Geum.ru

Червякова Марина Владимировна, преподаватель кафедры пми программа

Вид материалаПрограмма

Содержание


декан факультета)
Требования к уровню освоения содержания дисциплины
Объем дисциплины и виды учебной работы
Виды итогового контроля самостоятельной работы без отчетностей
Аудиторные занятия
Содержание дисциплины
Теория графов.
Комбинаторный анализ.
Разделы дисциплины и виды занятий и работ
Раздел дисциплины
Лабораторный практикум
Практические занятия
Теория графов.
Комбинаторный анализ.
Теория кодирования.
Наименование практических занятий
Расчетно-графическая работа
Задача РГР
Краткое содержание РГР
1. Входной контроль знаний студентов
...
Полное содержание
Подобный материал:
ФЕДЕРАЛЬНОЕ АГЕНТСВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

Тихоокеанский государственный университет
УТВЕРЖДАЮ

Проректор по учебной работе

________________С.В. Шалобанов

«______»_____________200__г.


ПРОГРАММА ДИСЦИПЛИНЫ

по кафедре Прикладная математика и информатика

ДИСКРЕТНАЯ МАТЕМАТИКА



Утверждена научно-методическим советом университета для направлений подготовки (специальностей) в области информатики и вычислительной техники,


Хабаровск 2006 г.

Программа разработана в соответствии с требованиями государственного образовательного стандарта, предъявляемыми к минимуму содержания дисциплины и в соответствии с примерной программой дисциплины, утвержденной департаментом образовательных стандартов профессионального образования с учетом особенностей региона и условий организации учебного процесса Тихоокеанского государственного университета


Программу составили

Хан Сун Э, к.ф.м.н, доцент кафедры ПМИ

Червякова Марина Владимировна, преподаватель кафедры ПМИ


Программа рассмотрена и утверждена на заседании кафедры ПМИ

протокол № ____ от «_____»__________200_ г

Зав.кафедрой _________________ «______»_________200_ г. Зарубин А.Г.


Программа рассмотрена и утверждена на заседании УМК и рекомендована к изданию протокол № ____ от «_____»__________200_ г

Прекдседатель УМК _________________ _________200_ г ________________


Подпись дата Ф.И.О.


Директор института _________________ _________200_ г ________________


Подпись дата Ф.И.О.

(декан факультета)


Цели и задачи дисциплины


Целью преподавания дисциплины является обеспечение базовой математической и информационной подготовки будущих специалистов по дискретной математике. Понятия, методы и алгоритмы, разработанные в теории дискретной математики, широко используются при математическом моделировании различных задач науки и техники, приближенных решениях различных модельных задач и во всех технических специальных дисциплинах и расчетах.

Преподавание математики в высших учебных заведениях имеет цель: формирование личности студентов, развитие их интеллекта и способностей к логическому и алгоритмическому мышлению; обучение основным математическим методам, необходимым для анализа и моделирования устройств, процессов и явлений, при описании оптимальных решений и выбора наилучших способов реализации этих решений, методам обработки и анализа результатов экспериментальных данных.

Задачи преподавания дискретной математики состоят в том, чтобы на примерах математических понятий и методов продемонстрировать сущность научного подхода, специфику математики и ее роль в осуществлении научно-технического прогресса; научить студентов приемам исследования и решения математически формализованных задач, выработать у студентов умение анализировать полученные результаты, привить им навыки самостоятельного изучения литературы по математике и ее приложениям.

Основные задачи изучения дисциплины состоят в том, чтобы студент свободно владел необходимым объемом фундаментальных знаний, позволяющих активно применять полученные знания при математическом моделировании различных процессов.


Требования к уровню освоения содержания дисциплины

Математическое образование должно быть фундаментальным и в то же время иметь четко выраженную прикладную направленность, быть в известной мере индивидуализированным (часть разделов программы может изучаться по выбору студента).

Фундаментальность математической подготовки включает в себя достаточную общность математических понятий и конструкций, обеспечивающую широкий спектр их применимости, разумную точность формулировок математических свойств изучаемых объектов, логическую строгость изложения математики, опирающуюся на адекватный современный математический язык.

Будущие специалисты по прикладной математике, автоматике и автоматизированному управлению, информационным системам, вычислительной технике, изучившие дисциплину «Дискретная математика», должны знать ее ключевые понятия и положения, которые могут использоваться в дальнейшем при изучении ряда профилирующих дисциплин. Студенты должны овладеть методами и алгоритмами, разработанными в дискретной математике, для исследования и решения задач, возникающих в самых различных областях человеческой деятельности. В идеале, специалисты должны научится создавать новые, собственные модели и теории, естественно, такое владение математикой требует существенно больших знаний и навыков.


Объем дисциплины и виды учебной работы
Наименование
По учебным планам основной траектории обучения

С максимальной трудоемкостью
С минимальной трудоемкостью
Общая трудоемкость дисциплины

По ГОС

По УП

180

153

140

153

Изучается в семестрах
3
2
Виды итогового контроля по семестрам

Зачет

Экзамен

Курсовой проект (КП)

Курсовая работа (КР)

Виды итогового контроля самостоятельной работы без отчетностей

Расчетно-графические работы (РГР)

Реферат (РФ)

Домашние задания (ДЗ)


3

2

2


2

Аудиторные занятия:

Всего

В том числе: лекции (Л)

Лабораторные работы (ЛР)

Практические занятия (ПЗ)

85

51


34

85

34

34

17
Самостоятельная работа

Общий объем часов (С2)

В том числе: на подготовку к лекциям

на подготовку к ЛР

на подготовку к ПЗ

на выполнение КП

на выполнение КР

на выполнение РГР

на написание РФ

на выполнение ДЗ

на экзаменационную сессию

68

34


34

68

34

24


10


Содержание дисциплины

Теория множеств. Понятие множества. Способы задания множеств. Пустое множество. Подмножество. Равные множества. Булеан. Число элементов булеана конечного множества. Универсальное множество. Операции над множествами. Теорема о пяти возможностях. Свойства операций над множествами. Кортеж, его длина. Декартово произведение двух множеств. Бинарное отношение. Область определения и область значений отношения. Матрица отношений. Операции пересечения, объединения и дополнения над отношениями. Обратное отношение. Тождественное отношение. Произведение отношений, степень отношения. Рефлексивность, иррефлексивность, симметричность, антисимметричность, транзитивность. Отношение эквивалентности. Классы эквивалентности, их свойства. Фактор-множество множества по эквивалентности. Разбиение. Теорема о связи эквивалентности и разбиения. Предпорядок. Частичный порядок. Линейный порядок. Частично и линейно упорядоченные множества. Диаграммы Хассе. Наибольший (наименьший) элемент частично упорядоченного множества. Максимальный (минимальный) элемент частично упорядоченного множества. Вполне упорядоченное множество. Функция. Образ, прообраз. Инъекция, сюръекция, биекция. Сложная функция. Обратная и обратимая функция. Теорема об обратной функции. Равномощные множества. Мощность. Конечные и бесконечные множества. Счетные множества. Теорема о конечном множестве.


Теория графов. Граф, орграф, каноническое соответствие, нижний граф, инцидентность, смежность, петля, кратные ребра, псевдограф, мультиграф, степень вершины, полустепень захода, полустепень исхода, изолированная вершина, висячая вершина. Простой граф, полный граф, помеченный граф, взвешенный граф, однородный граф, нулевой граф, пустой граф, подграф, собственный подграф, остовной граф. Изоморфизм графов. Дополнение графа, объединение, пересечение и соединение графов, удаление вершины и удаление ребра. Представления графов в виде матриц смежности вершин и инцидентности, списков вершин и ребер. Маршрут, замкнутый маршрут, цепь, простая цепь, цикл, простой цикл. Ацикличный граф. Длина маршрута. Геодезическая. Расстояние между вершинами. Диаметр графа. Связность вершин. Связный граф. Отношение связности. Компоненты связности. Слабая связность, сильная связность, односторонняя связность. Дерево, лес. Эйлеровый и гамильтоновый графы. Критерий Эйлера. Достаточные признаки гамильтоновых графов. Плоский граф. Планарный граф. Формула Эйлера. Теорема Понтрягина – Куратовского. Сеть. Критический путь в сети. Поток, максимальный поток, минимальный срез. Теорема Форда – Фалкерсона.


Комбинаторный анализ. Основные формулы комбинаторики.


Теория кодирования. Задача кодирования. Типы шифровок. Алфавитное кодирование. Разделимая схема кодирования. Неравенство Макмиллана. Префиксное кодирование. Оптимальное кодирование. Алгоритм Фано. Теорема Хаффмана. Помехоустойчивое кодирование. Кодирование Хемминга.

Разделы дисциплины и виды занятий и работ





№
Раздел дисциплины
Л
ЛР
ПЗ
РГР
С2


Теория множеств
*
*
*
*




Теория графов
*
*
*
*
*


Комбинаторный анализ
*



*
*
*


Теория кодирования
*
*
*



*

Лабораторный практикум и его взаимосвязь с содержанием лекционного курса

№

п/п
№

раздела по варианту содержания
Наименование лабораторной работы





Позиционные и непозиционные системы счисления.





Таблицы истинности логических функций


1
Диаграммы Эйлера ­– Венна


1
Свойства отношений, заданных матрицами


2
Алгоритмы поиска в глубину и ширину


2
Алгоритмы Прима и Дейкстры


2
Алгоритм Форда – Фалкерсона


4
Алгоритмы кодирования Фано и Хаффмана



Практические занятия

Теория множеств.

Задание. Решение задач по теме: отношения, операции над ними, свойства отношений, отображение, мощности множеств. Время на выполнение задания – 4 (10) часов

Оснащение. Для практических занятий целесообразно использовать   Элементы теории множеств: Метод.указ.для студ.,изучающих курс"Дискретная математика" / Сост.Т.М.Попова. Хабаровск: Изд-во ХГТУ, 2002, Дискретная математика. В 2ч. / Сафьянова Е.Н Томск: Изд-во ТУСУР, 2000, Дискретная математика для программистов / Хаггарти М.: Издательский дом «Вильямс», 2002, сборники задач на усмотрение преподавателя.


Теория графов.

Задание. Решение задач по теме: виды графов, алгоритмы на графах и орграфах.

Время на выполнение задания – 8 (16) часов

Оснащение. Для практических занятий целесообразно использовать Дискретная математика и комбинаторика / Д.А.Андерсон. М.: Издательский дом «Вильямс», 2003, Введение в дискретную математику / Б.М.Логинов. Калуга: Облиздат, 1998, сборники задач на усмотрение преподавателя.


Комбинаторный анализ.

Задание. Решение задач по теме: основные формулы комбинаторики.

Время на выполнение задания – 2 (4) часа

Оснащение. Для практических занятий целесообразно использовать Дискретная математика и комбинаторика / Д.А.Андерсон. М.: Издательский дом «Вильямс», 2003, Дискретная математика для программистов / Хаггарти М.: Издательский дом «Вильямс», 2002, сборники задач на усмотрение преподавателя.


Теория кодирования.

Задание. Решение задач по теме: алгоритмы Фано, Хаффмана, Хемминга.

Время на выполнение задания – 3 (4) часа.

Оснащение. Для практических занятий целесообразно использовать Дискретная математика и комбинаторика / Д.А.Андерсон. М.: Издательский дом «Вильямс», 2003,  сборники задач на усмотрение преподавателя.

Практические занятия и их взаимосвязь с содержанием лекционного курса




№ п/п
№ раздела по варианту содержания
Наименование практических занятий


1
Множества и отношения. Виды отношений.


1
Отображения. Операции. Мощность множеств.


2
Способы задания графов и операции над ними.


2
Деревья. Алгоритмы в графах.


2
Алгоритмы в орграфах.


2
Сети и потоки.


3
Формулы комбинаторики.


4
Кодирование Фано, Хаффмана, Хемминга.



Расчетно-графическая работа


Цель РГР: совершенствование основных математических методов и подходов к решению задач по теме множества, графы, формулы комбинаторики, схемы кодирования, выбора наилучших способов реализации этих решений, на основании теоретического курса и практических занятий.

Задача РГР: овладение необходимым объемом фундаментальных знаний и приемов, позволяющих активно применять полученные знания при решение задач по темам множества, графы, комбинаторика, кодирование.

Краткое содержание РГР:

1 часть содержит 5 задач по множествам,

2 часть содержит 4 задачи на графы,

3 часть содержит 8 задач по использованию формул комбинаторики,

4 часть содержит 2 задачи на алгоритмы Хаффмана и Хемминга.


Время на выполнение РГР – 10 часов


Контроль знаний студентов

1. Входной контроль знаний студентов

  • Понятия множества
  • Понятие отношения
  • Системы счисления



2. Текущий контроль знаний студентов


Контроль достижения целей обучения осуществляется с помощью: - двух, трех контрольных работ в течение семестра по разделам и темам курса.

Главной целью проведения текущих контрольных работ является установление уровня и характера усвоения студентами основных понятий, умений и навыков, формируемых в процессе изучения курса

Примерное содержание контрольных работ: (содержание и количество контрольных работ может меняться.)

Контрольная работа 1 «Множества» содержит 5 задач по операциям над множествами и отношениями, видам отношений, функций, мощности.

Контрольная работа 2 «Графы» содержит 5 задач на усвоение основных понятий теории графов, операций над графами, алгоритмов в графах.

Контрольная работа 3 «Комбинаторика и кодирование» содержит 8 задач по использованию основных формул комбинаторики и алгоритмов Хаффмана и Хэмминга.


3.Выходной контроль знаний студентов

Дисциплина завершается устными экзаменами по окончанию каждого семестра. На экзаменах проверяется степень усвоения студентами основных понятий дисциплины, понимание их взаимосвязи, умение доказывать основные теоремы, а также навыки в решении задач по каждому из разделов дисциплины.

Экзаменационные вопросы
  1. Понятие множества. Способы задания множеств. Пустое множество. Подмножество. Равные множества. Булеан. Мощность булеана конечного множества.
  2. Универсальное множество. Операции над множествами. Теорема о пяти возможностях.
  3. Свойства операций над множествами.
  4. Кортеж, его длина. Декартово произведение двух множеств. Бинарное отношение. Область определения и область значений отношения. Матрица отношений. Операции пересечения, объединения и дополнения над отношениями.
  5. Обратное отношение. Тождественное отношение. Произведение отношений. Степень отношения. Свойства рефлексивности, иррефлексивности, симметричности, антисимметричности, транзитивности.
  6. Отношение эквивалентности. Классы эквивалентности, их свойства. Фактор-множество множества по эквивалентности.
  7. Предпорядок. Частичный порядок. Линейный порядок. Линейно упорядоченное множество. Диаграммы Хассе. Наибольший (наименьший) элемент. Максимальный (минимальный) элемент. Вполне упорядоченное множество.
  8. Функция. Образ, прообраз. Инъекция, сюръекция, биекция. Сложная функция. Обратная и обратимая функция. Теорема об обратной функции.
  9. Равномощные множества. Мощность. Конечные и бесконечные множества. Счетные множества. Теорема о конечном множестве.
  10. Графы. Основные понятия (граф, орграф, каноническое соответствие, нижний граф, инцидентность, смежность, петля, кратные ребра, псевдограф, мультиграф, степень вершины, полустепень захода, полустепень исхода, изолированная вершина, висячая вершина, простой граф, полный граф).
  11. Помеченный граф, взвешенный граф, однородный граф, нулевой граф, пустой граф, подграф, собственный подграф, остовной граф. Изоморфизм графов.
  12. Дополнение графа, объединение и соединение графов, удаление вершины и удаление ребра. Представления графов.
  13. Маршрут, замкнутый маршрут, цепь, простая цепь, цикл, простой цикл. Ацикличный граф. Длина маршрута. Геодезическая. Расстояние между вершинами. Диаметр графа.
  14. Связность вершин. Связный граф. Отношение связности. Компоненты связности. Слабая связность, сильная связность, односторонняя связность. Дерево, лес. Эйлеровый и гамильтоновый графы.
  15. Плоский граф. Планарный граф. Формула Эйлера. Теорема Понтрягина – Куратовского.
  16. Сети и потоки. Максимальный поток. Минимальный срез. Теорема Форда – Фалкерсона.
  17. Основные формулы комбинаторики.
  18. Задача кодирования. Типы шифровок. Алфавитное кодирование. Неравенство Макмиллана.
  19. Префиксное кодирование. Оптимальное кодирование. Алгоритм Фано. Теорема Хаффмана.
  20. Помехоустойчивое кодирование. Кодирование Хеминга.



Учебно-методическое обеспечение дисциплины



Основная литература.
  1. Новиков Ф.А. Дискретная математика для программистов: Учеб. пособие для вузов / Ф. А. Новиков. - 2-е изд. - СПб.: Питер, 2005. - 368с.
  2. Белоусов А.И. Дискретная математика: Учеб. для втузов / А.И.Белоусов, С. Б. Ткачев; Под ред.: В.С. Зарубина, А.П. Крищенко. - 2-е изд., стер. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. - 744с.
  3. Сафьянова Е.Н. Дискретная математика. В 2ч.: Учеб. пособие для вузов. Ч.1 / Е. Н. Сафьянова. - Томск: Изд-во ТУСУР, 2000. - 106с.
  4. Сафьянова Е.Н. Дискретная математика. В 2ч.: Учеб. пособие для вузов. Ч.2 / Е. Н. Сафьянова. - Томск: Изд-во ТУСУР, 2000. - 99с.
  5. Элементы теории множеств: Метод.указ.для студ.,изучающих курс"Дискретная математика" / Сост.Т.М.Попова. - Хабаровск: Изд-во ХГТУ, 2002. - 15с.
  6. Андерсон Д.А. Дискретная математика и комбинаторика / Д.А. Андерсон. – М.: Издательский дом «Вильямс», 2003. – 960 с.


Дополнительная литература
  1. Акимов О.Е. Дискретная математика: Логика, группы, графы / Акимов Олег Евгеньевич. - 2-е изд., доп. - М.: Лаборатория Базовых Знаний, 2003. - 376с.
  2. Редькин Н.П. Дискретная математика: Курс лекций для студ.-механиков: Учеб. пособие для вузов / Н. П. Редькин. - СПб.: Лань, 2003. - 96с.
  3. Логинов Б.М. Введение в дискретную математику / Б.М.Логинов. – Калуга: Облиздат, 1998. – 423 с.



Материально – техническое обеспечение дисциплины


Для проведения лабораторных работ требуется компьютерный класс на базе IBM PC Pentium. Количество компютеров – не менее 15. Для выполнения работ необходимо установить на компьютерах прикладные программные пакеты Borland Delphi, C++ Builder или Visual Studio.


Методические рекомендации по организации изучения дисциплины


Программа определяет общий объем знаний, а не порядок изучения предмета. Тем не менее, построение соответствующих математических курсов должно проводиться так, чтобы у студента сложилось целостное представление об основных этапах становления современной математики и ее структуре, об основных математических понятиях и методах, о роли и месте дискретной математики в различных сферах человеческой деятельности.

Для того, чтобы студент воспринимал ценности математики как науки и свободно владел математическими методами в приложениях к техническим наукам, конкретная реализация программы должна иметь следующую структуру.

Математические курсы, соответствующие данной программе, должны содержать лекции, практические занятия в аудитории, индивидуальные занятия студентов с преподавателем и самостоятельную работу студентов. Целью лекций является изложение теоретического материала и иллюстрация его примерами и задачами. Основным теоретическим результатам должны сопутствовать пояснения об их приложениях к другим разделам математики и к техническим наукам. Желательно также кратко излагать историю появления наиболее важных понятий и результатов. Курс лекций должен строиться на основе четких формулировок и доказательств основных теорем, так как лишь при таком подходе студенты приобретают математическую культуру, необходимую для дальнейшего изучения инженерных дисциплин. Недопустимо сводить чтение лекций только к разбору примеров и алгоритмов их решения. Целью практических занятий и лабораторных работ является закрепление теоретического материала лекций и выработка умения решать примеры и задачи для последующего применения математических методов в технических приложениях. Важнейшей частью математических курсов являются индивидуальные занятия с преподавателем. Поэтому изучаемый курс должен содержать одну расчетную работу и две-три контрольные работы в течение семестра.

Организация самостоятельной работы предполагает, что:
  1. отдельные темы могут быть отнесены на самостоятельное изучение;
  2. на лекциях предлагается значительное количество контрольных вопросов и упражнений, служащих для проверки усвоения теории;
  3. на практических занятиях регулярно задаются домашние задания, которые проверяют усвоение методов и приемов решения разбираемых на практических занятиях задач, закрепляют алгоритмические умения и навыки.

Самостоятельная работа не расширяет существенно рамки программы, она призвана закрепить излагаемый на лекциях и практических занятиях материал, а также приучает студентов к самостоятельному овладению новым материалом.

Знания, полученные при изучении дисциплины «Дискретная математика» применяются при изучении широкого спектра профильных, специальных предметов.

Программа рассчитана на 153 часа.

Программа составлена в соответствии с государственными образовательными стандартами высшего профессионального образования.


Словарь терминов

Алфавитное кодирование. Если каждой букве первого алфавита соответствует некоторое слово, составленное из букв другого алфавита, то говорят, что задано алфавитное кодирование.

Асимметричность. Бинарное отношение R, заданное на множестве А, асимметрично, если для любых двух элементов a и b из А, таких что 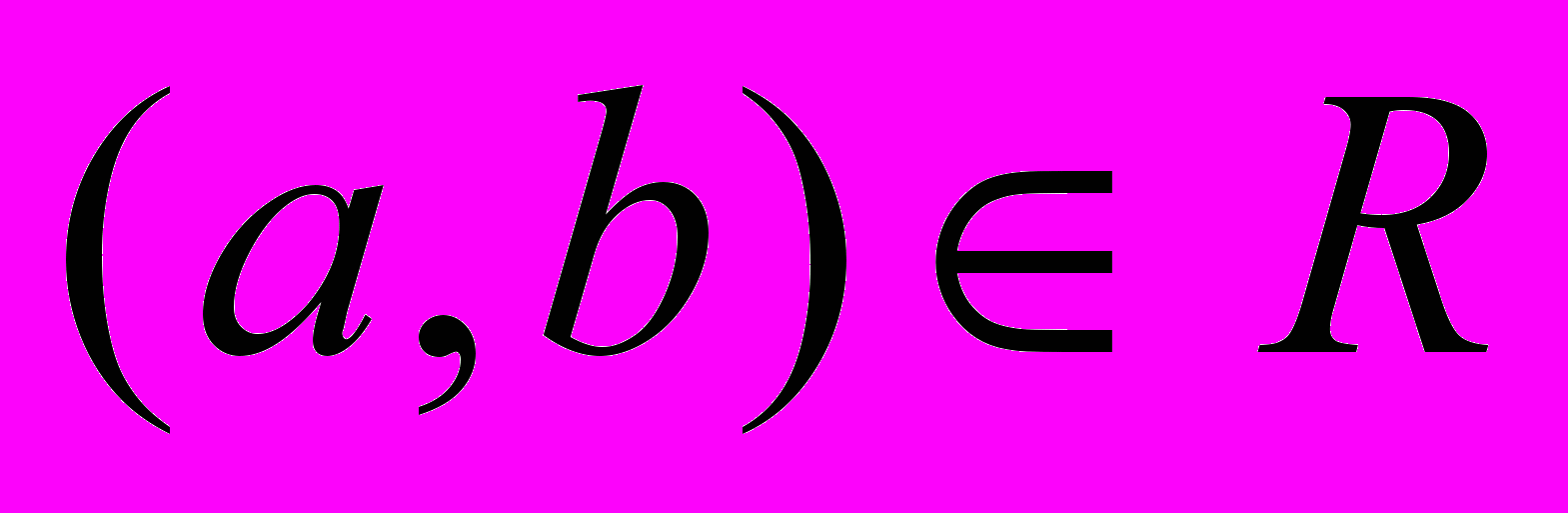, 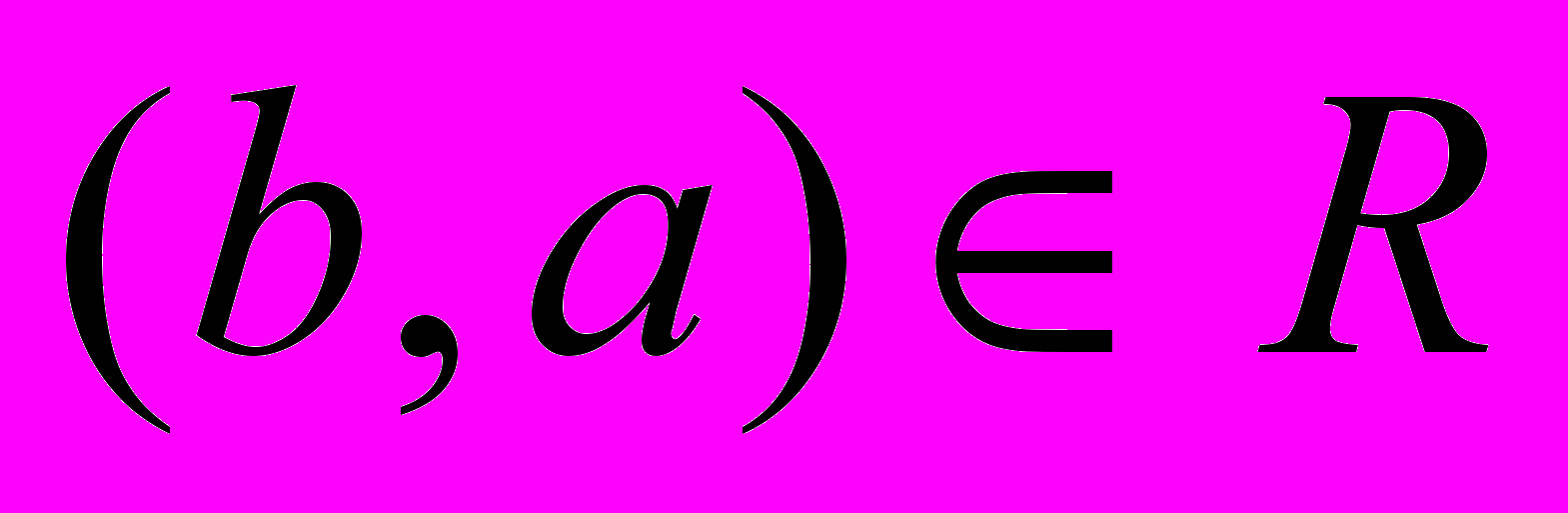следует, что .



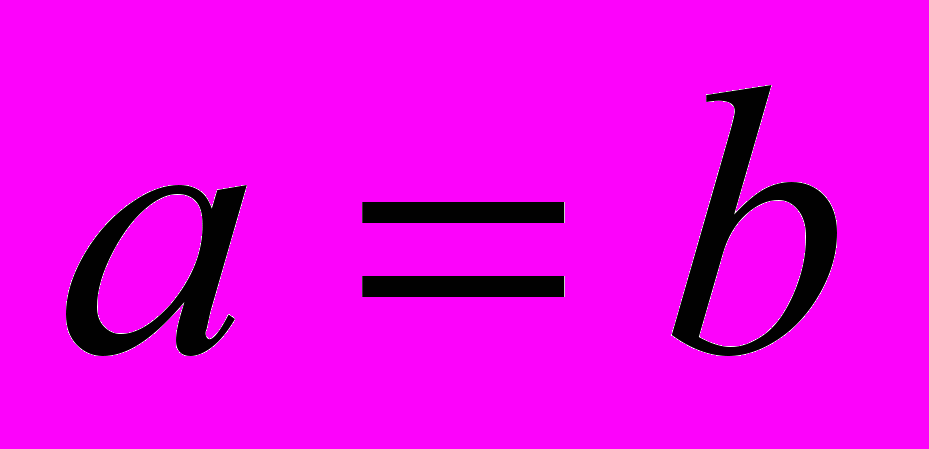Бинарное отношение. Некоторое подмножество декартова произведения двух множеств определяет бинарное отношение, заданное на этих множествах.


Булеан множества. Множество всех подмножеств данного множества называется его булеаном.


Граф. Под графом понимают систему двух множеств, первое из которых не пусто, элементы его называются вершинами, а второе множество состоит из некоторых пар вершин, которые называются ребрами, при этом говорят, что ребро инцидентно своим вершинам.


Декартово произведение двух множеств. Декартовым произведением двух множеств называется множество упорядоченных пар, первая компонента которых принадлежит первому множеству, а вторая компонента – второму.


Дерево. Связный, ацикличный граф называют деревом.


Замкнутый маршрут. Маршрут называют замкнутым, если в нем начальная вершина совпадает с конечной.


Изоморфизм графов. Граф 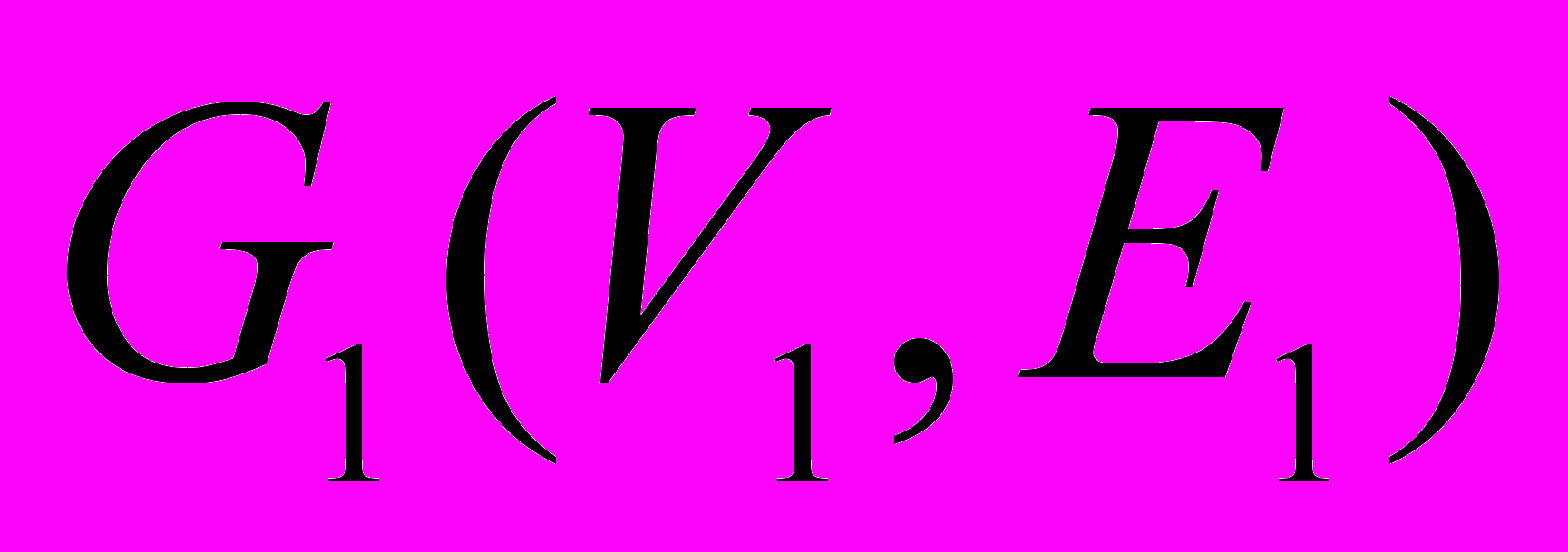изоморфен графу 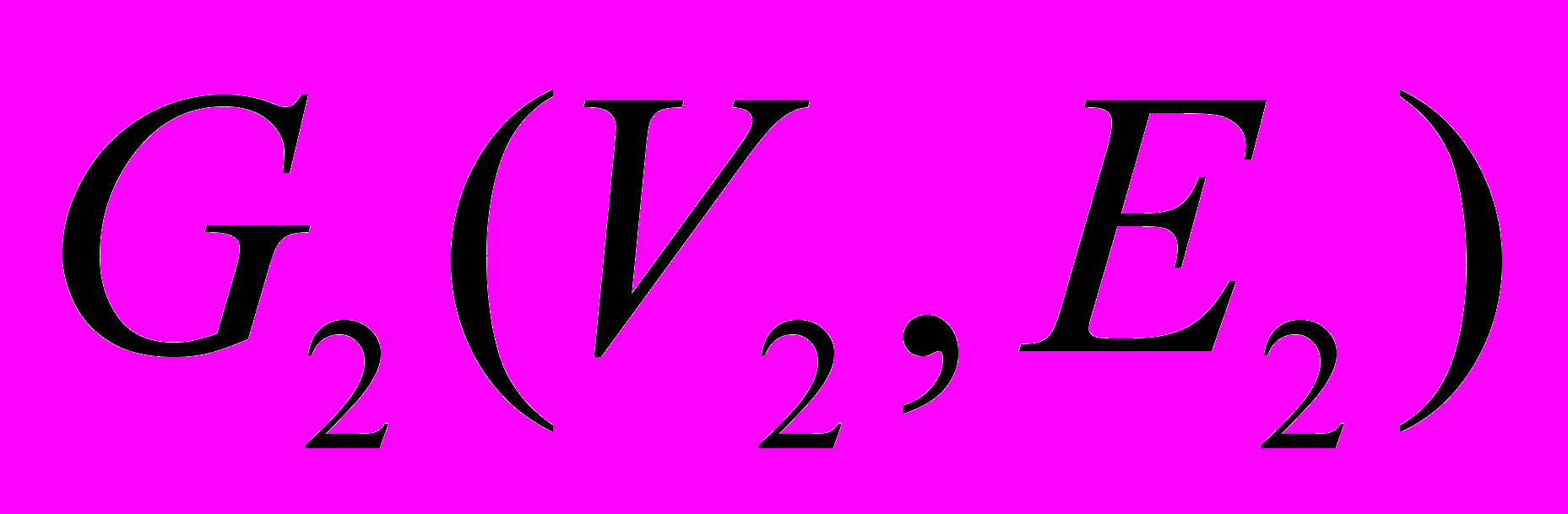, если существуют две биекци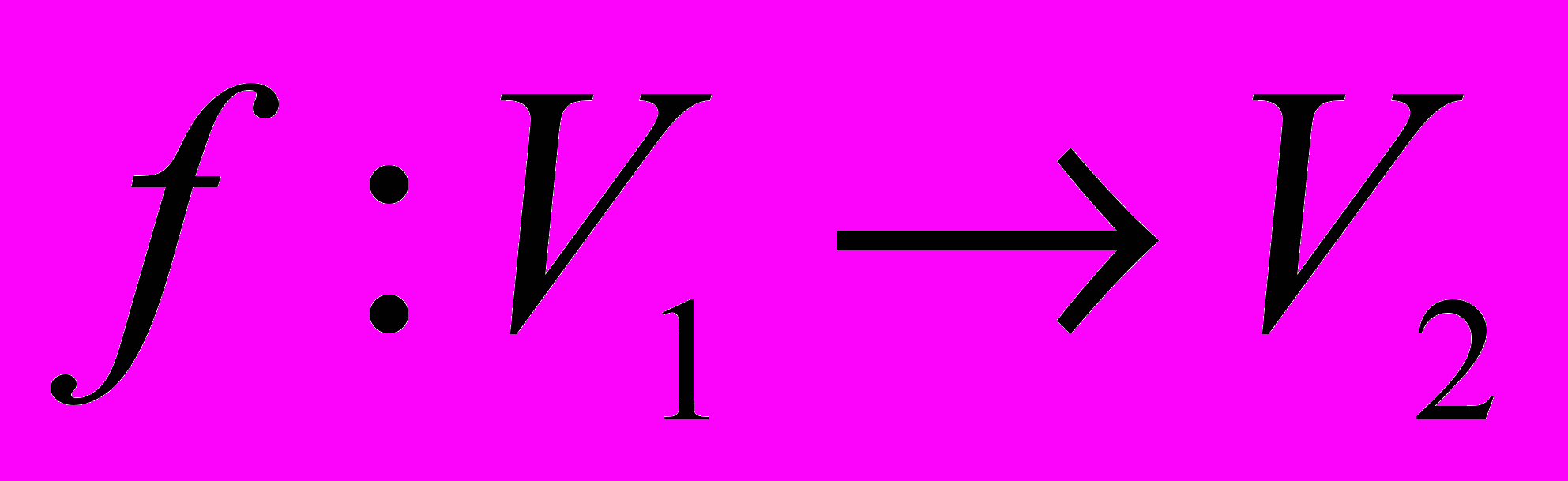и и 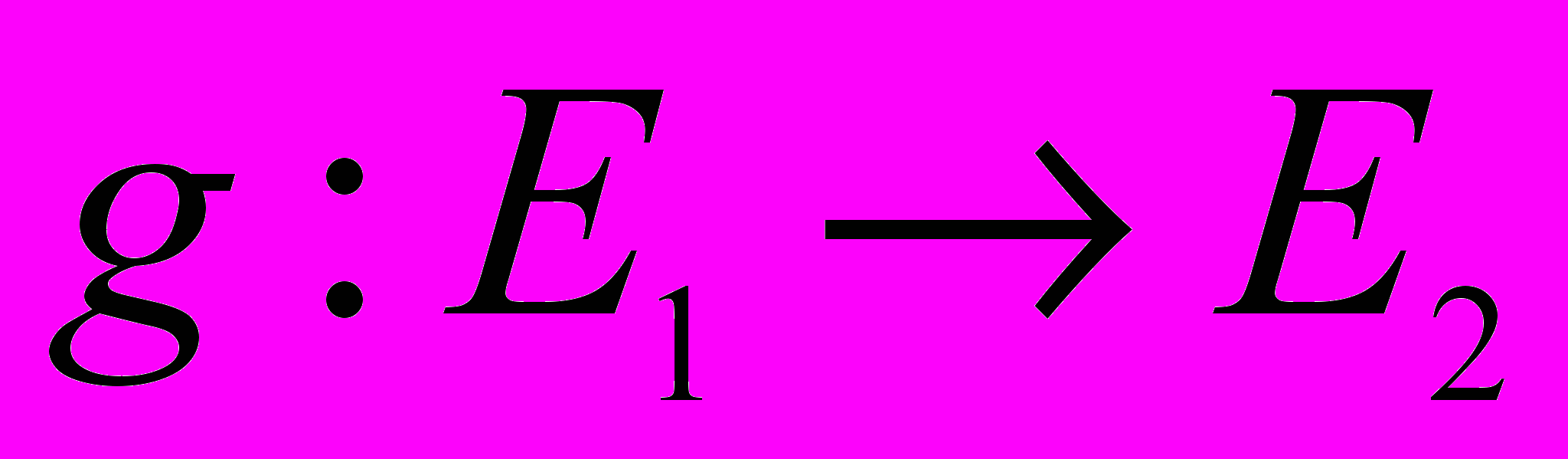такие, что 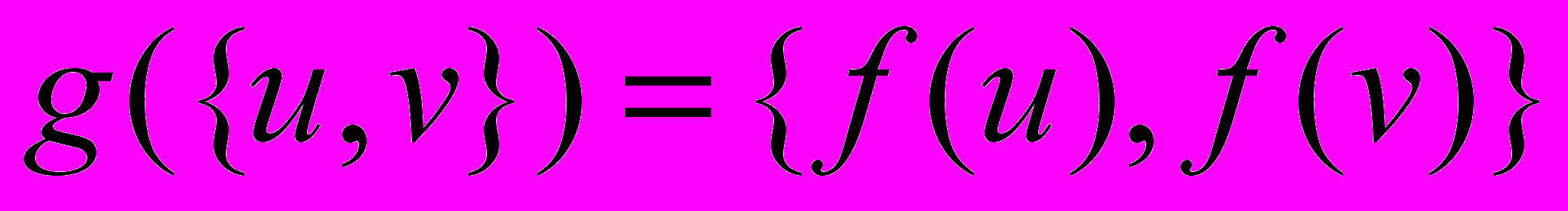, где вершины 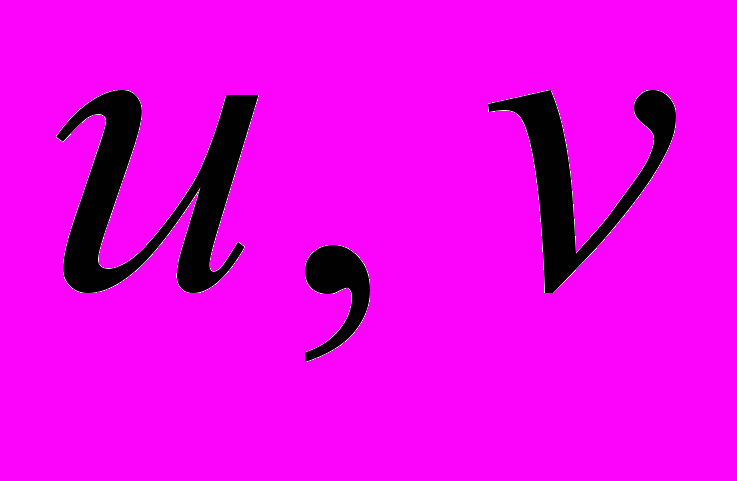принадлежат множеству .


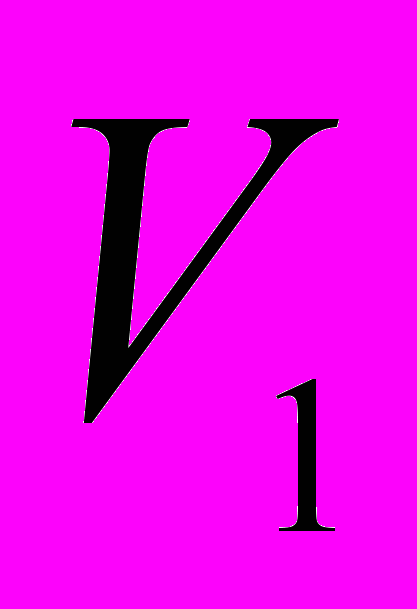Иррефлексивность. Бинарное отношение R, заданное на множестве А, иррефлексивно, если любая упорядоченная пара 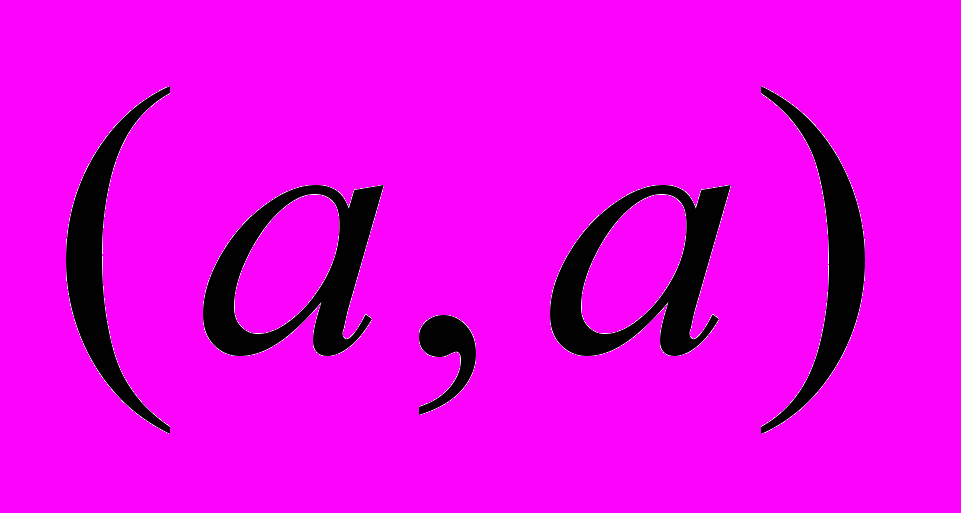не принадлежит R при каждом а из А.


Исток. Вершина, у которой полустепень захода равна 0, называется истоком.


Маршрут. Последовательность вершин и ребер, в которой каждое ребро инцидентно соседним вершинам, называют маршрутом в графе.


Матрица инцидентности. Матрицей инцидентности графа называется матрица, каждый элемент которой равен 1 или 0 в зависимости от того, инцидентна ли вершина ребру или нет.


Матрица смежности. Матрицей смежности вершин графа называется матрица, каждый элемент которой равен 1 или 0 в зависимости от того, смежные или нет соответствующие вершины данного графа.


Однородный граф. Граф называется однородным, если степень каждой его вершины одинаковая.


Оптимальное кодирование. Оптимальным называется кодирование с минимальной длиной кодов.


Орграф. Под орграфом понимают систему двух множеств, первое из которых не пусто, элементы его называются вершинами, а второе множество состоит из некоторых упорядоченных пар вершин, которые называются дугами.


Остов. Остовом называют собственный подграф данного графа, содержащий все его вершины, являющийся деревом.


Петля. Если ребро инцидентно только одной вершине, то оно называется петлей.


Подстановка. Биекция на конечном множестве 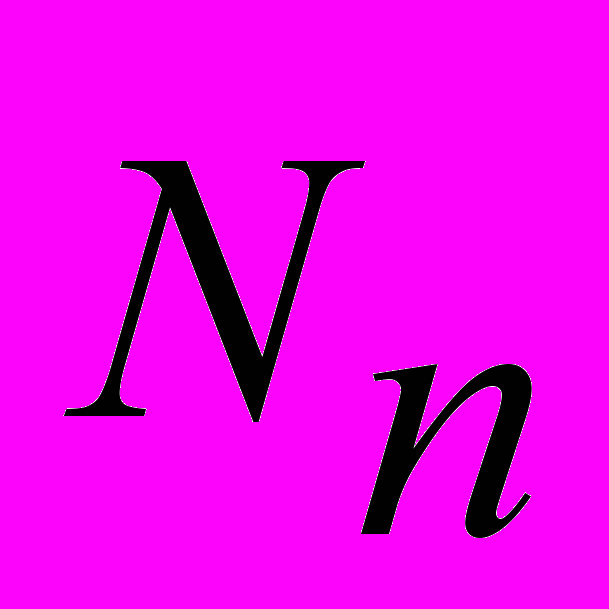называется подстановкой.


Полный граф. Граф называют полным, если любая пара вершин в нем смежна.


Полустепень. Для орграфа число исходящих из вершины ребер называют полустепенью исхода, а число входящих в вершину ребер – полустепенью захода.


Поток. Потоком в сети называют неотрицательную функцию 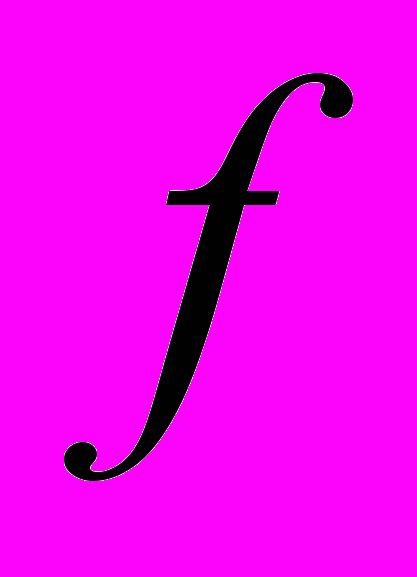, определенную на множестве ребер сети, для которой выполнены два условия: 1) поток каждого ребра не превосходит веса данного ребра; 2) сумма выходящих из некоторой вершины потоков (за исключением истока) равна сумме входящих в эту вершину потоков (за исключением стока).


Префикс. Если слово состоит в свою очередь из двух слов, то его начальная (левая) часть называется префиксом.


Префиксная схема кодирования. Схема называется префиксной, если элементарный код одной буквы не является префиксом кода другой буквы.


Простая цепь. Цепь, в которой все вершины различны, называется простой.


Равномощные множества. Два множества называют равномощными, если существует биекция из одного множества в другое.


Разделимая схема кодирования. Схема называется разделимой, если любое слово разлагается на элементарные коды единственным образом.


Рефлексивность. Бинарное отношение R, заданное на множестве А, рефлексивно, если каждая упорядоченная пара 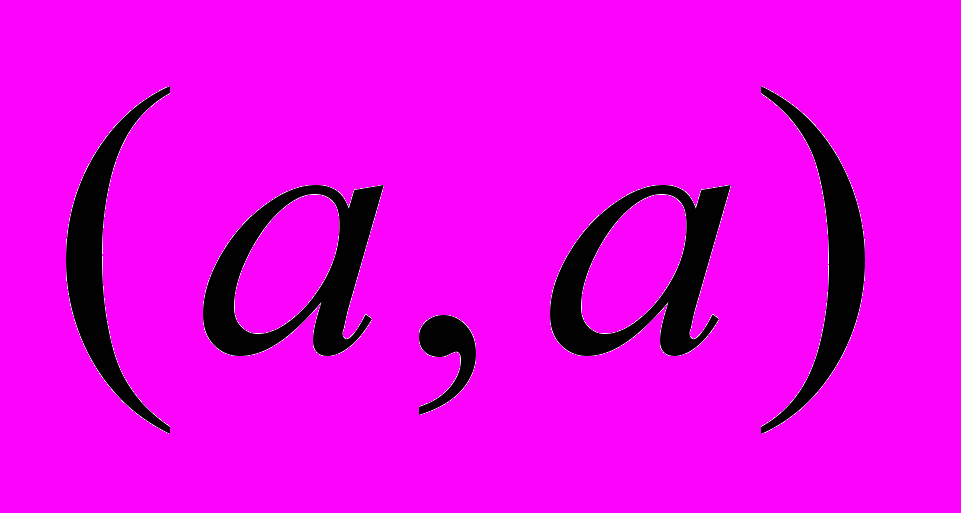принадлежит R при произвольном а из А.


Связные вершины. Вершины, между которыми существует маршрут, начинающийся в одной из них и заканчивающийся в другой, называют связными.


Связный граф. Граф называется связным, если любые две его вершины являются связными.


Сеть. Сетью называют слабосвязный, ацикличный орграф с одним истоком и одним стоком.


Симметричность. Бинарное отношение R, заданное на множестве А, симметрично, если для любых двух элементов a и b из А, таких что 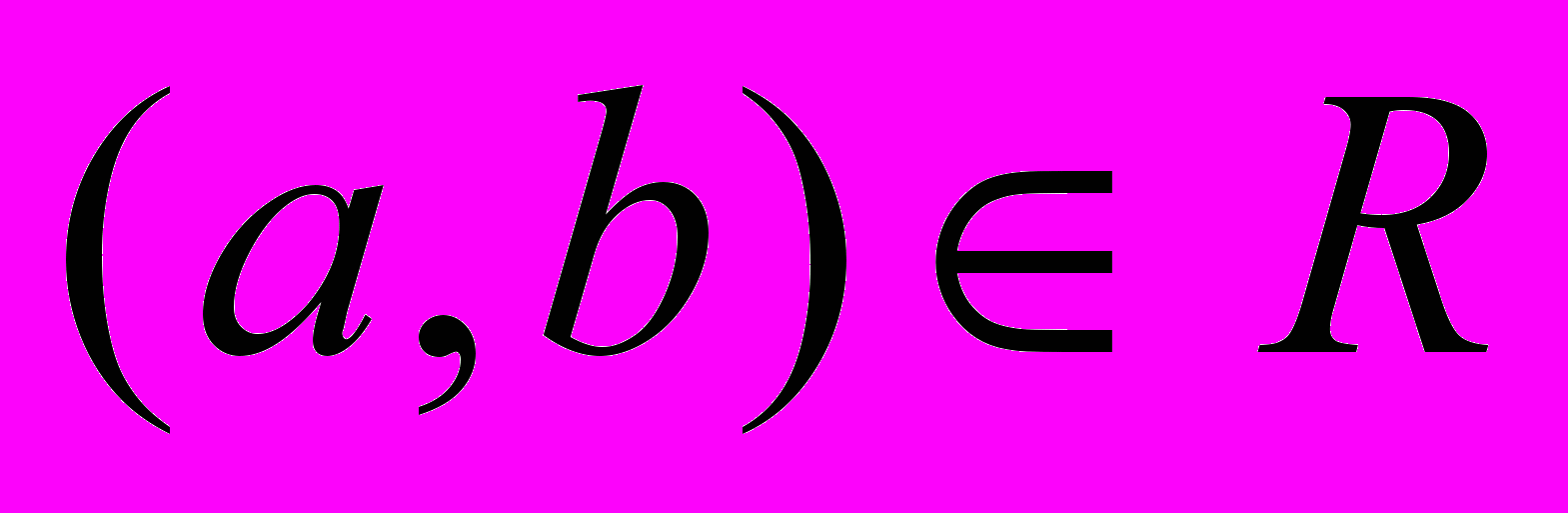, следует, что .


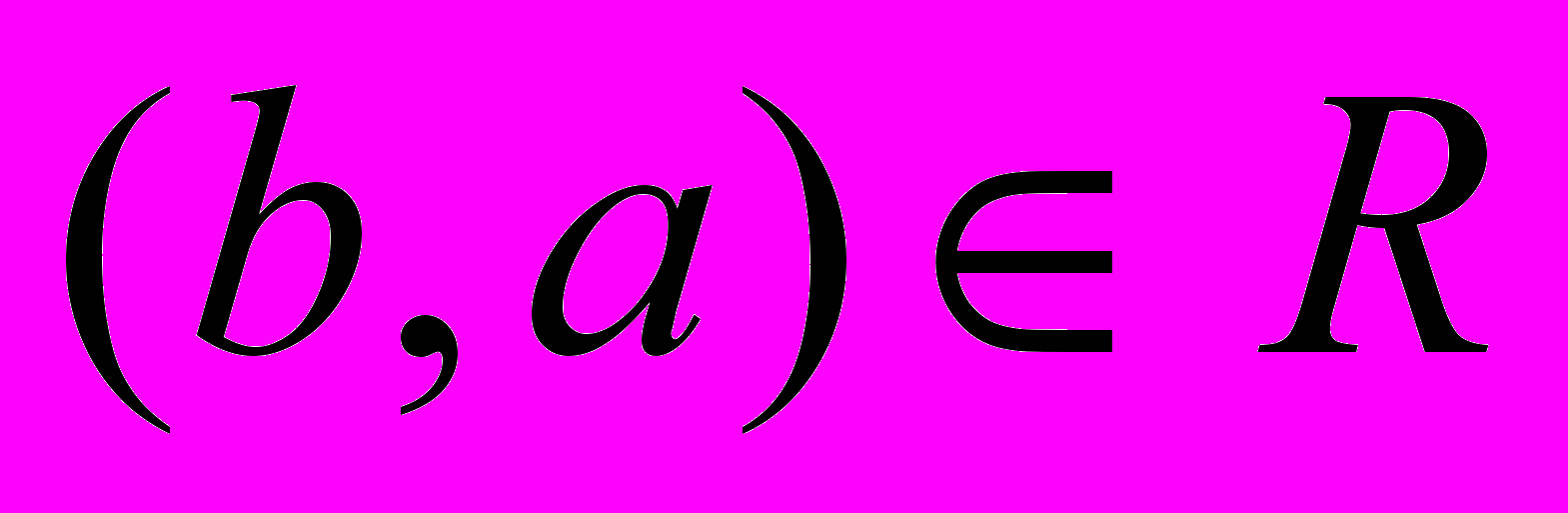Слово. Последовательность букв данного алфавита называют словом.


Смежные вершины. Вершины инцидентные одному и тому же ребру называют смежными.


Степень вершины. Число инцидентных вершине ребер называют ее степенью.


Сток. Вершина, у которой полустепень исхода равна 0, называется стоком.


Транзитивность. Бинарное отношение R, заданное на множестве А, транзитивно, если для любых трех элементов a, b и с из А, таких что 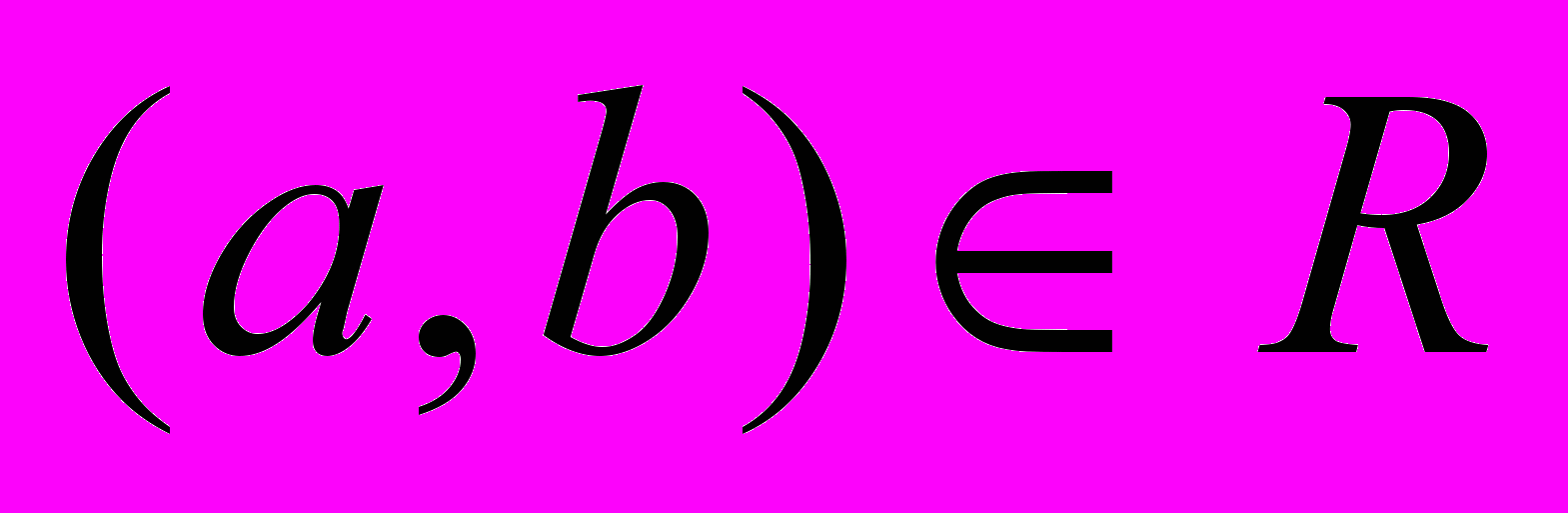, 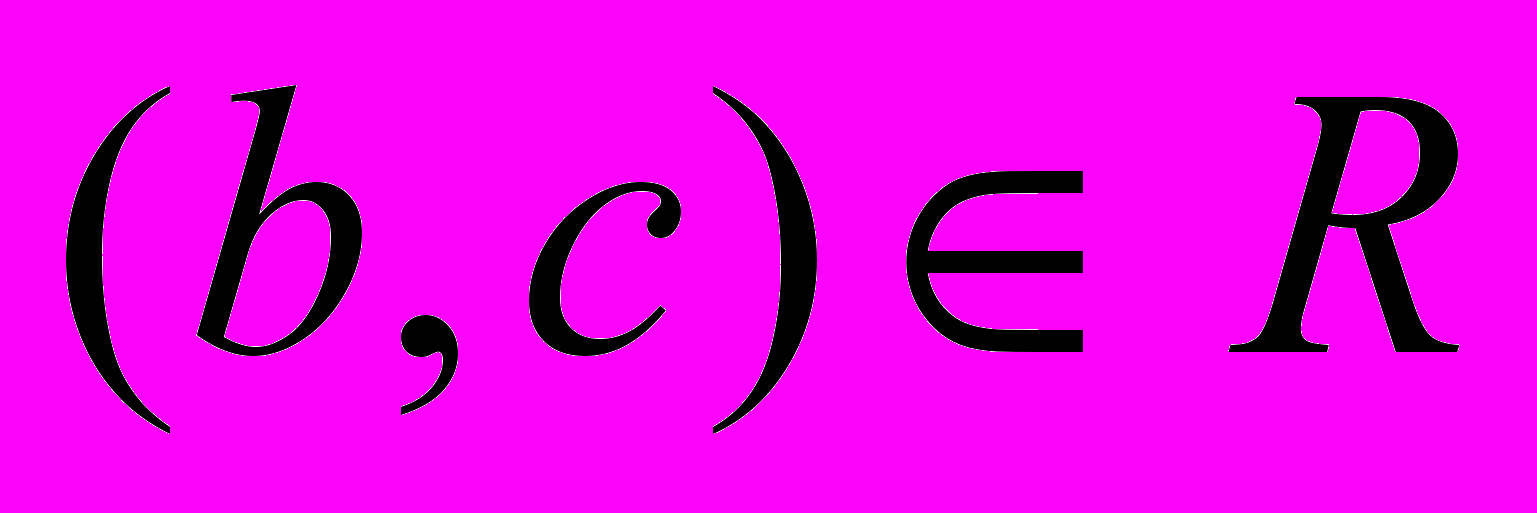следует, что .


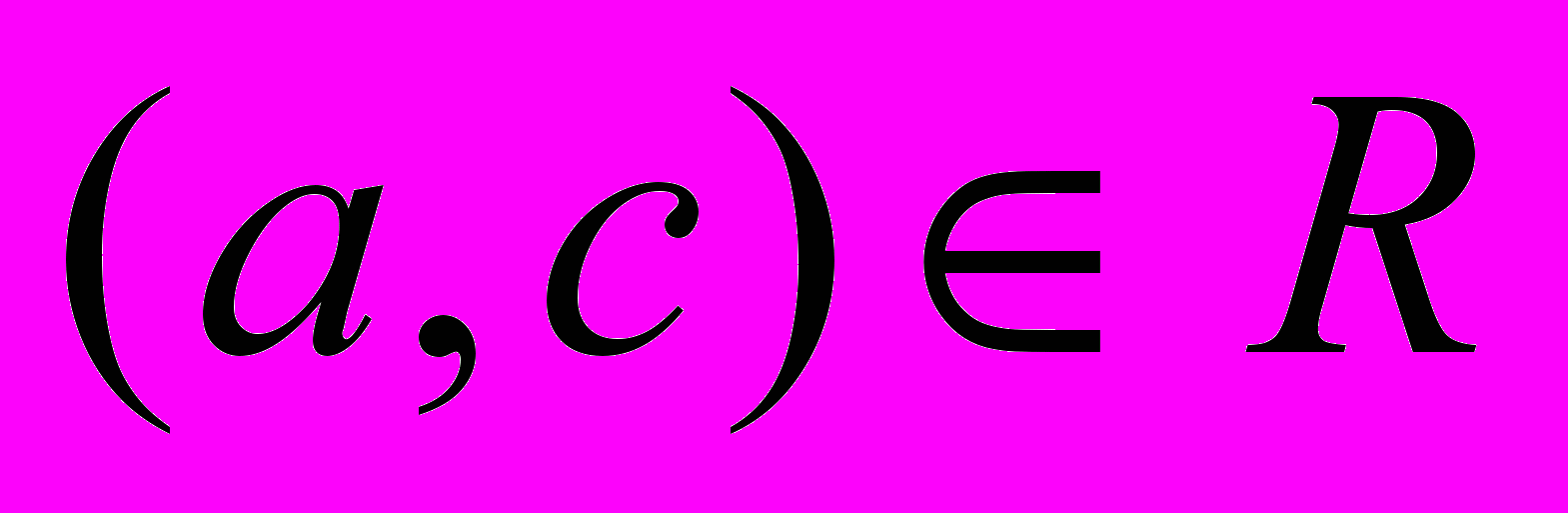Частичный порядок. Бинарное отношение R, заданное на множестве А, называют частичным порядком, если оно рефлексивно, асимметрично и транзитивно.


Цепь. Маршрут, в котором все ребра различны, называют цепью.


Цикл. Замкнутый маршрут, в котором все ребра различны, называется циклом.


Эквивалентность. Бинарное отношение R, заданное на множестве А, эквивалентно, если оно рефлексивно, симметрично и транзитивно.