Зарубин Анатолий Георгиевич, д ф. м н., профессор, завкафедрой пми попова Татьяна Михайловна, к ф. м н, доцент кафедры пми программа
| Вид материала | Программа |
- Попова Татьяна Михайловна, к ф. м н, доцент кафедры пми программа, 222.32kb.
- Агапова Елена Григорьевна, к ф. м н, доцент кафедры пми программа, 264.73kb.
- Агапова Елена Григорьевна, к ф. м н., доцент кафедры пми программа, 252.11kb.
- Червякова Марина Владимировна, преподаватель кафедры пми программа, 217.91kb.
- Лахман Анатолий Георгиевич канд юрид наук, доцент, профессор кафедры гражданского права, 177.89kb.
- Правосознание и правовое регулирование как понятия и реальность, 181.91kb.
- Красильников Дмитрий Георгиевич, Пунина Ксения Александровна учебно-методический комплекс, 856.5kb.
- Коноплянник Татьяна Михайловна, профессиональный аудитор-консультант, лауреат конкурс, 39.26kb.
- Минина Вера Николаевна, д соц н., профессор кафедры организационного поведения и управления, 222.64kb.
- Зачеты, 37.94kb.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
Тихоокеанский государственный университет
| | УТВЕРЖДАЮ Проректор по учебной работе ________________С.В. Шалобанов «______»_____________2009 г. |
ПРОГРАММА ДИСЦИПЛИНЫ
по кафедре Прикладная математика
Интегральные уравнения и вариационное исчисление
Утверждена научно-методическим советом университета для университета для направлений подготовки (специальностей) в области информатика и вычислительная техника. Специальности 010400 «Физика»
Хабаровск 2006 г.
Программа разработана в соответствии с требованиями государственного образовательного стандарта, предъявляемыми к минимуму содержания дисциплины и в соответствии с примерной программой дисциплины, утвержденной департаментом образовательных стандартов профессионального образования с учетом особенностей региона и условий организации учебного процесса Тихоокеанского государственного университета
Программу составили
Зарубин Анатолий Георгиевич, д.ф.м.н., профессор, завкафедрой ПМИ Попова Татьяна Михайловна, к.ф.м.н, доцент кафедры ПМИ
Программа рассмотрена и утверждена на заседании кафедры ПМИ
протокол № ____ от «_____»__________2009 г
Завкафедрой _________________ «______»_________2009 г. Зарубин А.Г.
Программа рассмотрена и утверждена на заседании УМК и рекомендована к изданию протокол № ____ от «_____»__________2009 г
Председатель УМК _________________ проф. В.А. Кныр
Подпись Ф.И.О.
Декан ФММиПУ _________________ А.З.Син _ ________2009 г
Подпись Ф.И.О. дата
Цели и задачи дисциплины
Дисциплина Интегральные уравнения и вариационное исчисление является одной из математических дисциплин, в которой содержаться основные сведения из теории интегральных уравнений и вариационного исчисления. Эти сведения необходимы студентам для дальнейшего освоения специальных дисциплин, таких, как математическая физика, квантовая механика, и других.
Для изучения дисциплины студенты должны знать основы математического анализа, дифференциальное и интегральное исчисление, теорию функциональных рядов, рядов Фурье, теорию дифференциальных уравнений, теорию функции комплексного переменного.
2. Требования к уровню освоения содержания дисциплины.
В результате изучения дисциплины студент должен
знать: постановку основной задачи вариационного исчисления, уравнение Эйлера для задач с неподвижными границами, условие трансверсальности для задач с подвижными границами, постановку задач на условный экстремум,
достаточные условия экстремума,
определение и свойства вполне непрерывных операторов, классификацию интегральных уравнений, постановку задач для однородных и неоднородных уравнений Фредгольма и Вольтерра первого и второго рода, свойства их решений, определение и способы решения некорректно поставленных задач ( на примере интегрально уравнения Фредгольма первого рода).
уметь: решать вариационные задачи с неподвижными и подвижными границами, границами, задачи на условный экстремум, определять тип экстремума,
решать интегральные уравнения с вырожденными ядрами, находить собственные функции и собственные значения однородных уравнений Фредгольма второго рода, строить резольвенты и решать с их помощью
неоднородные уравнения Фредгольма второго рода.
иметь навыки: решения вариационных задач, решения интегральных уравнений
Объем дисциплины и виды учебной работы
Наименование | По учебным планам основной траектории обучения |
| С максимальной трудоемкостью | |
Общая трудоемкость дисциплиныПо ГОС По УП | 68 |
| Изучается в семестрах | 6 |
Виды итогового контроля по семестрамЗачет Экзамен Курсовой проект (КП) Курсовая работа (КР) Виды итогового контроля самостоятельной работы без отчетностей Расчетно-графические работы (РГР) Реферат (РФ) Домашние задания (ДЗ) | 6 |
| Аудиторные занятия: Всего В том числе: лекции (Л) Лабораторные работы (ЛР) Практические занятия (ПЗ) | 68 17 17 |
Самостоятельная работаОбщий объем часов (С2) В том числе: на подготовку к лекциям на подготовку к ЛР на подготовку к ПЗ на выполнение КП на выполнение КР на выполнение РГР на написание РФ на выполнение ДЗ на экзаменационную сессию | 34 17 17 |
Содержание дисциплины
Введение в теорию вариационного исчисления. Линейное пространство. Линейное нормированное пространство Понятие функционала. Первая вариация функционала. Необходимое условие экстремума. Выпуклый функционал на выпуклом множестве. Достаточное условие выпуклости. Теорема об экстремуме выпуклого функционала.
Вариационная задача с закрепленными границами. Уравнение Эйлера. Задачи на условный экстремум.
Задача с подвижной границей. Достаточные условия экстремума. Понятие о прямых методах вариационного исчисления.
Классификация линейных интегральных уравнений. Уравнения Фредгольма и Вольтерра первого и второго рода. Примеры физических задач, приводящих к интегральным уравнениям.
Линейные операторы в бесконечномерном евклидовом пространстве Вполне непрерывный оператор. Теорема существования собственного значения и собственного вектора у симметричного вполне непрерывного оператора. Построение последовательности собственных значений и собственных векторов.
Однородное уравнение Фредгольма второго рода. Существование собственных значений и собственных функций у интегрального оператора с симметричным ядром. Вырожденные ядра. Теорема Гильберта-Шмидта.
Неоднородное уравнение Фредгольма второго рода. Принцип сжатых отображений. Уравнение Фредгольма с "малым l ". Уравнение Фредгольма с вырожденным и невырожденным ядром. Теоремы Фредгольма.
Уравнение Вольтера первого и второго рода. Существование и единственность решения. Принцип сжимающих отображений.Резольвента для уравнения Вольтерра Метод последовательных приближений.
Понятие о корректно и некорректно поставленных задачах
Уравнение Фредгольма первого рода как пример некорректно поставленной задачи. Сглаживающий функционал. Построение приближенного решения уравнения Фредгольма первого рода Метод А.Н. Тихонова регуляризации решения уравнения Фредгольма первого рода.
Разделы дисциплины и виды занятий и работ
для специальности Ф
| № | Раздел дисциплины | Л | ПЗ | РГР | ДЗ | С2 |
| | Введение в теория вариационного исчисления | * | | | | * |
| | Вариационная задача с закрепленными границами | * | * | | | |
| | Задача с подвижной границей | * | * | | | |
| | Классификация линейных интегральных уравнений | * | * | | | |
| | Линейные операторы | * | | | | * |
| | Однородное уравнение Фредгольма второго рода | * | * | | | |
| | Неоднородное уравнение Фредгольма второго рода | * | * | | | |
| | Уравнение Вольтера. | * | * | | | |
| | корректно и некорректно поставленные задачи | * | * | | | |
Практические занятия
1. Вариационное исчисление
Оснащение: 1. Л. Э. Эльсгольц. Дифференциальные уравнения и вариационное исчисление. М., Наука., 2006г
Задачи с неподвижными границами. Уравнение Эйлера.[1] часть 2, гл.6 1-20 стр.324-326
Задачи с подвижными границами. Условие трансверсальности. [1] часть 2, гл.7 1-8 стр.349-350
Задачи на условный экстремум. [1] часть 2, гл.9 1-5 стр 393
Достаточные условия экстремума. [1] часть 2, гл.8 1-8 стр 373
2. Интегральные уравнения
Оснащение. 2. М.Л.Краснов, А.И.Киселев, Г. И. Макаренко.Интегральные уравнения. Задачи и примеры с подробными решениями. УРСС., Москва, 2003г
Уравнения Фредгольма. Определение собственных чисел и собственных функций однородных уравнений Фредгольма. Построение резольвенты. Неоднородные уравнения с симметричным ядром. . [2], 123-128,135-140, 165-170.
Исследование задачи Штурма-Лиувилля сведением к уравнению Фредгольма второго рода. . [2], 112-115,219-225.
Уравнения Вольтерра первого и второго рода. Уравнение с ядром, зависящим от разности аргументов. Решение методом преобразования Лапласа. [2], 156,157,234-240
Практические занятия и их взаимосвязь с содержанием лекционного курса
| № п/п | № раздела по варианту содержания | Наименование практических занятий |
| | 1,2 | Задачи с неподвижными границами |
| | 1,3 | Задачи с подвижными границами |
| | 1 | Задачи на условный экстремум |
| | 1,2,3 | Достаточные условия экстремума |
| | 4,5,6,7 | Уравнения Фредгольма |
| | 4, 5,8,9 | Уравнения Вольтерра первого и второго рода |
Контроль знаний студентов
2. Текущий контроль знаний студентов
Контроль достижения целей обучения осуществляется с помощью: одной - двух, контрольных работ в течение семестра по разделам и темам курса. Главной целью проведения текущих контрольных работ является установление уровня и характера усвоения студентами основных понятий, умений и навыков, формируемых в процессе изучения курса. Контрольные работы рекомендуется проводить в рамках внеаудиторных занятий (домашние индивидуальные задания).
Примерное содержание контрольных работ: (содержание и количество контрольных работ может меняться.)
Контрольная работа 1 «Вариационное исчисление» содержит 2-3 задачи на построение функционала и решение задач. Время на выполнения 1-2 часа.
Контрольная работа 2 «Интегральные уравнения » содержит 2-3 задачи на технику построения аналитических и приближенных решений. Время на выполнение 1-2 часа.
- Выходной контроль знаний студентов
Дисциплина завершается зачетом по окончанию семестра. На зачете проверяется степень усвоения студентами основных понятий дисциплины, понимание их взаимосвязи, умение доказывать основные теоремы, а также навыки в решении задач по каждому из разделов дисциплины.
Вопросы
1.. Классификация линейных интегральных уравнений
2. Понятие вполне непрерывного оператора. Теорема существования собственного значения и собственного вектора для вполне непрерывного симметричного оператора.
3. Постановка задачи Штурма-Лиувилля.
4. Альтернатива Фредгольма
5. Уравнение Фредгольма первого рода как пример некорректно поставленной задачи.
6. Понятие функционала и его первой вариации.
7. Вариационная задача с закрепленными концами и уравнение Эйлера.
8. Достаточные условия экстремума.
.
Учебно-методическое обеспечение дисциплины
- Анхейзер Н.И. Лекции по вариационному исчислению. М.: Гостехиздат, 1955. – 320 с.
- Ванько Вячеслав Иванович. Вариационное исчисление и оптимальное управление: Учеб.для вузов / Ванько Вячеслав Иванович, О. В. Ермошина, Г. Н. Кувыркин; Под ред.:В.С.Зарубина.А.П.Крищенко. - 2-е изд. - М.: Изд-во МГТУ им.Н.Э.Баумана, 2001. - 488с.
- Виноградова П.В., Зарубин А.Г. Вариационное исчисление. – Хабаровск, Изд-во ТОГУ, 2006.
- Гельфанд И.М. Вариационное исчисление. М.: Наука, 1969. – 410 с.
- Карташев А.П. Обыкновенные дифференциальные уравнения и основы вариационного исчисления. М.: Наука, 1986. – 308 с.
- Краснов Л.М. Макаренко Г.И., Киселев А.И. Вариационное исчисление. М. Наука, 1973. 290 с.
- М.Л.Краснов, А.И.Киселев, Г. И. Макаренко. Интегральные уравнения. Задачи и примеры с подробными решениями. УРСС., Москва, 2003г
- Михлин С.Г. Вариационные методы в математической физике. М.: Наука, 1970. 512 с.
- Сабитов Камиль Басирович. Функциональные, дифференциальные и интегральные уравнения/ Сабитов Камиль Басирович. - М.: Высш.шк., 2005.
- Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. М., Эдиториал УРСС, 2000, Наука., 2006г..
Методические рекомендации по организации изучения дисциплины
Программа определяет общий объем знаний, а не порядок изучения предмета. Тем не менее, построение соответствующих математических курсов должно проводиться так, чтобы у студента сложилось целостное представление об основных этапах становления современной математики и ее структуре, об основных математических понятиях и методах, о роли и месте математики в различных сферах человеческой деятельности.
Для того, чтобы студент воспринимал ценности математики как науки и свободно владел математическими методами в приложениях к техническим наукам, конкретная реализация программы должна иметь следующую структуру.
Математические курсы, соответствующие данной программе, должны содержать лекции, практические занятия в аудитории, индивидуальные занятия студентов с преподавателем и самостоятельную работу студентов. Целью лекций является изложение теоретического материала и иллюстрация его примерами и задачами. Основным теоретическим результатам должны сопутствовать пояснения об их приложениях к другим разделам математики и к техническим наукам. Желательно также кратко излагать историю появления наиболее важных понятий и результатов. Курс лекций должен строиться на основе четких формулировок и доказательств основных теорем, так как лишь при таком подходе студенты приобретают математическую культуру, необходимую для дальнейшего изучения математики и инженерных дисциплин. Недопустимо сводить чтение лекций только к разбору примеров и алгоритмов их решения Целью практических занятий является закрепление теоретического материала лекций и выработка умения решать примеры и задачи для последующего применения математических методов в технических приложениях. Важнейшей частью математических курсов являются индивидуальные занятия с преподавателем. Поэтому каждый семестр должен содержать одну расчетную работу и две-три контрольные работы в течение семестра.
Самостоятельная работа предполагает, что: отдельные темы могут быть отнесены на самостоятельное изучение; на лекциях предлагается значительное количество контрольных вопросов и упражнений, служащих для проверки усвоения теории; на практических занятиях регулярно задаются домашние задания, которые проверяют усвоение методов и приемов решения разбираемых на практических занятиях задач, закрепляют алгоритмические умения и навыки. Самостоятельная работа не расширяет существенно рамки программы, она призвана закрепить излагаемый на лекциях и практических занятиях материал, а также приучает студентов к самостоятельному овладению новым материалом.
Задача вариационного исчисления - минимизация интегрального функционала при заданных краевых условиях.
Интегральные уравнения – уравнения, содержащие неизвестную функцию под знаком интеграла.
Уравнение Фредгольма – линейное интегральное уравнение вида (уравнение 2-го рода)
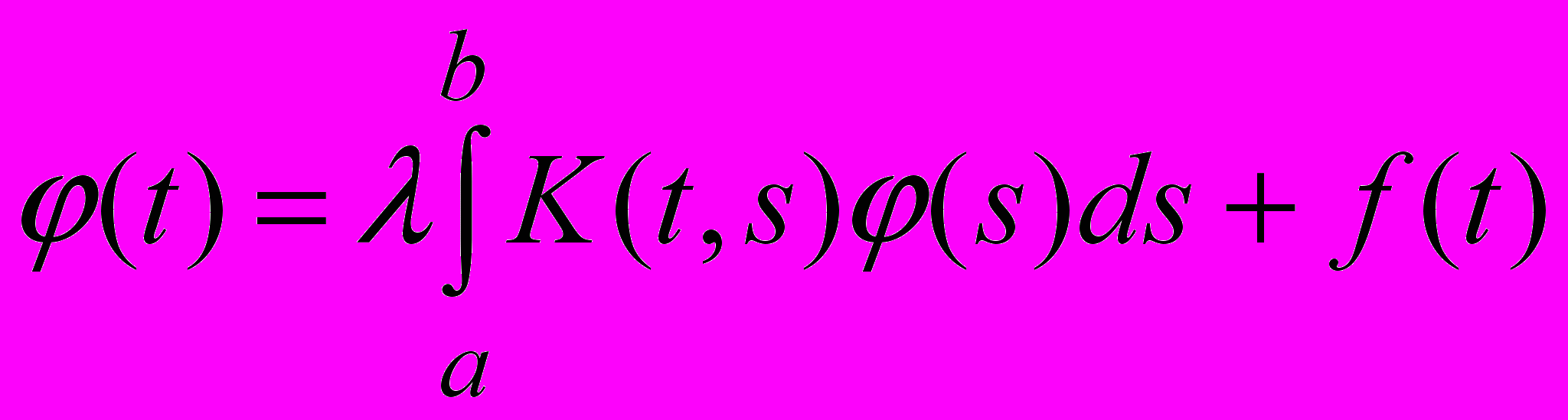, уравнение Фредгольма 1-го рода характеризуется отсутствием члена, содержащего неизвестную функцию вне интеграла.Уравнение Вольтера 2-го рода - линейное интегральное уравнение вида
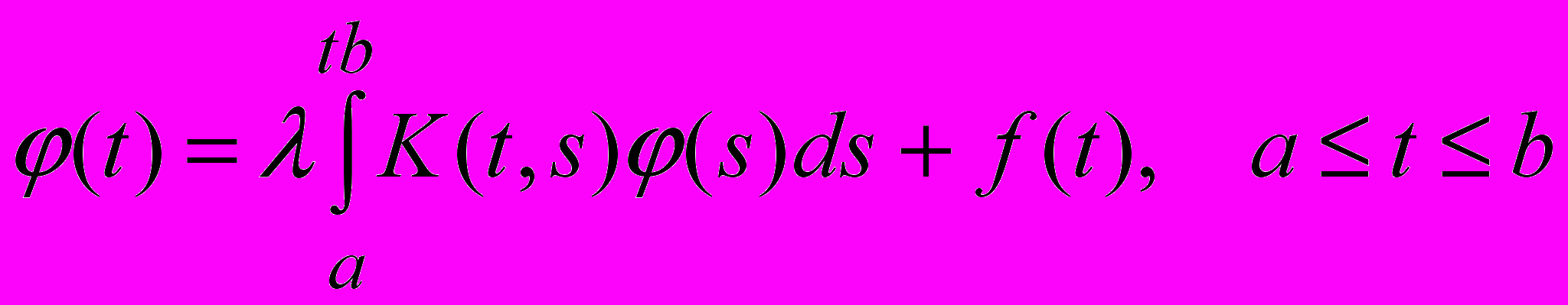, уравнение Вольтерра 1-го рода характеризуется отсутствием члена, содержащего неизвестную функцию вне интеграла.Задача Абеля – обобщение задачи и таутохроне: найти кривую, скользя вдоль которой без трения тяжелая частица достигает своего самого низкого положения за одно и то же время, независимо от начального положения.
Задача о брахистохроне – между точками, расположенными на различной высоте, провести кривую таким образом, что время падения тела вдоль кривой было минимальным.
Альтернатива Фредгольма. Условия, при которых операторное уравнение однозначно разрешимо, имеет бесконечное множество решений или неразрешимо.
Метрическое пространство – множество, с заданной на нем метрикой.
Метрика - неотрицательное число
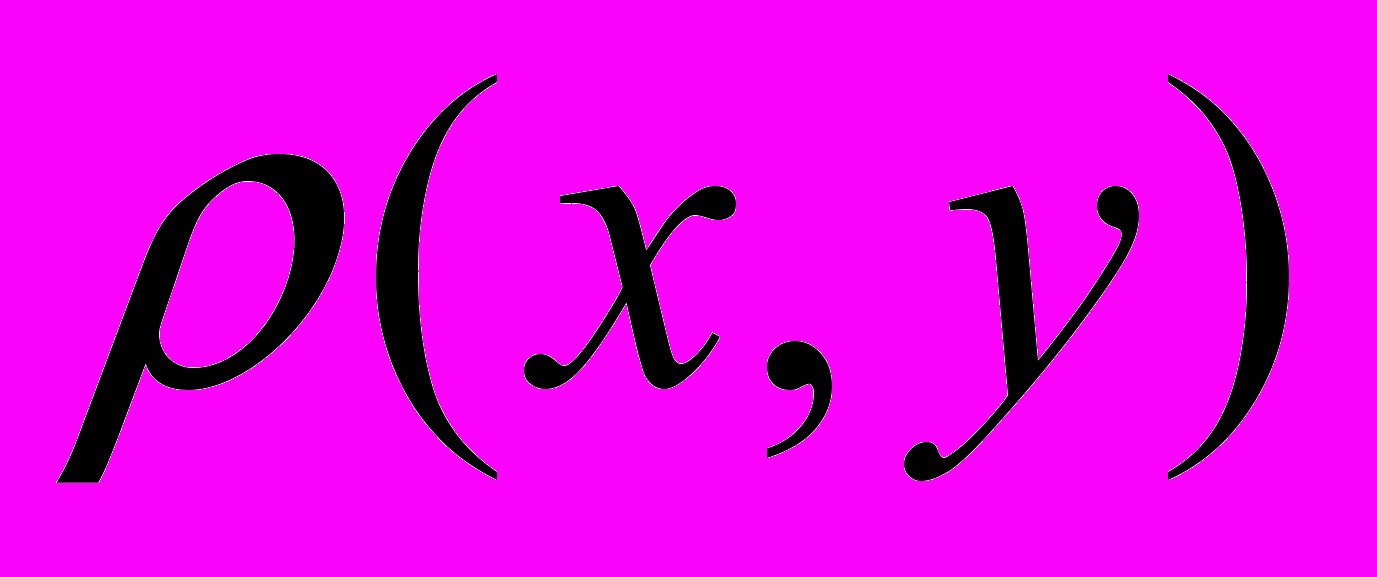, поставленное в соответствие каждой паре элементов 
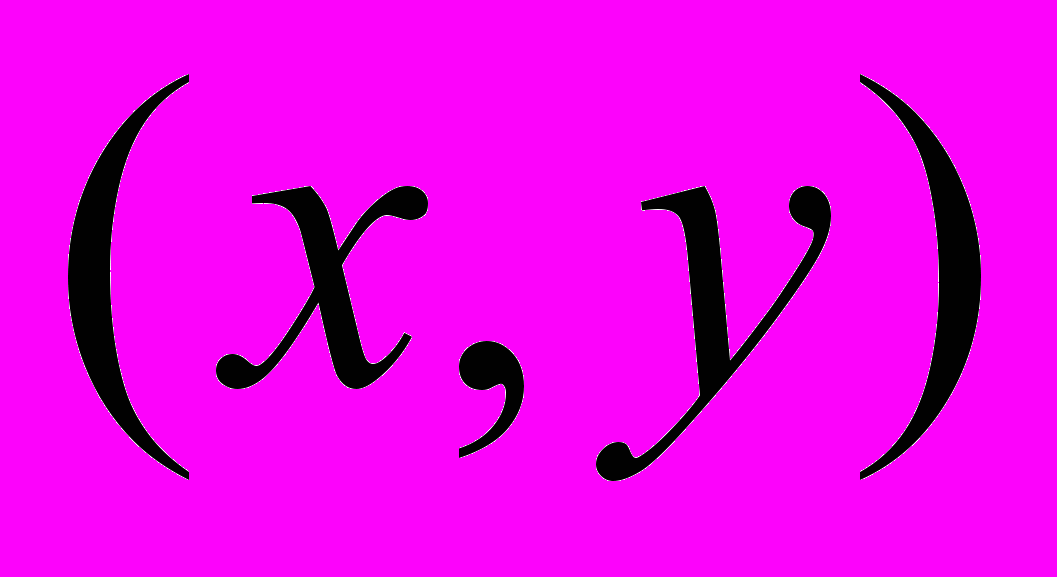множества, удовлетворяющее аксиомам: 1) 
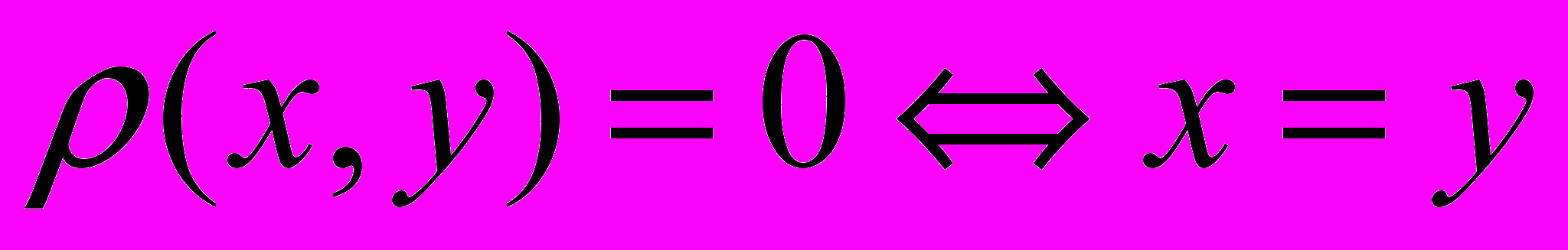, 2)
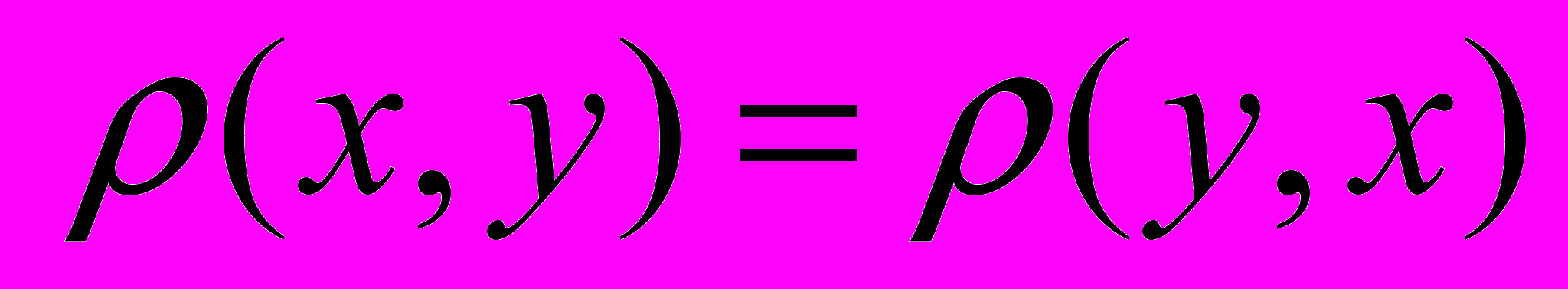, 3)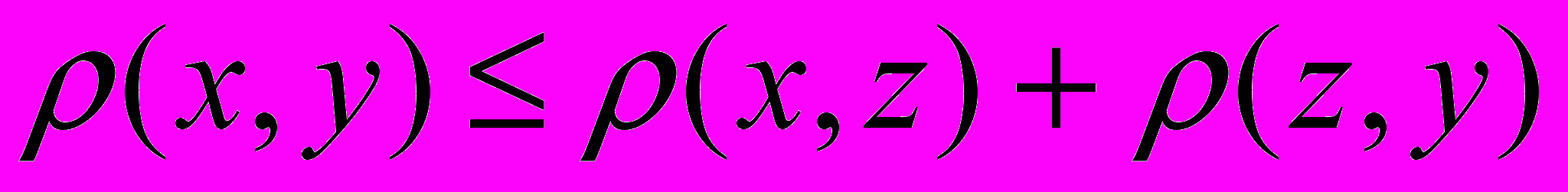 
.Полное пространство – метрическое пространство, в котором каждая фундаментальная последовательность сходится к элементу этого пространства.
Фундаментальная последовательность. Если для любого сколь угодно малого положительного ε существует
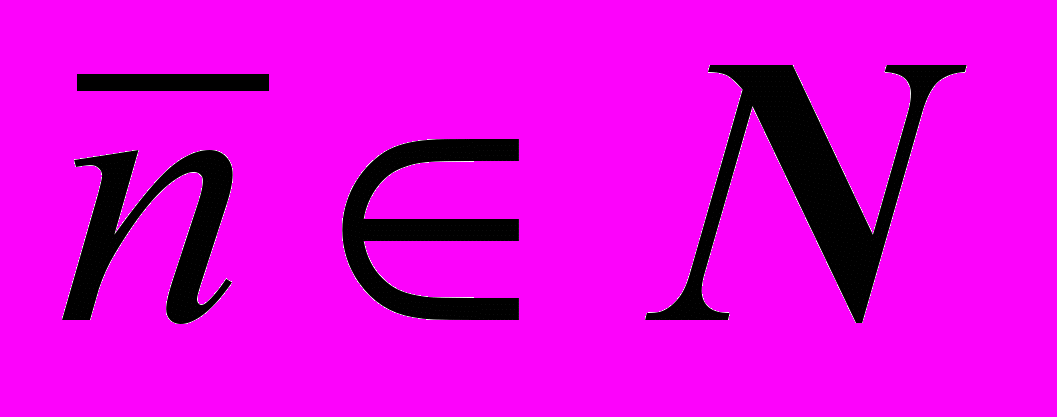такое что для любых 
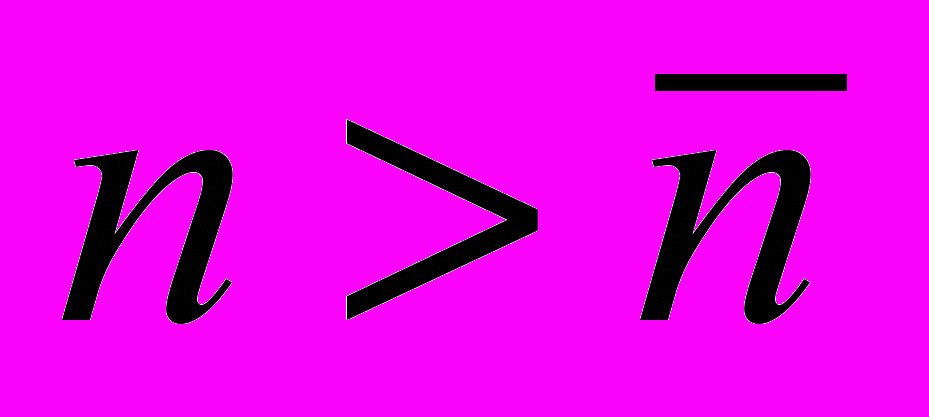и для любых m имеет место неравенство 
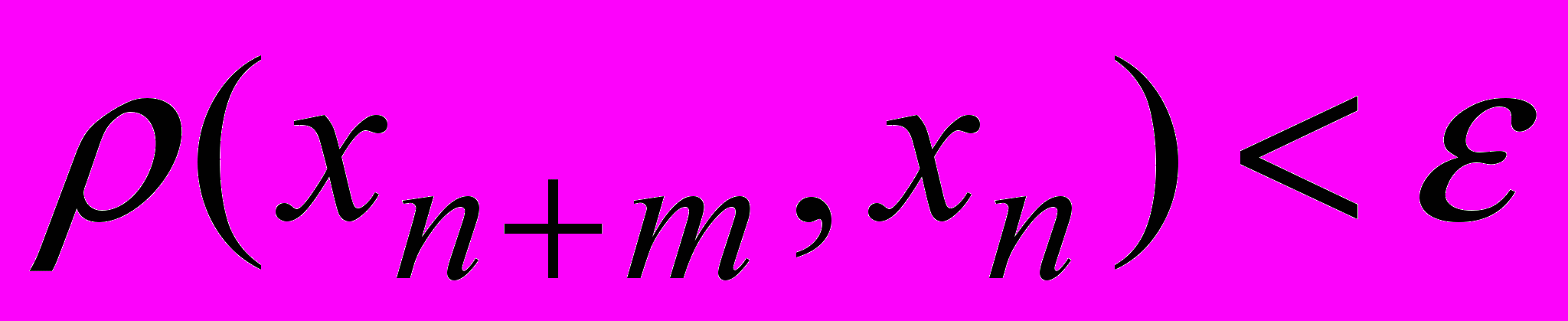.Сходящаяся последовательность – последовательность, предел которой существует и конечен.
Линейный оператор – оператор
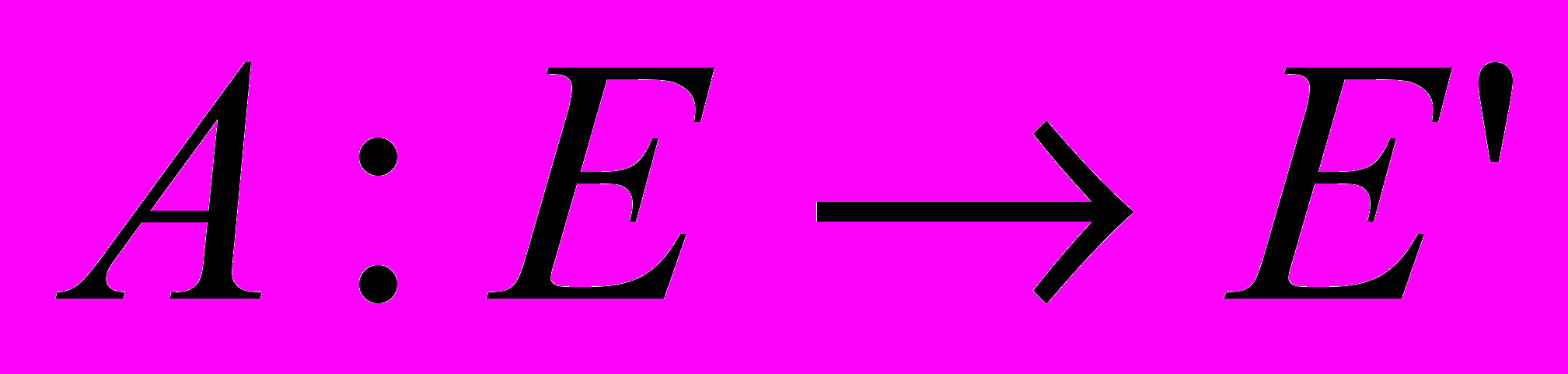, такой что для любых 
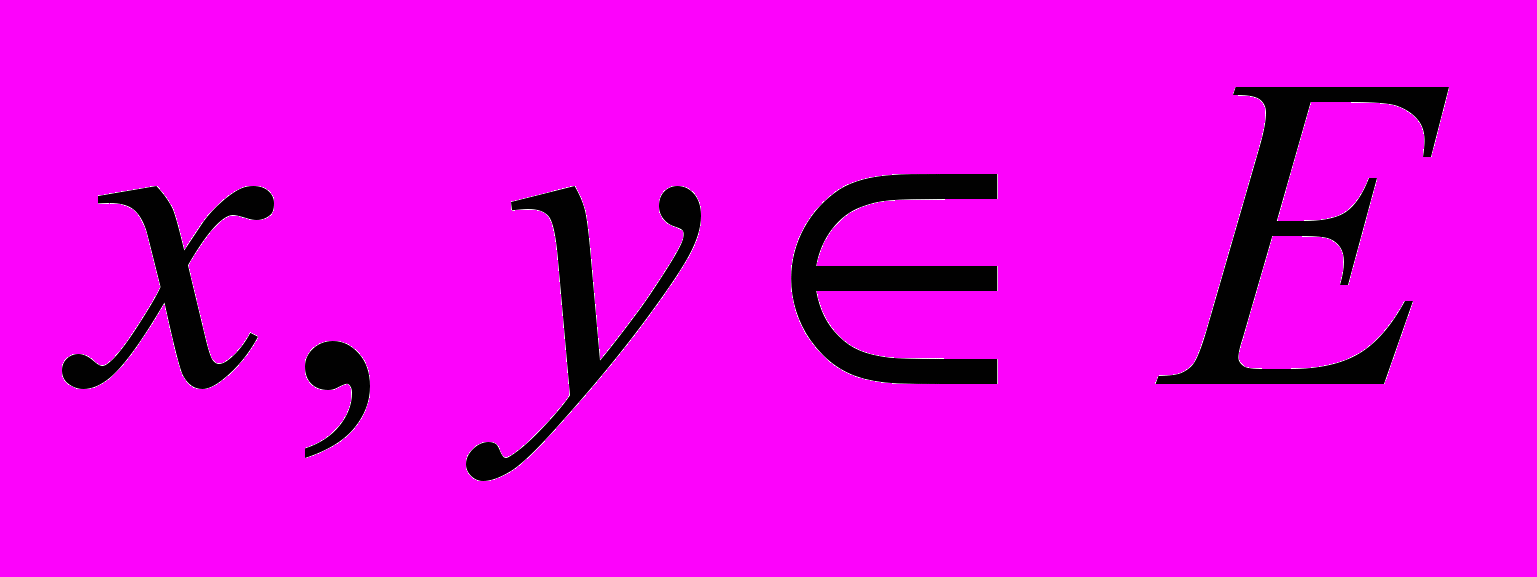и любых чисел 
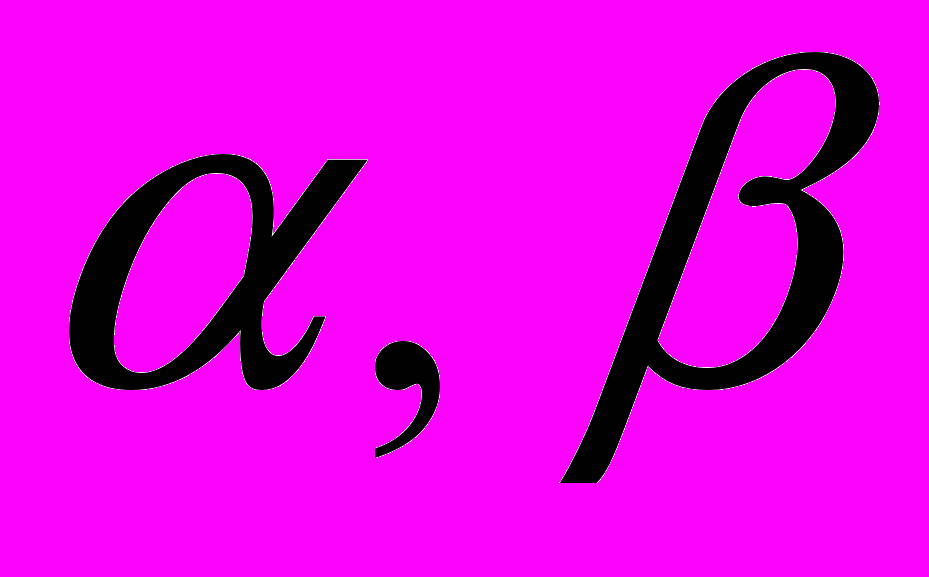имеет место соотношение 
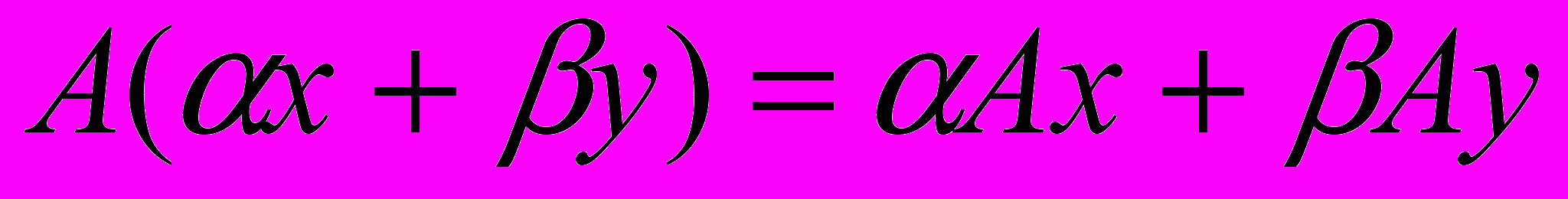.Сжимающий оператор – оператор, обладающий свойством, что для всех
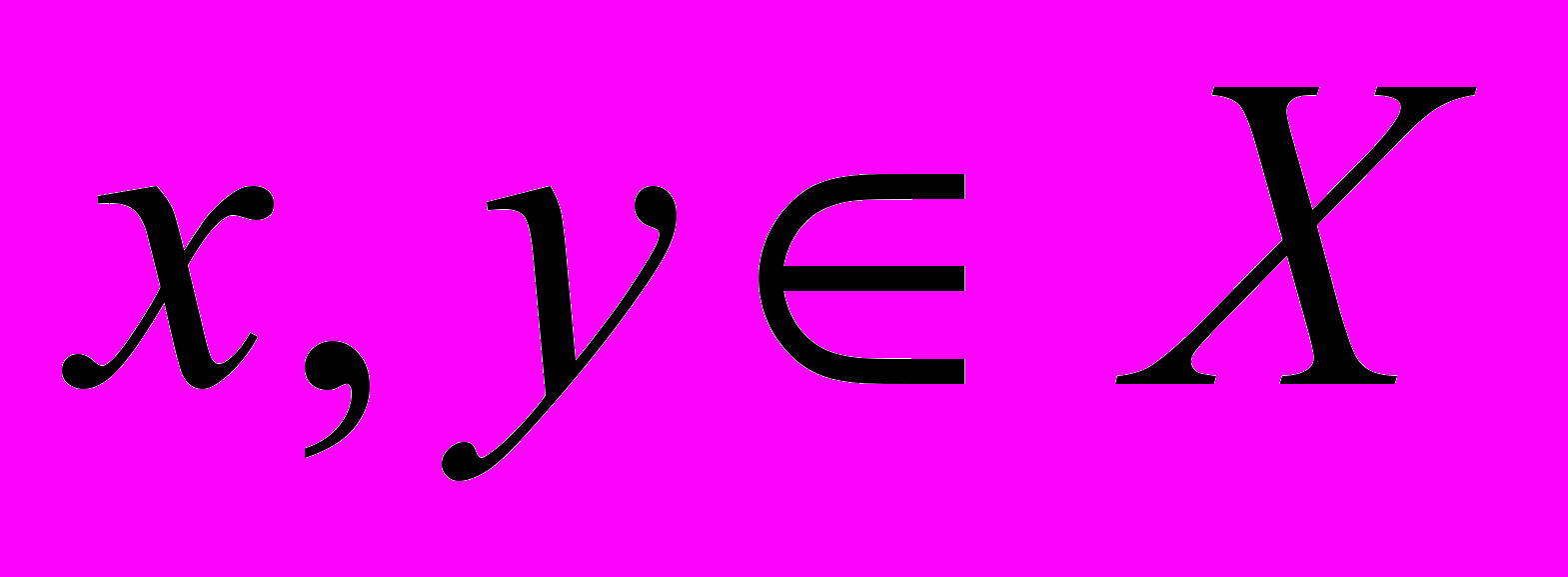выполнено 
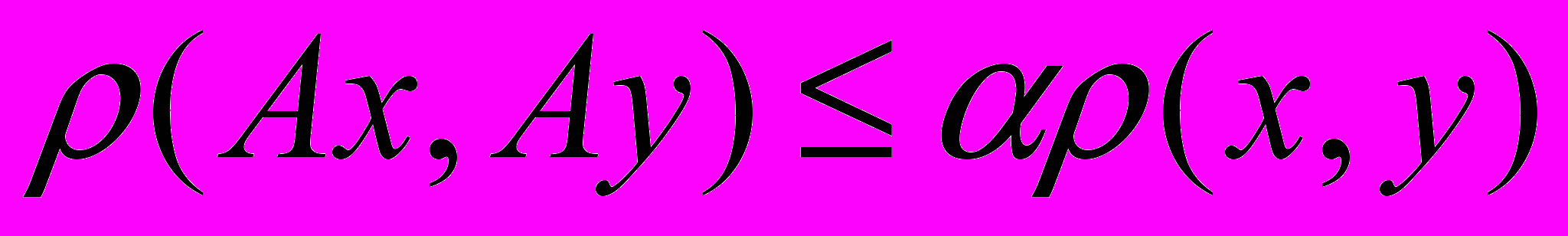, где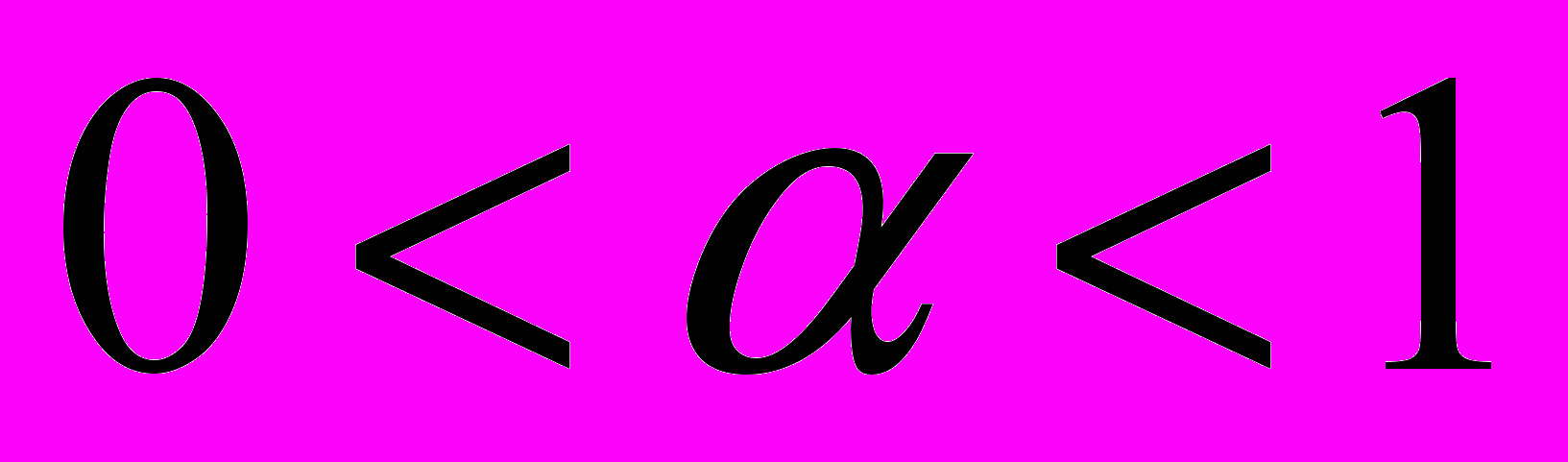 
.Линейное нормированное пространство – линейное пространство, в котором каждому элементу поставлена в соответствие число, норма элемента.
Норма элемента – каждому элементу х поставлено в соответствие действительное число
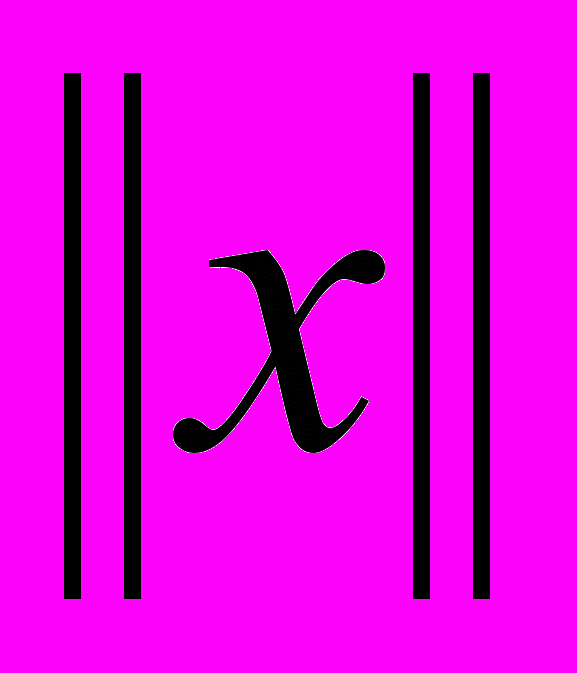, удовлетворяющее аксиомам: 1) 
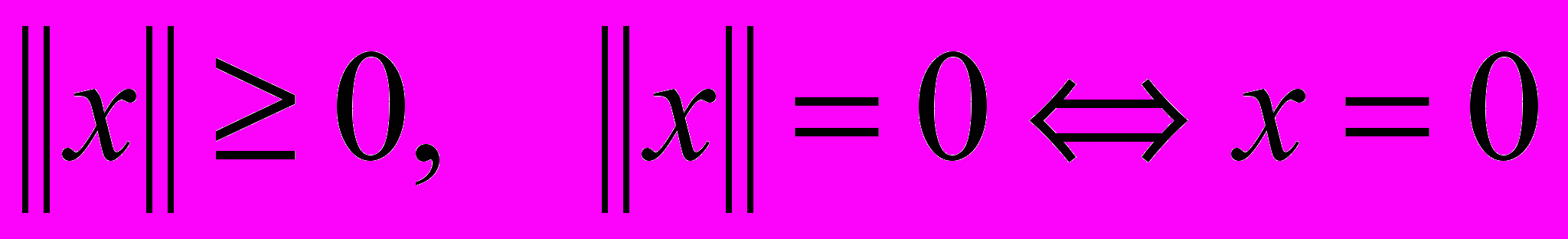, 2) 
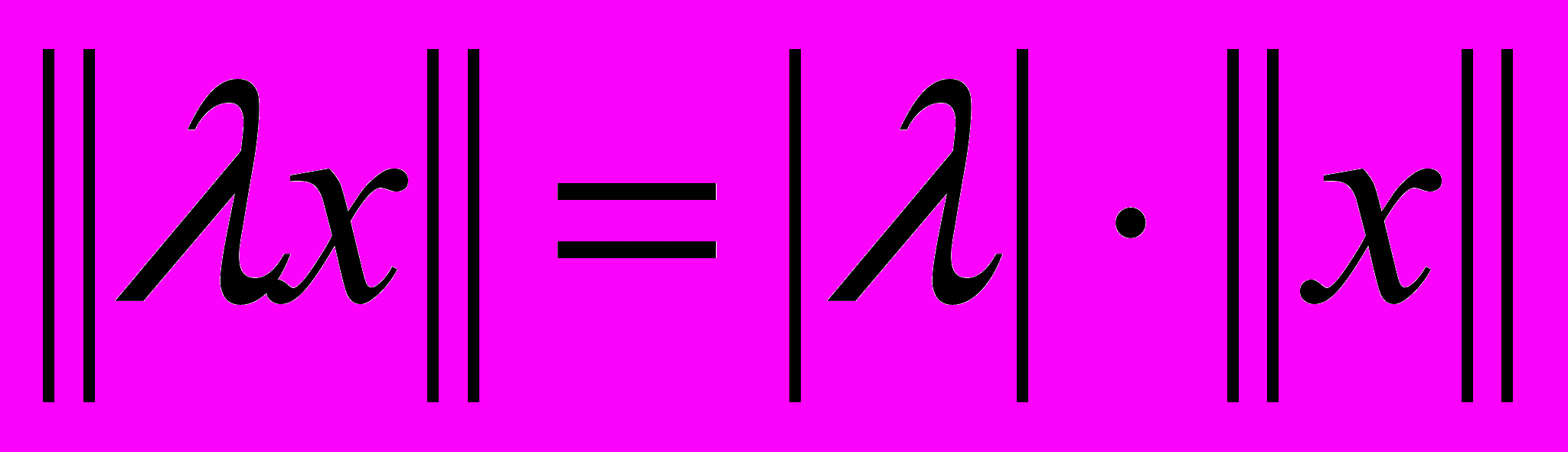, 3)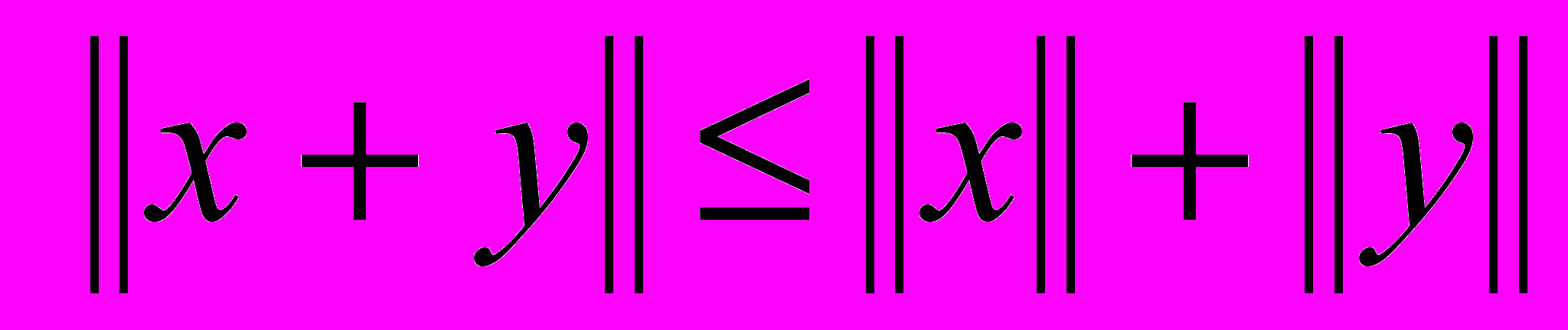
.Вполне непрерывный оператор – оператор, определенный на линейном нормированном пространстве, отображающий всякое ограниченное множество в компактное множество.
Компактное множество – множество метрического пространства, в котором всякая его последовательность содержит сходящуюся подпоследовательность.