Агапова Елена Григорьевна, к ф. м н., доцент кафедры пми программа

Вид материала

Программа

Содержание Цели и задачи изучаемой дисциплины Требования к уровню освоения содержания дисциплины. Объём дисциплины и виды учебной работы Общая трудоёмкость дисциплины Изучается в семестрах Вид итогового контроля самостоятельной работы без отчетностей Аудиторные занятия Самостоятельная работа Основы теории погрешностей Численные методы решения систем линейных уравнений Численные методы решения скалярных уравнений Численные методы решения систем нелинейных уравнений Спектральная задача Интерполирование функций Раздел дисциплины Лабораторный практикум Наименование лабораторной работы Лабораторный практикум Порядок выполнения Используемое оборудование ... Полное содержание

Подобный материал:

• Агапова Елена Григорьевна, к ф. м н, доцент кафедры пми программа, 264.73kb.
• Зарубин Анатолий Георгиевич, д ф. м н., профессор, завкафедрой пми попова Татьяна Михайловна,, 146.14kb.
• Попова Татьяна Михайловна, к ф. м н, доцент кафедры пми программа, 222.32kb.
• Богуславская Елена Львовна, к ф. н., доцент кафедры перевода и переводоведения Ургпу,, 379.6kb.
• Мамонтова Елена Анатольевна, к э. н., доцент кафедры Иип сонина Галина Васильевна., 13.24kb.
• Российский Экономический Университет им. Г. В. Плеханова факультет дистанционного обучения, 405.79kb.
• Состав оргкомитета: Шишло Елена Григорьевна, 82.13kb.
• Таболова Елена Мэлсовна, кандидат психологических наук, доцент кафедры социальной работы, 364.62kb.
• Рабочая программа курса Практикум на ЭВМ. Специальность 510200, Прикладная математика, 87.68kb.
• Иванова Елена Николаевна Доцент Леанович Елена Борисовна Минск 2010 оглавление список, 445.62kb.

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

Тихоокеанский государственный университет

Утверждаю Проректор по учебной работе ______________ С.В. Шалобанов “_____” ________________200_ г.

Программа дисциплины


по кафедре Прикладная математика и информатика


вычислительные методы

линейной алгебры


Утверждена научно-методическим советом университета

для направлений подготовки (специальностей) в области информатики и вычислительной техники. Специальности ПМ.


Хабаровск 2007 г.


Программа разработана в соответствии с требованиями государственного образовательного стандарта, предъявляемыми к минимуму содержания дисциплины и в соответствии с примерной программой дисциплины, утвержденной департаментом образовательных программ и стандартов профессионального образования с учетом особенностей региона и условий организации учебного процесса Тихоокеанского государственного технического университета.


Программу составила

Агапова Елена Григорьевна, к.ф.-м.н., доцент кафедры ПМИ

Программа рассмотрена и утверждена на заседании кафедры протокол № ______ от «____»__________________ 200_г
Завкафедрой__________«__»______ 200_г		_Зарубин А. Г.____
Подпись дата		Ф.И.О.
Программа рассмотрена и утверждена на заседании УМК и рекомендована к изданию протокол № ______ от «____»_____________ 200_г
Председатель  УМК  _______«__»_______ 200_г			__Попова Т. М.________
Подпись Дата			Ф.И.О.

Декан ФММПУ   __________«___»_______ 200_г	Син А.З. _______
Подпись дата	Ф.И.О.

^ Цели и задачи изучаемой дисциплины


Цель курса - формирование у студента представлений о методах решения задач на ЭВМ. Основные задачи курса - углубление математического образования и развитие практических навыков в области прикладной математики. Студенты должны быть готовы использовать полученные в этой области знания, как при изучении смежных дисциплин, так и в профессиональной деятельности, в частности при обучении информатике старшеклассников средней школы.

Курс включает в себя изучение элементов теории погрешностей и теории приближений, основные численные методы алгебры и математического анализа. Подробно рассмотрены различные методы построения интерполяционных многочленов.

Главная особенность обучения основам численных методов, которая все отчетливее проявляется в последние годы, связана с интенсификацией процессов использования различных специализированных математических пакетов и систем программирования вычислительных методов как инструмента решения прикладных задач. В связи с этим, явное включение в содержание дисциплины вопросов, раскрывающих применение современных информационных технологий в прикладной математике, является необходимым требованием времени.

Теория приближенного решения математических задач постоянно пополняется все более совершенными численными методами, появление которых стимулируется как особенностями машинной математики, так и расширением функциональных возможностей прикладных программных средств. Все это требует определенного уровня понимания, который необходимо обеспечить в рамках дисциплины «Численные методы».

Излагаемый на лекциях теоретический материал закрепляется и отрабатывается в ходе выполнения лабораторных работ, которые должны развить у студента умение:


^ Требования к уровню освоения содержания дисциплины.


Математическое образование должно быть фундаментальным и в то же время иметь четко выраженную прикладную направленность, быть в известной мере индивидуализированным (часть разделов программы может изучаться по выбору студента).

Фундаментальность математической подготовки включает в себя достаточную общность математических понятий и конструкций, обеспечивающую широкий спектр их применимости, разумную точность формулировок математических свойств изучаемых объектов, логическую строгость изложения математики, опирающуюся на адекватный современный математический язык.


^ Объём дисциплины и виды учебной работы

Наименование	По учебным планам основной траектории обучения
^ Общая трудоёмкость дисциплины
по ГОС	119
по УП	119
^ Изучается в семестрах	5
Вид итогового контроля по семестрам
зачет
экзамен	5
Курсовой проект (КП)
Курсовая работа (КР)
^ Вид итогового контроля самостоятельной работы без отчетностей расчетно-графические работы (РГР)
Реферат (РФ)
Домашние задания (ДЗ)
^ Аудиторные занятия:
всего	68
В том числе: лекции (Л)	34
Лабораторные работы (ЛР)	34
Практические занятия (ПЗ)
^ Самостоятельная работа
общий объем часов (С2)	51
В том числе на подготовку к лекциям	17
на подготовку к лабораторным работам	34
на подготовку к практическим занятиям
на выполнение КР
на выполнение РГР
на написание РФ
на выполнение ДЗ
на экзаменационную сессию

Содержание дисциплины

1. ^ ОСНОВЫ ТЕОРИИ ПОГРЕШНОСТЕЙ
   

Точные и приближенные значения величин, точные и приближенные числа.

Источники классификаций погрешностей. Абсолютная и относительная погрешности. Верные знаки, связь количества верных знаков и относительной погрешности. Правила округления и погрешность округления. Основные задачи теории погрешностей, способы их решения. Применение дифференциального исчисления при оценке погрешности. Обратная задача теории погрешностей. Оценка погрешностей вычислений, возникающих в ЭВМ.

2. ^ ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
   

Прямые методы решения систем линейных алгебраических уравнений. Метод

Гаусса, его применение для обращения и вычисления определителей матриц. Метод прогонки. Полные метрические пространства. Теорема о сжимающих отображениях в полном метрическом пространстве и ее следствия. Применение теоремы о сжимающих отображениях при решении системы линейных уравнений: простые итерации, метод Зейделя. Погрешности округления при практической реализации итерационного процесса. Оценка погрешности решения системы линейных алгебраических уравнений. Понятие об обусловленности. Понятие о методе Ньютона решения такой системы. Практические схемы решения на ЭВМ.

3. ^ ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СКАЛЯРНЫХ УРАВНЕНИЙ
   

Методы отделения и уточнения корней, геометрический смысл. Сходимость,

погрешность методов: половинного деления, Ньютона, секущих, простых итераций. Приближенное вычисление корня уравнения с заданной точностью методом половинного деления. Метод простой итерации численного решения уравнений. Условия сходимости итерационной последовательности. Практические схемы вычисления приближенного значения корня уравнения с заданной точностью методом простой итерации. Сходимость и устойчивость численного метода.

4. ^ ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
   

Теорема о сжимающих отображениях в полном метрическом пространстве. Понятие об обусловленности. Понятие о методе Ньютона решения такой системы. Практические схемы решения на ЭВМ.

5. ^ СПЕКТРАЛЬНАЯ ЗАДАЧА
   

Численные методы решения задач на собственные значения и собственные векторы матриц. Метод вращения Якоби, степенной метод. Метод Крылова. Метод Даниловского.

6. ^ ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
   

Задачи, приводящие к аппроксимации одной функции другой. Алгебраический интерполяционный многочлен: единственность, форма Лагранжа, оценка погрешности интерполирования. Схема Эйткена. Разделенные разности. Первый и второй многочлены Ньютона. Связь разделенной разности и производной. Практическая оценка погрешности интерполирования. Обратное интерполирование. Многочлены Чебышева, их применение для минимизации оценки погрешности интерполирования. Понятие о сходимости интерполяционного процесса. Понятия о сплайнах. Практические схемы интерполирования на ЭВМ.

Таблица 2 – Разделы дисциплины и виды занятий и работ

№	^ Раздел дисциплины	Л	ЛР	РГР	ДЗ	С2
1	2	3	4	5	6	7
	Основы теории погрешностей.	*	*			*
	Численные методы решения систем линейных уравнений.	*	*
	Численные методы решения скалярных уравнений.	*	*
	Численные методы решения систем нелинейных уравнений.	*	*
	Спектральная задача.	*	*			*
	Интерполирование функций.	*	*			*

^ Лабораторный практикум

Таблица 3 – Лабораторный практикум и его взаимосвязь с содержанием лекционного курса

№ п./п.	№ раздела по варианту содержания	^ Наименование лабораторной работы
	1	1. Метод Гаусса
	2	2. Прямое и итерационное решение систем линейных алгебраических уравнений 2.1. Методом квадратных корней 2.2. Метод простых итераций и метод Зейделя
	3	3. Численное решение алгебраических проблем собственных значений 3.1. Метод Крылова 3.2. Метод Данилевского
	4	4. Методы решения скалярных уравнений 4.1. Отделение и уточнение корня с помощью методов половинного деления, хорд, Ньютона, секущих 4.2. Итерационные методы
	5	5. Решение систем нелинейных уравнений
	6	6. Интерполяция

Лабораторный практикум приводится в виде перечня лабораторных работ с их краткой характеристикой, отражающей цели и задачи работы (задание), порядок выполнения (исполнение), используемое оборудование (оснастка), оценку результатов работы (оценка) и время, отводимое на выполнение лабораторной работы.

^

Лабораторный практикум

1. Метод Гаусса
   

Задание: Решить систему методом Гаусса. Предусмотреть постолбцовый выбор главного элемента и итерационное уточнение решения до достижения точности ε=10^-12 по евклидовой норме невязки. Найти обратную матрицу. Вычислить определитель матрицы.

^ Порядок выполнения: Составить программу, выполнить программу, сохранить программу и результаты. Составить отчет по лабораторной работе. Ответить на вопросы преподавателя (защитить лабораторную работу).

^ Используемое оборудование: персональный компьютер.

Время выполнения работы – 2 часа

2. Прямое и итерационное решение систем линейных алгебраических уравнений
   
   1. Методом квадратных корней
      

^ Задание: Решить систему линейных уравнений методом квадратных корней.

Порядок выполнения: Составить программу, выполнить программу, сохранить программу и результаты. Составить отчет по лабораторной работе. Ответить на вопросы преподавателя (защитить лабораторную работу).

^ Используемое оборудование: персональный компьютер

Время выполнения работы – 4 часа

2. Метод простых итераций и метод Зейделя
   

Задание: Решить систему линейных уравнений методом простой итерации и методом Зейделя. Провести сравнительный анализ примененных методов.

^ Порядок выполнения: Составить программу, выполнить программу, сохранить программу и результаты. Составить отчет по лабораторной работе. Ответить на вопросы преподавателя (защитить лабораторную работу).

^ Используемое оборудование: персональный компьютер

Время выполнения работы – 4 часа

3. Численное решение алгебраических проблем собственных значений
   
   1. Метод Крылова
      

Задание: Найти собственные значения и собственные вектора матрицы. Выполнить проверку.

^ Порядок выполнения: Составить программу, выполнить программу, сохранить программу и результаты. Составить отчет по лабораторной работе. Ответить на вопросы преподавателя (защитить лабораторную работу).

^ Используемое оборудование: персональный компьютер

Время выполнения работы – 4 часа

2. Метод Даниловского
   

Задание: Найти собственные значения и собственные вектора матрицы. Выполнить проверку.

^ Порядок выполнения: Составить программу, выполнить программу, сохранить программу и результаты. Составить отчет по лабораторной работе. Ответить на вопросы преподавателя (защитить лабораторную работу).

^ Используемое оборудование: персональный компьютер

Время выполнения работы – 4 часа

4. Методы решения скалярных уравнений
   

1. Отделение и уточнение корня с помощью методов половинного деления, хорд, Ньютона, секущих
   

Задание: Найти корень уравнения с точностью ε=10^-12 каждым из следующих способов: методом половинного деления; методом хорд; методом Ньютона; методом секущих. Сравнить методы по числу итераций и по вычислительным затратам.

^ Порядок выполнения: Составить программу, выполнить программу, сохранить программу и результаты. Составить отчет по лабораторной работе. Ответить на вопросы преподавателя (защитить лабораторную работу).

^ Используемое оборудование: персональный компьютер.

Время выполнения работы – 4 часа

2. Итерационные методы
   

Задание: Найти корень уравнения с точностью ε=10^-12 методом простых итераций. Предварительно привести уравнение к виду, пригодному для проведения итераций; доказать существование и единственность корня; выбрав начальное приближение, сделать априорную оценку количества шагов метода простых итераций.

^ Порядок выполнения: Составить программу, выполнить программу, сохранить программу и результаты. Составить отчет по лабораторной работе. Ответить на вопросы преподавателя (защитить лабораторную работу).

^ Используемое оборудование: персональный компьютер.

Время выполнения работы – 4 часа

4. Решение систем нелинейных уравнений
   

Задание: Решить систему нелинейных уравнений методом Ньютона.

^ Порядок выполнения: Составить программу, выполнить программу, сохранить программу и результаты. Составить отчет по лабораторной работе. Ответить на вопросы преподавателя (защитить лабораторную работу).

^ Используемое оборудование: персональный компьютер

Время выполнения работы – 4 часа

6. Интерполяция

Задание: Записать подходящее для приближенного вычисления значений y = f(x) интерполяционные многочлены Лагранжа первой и второй степени.

^ Порядок выполнения: Составить программу, выполнить программу, сохранить программу и результаты. Составить отчет по лабораторной работе. Ответить на вопросы преподавателя (защитить лабораторную работу).

Используемое оборудование: персональный компьютер

Время выполнения работы – 4 часа

Контроль знаний студентов


^ 1. Вопросы входного контроля

1. Арифметические действия с числами.
   
2. Абсолютная и относительная погрешности числа.
   
3. Определитель матрицы: определение и вычисление.
   
4. Обратная матрица: определение и вычисление.
   
5. Решение систем линейных алгебраических уравнений: метод Крамера, матричный метод, метод Гаусса.
   
6. Спектральная задача: характеристическое уравнение, собственные числа и собственные вектора.
   
7. Основная теорема алгебры.
   
8. Принцип вложенных отрезков.
   
9. Теорема Ферма.
   

^ 2. Вопросы текущего контроля знаний

1. Погрешности основных арифметических операций. Погрешности элементарных функций.
   
2. Прямая задача теории погрешностей и способы ее решения.
   
3. Метод простой итерации решения уравнений и его реализация на ЭВМ.
   
4. Общая характеристика точных методов решения систем линейных уравнений на ЭВМ. Метод Гаусса.
   
5. Метод касательных численного решения уравнений и его реализация на ЭВМ.
   
6. Метод хорд численного решения уравнений и его реализация на ЭВМ.
   
7. Метод простой итерации решения систем нелинейных уравнений.
   
8. Задача аппроксимации функции.
   
9. Многочленная интерполяция.
   
10. Построение интерполяционного многочлена с помощью системы линейных уравнений.
    
11. Интерполяционные формулы Ньютона.
    
12. Интерполяционный многочлен Лагранжа и оценка его погрешности.
    
13. Интерполяционный многочлен Ньютона для равномерной сетки.
    
14. Обратное интерполирование для равномерной и неравномерной сетки. Интерполяционный многочлен Чебышева.
    
15. Метод наименьших квадратов, наилучшее квадратичное приближение. Вычисление значений параметров среднеквадратичных приближений. Реализация метода наименьших квадратов на ЭВМ.
    

^ 3. Вопросы выходного контроля

1. Источники погрешностей значения величин и их классификация.
   
2. Погрешности основных арифметических операций. Погрешности элементарных функций.
   
3. Прямая задача теории погрешностей и способы ее решения.
   
4. Обратная задача теории погрешностей и ее решение методом равных влияний.
   
5. Представление в ЭВМ чисел с плавающей точкой; погрешность машинного округления; принципы оценки погрешности результатов вычислений.
   
6. Метод простой итерации решения уравнений и его реализация на ЭВМ.
   
7. Метод касательных численного решения уравнений и его реализация на ЭВМ.
   
8. Метод хорд численного решения уравнений и его реализация на ЭВМ.
   
9. Общая характеристика точных методов решения систем линейных уравнений на ЭВМ. Метод Гаусса.
   
10. Метод простой итерации решения систем нелинейных уравнений.
    
11. Задача аппроксимации функции.
    
12. Многочленная интерполяция.
    
13. Построение интерполяционного многочлена с помощью системы линейных уравнений.
    
14. Интерполяционные формулы Ньютона.
    
15. Интерполяционный многочлен Лагранжа и оценка его погрешности.
    
16. Интерполяционный многочлен Ньютона для равномерной сетки.
    
17. Обратное интерполирование для равномерной и неравномерной сетки. Интерполяционный многочлен Чебышева.
    
18. Метод наименьших квадратов, наилучшее квадратичное приближение. Вычисление значений параметров среднеквадратичных приближений. Реализация метода наименьших квадратов на ЭВМ.
    

Учебно-методическое обеспечение дисциплины

1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы: учебное пособие для вузов. – М.: Наука, 1987.
   
2. Бахвалов Н. С., Лапин А.В., Чижонков Е.В. Численные методы в задачах и упражнениях. Учеб. пособие. /Под ред. В.А. Садовничего. – М.: Высшая школа, 2000.
   
3. Березин И.С., Жидков Н.П. Методы вычислений. В 2-х ч. – М.: Физматгиз, 1962.
   
4. Васильков Ю.В., Василькова Н.Н. Компьютерные технологии вычислений в математическом моделировании: Учеб. пособие.-М.: Финансы и статистика, 1999.
   
5. Волков Е.А. Численные методы. - М.: Наука, 1982.
   
6. Воробьева Г.Н., Данилова А.Н. Практикум по вычислительной математике.- М.: Высш. шк., 1990
   
7. Демидович Б.Н., Марон И.А. Основы вычислительной математики.- М.: Наука, 1970.
   
8. Заварыкин В.М., Житомирский В.Г., Лапчик М.П. Численные методы.- М.: Просвещение, 1991
   
9. Калиткин Н.П. Численные методы.- М.: Наука, 1978.
   
10. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах.- М.: Наука, 1972.
    
11. Лапчик М.П., Рагулина М.И., Стукалов В.А. Численные методы: Учеб. пособие для пед. вузов.-М.: Академия, 2001.
    
12. Марчук Г.И. Методы вычислительной математики.- М.: Наука, 1989.
    
13. Мысовских И.П. Лекции по методам вычислений.-М.: Наука, 1993.
    
14. Ракитин В.И., Первушкин В.Е. Практическое руководство по методам вычислений с приложением программ для персональных компьютеров: Учеб. пособие.- М.: Высш. шк., 1998.
    
15. Самарский А.А., Гулин А.В. Численные методы.- М.: Наука, 1989.
    
16. Сборник задач по методам вычислений: Учеб. пособие: Для вузов/Под ред. П.И. Монастырного.-М.: Физматлит, 1994.
    
17. Тихонов А.Н., Костомаров Д.П. Вводные лекции по прикладной математике.- М.: Наука, 1984.
    
18. Хемминг Р.В. Численные методы для научных работников и инженеров. - М.: Наука, 1979.
    

Материально-техническое обеспечение дисциплины


Для выполнения лабораторного практикума необходимо следующее оборудование:

1. Персональный компьютер типа IBM PC с техническими характеристиками:
   
   1. Процессор Pentium IV с тактовой частотой 2 ГГц и выше;
      
   2. Оперативная память не менее 512 Мб;
      
   3. Жесткий диск не менее 40 Гб;
      
   4. Монитор 17’
      
   5. Дополнительное оборудование (по возможности)
      
      1. Принтер;
         
      2. Сканер;
         
      3. ^ CD, DVD-ROM.
         
2. На ПК должно быть установлено следующее программное обеспечение:
   
   1. Операционная система Windows (2000, WP и т.д.)
      
   2. Антивирусная программа (AVP, DrWeb и т.д.)
      
   3. Архиваторы (RAR, ZIP)
      
   4. Среды программирования(QBasic, Pascal, Delfi, C++ или др.)
      
   5. MS Office XP, 2003
      
   6. Математические пакеты MathCad, Maple, Statistica
      
   7. Система автоматизированного проектирования AutoCad
      

Методические рекомендации по организации изучения дисциплины


Курс освещает историю развития теории вычислительных методов линейной алгебры, основные понятия, свойства, применение в исследованиях и приложения в технических системах.

Наряду с методами численной реализации решений задач линейной алгебры рассматриваются методы решения задач математического анализа: метод половинного деления.

При реализации программы курса основные понятия и основные предложения (теоремы) должны иллюстрироваться примерами.


^ Лабораторный практикум проводится после изучения крупных разделов курса или же, наоборот, может предварять их изучение, создавая опытно-экспериментальный образ предстоящего теоретического материала.


Самостоятельная работа предполагает, что:

1. отдельные темы могут быть отнесены на самостоятельное изучение;
   
2. на лекциях предлагается значительное количество контрольных вопросов и упражнений, служащих для проверки усвоения теории;
   

Программа составлена в соответствии с государственными образовательными стандартами высшего профессионального образования по направлениям подготовки в области техники и технологии.

^ Словарь терминов и персоналий


Абсолютной погрешностью приближения х^* называется величина: 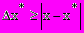, где х - точное значение некоторого числа, х^* - приближенное, т.е. точное значение числа х заключено в границах .


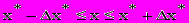Аппроксимацией называется замена одной функции другой близкой к исходной и обладающей "хорошими" свойствами, позволяющими легко производить над ней те или иные аналитические или вычислительные операции.


^ Вычислительной погрешностью называется погрешность, возникающая за счет округлений.


Ведущими (главными) элементами называются числа, на которые производится деление в методе Гаусса.


^ Вековым определителем называется определитель det(A-λE).


Второй интерполяционной формулой Ньютона называется формула вида

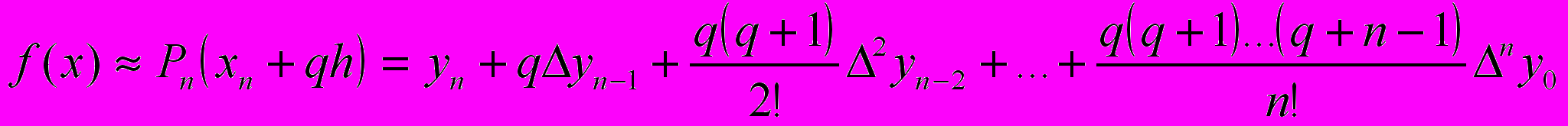, где .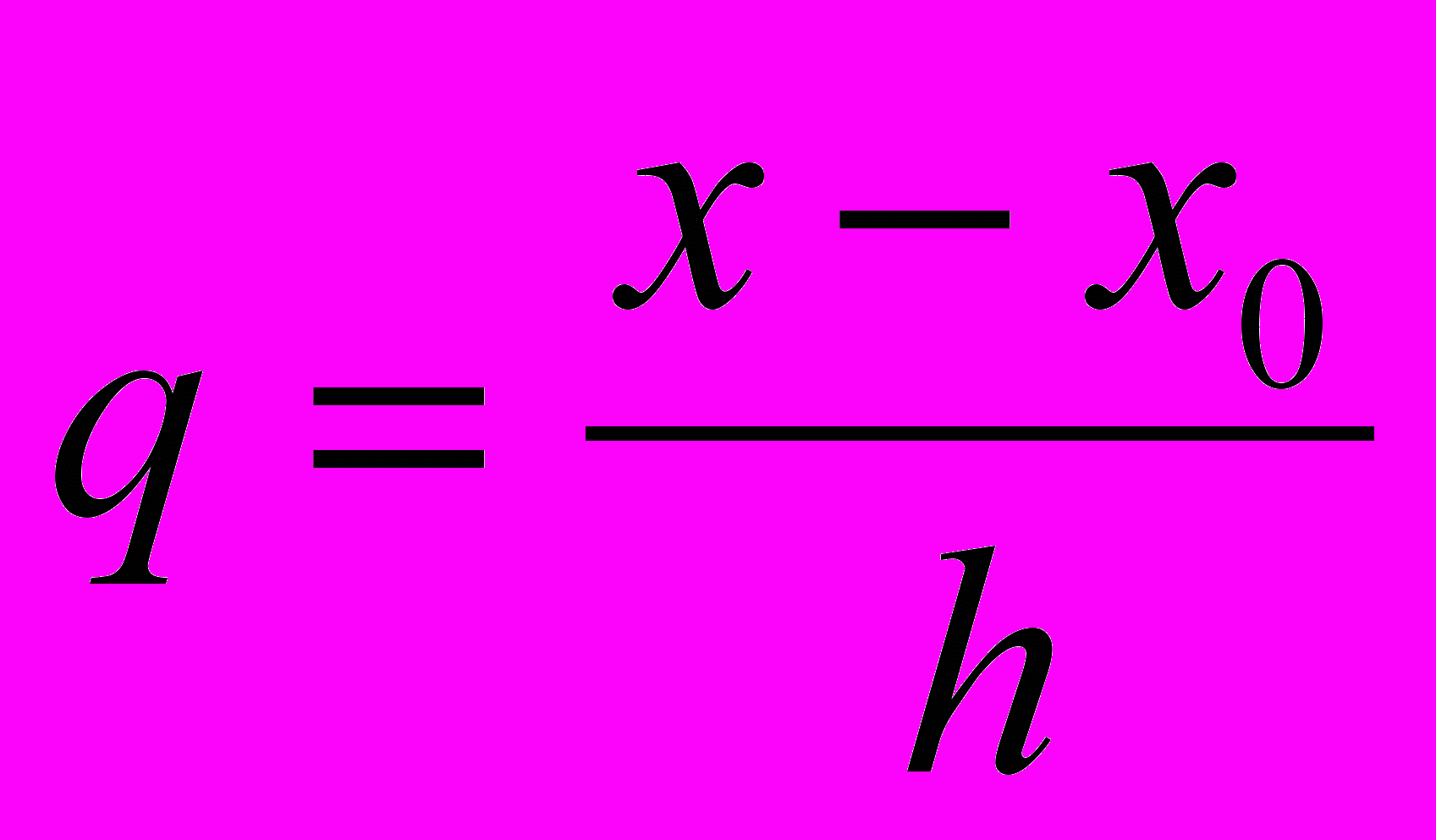


Значащими цифрами числа называются все цифры в его записи, начиная с первой ненулевой слева.


Интерполяцией функции f называется приближенное восстановление функции f по формуле .


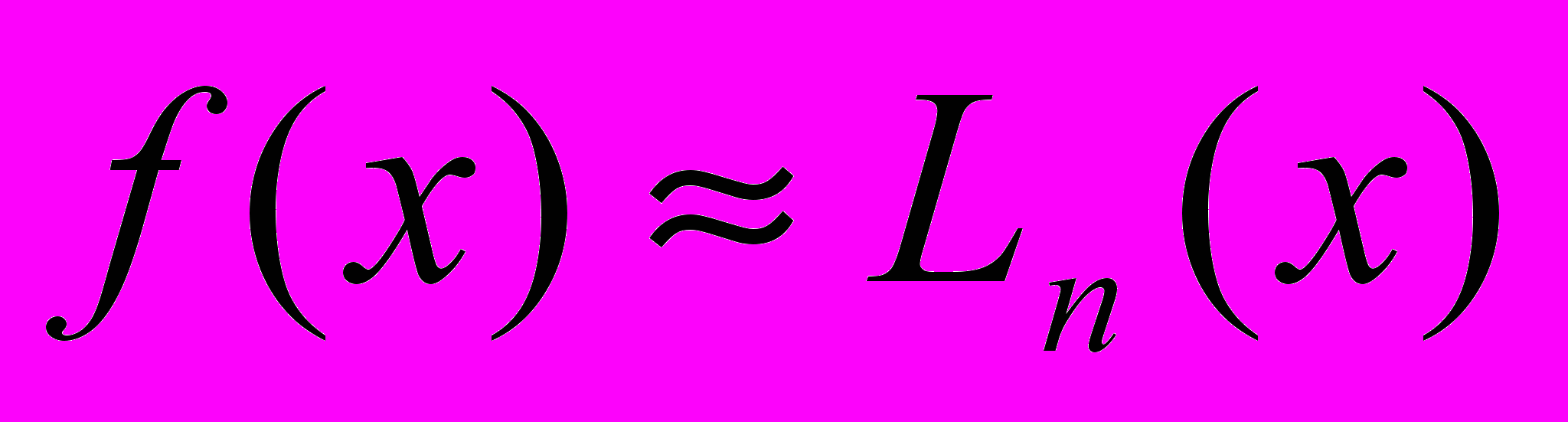^ Интерполяционным многочленом называется алгебраический многочлен L_n(x) степени n, который в точках x_i принимает заданные значения L_n(x_i) = f_i.


Интерполяционным сплайном называется кубический сплайн, принимающий в узлах х_i те же значения f_i, что и некоторая функция f.


Интерполяционным многочленом Лагранжа называется интерполяционный многочлен вида

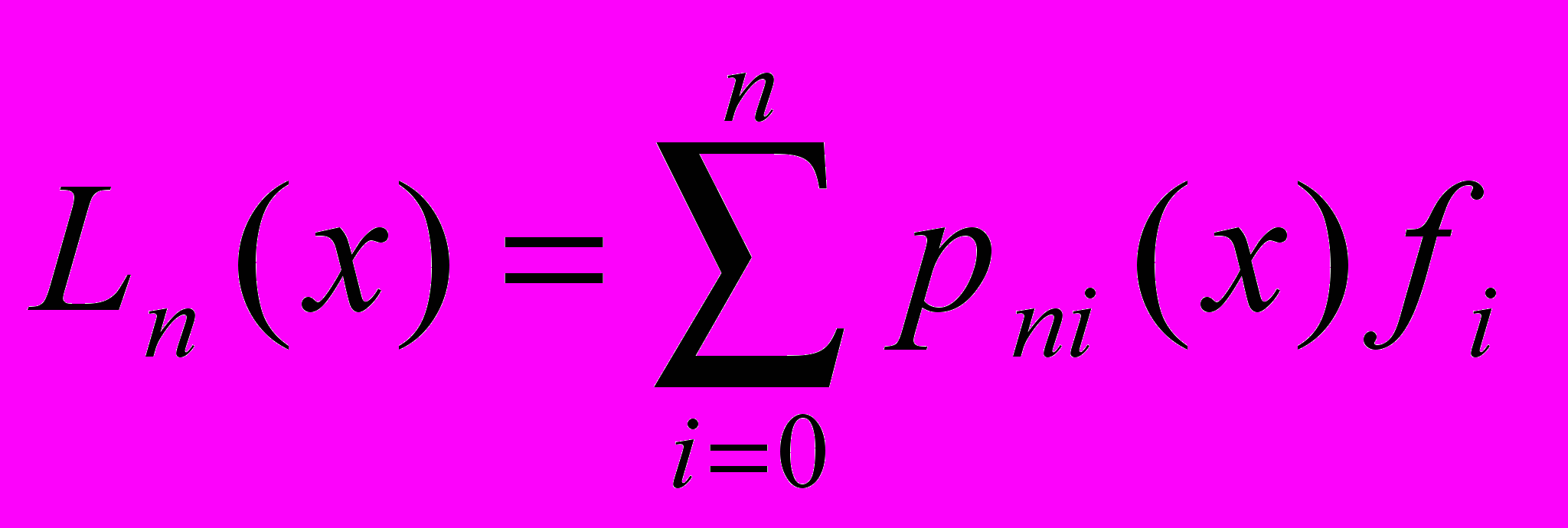, где 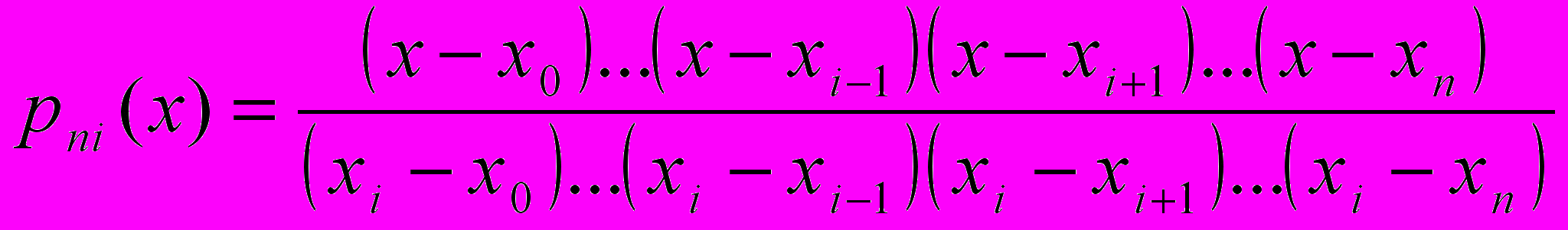, i=0, 1, …, n.


Итерационным методом называется метод, в котором точное решение может быть получено лишь в результате бесконечного повторения единообразных действий.


^ Матрицей с диагональным преобладанием называется матрица, элементы которой удовлетворяют условию: 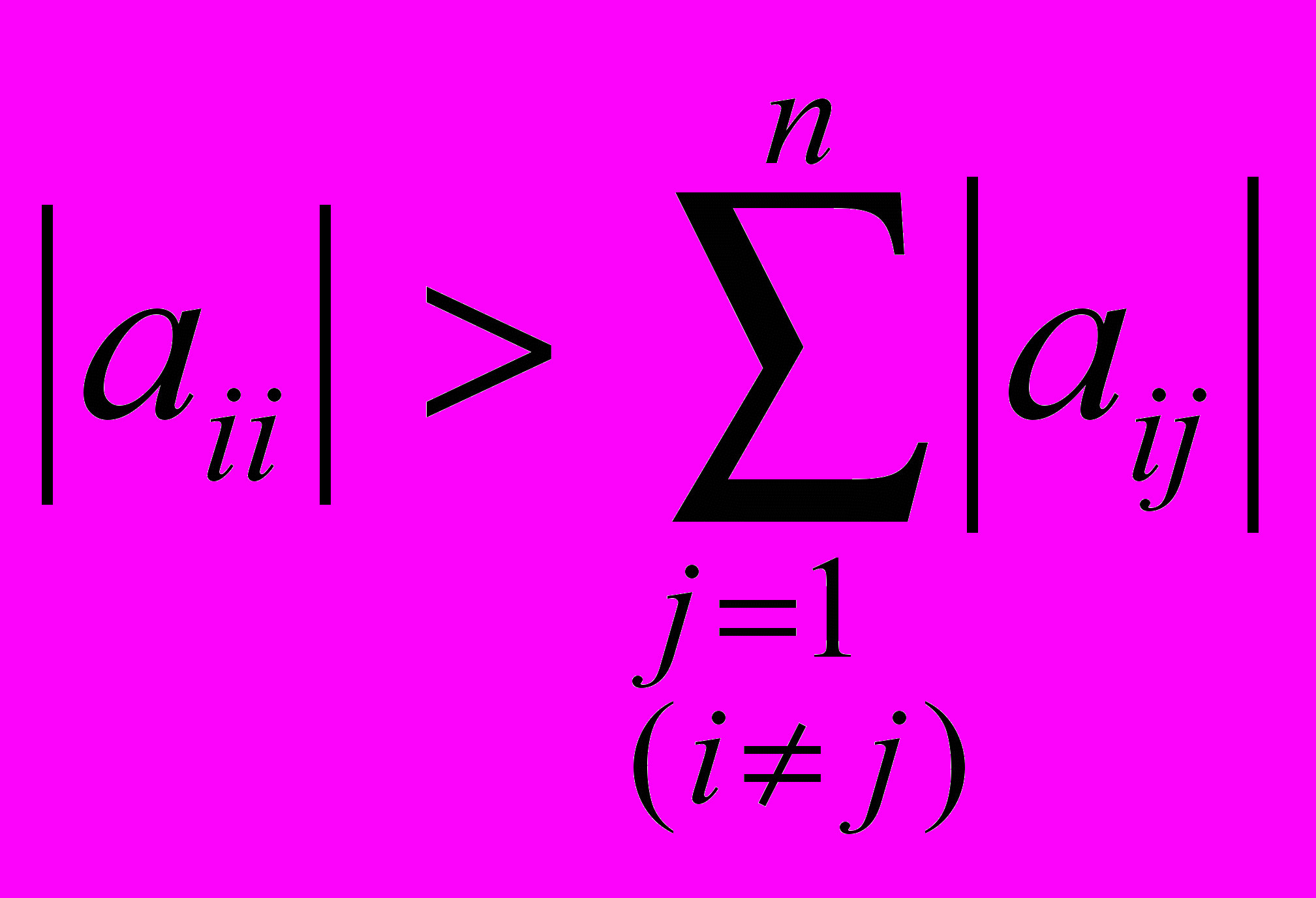i=1, 2,…n.


Метод Зейделя для системы линейных уравнений X=CX+D состоит в том, что итерации производятся по формуле

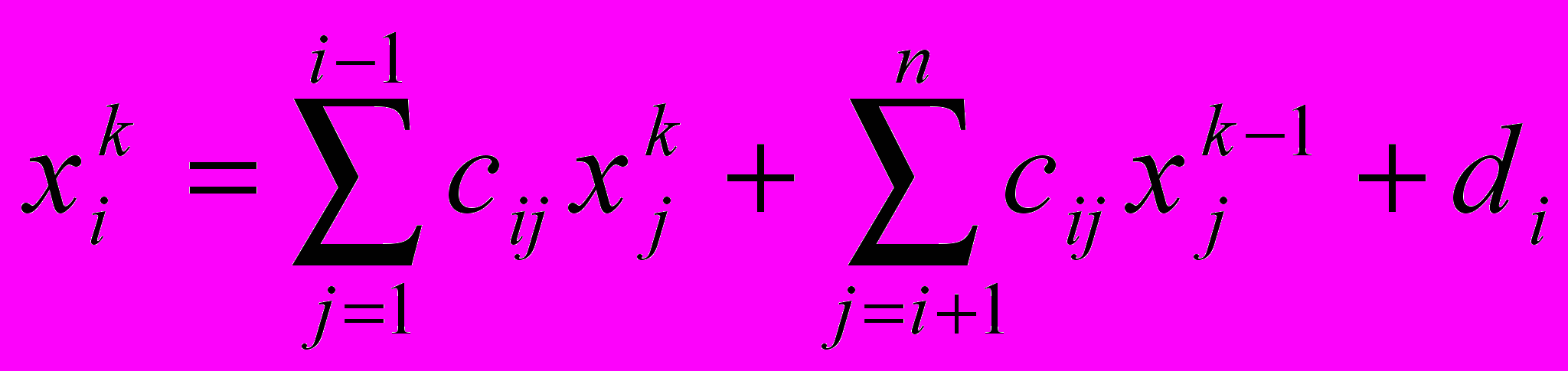, где x_i⁰ произвольны, i=1, 2,…, n, k=1, 2,…


Метод Ньютона (касательных) решения нелинейного уравнения f(x)=0 состоит в том, что итерации производятся по формуле .


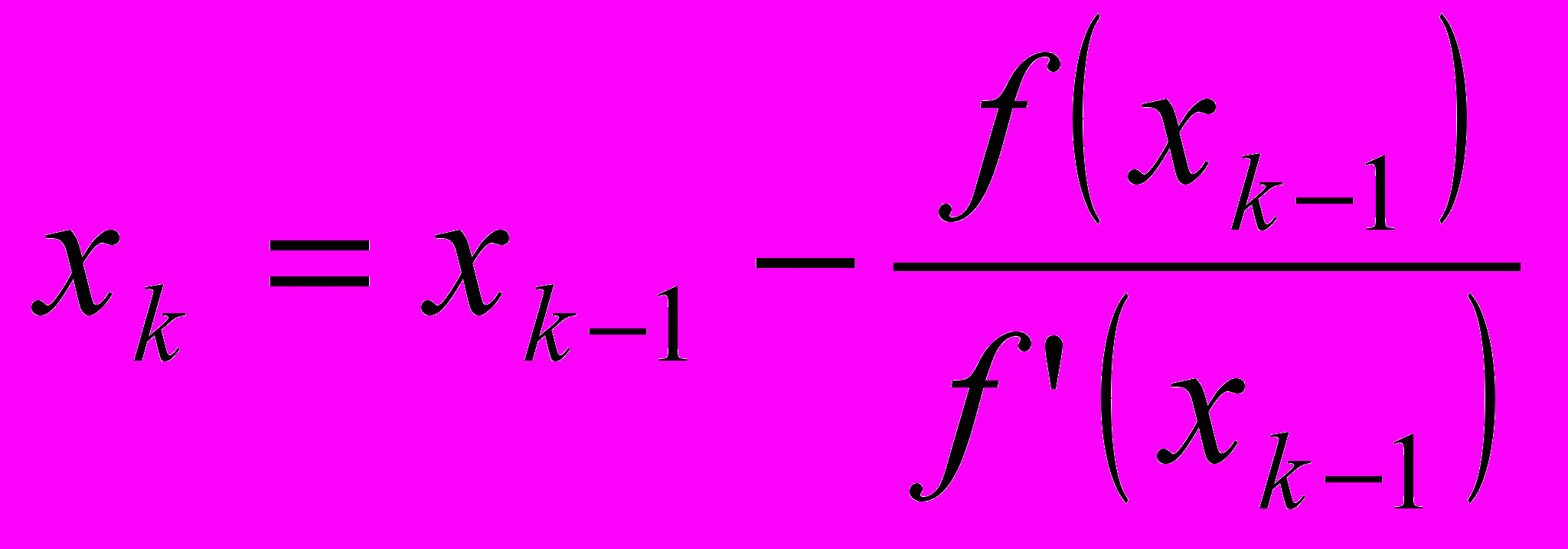^ Метод простых итераций для системы линейных уравнений X=BX+b состоит в том, что итерации производятся по формуле X^k = BX^k-1 +b , k=1, 2,…


Невязкой для системы линейных уравнений Ax=b называется величина b-Ax*.


Невязкой для уравнения f(x)=0 называется величина f(x_k+1) .


Относительной погрешностью называется отношение абсолютной погрешности к абсолютному значению приближенной величины: 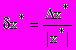, при условии, что .


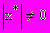Ошибкой для уравнения f(x)=0 называется разность корня x и приближенного решения

x* : x-x*.


Первой интерполяционной формулой Ньютона называется формула вида

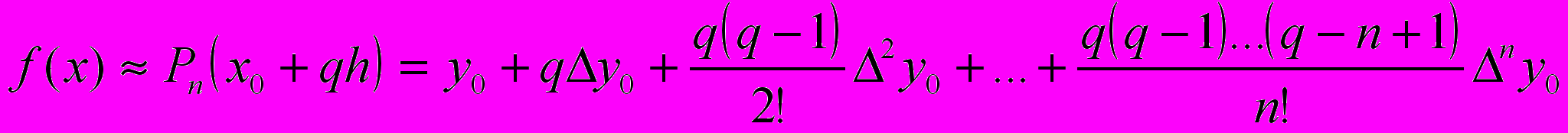, где .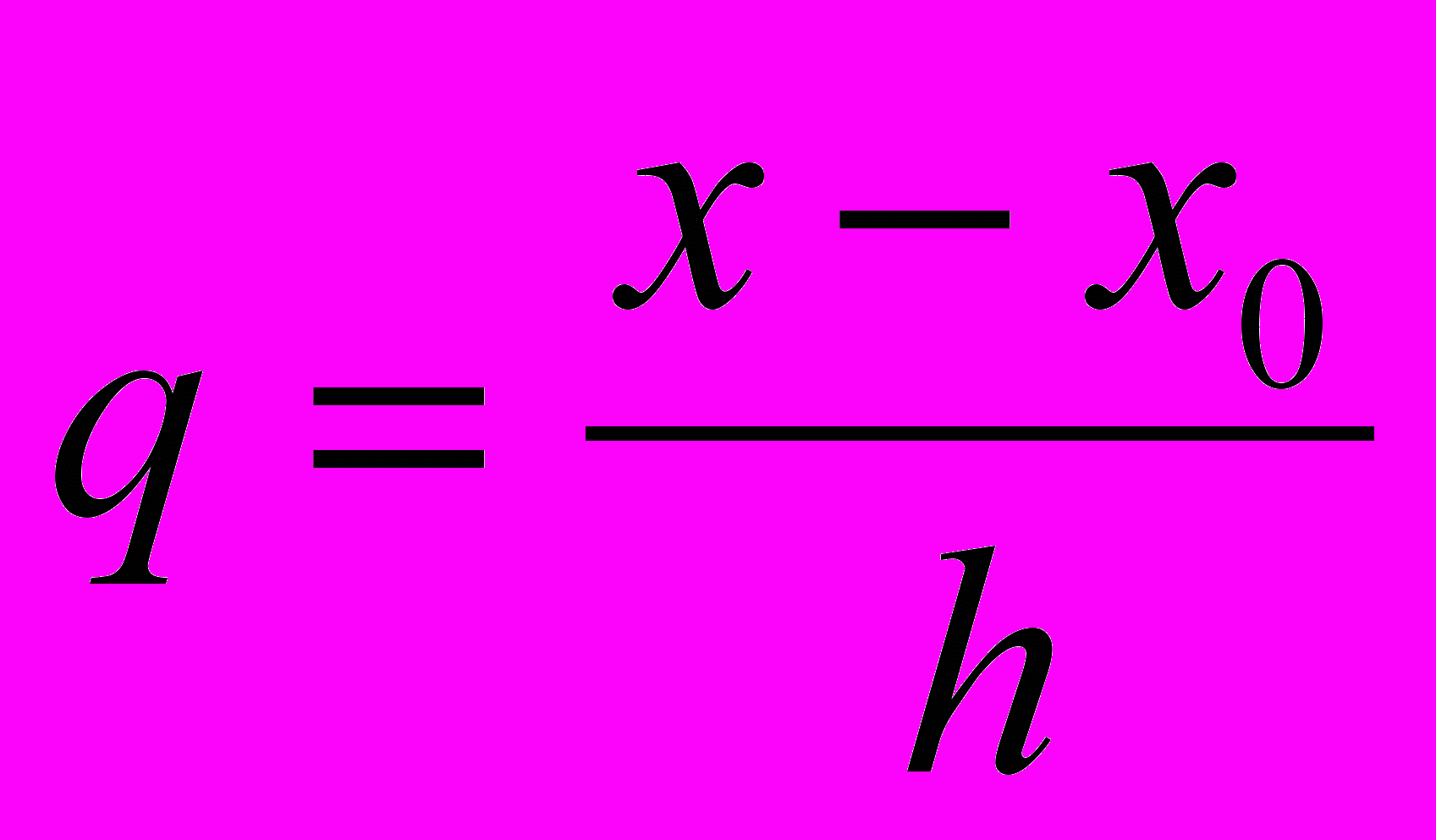


^ Полной проблемой собственных значений называется задача нахождения всех собственных значений и собственных векторов числовой матрицы.


Поправкой для элемента x_k+1 последовательности {x_k } приближений к корню x уравнения f(x)=0 называется величина x_r+1 – x_k .


Собственным вектором квадратной матрицы А называется такой вектор 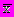, для которого выполняется соотношение: 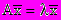, где  - собственное значение матрицы А.


Собственным значением квадратной матрицы А называется такое число , для которого выполняется соотношени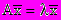е: , где 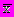- некоторый не нулевой вектор.


Сплайном называется функция, которая вместе с несколькими производными непрерывна на всем заданном отрезке [a, b], а на каждом частичном отрезке [x_i , x_i+1 ] в отдельности является некоторым алгебраическим многочленом.


Узлами интерполяции называются точки x_i , i=0, 1,…, n.


Упрощенный метод Ньютона (касательных) решения нелинейного уравнения f(x)=0 состоит в том, что итерации производятся по формуле

.


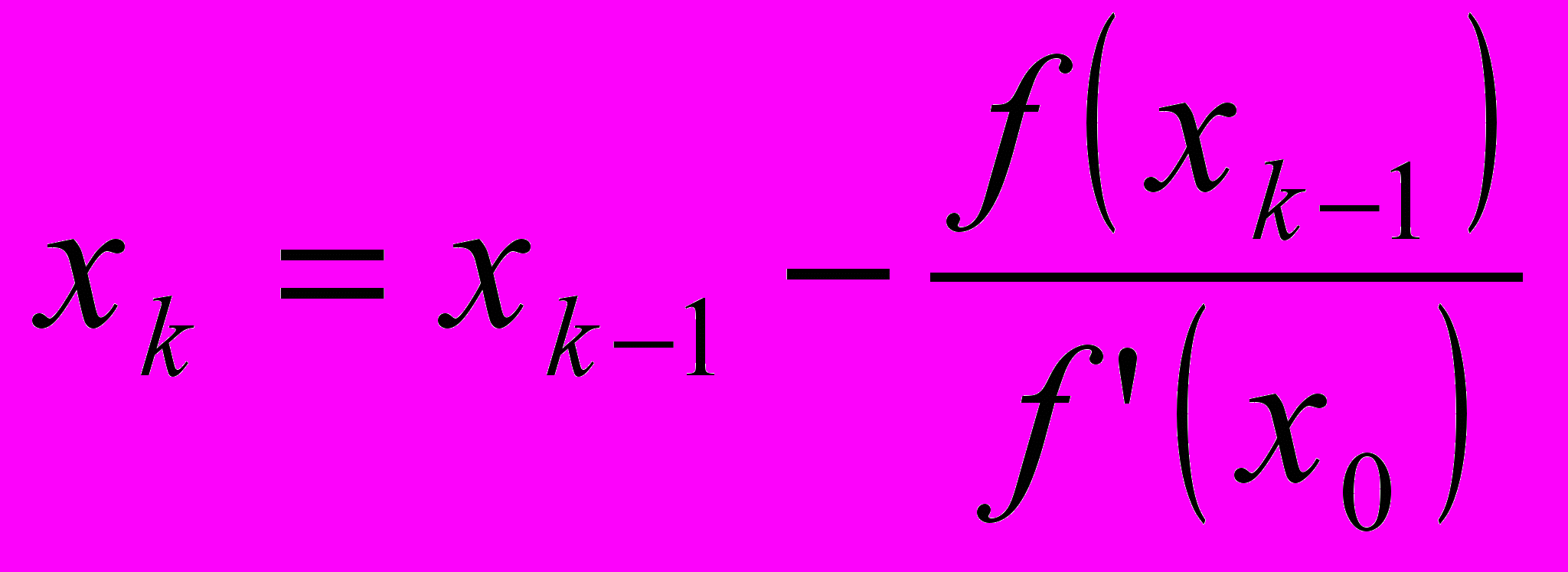^ Частичной проблемой собственных значений называется задача нахождения одного или нескольких собственных чисел  и соответствующих им собственных векторов.


Числом (мерой) обусловленности матрицы А называется положительное число

//А//∙//А^-1//=cond A.


Экстраполяцией называется приближенное восстановление функции f по формуле 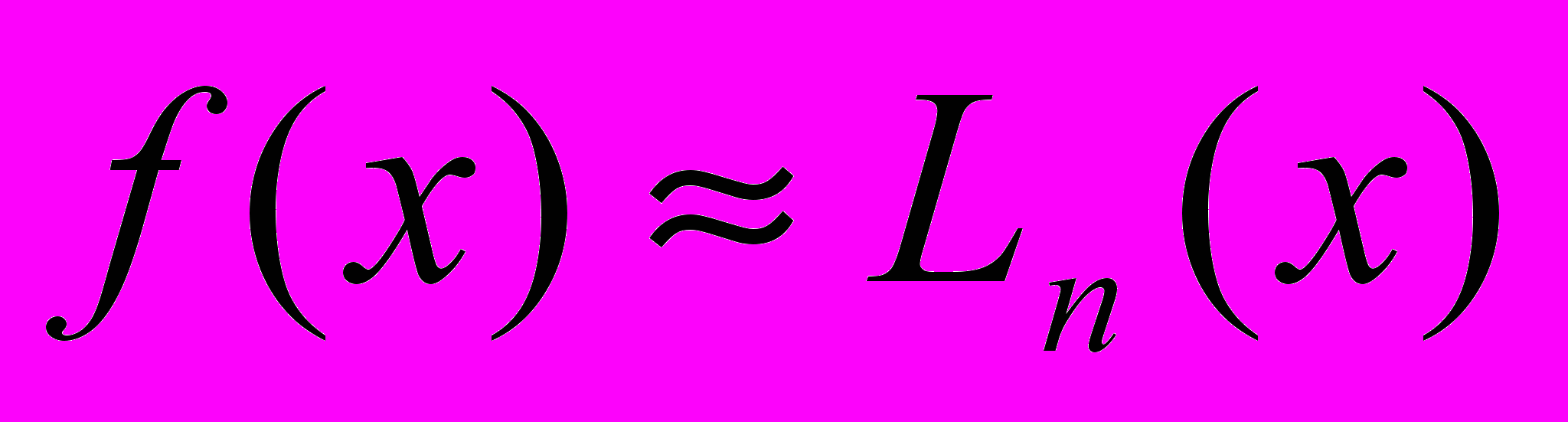, где x расположен вне минимального отрезка, содержащего все узлы интерполяции x₀ , x₁ ,…, x_n