Рабочая учебная программа по дисциплине «математический анализ» специальность
| Вид материала | Рабочая учебная программа |
- Рабочая учебная программа дисциплины (модуля) Математический анализ, 233.89kb.
- Рабочая программа учебной дисциплины «Математический анализ» Специальность «Математические, 187.35kb.
- Рабочая программа по дисциплине с 1 Математический анализ, 302.06kb.
- Российской Федерации " мати", 156.34kb.
- Рабочая программа дисциплины «Математический анализ ii» Направление, 132.24kb.
- Рабочая программа по дисциплине б 1математика. Математический анализ шифр и название, 259.57kb.
- Рабочая программа по курсу (дисциплине) "Математический анализ" для студентов фмф (специальность, 97.79kb.
- Программа по дисциплине математический анализ, 133.35kb.
- Рабочая программа по дисциплине «Учет и анализ банкротств» специальность 060500 «Бухгалтерский, 128.85kb.
- Рабочая учебная программа по дисциплине «Моделирование рынка ценных бумаг» ен., 282.34kb.
Федеральное агентство по образованию
Государственное образовательное учреждение
Высшего профессионального образования
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ УНИВЕРСИТЕТ
Филиал в г. Воскресенске
Кафедра Прикладной математики
«УТВЕРЖДАЮ»
Зав. кафедрой
ктн, профессор Баринов А.Н.
«__» ______________200_г.
РАБОЧАЯ УЧЕБНАЯ ПРОГРАММА
по дисциплине «МАТЕМАТИЧЕСКИЙ АНАЛИЗ»
специальность 080116 «Математические методы в экономике»
(второй год обучения)
Составитель: старший преподаватель кафедры Прикладной математики Меньшова И.В.
Рассмотрено на заседании кафедры
Протокол №__
от «__» ______________200_г.
Воскресенск, 2010
-
Рабочая учебная программа
ВВЕДЕНИЕ
В современной науке и технике математические методы исследования, моделирования и проектирования играют всё большую роль. Это обусловлено совершенствованием вычислительной техники, благодаря которой существенно расширяется возможность успешного применения математики при решении конкретных задач.
Курс «Математического анализа» является фундаментом математического образования экономиста-математика и имеет важное значение для успешного изучения таких дисциплин, как «Теория вероятностей», «Математическая статистика», «Исследование операций», «Эконометрика», «Экономическая теория» и др., предусмотренных учебным планом.
Данная программа построена в соответствии с требованиями Государственного образовательного стандарта высшего профессионального образования к дисциплине «Математический анализ». Учебная программа разработана на основе учебного плана специальности 061800 «Математические методы в экономике».
Выписка из Государственного образовательного стандарта высшего профессионального образования ОПД.Ф.ОО. МАТЕМАТИЧЕСКИЙ АНАЛИЗ.
Множество. Окрестность точки. Функциональная зависимость. Предел числовой последовательности. Предел функции. Эквивалентные функции. Непрерывность функции в точке. Числовые множества и последовательности. Непрерывные функции. Производная и дифференциал. Дифференцируемые функции. Выпуклость функции. Неопределенный, определенный и несобственные интегралы. Функции нескольких переменных. Приложения к общей экономической теории. Кратные интегралы. Неявная функция. Выпуклые функции. Функциональные последовательности и ряды. Степенные ряды. Дифференциальные уравнения. Обыкновенные разностные уравнения.
-
Организационно-методический раздел
Курс «Математический анализ» читается студентам специальности 080116 «Математические методы в экономике» в первом, втором, третьем и четвертом семестрах.
-
Цель курса
Цель курса "Математический анализ" - ознакомление с фундаментальными методами исследования переменных величин посредством анализа бесконечно малых, основу которого составляет теория дифференциального и интегрального исчисления. Объектами изучения в данной дисциплине являются, прежде всего, функции. С их помощью могут быть сформулированы как законы природы, так и разнообразные процессы, происходящие в экономике. Отсюда объективная важность математического анализа как средства изучения функций. Дисциплина "Математический анализ" отражает важное направление развития современной математики, в ней рассматриваются вопросы, связанные с методами вычислений.
-
Задачи курса
Основные задачи изучения данного курса заключаются в приобретении студентами теоретических знаний и практических навыков по следующим направлениям: развитие у студентов творческого и логического мышления, подготовка студентов к умению точной математической постановки изучаемой экономической проблемы и ее решению с помощью современной вычислительной техники.
-
Место курса в профессиональной подготовке выпускника
Курс «Математический анализ» на втором годе обучения изучается общим объёмом 154 часа специальностью 061800 «Математические методы в экономике».
Усвоение курса в третьем и четвертом семестрах основано на знаниях, полученных при изучении курса «Математического анализа», читаемого в первом и втором семестрах. В свою очередь дисциплина является базовой для таких дисциплин, как «Теория вероятностей и математическая статистика», «Экономическая теория», «Исследование операций», «Эконометрика» и др.
Курс изучается в форме лекций и практических занятий. В ходе практических занятий студент должен приобрести навыки решения типовых задач с применением изучаемого теоретического материала. Предусмотрена самостоятельная подготовка студентов. Они выполняют индивидуальные задания, сдают экзамен.
В целом, изучение дисциплины направлено на подготовку студентов специальности «Математические методы в экономике» к умению применять методы математического анализа к решению конкретных экономических задач на микро- и макроуровне.
-
Требования к уровню освоения содержания курса
В результате изучения дисциплины студенты должны:
- знать основные определения и понятия изучаемых разделов математического анализа, уметь формулировать и доказывать основные результаты этих разделов.
- уметь анализировать функции, заданные в виде графика, таблицы или уравнения, а также понимать связь между различными формами представления функций; понимать смысл производной как скорость изменения и локального линейного приближения, а также уметь применять производную для решения широкого круга прикладных задач в экономике;
- понимать смысл определенного интеграла как предела интегральной суммы и как итоговое изменение величины, а также уметь применять интегралы для решения широкого круга прикладных задач в экономике; понимать взаимосвязь между производной и определенным интегралом; уметь, исходя из описания простой физической или экономической задачи, построить математическую модель явления, используя функцию, дифференциальное уравнение или интеграл;
- использовать методы математического анализа для решения задач, обоснования результатов расчётов и рассуждений.
2.Содержание курса (второй год обучения)
2.1. Темы и краткое содержание
Тема 1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Понятие функции нескольких действительных переменных. Область определения. Линии и поверхности уровня. Элементарные функции нескольких переменных. Предел функции в точке. Непрерывность функции. Теоремы Вейерштрасса. Равномерная непрерывность функций.
Частные производные функции нескольких переменных. Дифференцируемость функции в точке. Связь дифференцируемости с существованием частных производных. Геометрический смысл дифференцируемости. Дифференцируемость сложных функций и инвариантность формы первого дифференциала. Приращение функции в данном направлении. Производная по направлению. Градиент. Производные и дифференциалы высших порядков. Теорема о равенстве смешанных производных. Неявные функции. Теоремы существования, дифференцируемости неявных функций. Вычисление производных неявных функций.
Экстремум функции нескольких переменных. Необходимые условия экстремума в терминах первого дифференциала. Достаточные условия экстремума. Понятие об условном экстремуме. Общая схема отыскания наибольших и наименьших значений функции нескольких переменных.
Эмпирические формулы. Метод наименьших квадратов. Нахождение методом наименьших квадратов коэффициентов квадратичной и линейной зависимостей.
Функции нескольких переменных в экономическом анализе. Производственная функция. Функция полезности. Предельная полезность. Предельная норма замещения. Кривые безразличия.
Тема 2. ИНТЕГРИРОВАНИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Двойные и тройные интегралы Римана. Условие интегрируемости функции и классы интегрируемых функций. Свойства интеграла Римана. Сведение кратных интегралов к повторным. Замена переменных. Общая схема применения кратных интегралов Римана к задачам геометрии.
Тема 3. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
3.1. Дифференциальные уравнения первого порядка.
Частные и общие решения. Задача Коши. Теорема существования и единственности решения задачи Коши. Основные классы уравнений, интегрируемых в квадратурах: уравнения с разделяющимися переменными, однородные, линейные, Бернулли, в полных дифференциалах. Математические модели экономической динамики с непрерывным временем.
3.2. Дифференциальные уравнения высших порядков.
Задача Коши. Уравнения, допускающие понижения порядка. Линейные дифференциальные уравнения высших порядков, однородные и неоднородные. Структура общего решения. Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами.
3.3. Системы дифференциальных уравнений.
Нормальная система дифференциальных уравнений. Задача Коши. Теорема существования и единственности решения задачи Коши. Метод исключения для решения нормальных систем дифференциальных уравнений. Системы линейных дифференциальных уравнений. Решение систем линейных дифференциальных уравнений с постоянными коэффициентами.
3.4. Разностные уравнения.
Задача Коши. Линейные разностные уравнения. Модели экономической динамики с дискретным временем.
2.2. Распределение часов дисциплины по темам и формам занятий
| № п/п | Наименование тем | Всего часов | Аудиторные занятия (в том числе) | Самостоятельная работа | |
| лекции | ПЗ | ||||
| 1 | ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ | 31 | 9 | 8 | 14 |
| 2 | ИНТЕГРИРОВАНИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ | 26 | 5 | 5 | 16 |
| 3 3.1 3.2 3.3 3.4 | ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ Дифференциальные уравнения первого порядка. Дифференциальные уравнения высших порядков. Системы дифференциальных уравнений. Разностные уравнения. | 28 23 19 23 | 6 6 4 2 | 14 9(1час к.р.) 7 6 | 8 8 8 15 |
| ВСЕГО по курсу | 154 | 34 | 51 | 69 | |
2.3. Основные виды занятий и особенности их проведения при изучении данного курса
2.3.1. Лекционные занятия
Лекции построены как типичные лекционные занятия по математическому анализу в соответствии с требованиями государственного стандарта для подготовки специалистов специальности 061800 «Математические методы в экономике».
Недельная аудиторная нагрузка составляет два часа в третьем семестре и один час - в четвертом. На лекции преподаватель излагает теоретический материал, который по мере необходимости иллюстрируется примерами.
2.3.2. Практические занятия
Занятия по практике построены как типичные практические занятия по математическому анализу в соответствии с требованиями государственных стандартов для подготовки специалистов специальности 061800 «Математические методы в экономике». Недельная аудиторная нагрузка составляет два часа в каждом семестре изучения дисциплины. На практических занятиях студент под руководством преподавателя изучает методы решения конкретных задач математического анализа и приобретает навыки решения этих задач.
2.4. Взаимосвязь аудиторной и самостоятельной работы студентов при изучении курса
В ходе изучения курса математического анализа студент слушает лекции по большинству тем, посещает практические занятия, занимается индивидуально. Индивидуальные занятия включают закрепление тем, изучаемых аудиторно, и самостоятельное изучение некоторых тем. Освоение курса предполагает, помимо посещения лекций и практических занятий, выполнение аудиторных контрольных работ. Особое место в овладении данным курсом отводится самостоятельной работе по решению текущих и индивидуальных домашних заданий. Учебным планом предусмотрены консультации, которые студент может посещать по желанию.
-
Формы промежуточного и итогового контроля
Курс «Математического анализа» завершается экзаменом в каждом из двух семестров. Обязательным условием допуска студента к экзамену является успешное выполнение индивидуальных домашних заданий и аудиторных контрольных работ. Экзамен проводится в письменно-устной форме. В экзаменационные билеты включаются теоретические и практические вопросы. Для успешной сдачи экзамена студент должен продемонстрировать знание основных теоретических положений курса «Математического анализа» и показать свои навыки применения теории при решении конкретных практических задач. После выполнения письменной части студент делает необходимые пояснения. При спорности выставляемой оценки студент отвечает на дополнительные вопросы преподавателя.
-
Учебно-методическое обеспечение дисциплины
Рекомендуемая литература (основная).
- Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов, Т.1, 2: Учебное пособие для втузов. – М.: Наука
- Берман Г.Н. Сборник задач по курсу математического анализа: Уч. пособие. – СПб., Изд-во – Профессия.
- Математика в экономике: Учебник: В 2-х ч. Ч.1,2/ А.С. Солодовников, В.А. Бабайцев, А.В. Браилов, И.Г. Шандро. – М.: Финансы и статистика.
- Сборник задач по высшей математике. 1,2 курс/ [К.Н. Лунгу и др.] ; под ред. С.Н. Федина. – М.: Айрис-пресс.
-
Рекомендуемая литература (дополнительная).
- Ильин В.А., Позняк Э.Г. Основы математического анализа: Учеб.: В 2 ч.: М., Наука, 1982.
- Ильин В.А., Садовничий В.А., Сендов Бл.Х. Математический анализ: Учеб.: М., Наука, 1979. 719 с.
- Ильин В.А., Садовничий В.А., Сендов Бл.Х. Математический анализ: Учеб.: В 2 ч. М.: Изд-во Моск. Ун-та, 1985-1987.
- Кудрявцев Л.Д. Курс математического анализа: Учеб.: В 2-х т. М.: Наука, 1981.
- Никольский С.М. Курс математического анализа: Учеб.: В 2-х т. М.: Наука, 1983.
- Натансон И.П. Теория функций вещественной переменной: Учеб. пособие. М.: Наука, 1974. 480 с.
- Демидович Б.П. Сборник задач и упражнений по математическому анализу: Учеб. пособие. М.: Наука, 1979.527 с.
- Кудрявцев Л.Д. и др. Сборник задач по математическому анализу: Учеб. пособие: В 2 ч. М.: Наука, 1984-1986.
- Смирнов В.И. Курс высшей математики: Учеб.: В 4 т. М.: Наука, 1981. Т. 1-2.
- Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления: Учеб. пособие. В 3 т. М.: Наука, 1969-1970.
-
Материалы, устанавливающие содержание и порядок проведения промежуточных и итоговых аттестаций.
Вопросы к экзамену II курс (3 семестр)
- Дайте определение функции двух переменных, ее области определения и области значений. Приведите примеры функций нескольких переменных в экономике.
- Дайте определения линий и поверхностей уровня. Приведите примеры линий уровня в экономике.
- Как определяется расстояние между точками в n-мерном пространстве?
- Дайте определения ε-окрестности и ограниченного множества в n-мерном пространстве.
- Дайте определения внутренней, внешней и граничной точек n-мерного пространства.
- Дайте определения открытого и замкнутого множеств.
- Дайте определения предела функции двух переменных в точке.
- Дайте определение непрерывности в точке функции двух переменных.
- Что называется полным и частичным приращениями функции двух переменных.
- Дайте определение частной производной для функции двух переменных и объясните ее геометрический смысл.
- Докажите достаточное условие дифференцируемости функции.
- Сформулируйте понятие полного дифференциала функции двух переменных.
- Дайте определение сложной функции для функции двух переменных.
- Докажите правило нахождения производной сложной функции.
- Дайте определение производной по направлению функции двух переменных.
- Что называется градиентом функции двух переменных?
- Докажите основное свойство градиента.
- Как определяются предельная полезность и предельная норма замещения?
- Дайте определения эластичности функции двух переменных в точке.
- Объясните смысл коэффициентов производственной функции Кобба-Дугласа.
- Дайте определение однородной функции.
- Приведите формулу Эйлера.
- Как определяются частные производные высших порядков?
- Дайте определение точки экстремума функции двух переменных.
- Докажите необходимое условие экстремума функции двух переменных.
- Сформулируйте достаточное условие экстремума функции двух переменных.
- В чем заключается метод множителей Лагранжа нахождения условного экстремума функции двух переменных?
- Дайте определение эмпирических формул.
- В чем заключается метод наименьших квадратов?
- Выведите формулу для нахождения методом наименьших квадратов коэффициентов линейной функции.
- Дайте определение двойного интеграла и укажите его геометрический смысл для неотрицательной функции.
- Перечислите основные свойства двойного интеграла (линейность, аддитивность, монотонность, оценка, среднее значение).
- Как двойной интеграл вычисляется в декартовых координатах?
- Как производится замена переменных в двойном интеграле?
- Как двойной интеграл вычисляется в полярных координатах?
- Перечислите геометрические приложения двойного интеграла.
2. Вопросы к экзамену II курс (4 семестр)
- Понятие дифференциального уравнения, его общее и частное решения. Интегральная кривая. Порядок дифференциального уравнения.
- Общий вид дифференциального уравнения I порядка, его геометрический смысл. Изоклины.
- Теорема о существовании и единственности решения задачи Коши для дифференциального уравнения I порядка. Геометрический смысл задачи Коши. Особые решения.
- Дифференциальные уравнения с разделяющимися переменными: общий вид; нахождение решения.
- Автономные дифференциальные уравнения. Теорема о решении автономного дифференциального уравнения, её геометрический смысл. Стационарное решение.
- Модель естественного роста. Модель естественного роста в условиях конкурентного рынка.
- Неоклассическая модель роста.
- Однородные дифференциальные уравнения I порядка: общий вид; нахождение решения.
- Линейные уравнения I порядка. Уравнение Бернулли. Метод Бернулли. Метод Лагранжа (вариации произвольной постоянной).
- Уравнение в полных дифференциалах. Интегрирующий множитель Необходимое и достаточное условие полного дифференциала.
- Дифференциальные уравнения высших порядков. Теорема о существовании и единственности решения задачи Коши для дифференциальных уравнений высших порядков. Общий и частный интегралы.
- Уравнения, допускающие понижение порядка: общий вид; нахождение решения.
- Линейные дифференциальные уравнения высших порядков. Линейный оператор n-го порядка. Свойство линейного оператора.
- Теорема о решении линейного неоднородного уравнения.
- Свойство линейных уравнений.
- Линейные однородные дифференциальные уравнения. Определитель Вронского. Теорема о значении определителя Вронского в случае линейно независимых решений.
- Фундаментальный набор решений. Теорема об общем решении линейного однородного дифференциального уравнения.
- Линейные однородные дифференциальные уравнения с постоянными коэффициентами: общий вид; характеристическое уравнение; нахождение решения.
- Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами. Метод вариации произвольной постоянной.
- Линейные неоднородные дифференциальные уравнения. Метод неопределённых коэффициентов.
- Системы дифференциальных уравнений. Решение системы дифференциальных уравнений. Теорема о существовании и единственности решения задачи Коши для систем дифференциальных уравнений.
- Метод сведения системы к одному дифференциальному уравнению.
- Решение однородных линейных систем с постоянными коэффициентами.
- Решение неоднородных линейных систем с постоянными коэффициентами.
- Разностные уравнения.
- Линейные разностные уравнения. Фундаментальный набор решений. Теоремы о нахождении решений линейных разностных уравнений. Определитель Казоратти.
- Модель Самуэльсона - Хикса.
- Паутинная модель рынка.
- Задача об определении текущей стоимости купонной облигации.
-
Задачи к экзамену II курс (3 семестр)
1. Найти область определения функций:
а) z =
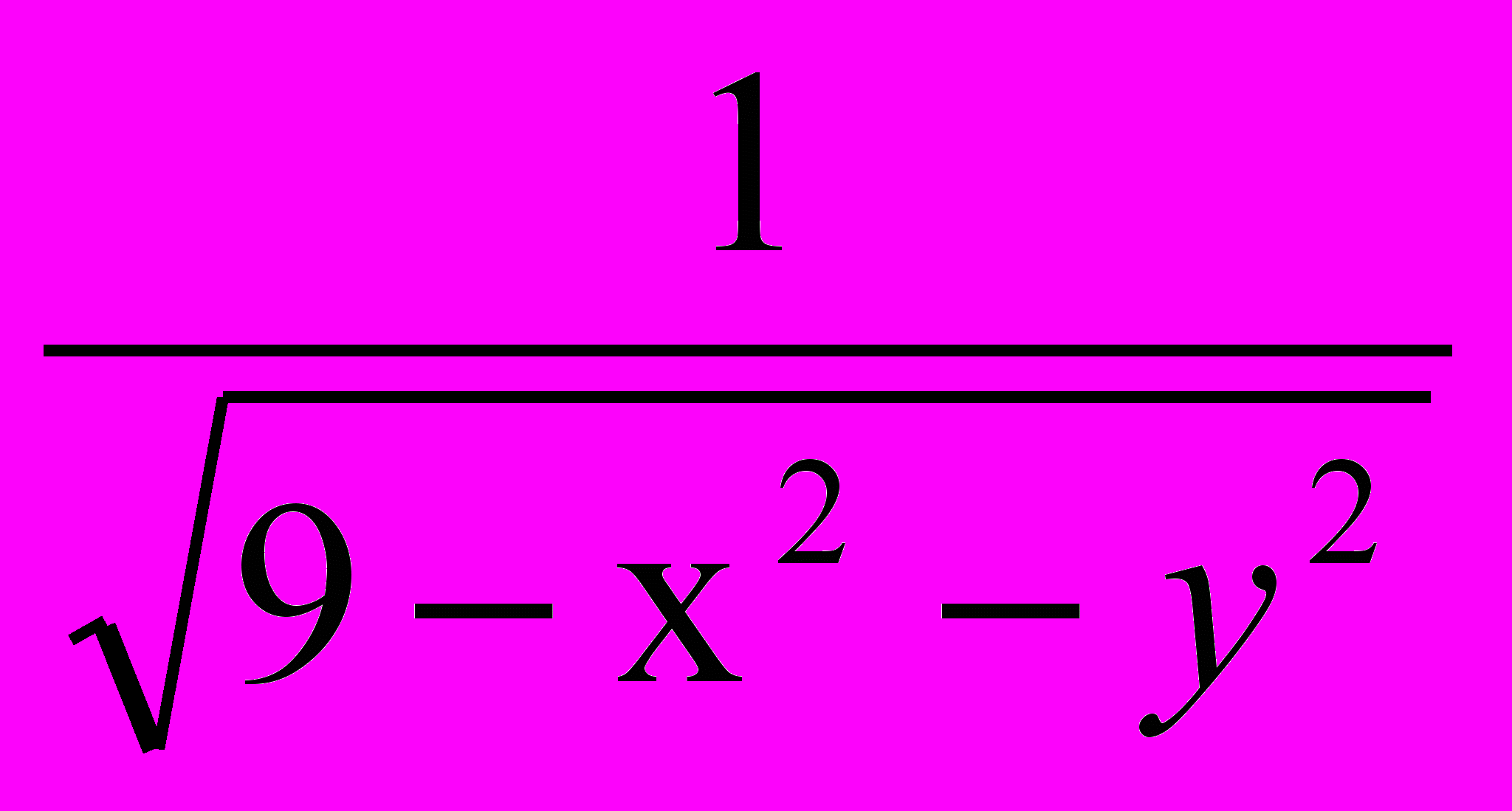 ; б) z = arcsin(x + y);
; б) z = arcsin(x + y);в) u = ln(x2 + y2 + z2 – 1); г) u =
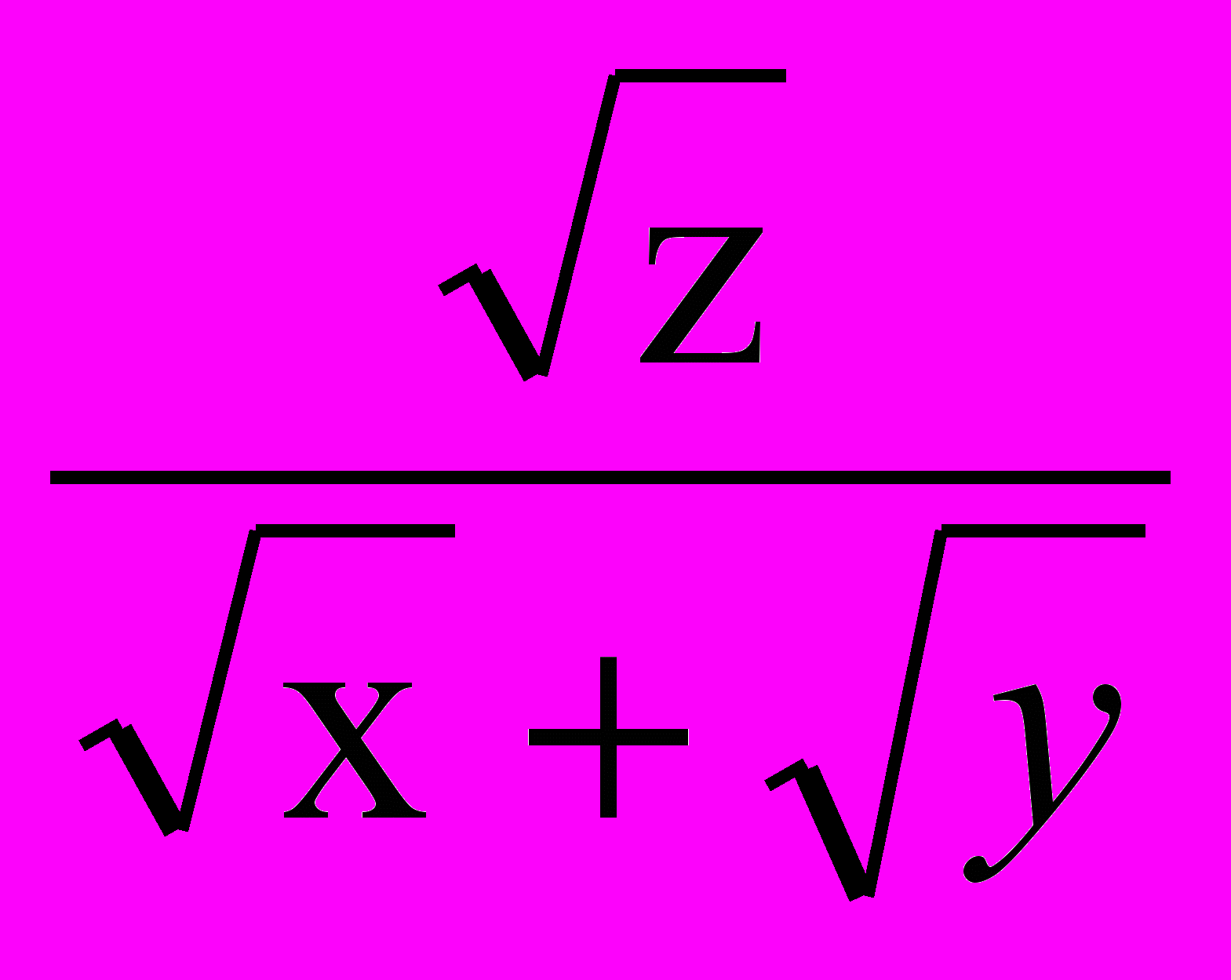 ;
;д) z =
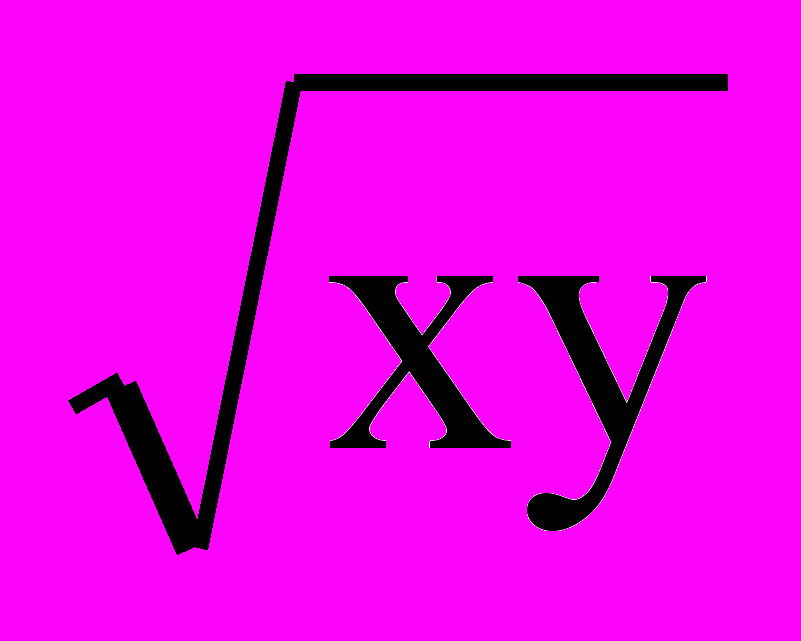 .
.2. Построить линии уровней следующих функций (для z = 1, 2, 3):
а) z = x + y; б) z = x2 – y2;
в) z = x2 + y2 – 3; г) z =
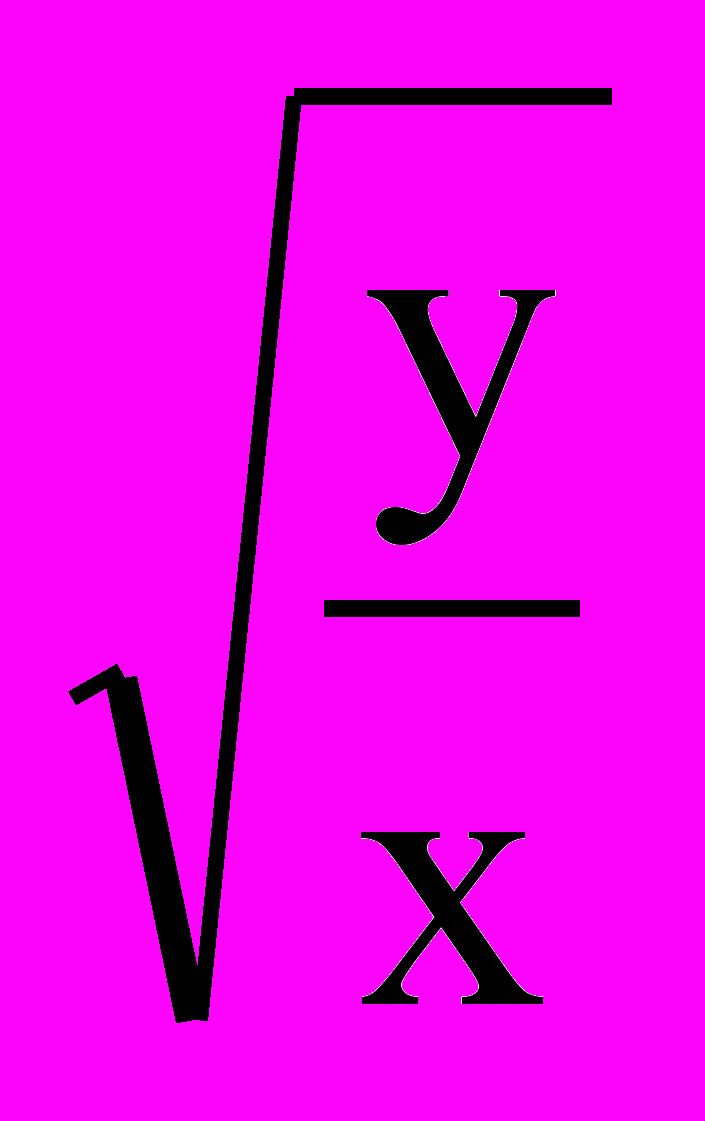 ;
;д) z =
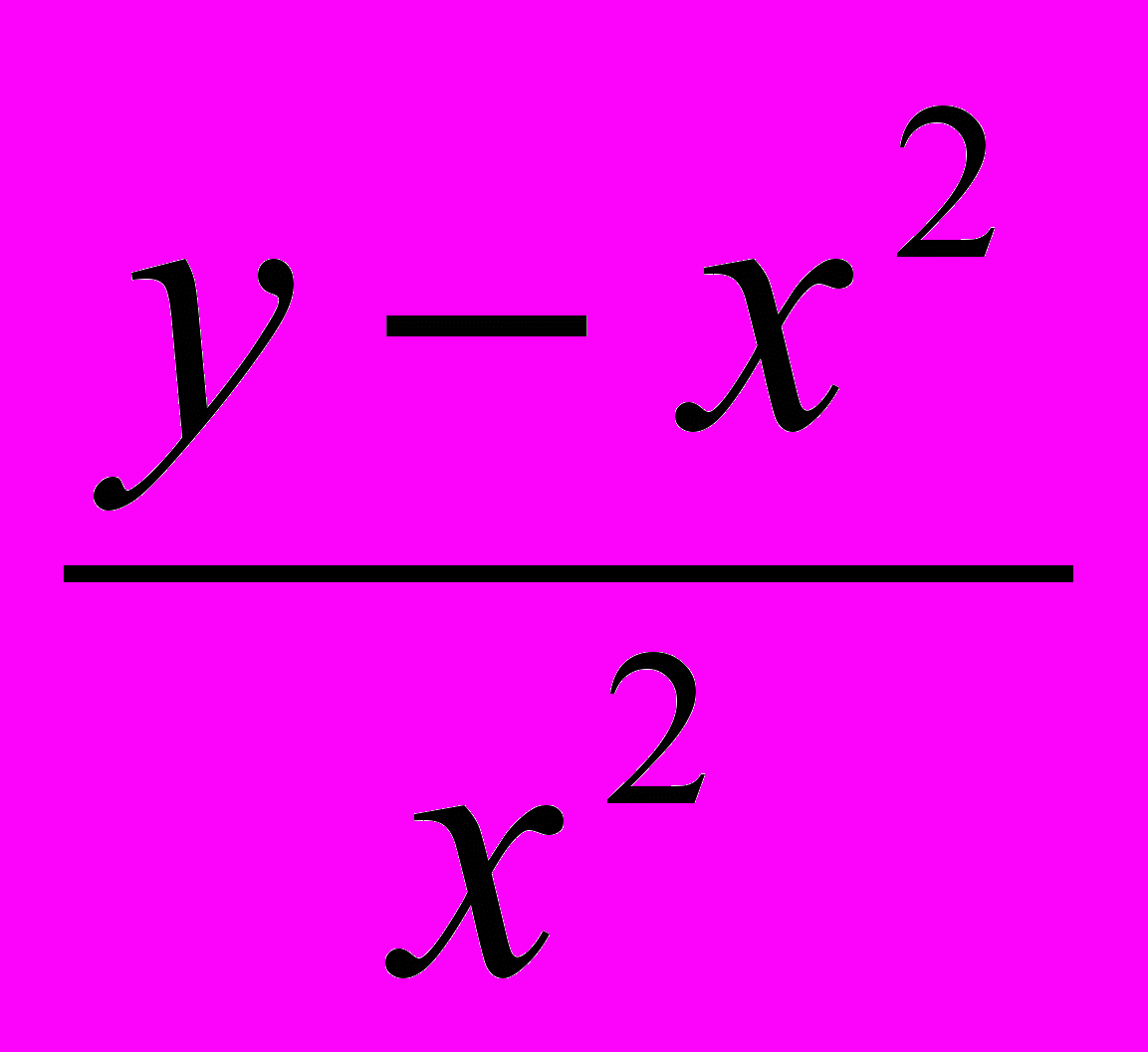 ; е) z = ln(xy);
; е) z = ln(xy);ж) z = exy.
3. Построить поверхности уровней функций (для u = 0, 1, 2):
а) u = 2x + y + 3z;
б) u = x2 + y2 + z2;
в) u = 4x2 + 9y2 + z2.
4. Показать, что данные функции удовлетворяют приведенным
уравнениям:
а)
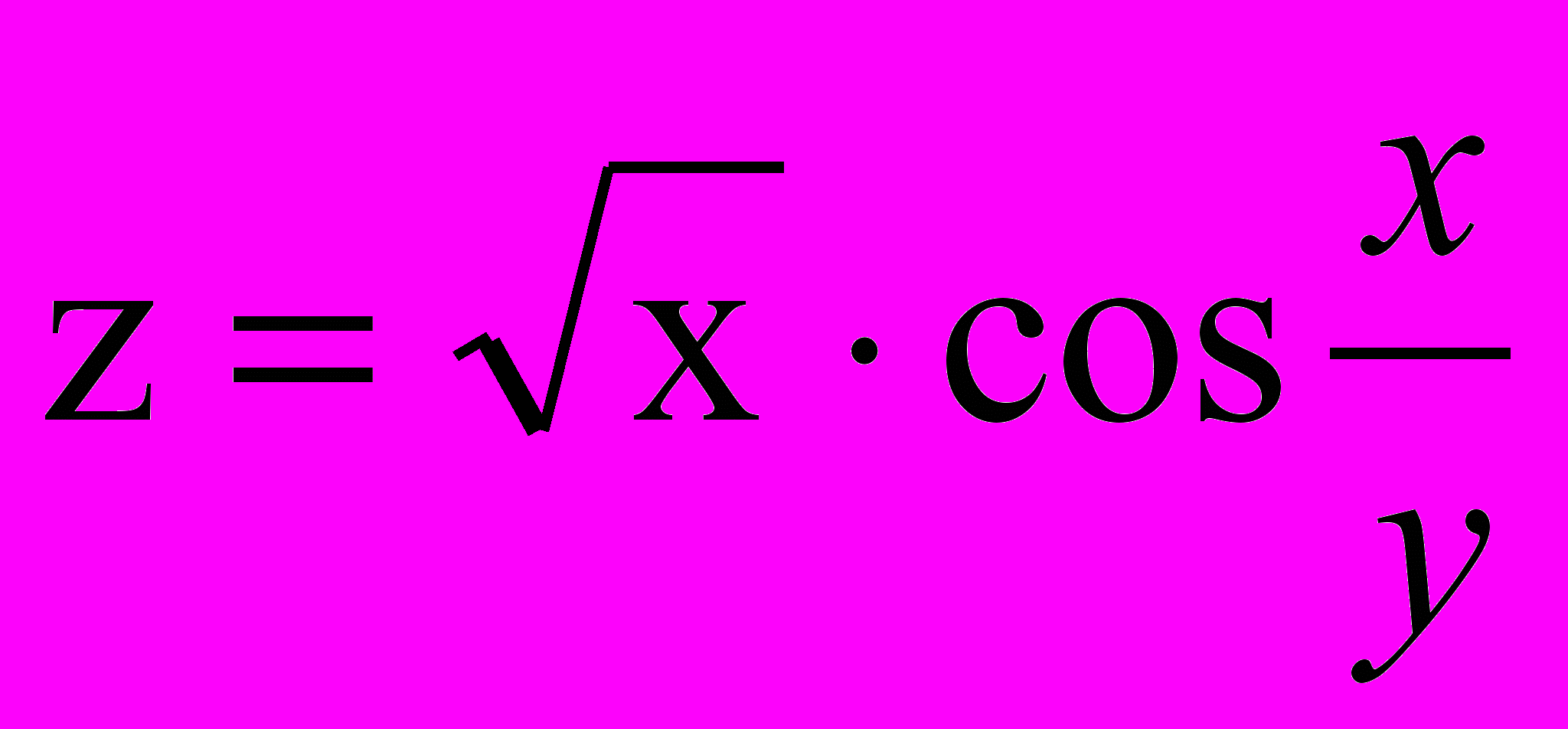 ;
; 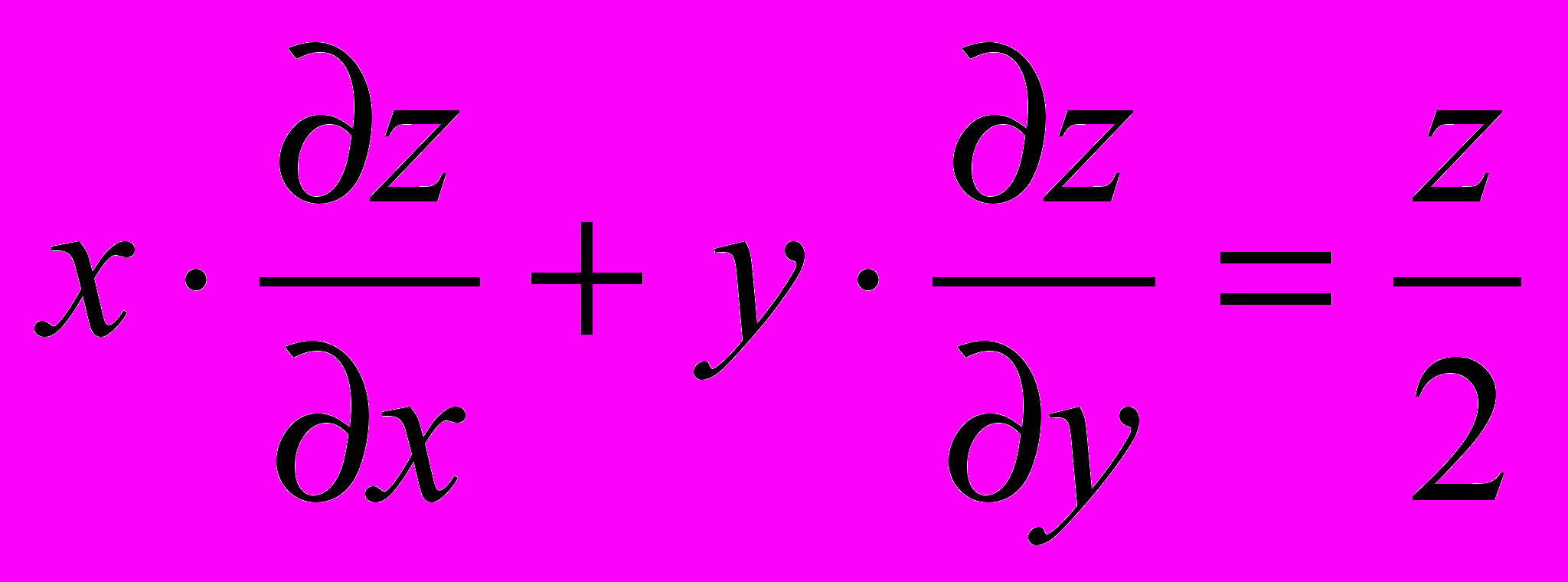 ;
;б)
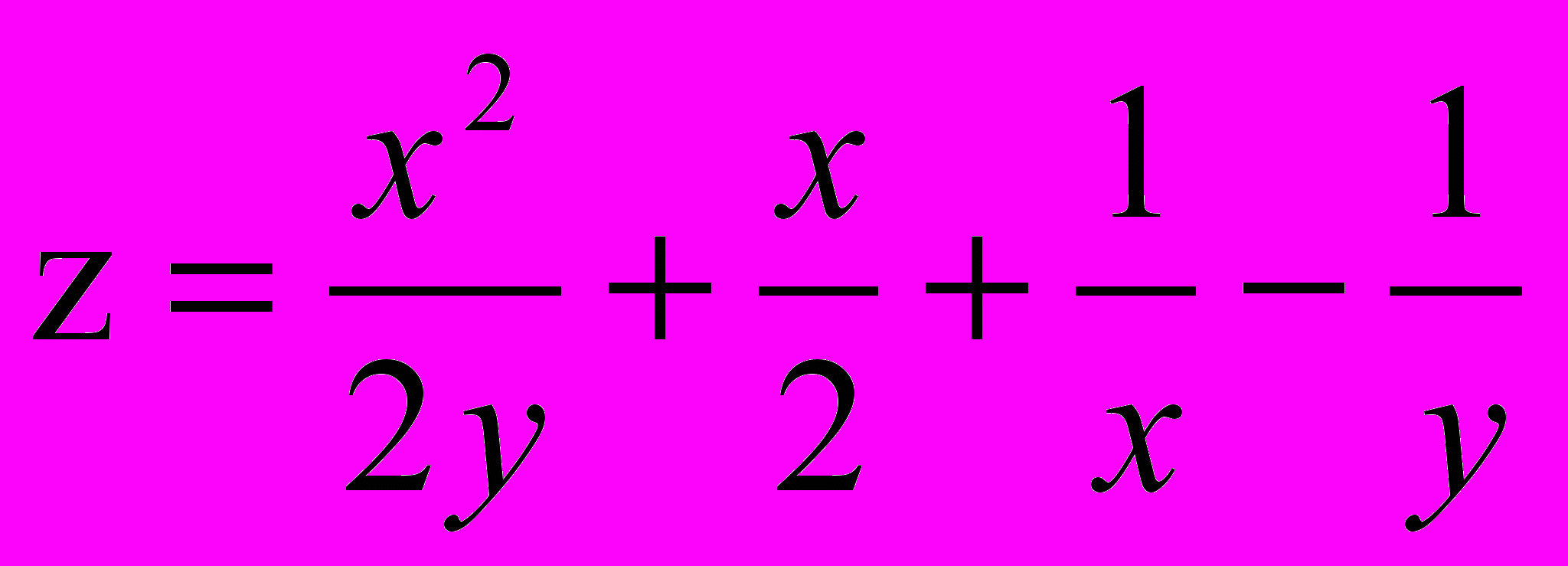 ;
; 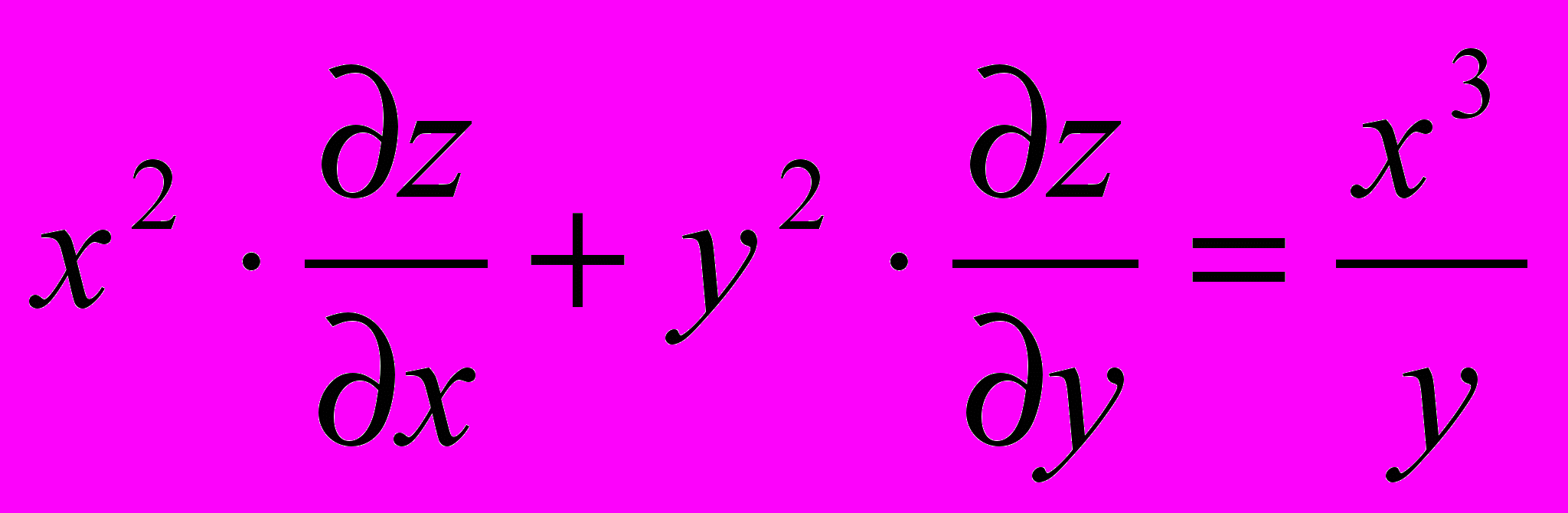 ;
;в)
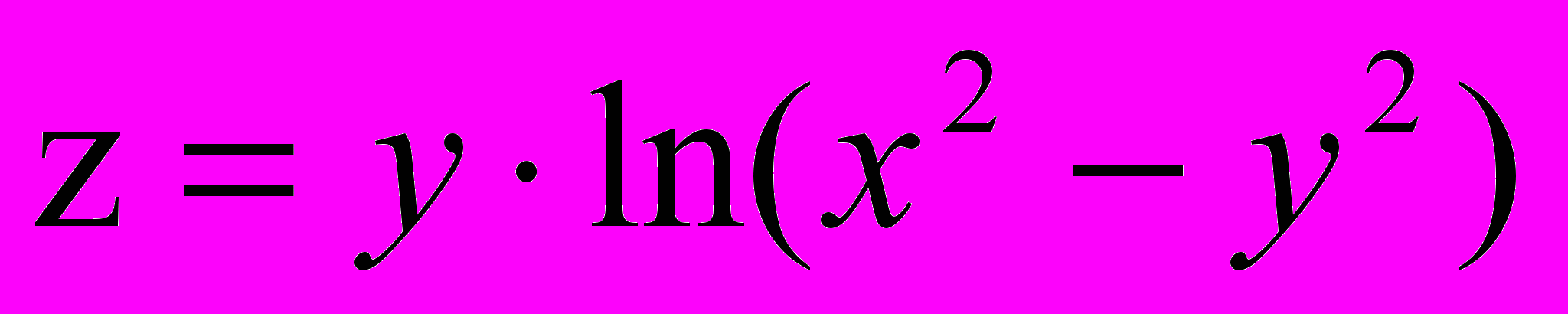 ;
; 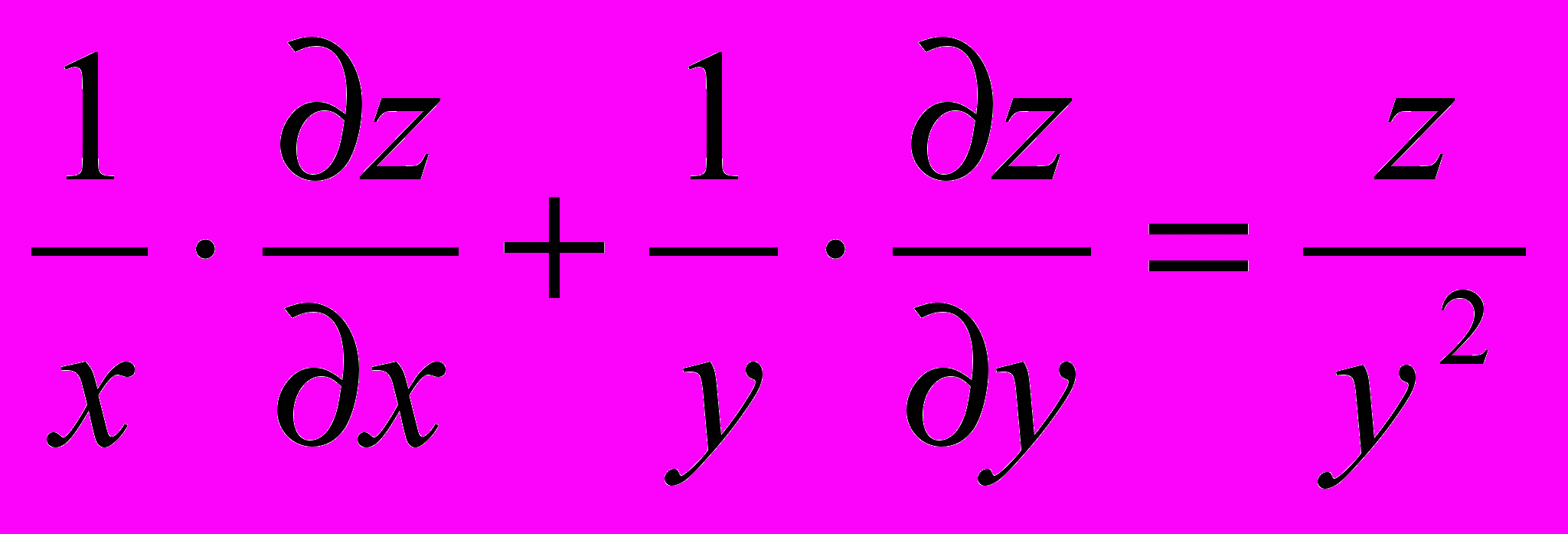 .
.5
 . Найти производные приведенных функций по направлению вектора e в
. Найти производные приведенных функций по направлению вектора e в заданной точке:
 а) z = x3y – 5xy2 + 8; e = (1; 1); М0(1; 1);
а) z = x3y – 5xy2 + 8; e = (1; 1); М0(1; 1); б) z = ln
б) z = ln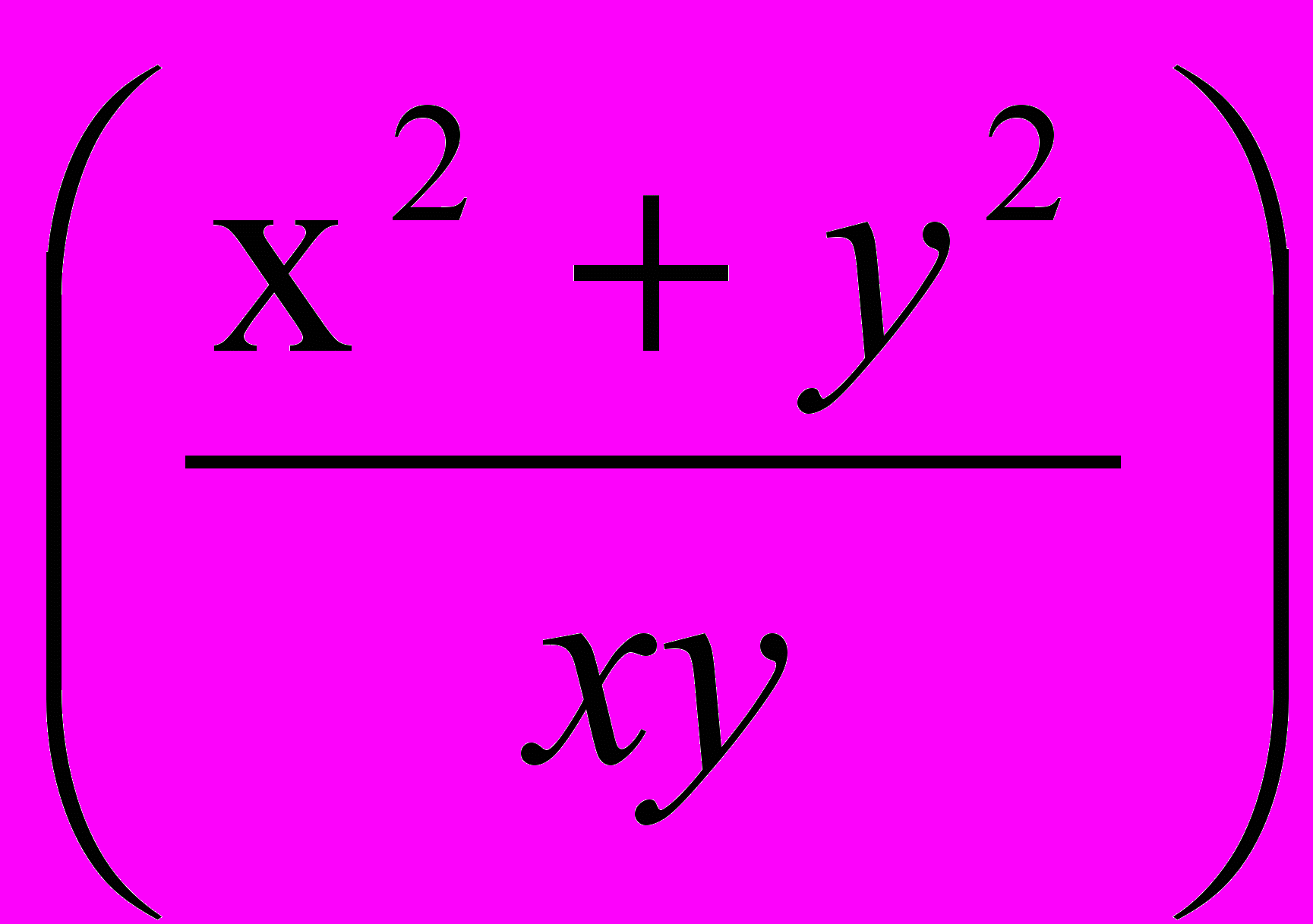 ; e = (6; 8); М0(1; 2);
; e = (6; 8); М0(1; 2); в) u = arccos
в) u = arccos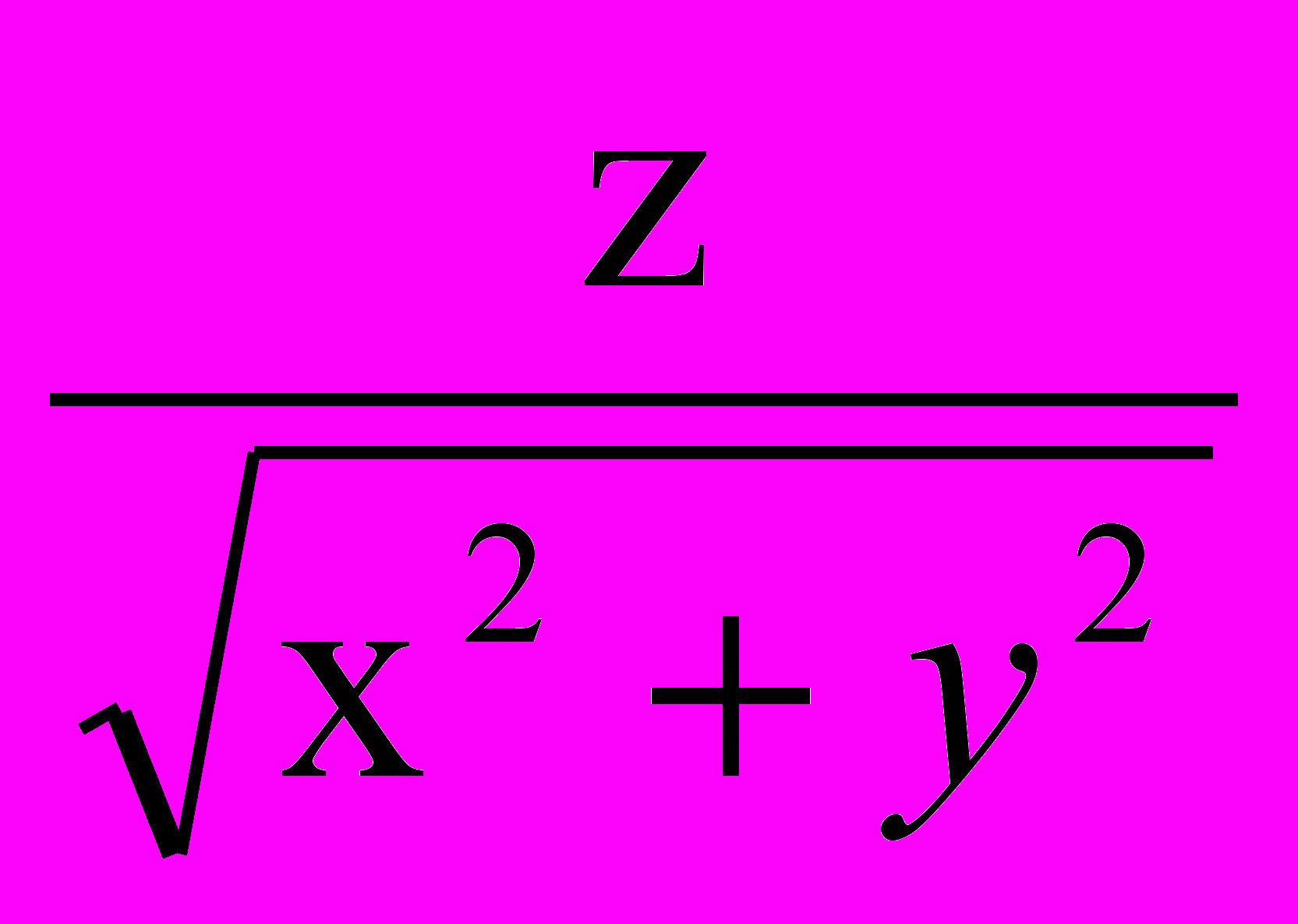 ; e = (2; 1; 2); М0(1; 1; 1).
; e = (2; 1; 2); М0(1; 1; 1).6. Построить линии уровня функции z = 4 – x2 – y2. Найти величину и
направление grad z в точке М0(1; 2).
7. Найти grad z и |grad z|:
а) z = (x – y)2 в точке М0(1; 1);
б) z =
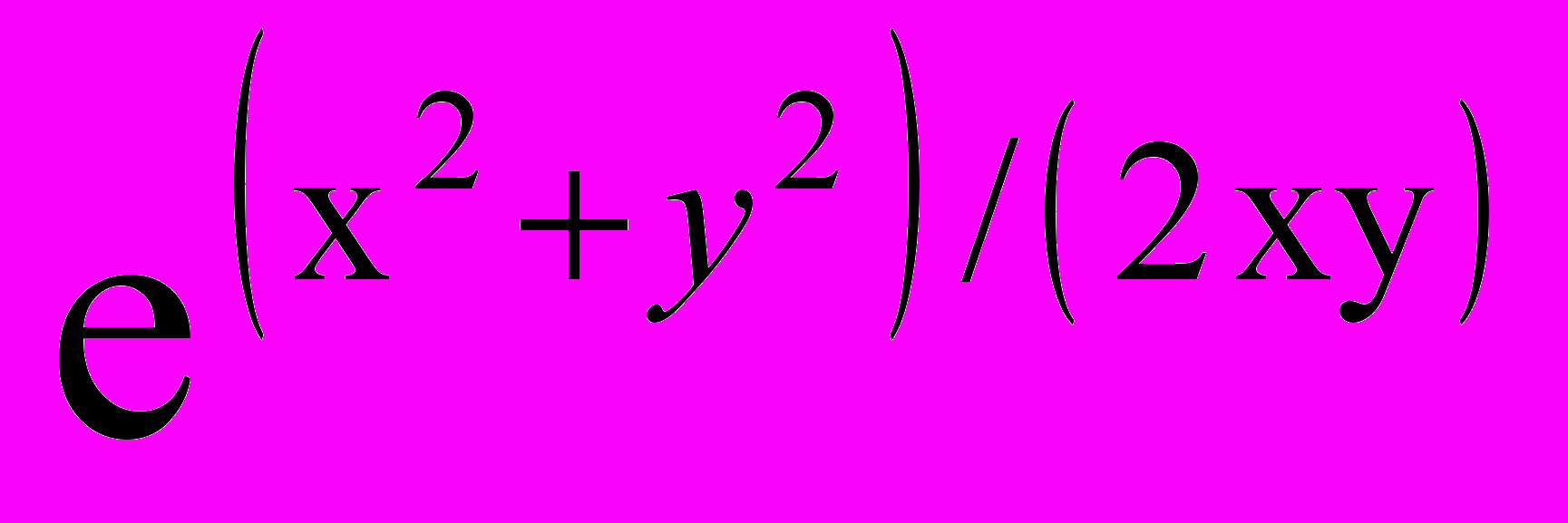 в точке М0(1; 1).
в точке М0(1; 1).8. Вычислить приближенно:
а)
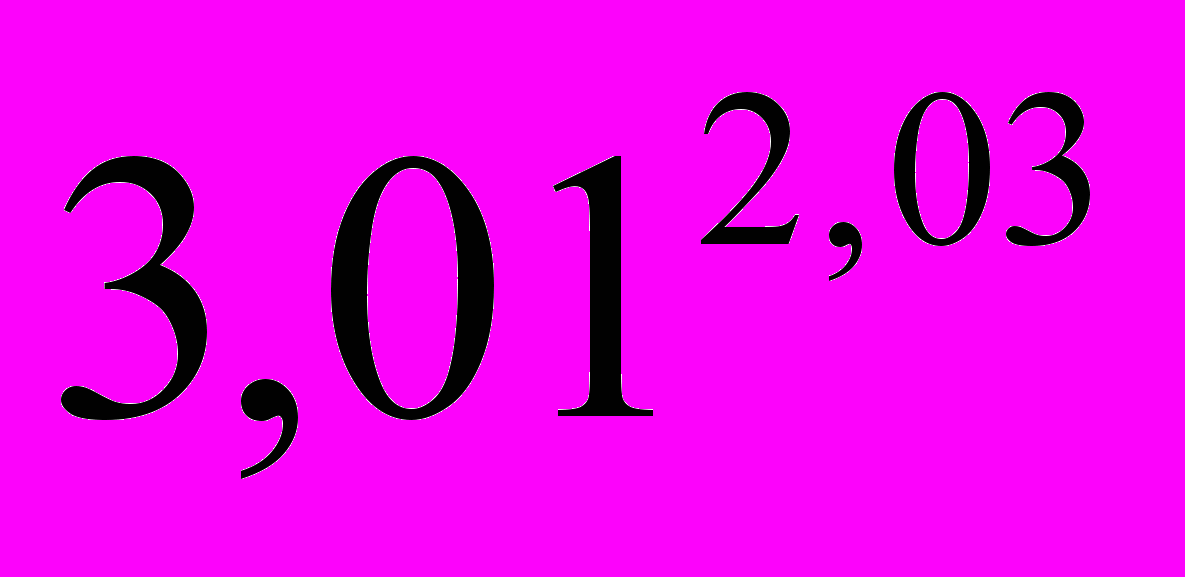 ;
;б) ln(8,001 + 0,993);
в)
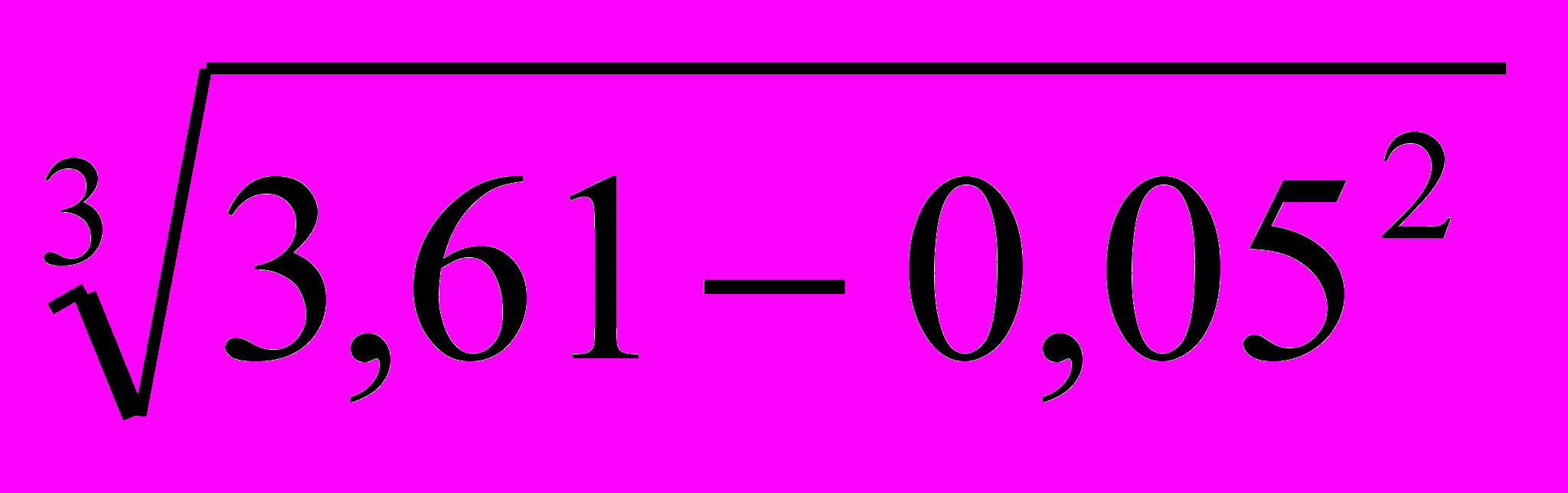 .
.9. Показать, что функция z =
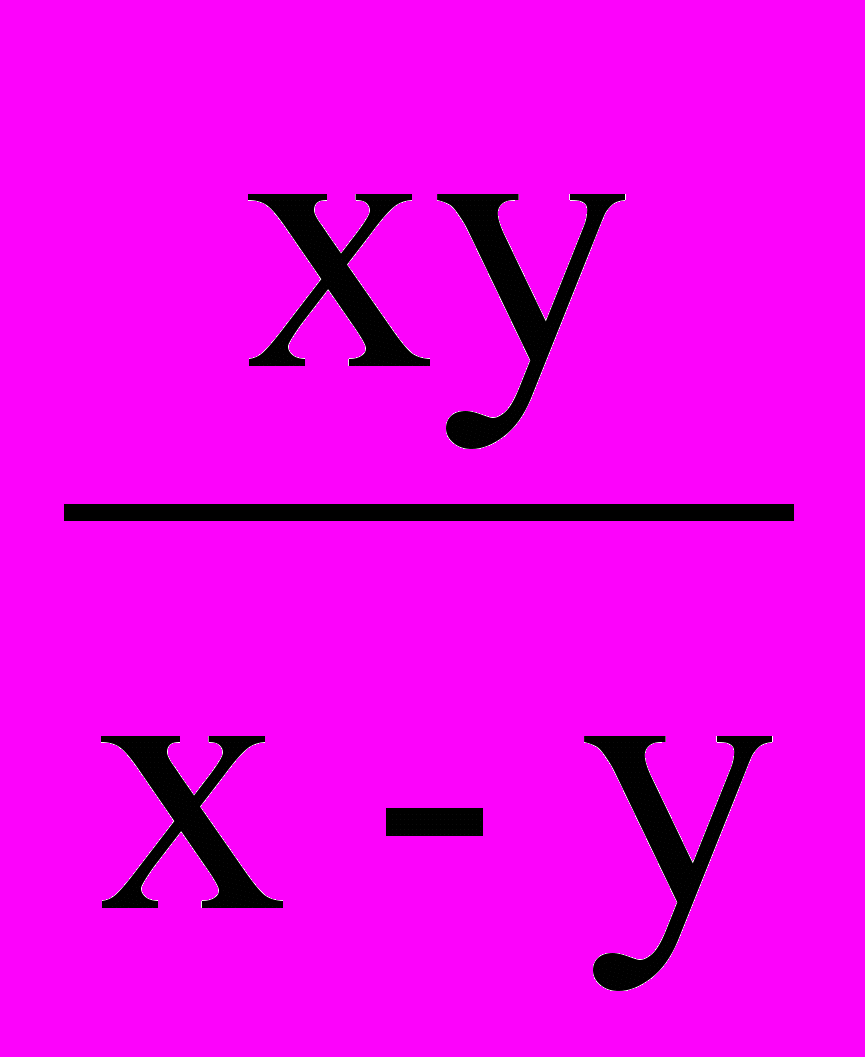 удовлетворяет уравнению
удовлетворяет уравнению 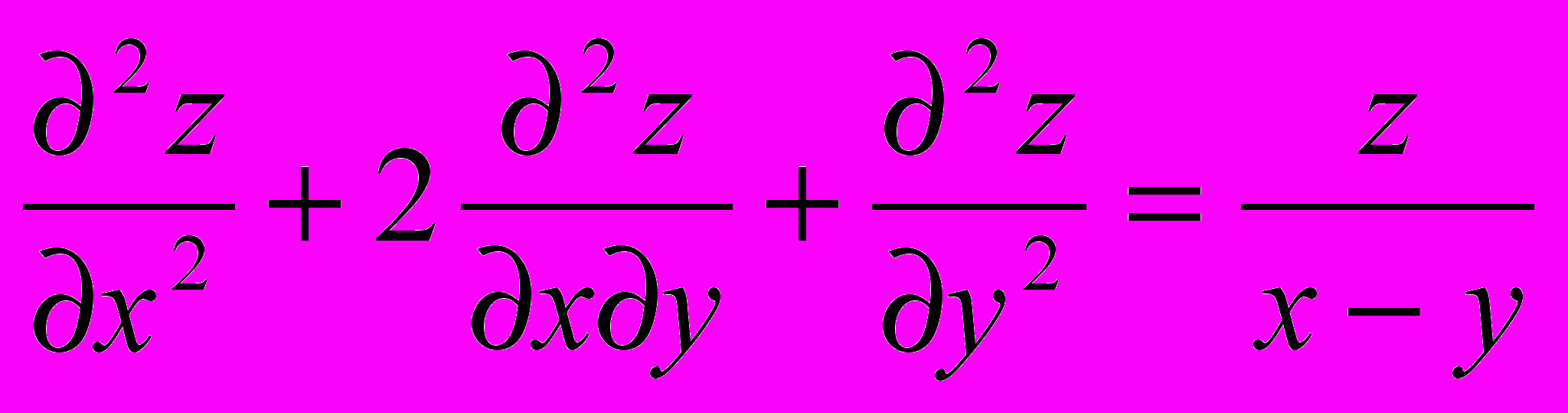 .
.10. Найти экстремумы функции:
а) z = x2 – xy + y2 + 9x – 6y + 20;
б) z = xy2 – xy – xy3 (x > 0, y > 0);
в) z = 3x2 – x3 + 3y2 + 4y;
г) z = y
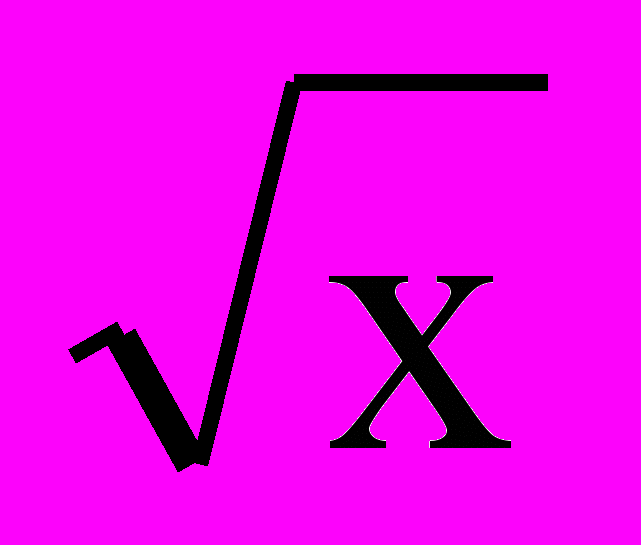 - y2 – x + 6y;
- y2 – x + 6y;д) z = 4 -
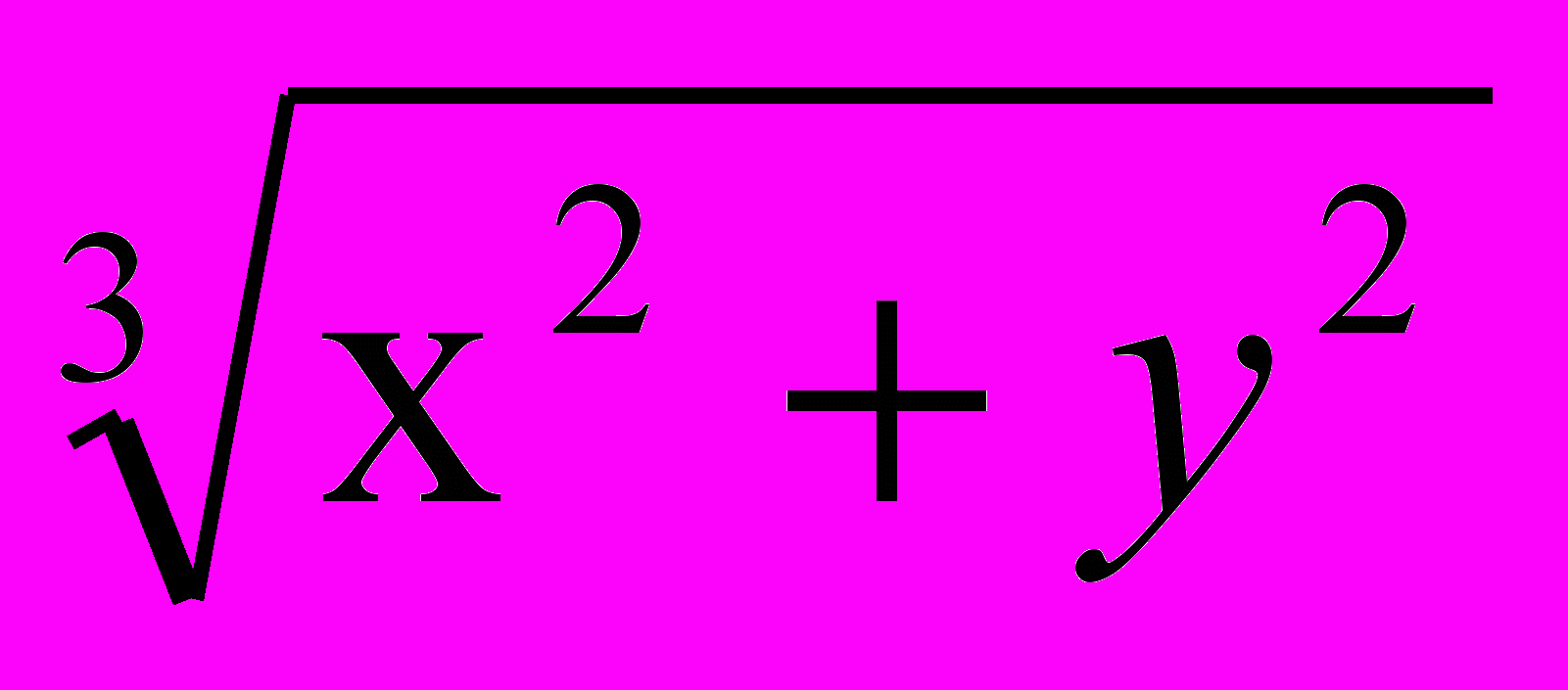 .
.11.Найти условные экстремумы функций:
а) z = x2 + y2 – xy + x + y – 4 при x + y + 3 = 0;
б) z =
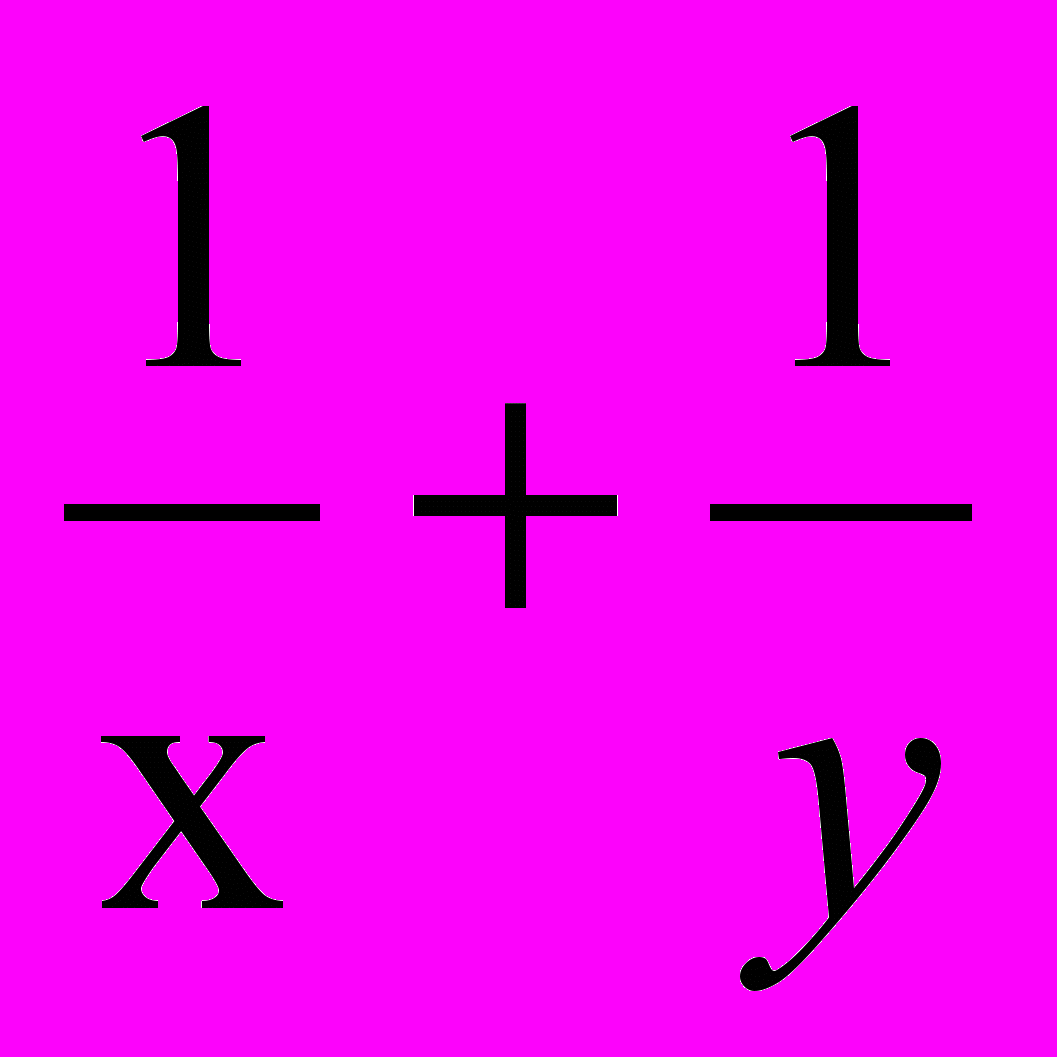 при x + y = 2;
при x + y = 2;в) z = x + 2y при x2 + y2 = 1;
г) z = x + y при
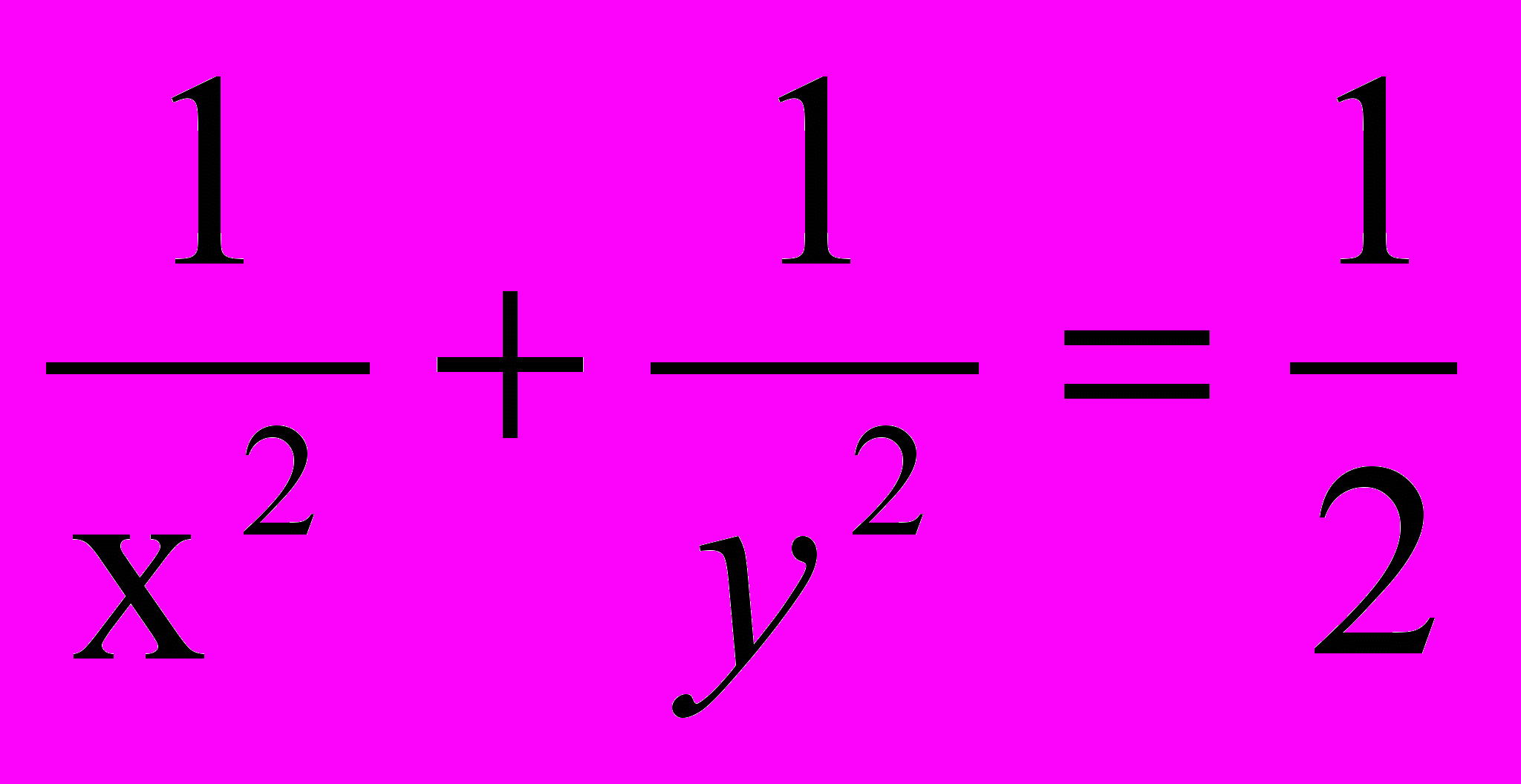 .
.12.Найти уравнение касательной плоскости к поверхности 4x2+3y2+5z2=1 в точке P0
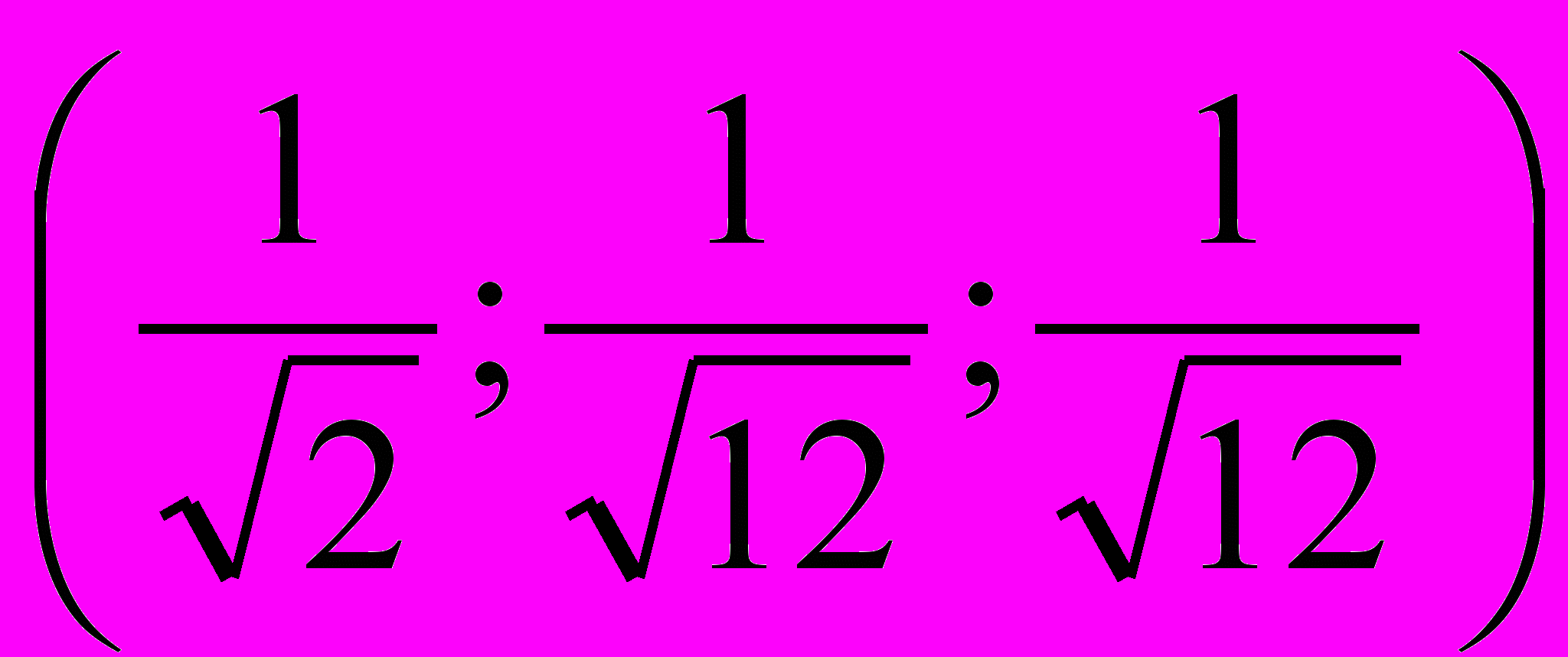 .
.13.
а) Получить линейную зависимость y = ax + b по следующим данным:
-
x
1
2
3
4
5
6
y
6
8
10
9
12
11
б) В результате исследования зависимости между сроком эксплуатации
автомобиля и расходами на его ремонт получены следующие данные:
-
t, лет
1
2
3
4
5
6
7
8
S, тыс. руб.
120
140
230
370
445
570
655
770
Найти:
- линейную зависимость стоимости ремонта автомобиля от срока
эксплуатации;
- предполагаемую величину затрат на ремонт за 10-й год эксплуатации.
в) Прибыль предприятия за некоторый период деятельности по годам
приведена ниже:
-
Год t
1
2
3
4
5
6
7
Прибыль π
54
57
62
65
67
69
70
Требуется:
- составить квадратичную зависимость прибыли по годам деятельности
предприятия;
- определить ожидаемую прибыль для 8-го года деятельности.
14.
а) Предприниматель решил выделить на расширение своего дела 150 тыс. руб. Известно, что если на приобретение нового оборудования затратить x тыс. руб., а на зарплату вновь принятых работников y тыс. руб., то прирост объема продукции составит Q = 0,001x0,6y0,4. Как следует распределить выделенные денежные ресурсы, чтобы прирост объема продукции был максимальным?
б) Общие издержки производства заданы функцией TC = 0,5x2 + 0,6xy + 0,4y2 + 700x + 600y + 2000, где x и y – соответственно количество товаров А и В. Общее количество произведенной продукции должно быть равно 500 ед. Сколько единиц товара А и В нужно производить, чтобы издержки на их изготовление были минимальными?
15. Оценить интеграл
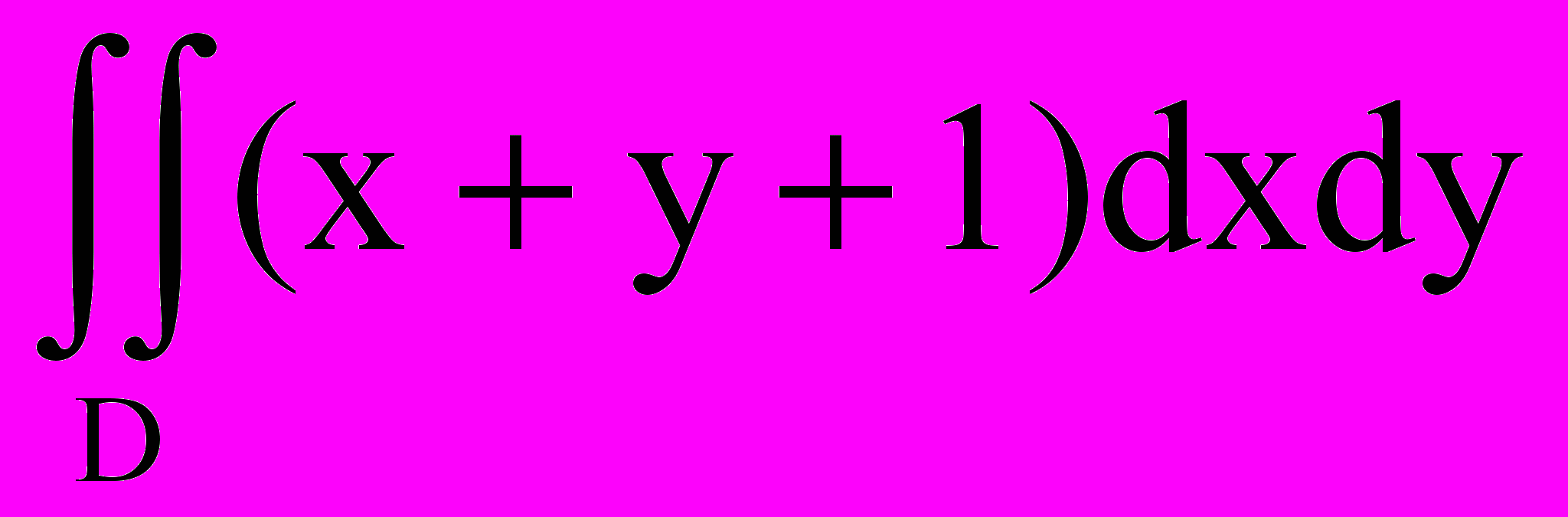 , где D – круг x2 + y2 ≤ 4.
, где D – круг x2 + y2 ≤ 4.16. Вычислить интегральное среднее значение функции f(x, y) = x + 6y в области D – треугольнике, ограниченном прямыми y = x, y = 5x, x = 1.
17. Изменить порядок интегрирования
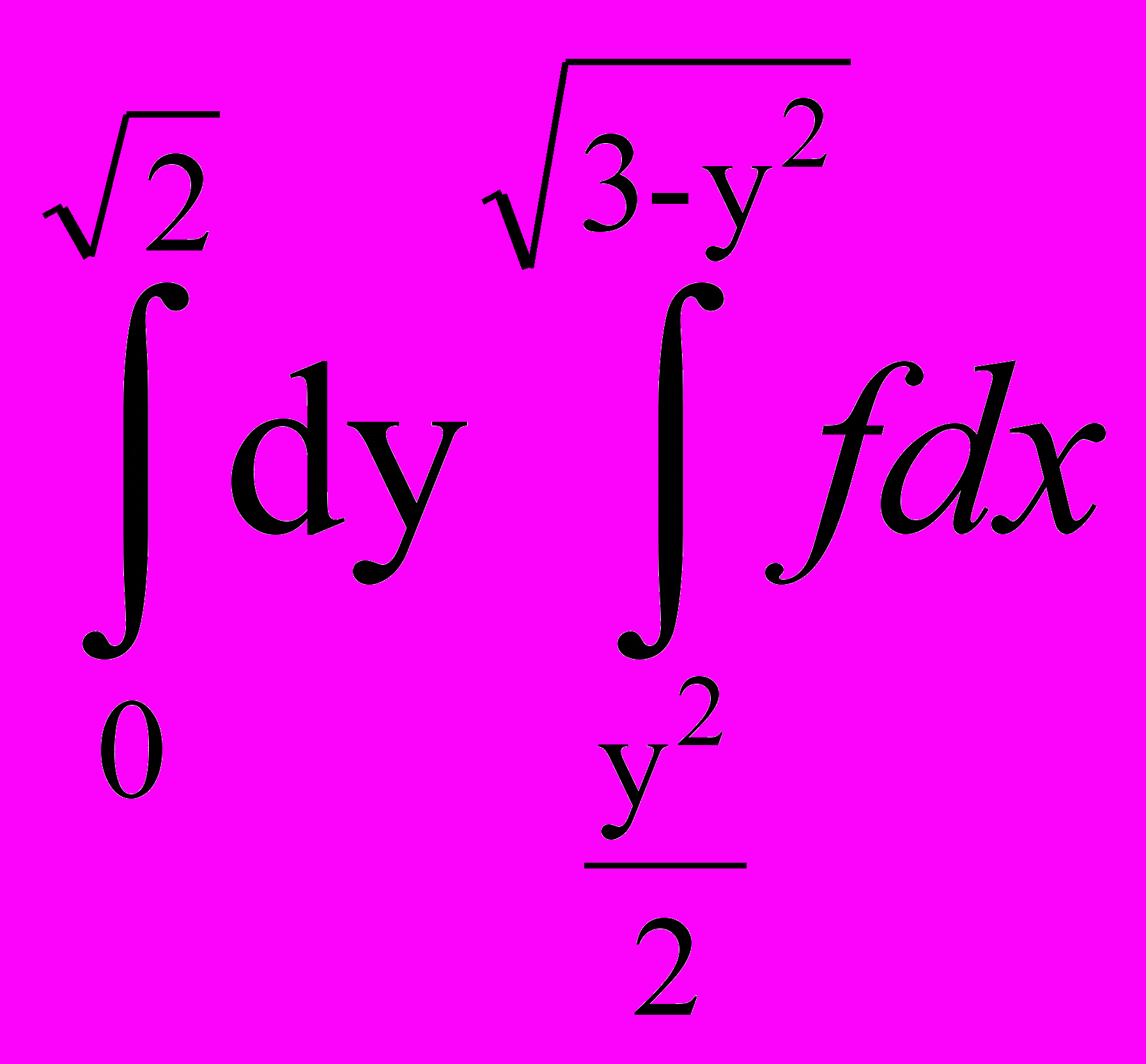 .
.18. Вычислить двойной интеграл
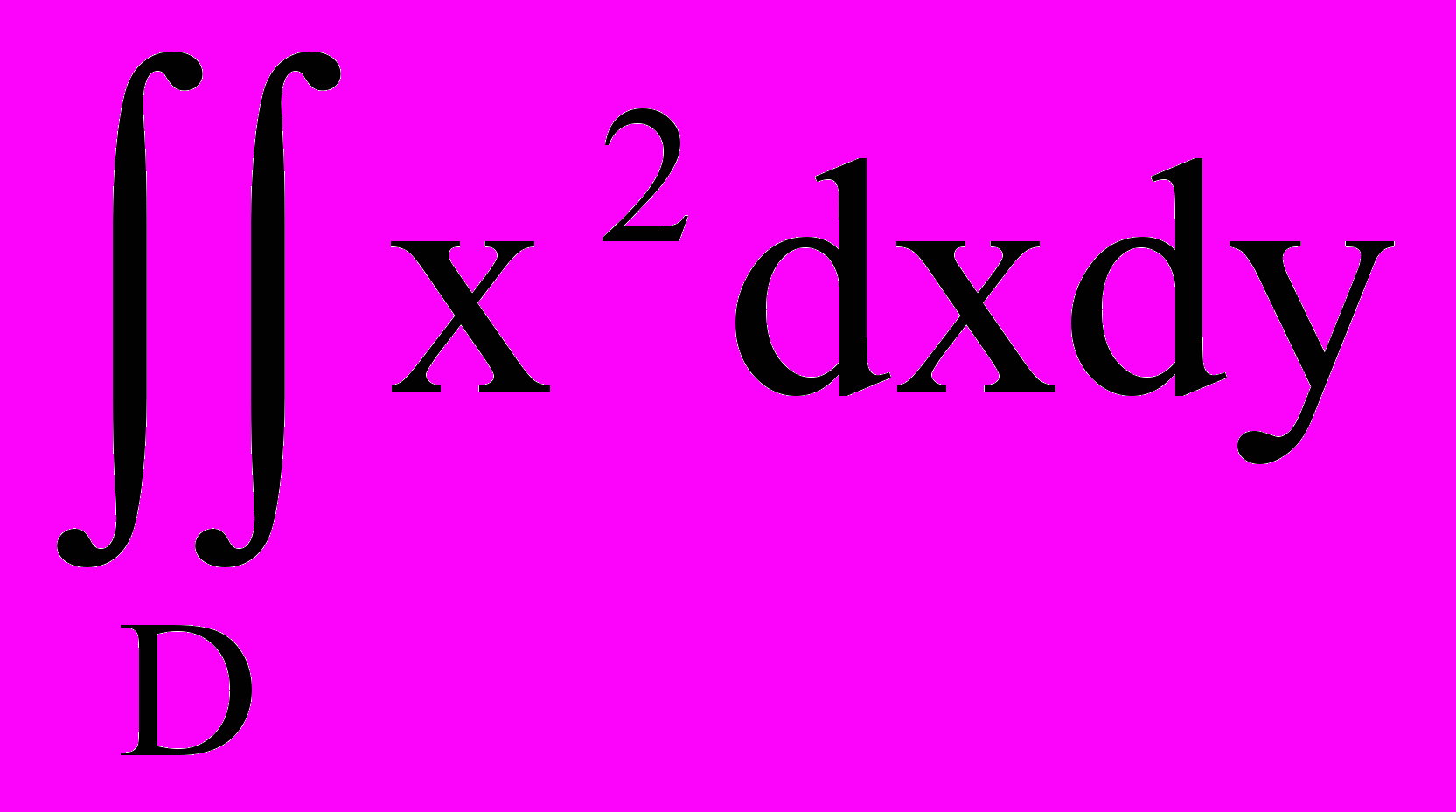 , где D – область, ограниченная прямыми: y = x; y = -x; x = 2.
, где D – область, ограниченная прямыми: y = x; y = -x; x = 2.19. Переходя к полярным координатам, вычислить интеграл
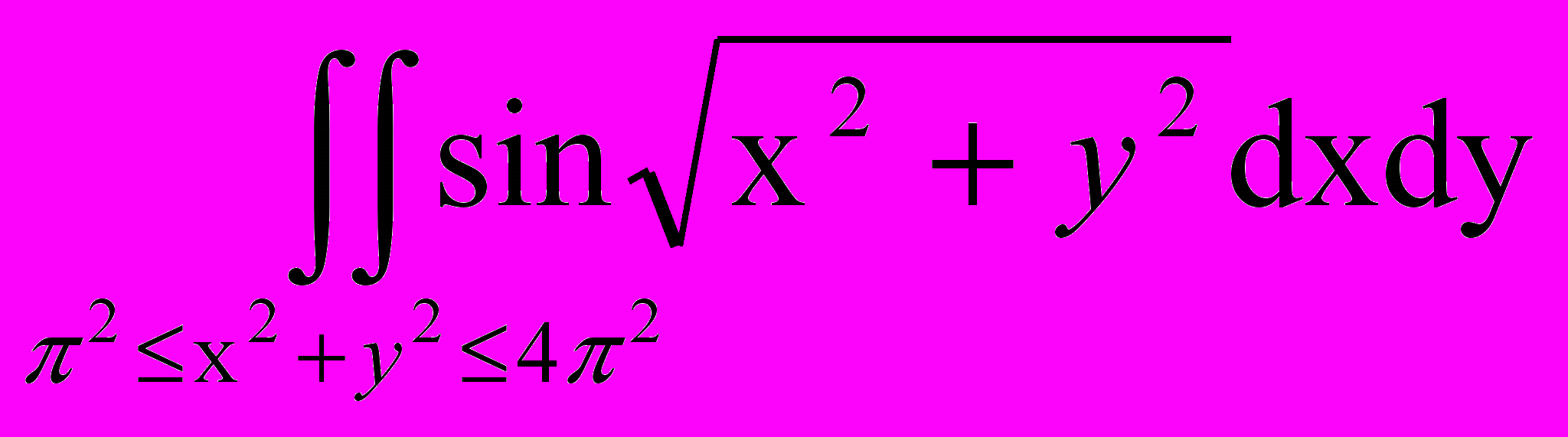 .
.20. Вычислить объем тела, ограниченного поверхностями: z = 0, z = 3 – x2 – y2.
21. Вычислить площадь фигуры, ограниченную линиями: y = x2 + 4x, y = x + 4.
22. Оценить интеграл
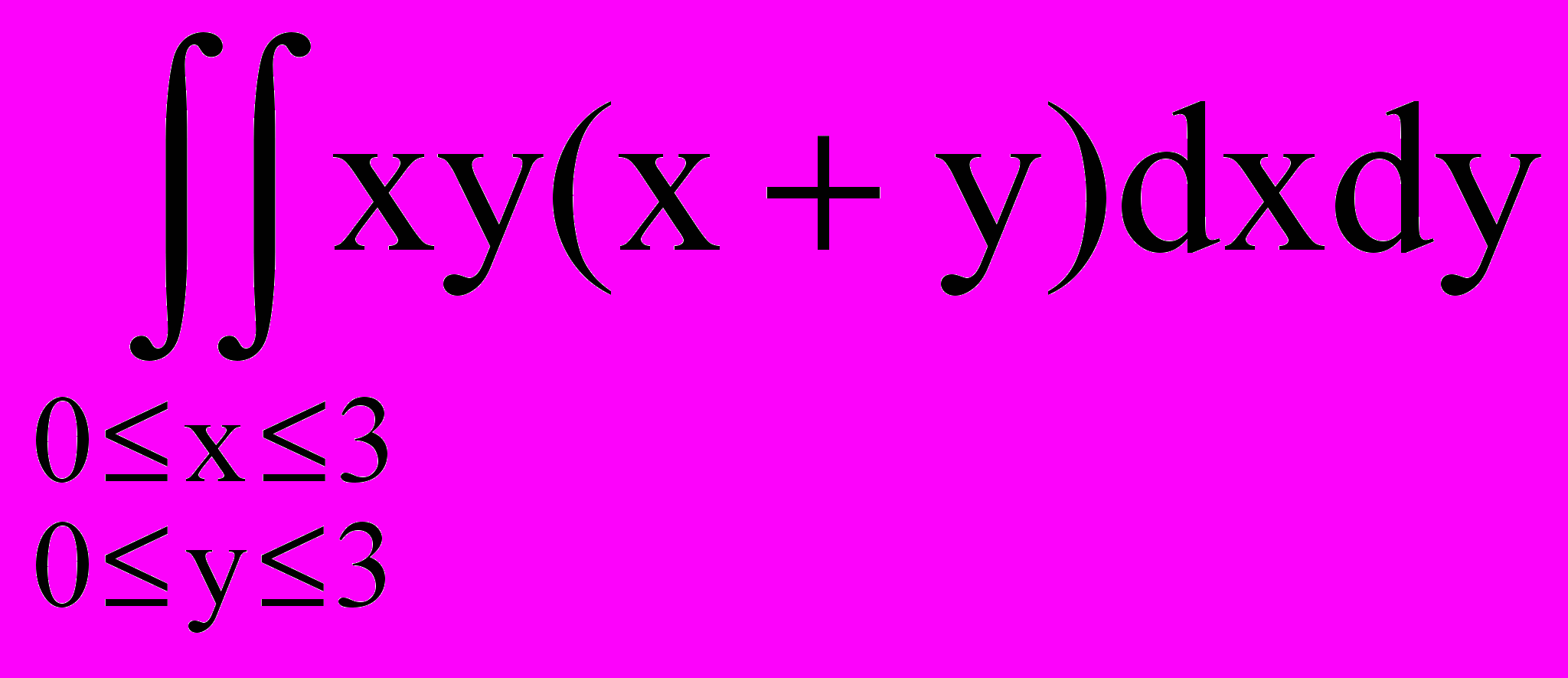 .
.23. Вычислить объем тела, ограниченного поверхностями: z =
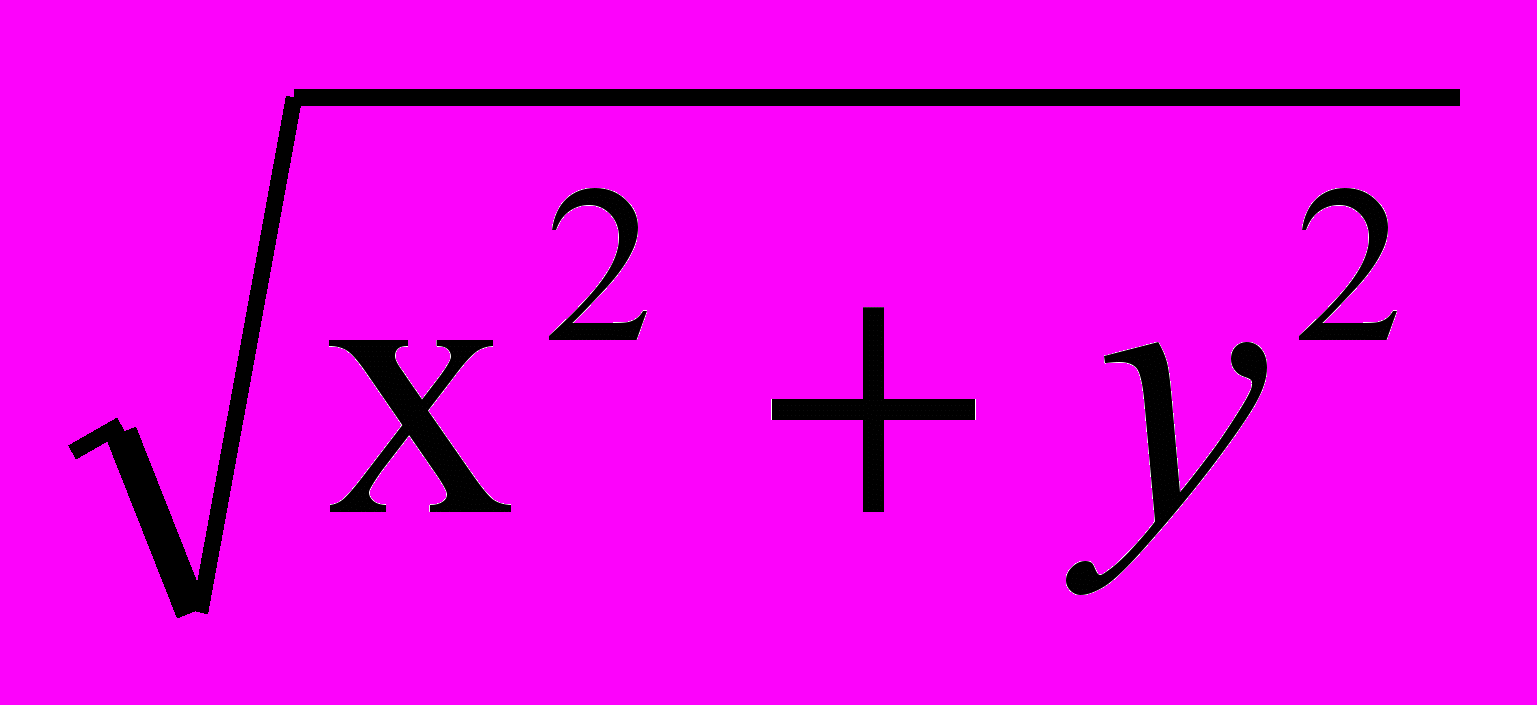 ;
; 3z = x2 + y2.
-
Задачи к экзамену II курс (4 семестр)
I. Решить дифференциальные уравнения.
1. ху'-у=у3; Ответ:
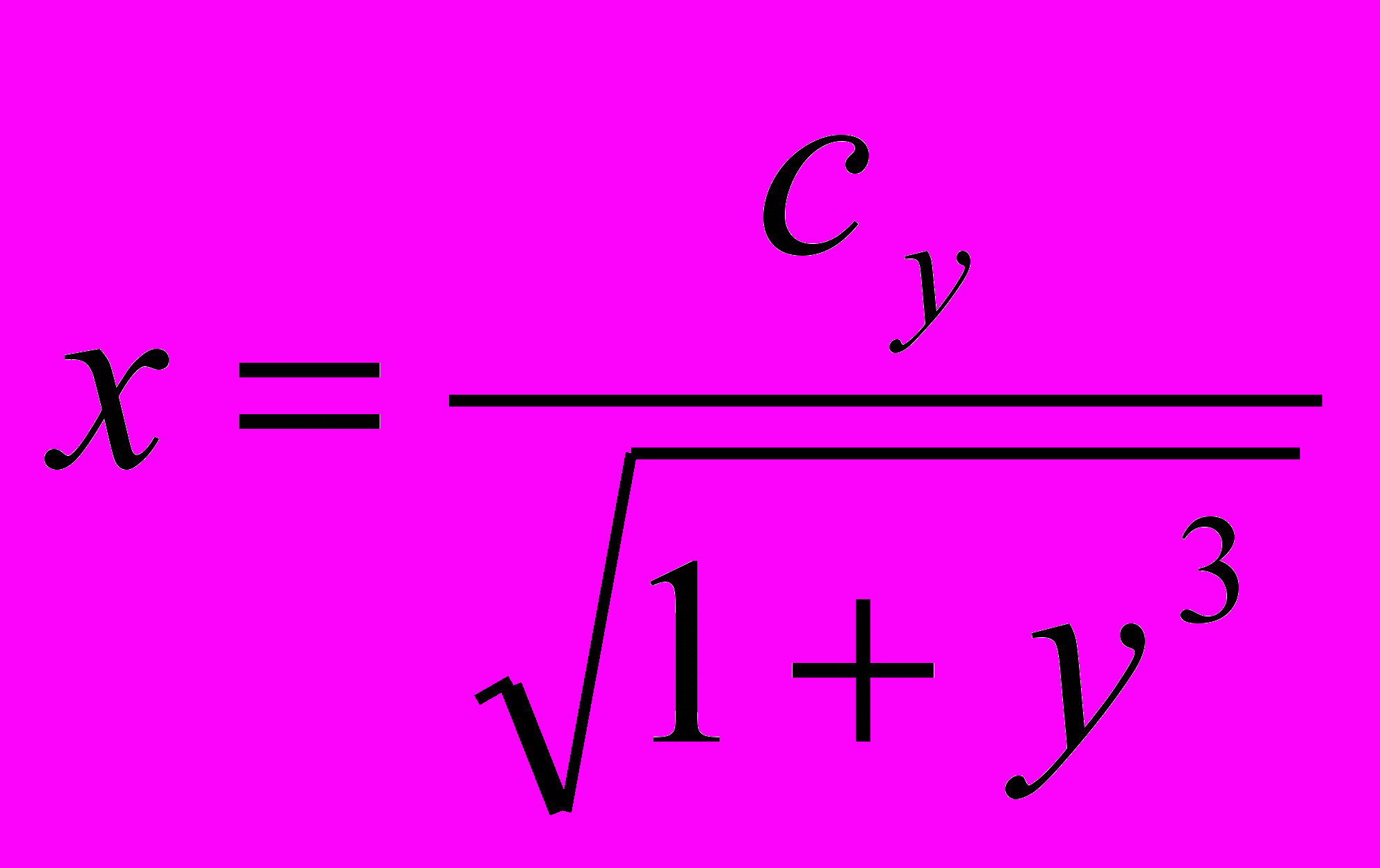
2. ху*у'=1-х2 ; Ответ: х2+у2=ln(cх2)
3. у-ху'=1+х2у'; Ответ:
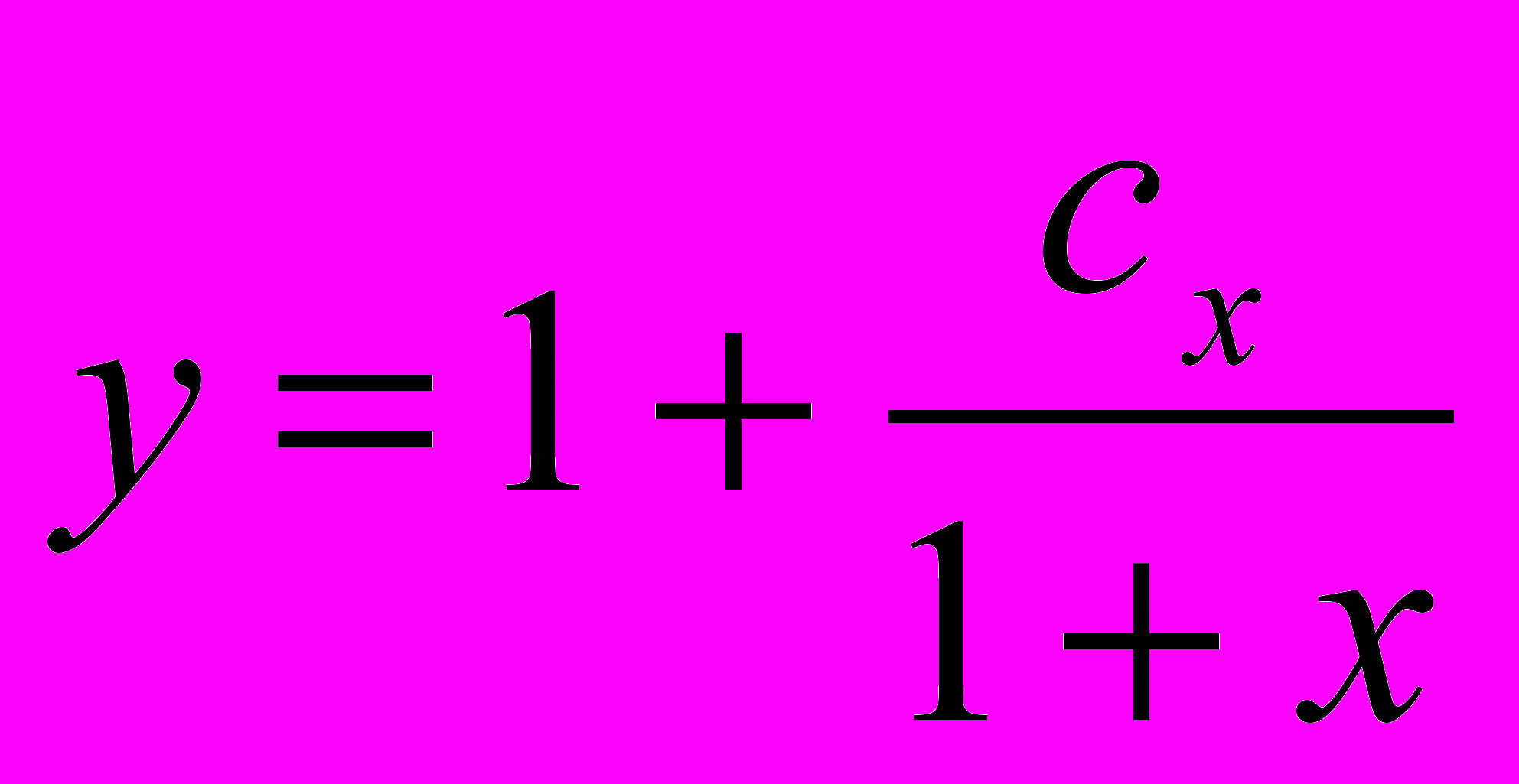
4. хуdx+(x+1)dy=0; Ответ: у=с(х+1)*℮-х
5.
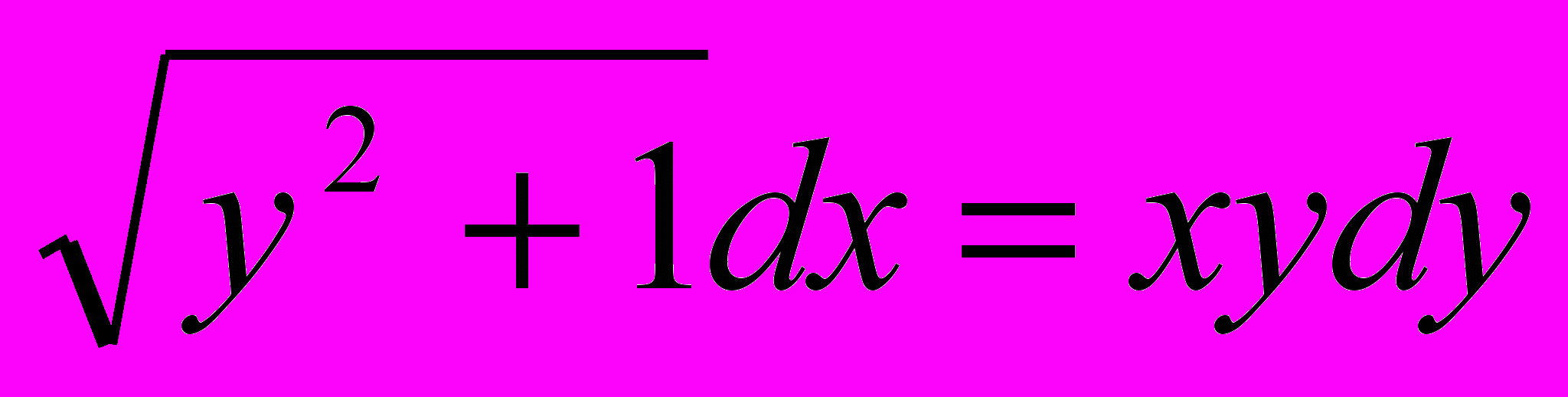 ; Ответ:
; Ответ: 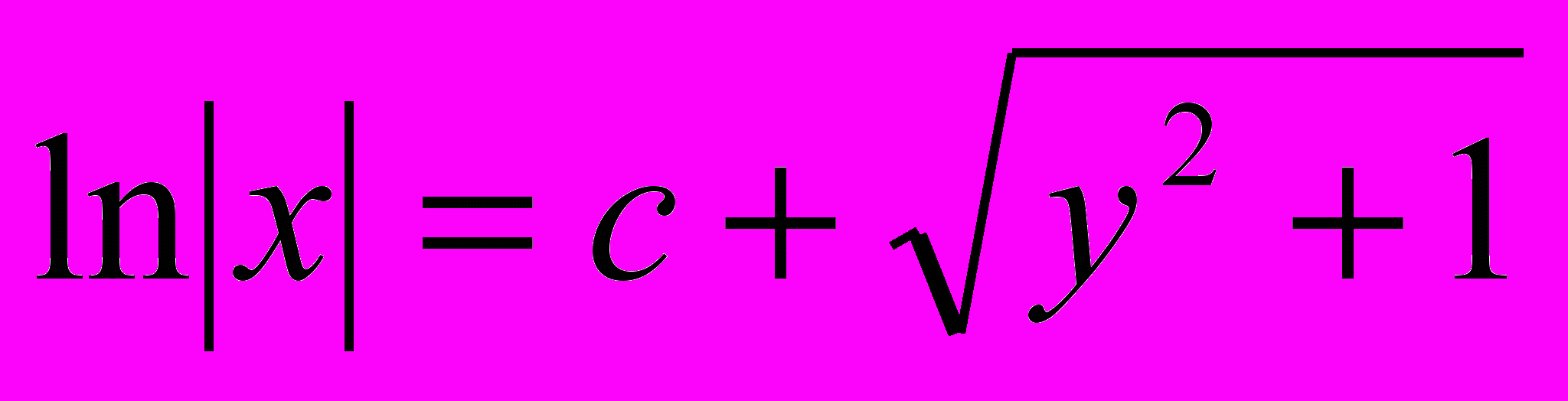 , х=0
, х=06. 2х2уу'+у2=2; Ответ:
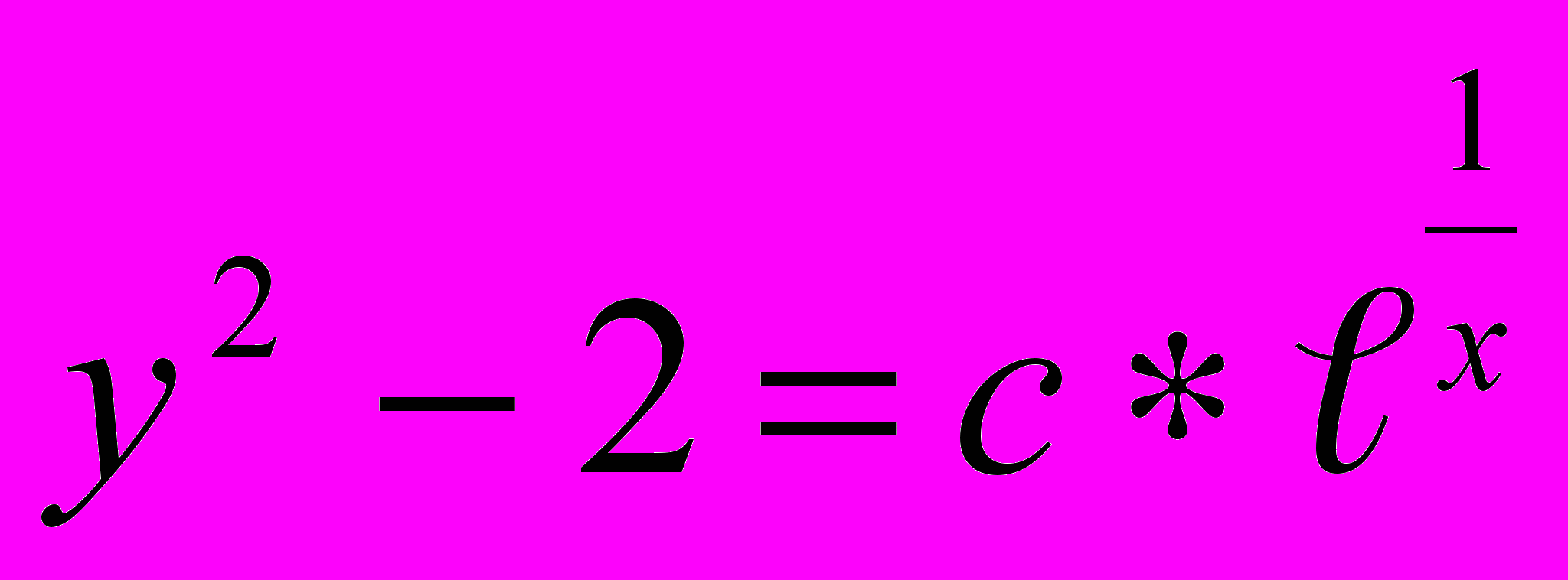
7. уу'+х=1; Ответ: у2+х2-2х=с
8. у'=10х+у Ответ: у=-ln(c-10x)
9. у'-у=2х-3; Ответ: 2х+у-1=с*℮х
10. (сделайте замену переменных):
(2х-у)dx+(4x-2y+3)dy=0; Ответ: 5х+10у+с=3ln(10x-5y+6)
II. Решить дифференциальные уравнения.
1.
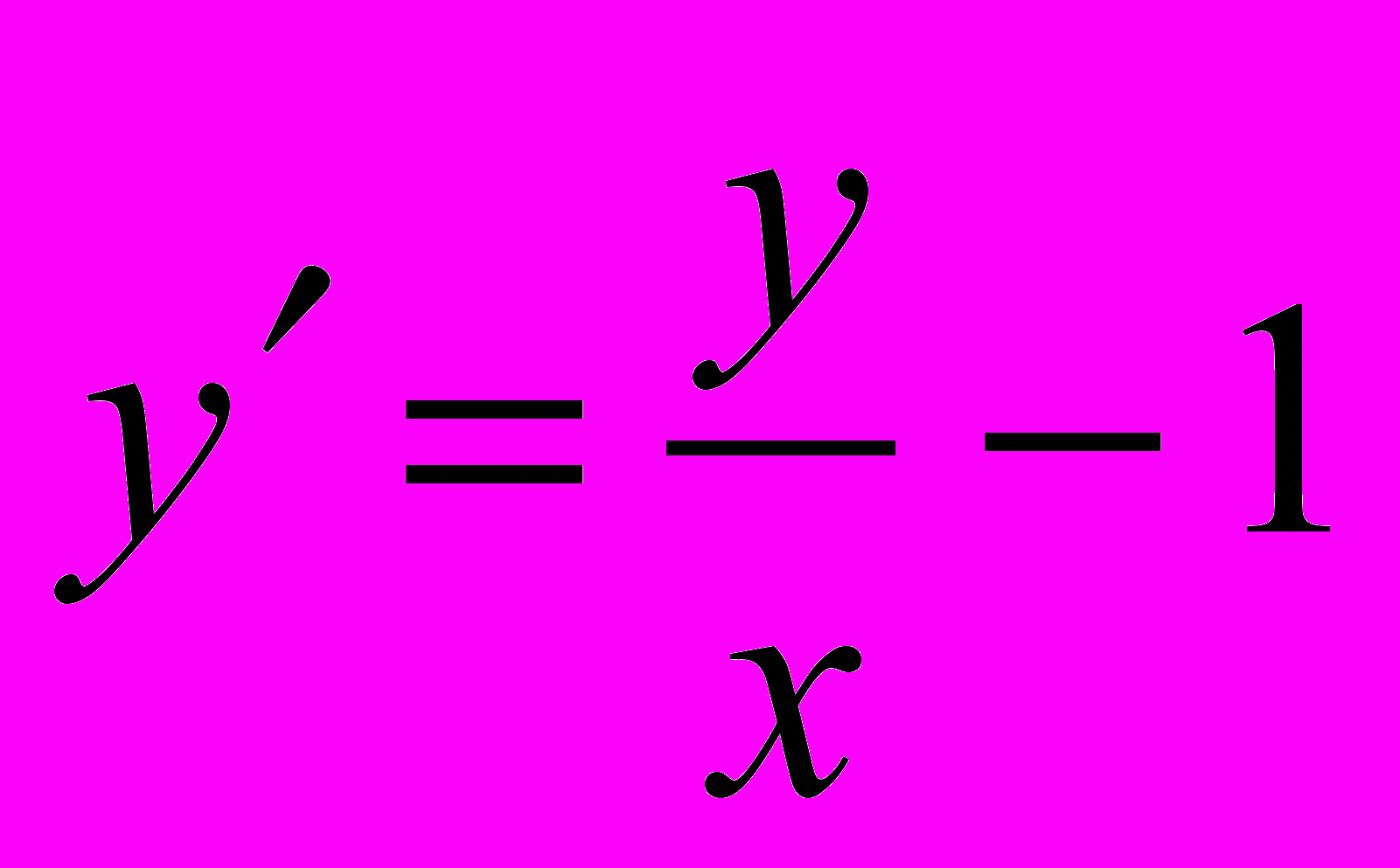 ; Ответ:
; Ответ: 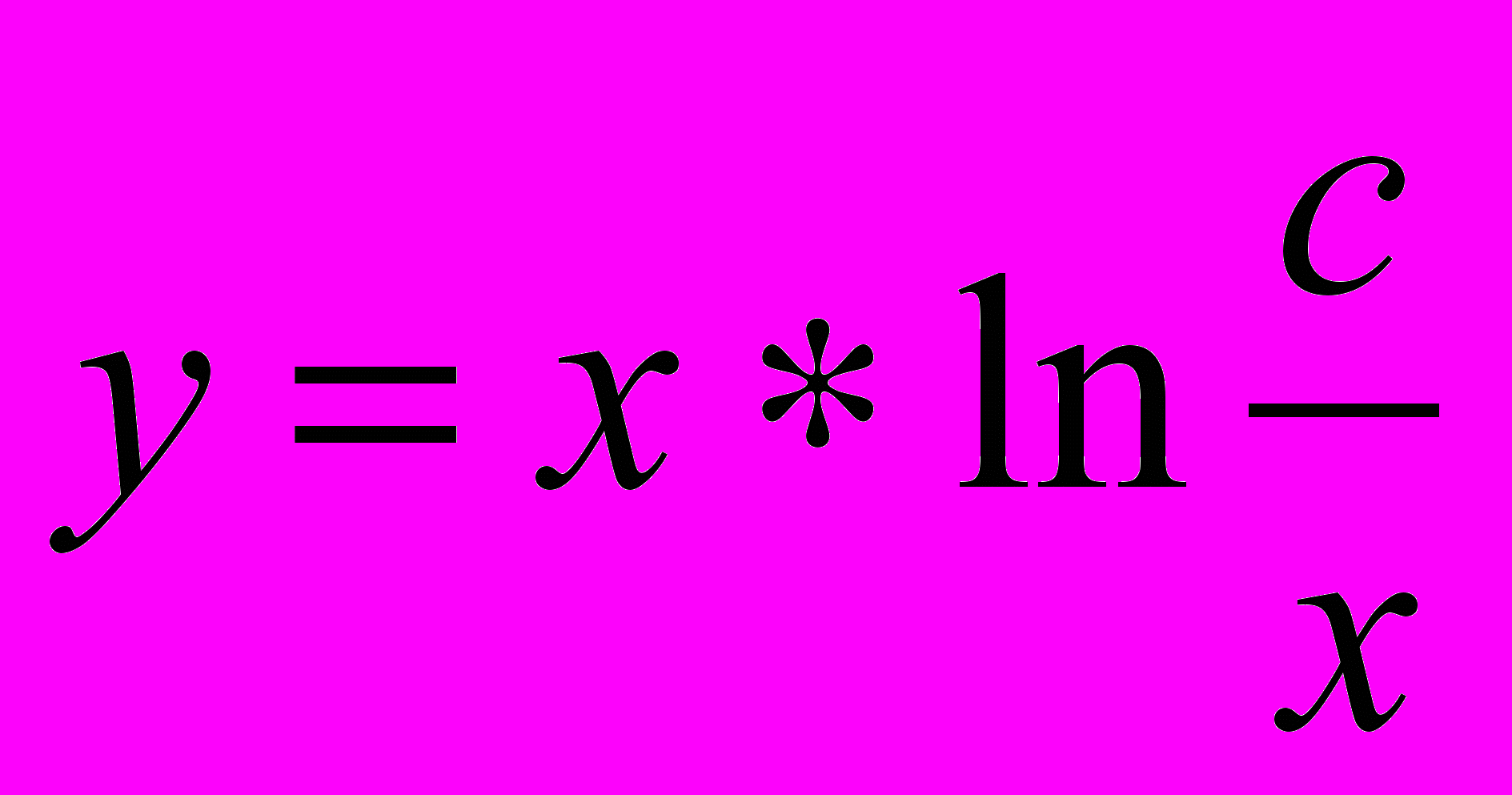
2. (х-у)*уdx-x2dy=0; Ответ:
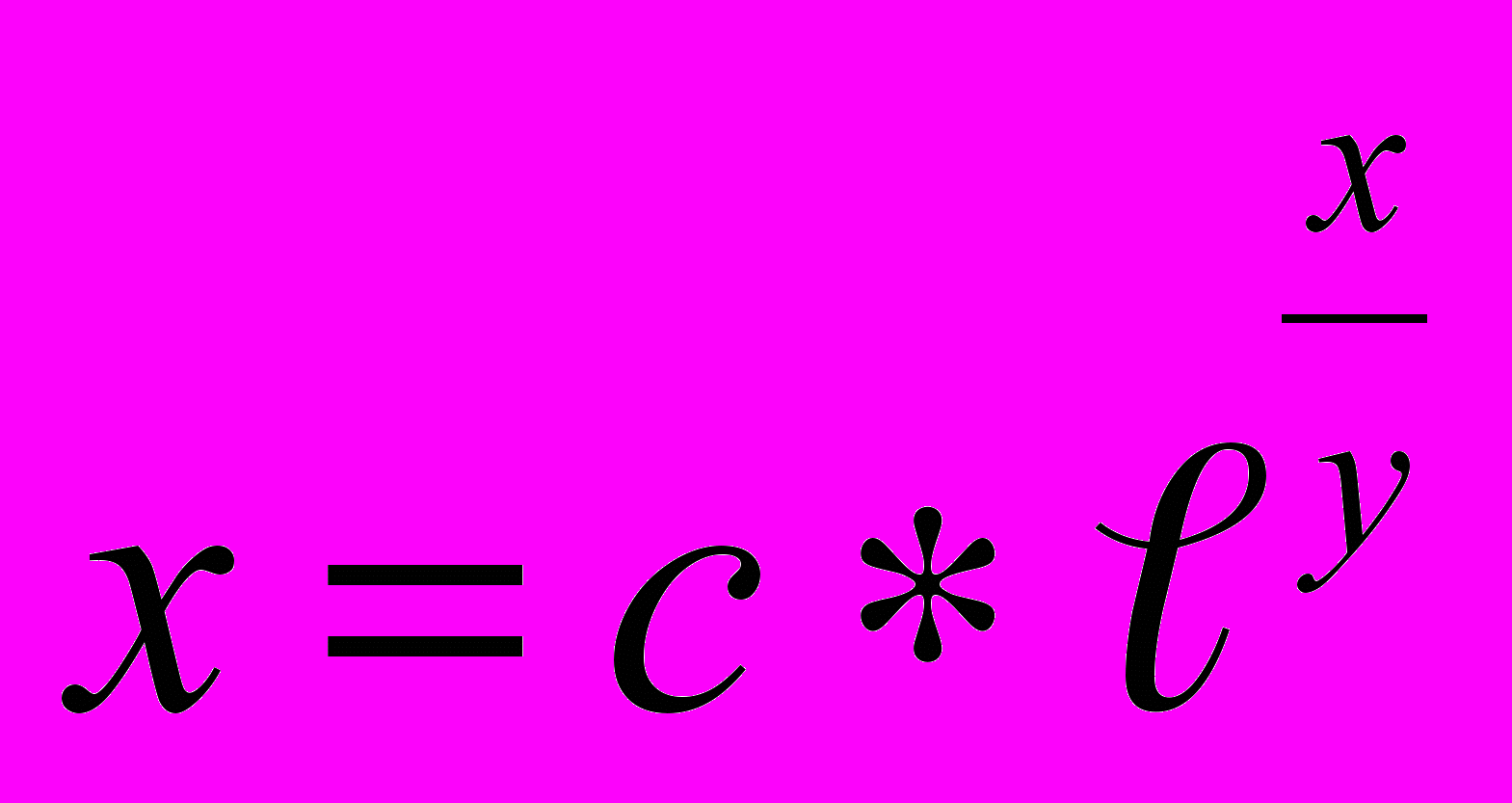 ; у=0
; у=03. (х2+у2)dx-2xydy=0; Ответ: (х-с)2-у2=с2
4.
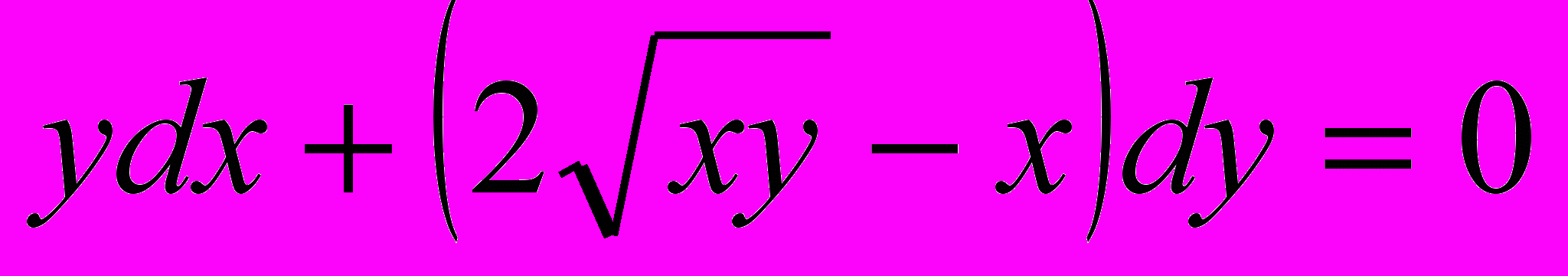 ; Ответ:
; Ответ: 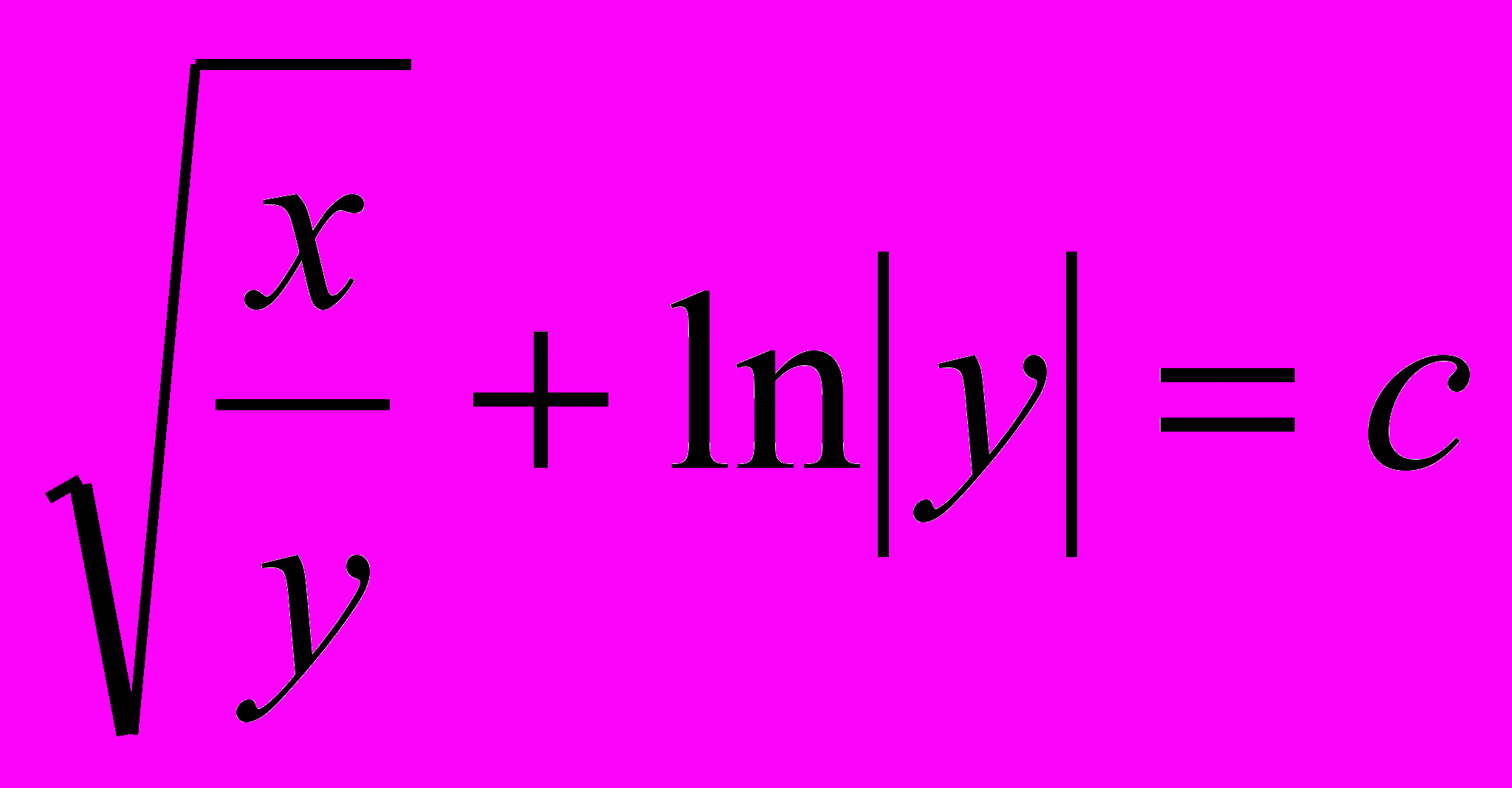 , у=0
, у=05. ydy+(x-2y)dx=0; Ответ: х=(у-х)*lnc(y-x), у=х
6.
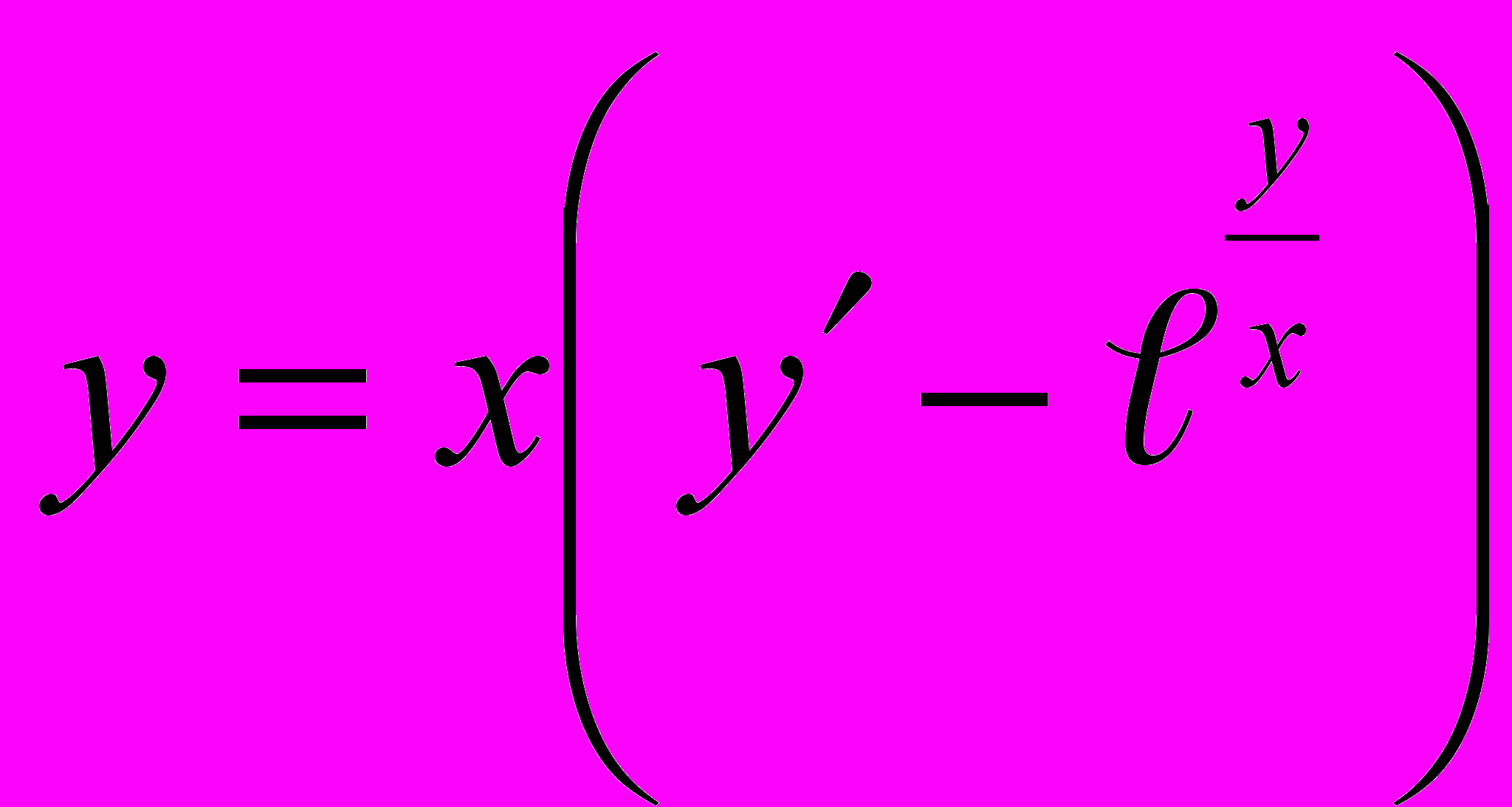 ; Ответ:
; Ответ: 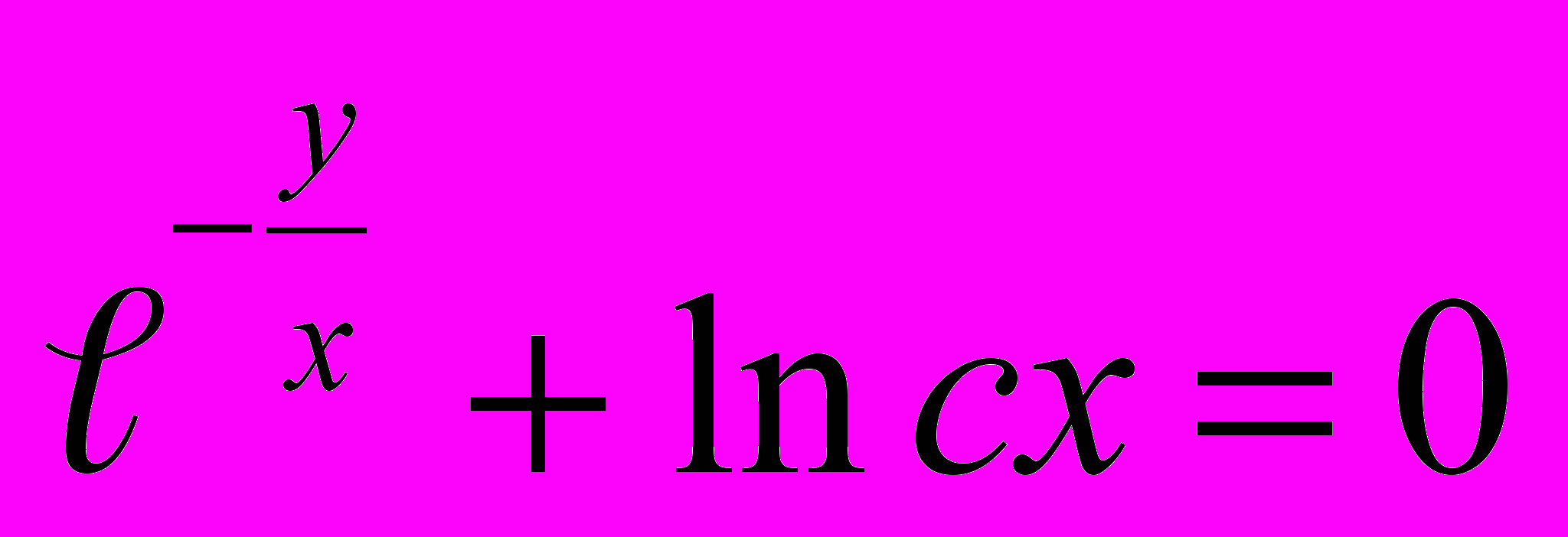
III. Решить дифференциальные уравнения.
1.
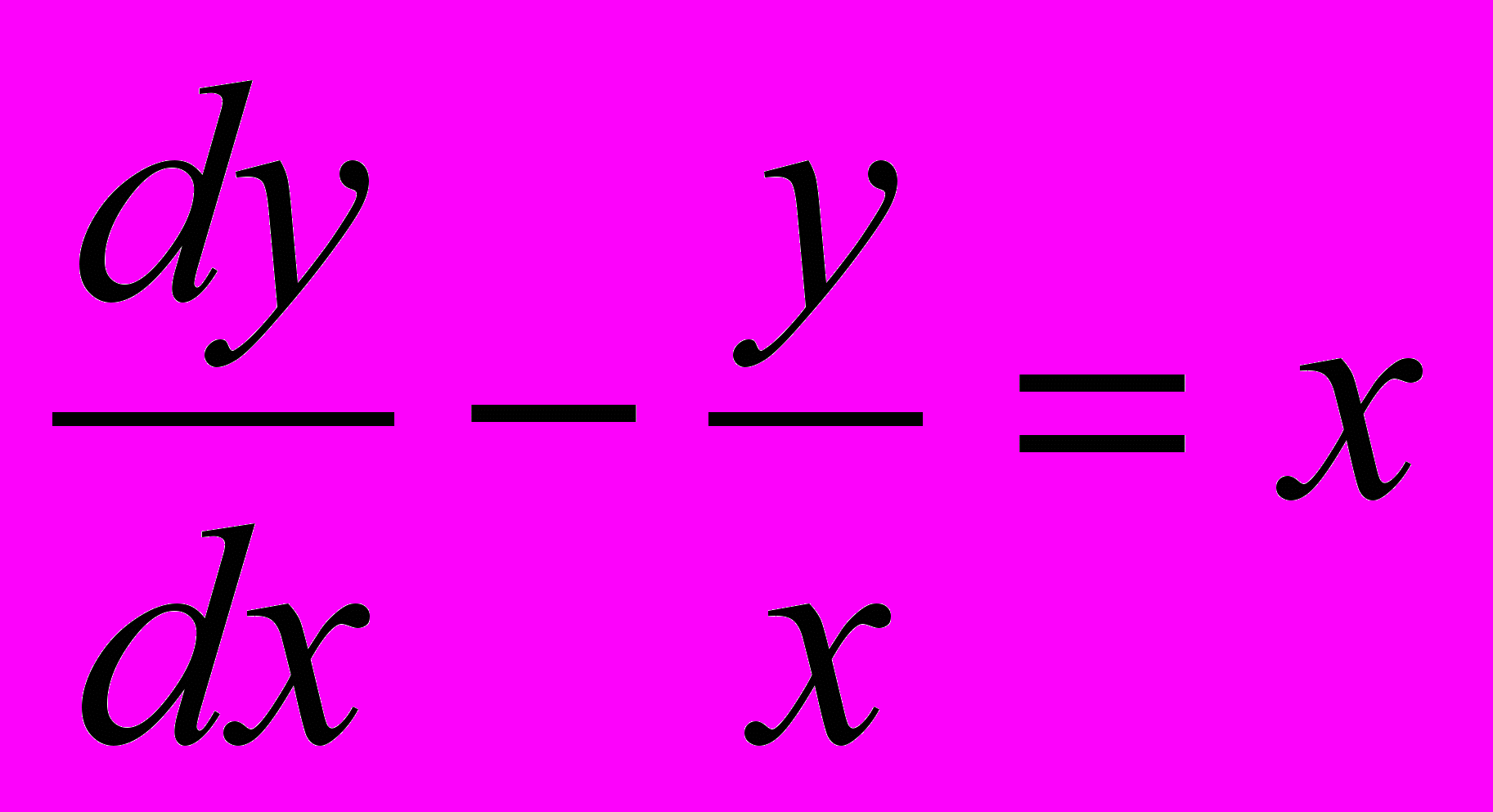 ; Ответ: у=сх+х2
; Ответ: у=сх+х22.
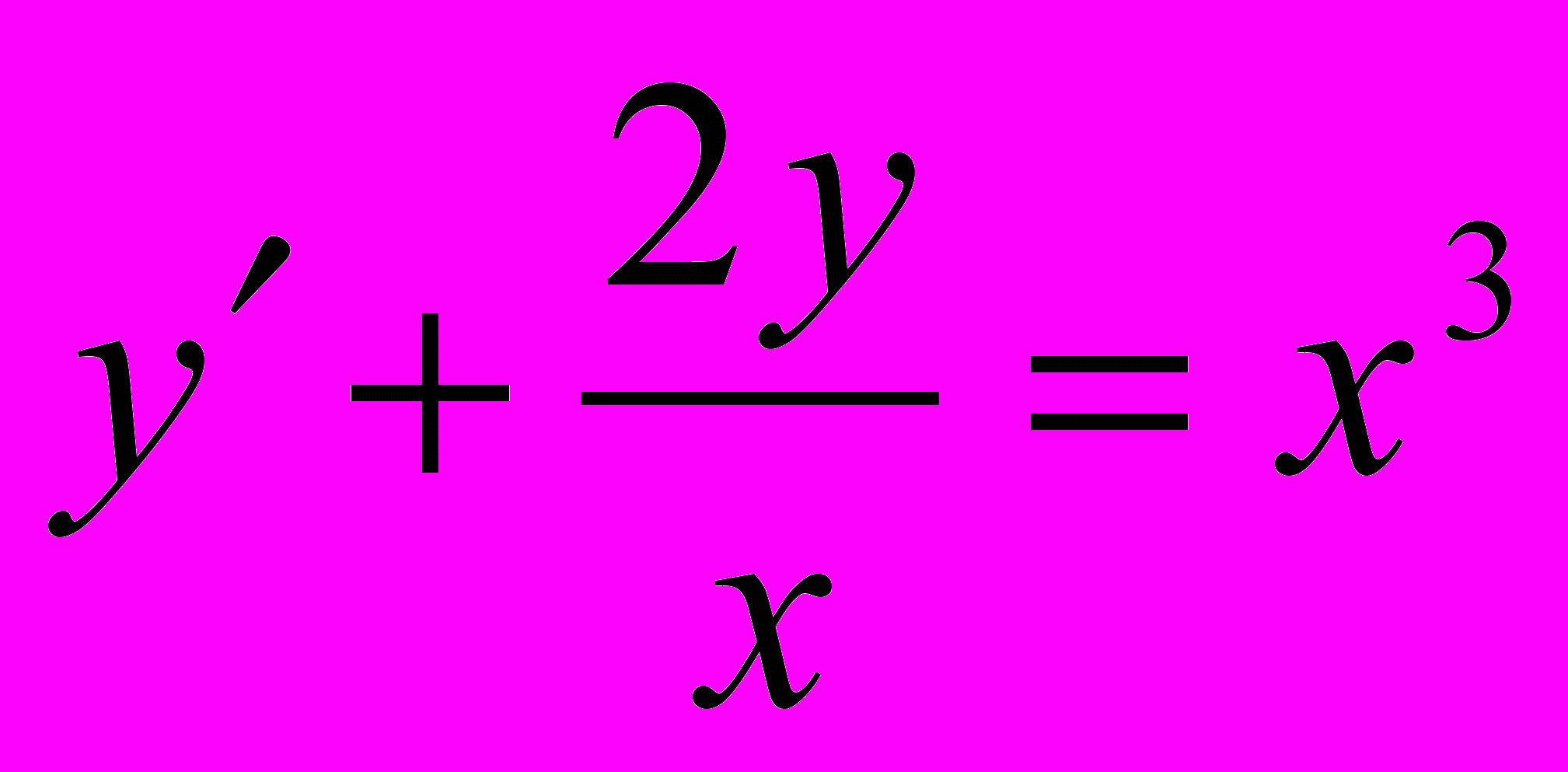 ; Ответ:
; Ответ: 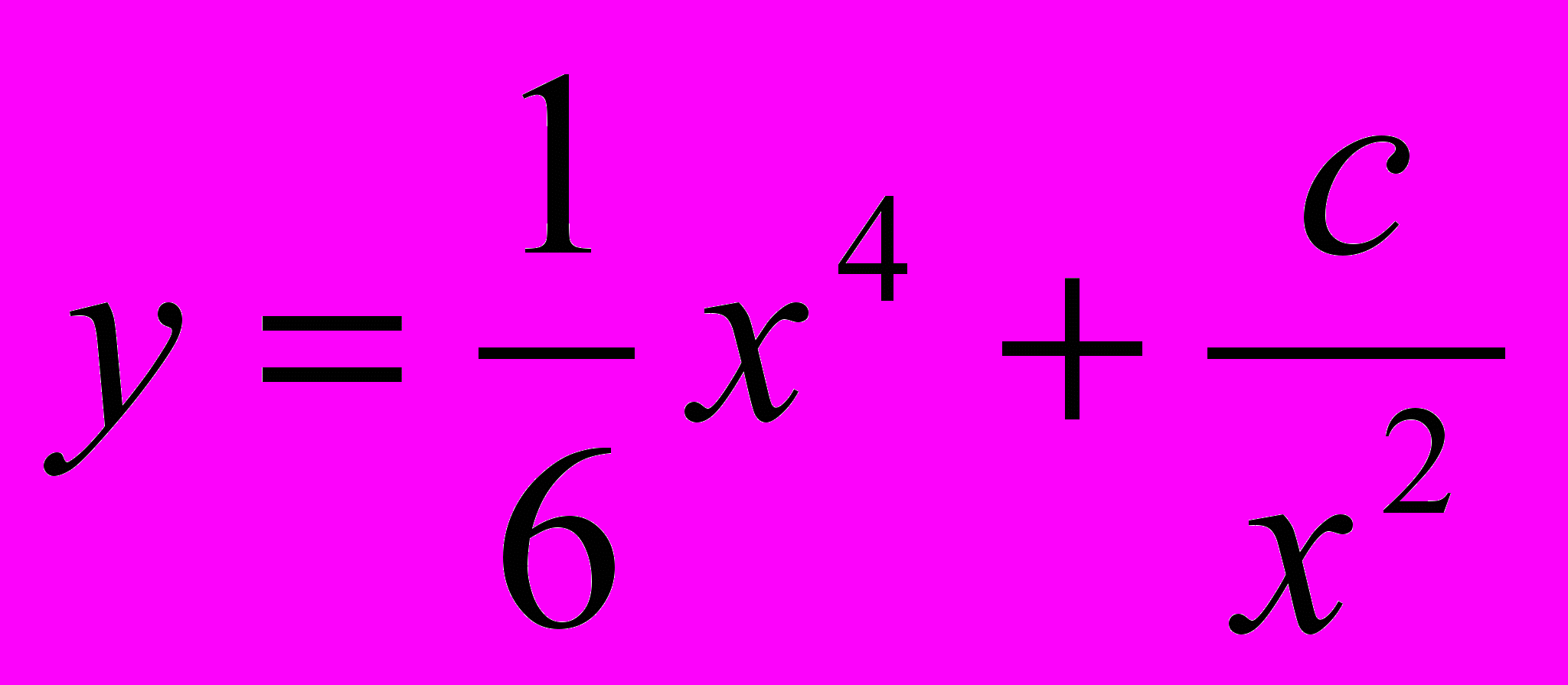
3. у2dx-(2xy+3)dy=0; Ответ:
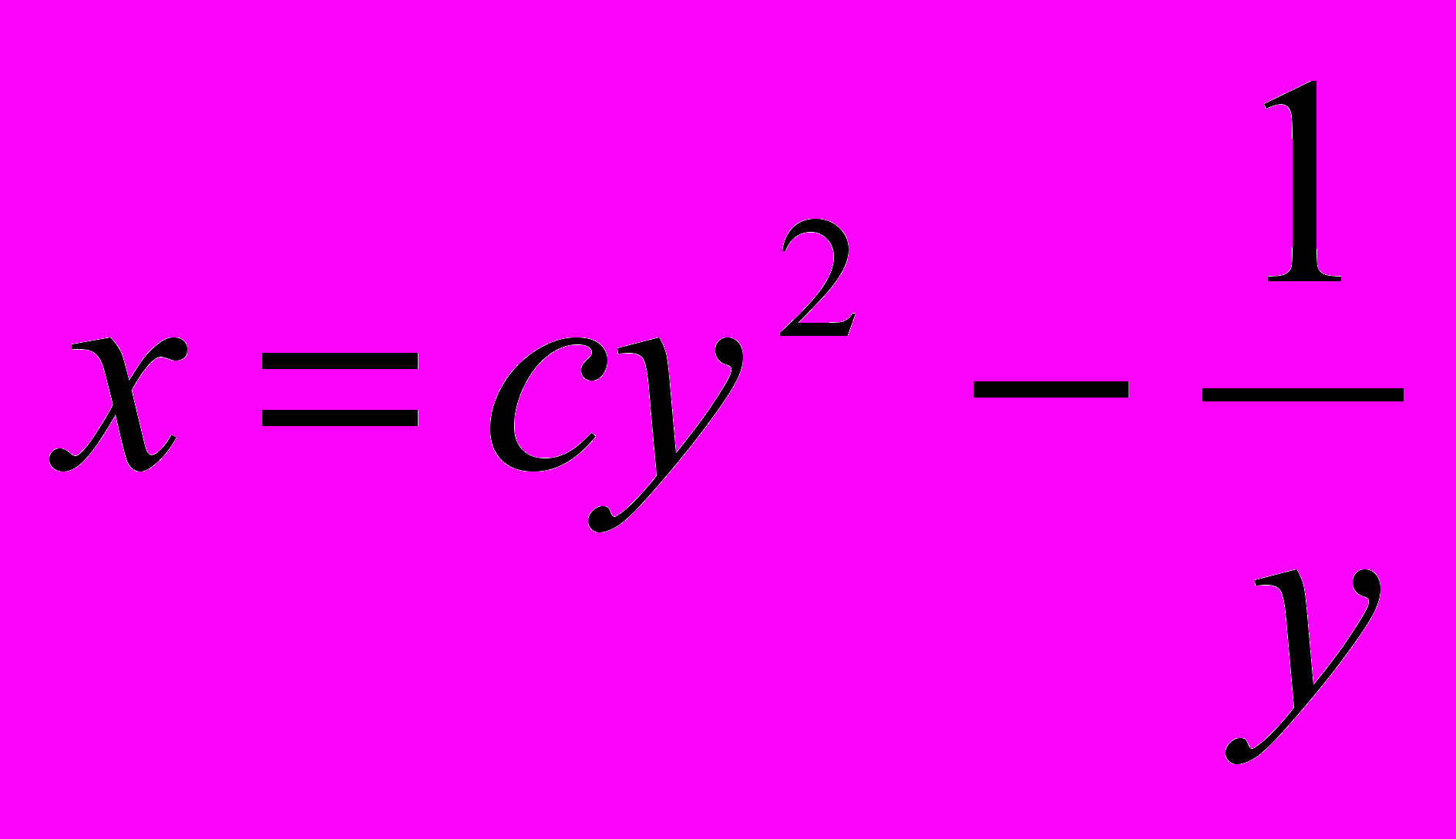
4. у'-у=℮х; Ответ: у=(х+с)*℮х
5. ху'-2у=х, у(1)=-1; Ответ: у=-х
IV. Решить задачи.
1. Определить численность населения России через 20 лет, считая, что скорость прироста населения пропорциональна его наличному количеству, и зная, что население России в 2000 году составляло 145 миллионов человек, а прирост населения за 2000 год был равен 2%.
Ответ:
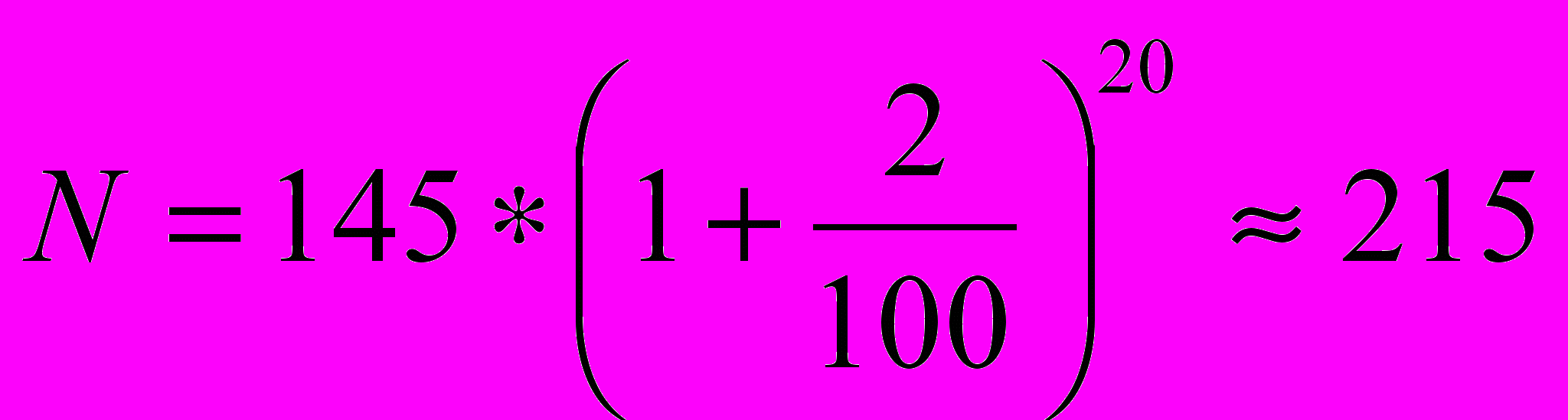 (миллионов человек)
(миллионов человек)2. Тело движется со скоростью, пропорциональной пройдённому пути. Какой путь пройдёт тело за 5 секунд от начала движения, если известно, что за 1 секунду оно проходит 8 метров, а за 3 секунды – 40 метров?
Ответ: 200 метров.
3. Найти уравнение кривой, проходящей через точку А(4; 1) для которой:
а) отрезок любой касательной к кривой, заключенной между осями координат, делится точкой касания пополам;
б) отрезок касательной между точкой касания и осью абсцисс делится пополам в точке пересечения с осью ординат.
Ответ: а)
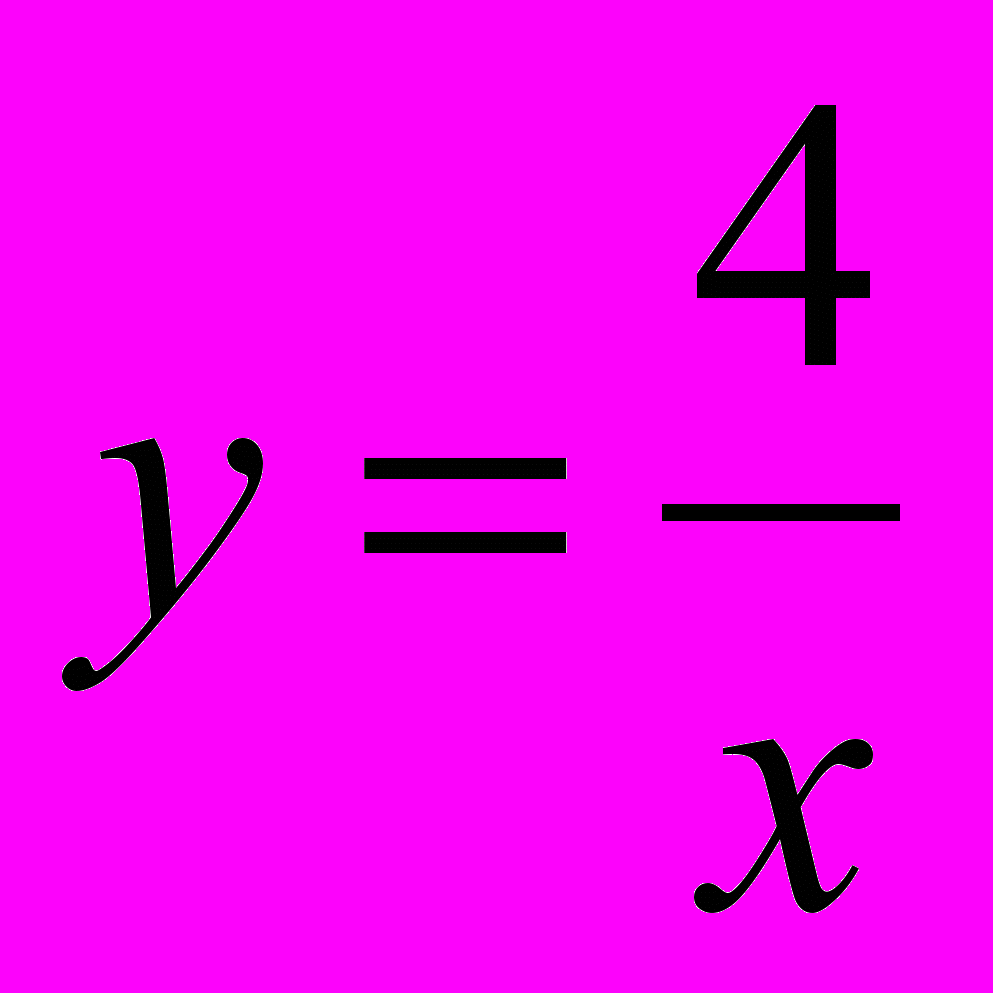 ; б)
; б) 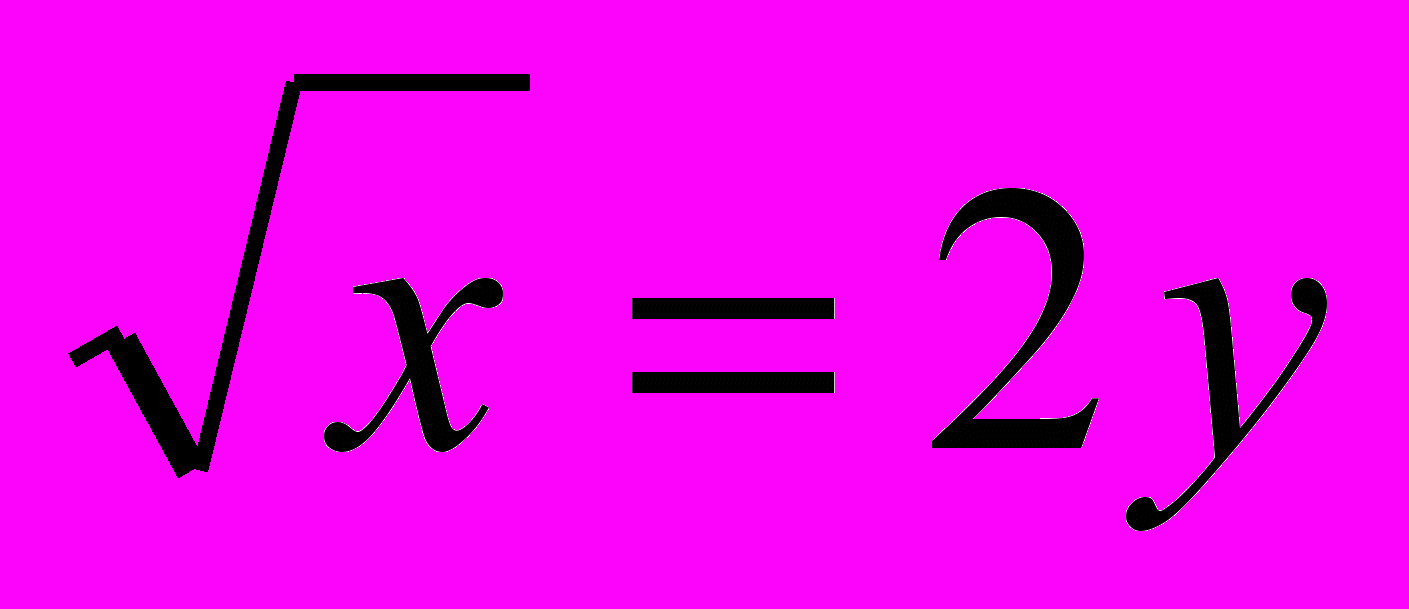 .
.4. Найти выражение объёма реализованной продукции у=у(t) и его значение при t=2, если известно, что кривая спроса имеет вид Р(у)=3-2у, норма акселерации
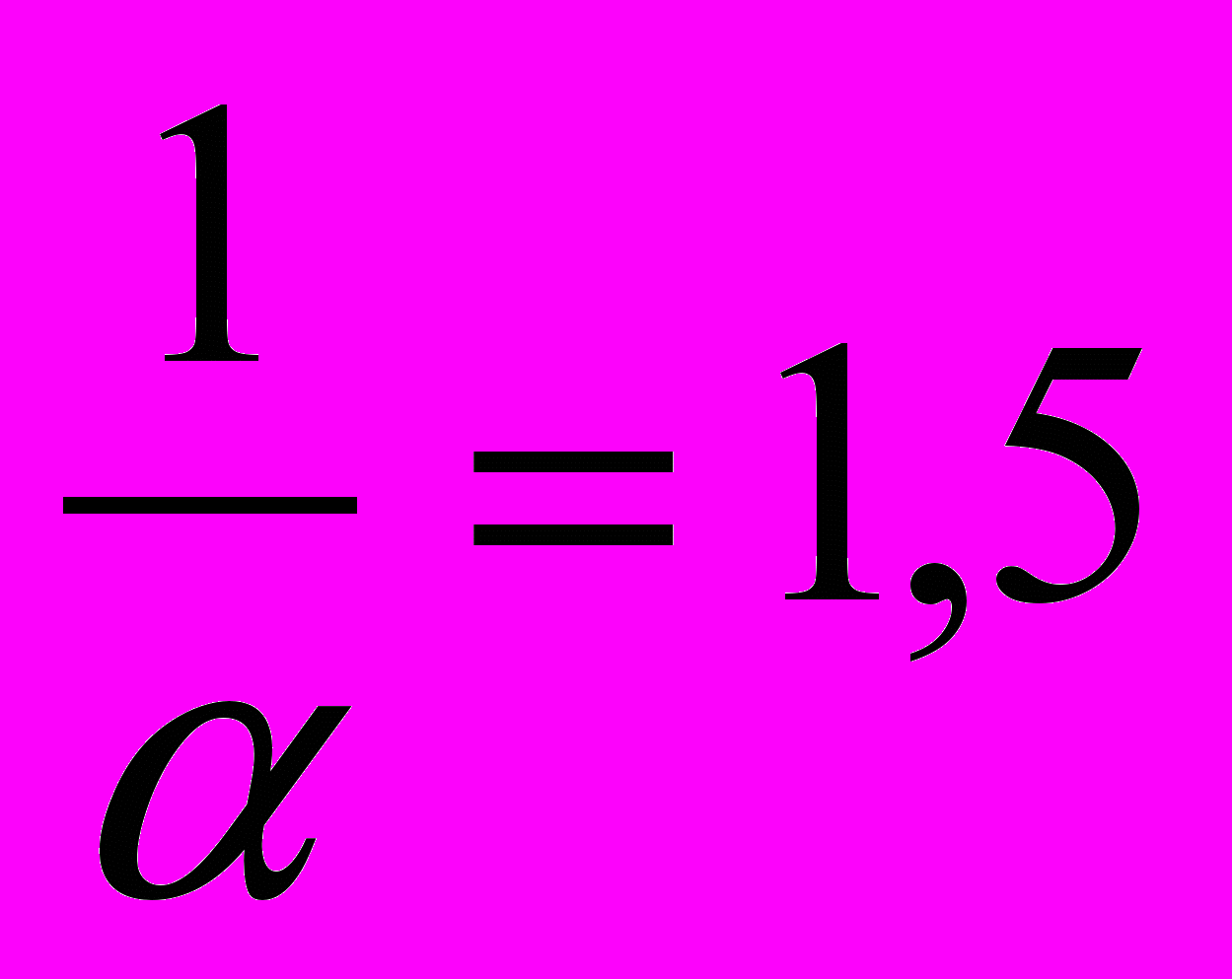 , норма инвестиций β=0,6; у(0)=1.
, норма инвестиций β=0,6; у(0)=1.Ответ:
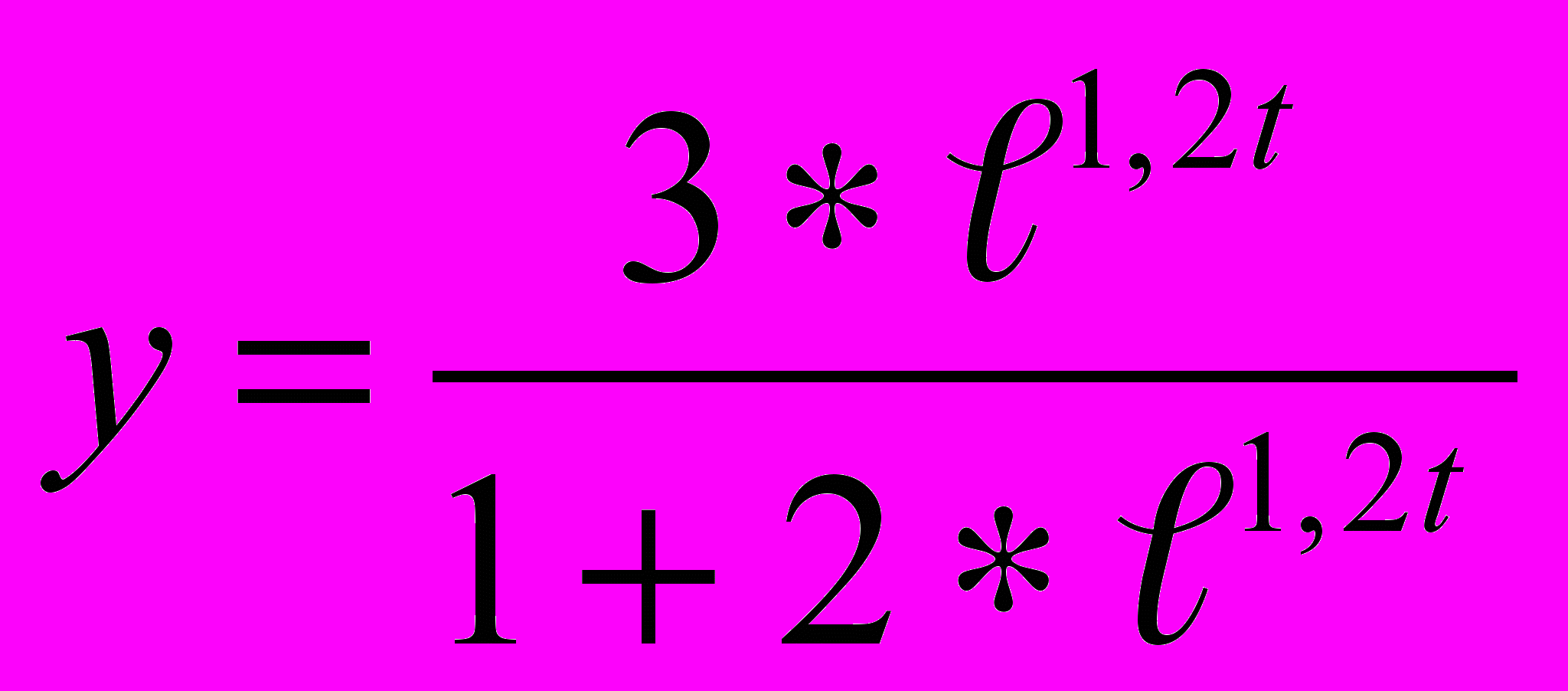 ;
; 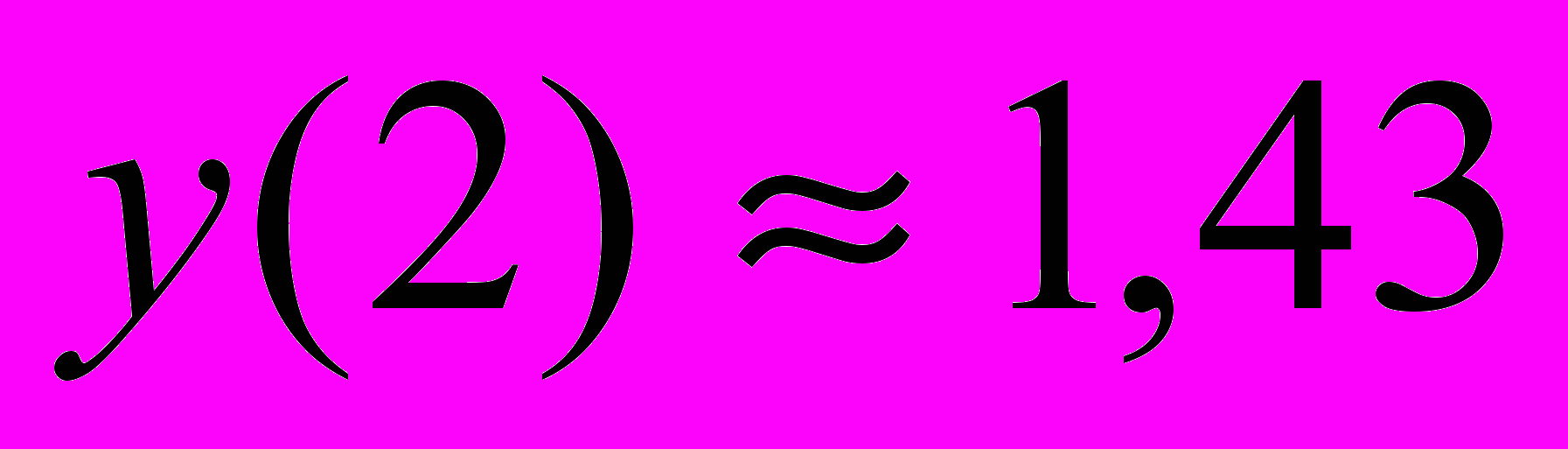
V. Решить дифференциальные уравнения.
1. у'''=℮2х Ответ:
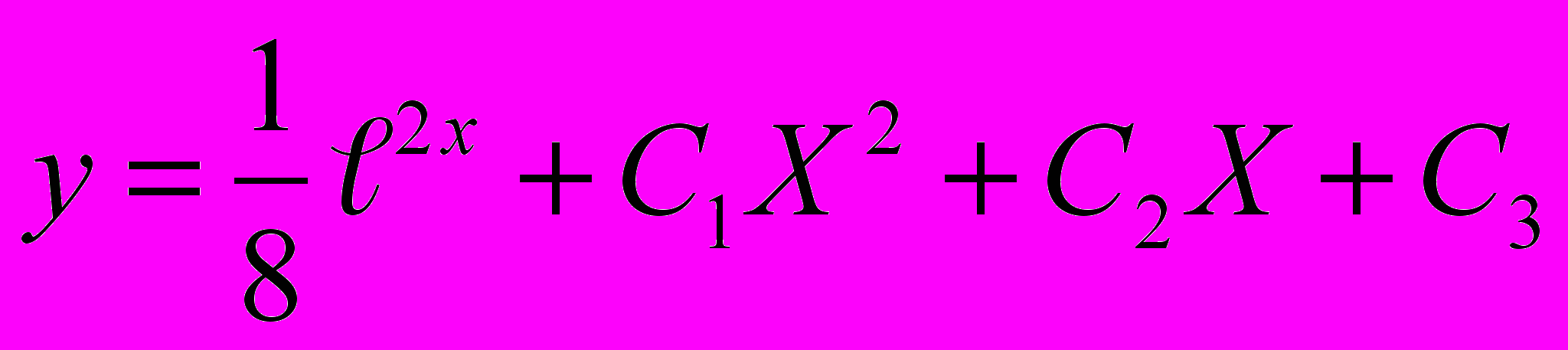
2. х(у''+1)+у'=0 Ответ:
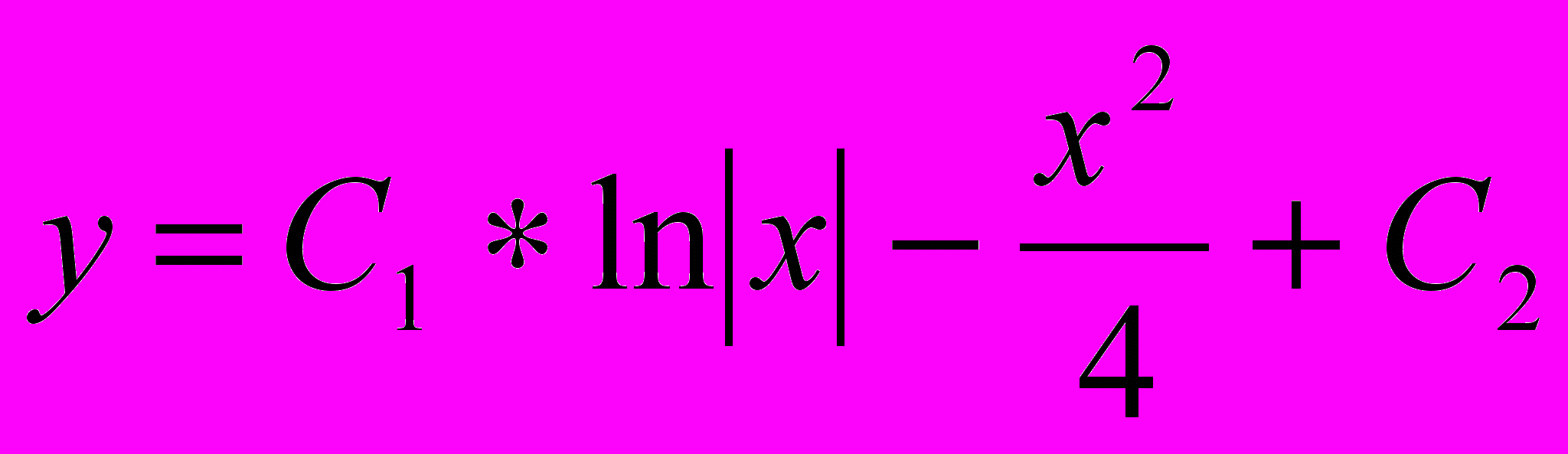
3. уу''=(у')2-(у')3, у(0)=1; у'(0)=2 Ответ:
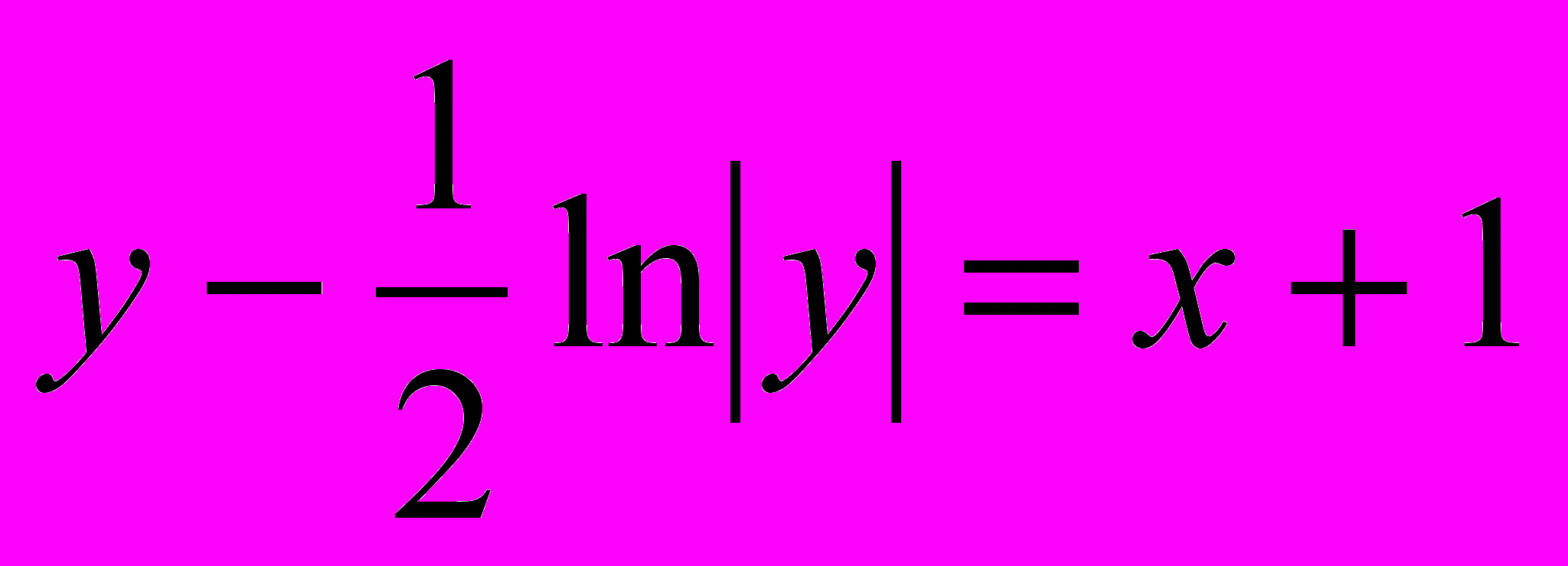
4. 2у(у')+у''=0, у(0)=0; у'(0)=-3 Ответ: у3-у=3х
VI. Решить дифференциальные уравнения.
1. у''-4у=3х2+2х+1 Ответ:
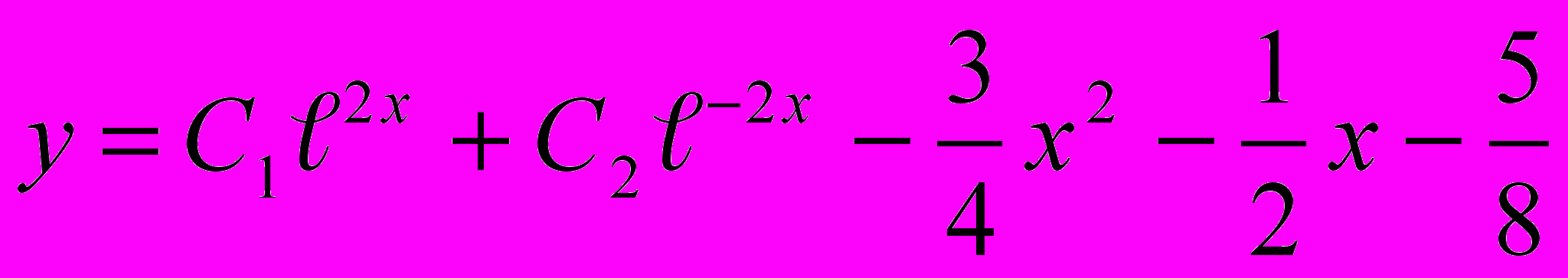
2. у''+у'-2у=х2+3 Ответ:
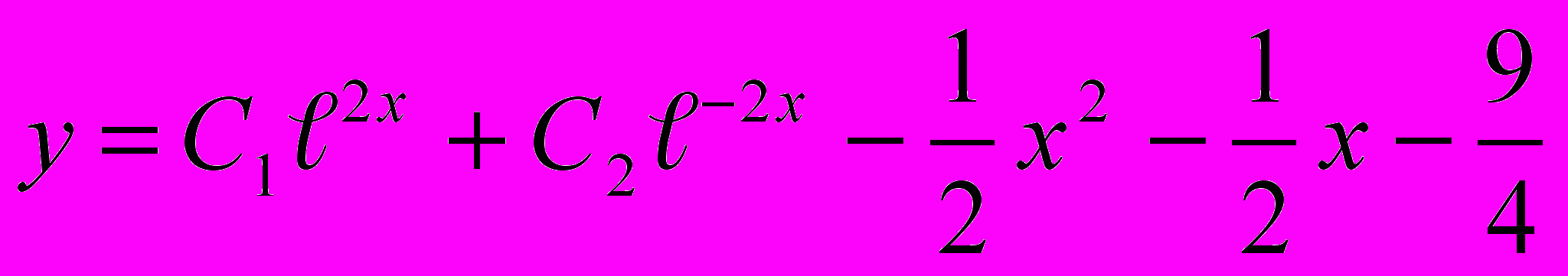
3. у''-5у'=3х+1 Ответ: у=С1+С2℮5х-0,3х2-0,32х
4. у''+4у'=2х-1 Ответ:
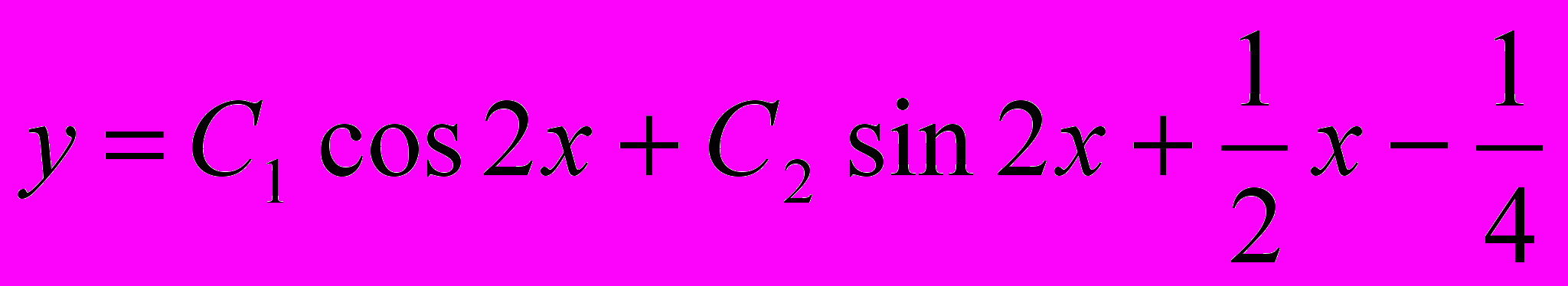
5. у''-4у=℮2х Ответ:
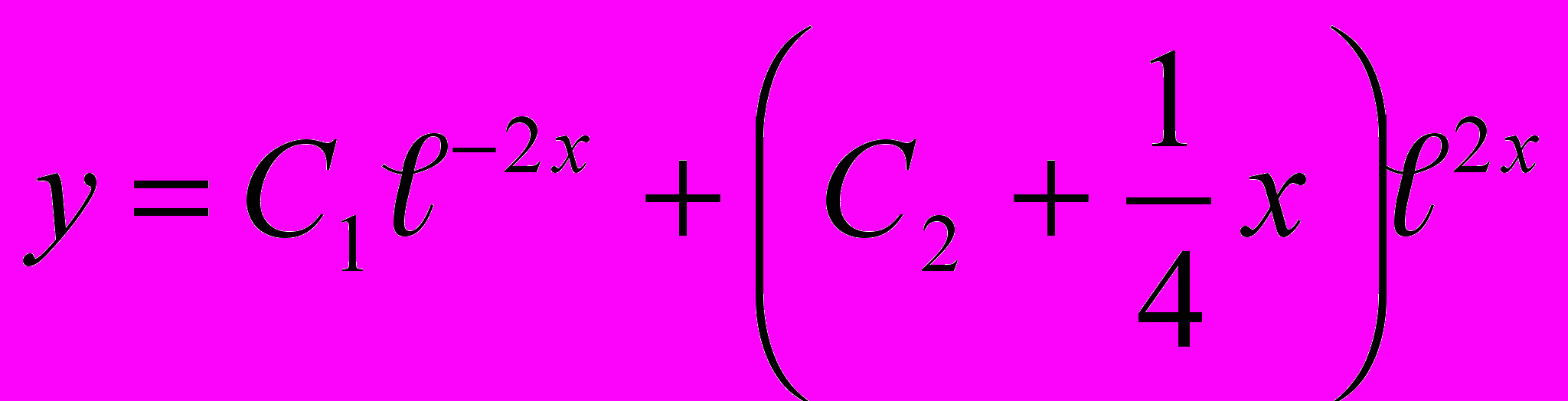
6. у''+у'-2у=℮2х Ответ:
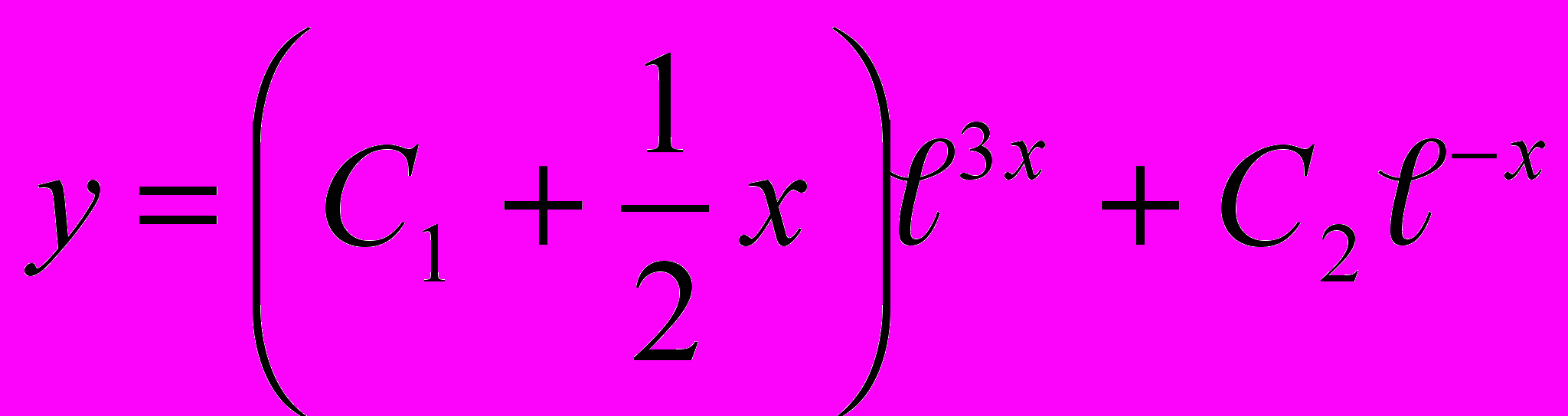
7. . у''+4у=sin2x+2cos2x Ответ:
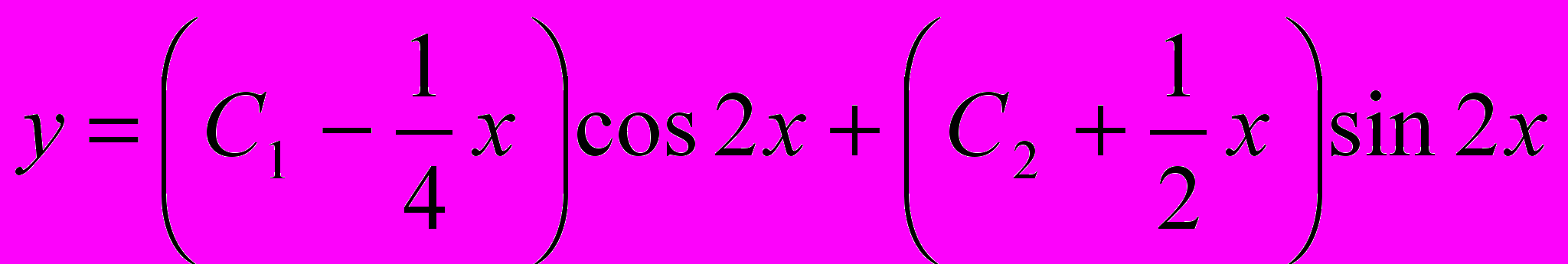
8. у''+1=cosx Ответ:
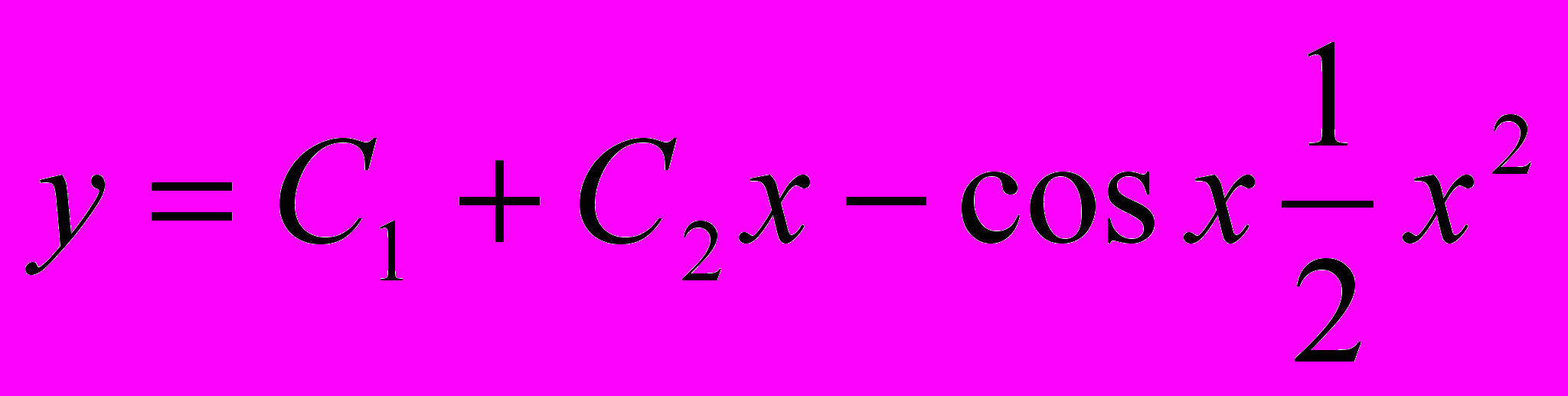
VII. Решить дифференциальные уравнения.
1. у''+у=ctgx Ответ:
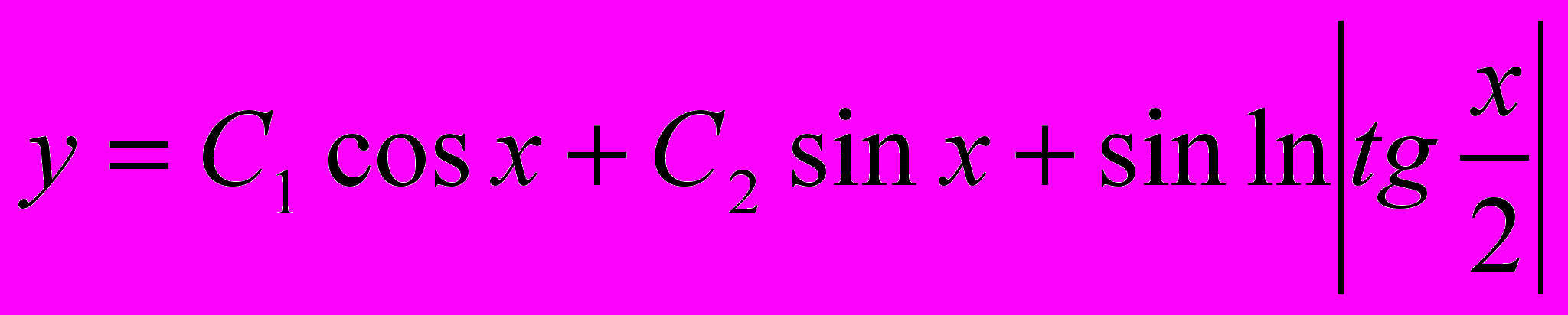
2.
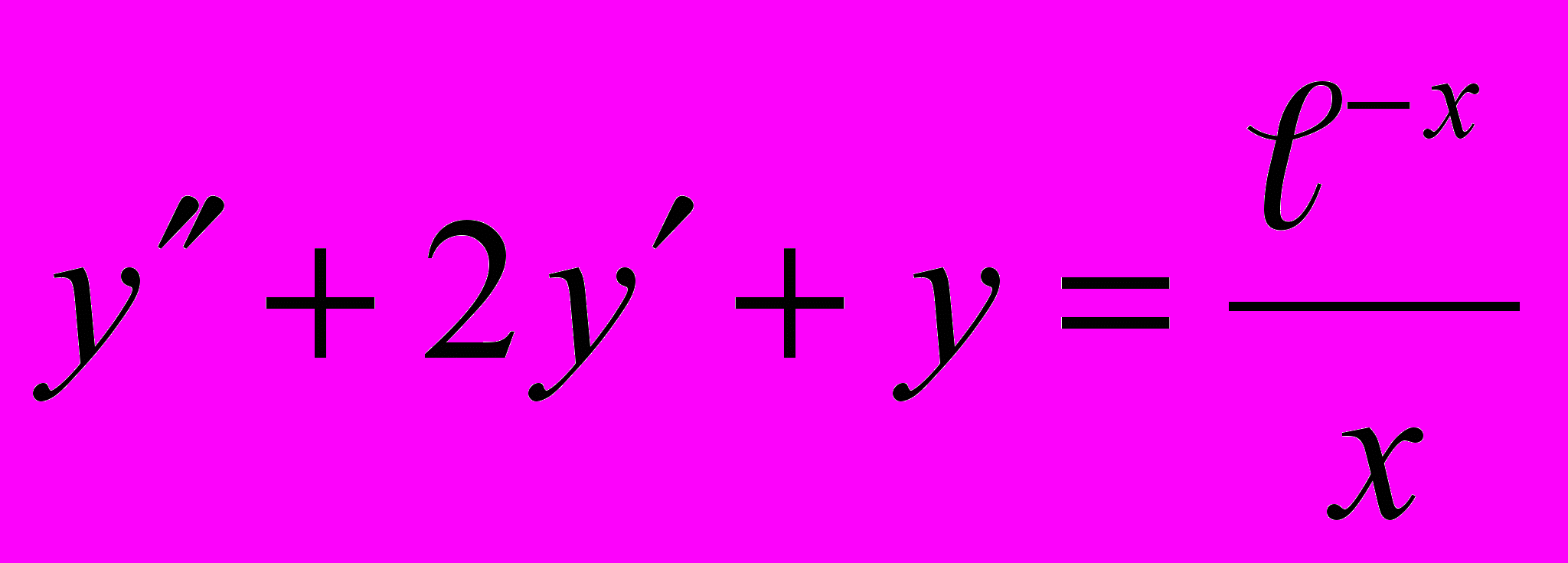 Ответ:
Ответ: 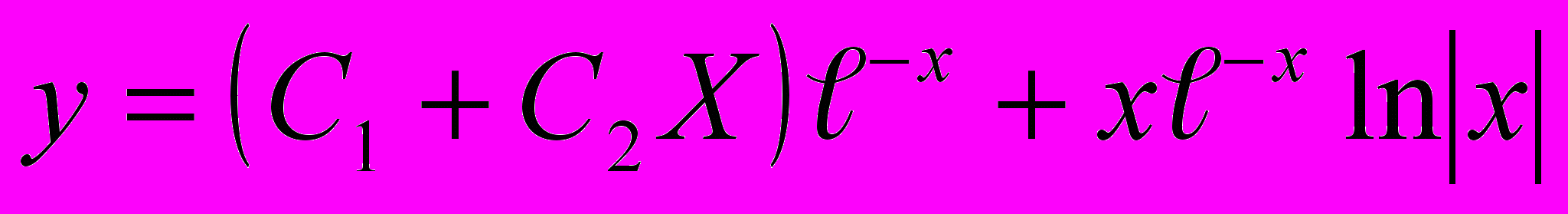
VIII. Решить системы дифференциальных уравнений.
1.
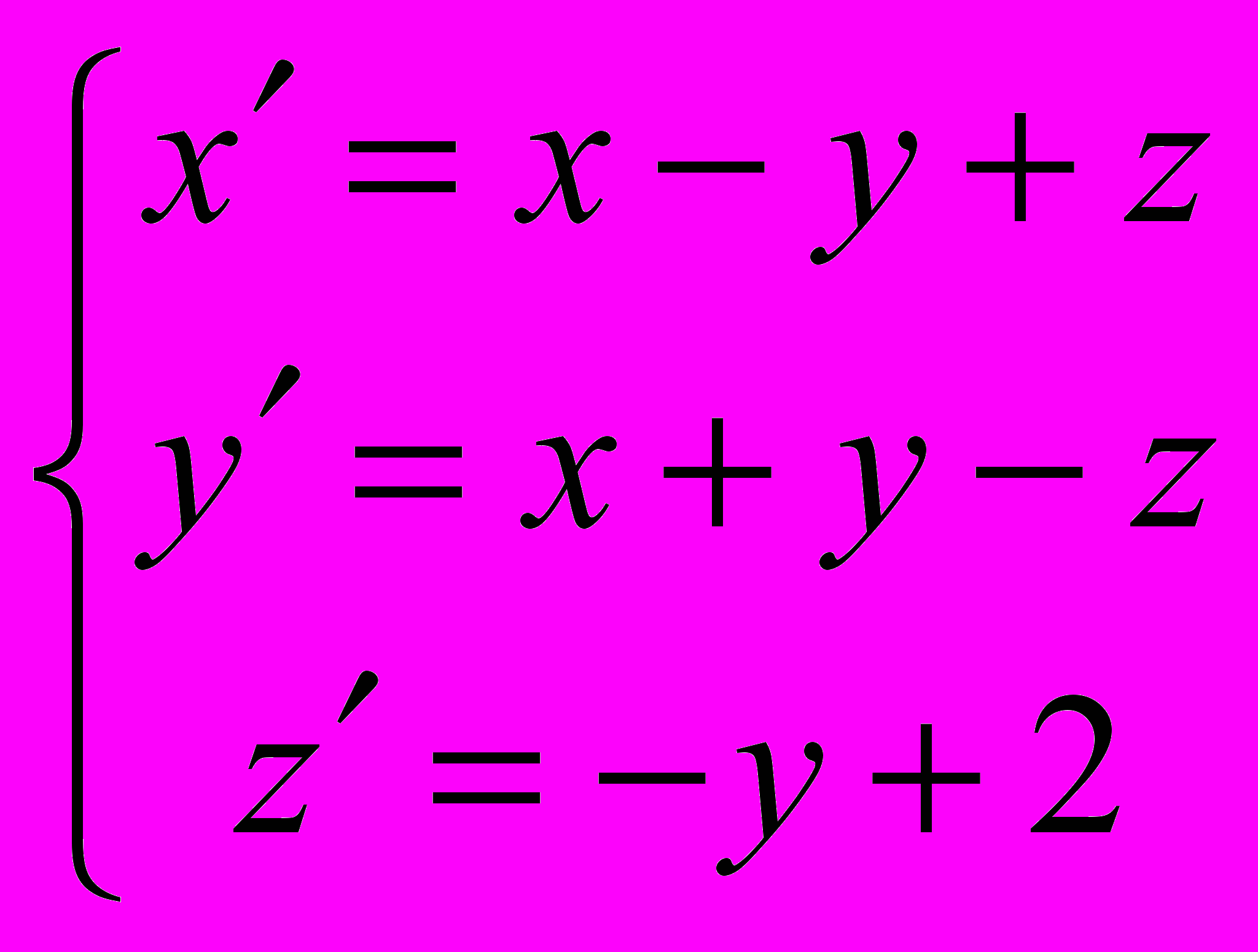 Ответ:
Ответ: 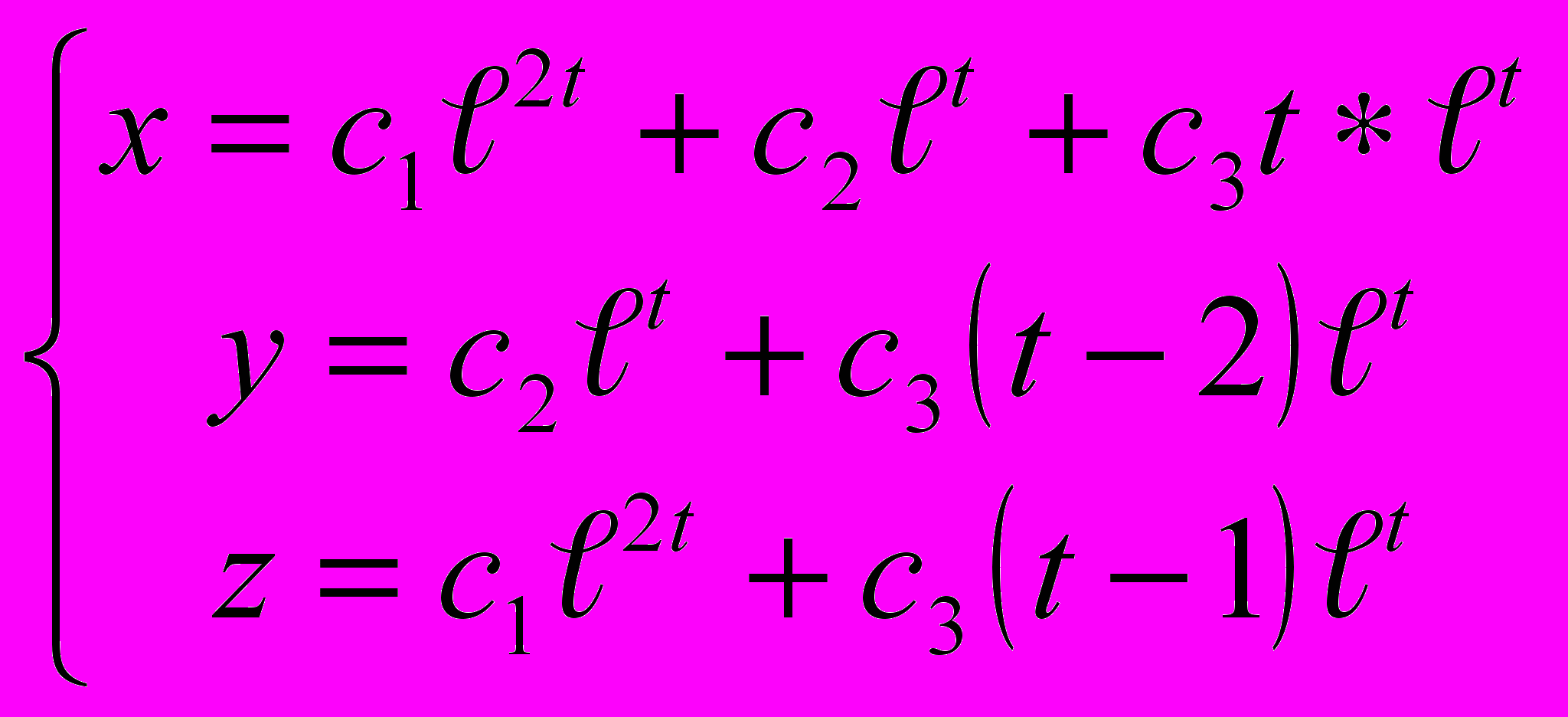
2.
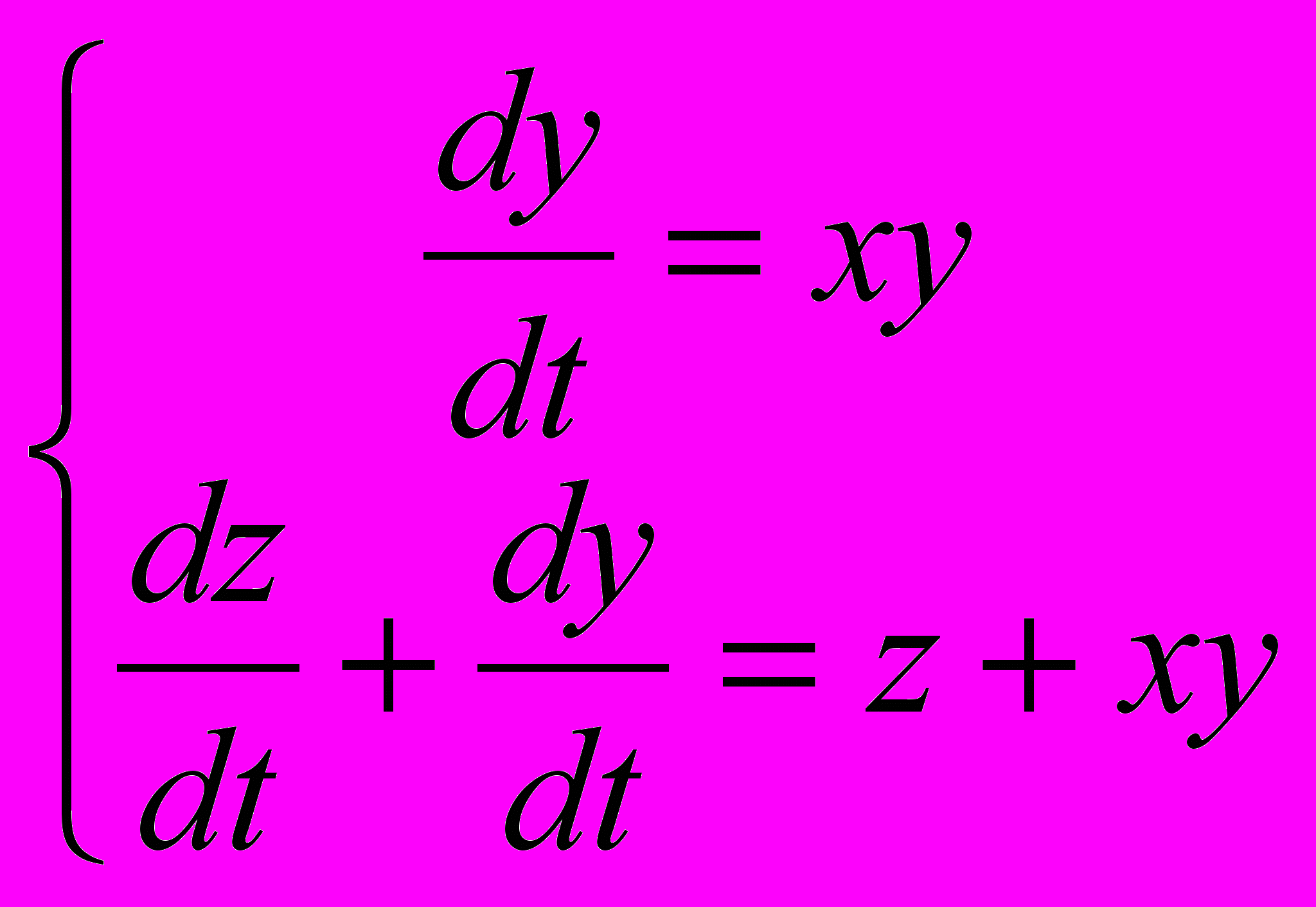 Ответ:
Ответ: 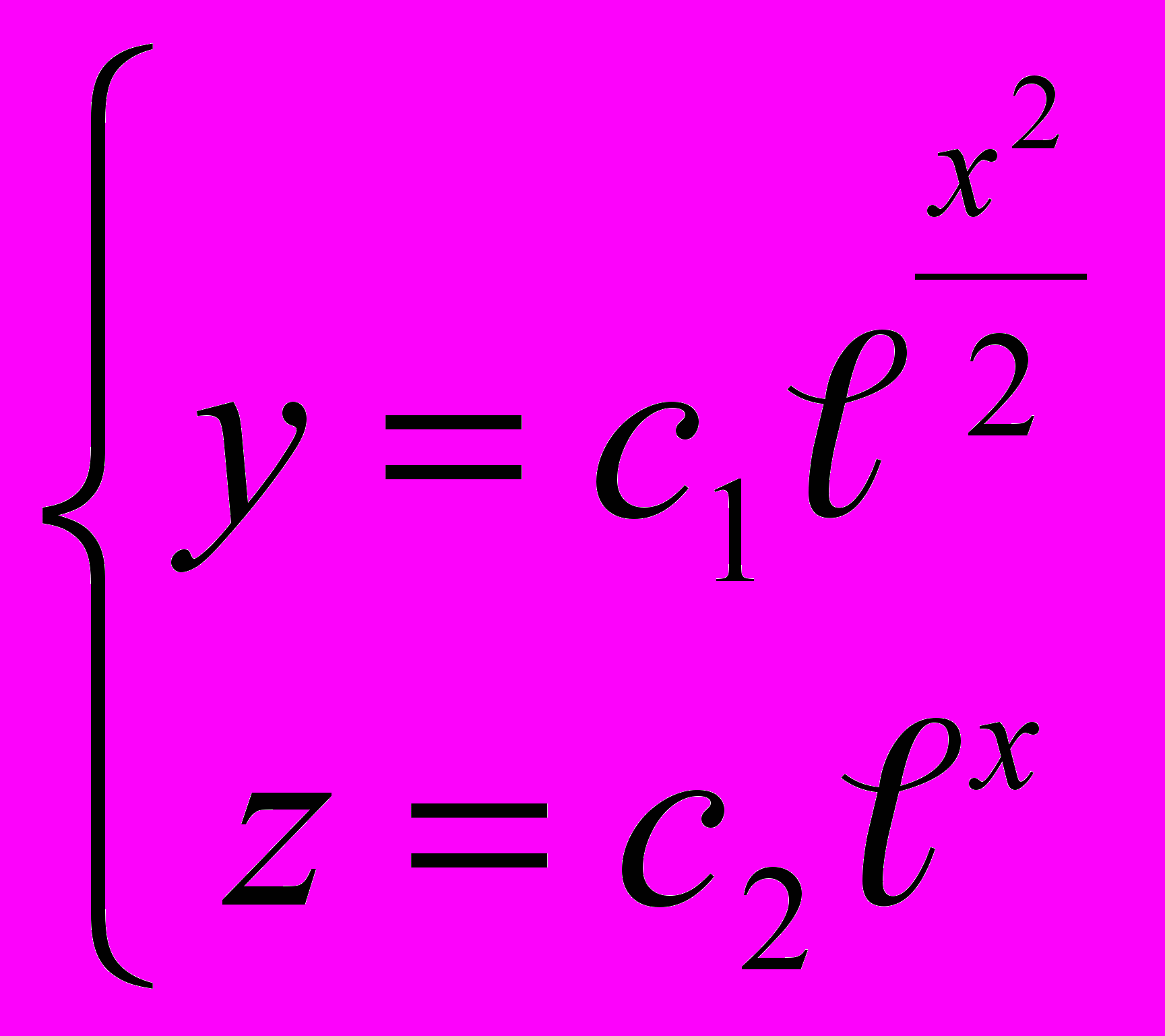
IX. Найти решение разностных уравнений.
- yn+2-4yn+1+3yn=0
- yn+2-4yn+1+yn=0
- yn+2+6yn+1+5yn=0
- yn+2+4yn+1+6yn=0
- yn+2+3yn+1-4yn=5*(-4)n
- 2yn+2-3yn+1 -5yn=2n+3
