И. В. Дробышева кандидат педагогических наук, профессор

Вид материала

Документы

Содержание Информационные технологии в научно-исследовательской, проектной деятельности школьников и студентов 1 этап. Начальные общеобразовательные условия, с которых обучаемый начинает заниматься научно-исследовательской деятельностью. 2 Собственная поисковая деятельность является необходимым условием развития личности учащихся, пропедевтикой их дальнейшей карьеры

Подобный материал:

• Федеральными Государственными Требованиями детство примерная основная общеобразовательная, 3629.29kb.
• Федеральными Государственными Требованиями детство примерная основная общеобразовательная, 7829.77kb.
• Декан, кандидат педагогических наук, доцент Е. В. Шустова Доктор педагогических наук,, 538.89kb.
• Программа воспитания и обучения в детском саду, 3936.51kb.
• Программа воспитания и обучения в детском саду, 3919.5kb.
• Программа воспитания и обучения в детском саду, 3924.08kb.
• Программа воспитания и обучения в детском саду, 3718.01kb.
• Л. Р. Муминова доктор педагогических наук, профессор; Е. В. Оганесян кандидат педагогических, 2948.06kb.
• «Слова о Полку Игореве», 3567.27kb.
• Умк занкова Дидактическая система развивающего обучения Л. В. Занкова академик, доктор, 139.44kb.

ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ В НАУЧНО-ИССЛЕДОВАТЕЛЬСКОЙ, ПРОЕКТНОЙ ДЕЯТЕЛЬНОСТИ ШКОЛЬНИКОВ И СТУДЕНТОВ

А.А. Русаков, В.Н. Яхович

Московский государственный гуманитарный университет
им. М.А. Шолохова, г. Москва, Россия, e-mail: arusakov@space.ru;
Орловский государственный университет, г. Орел, Россия,
e-mail: yakhovichvn@mail.ru

Продолжающийся процесс информатизации общества оказывает заметное влияние на сферу образования, главной целью которого становится создание обучаемому условий, позволяющих адаптироваться и развиваться в условиях постоянного возрастания потоков информации.

Информатизация образования направлена на повышение качества образования, формирование информационной культуры, нового мировоззрения, основанного на понимании определяющей роли информации и информационных процессов в окружающем мире, социализацию учащихся в постоянно изменяющейся информационной среде.

Научно-исследовательская деятельность учащихся (школьников и студентов) по математике и информатике – это, прежде всего, формирование дидактических условий, в которых обучаемые получают новые импульсы:

• для более глубокого освоения предмета;
  
• для развития опережающего обучения;
  
• для мотивации разработки своего собственного образовательного продукта;
  
• для последовательного перехода учащегося из объектной роли через субъектную к творческой и обучающей роли для своих товарищей;
  
• для выявления субъективной новизны результата этой деятельности и процесса ее выполнения (субъективность заключается в том, что результаты исследования являются совершенно новыми и зачастую неожиданными для самого обучаемого);
  
• для проведения собственного научно-исследовательского проекта, который иногда (и это, безусловно, достижение) заканчивается новым результатом или открытием в науке (с дальнейшей публикацией в научном журнале);
  
• для осмысления нерешенных задач и знакомства с проблемами внутри математического (естественно-научного), информатического и компьютерного знаний [1].
  

Несмотря на наличие индивидуальных особенностей у каждого конкретного школьника и студента можно выделить некоторые общие этапы введения его в научно-исследовательскую работу.

1 этап. Начальные общеобразовательные условия, с которых обучаемый начинает заниматься научно-исследовательской деятельностью.

2 этап. Включает в себя активную позицию преподавателя при вовлечении учащегося в научно-исследовательскую деятельность, которая на данном этапе является подготовительной – введение в тематику будущего исследования, знакомство с понятийным аппаратом той области математического и/или информатического знания, внутри которой планируется дальнейшая исследовательская работа. Мотивация активной позиции учащегося, который должен прорешать определенный минимум задач по выбранной тематике, усвоить понятия. Создается язык общения.

Этот этап для некоторых обучаемых оказывается достаточно трудным, и они отсеиваются, выбирая для себя другое направление учебной деятельности, более близкую для себя тематику (учитывая это обстоятельство, изначально набирается некоторая группа учащихся, от которой, к концу второго этапа остаются несколько человек). С учащимися прошедшими первоначальный отбор и продолжается дальнейшая работа, проектируются индивидуальные траектории их научно-исследовательской деятельности.

3 этап. Корректируются индивидуальные траектории научно-исследовательской деятельности, сужается тематика, которая на данном этапе все еще достаточно широка. В этом поле ставится задача поиска источников (литературы, учебной и научной), их изучения, осмысления проекта, хотя бы реферативного.

По выбранной теме учащийся совместно с учителем подбирает литературу, по которой знакомится с необходимым понятийным аппаратом и решает учебные и нацеленные задачи, имеющие субъективную новизну для обучаемого, делится результатами со своими товарищами (решение у доски, доклад на семинаре и т.п.).

4 этап. Оформление результатов работы. Это не всегда обязательный, но очень важный этап исследования учащегося. Не каждому удается правильно подать полученный результат (при постоянной коррекции целей и постоянном дозировании), показать свою работу, пусть не новые для естественно-научного, компьютерно-информатического знания, но самостоятельно решенные задачи, свой собственный алгоритм, свой программный продукт.

В том же случае, когда руководитель видит значительное продвижение обучаемого по предложенной ему траектории, то данный этап промежуточной фиксации и оформления возможно или продлить, или отсрочить, или вовсе опустить (решение сугубо индивидуальное).

5 этап. На этом этапе, когда студентами накоплен достаточный материал, уже можно говорить и обсуждать пути подходов к решению исследовательской задачи.

Данный этап в свою очередь разбивается на микроцели, в какой-то мере повторяющие предыдущие этапы, в соответствии с мнением А.Н. Колмогорова о том, что обучение математике должно состоять из нескольких ступеней – витки обучения по спирали, с выходом на все более и более высокий уровень.

Для знакомства с узкоспециализированной задачей необходим более глубокий понятийный аппарат. Теперь обучаемому не достаточно общедоступной литературы – набор возможных источников сужается вплоть до научных статей, диссертационных исследований и т.п.

Постоянное дозирование материала.

Постоянная мотивация дальнейшего продвижения в решении поставленной задачи в ходе общения с учащимися.

Постоянная коррекция целевой функции – какие задачи обучаемый должен решить на данном этапе, в соответствии с достигнутым уровнем развития математической и информатической подготовки по конкретной тематике исследования.

Поддержание субъективной уверенности в возможности решения обучаемым поставленной задачи на каждом этапе.

Прослушивание выступления учащегося у доски.

Индивидуальные беседы.

Конечная цель – получение объективно нового результата в науке.

«Думаю, вообще очень немногое может быть сравнимо с тем чувством, которое овладевает человеком, когда он сделал научное открытие. Он узнал новое, еще совершенно неизвестное, своим открытием принес пользу людям. Именно это, видимо, и дает то наивысшее удовлетворение, какое только возможно для ученого» М.В. Келдыш.

6 этап. Оформление полученного результата в виде презентации или доклада на конференцию, или в виде публикации в научный журнал.

Собственная поисковая деятельность является необходимым условием развития личности учащихся, пропедевтикой их дальнейшей карьеры ученого.

Одной из организационных форм вовлечения в исследовательскую работу учащихся может служить предмет математического практикума. Математический практикум предназначен для студентов, обучающихся практическому программированию (на компьютерах любого типа), сегодня его можно смело называть «Компьютерный практикум». Цели практикума: дать конкретное представление о важнейших прикладных методах, связанных с математическим анализом; на конкретных примерах отработать приемы решения задач с помощью компьютеров; в конечном счете, продемонстрировать плодотворность взаимодействия, сочетания «математические методы + возможности компьютера». Математический практикум, таким образом, поддерживает два курса – математики и программирования, равно как и опирается на них.

Р
(1)
ассматриваемый практикум посвящен анализу нелинейных одномерных динамических систем с дискретным временем. С точки зрения чистой математики речь идет об исследовании поведения последовательностей, заданных рекуррентно:

,

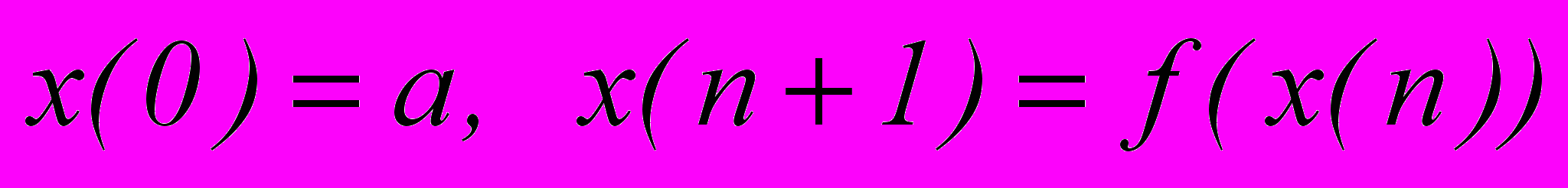где f – заданная числовая функция, одна и та же для всех n. Слово «поведение» по отношению к последовательностям расшифровывается многообразно, в соответствии с разнообразными возможностями: последовательность может быть ограниченной и неограниченной; возрастающей, убывающей или немонотонной; постоянной, периодической (типа x(n)=(-1)ⁿ или x(n)=sin n^o) или непериодической; сходящейся (стабилизирующейся, как сказал бы прикладник; имеющей предел, как сказал бы математик), стремящейся к бесконечности или вообще ведущей себя нерегулярно, хаотично …

С точки зрения прикладной математики ведется наблюдение за изменением во времени (эволюцией) некоторой величины х. Идеально было бы знать зависимость х от t – функцию x=x(t) – с тем, чтобы делать какие-то предсказания о ходе эволюции. В реальности часто бывает так, что, во-первых, мы можем следить за величиной х не постоянно, а через определенный промежуток времени (например, при метеорологических наблюдениях). Приняв этот промежуток времени за 1, осуществляется переход от функции x(t) (tR) к последовательности:

{x(0), x(1), x(2), …, x(n), x(n+1), …},

описывающей изменение величины х во времени – в дискретном времени.

Далее, идея заключается не в измерении х, а в предсказании поведения x(n), в идеале предполагающем априорное знание последовательности x(n). И здесь в реальности имеет место второе обстоятельство: чаще мы не можем написать формулу для x(n), но можем по значению x(n) предсказать значение x(n+1) – указать закон изменения

f: x(n)  x(n+1).

Если это простая функциональная связь вида (1), то приходим к итерационным последовательностям.

Получив уравнение вида (1), естественно попытаться получить из него явную формулу для x(n), после чего, изучить поведение последовательности x(n) средствами математического анализа.

Так задание практикума «Итерации» состоит в разработке достаточно универсальной программы, которая по запрограммированной функции f(x) строила бы геометрическую интерпретацию итерационных последовательностей, так называемые «лестницы Ламмерея» для этой функции.

Например, рассматривается следующая задача:

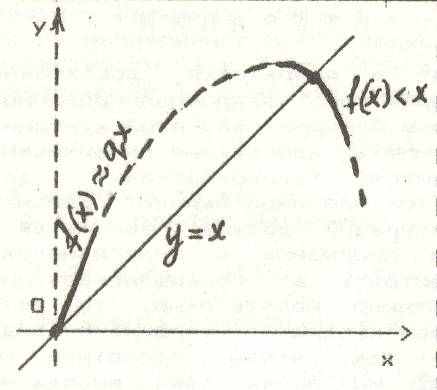
Пусть X(n) – величина нашего вклада в сбербанке в n-м году. Наше поведение следующее: ежегодно мы вносим А$, а тратим В$. Банк же ежегодно начисляет Р% к нашему вкладу. Написать формулу для Х(n).

В ходе практикума учащимся дается представление о том, что во многих приложениях итерируемая функция f должна обладать некоторыми априорными свойствами, например, «биологические» законы эволюции должны описываться функциями определенного вида (см. рис.), простейшими из которых являются квадратичные функции вида f(x)=ax(b-x), где a, b > 0.

Зачастую решение задачи исследовательского проекта по математике (с определенной степенью точности) может быть найдено при помощи компьютерной программы, что позволяет выдвинуть гипотезу и только затем построить ее строго математическое подтверждение.

Примером такого проекта может служить работа «Коэффициент растяжения кривой Пеано-Гильберта», выполненная в 2002/2003 уч. г. учащимся лицея «Вторая школа» Константином Бауманом под руководством А.А. Русакова и занявшая первое место по секции «Математика» на Международной конференции «III Колмогоровские чтения», посвященной столетию великого ученого – математика и педагога А.Н. Колмогорова.

В своей работе [2] школьник получил точное значение коэффициента растяжения кривой Пеано-Гильберта (С=6). Этот результат применим в классификационном анализе данных, позволяет совершенствовать технику развертки изображения на технических дисплеях.

Полученный Константином результат не был сразу очевиден. Ему никак не удавалось доказать и получить более точную оценку константы гельдеровости С. Математическими методами была получена лишь оценка 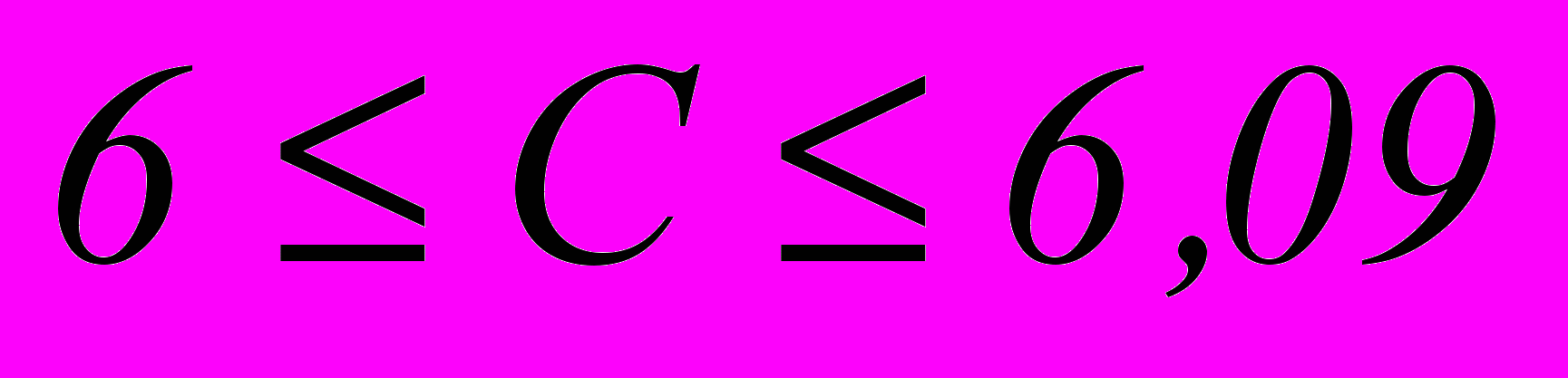. Поэтому было решено воспользоваться компьютерной программой, составленной другим учеником А.А. Русакова – Щепиным Никитой, реализующей алгоритм сокращенного перебора для оценки коэффициента растяжения С [3]. Неоднократное использование и получение оценок для константы с помощью программы Никиты увеличило степень уверенности в том, что С=6, после чего задача состояла в поиске путей доказательства этого факта. После неоднократных попыток доказать, что коэффициент растяжения кривой Пеано-Гильберта в точности равен 6 и долгой, упорной работы, ему это удалось.

Нам кажется интересной постановка исследовательской задачи, содержащая в себе необходимость применения методов численного решения, требующая составления компьютерной программы на одном из языков программирования, с выходом на вычислительные методы, работу с калькулятором и на «компьютерный практикум». Здесь, кроме понимания тесной взаимосвязи математики и информатики, учащийся получает навыки алгоритмизации, построения логической последовательности шагов решения предложенной задачи.

Рассмотрим следующую задачу.

Н
(1)
айти действительные решения кубического уравнения



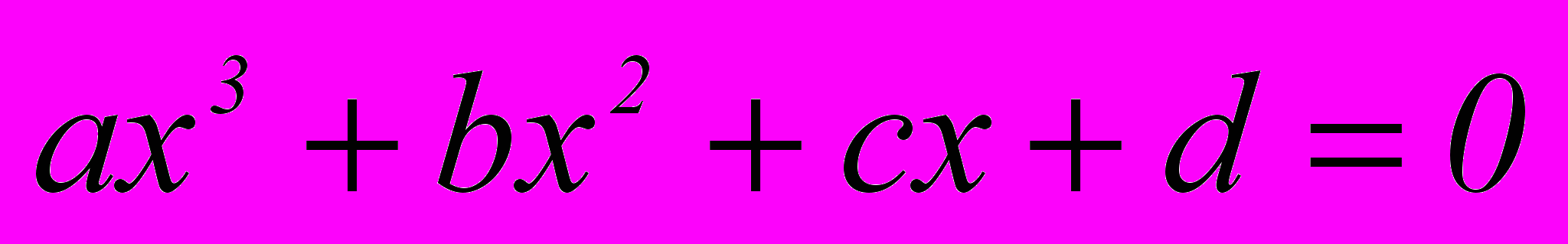
с действительными коэффициентами, удовлетворяющими следующим условиям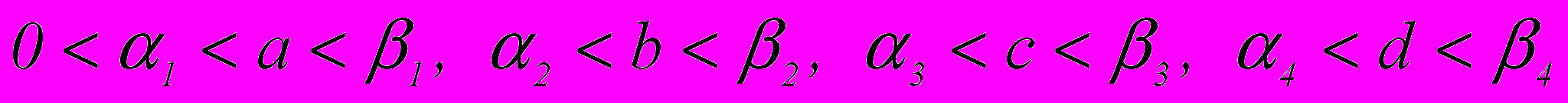, где 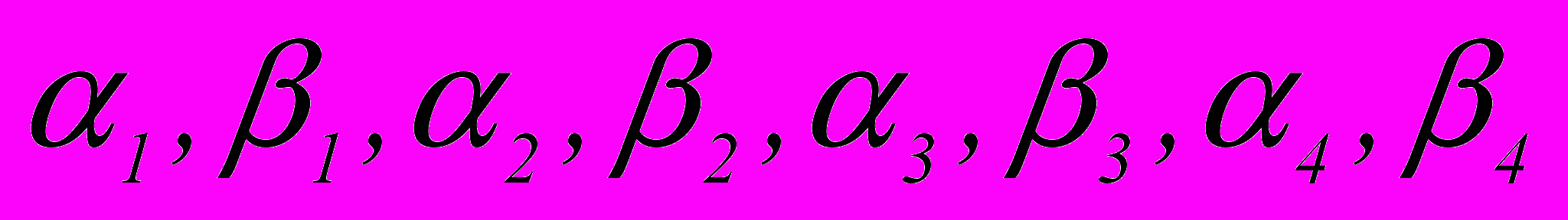– некоторые задаваемые числа, с любой наперед заданной точностью h=10– S, где s – заданное натуральное число.

Решение данной задачи, кроме изучения соответствующей литературы, требует от учащегося решения следующих подзадач.

Нахождение отрезка, внутри которого будут расположены действительные корни данного уравнения при заданных h и L=max().

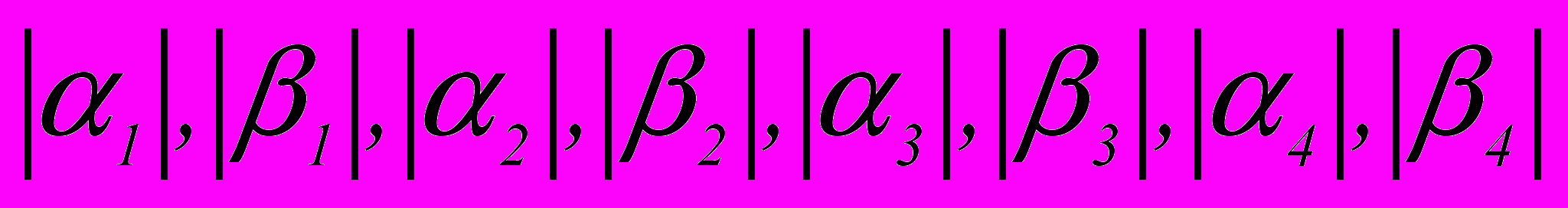Составление компьютерной программы нахождения действительных корней уравнения (1) одним из численных методов: методом бинарного поиска (метод бисекций), методом итераций, методом касательных (метод Ньютона) или др.

Отметим, что построенная выше траектория введения обучаемого в научно-исследовательскую работу не может служить однозначной рекомендацией для организации научно-исследовательской работы учащихся. Многие вопросы все еще остаются нерешенными. Как выбрать задачу посильную учащемуся? Как сделать так, чтобы он не бросил заниматься научно-исследовательской темой (не потерял интерес к математике)? Как почувствовать, увидеть необходимость «компьютерной поддержки»? Как убедить его не останавливаться на уже достигнутом, когда полученный промежуточный субъективно новый результат кажется учащемуся настоящим открытием? И другие.

Несмотря на все постоянно возникающие вопросы и проблемы, вовлечение учащихся в научно-исследовательскую работу позволяет в ходе учебной деятельности использовать приемы, соответствующие методам изучаемой науки и современному уровню развития информационных технологий, не ограничиваясь пассивным усвоением обучаемым новых знаний, а, развивая его творческий потенциал в процессе изучения многочисленных источников и выработки умения взглянуть на них с новой точки зрения; нахождения учащимся собственного оригинального решения поставленной проблемы; постановке новых вопросов в уже известном и др.


Литература

1. Русаков, А.А. Новые информационные технологии и традиционное математическое образование / А.А. Русаков, В.Н. Яхович // Педагогическая информатика, 2006. – № 2. – С. 11-16.
   
2. Бауман, К.Е. Коэффициент растяжения кривой Пеано : (первое место по секции "Математика") / К.Е. Бауман // Тезисы Международной научной конференции школьников "Колмогоровские чтения 2003". – 2003.
   
3. Щепин, Н.Е. Конструктор непрерывных раскладок кубиков / Н.Е. Щепин // Программа конференции-конкурса «Юниор» министерства образования РФ, московского комитета народного образования, МИФИ. – 2003.