Учебная программа для специальности (рабочий

Вид материала

Программа

Содержание Одобрена и рекомендована к утверждению на заседании Совета факультета математики и информатики Пояснительная записка 1.2. Формы и методы обучения и воспитания 1.4. Требования к компетентности (согласно образовательного стандарта специальности) 1.5. Распределение общих и аудиторных часов по семестрам Содержание учебного материала Требования к курсовой работе (проекту) 3.2. Объем задания 4. Учебно-методическая карта дисциплины Основная литература Дополнительная литература 5.2. Перечень средств диагностики результатов учебной деятельности 6. Протокол согласования учебной программы Название дисциплины, с которой требуется согласование Дополнения и изменения к учебной программе

Подобный материал:

• Учебная программа для специальности: ( рабочий вариант) 1-310306 Экономическая кибернетика, 111.14kb.
• Учебная программа для специальности: ( рабочий вариант) 1-25, 147.69kb.
• Учебная программа для специальности: ( рабочий вариант) 1-25 01 10 коммерческая деятельность, 341.14kb.
• Учебная программа для специальности: ( рабочий вариант) 1-25 01 04 "Финансы и кредит", 141.19kb.
• Программа (рабочий вариант) для специальности: 1-31 01 01 Биология, 1-33 01 01 Биоэкология,, 307.03kb.
• Учебная программа для специальностей: ( рабочий вариант) Специальность, 236.69kb.
• Учебная программа для специальностей: ( рабочий вариант) 1-25 01 04 «Финансы и кредит», 335.77kb.
• Учебная программа для специальности: (рабочий, 259.32kb.
• Учебная программа для специальности: (рабочий, 199.2kb.
• Учебная программа для специальности: ( рабочий вариант) 1-25, 193.29kb.

Ф 27-019

Учреждение образования

“Гродненский государственный университет имени Янки Купалы”

УТВЕРЖДАЮ

Декан факультета

математики и информатики____

___________________ Е.Н. Ливак

«___» _______ 20 г.


Регистрационный № УД- _____/р.

ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ

Учебная программа для специальности

(рабочий вариант)

I - 31 03 01-02 математика»

Факультэт	Математики и информатики
	(назва факультэта)
Кафедра	Теории функций, функционального анализа и прикладной математики
Курс	3, 4
Семестр	5, 6, 7

Лекции ______110_______ (количество часов)	Экзамен ___6,7_____ (семестр)
Практические (семинарские) занятия ____110_________ (количество часов)	Зачёт ___5_____ (семестр)
Лабораторные занятия _____________ (количество часов)	Курсовая работа (проект)___
Всего аудиторных часов по дисциплине ____220________ (количество часов)
Всего часов по дисциплине _____340_______ (количество часов)	Форма получения высшего образования очная
Составил Мисюк В.Р. канд. физ.-мат. наук, доцент

2011 г.



Учебная программа (рабочий вариант) составлена на основе типовой программы ТД-G 217/тип. от 04.08.2009

____________________________________________________________

(название типовой учебной программы (учебной программы), дата утверждения, регистрационный номер)


Рассмотрена и рекомендована к утверждению в качестве рабочего варианта на заседании кафедры теории функций, функционального анализа и прикладной математики


23 мая 2011 г., протокол N° 5

Заведующий кафедрой

________ Ю.М. Вувуникян

(И.О.Фамилия)

Одобрена и рекомендована к утверждению на заседании Методической комиссии по специальности (ям)

24 мая 2011 г., протокол N°_6_

Председатель

_________Н.П. Макарова(И.О.Фамилия)

Одобрена и рекомендована к утверждению на заседании Совета факультета математики и информатики

25 мая_2011 г., протокол N°5

Учёный секретарь

_______________ _____________________

(И.О.Фамилия)

1. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
   

0. 1.1 Цель преподавания дисциплины
   

Формирование фундаментальных знаний и практических навыков применения методов функционального анализа в научных и практических приложениях


1.2. Формы и методы обучения и воспитания

Лекции

Самостоятельная работа

Работа в группах


1.3 Рекомендации по организации самостоятельной работы студентов

- Изучение основных теоретических положений курса.

- Освоение практических навыков применения методов функционального анализа.

Самостоятельная работа студентов может быть реализована на лабораторных занятиях (с непосредственной консультационной поддержкой преподавателя),


1.4. Требования к компетентности (согласно образовательного стандарта специальности)


В результате изучения учебной дисциплины студент должен:

– знать: основные понятия теории метрических пространств, теории меры, теории интеграла Лебега, теории нормированных пространств и линейных операторов в нормированных пространствах.

– уметь: доказывать свойства основных понятий теории метрических пространств, теории меры, теории интеграла Лебега, теории нормированных пространств и линейных операторов в нормированных пространствах.

– владеть навыками: вычисления меры и интеграла Лебега, нормы ограниченного линейного оператора, резольвентного множества и спектра, решения интегрального уравнения Фредгольма второго рода с вырожденными ядрами.

Быть компетентным: в исследовании на разрешимость корректность разрешимости уравнения Ах=у с линейным непрерывным оператором А; в использовании основных понятий функционального анализа при изучении других математических дисциплин.


1.5. Распределение общих и аудиторных часов по семестрам

Распределение нагрузки по семестрам

5 семестр: 36 ч. – лекции, 36 ч. – практика,

6 семестр: 30 ч. – лекции, 30 ч. – практика,

7 семестр: 44 ч. – лекции, 44 ч. – практика

2. СОДЕРЖАНИЕ УЧЕБНОГО МАТЕРИАЛА
   

№ п/п	Наименование раздела, темы дисциплины	Содержание в соответствии с учебной программой
	Введение
1	Метрическое пространство	Метрическое пространство. Неравенство Гельдера и Минковского. Сходящиеся последовательности в метрическом пространстве. Полные метрические пространства. Теорема о пополнении метрических пространств. Непрерывные отображения. Полнота пространства ℓp. Неполнота пространства Rp[a,b]. Теорема о вложенных шарах. Теорема Бэра о категориях. Теорема Банаха о нигде не дифференцируемых функциях. Принцип сжимающих отображений.
2	Теория меры	Система множеств. Кольцо, порожденное полукольцом. Сигма-алгебра. Элементы теории множеств. Кольцо и алгебры множеств. Мера на полукольце. Продолжение меры с полукольца на минимальное кольцо. δ- аддитивная мера. Верхняя мера. Мера Лебега. Класс измеримых по Лебегу множеств. Мера Лебега в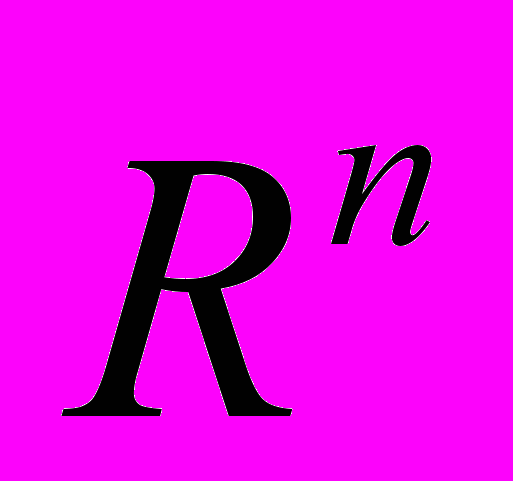 . Борелевские множества. Множества меры нуль.
3	Измеримые функции и теория интегралов Лебега	Измеримые функции и их свойства. Сходимость почти всюду и сходимость по мере. Теорема Лебега, Рисса, Егорова и Лузина об измеримых функциях. Простые функции и определение интеграла Лебега. Свойства интеграла Лебега (линейность, монотонность, δ-аддитивность). Предельный переход под знаком интеграла Лебега. Сравнение интегралов Лебега и Римана. Пространство Lp и его полнота. Произведение мер. Теорема Фубини.
4	Интеграл Римана-Стилтьеса	Монотонные функции. Дифференцирование монотонных функций. Функции ограниченной вариации. Канторова лестница. Сингулярные и абсолютно непрерывные функции. Интеграл Римана-Стилтьеса и его свойства.
5	Векторные пространства.	Примеры векторных пространств, линейные функционалов и линейных отображения векторных пространств. Прямое произведение векторных пространств. Сумма ВП и фактор-пространство ВП. Нормированные пространства. Основные определения и свойства. Сходящиеся и фундаментальные последовательности в НП. Ряды в НП. Примеры НП
6	Линейные операторы и функционалы в НП.	Линейные непрерывные операторы в НП. Ограниченные линейные операторы. Теорема о связи между непрерывностью и ограниченностью линейного оператора. Ограниченные линейные функционалы. Норма оператора и ее свойства. Виды сходимости в сопряженном пространстве. Виды сходимости в пространстве линейных непрерывных операторов. Полнота пространства линейных непрерывных операторов и сопряженного пространства. Равномерная ограниченность и равномерная непрерывность последовательности операторов. Полунормы и их свойства. Выпуклые множества и их свойства. Теорема Хана-Банаха (общий случай). Теорема Хана-Банаха в НП.
7	Элементы спектральной теории операторов.	Обратные операторы. Теорема о непрерывной обратимости оператора I-A. Теорема об открытости множества непрерывных обратимых операторов. Резольвентное множество. Спектр оператора и его свойства. Теорема Банаха об обратимом операторе
8	Гильбертово пространство.	Гильбертово пространство. Определение евклидового пространства. Примеры евклидовых пространств. Неравенство Буняковского–Коши–Шварца Ортогональные системы. Теорема Пифагора. Существование ортонормированного базиса в сепарабельном евклидовом пространстве.
9	Интегральные уравнения.	Интегральные уравнения Вольтера и Фредгольма I и II родов. Полная непрерывность оператора Фредгольма в пространстве квадратично-суммируемых функций и пространстве непрерывных функций.
10	Топологические векторные пространства	Определение топологического векторного пространства. Существование в ТВП базиса из уравновешенных множеств. Секвенциальная полнота. Аксиомы отделимости. Теорема о регулярности отделимого ТВП. Определение Колмогорова-фон Неймана ограниченного множества в ТВП. Линейные непрерывные операторы в ТВП. Теорема об ограниченности линейного непрерывного оператора в ТВП. Примеры ТВП.
11	Локально выпуклые пространства.	Определение ЛВП. Примеры ЛВП. Существование в ЛВП базиса из бочек. Бочечные пространства. Определяющая система преднорм. Примеры определяющих семейств. Метризуемые ЛВП.
12	Пространство основных функций. Обобщённые функции.	Финитные функции и их свойства. Основные функции. Определение топологии пространства основных функций. Ограниченные множества в пространстве основных функций. Критерий ограниченности множества в пространстве D. Определение обобщённой функции. Примеры обобщённых функций. Дифференцирование обобщённых функций. Примеры. Первообразная и интеграл от обобщённых функций. Преобразование Фурье в пространстве основных и обобщённых функций.

3 . ТРЕБОВАНИЯ К КУРСОВОЙ РАБОТЕ (ПРОЕКТУ)¹


3.1. Цель курсовой работы (проекта) по дисциплины

______________________________________________________________________________________________________________________________

______________________________________________________________________________________________________________________________


3.2. Объем задания²

__________________________________________________________________________________________________________________________________________________

__________________________________________________________________________________________________________________________________________________


3.3. Примерная тематика курсовых работ (проектов)


Приближения функций в различных функциональных пространствах

___

4. Учебно-методическая карта дисциплины

Номер недели	Темы занятий	Вопросы, которые изучаются на занятиях	Занятия (часы)				Матэрыяльнае забяспячэнне заняткаў	Літаратура	Форма кантроля знаний
			лекции	практич. семинар	лабораторные	Контролир. самост. работа
1	2	3	4				5	6	7
1	Метрическое пространство	Определение метрического пространства. Неравенство Гельдера и Минковского. Сходящиеся последовательности в метрическом пространстве.	2	2			Презентация №1
2	Полные метрические пространства	Полные метрические пространства. Теорема о пополнении метрических пространств. Непрерывные отображения.	2	2			Презентация №2,3
3	Критерий полноты метрического пространства	Полнота пространства ℓp. Неполнота пространства Rp[a,b]. Теорема о вложенных шарах.		2		2л	Презентация №4
4	Категории множеств в метрическом пространстве	Теорема Бэра о категориях. Теорема Банаха о нигде не дифференцируемых функциях.	2	2			Презентация №5
5	Принцип сжимающих отображений.	Принцип сжимающих отображений и основные примеры.	2	2			Презентация №6
6	Элементы теории множеств.	Система множеств. Кольцо, порожденное полукольцом. Кольцо и алгебры множеств. Сигма алгебры.	4	4			Презентация №6
7	Мера на системах множеств	Мера на полукольце. Продолжение меры с полукольца на минимальное кольцо. Ϭ- аддитивная мера. Верхняя мера	4	2			Презентация №7
8	Измеримые по Лебегу множества	Мера Лебега. Класс измеримых по Лебегу множеств. Мера Лебега в 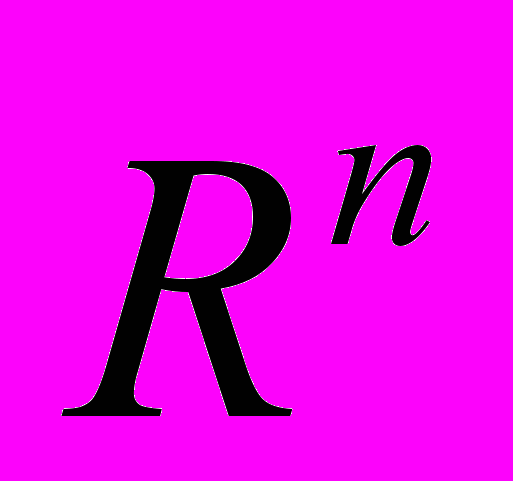. Борелевские множества. Множества меры нуль.	4	4			Презентация №8
9	Измеримые функции	Измеримые функции и их свойства. Сходимость почти всюду и сходимость по мере. Теорема Лебега, Рисса, Егорова и Лузина об измеримых функциях	2	4		2л	Презентация №9
10	Интеграл Лебега от простых функций	Простые функции и определение интеграла от простых функций Лебега. Свойства интеграла Лебега от простых функций.	2	2			Презентация №10,11
11	Функции, суммируемые по Лебегу.	Общее определение интеграла Лебега и его корректность. Свойства интеграла Лебега (линейность, монотонность, Ϭ-аддитивность, абсолютная непрерывность и т.д.).	2	2			Презентация №10,11
12	Предельный переход под знаком интеграла Лебега	Теоремы Лебега, Леви, Фату о предельном переходе под знак интеграла Лебега. Интеграл Лебега по множеству бесконечной меры. Сравнение интегралов Лебега и Римана.	2	2			Презентация №12
13	Пространство Лебега.	Пространство Lp и его полнота. Произведение мер. Теорема Фубини.	4	4			Презентация №13
14	Монотонные функции и функции ограниченной вариации	Монотонные функции и их точки разрыва. Функция скачков и связь со свойством монотонности функции. Дифференцирование монотонных функций. Функции ограниченной вариации и их свойства. Канторова лестница и понятие сингулярной функции.	2	2			Презентация №14
15	Абсолютно непрерывные функции. Интеграл Римана-Стилтьеса.	Абсолютно непрерывные функции и теорема вложения. Неопределённый интеграл Лебега. Определение интеграла Римана-Стилтьеса и его свойства.	2	2			Презентация №15,16
16	Векторные пространства. Линейные отображения векторных пространств Прямое произведение векторных пространств. Сумма ВП и фактор-пространство ВП.	Примеры векторных пространств, линейные функционалов и линейных отображения векторных пространств. Введение векторной структуры в прямом произведении	2	2			Презентация №17
17	Нормированные пространства. Основные определения и свойства.	Свойства нормированных пространств	2	2			Презентация №18
18	Сходящиеся и фундаментальные последовательности в НП. Ряды в НП.	Свойства сходящихся и фундаментальных последовательностей. Абсолютно сходящиеся ряды в НП	2	2			Презентация№19
19	Примеры НП	Примеры пространств последовательностей, непрерывных и непрерывно- дифференцируемых функций	2	2			Презентация№19
20	Линейные непрерывные операторы в НП. Ограниченные линейные операторы. Теорема о связи между непрерывностью и ограниченностью линейного оператора. Ограниченные линейные функционалы.	Основные свойства непрерывных и ограниченных операторов	2	2			Презентация№19
21	Норма оператора и ее свойства. Виды сходимости в сопряженном пространстве. Виды сходимости в пространстве линейных непрерывных операторов.	Оценка и вычисление норм конкретных операторов	2	2			Презентация№20
22	Полнота пространства линейных непрерывных операторов и сопряженного пространства.	Полнота сопряженного пространства	2	2			Презентация№21
23	Теорема Банаха-Штейнгауза (принцип равномерной ограниченности). Теорема о непрерывности предела сильно сходящейся последовательности линейных непрерывных операторов.	Равномерная ограниченность и равномерная непрерывность последовательности операторов		2		2л	Презентация№22
24	Полунормы и их свойства. Выпуклые множества и их свойства. Теорема Хана-Банаха (общий случай)	Шар по полунорме и его свойства. Функционал Минковского	2	2			Презентация№23
25	Теорема Хана-Банаха в НП.	Теорема о достаточном числе линейных непрерывных функционалов.	2	2			Презентация№24
26	Обратные операторы. Теорема о непрерывной обратимости оператора I-A. Теорема об открытости множества непрерывных обратимых операторов.	Левые и правые обратные операторы.	2	2			Презентация№25
27	Теорема об операторах, удовлетворяющих энергетическим неравенствам	Примеры операторов, удовлетворяющих энергетическим неравенствам		2
28	Теорема Банаха об обратимом операторе	Сравнение норм	2	2
29	Резольвентное множество. Спектр оператора и его свойства. Пример.	Теорема о свойствах резольвентного множества	2	2
30	Определение евклидового пространства. Примеры евклидовых пространств	Неравенство Буняковского–Коши–Шварца	2	2			Презентация№26
31	Ортогональные системы. Теорема Пифагора. Существование ортонормированного базиса в сепарабельном евклидовом пространстве	Ортогонализация Гильберта-Шмидта	2	2			Презентация№27
32	Классификация линейных интегральных уравнений. Оператор Фредгольма и его свойства.	Интегральные уравнения Вольтера и Фредгольма I и II родов	2	2
33	Полная непрерывность оператора Фредгольма в пространстве квадратично-суммируемых функций и пространстве непрерывных функций	Относительно компактные множества и компактные операторы. Теорема о компактности равномерно сходящещейся последовательности компактных операторов	2	2
34	Композиции операторов Фредгольма. Степени операторов Фредгольма.	Свертка ядер операторов Фредгольма	2	2
35	Построение резольвентной функции и решение с её помощью интегрального уравнения Фредгольма второго рода. Интегральные уравнения Фредгольма второго рода с вырожденными ядрами.	Операторный ряд Неймана и достаточные условия его сходимости. Решение интегральных уравнений Вольтерра и Фредгольма с помощью резольвентной функции	2	4
36	Сопряжённые операторы Фредгольма. Эрмитовы ядра. Решение интегральных уравнений Фредгольма с эрмитовыми ядрами.	Применение теоремы Гильберта-Шмидта к решению интегральных уравнений	4	4
37	Определение топологическоговекторного пространства.	Система окрестностей нуля в ТВП. Базисы окрестностей нуля. Поглощающие множества в векторных пространствах. Свойство поглощаемости окрестности нуля в ТВП.	4	2
38	Существование в ТВП базиса из уравновешенных множеств. Секвенциальная полнота.	Уравновешенные множества и их свойства. Сходящиеся и фундаментальные последовательности в ТВП.	2	2
39	Аксиомы отделимости. Теорема о регулярности отделимого ТВП.	Хаусдорфовость отделимого ТВП	2
40	Определение Колмогорова фон Неймана ограниченного множества в ТВП. Линейные непрерывные операторы в ТВП. Теорема об ограниченности линейного непрерывного оператора в ТВП. Примеры ТВП,	Борнология. Свойства борнологий. Линейные непрерывные операторы и функционалы в ТВП. Ограниченные линейные операторы.	4	2
41	Определение ЛВП. Примеры ЛВП. Существование в ЛВП базиса из бочек. Бочечные пространства.	Выпуклые множества и их свойства. Абсолютно выпуклые, центральные множества и бочки. Шары по преднорме. Теоремы о свойствах шара по преднорме.	2
42	Определяющая система преднорм. Примеры определяющих семейств	Функционал Минковского и его свойства. Построение топологии с помощью определяющего семейства преднорм.	2	2
43	Метризуемые ЛВП.	ЛВП со счётным определяющим семейством преднорм.	2
44	Финитные функции и их свойства. Основные функции. Определение топологии пространства основных функций.	Носитель непрерывной функции. Пример С.Л. Соболева основной функции.	2	2
45	Ограниченные множества в пространстве основных функций. Критерий ограниченности множества в пространстве D.	Характеризация сходящихся и фундаментальных последовательностей основных функций. Секвенциальная полнота пространства D.	2	4
46	Определение обобщённой функции. Примеры обобщённых функций.	Операции над обобщёнными функциями.		4		2л
47	Дифференцирование обобщённых функций. Примеры. Первообразная и интеграл от обобщённых функций.	Производные высших порядков от обобщённых функций.	2	4
48	Преобразование Фурье в пространстве основных и обобщённых функций.	Преобразование Фурье в пространствах S, D, , 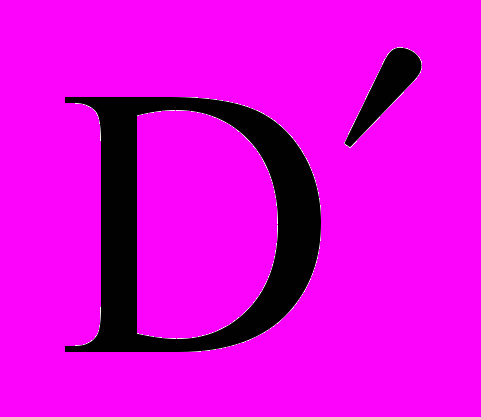.	2	4
		ИТОГО	102	110		8л

5. ИНФОРМАЦИОННО-МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ

ПО ДИСЦИПЛИНЕ


5.1. Перечень рекомендуемой литературы

Основная литература

1. Садовничий В.А. Теория операторов. – М.: МГУ, 1986.
   
2. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. – М.: Наука, 1972. – 496с.
   
3. Рудин У. Функциональный анализ. – М.: Мир, 1975. – 448с.
   
4. Люстерник Л.А., Соболев В.И. Краткий курс функционального анализа. – М: Высшая шк., 1982.
   
5. Канторович Л.В., Акилов Г.П. Функциональный анализ. – М.: Наука,1984. –752с.
   
6. Данфорд Н., Шварц Дж.Т., Линейные операторы. Общая теория. – М.: Изд. ин. лит., 1962. – 896 с.
   
7. Эдвардс Р. Функциональный анализ: Теория и приложения. – М.: Мир, 1969. – 1071с.
   
8. Антоневич А.Б., Радыно Я.В. Функциональный анализ и интегральные уравнения. – Минск: Изд. университетское, 1984. – 352с.
   
9. Антоневич А.Б., Князев П.Н., Радыно Я.В. Задачи и упражнения по функциональному анализу. – Минск: Высшая шк., 1978. – 206 с.
   
10. Вувуникян Ю.М. Обобщённые функции и преобразование Фурье. – Гродно: ГрГУ, 1983. – 37 с.
    
11. Вувуникян Ю.М. Методические указания по разделу «Основы теории обобщённых функций» курса « Функциональный анализ и интегральные уравнения» для студентов специальности 01.01. – Гродно: ГрГУ, 1988. – 48с.
    
12. Вувуникян Ю.М. Методические указания по курсу « Функциональный анализ и интегральные уравнения» для студентов специальности 2013. – Гродно: ГрГУ, 1986. – 45с.
    
13. Антоневич А.Б., Вувуникян Ю.М., Забрейко П.П. и др. Методические указания к лабораторным работам по курсу « Функциональный анализ и интегральные уравнения» для студентов специальности 01.01. – Гродно: ГрГУ, 1986. – 64 с.
    

Дополнительная литература

1. Бурбаки Н. Топологические векторные пространства. – М.: Изд. ин. лит-ра, 1959. – 410с.
   
2. Владимиров В.С. Обобщённые функции в математической физике. – М.: Наука, 1076. – 280с.
   
3. Владимиров В.С. Уравнения математической физики. – М.: Наука, 1981. – 512с.
   
4. Гельфанд И.М., Шилов Г.В. Обобщённые функции. – М.: Физматгиз, 1958, - Т.1. – 440с.
   
5. Дьедонне Ж. Основы современного анализа. – М.: Мир, 1964. – 432 с.
   
6. Иосида К. Функциональный анализ. – М.: Мир, 1967. – 624с.
   
7. Катран А. Дифференциальное исчисление, дифференциальные формы. – М.: Мир, 1971. – 392с.
   
8. Кирилов А.А., Гвишиани А.Д., Теоремы и задачи функционального анализа. – М.: Наука, 1970. – 384с.
   
9. Коллатц Л. Функциональный анализ и вычислительная математика. – М.: Мир, 1969. – 496 с.
   
10. Натансон И.П. Теория функций вещественной переменной. – М.: наука, 1974.
    
11. Робертсон А., Робертсон В. Топологические векторные пространства. – М.: Наука, 1967. – 260с.
    
12. Шефер Х. Топологические векторные пространства. – М.: Мир, 1971. – 360с.
    
13. Шилов Г.Е. Математический анализ: Второй специальный курс. – М.: МГУ, 1984. – 208с.
    

5.2. Перечень средств диагностики результатов учебной деятельности

1. Проверка индивидуальных заданий.
   
2. Контрольные работы
   
3. Зачёт.
   
4. Экзамен
   

6. ПРОТОКОЛ СОГЛАСОВАНИЯ УЧЕБНОЙ ПРОГРАММЫ

ПО ИЗУЧАЕМОЙ УЧЕБНОЙ ДИСЦИПЛИНЕ

С ДРУГИМИ ДИСЦИПЛИНАМИ СПЕЦИАЛЬНОСТИ

Название дисциплины, с которой требуется согласование	Название кафедры	Предложения об изменениях в содержании учебной программы по изучаемой учебной дисциплине	Решение, принятое кафедрой, разработавшей учебную программу (с указанием даты и номера протокола)3
1.Мат анализ. ТФКП	МА, ТФФА		Утверждаем Пр №5 от 23.05.2011
2. аналитическая геометрия	АГиМПМ, ТФФА		Утверждаем Пр №5 от 23.05.2011

7. ДОПОЛНЕНИЯ И ИЗМЕНЕНИЯ К УЧЕБНОЙ ПРОГРАММЕ
   

на ____ / _____ учебный год

№ п/п	Дополнения и изменения	Основание

Учебная программа пересмотрена и одобрена на заседании кафедры

(протокол № __ от _______ 20__ г.)

Заведующий кафедрой

доктор физ.-мат. навук, доцент ______________ Ю.М. Вувуникян

УТВЕРЖДАЮ

Декан факультета

кандидат тех.наук, доцент___ ______________ Е.Н. Ливак

(степень, звание) (И.О.Фамилия)