И в авторской редакции. Удк 536. 7 +"7"+ (201) +53+57 +577. 4+211 Вейник А. И., «Термодинамика реальных процессов», Мн.: "Навука I тэхнiка", 1991. 576 с. Isbn 5-343-00837. Вмонографии приводятся ряд новых закон

Вид материала

Закон

Содержание 1. Вывод основного уравнения ОТ для ансамбля простых явлений. U (полный дифференциал dU 1 = 2, уравнения (31)-(34) приобретают вид dU = P 2. Виды работы. 3. Специфическая мера интенсивности силового Р. Как уже упоминалось, в частном случае эта величина представляет собой универсальную меру интенсивности силового взаимо­действ 4. Универсальная мера количества силового поведения ансамбля, или энергия. 5. Контрольная поверхность, система и окружающая среда. 6. Внутренние и внешние степени свободы системы. 7. Первое начало ОТ, или закон сохранения энергии.

Подобный материал:

• Впервые в авторской редакции, 9591.86kb.
• Конспект лекций Кемерово 2004 удк: 637. 992, 2553.59kb.
• Хавронюк Микола Іванович удк 343 (4: 447) Кримінальне закон, 3077.54kb.
• М. М. Ничипорчук национальный исследовательский ядерный университет «мифи» моделирование, 9.59kb.
• Удк [544. 77: 577. 112. 824]: 535, 64.03kb.
• Хавронюк Микола Іванович удк 343 (4: 447) кримінальне закон, 684.97kb.
• Учебное пособие и Учебный словарь-минимум по религиоведению. М.: Гардарики, 2000. 536, 8576.03kb.
• Учебное пособие и Учебный словарь-минимум по религиоведению. М.: Гардарики, 2000. 536, 8588.39kb.
• И. А. Бунин принадлежал к тем реалистам рубежа веков, которым была дорога сущность, 164.9kb.
• Формирование гендерного подхода к обучению и воспитанию учащихся в школе 343, 102kb.

Глава VII. Первое начало ОТ.


1. Вывод основного уравнения ОТ для ансамбля простых явлений.


Мы теперь располагаем экстенсорами Ε (см. соотношение (27)), играющими роль аргумента N₁ в уравнении (14). Этого вполне достаточно, чтобы написать основное уравнение ОТ применительно к ансамблю простых явле­ний и определить все остальные величины, входящие в уравне­ния (14) и (15), в частности найти неизвестную меру N₄ , обозна­ченную нами через U (см. выражение (29)). Благодаря этому мы, наконец, сформулируем наиболее общие, универсальные и достоверные количественные принципы, или начала, которые обнаруживаются на первом - начальном - этапе эволюции вещества и его поведения. Таким образом, будет замкнута цепочка дедуктивных рассуждений (2) и завершено построе­ние обещанного выше общего метода дедукции, который берет свое начало от весьма общих философских концепций и затем в ходе рассуждений опускается до уровня числового выражения свойств конкретных явлений.

Мы убедимся, что основное уравнение (14), написанное для ансамбля простых явлений, представляет собой не что иное, как первое начало ОТ. Дальнейшая расшифровка характеристик и связей, содержащихся в первом начале, приведет к формули­ровке остальных шести начал. На этом завершится построение общего метода дедукции. Разработанный таким способом аппа­рат ОТ будет использован для изучения отдельных явлений эволюционного ряда (24).

Основное уравнение ОТ применительно к ансамблю простых явлений получается из соотношений (14), (27) и (29). Имеем

_{U = F(E1 ; E2 ; ... ; Ei) (30)}

Мера количества поведения вещества ансамбля U есть одно­значная функция всех мер Ε количества вещества; число ве­ществ различного сорта, из которых построен ансамбль, равно l . Как уже отмечалось, нам пока известно семь таких разно­родных веществ. Вида функции F мы не знаем.

Абсолютные значения многих характеристик явления обычно найти труднее, чем изменения этих характеристик. Поэтому уравнение (30) надо преобразовать таким образом, чтобы в него входили только изменения (разности) соответствующих вели­чин. Для этого достаточно продифференцировать выраже­ние (30).

В соответствии с хорошо известными правилами дифферен­цирования функции нескольких переменных полное изменение меры U (полный дифференциал dU ) определяется в виде суммы произведений скорости приращения функции с аргументом на приращение этого аргумента, то есть

dU = Дж, (31)

или

dU = 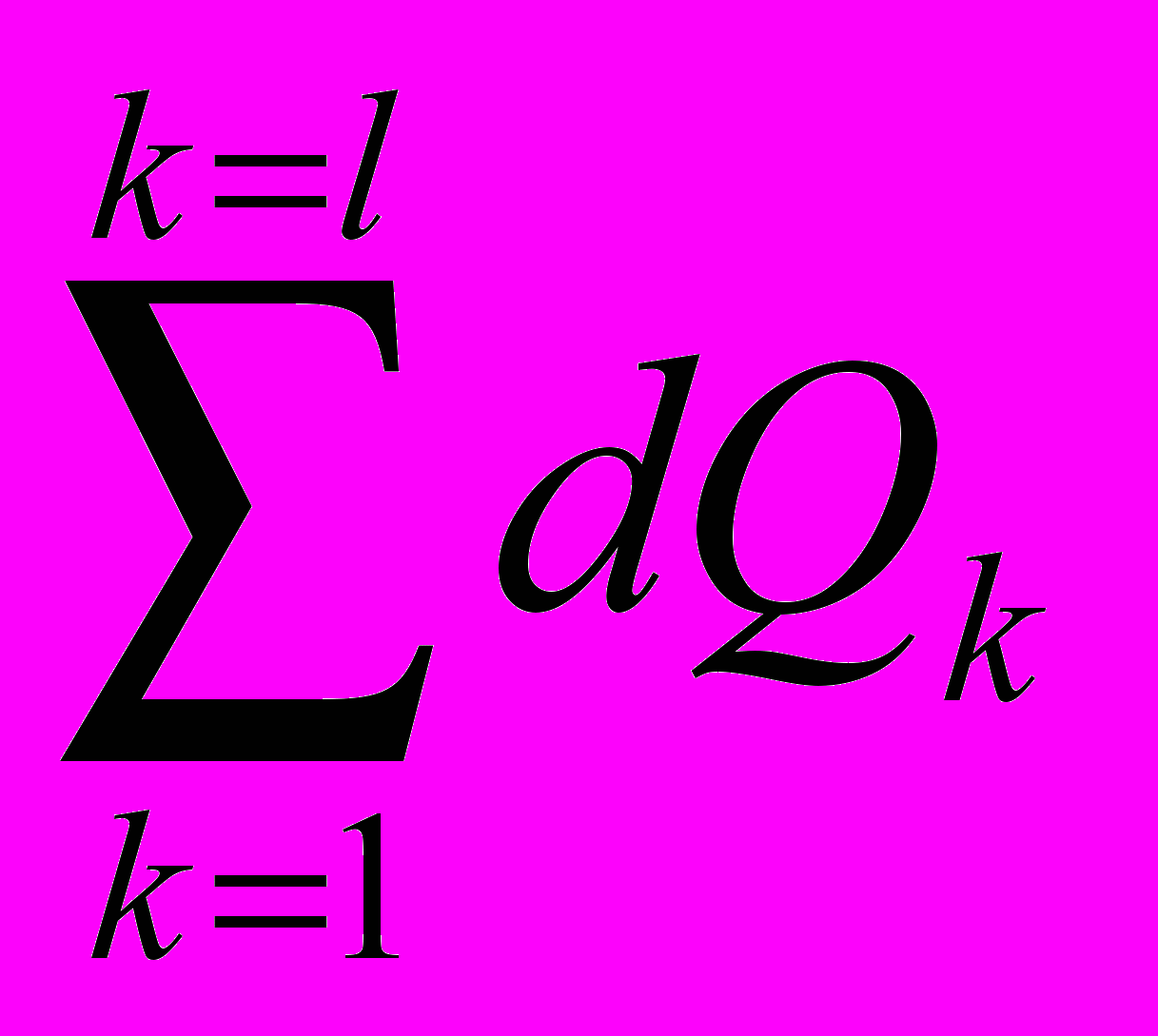Дж, (32)

где P_k = (U/E_k)_Ein (33)

dQ_k = P_kdE_k Дж (34)


Индекс Еin стоящий внизу скобки, говорит о том, что при диф­ференцировании все остальные экстенсоры, кроме данного, k-того, остаются постоянными (инвариантными).

Равенство (31) в аналитической форме выражает общее дифференциальное уравнение первого начала ОТ. Определен­ные совокупности найденных величин обозначены буквами Ρ и Q ; смысл этих символов, как и самого уравнения, включая его размерность, выясняется ниже.

Для большей наглядности свои рассуждения мы нередко будем иллюстрировать самыми простыми примерами, в которых ансамбль состоит всего из двух разнородных веществ, опреде­ляемых двумя экстенсорами (l = 2). При этом основные идеи ОТ сохраняют свою силу, но дифференциальные уравнения оказы­ваются наименее громоздкими.

Итак, в частном случае, когда 1 = 2, уравнения (31)-(34) приобретают вид

dU = P₁dE₁ + P₂dE₂ Дж, (35)

или

dU = dQ₁ + dQ₂ Дж, (36)

где P₁ = (U/E₁)_E2 ; P₂ = (U/E₂)_E1 (37)

dQ₁ = P₁dE₁ ; dQ₂ = P₂dE₂ (38)

Индекс Е₂ внизу первой скобки означает, что при дифферен­цировании меры U по Е₁ постоянной считается величина Е₂ ; индекс Е₁ у второй скобки говорит о постоянстве величины Е₁ .

В еще более простом гипотетическом частном случае, если ансамбль содержит только одно вещество (l = 1), то основное дифференциальное уравнение ОТ записывается следующим образом:

dU = PdE Дж (39)

или dU = dQ Дж (40)

где P = dU/dE (41)

dQ = PdE (42)

Мы добились того, что в найденном дифференциальном уравнении первого порядка (31) отсутствует неизвестная функ­ция F . Кроме того, главные количественные меры входят в это уравнение в виде интересующих нас изменений (разностей). Теперь нам предстоит внимательно рассмотреть физический смысл самого уравнения и всех содержащихся в нем характе­ристик [ТРП, стр.91-93].


2. Виды работы.


В уравнении (31) хорошо нам известными характеристиками являются только экстенсоры Е . Но для одного частного слу­чая - силового взаимодействия - мы знаем также фактор интенсивности, или интенсиал, каковым служит сила Р_х . В этом частном случае произведение интенсиала на изменение экстенсора dE_x (перемещение dx) равно работе dQ_x , которая изме­ряется в джоулях (см. формулу (28)). Следовательно, все остальные слагаемые правой части уравнения (31) также дол­жны представлять собой работы, измеряемые в джоулях. Этот факт отражен в уравнении, записанном в форме (32).

Интересная особенность вопроса заключается в том, что каждая из работ сопряжена со своим специфическим экстенсором, имеющим особую размерность. В любом таком конкрет­ном случае экстенсор «окрашивает» работу в свой специфи­ческий «цвет». Например, приходится различать работы кинети­ческую, механическую, электрическую и т.д. В этом смысле обсуждаемые работы можно рассматривать как специфические.

Вместе с тем любая данная работа в целом есть универсальная мера силового взаимодействия данного вещества с ансамблем, ибо измеряется в одних и тех же единицах - джоулях - и состоит из универсальной меры интенсивности силового взаимодействия, или силы, измеряемой в ньютонах, и универсальной меры экстенсивности силового взаимодействия, или перемещения, измеряемого в метрах. Это дает основание считать работу некоей универсальной мерой количества воздей­ствия на ансамбль. В термодинамике величину dQ часто именуют обобщенной работой.

Здесь мы сталкиваемся с удивительно органичным сочета­нием универсального (обобщенного) и специфического (кон­кретного), одновременно присутствующих в одном из основных понятий теории. Это хорошо перекликается с высказанной ранее идеей о целесообразности и плодотворности синтеза обобщен­ного и конкретного подходов.

Работа совершается в процессе подвода или отвода от ансамбля определенного количества вещества, мерой которого служит экстенсор dE . Этот подвод или отвод можно рассматри­вать как некое специфическое воздействие на ансамбль вещест­вом определенного сорта. Следовательно, специфической мерой количества воздействия на ансамбль является изменение экстенсора dE .

Таким образом, изменение количества вещества ансамбля, определяемое экстенсором dE , одновременно сопровождается двумя видами воздействий - специфическим и универсальным. Мерой количества специфического воздействия служит экстен­сор dE , а мерой количества универсального - работа dQ .

Нетрудно сообразить, что специфическая мера количества воздействия на ансамбль, или величина dE , одновременно явля­ется специфической мерой экстенсивности силового взаимо­действия между ансамблем и квантами подводимого или отводимого вещества определенного сорта. Здесь также сталки­ваются между собой две противоположные сущности - кон­кретная и обобщенная, ибо специфическая особенность вещества накладывается на универсальное свойство перемещения: ведь обе величины - dE и dx , - будучи аргументами в основном уравнении ОТ, с равным успехом определяют одну и ту же обоб­щенную работу dQ (см. формулы (28) и (34)).

Хотя работы, определяемые выражениями (28) и (34), друг другу равны, у них имеется и существенное различие. Разуме­ется, оно касается только правых частей уравнений, ибо левые тождественны между собой. Имеющееся различие заключается в том, что работа (28) выражена через предельно универ­сальные характеристики процесса - силу и перемещение, а работа (34) - через специфические характеристики того же процесса. О специфичности экстенсора говорилось уже доста­точно, теперь предстоит заняться мерой Р [ТРП, стр.93-95].


3. Специфическая мера интенсивности силового

взаимодействия, или интенсиал.


Очередной важной характеристикой уравнения (31), смысл которой подлежит расшифровке, является величина Р. Как уже упоминалось, в частном случае эта величина представляет собой универсальную меру интенсивности силового взаимо­действия, или силу Р_х , то есть служит фактором интенсивности, или интенсиалом. Поэтому и во всех остальных случаях вели­чина Ρ тоже должна выполнять роль интенсиала. Однако при­менительно к каждому конкретному экстенсору интенсиал при­обретает свою специфическую «окраску», включая специфи­ческую размерность, отличную от размерности Р_х , и т.д. В этих условиях интенсиал является специфической мерой интенсив­ности силового взаимодействия между ансамблем и квантами вещества.

Специфичность, в частности, проявляется в том, что данный интенсиал избирательно воздействует только на сопряженное с ним вещество и не влияет на все остальные. Например, элек­трический потенциал способен воздействовать только на элек­трический заряд и безразличен к массе. В свою очередь, квадрат скорости воздействует на массу и оставляет в покое электри­ческий заряд.

Следовательно, каждый конкретный интенсиал служит спе­цифическим аналогом силы. Аналогом, но не самой силой, ибо единицей измерения силы является ньютон, а каждый интен­сиал, сопряженный с соответствующим веществом, имеет свою собственную специфическую размерность, отличную от размер­ности силы.

Для каждого конкретного вещества мера Ρ легко определя­ется из общего выражения (34), где известны экстенсоры и раз­мерность работы. Например, для упомянутых выше экстенсоров – массы m (кг), объема V (м³) и электрического заряда, или электриора,  (Кл) интенсиалы имеют следующие раз­мерности:

[P_m] = Дж/кг = (Нм)/(Нс²/м) = м²/с² ;

[P_v] = Дж/м³ = (Нм)/м³ = Н/м² ;

[P_] = Дж/Кл = (ВАс)/Кл = (ВКл)/Кл = В .

Как видим, интенсиал применительно к массе имеет смысл квадрата скорости (Р_m = ²), применительно к объему - давления (Р_v = р) и применительно к электрическому заряду - электрического потенциала (Ρ_ψ = φ). Произведение каждого из этих интенсиалов на изменение сопряженного с ним экстенсора дает соответствующую работу. Со всеми этими частными характеристиками различных явлений мы хорошо знакомы.

Кроме того, ранее мы убедились, что интенсиал Р_х опреде­ляет силовое поведение вещества в процессе образования или распада ансамбля, то есть является мерой качества поведения вещества Ν₅ применительно к ансамблю простых явлений. Сле­довательно, и все остальные частные интенсиалы также явля­ются каждый мерой качества поведения соответствующего вещества. Например, ² - это мера качества поведения кинети­ческого вещества, φ - электрического и т.д. [ТРП, стр.95-96].


4. Универсальная мера количества силового поведения ансамбля, или энергия.


Следующей, самой важной характеристикой уравнения (31) служит мера U, играющая роль величины Ν₄ в уравнениях (14) и (26).

Известно, что у любого правильно составленного уравнения все слагаемые имеют одинаковую размерность. Поэтому мера U тоже должна иметь размерность работы (Дж). Кроме того, мы знаем, что при образовании и распаде ансамбля совер­шаемая работа каким-то образом аккумулируется ансамблем и затем может вновь проявиться в виде работы. Иными словами, величина U определяет количество силового поведения, заклю­ченного в ансамбле. Перечисленными свойствами обладает хорошо известная мера, именуемая энергией.

Хотя работа и энергия имеют одну и ту же размерность, Они по сути дела представляют собой совершенно различные харак­теристики. Работу можно назвать мерой количества поведения, обусловленного перемещением порций веществ в процессе обра­зования или распада ансамбля; когда процесс прекращается, тогда перемещения нет и работа равна нулю. Энергия - это мера количества поведения, которое накапливается в ансамбле в ходе его образования и совершения работы. Количественная связь между обоими этими видами поведения определяется уравнением (31).

Весьма примечательно - об этом свидетельствует непосред­ственный опыт, - что аккумулированная энергия обычно сохра­няет в ансамбле свою специфическую «окраску», сопряженную с «окраской» совершаемой работы, которая, в свою очередь определяется сортом подводимых или отводимых квантов ве­щества. Поэтому, как и в случае работы, требуется разли­чать кинетическую, электрическую и другие составляющие энер­гии; об исключениях из этого правила говорится ниже. Вместе с тем сама по себе мера U обладает предельной универсаль­ностью.

По своей универсальности энергия стоит на одном уровне и органически связана с такими характеристиками, как сила и перемещение. Поэтому сила есть универсальная мера качества поведения вещества, причем поведение проявляется в виде притяжения и отталкивания, а энергия - это универ­сальная мера количества силового поведения ансамбля, которое проявляется в удержании квантов друг подле друга. Следова­тельно, меру U можно назвать также энергией связи между квантами, заключенной в ансамбле.

Универсальность понятия энергии обусловлена еще и тем, что оно применимо не только ко всем разнородным простым ве­ществам, но и ко всем без исключения более сложным формам явлений. Это прямо вытекает из правила вхождения, согласно которому всякое сложное явление включает в себя более про­стые. Поэтому с помощью энергии можно оценивать количество примитивного силового поведения, заключенного в любом слож­ном явлении, включая общество и т.д. Разумеется, на сложном уровне наряду с силовой явления располагают также возмож­ностями использовать и другие, более совершенные формы пове­дения, для оценки количества которых впоследствии будет най­дена своя особая мера. Что же касается простого уровня, то на нем силовой примитив - это единственно возможный, един­ственно доступный для явления способ поведения, а энергия - единственная мера, определяющая количество этого поведения.

Весьма важно, что за спиной энергии, как и силы, всегда стоят свои особые вещества, которые цементируют ансамбль в единое целое. Однако энергия-мера и упомянутые вещества суть принципиально различные вещи. Поэтому энергию недо­пустимо отождествлять ни с веществом, ни с какими бы то ни было иными объектами или понятиями. Согласно ОТ, ника­кого другого смысла, кроме указанного - быть универсальной мерой количества поведения на уровне ансамбля простых явле­ний, - энергия не имеет и иметь не может.

В связи с приведенной здесь формулировкой понятия энер­гии необходимо обратить внимание на то разнообразие во взгля­дах и определениях, которое господствует в современной науке. Впервые понятие энергии возникло в механике. Намеки на это понятие содержатся уже в комментариях Филопона (VI в.) на труды Аристотеля - речь идет об «импето» [53, с.25]. В XVII в. Гюйгенсом, Лейбницем и другими кинетическая энер­гия, или «живая сила», была определена как произведение массы на квадрат скорости [53, с.94]; в XIX в. Кориолис испра­вил это выражение, введя в него множитель, равный одной вто­рой [53, с.95]. Так энергия оказалась связанной с кинети­ческими представлениями.

Примерно в тот же период формировалось понимание теп­лоты как движения внутренних частей тел (Бэкон, Кеплер). В частности, в 1752 г. Эйлер писал: «То, что теплота заключа­ется в некотором движении малых частиц тела, теперь уже достаточно ясно» [53, с.168]. Создание Кренигом, Клаузиусом, Максвеллом и другими кинетической теории теплоты [53, с.237] послужило основанием отождествлять энергию с теплотой (че­рез кинетическую энергию молекул).

Далее при анализе законов излучения абсолютно черного тела Планк ввел понятия кванта действия и квантов (порций) энергии, которые излучаются телом в окружающую среду [53, с.338]. Эти порции энергии были затем отождествлены с кван­тами света, или фотонами. В результате под энергией теперь часто понимают просто фотоны, или так называемое электро­магнитное поле.

Таким образом, в ходе исторического развития науки энер­гия превратилась в одну из наиболее трудно доступных для по­нимания категорий. Согласно традиционному мышлению, энер­гия есть одновременно кинетическая энергия, теплота, фотоны (свет), электромагнитные волны; ее принято выражать (а ино­гда и отождествлять) через массу, считать, что она порождается гравитацией, и т.д. В некоторых из имеющихся определений можно видеть явное отождествление энергии-меры с той сущ­ностью, которую эта мера призвана определять. Нечто похожее мы наблюдали ранее в случае определения понятия силы. Все это, конечно, не способствует выявлению истинного физического смысла понятия энергии.

Теперь должно быть совершенно ясно, что энергия - это универсальная мера (и только мера!) количества простого сило­вого поведения, заключенного в теле. Энергия сопоставляется с работой в уравнении (31) и измеряется в джоулях. Будучи мерой, энергия, как и всякая другая мера, предназначена для подстановки в расчетные формулы; фотоны в формулу не под­ставишь.

Подведем некоторые итоги. Перед нами стояла задача - определить физический смысл количественных мер, входящих в общее уравнение ансамбля простых явлений (26), и таким образом, избавившись от нулей, придать этому уравнению доступную для практического использования форму. Непосредственно глядя на уравнение (26) и готовый ансамбль, этого сде­лать было нельзя. Пришлось рассмотреть физический механизм (процесс) образования ансамбля из отдельных порций вещества. Такой подход представляется наиболее простым, наглядным и экономным из всех возможных. В ходе рассужде­ний логика привела к детальному ознакомлению с особен­ностями таких понятий, как универсальное и специфические взаимодействия, перемещение, сила и работа. На этом фунда­менте с помощью известных экстенсоров (см. формулу (27)) было выведено основное уравнение ОТ для ансамбля простых явлений (31), параллельно был уточнен смысл некоторых из упомянутых понятий, особенно это касается энергии. В резуль­тате такие количественные меры уравнения (26), как N₄ и N₅ , получили для ансамбля простых явлений конкретное выражение и толкование.

Предстоит дальнейшая расшифровка выведенного уравне­ния (31) и содержащихся в нем связей. Однако теперь в логику рассуждений целесообразно ввести весьма плодотворные поня­тия и методы, выработанные в течение последнего столетия в термодинамике [ТРП, стр.96-99].


5. Контрольная поверхность, система и окружающая среда.


Анализ уравнения (31) очень сильно облегчается, если ввести такие понятия, как контрольная поверхность, система и окру­жающая среда. Под контрольной понимается некая замкнутая поверхность, мысленно окружающая данный ансамбль. Понятие контрольной поверхности играет важную роль, поскольку с ее помощью изучаемый ансамбль отделяется от всех остальных ансамблей Вселенной. Разумеется, такое отделение можно совершить только мысленно, ибо в реальных условиях все ан­самбли связаны друг с другом веществом взаимодействия.

В термодинамике данный ансамбль, ограниченный контроль­ной поверхностью, принято называть системой, или телом, а все, что находится за пределами контрольной поверхности, - окру­жающей средой. Изучая систему, мы вправе не интересоваться свойствами окружающей среды. Окружающая среда должна волновать нас только в той мере, в какой она служит источником специфических и универсальных воздействий на систему. Такой подход к изучению ансамбля очень плодотворен, поэтому мы будем широко использовать его в дальнейшем.

В общем случае система может состоять из одного ансамбля, совокупности многих ансамблей или даже фрагмента отдель­ного ансамбля. При этом система может принадлежать любому из количественных уровней мироздания: микро-, макро-, мега- и тому подобным мирам.

Известны различные виды специфических и универсальных воздействий окружающей среды на систему. Один из них заклю­чается в переносе через контрольную поверхность определен­ного количества вещества dE . Сам по себе процесс переноса говорит о наличии специфического воздействия. Но одновре­менно совершается работа dQ , равная произведению экстенсора dE на интенсиал Р . Следовательно, перенос вещества свидетель­ствует также и о наличии универсального воздействия. Процесс переноса сравнительно легко обнаруживается, если наблю­дать за тем, что происходит непосредственно на контрольной поверхности.

Второй вид воздействия связан с эффектом экранирования веществами друг друга в пределах системы. В состоянии экрани­рования и после нарушения этого состояния вещество ведет себя по-разному, что существенно влияет на свойства системы. Прекращение экранирования во многих отношениях равно­сильно появлению в системе вещества. Например, соответ­ствующие условия возникают, если нейтрон, в котором взаимно скомпенсированы (экранированы) положительный и отрица­тельный электрические заряды, распадается на протон и элек­трон. При этом в системе как бы появляются положительное и отрицательное электрические вещества. С другими весьма рас­пространенными примерами экранирования придется столк­нуться в гл. XIII.

Очень большой интерес представляет также третий вид изме­нений экстенсора системы - за счет парена. Этот процесс пока наименее исследован, но ему предстоит большое будущее.

При изучении и расчетах второй и третий виды воздействий могут быть сведены к первому путем соответствующего выбора контрольной поверхности, системы и окружающей среды. При этом экранированное вещество и вещество парена мысленно относятся к окружающей среде, хотя на самом деле они нахо­дятся в пределах системы. Нарушение экранирования и появле­ние вещества из парена условно рассматриваются как перенос вещества через контрольную поверхность. С похожими услов­ными методами выбора контрольной поверхности, системы и окружающей среды приходится сталкиваться также при изу­чении химических и фазовых превращений [17, с.303; 21, с.205].

Следовательно, в качестве основного вида воздействий окру­жающей среды на систему можно принять первый, который со­провождается переносом через контрольную поверхность ве­щества в количестве dE . Этот вид является наиболее общим, к нему могут быть сведены все остальные, поэтому ниже его изучению уделяется наибольшее внимание.

Введение понятий контрольной поверхности, системы и окру­жающей среды, а также установление основного вида воздей­ствий позволяют очень четко обозначить принадлежность вели­чин, содержащихся в уравнении (31), то есть определить, какие из них относятся к системе, какие - к контрольной поверхности и окружающей среде. Например, совершенно очевидно, что величина dU должна принадлежать системе, поскольку энергия определяет связь между всеми веществами, образующими сис­тему. В термодинамике энергию U принято называть внутрен­ней. Однако в ОТ существует только одна энергия - мера, поэ­тому такая конкретизация названия не имеет особого смысла.

В противоположность энергии экстенсор dE относится к окружающей среде, ибо в процессе взаимодействия вещество в количестве dE переходит из окружающей среды в систему. Этот процесс сопровождается совершением работы dQ . Работу совершает окружающая среда над системой, поэтому величина dQ также принадлежит окружающей среде.

Следовательно, в целом левая часть уравнения (32), а зна­чит, и (31) относится к системе, а правая - к окружающей среде. При этом положительному приращению величины экстенсора системы dE (переходу вещества из окружающей среды в систему) соответствует положительная работа dQ (окружаю­щей среды над системой) и положительное приращение (воз­растание) энергии dU системы. В этом заключается правило знаков для энергии, работы и экстенсора.

Необходимо отметить, что в термодинамике в качестве некоего исключения принято считать так называемую механи­ческую работу, связанную с изменением объема системы. В этом случае положительное приращение dU получается при отри­цательном приращении объема dV : при совершении положи­тельной работы система сжимается - ее объем уменьшается. Поэтому механическую работу обычно записывают в виде

dQ_v = - pdV Дж, (43)

или dL = pdV Дж,

где использовано известное обозначение

dQ_v = - dL Дж.

О
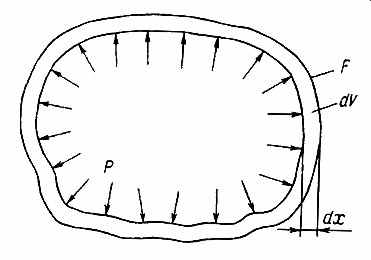
днако ниже по мере расшифровки физического смысла введенных понятий станет ясно, что во всех случаях положи­тельному dU отвечают положительные dQ и dE . Причина кажу­щегося исключения для механических явлений заключена толь ко в неадекватном способе традиционного выбора механическо­го экстенсора, то есть объема V (см. параграфы 2 и 4 гл. XV). Кстати, на примере механической работы легко показать органическую связь, существующую между уравнениями (28) и (43) и таким образом перекинуть мост к общему уравнению (34). Для этого достаточно обратиться к рис. 1, где изображена система, изменившая свой объем на величину dV под действием давления р ; площадь контрольной поверх­ности равна F.


Рис.1. Схема для определения связи между формулами (28) и (43).


Находим

dQ_x = P_xdx = pFdV/F = pdV = dQ_v = dQ_k (44)

где P_x = pF ; dx = dV/F .

Здесь знак минус опущен (рассматривается абсолютное значе­ние работы); давление р, равномерно распределенное по пло­щади F , выражено через силу Р_х ; приращение объема dV, отне­сенное к площади, дает перемещение контрольной поверхности на расстояние dx [ТРП, стр.99-102].


6. Внутренние и внешние степени свободы системы.


Установим далее физический смысл величины l, которая входит в правую часть уравнения (31), принадлежащую окружающей среде.

Допустим, что данная система, определяемая уравнением (27), внутренне восприимчива к l конкретным веществам, она способна приобретать и терять через контрольную поверхность эти вещества. Тогда такую систему можно определить как обла­дающую l внутренними степенями свободы. Следовательно, под внутренними степенями свободы мы будем понимать располага­емые, потенциально заложенные в системе возможности вза­имодействий с окружающей средой.

Однако реализация имеющихся возможностей зависит не только от свойств системы, но не в меньшей мере и от свойств окружающей среды. Ведь последняя на границе с системой - на контрольной поверхности - располагает вполне определен­ными своими внутренними степенями свободы. В общем слу­чае количество этих степеней, внешних по отношению к системе, равно l_е , причем не все степени из числа l_е обязательно совпада­ют со степенями из числа l . Очевидно, что взаимодействие меж­ду системой и окружающей средой возможно только по сопря­женным степеням свободы, когда система и среда одновременно способны воспринимать и терять соответствующие вещества.

Если число сопряженных между собой степеней свободы системы и среды обозначить через n , то должно соблюдаться требование [18, с.61; 21, с.47]

n  1 (45)

Величина n характеризует фактически реализуемые взаимодей­ствия между системой и окружающей средой, то есть опреде­ляет внешние степени свободы системы, зависящие от свойств окружающей среды.

Отсутствие какой-либо конкретной степени свободы - вну­тренней или внешней - говорит о внутренней или внешней изо­ляции системы по отношению к соответствующему веществу. Например, жидкости и твердые тела практически несжимаемы, то есть внутренне изолированы по отношению к объему, поэ­тому они не могут быть использованы в качестве рабочего тела в тепловом двигателе; фарфор и стекло внутренне изолированы по отношению к электрическому заряду, значит, они не могут служить проводниками электричества. Аналогично внешняя изоляция системы по отношению к объему может быть достиг­нута путем применения жесткой окружающей среды (обо­лочки), как в калориметрической бомбе; внешняя электрическая изоляция обеспечивается с помощью оболочки из фарфора, стекла и т.п.

Теперь должно быть ясно, что уравнение (31) выведено при условии, когда l = l_e = n . Это соответствует крайнему частному случаю полного совпадения всех внутренних и внешних степе­ней свободы системы. В противоположном крайнем случае, когда все степени свободы не совпадают между собой, величина n = 0 , при этом система полностью внешне изолирована, взаимо­действие между нею и окружающей средой невозможно.

Из сказанного следует, что в уравнение (31) вместо вели­чины l правильно подставлять величину n , которая является характеристикой не только системы, но и окружающей среды и однозначно определяет условия взаимодействия системы с последней [ТРП, стр.102-103].


7. Первое начало ОТ, или закон сохранения энергии.


Теперь все величины, входящие в основное уравнение (31) для ансамбля простых явлений, нам известны. Необходимо обоб­щить полученные результаты и установить смысл уравнения в целом.

Мы убедились, что левая часть соотношения (31) определяет изменение энергии системы, а правая - внешние работы, кото­рые на контрольной поверхности совершает окружающая среда над системой. Работы совершаются в процессе переноса веществ через контрольную поверхность. Для этих условий ура­внение (31) утверждает факт существования однозначной связи между изменением энергии системы и суммой внешних работ, причем сумма работ, совершаемых над системой, равна изме­нению энергии последней.

Уравнение (31) с равным успехом может быть применено также к окружающей среде. По отношению к последней совер­шаемые работы оказываются отрицательными. Поэтому изме­нение энергии среды dU_c тоже должно быть отрицательным. Поскольку в обоих случаях рассматриваются одни и те же работы, постольку должно быть справедливо равенство

dU + dU_c = 0 (46)

Как видим, на сколько увеличивается энергия системы, на столько же уменьшается энергия окружающей среды. Иными словами, суммарное изменение энергии системы и среды равно нулю, то есть совокупная энергия системы и среды остается неизменной при любых процессах их взаимодействия.

Следовательно, соотношение (31) представляет собой не что иное, как уравнение закона сохранения энергии, или просто закона энергии. Это уравнение выведено для первого - началь­ного - шага эволюционного развития явлений. Поэтому закон энергии заслуживает наименования первого начала ОТ. Из уравнения (31) в качестве частных случаев получаются все из­вестные уравнения этого типа: уравнение первого закона термо­динамики, уравнение Гиббса и т.д. (см. параграфы 19 гл. XV и 3 гл. XX).

Первое начало в наиболее общем виде выражает идею сохра­нения количества поведения вещества при любых взаимо­действиях системы и окружающей среды. Оно справедливо для любого уровня мироздания и любой по сложности формы явле­ния, то есть представляет собой предельно универсальный, абсо­лютный закон природы. В самой общей формулировке первое начало гласит: энергия (количество поведения вещества) Вселенной постоянна.

Впервые идея сохранения в самом общем виде как основной принцип развития мира зародилась еще в древности. Например, греческий философ Эмпедокл (450 лет до н.э.) учил, что ничего не может происходить из ничего и ничто не может быть уничто­жено. В простейшей форме эта идея получила количественное выражение в законе рычага Архимеда. Согласно этому закону, сила обратно пропорциональна перемещению (золотое правило механики), что соответствует постоянству их произведения, то есть работы. Леонардо да Винчи распространил этот закон на вращательное движение (ворот). При этом постоянным оказывается произведение вращательного момента на угол пово­рота. В 1842 г. Р. Майер экспериментально открыл закон экви­валентности теплоты и работы и определил числовое значение механического эквивалента теплоты. В 1843 г. Д. Джоуль и не­зависимо от него в 1844 г. Э.X. Ленц установили закон сохра­нения энергии применительно к термическим и электрическим явлениям (закон Джоуля-Ленца). Наконец, в 1847 г. Гельмгольц обобщил этот закон, распространив его на все формы движения материи. Термин «энергия» происходит от греческого слова energeia - деятельность.

Таким образом, закон сохранения энергии был установлен экспериментально и всегда считался чисто опытным законом, который невозможно получить теоретически. Однако парадигма ОТ позволяет по-новому взглянуть на мир, благодаря чему уда­ется аналитически вывести уравнение, определяющее одно из важнейших свойств природы. В данном случае упомянутый выше метод эстафеты сопровождается передачей в ОТ самого замечательного закона естествознания.

Чтобы не возникало неясностей при практическом использо­вании уравнения (31), надо сделать несколько пояснений, касающихся математических символов d , входящих в это ура­внение; о них еще не говорилось. Очевидно, что d перед U пред­ставляет собой полный дифференциал, то есть бесконечно малое изменение, бесконечно малую разность; в данном случае име­ется в виду разность значений энергии между двумя состоя­ниями системы. Аналогичный смысл полного дифференциала имеет знак d перед Е . Величина dE определяет количество пере­несенного через контрольную поверхность вещества, в соот­ветствии с этим изменяется и экстенсор системы.

В противоположность этому знак d перед Q не является диф­ференциалом, ибо работа dQ есть не изменение чего-либо, а про­сто бесконечно малая величина. Работа совершается в процессе переноса вещества через контрольную поверхность. В момент окончания процесса работа прекращается. О качественной и количественной стороне совершенной в закончившемся процессе работы можно судить только по косвенным признакам: по изменениям экстенсоров и энергии системы. Иными словами, работа не может содержаться в системе, поэтому она не может изменяться и, следовательно, dQ не есть дифференциал работы (не есть разность каких-то двух значений величины Q в сис­теме).

Отмеченное различие в физическом смысле знаков d в урав­нении (31) имеет принципиальное теоретическое и практическое значение. Например, оно делает невозможным одинаковый под­ход при определении величин Е , U и Q , что будет ясно из даль­нейшего изложения.

Как видим, знак d перед Q имеет условный смысл. Но опреде­ленная условность содержится также и в знаках d перед энер­гией и экстенсорами. Ведь исходное уравнение (30) найдено для макроскопической системы, его дифференцирование связано с устремлением в пределе к нулю каждого экстенсора. При этом система как бы последовательно переходит из макромира в ми­кромир, наномир и т.д., которые обладают неодинаковыми свой­ствами: континуальными (непрерывными), дискретными (кван­товыми) и т.д. Поэтому во избежание неясностей и недоразуме­ний надо четко представлять себе, что устремление dE к нулю происходит мысленно, условно, на том уровне свойств, которые рассматриваются в каждом данном конкретном случае, например на уровне макромира. Если фактические размеры системы при­ближаются к величинам отдельных порций (квантов) веществ, тогда скачкообразно начинают изменяться энергия и интенсиалы, а также коэффициенты А и К , которые появляются в третьем и пятом началах ОТ. Это обстоятельство необходимо учитывать. При этом следует различать дискретность экстенсоров и скачки в значениях величин U , P , А и К . Эти скачки применительно к каждой данной степени свободы уменьшаются с ростом числа квантов соответствующего вещества в системе. При решении подобных задач большую помощь могла бы оказать особая дискретная алгебра, сейчас делаются попытки ее разработки [ТРП, стр.104-106].