Й формой итогового контроля знаний, умений и навыков учащихся оставалась контрольная работа, при этом личностный рост ребенка оставался вне поля зрения педагога
| Вид материала | Контрольная работа |
- Контрольная работа является одним из видов самостоятельной учебной работы студентов-заочников,, 111.64kb.
- Работа социального педагога с семьёй, 185.92kb.
- Знаний Умений Навыков (зун) учащихся по информатике Письменная контрольная работа, 40.74kb.
- Л. Ф. Методы и формы контроля усвоения знаний учащихся по русскому языку Рассказ (сообщение,, 273.63kb.
- Хорошева Наталья Юрьевна Вилюйск 2006 оглавление введение. 3 Тестирование как вид контроля, 259.73kb.
- Модель оценки индивидуальных достижений учащихся, основанная на компетентностном подходе, 38.33kb.
- Доклад Контроль знаний и умений учащихся составная часть процесса обучения, 12.25kb.
- Курсовая работа является основным видом письменных работ, выполняемых обучающимися,, 114.24kb.
- Интерактивные формы работы по взаимодействию с семьей, 151.35kb.
- Методические рекомендации по подготовке к экзамену по Налоговому праву (2011-2012 учебный, 49.03kb.
Сообщение на районной секции
учителей математики
« Эффективные методы
осуществления контроля
за результатами учебной деятельности
учащихся на различных этапах
обучения математике »
учителя математики
МОУ «Стригуновская средняя
общеобразовательная школа»
Коровянской Татьяны
Александровны
- Борисовка 2006 -
Многие годы единственной формой итогового контроля знаний, умений и навыков учащихся оставалась контрольная работа, при этом личностный рост ребенка оставался вне поля зрения педагога. Сегодня совершенствование учебного процесса требует развития и внедрения новых, нетрадиционных форм обучения. Изменение форм обучения влечет за собой изменение в системе контроля. Она становится более гибкой, позволяющей, с одной стороны, организовывать контроль знаний, умений и навыков, а с другой стороны находить возможность развития интеллектуальных и творческих способностей учащегося.
То есть при выборе форм и методов проверки знаний нами двигало понимание важности активной деятельности ученика, превращающее его из пассивного объекта воздействия в активного субъекта деятельности.
Деятельность на уроке рассматривается нами как последовательная цепь действий: настройка (актуализация) - целеполагание - определение критериев успеха - планирование собственной деятельности - реализация плана - рефлексия - оценивание - коррекция собственной деятельности.
Для осуществления контроля в рамках личностно ориентированного образования необходимо, чтобы:
- уровень проверяемого материала опирался на реальные достижения учащихся;
- цели, поставленные учителем или сформулированные в процессе настройки с учащимися, были достигаемы;
- неудача рассматривалась бы как переход на более высокий уровень;
- происходило побуждение к разнообразным формам деятельности, имеющим опору на зону ближайшего развития;
- акцентировалось внимание на характер деятельности каждого ученика или на особенностях его личности;
- предупреждалось состояние тревожности, не допускалось перенапряжения уровня притязаний;
- подчеркивалась возможность решения более трудных задач.
Виды контроля можно выделить следующие :
- устный опрос;
- письменный опрос;
- зачеты;
- лабораторные или практические работы;
- самостоятельные и контрольные работы;
- и сочетающие различные вышеперечисленные виды.
В зависимости от логики учебных занятий, типа урока контроль за результатами учебной деятельности можно осуществлять на следующих этапах урока :
- актуализации субъективного опыта, опорных знаний и умений или комплекса знаний;
- этапе закрепления знаний;
- этапе применения полученных знаний и умений;
- при систематизации и обобщении.
Предлагаю некоторые формы и методы осуществления контроля за результатами учебной деятельности , которые можно использовать на различных этапах урока и вообще учебной деятельности.
1. Блиц – опрос
«Положительные и отрицательные числа»
- Любое положительное число больше 0.
- Любое отрицательное число больше 0.
- Любое положительное число меньше любого отрицательного.
- Из двух положительных чисел большим будет то, у которого модуль больше.
- Любое положительное число больше любого отрицательного.
- Из двух отрицательных чисел большим будет то, модуль которого меньше.
- Из двух отрицательных чисел большим будет то, модуль которого больше. И т.д.
Учащиеся отвечают на розданных листочках- карточках (ставят «+», если согласны с утверждением и «- » - если посчитали утверждение неверным):

Ф.И._______________________
1. 7. 13. 19. 25.
2. 8. 14. 20. 26.
3. 9. 15. 21.
4. 10. 16. 22.
5. 11. 17. 23.
6. 12. 18. 24.
Оценка ________
2. Вставка пропущенных знаков

Вместо * поставь такую цифру, чтобы неравенство стало верным.
а)- 382> - 38*; б)- 432*1 <- 43271; в) -17,*5 > - 17,35;
г) - 2
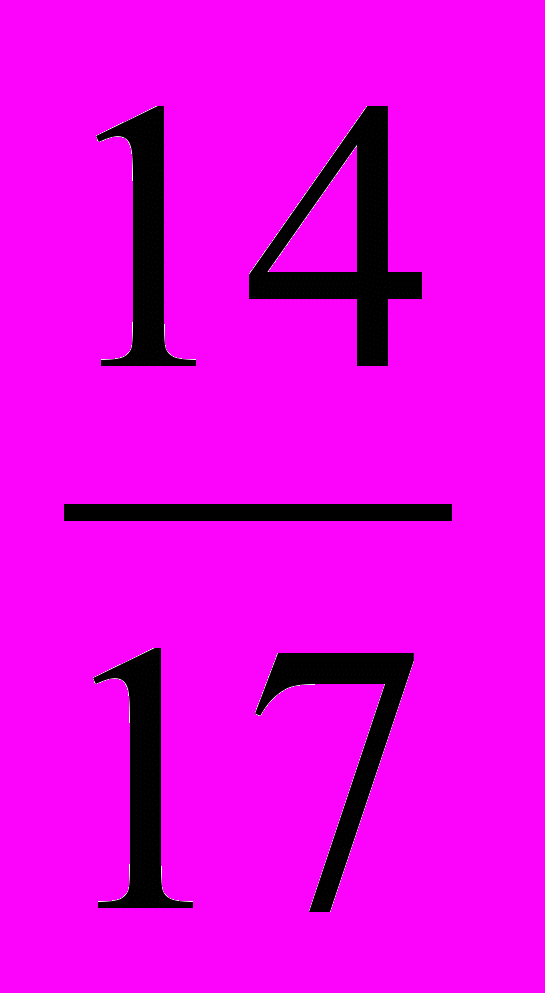 < - 2
< - 2 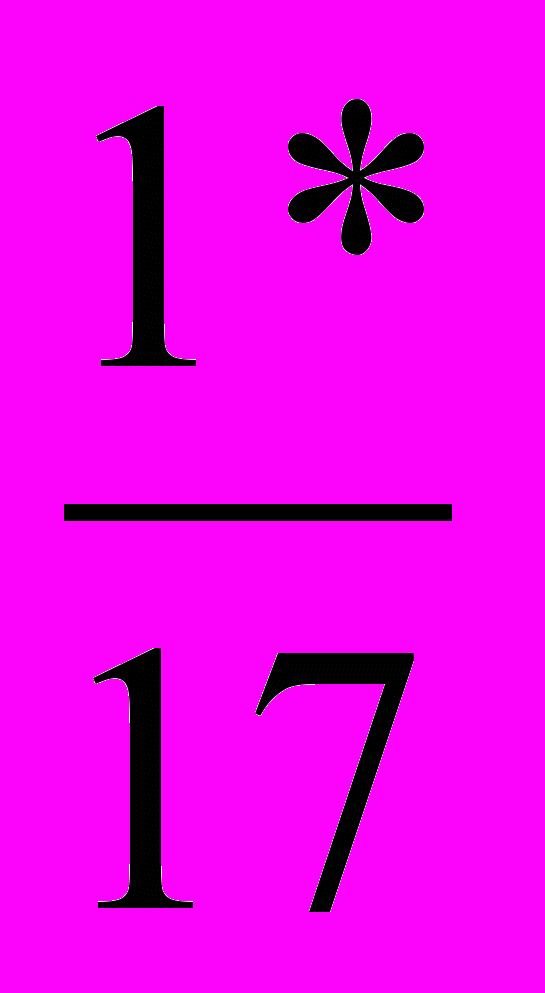 д)- 98
д)- 98  > - 98
> - 98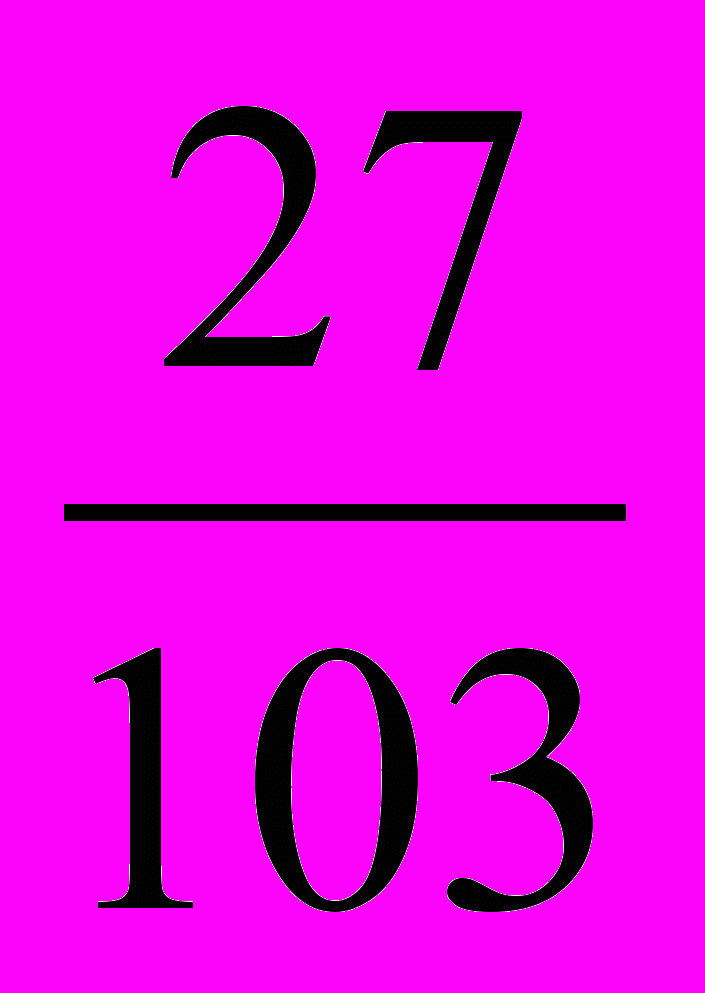 е)- 2*61,3<- 2861,3.
е)- 2*61,3<- 2861,3. - Незаконченные предложения


4. Выбор правильного ответа.
Пример :

Выбери правильный или предложи свой вариант ответа :
1. Смежными называются такие углы,
а) у которых одна сторона общая, а две другие дополнительные лучи;
б) у которых две стороны общие;
в) у которых стороны одного угла являются продолжениями сторон другого.
2. Вертикальными называются такие углы,
а) у которых одна сторона общая, а две другие дополнительные лучи;
б) у которых две стороны общие;
в) у которых стороны одного угла являются продолжениями сторон другого.
З. При пересечении двух прямых образуется смежных углов
а) одна пара;
б) две пары;
в) четыре пары.
4. При пересечении двух прямых образуется вертикальных углов
а) одна пара;
б) две пары;
в) четыре пары.
5. Свойство смежных углов:
а) они равны;
б) их сумма равна 180°;
в) свой вариант.
6. Свойство вертикальных углов:
а) они равны;
б) их сумма равна 180°;
в) свой вариант.
- Установление логических связей между элементами

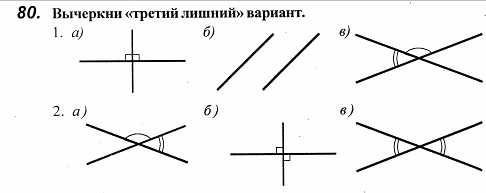
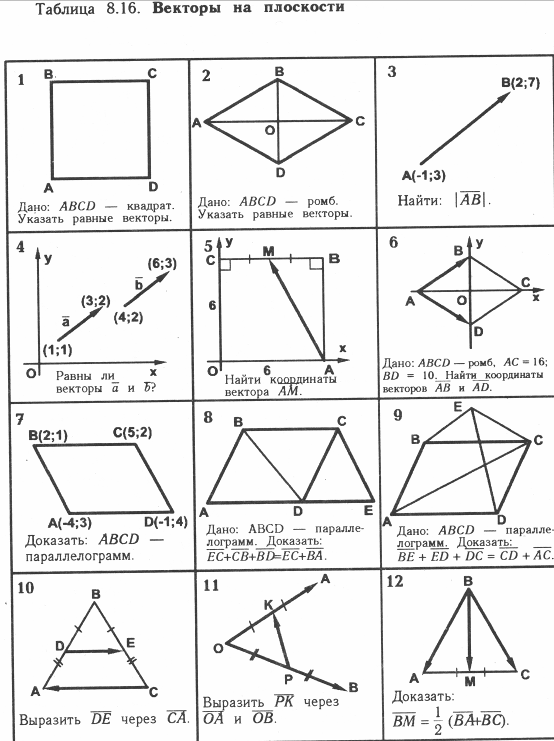
- Задачи на готовых чертежах
- Различные тесты ( прилагаются )
Групповые методы осуществления контроля за результатами учебной деятельности.
Урок-зачет
Основная цель этого урока — диагностика уровня усвоения знаний и умений каждым учащимся на определенном этапе обучения.
Практикуются различные виды зачетов: текущий и тематический, зачет-практикум, дифференцированный зачет, зачет-экстерн и др. Они предусматривают разные формы организации деятельности учителя и учащихся: форму экзамена, ринга, конвейера, общественного смотра знаний, аукциона и пр.
Если учащимся предварительно сообщается примерный перечень заданий, выносимых на зачет, то его называют открытым. Такой зачет проводится как завершающая проверка в конце изучаемой темы.
Приступая к ее изложению, учитель сообщает о содержании предстоящего зачета, об особенностях его организации и сроках сдачи. для проведения зачета из числа наиболее подготовленных учащихся выбираются консультанты. Они помогают распределить остальных учеников по группам из 3—5 человек и готовят учетные карточки, в которых фиксируются оценки за выполнение учениками каждого задания и итоговые оценки за зачет.
для каждого ученика, кроме консультантов, готовятся индивидуальные задания, включающие основные (соответствующие обязательному уровню Подготовки) и дополнительные вопросы и упражнения (их выполнение необходимо для получения хорошей или отличной оценки).
В начале урока, пока ученики выполняют задания, учитель проводит собеседование с консультантами: проверяет и оценивает их знания, а затем еще раз разъясняет методику проверки заданий.
Затем консультанты контролируют выполнение заданий в своих группах, а учитель выборочно проверяет работы учащихся, справившихся к этому моменту с основными заданиями.
Урок завершается заполнением учетных карточек промежуточными оценками, на основе которых учитель выставляет в журнал итоговую.
Урок-практикум
Главная задача урока-практикума - усиление практической направленности обучения. Он должен быть не только тесно связан с изученным материалом, но и способствовать его прочному, неформальному усвоению.
Основные формы проведения такого урока - практическая и лабораторная работы, на которых учащиеся самостоятельно упражняются в применении полученных знаний и умений.
Различают установочные, иллюстративные, тренировочные, исследовательские, творческие и обобщающие уроки-практикумы. На них преобладает групповая форма работы, при этом каждая группа, как правило, выполняет отличающуюся от других практическую или лабораторную работу согласно имеющейся инструкции.
Урок-соревнование
В основе этого урока лежит состязание команд при ответах на вопросы или решении чередующихся заданий, предложенных учителем, а форма проведения может быть самой разной: поединок, бой, эстафета, КВН, «Брейн-ринг>, «Счастливый случай», «Звездный час» и т.д.
В организации и проведении урока-соревнования вьщеляют три основных этапа: подготовительный, игровой и подведение итогов. Для каждого конкретного урока эта структура детализируется в соответствии с содержанием используемого материала и особенностями сюжета состязаний.
Контроль и развитие творчества детей
Изучение математики с самого начала предусматривает достаточно четкую структуру, в которой (казалось бы) нет места каким бы то ни было элементам творчества. Естественно, предусматриваются игровые моменты на ранних стадиях изучения математики, конкурсы и так далее. Но почему-то только говорят – красота математики, математика - интересная наука. На самом же деле возможности для творчества детей есть, и очень большие. При этом у учащихся повышается интерес к математике как к науке, предмету. Появляется желание самостоятельной проработки дополнительного материала. И в конце концов им просто начинает нравится эта достаточно сложная наука.
Итак, элементы математики, определенные мной как возможность для творчества:
- По учебной программе – номера, заранее предусматривающие художественное оформление.
- Различные самостоятельные графические построения.
- Небольшие “математические” сочинения – в основном пятые, шестые классы.
- Поиск вариантов решения задач и примеров.
- В свободное время поиск интересных математических загадок и логических задачек.
- Составление задач по готовым решениям.
- “Потерянные” решения, отдельные числа и цифры.
- Кроссворды, и многое другое.
По учебной программе – номера, предусматривающие заранее художественное оформление. Типа: в кружочках напишите числа и выполните указанные действия.

Такие задания даются отдельно с требованием выполнения на альбомных листах. Дети с большим удовольствием выполняют эти работы. На следующем уроке работы собираются, и выделяется несколько лучших работ. Выбираются три представителя “счетной комиссии” из первого, второго и третьего рядов. Каждому дается листик с фамилиями претендентов, карандаш. Представитель обходит свой ряд, подсчитывая голоса. По трем листам определяется победитель. Лучшая работа вывешивается на стенде “Лучшие работы Н-го класса” в кабинете.
Различные самостоятельные графические построения. В шестом классе при прохождении темы “Масштаб” для большей мотивации изучения предмета предлагалось нарисовать план своего дома.
Или тема «Координатная плоскость». Задание – придумать фигуру и расписать ее построение по координатам на плоскости.
И, конечно, к этому пункту следует добавить изготовление учащимися геометрических фигур, тел и иллюстраций к задачам по геометрии. Разукрашенные многогранники – интерес к ним у ученика не меньший, чем и к построениям.
Небольшие “математические” сочинения – в основном пятые классы. В данном случае детям дается тема (“Математика в жизни моих родителей”, “Где я вижу геометрические фигуры” и прочее), полученный в ответ материал дети с удовольствием читают друг другу. С проведением таких работ я стараюсь подгадать под декаду естественно-математического цикла. Тогда наиболее интересные и заслуживающие внимания работы идут в школьные газеты.
Поиск вариантов решения задач и примеров. Решать задачи не по действиям, а с помощью выражений, пользоваться свойствами сложения и вычитания при решении уравнений, а не находить скобки как неизвестные компоненты. В старших классах поиск более простого или короткого способа, который хотя бы использовался для проверки правильности решения задачи (Пример: Метод решения геометрических задач с помощью центра масс). Оригинальное решение, естественно. поощряется.
В свободное время поиск интересных математических загадок и логических задачек. Все начинается с первого урока, на который я готовлю наиболее интересные для данной возрастной группы задачи, загадки и прочее. Здесь возможностей много, соответствующая литература существует.
Составление задач на готовые решения. Это развивает речь, дети начинают потом более внимательно вчитываться в условия стандартных книжных задачек. Поскольку тетрадки для таких дополнительных заданий у детей на руках, то привожу прямо в докладе.
Пример: Давалось решение без условия:
120+40=160 (…) - …
314-160=154 (…) - …
Ответ: 154 …
Грикоров Юра, 5 класс : «В первый день чуть-чуть украли. И из-за этого собрали 120 кг картошки. Во второй день почти всю картошку сожрала медведка и поэтому собрали только 40 кг картошки. В третий день собрали 314 кг. На сколько кг картошки больше собрали в третий день, чем в первый и второй вместе взятые?»
Потерянные решения, отдельные числа и цифры. В этом случае в готовых решениях отсутствуют некоторые числа или цифры. Чаще всего в результате каких-либо интересных и смешных ситуаций. Детям интересно их находить и восстанавливать примеры. Тоже творчество.
Кроссворды и прочее. Это стандарт. Но и здесь можно более занимательно подать материал. Обычные проверочные работы на знание правил, свойств и определений (математические диктанты) можно предлагать в виде решения кроссворда. И тут нет ограничения на возраст учащихся. Это интересно всем. Также полезно давать возможность детям самим составлять их. Чаще всего их даже не надо выводить на мысль, они сами изъявляют желание.
