С 2007 Группа 04-102, 2 семестр

Вид материала

Закон

Содержание 30. Интерференция при отражении от тонких пленок. Пример расчета интерференционной картины для плоскопараллельной пластинки. 31. Кольца Ньютона. Радиусы темных и светлых колец.

Подобный материал:

• Лекций студентами Кафедра биологии дисциплина ботаника группа, 75.84kb.
• Темы рефератов по дисциплине: «Оcновы аудита» Сущность аудиторской деятельности, 153.15kb.
• Курс, группа у-5360, срок обучения 4 года 4 месяца, осенний семестр 2007-2008 учебного, 158.22kb.
• Список публикаций педагогов моу сош №102 в 2007-2008 учебном году, 38.48kb.
• Году в Республике Коми составил 103,0% к уровню 2007 года, что выше среднероссийского, 240.16kb.
• График контрольных мероприятий по учебным дисциплинам III курс I семестр группа 3394,3395, 94.19kb.
• Анализ ситуации на рынке производства сахара, 81.6kb.
• Сп 41-102-98, 1743.38kb.
• Никитина Ирина Александровна, д э. н., профессор, sizn@mail ru Бакалаврская программа, 154.15kb.
• Курс 5 Семестр: 9-10 Астана 2011 7 Сведения о преподавателях, 325.38kb.

30. Интерференция при отражении от тонких пленок. Пример расчета интерференционной картины для плоскопараллельной пластинки.

Интерференция - физическое явление, наблюдаемое при сложении волн (световых, звуковых и т. п.), усиление волн в одних точках пространства и ослабление в других (или сложение двух или более волн, при котором амплитуда результирующей волны зависит от разности фаз исходных волн в данной точке пространства)




Пусть на плоскопараллельную прозрачную пленку (пластинку) с показателем преломления n и толщиной d под углом  падает плоская монохроматическая волна (для простоты рассмотрим один луч).

На поверхности пленки в точке А волна частично отражается (луч 1- ) и частично преломляется (луч АВ). В точке В волна также частично отражается (луч ВС) и частично преломляется (луч 2- ). То же самое происходит в точке С.

Причем преломленная волна (луч 1" ) накладывается на волну непосредственно отраженную от верхней поверхности (луч 1- ). Эти две волны когерентны, если оптическая разность хода меньше длины когерентности l_ког, и в этом случае они интерферируют.

Оптическая разность хода двух волн =(AB+BC)n-(AD-/2),

где /2 - потеря полуволны при отражении луча 1- в точке А. Используя закон преломления n₁sin = n₂sin и учитывая, что в рассматриваемом случае n₁=1, n₂=n, можно показать, что .(17)

В точке наблюдения на экране будет максимум, если m и минимум, если (2m+1)/2[см.(15),(16)].

Возможность уменьшения вредного отражения света вследствие интерференции в тонких пленках широко используется в современных оптических приборах. Для этого на передние поверхности линз, призм наносят тонкие пленки с показателем преломления n= и толщиной d, которая определяется из условия минимума при интерференции волн, отраженных от границ раздела сред с n₁ и n и n и n₂

2dn=(2m+1)/2, m=0,1,2-(18)

Минимальная толщина пленки соответствует m=0

d=/(4n)

Такая оптика получила название просветленной оптики.

31. Кольца Ньютона. Радиусы темных и светлых колец.

Кольца Ньютона — кольцеобразные интерференционные максимумы и минимумы, появляющиеся вокруг точки касания слегка изогнутой выпуклой линзы и плоскопараллельной пластины. Интерференция возникает в воздушном зазоре между линзой и пластиной (отраженный свет).

Они наблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельный толстой стеклянной пла­стинки и плоско-выпуклой линзы с большим радиусом кривизны (рис. 52). Роль тонкой пленки, от поверхно­стей которой отражаются когерентные волны, играет воздушный зазор между пластинкой и линзой (вслед­ствие большой толщины пластинки и линзы за счет от­ражений от других поверхностей интерференционные полосы не возникают). При нормальном падении света полосы равной толщины имеют вид концентрических окружностей, при наклонном падении — эллипсов. Най­дем радиусы колец Ньютона, получающихся при паде­нии света по нормали к пластинке. В этом случае cos i₂ ~ 1 и оптическая разность хода равна удвоенной толщине зазора [см. формулу 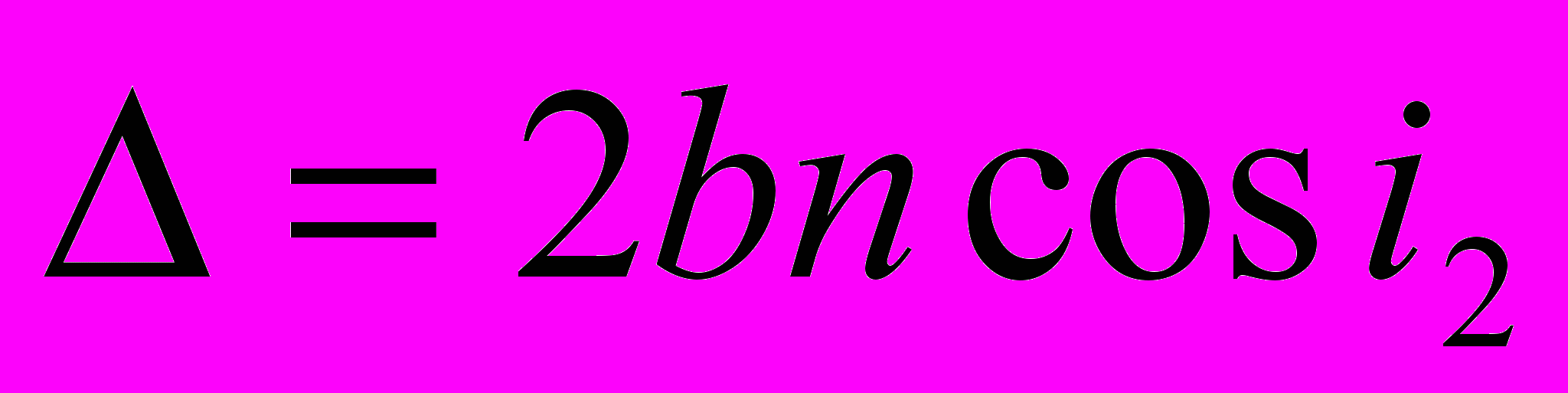; предполагается, что в зазоре п = 1]. Как следует из рис. 52: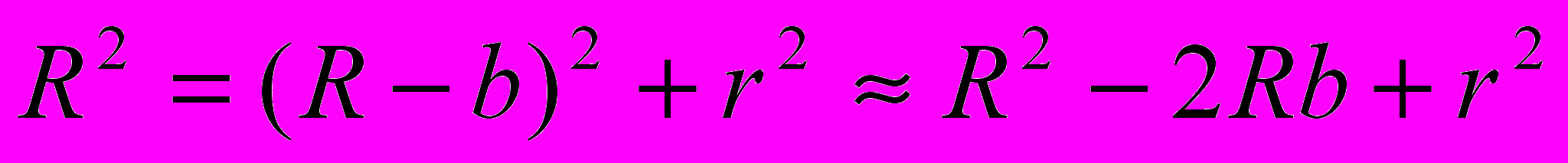



где R — радиус кривизны линзы, r — радиус окружно­сти, всем точкам. которой соответствует одинаковый за­зор b. Ввиду малости b мы пренебрегли величиной Ь² по сравнению с 2Rb.

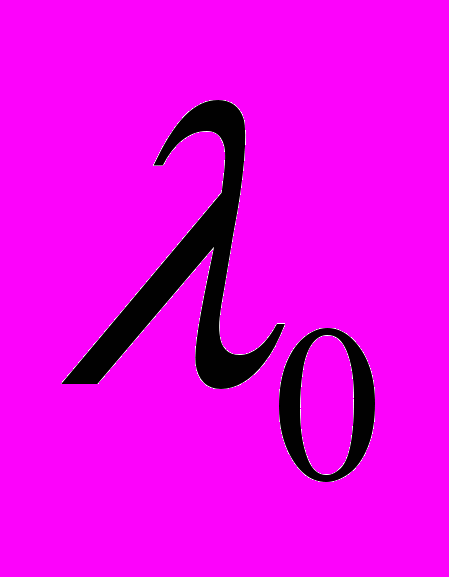В соответствии с (19.11) b = r²/2R. Чтобы учесть возникающее при отражении от пластинки изменение фазы на , нужно при вычислении к 2Ь = r²/R приба­вить /2. В результате получится: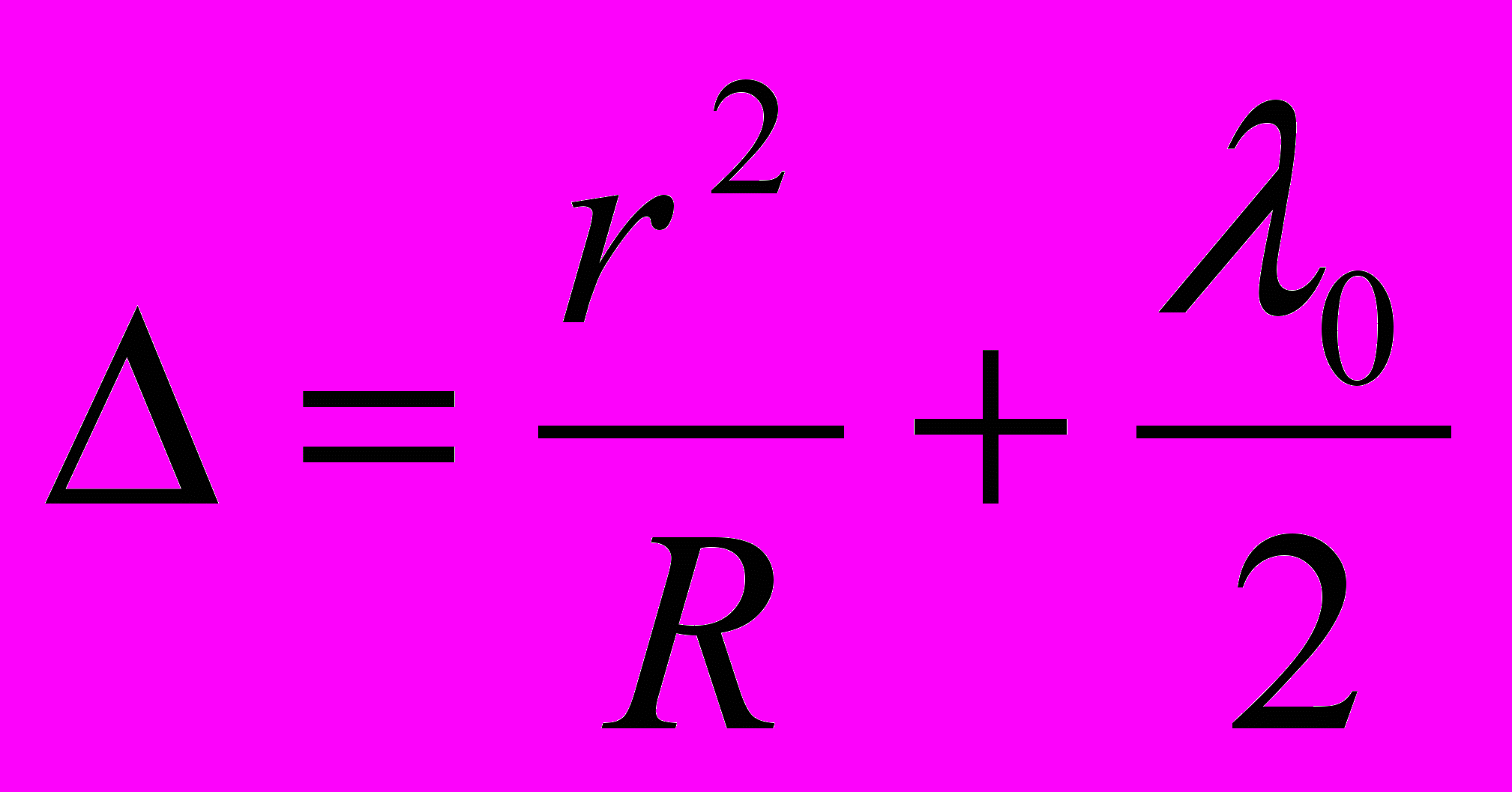



В точках, для которых 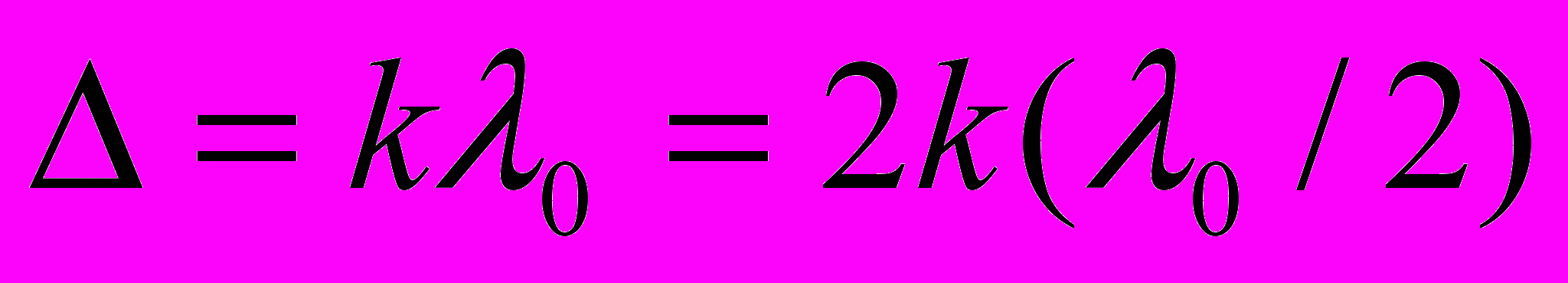возникнут максимумы; в точках, для которых 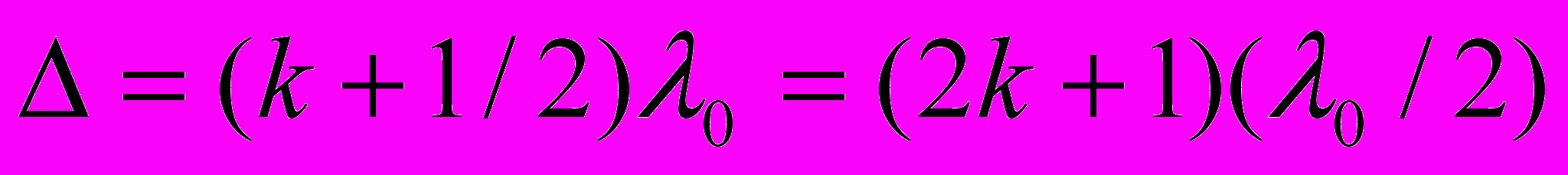,— минимумы интенсивности. Оба усло­вия можно объединить в одно: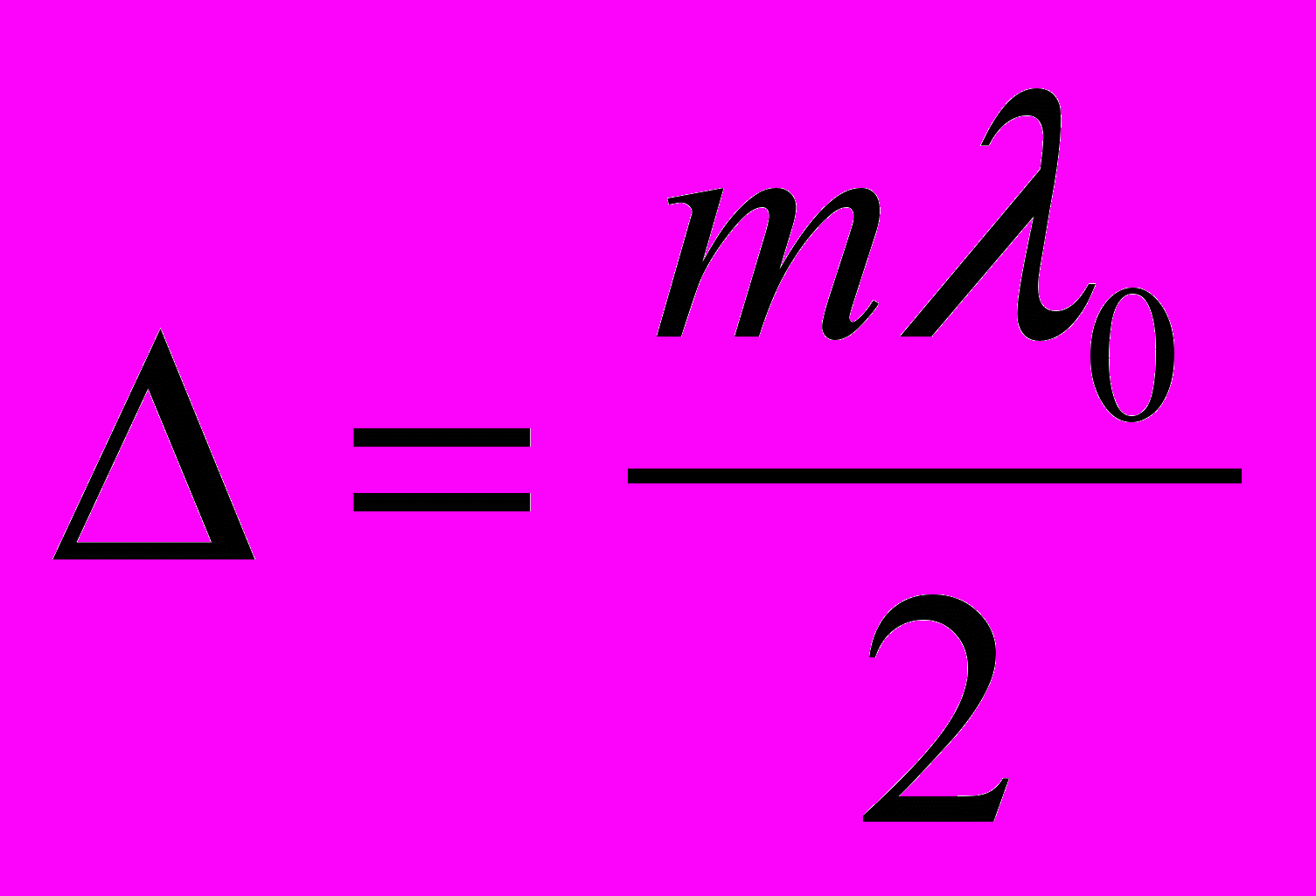



причем четным значениям m будут соответствовать мак­симумы, а нечетным — минимумы интенсивности.

Подставив сюда выражение (19.12) для и разре­шив получающееся уравнение относительно r, найдем радиусы светлых и темных колец Ньютона: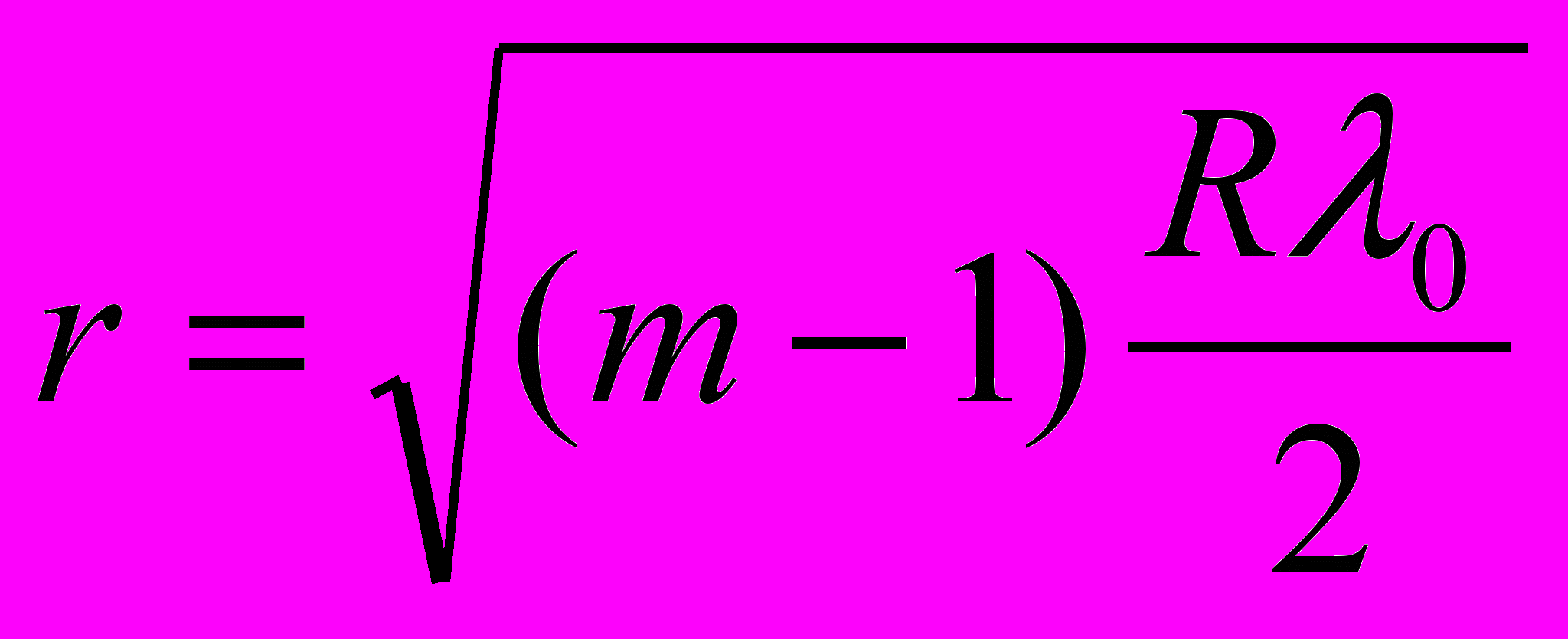

(m = 1, 2, 3…)

четным m соответствуют радиусы светлых колец, не­четным m — радиусы темных колец. Значению m = 1 соответствует r = 0, т. е. точка в месте касания пла­стинки и линзы. В этой точке наблюдается минимум ин­тенсивности, обусловленный изменением фазы на при отражении световой волны от пластинки.