С 2007 Группа 04-102, 2 семестр

• Лекций студентами Кафедра биологии дисциплина ботаника группа, 75.84kb.
• Темы рефератов по дисциплине: «Оcновы аудита» Сущность аудиторской деятельности, 153.15kb.
• Курс, группа у-5360, срок обучения 4 года 4 месяца, осенний семестр 2007-2008 учебного, 158.22kb.
• Список публикаций педагогов моу сош №102 в 2007-2008 учебном году, 38.48kb.
• Году в Республике Коми составил 103,0% к уровню 2007 года, что выше среднероссийского, 240.16kb.
• График контрольных мероприятий по учебным дисциплинам III курс I семестр группа 3394,3395, 94.19kb.
• Анализ ситуации на рынке производства сахара, 81.6kb.
• Сп 41-102-98, 1743.38kb.
• Никитина Ирина Александровна, д э. н., профессор, sizn@mail ru Бакалаврская программа, 154.15kb.
• Курс 5 Семестр: 9-10 Астана 2011 7 Сведения о преподавателях, 325.38kb.

29. Основные понятия в теории интерференции. Оптическая длина пути и оптическая разность хода. Условия максимумов и минимумов интенсивности света через разность фаз и оптическую разность хода. (см. также вопрос 27) Оптическая длина пути, оптический путь, между точками А и В прозрачной среды; расстояние, на которое свет (ссылка скрыта) распространился бы в вакууме за время его прохождения от А до В. Поскольку скорость света в любой среде меньше его скорости в вакууме, О. д. п. всегда больше реально проходимого светом расстояния (или, в предельном случае вакуума, равна ему). В оптической системе, состоящей из р однородных сред (траектория луча света в такой системе — ломаная линия), О. д. п. равна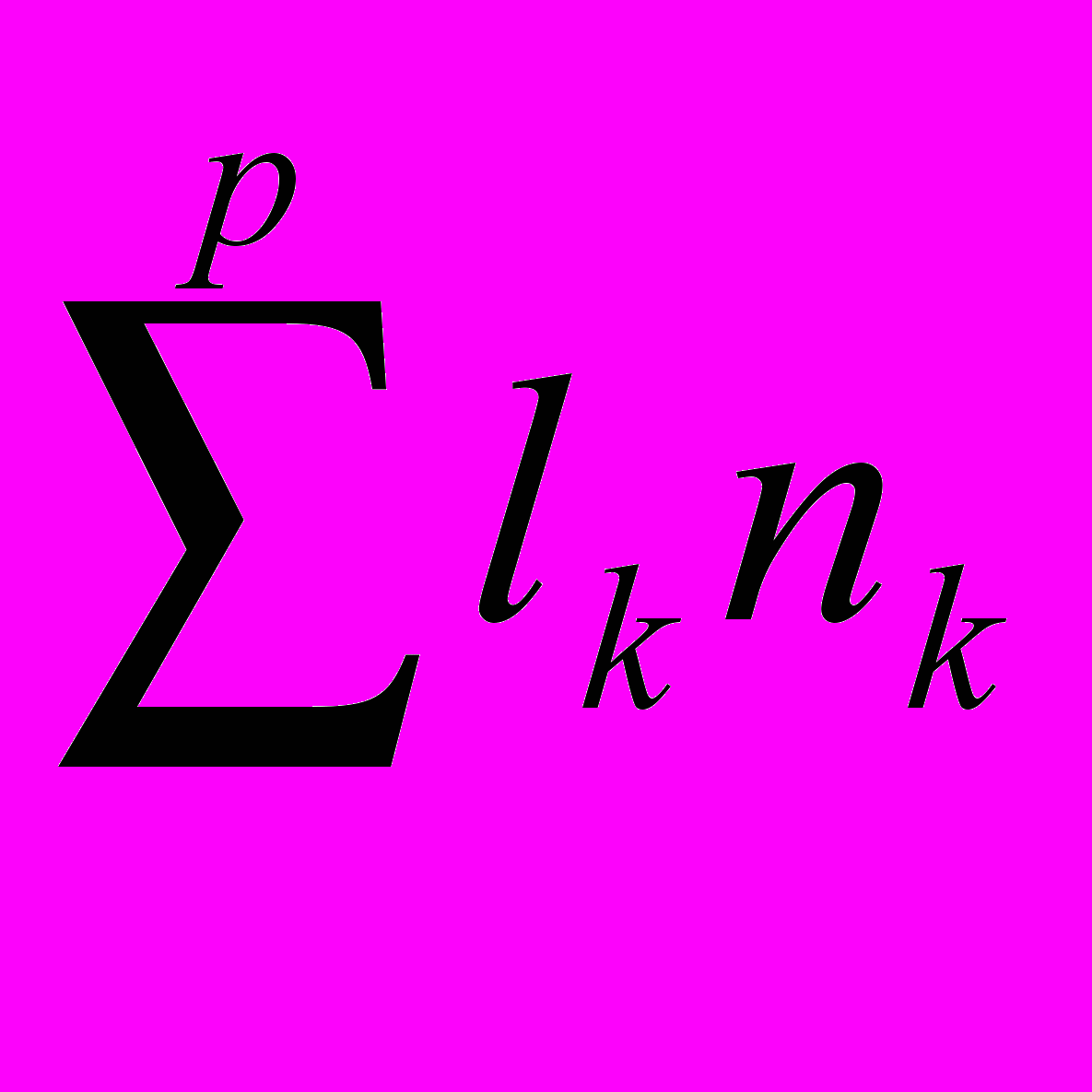, где lk — расстояние, пройденное светом в k-той среде (k = 1, 2,..., р), nk — показатель преломления этой среды,  — знак суммы. Для одной среды (р = 1) сумма сокращается до единственного члена ln . В оптически неоднородной среде (с плавно меняющимся n; траектория луча в такой среде — кривая линия), О. д. п. есть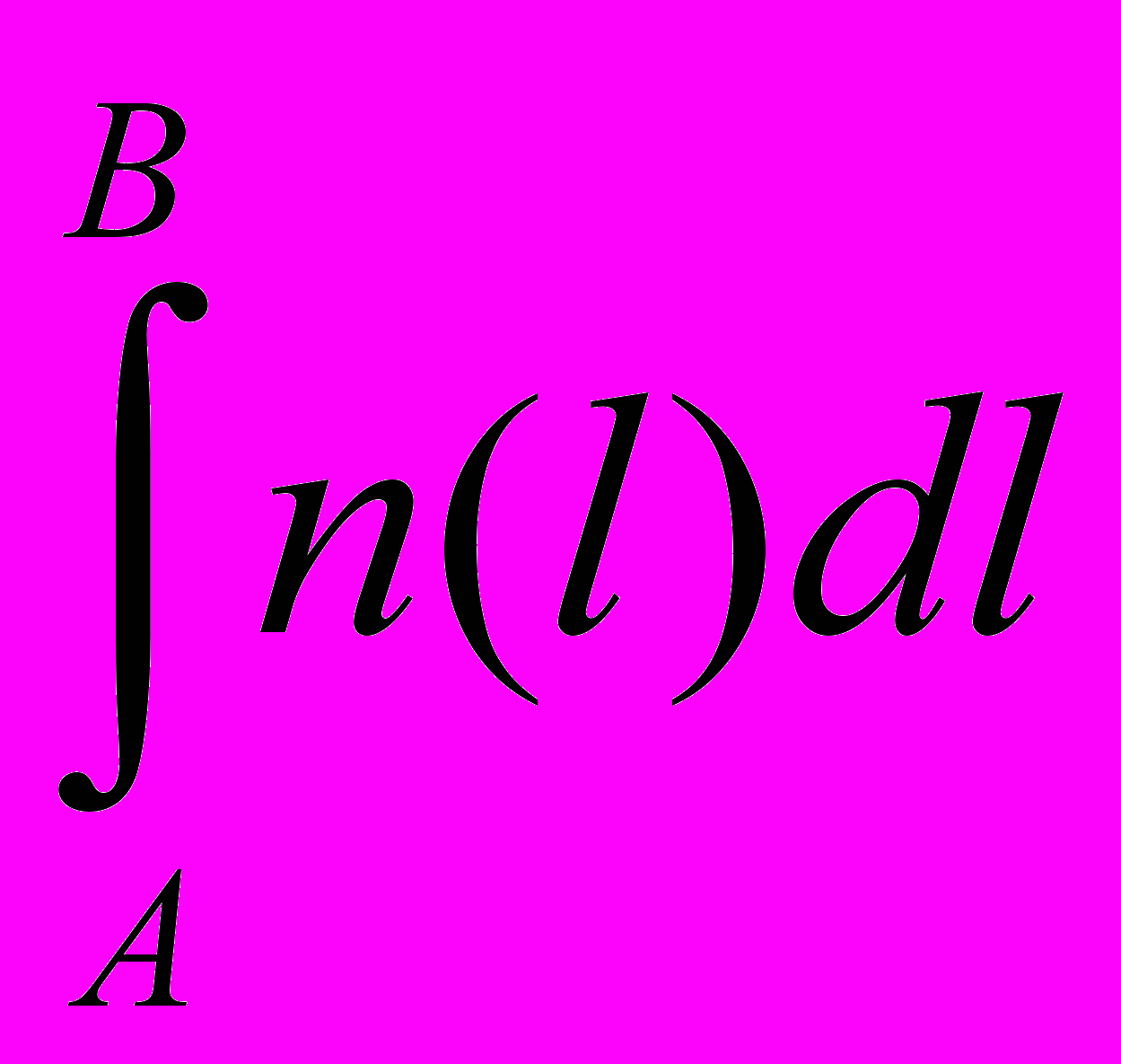, где dl — бесконечно малый элемент траектории луча. Понятие О. д. п. играет большую роль в оптике, особенно в ссылка скрыта и ссылка скрыта, позволяя сопоставлять пути, проходимые светом в средах, в которых скорость его распространения различна. Геометрическое место точек, для которых О. д. п., отсчитываемая от одного источника, одинакова, называется поверхностью световой волны; световые колебания на этой поверхности находятся в одинаковой ссылка скрыта. Разность хода лучей, разность ссылка скрыта двух световых лучей, имеющих общие начальную и конечную точки. Понятие Р. х. играет основную роль в описании ссылка скрыта и ссылка скрыта. Расчёты распределения световой энергии в ссылка скрыта основаны на вычислении Р. х. проходящих через них лучей (или пучков лучей). Оптическая разность хода. Вместо разности фаз интерферирующих волн удобно ввести в рассмотрение пропорциональную ей величину - оптическую разность хода, которая отличается множителем , где 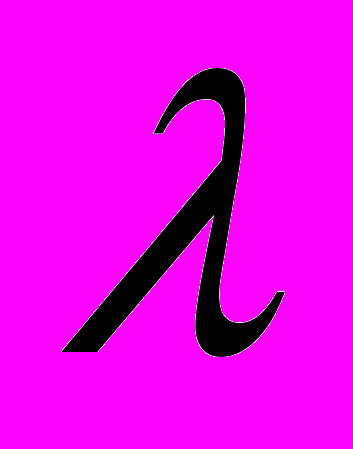- длина световой волны. Изменению разности фаз на 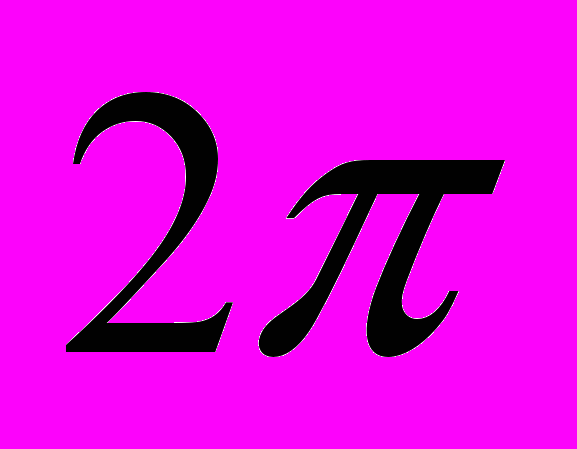соответствует изменение разности хода на . 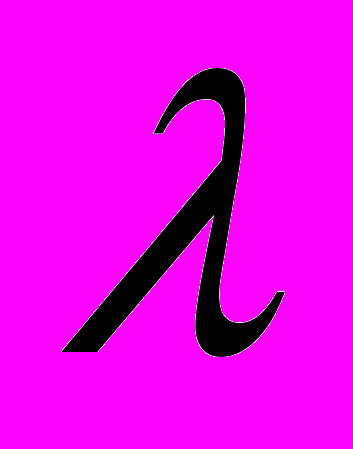В вакууме оптическая разность хода в отличие от разности фаз имеет наглядную интерпретацию. Если две интерферирующие волны испускаются одним источником света, то разность хода - это геометрическая разность длин путей, по которым два интерферирующих луча от одной точки источника достигли одной точки экрана. Например, в оптической схеме опыта Юнга, изображенной на рис. 18, разность хода для точки P на экране находится по формуле: . 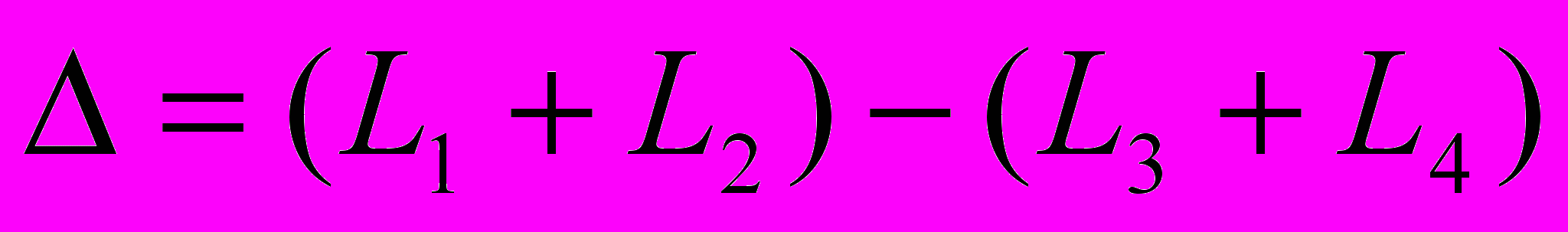В изотропной среде скорость света в n раз меньше, чем в вакууме, здесь n - показатель преломления среды. Частота света в среде и в вакууме одинакова, поэтому длина волны в среде в n раз меньше. 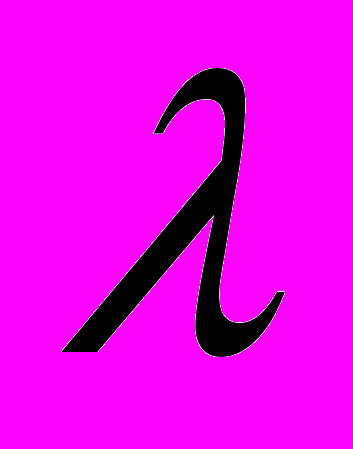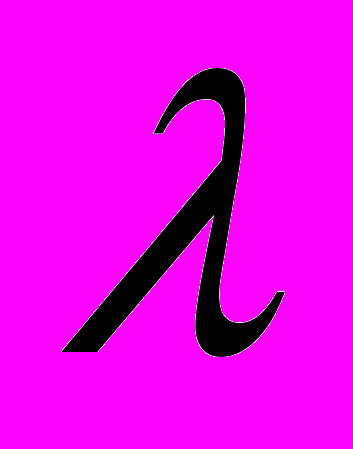В соответствии с соотношением вместо реального уменьшения длины волны можно рассматривать неизменную и соответствующее увеличение длины пути луча. С этой целью вводится понятие оптической длины пути, которая в n раз больше геометрической длины. Далее, употребляя термин "разность хода", всегда будем иметь в виду оптическую разность хода. Заменяя разность фаз интерферирующих волн оптической разностью хода, получаем следующее выражение для интенсивности интерференционной картины: . Приемники света в оптическом диапазоне реагируют на интенсивность света, а не на напряженность электрического или магнитного полей. Поэтому измеряемые в опыте величины, ширина полос и видность, также могут быть выражены через интенсивность, а значит и через оптическую разность хода. Следовательно, понятие оптической разности хода позволяет свести оптическую задачу по интерференции к геометрической задаче отыскания разности хода. Отметим, что разность хода лучей можно отсчитывать не только как разность длин путей от источника до точки наблюдения, но и как разность длин путей от двух точек любой поверхности равной фазы волны до точки наблюдения. При этом, конечно, две точки на поверхности равной фазы - не произвольные точки, а должны быть точками, через которые реально проходят лучи, попадающие в точку наблюдения. Так на рис. 18 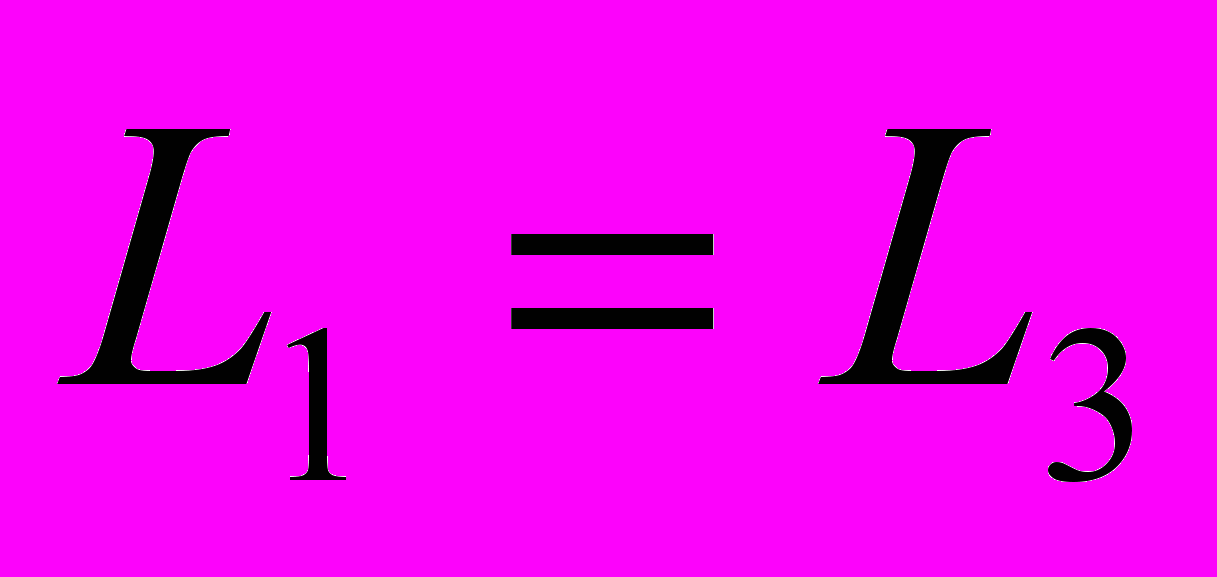, поэтому две щели находятся на поверхности равной фазы, и, следовательно, разность хода можно найти по упрощенной формуле . Этот прием часто используется при решении задач. 18.1.2.1. Условия максимума и минимума на разность фаз δ 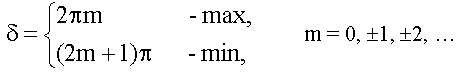18.1.2.2. Оптическая разность хода Пусть для простоты, начальные фазы α1 и α2 интерферирующих волн равны нулю, тогда: 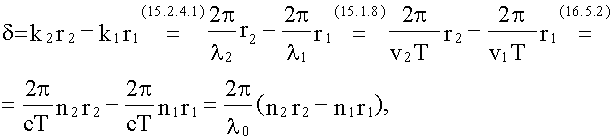здесь λ0 = cT - длина световой волны в вакууме. Оптической разностью хода называют величину: 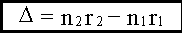. Тогда: 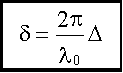. 18.1.2.3. Условия максимума и минимума на оптическую разность хода Из (18.1.2.1.) и (18.1.2.2.): После сокращения получим условия на Δ: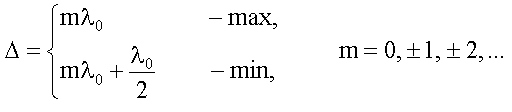