С 2007 Группа 04-102, 2 семестр
| Вид материала | Закон |
- Лекций студентами Кафедра биологии дисциплина ботаника группа, 75.84kb.
- Темы рефератов по дисциплине: «Оcновы аудита» Сущность аудиторской деятельности, 153.15kb.
- Курс, группа у-5360, срок обучения 4 года 4 месяца, осенний семестр 2007-2008 учебного, 158.22kb.
- Список публикаций педагогов моу сош №102 в 2007-2008 учебном году, 38.48kb.
- Году в Республике Коми составил 103,0% к уровню 2007 года, что выше среднероссийского, 240.16kb.
- График контрольных мероприятий по учебным дисциплинам III курс I семестр группа 3394,3395, 94.19kb.
- Анализ ситуации на рынке производства сахара, 81.6kb.
- Сп 41-102-98, 1743.38kb.
- Никитина Ирина Александровна, д э. н., профессор, sizn@mail ru Бакалаврская программа, 154.15kb.
- Курс 5 Семестр: 9-10 Астана 2011 7 Сведения о преподавателях, 325.38kb.
32. Дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля. Радиусы зон Френеля. Дифракция на круглом отверстии и непрозрачном диске.Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий (более широком смысле - любые отклонения при распространении волн от законов геометрической оптики ). Дифракционная картина – система чередующихся светлых и темных колец. Если препятствие имеет линейный характер (щель, нить, край экрана), то на экране возникает система параллельных дифракционных полос. Френель развил количественную теорию дифракционных явлений . В основу теории Френель положил принцип Гюйгенса, дополнив его идеей об интерференции вторичных волн. Р 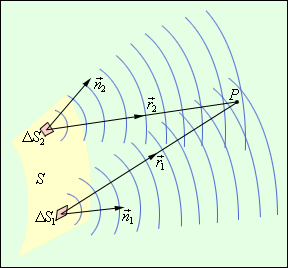 исунок ниже иллюстрирует принцип Гюйгенса–Френеля. исунок ниже иллюстрирует принцип Гюйгенса–Френеля.
Пусть поверхность S представляет собой положение волнового фронта в некоторый момент. Для того чтобы определить колебания в некоторой точке P, вызванное волной, по Френелю нужно сначала определить колебания, вызываемые в этой точке отдельными вторичными волнами, приходящими в нее от всех элементов поверхности S (ΔS1, ΔS2 и т. д.), и затем сложить эти колебания с учетом их амплитуд и фаз. При этом следует учитывать только те элементы волновой поверхности S, которые не загораживаются каким-либо препятствием. Рассмотрим в качестве примера простую дифракционную задачу о прохождении плоской монохроматической волны от удаленного источника через небольшое круглое отверстие радиуса R в непрозрачном экране :
Точка наблюдения P находится на оси симметрии на расстоянии L от экрана. В соответствии с принципом Гюйгенса–Френеля следует мысленно заселить волновую поверхность, совпадающую с плоскостью отверстия, вторичными источниками, волны от которых достигают точки P. В результате интерференции вторичных волн в точке P возникает некоторое результирующее колебание, квадрат амплитуды которого (интенсивность) нужно определить при заданных значениях длины волны λ, амплитуды A0 падающей волны и геометрии задачи. Для облегчения расчета Френель предложил разбить волновую поверхность падающей волны в месте расположения препятствия на кольцевые зоны (зоны Френеля) по следующему правилу: расстояние от границ соседних зон до точки P должны отличается на полдлины волны, то есть
Е 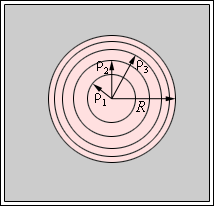 сли смотреть на волновую поверхность из точки P, то границы зон Френеля будут представлять собой концентрические окружности (рис. ниже). сли смотреть на волновую поверхность из точки P, то границы зон Френеля будут представлять собой концентрические окружности (рис. ниже).
Из рис. Выше легко найти радиусы ρm зон Френеля:
Так в оптике λ << L, вторым членом под корнем можно пренебречь. Количество зон Френеля, укладывающихся на отверстии, определяется его радиусом R:
Здесь m – не обязательно целое число. Результат интерференции вторичных волн в точке P зависит от числа m открытых зон Френеля. Легко показать, что все зоны имеют одинаковую площадь:
33. Дифракция Фраунгофера на щели. Распределение интенсивности света в дифракционной картине. Условия максимумов и минимумов интенсивности. Дифракционная решетка. Дифракция Фраунгофера на решетке. Условия максимумов и минимумов интенсивности.Дифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями и связанных с отклонениями от законов геометрической оптики. Дифракция, в частности, приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени.Различают два случая дифракции. Если источник света и точка наблюдения Р расположены от препятствия настолько далеко, что лучи, падающие на препятствие, и лучи, идущие в точку Р, образуют практически параллельные пучки, говорят о дифракции Фраунгофера или о д 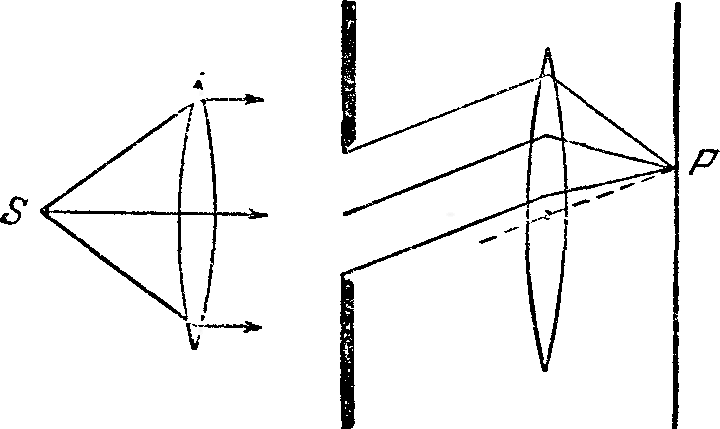 ифракции в параллельных лучах. В противном случае говорят о дифракции Френеля. Дифракцию Фраунгофера можно наблюдать, поместив за источником света S и перед точкой наблюдения Р по линзе так, чтобы точки S и Р оказались в фокальной плоскости соответствующей линзы (см рис.). ифракции в параллельных лучах. В противном случае говорят о дифракции Френеля. Дифракцию Фраунгофера можно наблюдать, поместив за источником света S и перед точкой наблюдения Р по линзе так, чтобы точки S и Р оказались в фокальной плоскости соответствующей линзы (см рис.).Р  ассмотрим экран с двумя щелями, на которые нормально падает плоская монохроматическая волна. Расчеты показывают, что интенсивность света за экраном будет зависеть от угла между направлением распространения света и п ассмотрим экран с двумя щелями, на которые нормально падает плоская монохроматическая волна. Расчеты показывают, что интенсивность света за экраном будет зависеть от угла между направлением распространения света и п ерпендикуляром к экрану : ерпендикуляром к экрану : где I0 - интенсивность света в центре дифракционной картины, когда открыта только одна щель, b - ширина щели, d - расстояние между щелями, k=2 / - волновое число, - длина волны света, - дополнительная разность хода между интерферирующими лучами (в случае наклонного падения плоской волны на экран или когда одна из щелей закрыта стеклянной пластинкой). Первый сомножитель в квадратных скобках описывает дифракцию Фраунгофера на одной щели, а второй сомножитель - интерференцию от двух точечных источников. Общая энергия, проходящая через одну щель, пропорциональна b, а ширина дифракционной картины пропорциональна 1/b. Поэтому, интенсивность света I0 в центре дифракционной картины будет пропорциональна b2. Если мы рассмотрим дифракцию на двух щелях, то в пределах первого дифракционного максимума мы можем наблюдать N интерференционных полос, где N=2d/b. Приведённый ниже рисунок показывает зависимость интенсивности света от угла в случае д 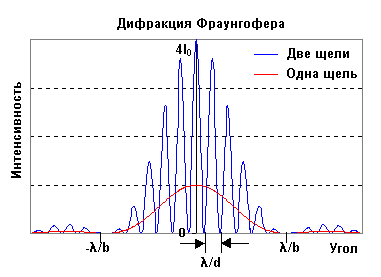 ифракции на одной щели (кривая красного цвета) и в случае дифракции на двух щелях (кривая синего цвета). Из рисунка видно, что в случае дифракции на двух щелях, огибающая интенсивности интерференционных полос повторяет кривую дифракции на одной щели. ифракции на одной щели (кривая красного цвета) и в случае дифракции на двух щелях (кривая синего цвета). Из рисунка видно, что в случае дифракции на двух щелях, огибающая интенсивности интерференционных полос повторяет кривую дифракции на одной щели.Говоря о дифракции Фраунгофера, мы подразумеваем случай, когда наблюдение дифракционной картины производится на достаточно большом расстоянии от экрана с щелями. Количественный критерий дифракции Фраунгофера описывается следующей формулой: z >> d2/ где z - расстояние от экрана с щелями до точки наблюдения. В непосредственной близости к щелям дифракционная картина будет описываться формулами. Условия max и min смотри в билете 31 34. Дифракционная решетка как спектральный прибор. Разрешающая способность дифракционной решетки. Угловая дисперсия.Дифракционная решетка — оптический прибор, работающий по принципу ссылка скрыта света, представляет собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесённых на некоторую поверхность. Описание явления : Фронт световой волны разбивается штрихами решетки на отдельные пучки когерентного света. Эти пучки претерпевают дифракцию на штрихах и интерферируют друг с другом. Так как для каждой длины волны существует свой угол дифракции, то белый свет раскладывается в спектр. Формулы: Расстояние, через которое повторяются штрихи на решетке, называют периодом дифракционной решетки. Обозначают буквой d. Если известно число штрихов (N), приходящихся на 1 мм решетки, то период решетки находят по формуле: 0,001*(1/N) Формула дифракционной решетки: d*sinα=k*λ, где d — период решетки, α — угол максимума данного цвета, k — порядок максимума, λ — длина волны. Угловой дисперсией спектральных приборов принято называть величину 
В случае решетки, как следует из  , угловая дисперсия равна , угловая дисперсия равна  Разрешающей способностью спектрального прибора принято называть отношение
где  – минимальный интервал между двумя близкими спектральными линиями, при котором они могут быть разрешены, то есть отделены одна от другой. – минимальный интервал между двумя близкими спектральными линиями, при котором они могут быть разрешены, то есть отделены одна от другой.35. Поляризация света. Степень поляризации. Закон Малюса.Поляризация — для ссылка скрыта направление колебаний вектора ссылка скрыта E. ссылка скрыта электромагнитное излучение может иметь: -Линейную поляризацию — в направлении, ссылка скрыта направлению распространения волны; -Круговую поляризацию — правую либо левую, в зависимости от направления вращения вектора индукции; -Эллиптическую поляризацию — случай, промежуточный между круговой и линейными поляризациями. Некогерентное излучение может не быть поляризованным, либо быть полностью или частично поляризованным любым из указанных способов. В этом случае понятие поляризации понимается статистически.  Для описания явлений поляpизации достаточно иметь в виду какую-нибудь одну плоскость. Мы остановимся на плоскости колебаний (Q). Плоскополяpизованный свет имеет еще одну хаpактеpистику: pасположение плоскости колебаний в пpостpанстве. Для описания явлений поляpизации достаточно иметь в виду какую-нибудь одну плоскость. Мы остановимся на плоскости колебаний (Q). Плоскополяpизованный свет имеет еще одну хаpактеpистику: pасположение плоскости колебаний в пpостpанстве.Если конец вектоpа Е в плоскости К, пеpпендикуляpной к лучу, описывает эллипс или окpужность, то свет соответственно называется поляpизованным по эллипсу или по кpугу. Волну, поляpизованную по эллипсу или по кpугу, можно pазложить pазличными способами на две плоскополяpизованные волны, как это показано на pис. 1.21 (по оси х по оси y).  Если конец вектоpа Е в плоскости К описывает беспоpядочные колебания, т. е. плоскость колебаний постоянно и беспоpядочно меняется, то свет называется естественным или неполяpизованным. Рис. 1.22 иллюстpиpует такую ситуацию. Естественные источники света излучают именно такой, неполяpизованный свет. Это ясно из того, что свет от обычных источников излучается отдельными атомами. Каждый атом излучает плоскополяpизованные волны, но плоскости их колебаний никак не согласованы между собой. Суммаpный свет получается сложным, неполяpизованным. Наконец, можно создать частично поляpизованный свет, в котоpом не все плоскости колебаний одинаково пpедставлены, а имеется некотоpая выделенность одних колебаний пеpед дpугими. Рис.1.23 иллюстpиpует колебания конца вектоpа Е в частично поляpизованном свете. Можно ввести величину, хаpактеpизующую степень поляpизации у частично поляpизованного света. Если конец вектоpа Е в плоскости К описывает беспоpядочные колебания, т. е. плоскость колебаний постоянно и беспоpядочно меняется, то свет называется естественным или неполяpизованным. Рис. 1.22 иллюстpиpует такую ситуацию. Естественные источники света излучают именно такой, неполяpизованный свет. Это ясно из того, что свет от обычных источников излучается отдельными атомами. Каждый атом излучает плоскополяpизованные волны, но плоскости их колебаний никак не согласованы между собой. Суммаpный свет получается сложным, неполяpизованным. Наконец, можно создать частично поляpизованный свет, в котоpом не все плоскости колебаний одинаково пpедставлены, а имеется некотоpая выделенность одних колебаний пеpед дpугими. Рис.1.23 иллюстpиpует колебания конца вектоpа Е в частично поляpизованном свете. Можно ввести величину, хаpактеpизующую степень поляpизации у частично поляpизованного света.Неполяpизованный или частично поляpизованный свет, так же как и поляpизованный по эллипсу, можно pазложить на два плоскополяpизованных луча. Этим обстоятельством на пpактике шиpоко пользуются для создания плоскополяpизованного света. Степенью поляризации называют выражение: 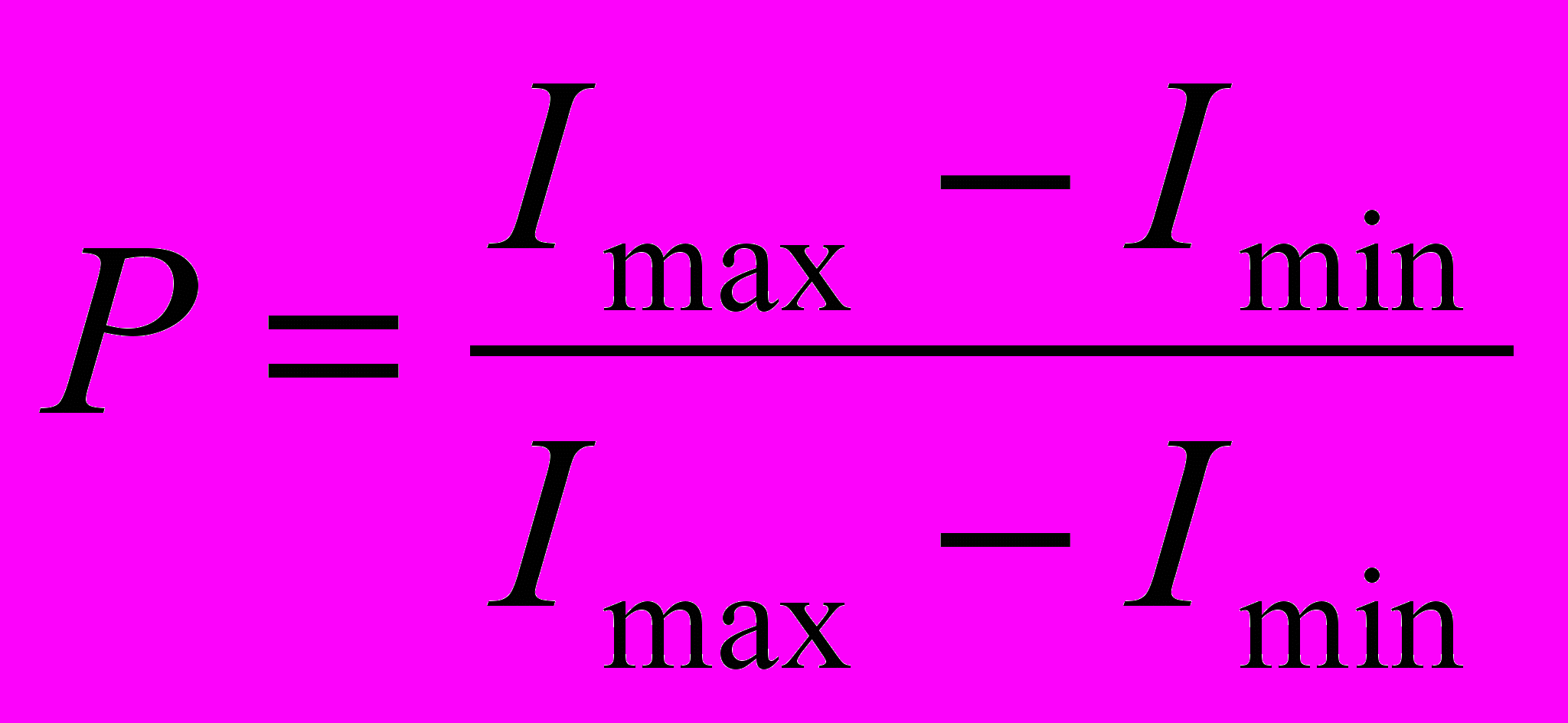 , I – итенсивность прошедшего света.(В знаменателе «+», ошибка автора картинки) , I – итенсивность прошедшего света.(В знаменателе «+», ошибка автора картинки)Для плосксполяризованного света 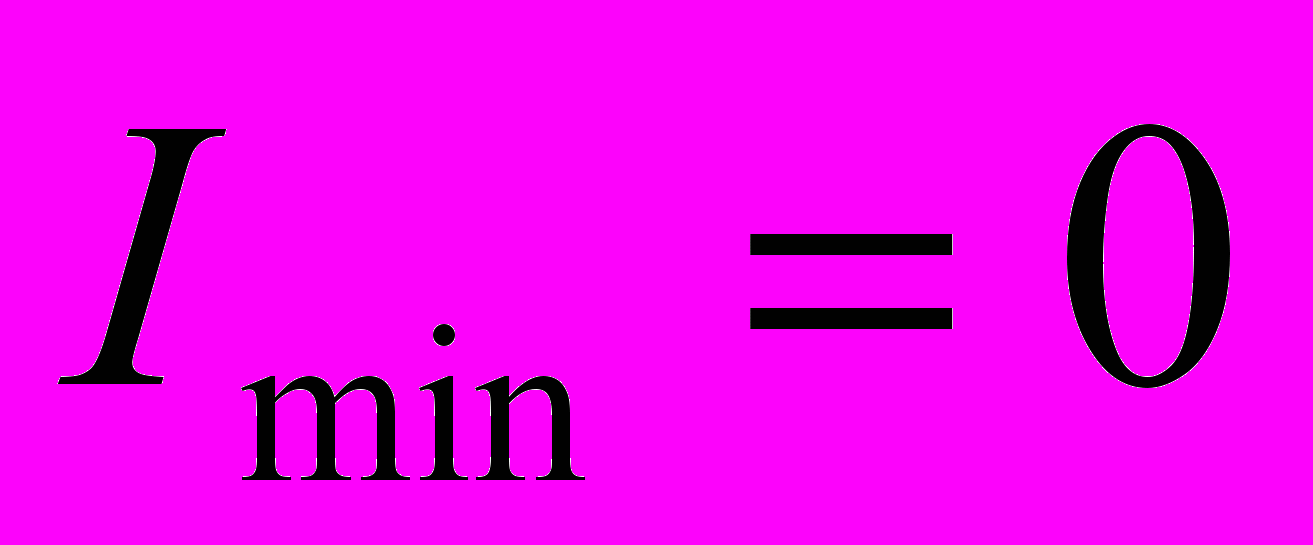 и Р = 1, для естественного света и Р = 1, для естественного света 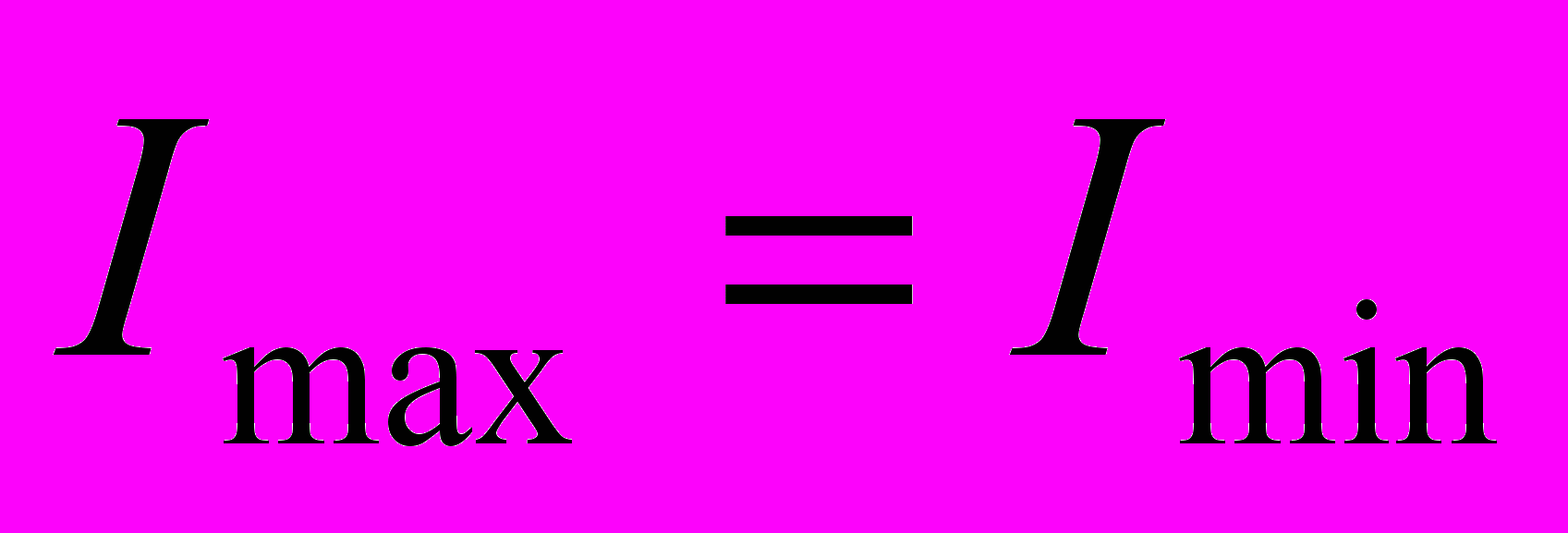 и Р = 0. и Р = 0. Если естественный свет проходит через два последовательно установленных поляроида, то интенсивность прошедшего света зависит от угла Δφ между разрешенными направлениями обоих поляроидов: Если естественный свет проходит через два последовательно установленных поляроида, то интенсивность прошедшего света зависит от угла Δφ между разрешенными направлениями обоих поляроидов: Это соотношение называют законом Малюса. 36. Поляризация света при отражении и преломлении света на границе раздела двух сред.Рассмотрим луч света, падающий на границу раздела двух сред: стекла с коэффициентом преломления n=1,5 и воздуха с коэффициентом преломления n=1. Часть света будет отражаться от границы раздела сред, а часть света будет проходить через границу, испытывая преломление. Суммарная энергия отраженного и преломленного луча в точности равна энергии падающего луча, но соотношение интенсивностей этих лучей будет зависеть от разницы показателей преломления сред, угла падения и поляризации падающего луча. Поляризация называется параллельной, если вектор электрического поля E лежит в плоскости падающего луча и нормали к границе раздела сред (см. рисунок ниже). В противном случае поляризация называется перпендикулярной. С 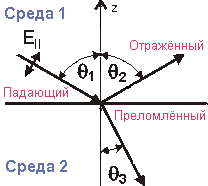 огласно формуле Френеля угол падения луча 1, угол отражения 2 и угол преломления 3 связаны следующими уравнениями: огласно формуле Френеля угол падения луча 1, угол отражения 2 и угол преломления 3 связаны следующими уравнениями:1 = 2 n1sin1 = n2sin3 Отражательная способность границы раздела сред для лучей с параллельной и перпендикулярной поляризацией R|| и R, а также пропускательная способность границы сред T и T описывается выражениями:  Для луча, падающего нормально к границе раздела, исчезает различие между перпендикулярной и параллельной компонентами, т.е.  |