Летней Математической Школы, проходившей 11-25 июня 2011 года под Костромой. Всодержание лекционных занятий изложено в опре­де­­лениях, задача

Вид материала

Задача

Содержание Материалы зачета Вопросы

Подобный материал:

• Отчет о Летней Школе пул ап день 29 июня, 77.18kb.
• Русской Онтологической Школы в г. Новосибирске, 13-17 июля 2011 года, в том числе лекции, 643.67kb.
• Программа VIII международной летней школы по русской литературе на Карельском перешейке, 53.89kb.
• Вторая- организация профильного обучения в школе, 1770.94kb.
• Конкурс на участие в летней школе " Права человека и медицина", 56.38kb.
• Г. Орел 29 июня 2011 года На основании плана работы Контрольно-счетной палаты, 316.4kb.
• Основная образовательная программа начального общего образования г. Пермь, 2011, 2132.92kb.
• Расписание занятий для студентов, 56.4kb.
• М к. Аммосова Педагогический институт Рабочая программа, 114.38kb.
• Пресс-обзор рынка недвижимости с 22 июня по 28 июня 2011 года, 1403.06kb.

Алгебра

1. Найти x и y, чтобы выполнялось x³ + y³ = x² + y² = xy + 1.
   

Ответ: x = y = 1.
Указание. Полезно сделать замену a = x + y, b = xy.

2. Разложите на множители выражение
   (а) (a – b)³ + (b – c)³ + (c – a)³;
   (б) (a + b + c)³ – a³ – b³ – c³;
   (в) (a² + b²)³ + (c² – a²)³ – (b² + c²)³;
   (г) 8a³(b + c) – b³(c + 2a) – c³(2a – b).
   

(а) Ответ: 3(a – b)(b – c)(c – a).
Указание: можно применить хитрое кубическое тождество.
(б) Ответ: 3(a + b)(b + c)(c + a).
Указание: угадать множители или применить формулу разности кубов.
(г) Указание. Один из множителей (2a + c).

3. Пусть 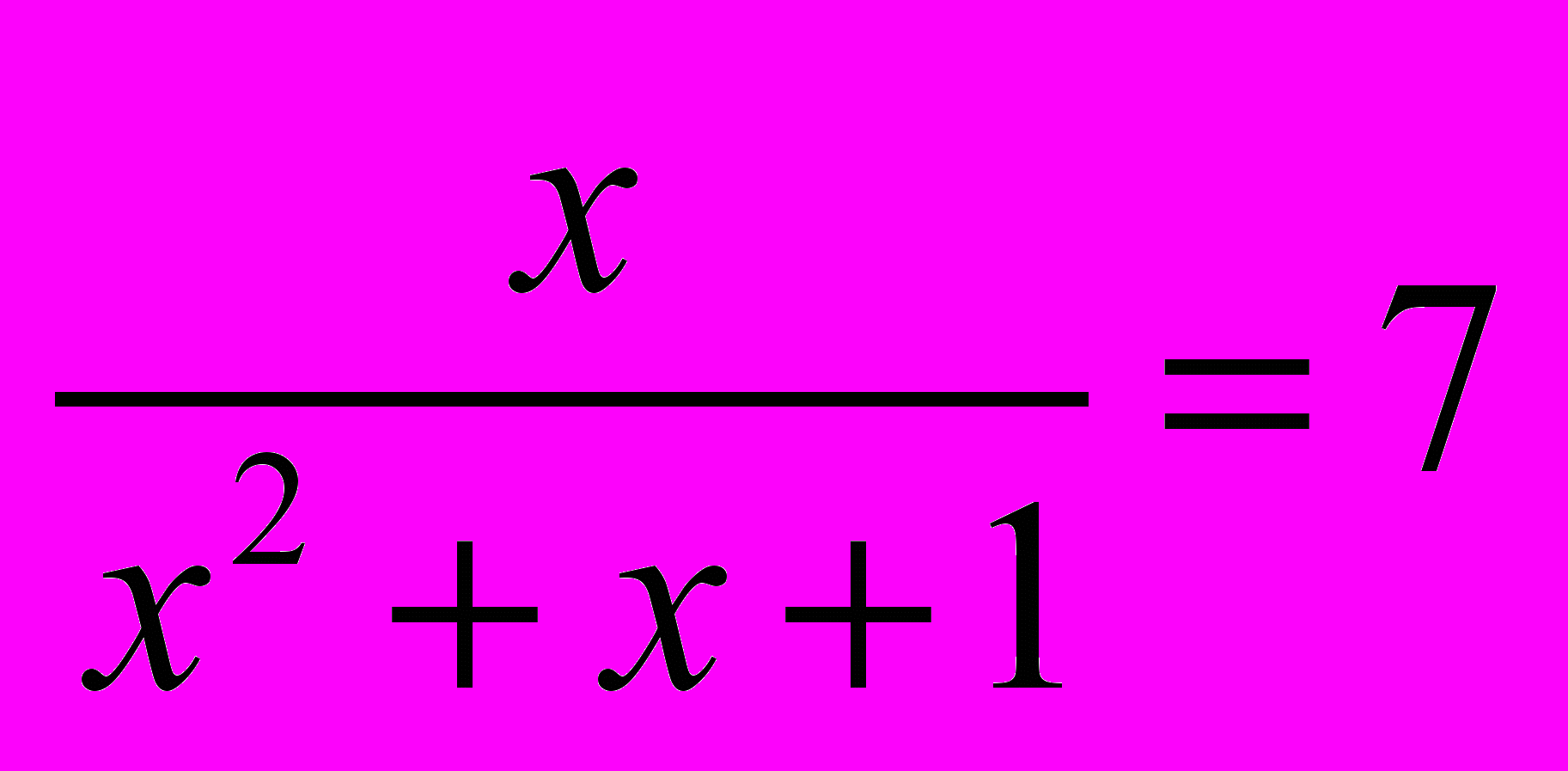. Найдите .
   
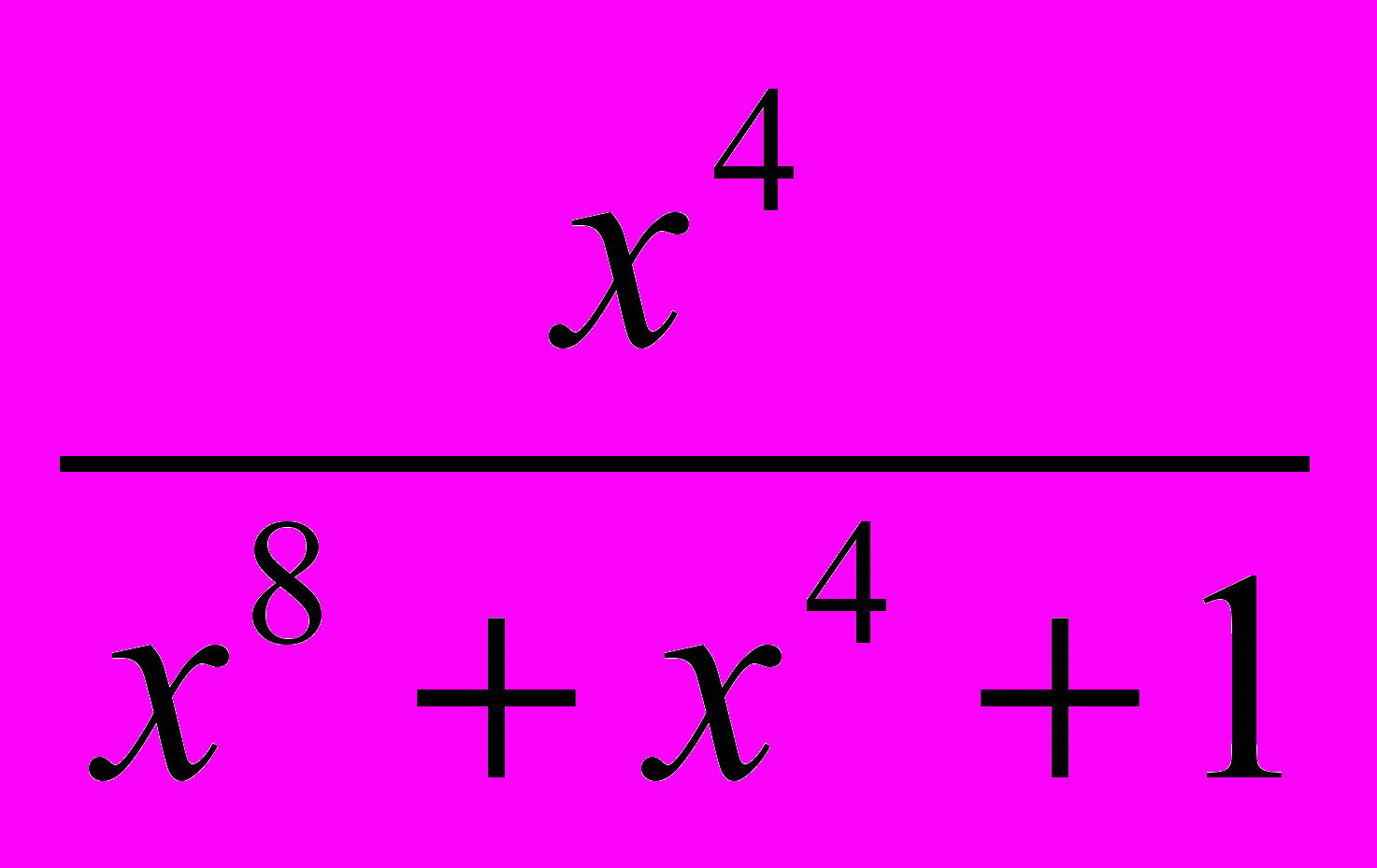4. Действительные числа a, b, c, d таковы, что a + b + c + d = 0, ab = cd.
   Какие значения может принимать сумма a³ + b³ + c³ + d³?
   

Решение. Сумма кубов раскладывается на множители, откуда получаем ответ:
a³ + b³ + c³ + d³ = 3(a + b)(cd – ab) = 0.
Источник: фольклор.

5. Упростите выражение:
   .
   

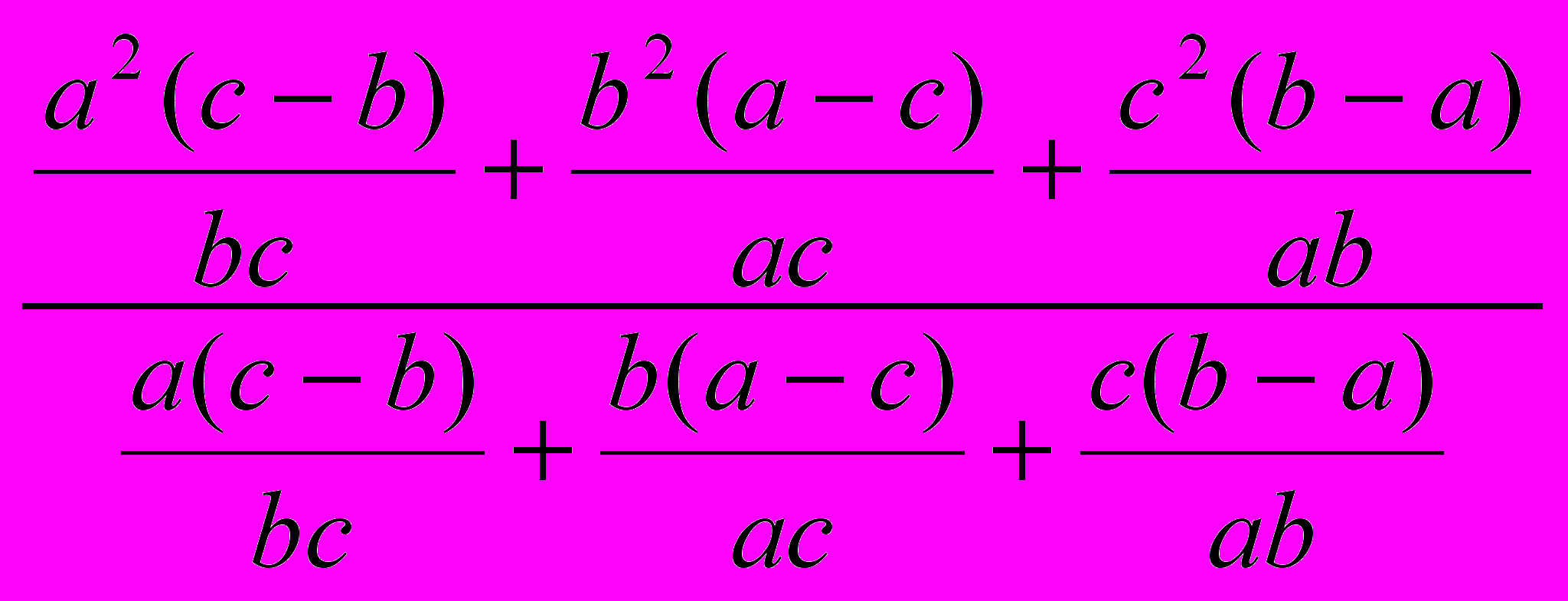Ответ: a + b + c.
Источник: фольклор.

6. Существуют ли натуральные числа a, b, c, удовлетворяющие равенству:
   (а) a¹⁰ + b¹⁰ = c¹¹,
   (б) a³ + b¹³ = c¹⁰,
   (в) a¹⁰ + b¹⁰ = c¹¹, где a — нечетное число,
   (г) a¹⁵ + b¹⁷ = c²⁰?
   

(а) Пример: a = b = c = 2.
(б) Пример: a = 2¹³, b = 2³, c = 2⁴.
Указание. Числа x = y = z = 2 удовлетворяют равенству a³⁹ + b³⁹ = c⁴⁰.
(в) Пример: a = с = 1 + 2¹⁰ = 1025, b = 2050.
Указание. Подберем b = ka. Тогда a¹⁰ + b¹⁰ = (1 + k¹⁰)  a¹⁰.
Значит, можно взять a = (1 + k¹⁰). В указанном примере k = 2.

7. В трех клетках клетчатого листа записаны числа, а остальные клетки пусты. Разрешается выбрать два числа из разных непустых клеток и записать в пустую клетку их сумму; также можно выбрать числа a, b, c из трех разных непустых клеток и записать в пустую клетку число ab + c². Докажите, что при помощи нескольких таких операций можно записать в одну из клеток квадрат суммы трех исходных чисел (какими бы они ни были).
   

Решение. Пусть исходные числа — x, y, z. Получим сначала числа x+y, y+z, z + x. Затем из клеток x, y + z, y получим x(y + z) + y²; аналогично, получим числа y(z + x) + z² и z(x + y) + x². Сложив их, получаем требуемое: x(y + z)+y² + y(z + x) + z² + z(x + y) + x² = x² +y² +z² + 2xy + 2yz + 2zx = (x + y + z)².
Источник: олимпиада Эйлера, 8 класс, автор — И. Богданов.

Инварианты

1. Черный ящик работает так: любые три числа a, b и c, попадающие в него, он перерабатывает в числа a + b – c, b + c – a, c + a – b. Можно ли с помощью этого ящика из чисел 1, 3, 8 получить числа –1, 3, 9?
   
2. На доске написаны числа 1, 2, 3, ..., 20. Разрешается стереть любые два числа a, b и вместо них записать число (а) a + b, (б) ab, (в) a + b – 1, (г) ab + a + b. Какое число может остаться на доске после 19 таких операций?
   
3. На доске написаны числа 1, 2, …, 1999. Разрешается стереть любые два числа и написать вместо них разность этих чисел. Можно ли добиться того, чтобы все числа на доске были нулями?
   
4. На столе стоят 50 стаканов, из них 25 — вверх дном. Можно ли, переворачивая по два стакана, поставить все стаканы правильно?
   
5. Круг разделен на 6 секторов, и в каждом написано число. Разрешается одновре­менно увеличивать на 1 числа в любых двух соседних секторах. Можно ли сде­лать все 6 чисел равными, если в начале они такие (именно в таком порядке): (а) 1, 0, 0, 0, 0, 0; (б) 1, 0, 1, 0, 0, 0?
   
6. В
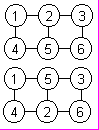
   кружочках расставлены числа как показано на верхнем рисунке. За ход разрешается к любым двум кружочкам, соединенными отрезком, прибавить одно и то же целое число.
   (а) Можно ли с помощью таких операций сделать все числа равными?
   (б) Можно ли с помощью таких операций сделать расстановку, показанную на нижнем рисунке?
   
7. Круг разделен на 6 секторов, в каждом из которых стоит фишка. За один ход разрешается сдвинуть любые две фишки в соседние с ними секторы. Можно ли с помощью таких операций собрать все фишки в одном секторе?
   
8. Имеются три автомата. Если одному из них на вход дать карточку, где написаны числа (m, n), то он выдаст карточку с числами (n, m). Если другому — выдаст (n + m, n). Если дать третьему — выдаст (m – n, n). Можно ли таким образом из карточки (12, 21) получить карточку (19, 86)?
   
9. У многочлена ax² + bx + c можно заменить x на (x – k) или поменять местами a и c. Можно ли такими операциями из многочлена (x² – 3x – 4) получить мно­гочлен (x² – x – 1)?
   
10. Двое играют в такую игру. В начале по кругу стоят числа 1, 2, 3, 4. Каждый своим ходом первый прибавляет к двум соседним числам по 1, а второй меняет любые два соседних числа местами. Первый выигрывает, если все числа станут равными. Может ли второй ему помешать?
    

Источник: РМО, 2005-2006, округ, 8 класс, №1.
Автор — Павел Мартынов.

11. Три автомата печатают карточки. Первый по карточке (a, b) печатает (a + 1, b + 1); второй по (a, b) печатает (a/2, b/2), если a и b — четные; третий по (a, b) и (b, c) печатает (a, c). Прочитанные автоматом карточки возвращаются. Можно ли, начав с карточки (5, 19), получить (а) (1, 50); (б) (1, 100)?
    
12. На доске написано целое число. Его последняя цифра запоминается, затем стирается и умноженная на 5 прибавляется к тому числу, что осталось на доске после стирания. Первоначально было написано число 7¹⁹⁹⁸. Может ли после применения нескольких таких операций получиться число 1998⁷?
    

Источник: РМО, 1997-1998, округ, 11 класс, №1.

13. Имеется три кучки камней. Сизиф таскает по одному камню из кучи в кучу. При каждом перетаскивании из кучи А в кучу Б записывается разность числа камней в кучах А и Б (до перекладывания). В некоторый момент оказалось, что все камни лежат в тех же кучах, в которых лежали первоначально. Сизиф получает плату, равную сумме записанных чисел. Какой наибольшей может быть эта сумма?
    

Указание 1. Назовем камни одной кучи знакомыми. Число, записываемое Сизифом, — изменение количества пар знакомых камней.
Указание 2. Инвариант — величина ab + bc + ca + S, где a, b, c — количества камней в кучах, S — текущий доход Сизифа.
Источник: РМО, 1994-1995, финал, 9 класс, № 3.
Автор — И. Изместьев.

Неравенства

1. Пусть s наименьшее из чисел x, 1 – y, y – x. Найти наибольшее значение s.
   
2. Положительные числа a, b, c и x, y, z удовлетворяют условиям a² + b² = c², x² + y² = z². Докажите, что ax + by  cz.
   

Источник: С.Г. Губа, Математика в Школе, 3-68.

3. Докажите, что для любых действительных чисел x и y выполнено неравенство
   x² + xy + y²  3(x + y – 1).
   

Источник: РМО,1992-1993, округ, 9 класс, № 1.

4. Докажите, что для любых положительных чисел x и y выполняется неравенство
   .
   

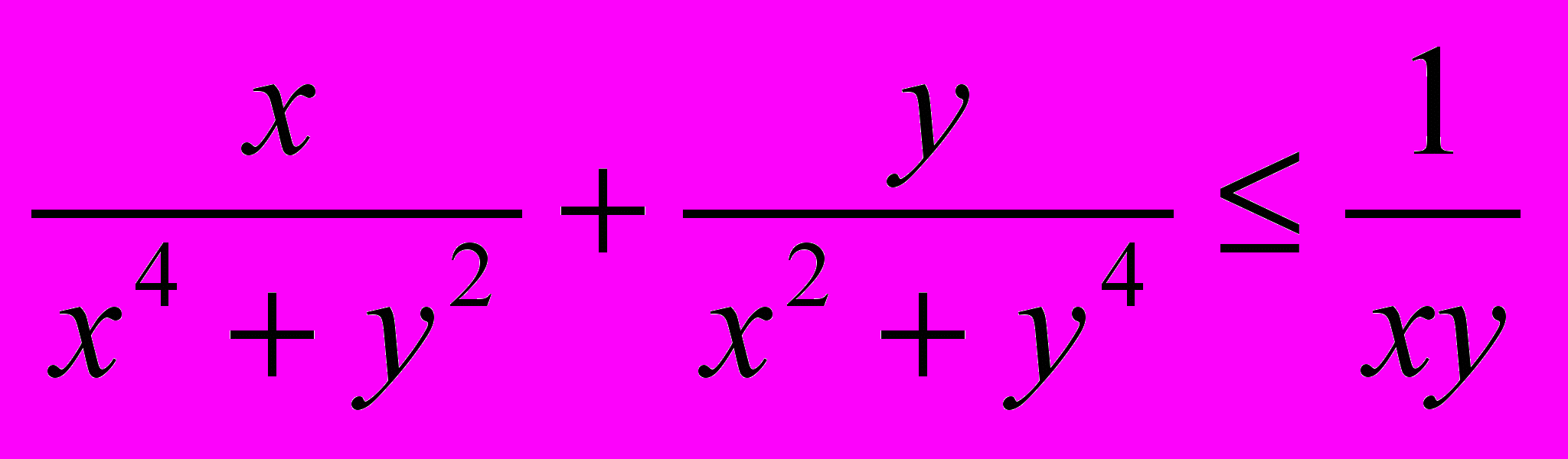Указание. Каждое слагаемое левой части не превосходит половины правой части.
Источник: РМО,1994-1995, округ, 9 класс, № 1.

5. Докажите, что если a, b, c — положительные числа и ab + bc + ca > a + b + c, то a + b + с > 3.
   

Решение. Используем неравенство a² + b² + c²  ab + bc + ca > a + b + c.
Добавим в левую часть до полного квадрата и усилим:
(a + b + c)²  2(a + b + c) + a² + b² + c² > 3(a + b + c).
Источник: РМО,1995-1996, округ, 10 класс, № 1.

6. Докажите, что если числа a, b, c и d принадлежат отрезку [1; 2], то
   .
   

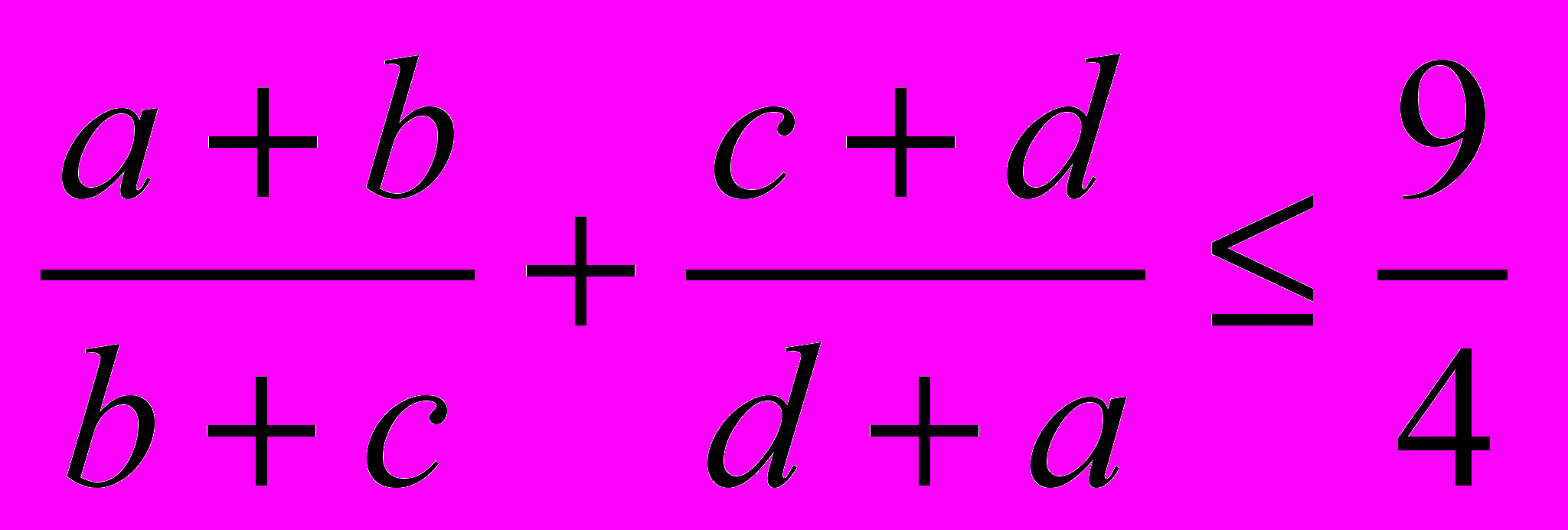Решение. Вычтем из каждой дроби в левой части по единице.
Получим (a – c) / (b + c) + (c – a) / (d + a)  1/4.
Пусть a > c, a – c < 1.
Тогда достаточно показать, что 1 / (b + c) – 1 / (d + a)  1/4, что очевидно следует из того, что 1 / (b + c) не более 1/2, а 1 / (d + a) не менее 1/4.

7. Решите в вещественных числах систему уравнений:
   
   

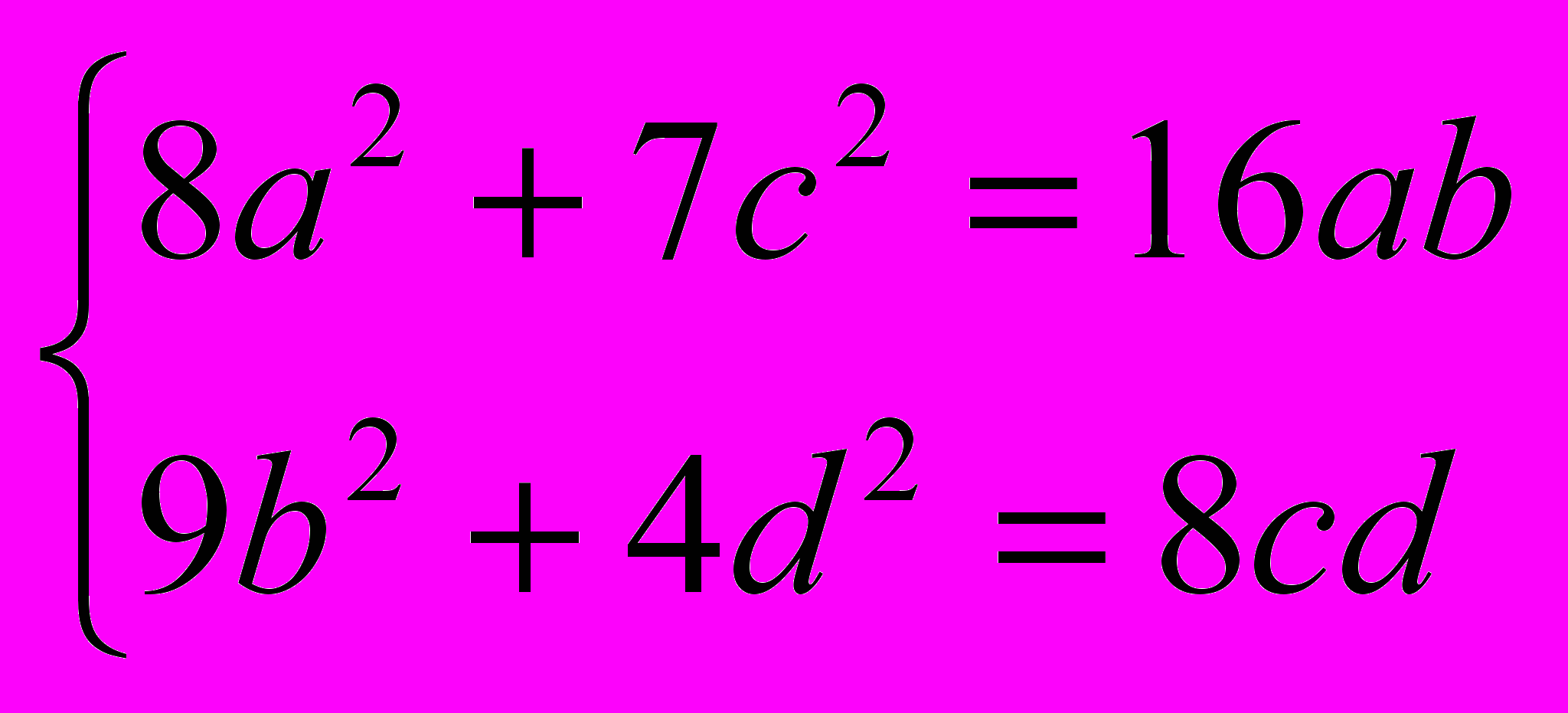
Источник: СПбМО-1995, 1 тур, 9 класс, автор – А. Храбров.

8. Докажите, что ни при каких действительных a, b и с три числа
   (b – c)(bc – a²), (c – a)(ca – b²) и (a – b)(ab – c²)
   не могут быть положительными одновременно.
   
9. Докажите, что если 0 < a₁, ..., a_n < 1, то (a₁ + ... + a_n + 1)² > 4(a₁² + ... + a_n²).
   

(Васильев Н.Б., Егоров А.А. Задачи всесоюзных математических олимпиад. Москва, Наука, 1988.)

Делимость

• Приведите пример восьми таких попарно различных натуральных чисел, что для любых двух чисел a и b выполнено: a не кратно b, но a² кратно b.
  

Пример 1: a⁸b¹⁶, a⁹b¹⁵, …, a¹⁶b⁸, где a и b — взаимно простые числа.
Пример 2: умножить произведение 8 простых чисел по очереди на каждое из этих простых чисел.
Источник: ММО, 1998, 8 класс, № 2.

• Натуральные числа m и n таковы, что НОК (m, n) + НОД (m, n) = m + n. Докажите, что одно из чисел m или n делится на другое.
  

Источник: РМО,1994-1995, округ, 10 класс, № 2.

1. Натуральные числа a, b, c таковы, что ab + ac = bc.
   Докажите, что НОД (a, b) + НОД (a, c) = НОД (b, c).
   

Источник: турнир Кванта.

2. Найдите все простые p такие, что число p² + 11 имеет ровно 6 различных делителей (включая единицу и само число).
   

Ответ: p =3.
Указание. Представьте сумму в виде (p – 1)(p + 1) + 12.
Источник: РМО,1994-1995, округ, 9 класс, № 1.

3. Найдите все натуральные числа, имеющие ровно шесть делителей, сумма которых равна 3500.
   

Ответ:1996.
Источник: РМО,1995-1996, округ, 9 класс, № 1.

4. Существуют ли 10 различных целых чисел таких, что все суммы, составленные из девяти из них, — точные квадраты?
   

Ответ: да.
Источник: РМО,1998-1999, округ, 10 класс, № 1.

5. Найдите все простые p и q, что p + q = (p – q)³.
   

Источник: РМО, 2000-2001, округ, 11 класс, № 1.

6. Существуют ли два различных натуральных числа a и b, что число a²⁰ + b²⁰ делится на a + b, a² + b², a³ + b³, …, a¹⁹ + b¹⁹?
   

Источник: Е. Черепанов, Квант-2000.

7. Существуют ли различные взаимно простые в совокупности натуральные числа a, b, c, большие 1, такие, что 2^a + 1 делится на b, 2^b + 1 делится на c, 2^c + 1 делится на a?
   

Ответ: да. Пример: a = 3, b = 9, c = 19.
Источник: РМО,1999-2000, округ, 9 класс, № 2.

8. * Можно ли все целые числа от 143 до 153 выписать в некотором порядке так, чтобы полученное 33-значное число было простым?
   

Указание. Все такие 33-значные числа дают одинаковый остаток при делении на 999.
Источник: кубок Ив. Сусанина, автор — С.И. Токарев.

Материалы зачета

Вопросы

1. Конечная аффинная плоскость.
   Её определение, порядок, число точек, прямых, пучков.
   
2. Модель конечной аффинной плоскости порядка p, где p — простое число. Определение точек, прямых. Указание всех прямых плоскости.
   
3. Доказательство выполнения аксиом в модели конечной аффинной плоскости.
   
4. Латинские и магические квадраты. Построение магического квадрата из пары ортогональных латинских квадратов.
   
5. Построение латинских квадратов порядка p, где p — простое число.
   Их попарная ортогональность.
   
6. Расстояние Хэмминга между словами. Поиск ошибок. Построение кода из набора попарно ортогональных латинских квадратов.
   
7. Числа Стирлинга для подмножеств. Определение. Рекуррентное соотношение. Построение треугольника. Разложение убывающей факториальной степени по степеням переменной.
   
8. Числа Стирлинга для циклов. Определение. Рекуррентное соотношение. Построение треугольника. Разложение возрастающей факториальной степени по степеням переменной.
   
9. Разложение числа Стирлинга (и того, и другого) в сумму произведений чисел Стирлинга и биномиальных коэффициентов.
   
10. Пентагональная теорема Эйлера. Её эквивалентность теореме о разбиениях.
    
11. Теорема Эйлера о разбиениях. Инволюция Франклина. Доказательство теоремы Эйлера и теоремы Файна.
    

Задачи

1. Докажите: если есть множество (x, y), где x, y — остатки при делении на n, то можно определить  (n) + 1 семейство параллельных прямых, где  (n) — фун­кция Эйлера — число натуральных чисел, меньших n и взаимно простых с n.
   
2. Докажите тождество .
   
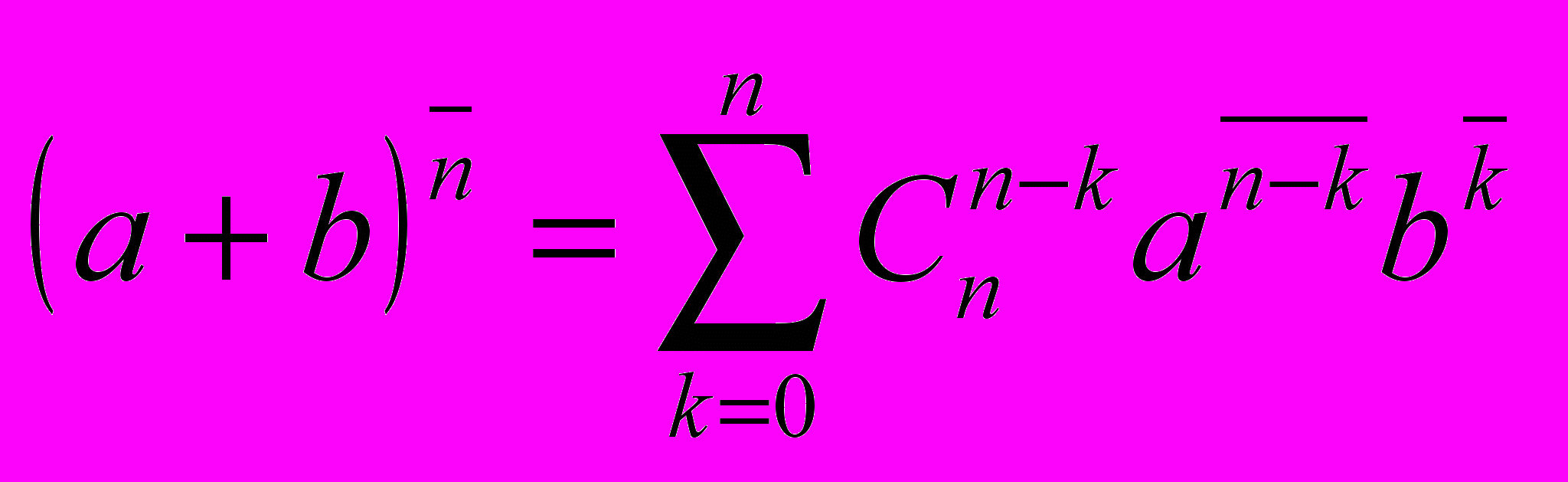3. Перед 9 школьниками положили 7 апельсинов и каждый взглядом выбрал один самый вкусный (по его мнению) апельсин. Все желания учеников назовем об­щим желанием. Сколько может быть различных общих желаний? Сколько из них таких желаний, когда ровно 4 апельсина оказываются никем невостребованными?
   
4. Существует ли двоичный код длины 20, содержащий 1000 кодовых слов и исправляющий любые комбинации из трех или менее ошибок?
   
5. Доказать, что максимальный двоичный код длины 5 с кодовым расстоянием, равным 3, содержит 4 кодовых слова. Укажите такой код.
   
6. Докажите, что число разбиений числа n не более чем с m частями равно числу разбиений числа n, в которых нет частей, превосходящих m.
   
7. Число разбиений числа (a – c) ровно с (b – 1) частями, не превосходящими c, равно числу разбиений числа (a – b) с (c – 1) частями не превосходящими b.
   

Указание. В диаграмму Юнга можно добавить одну строку из c элементов, удалить первый столбец и провести сопряжение полученного разбиения.