Geum.ru

Летней Математической Школы, проходившей 11-25 июня 2011 года под Костромой. Всодержание лекционных занятий изложено в опре­де­­лениях, задача

Вид материалаЗадача

Содержание


Проверка ошибок
Расстоянием Хемминга
Числа Стирлинга
Подобный материал:
1   2   3   4   5   6

Проверка ошибок

  1. Пусть послано несколько сообщений, закодированных последовательностями нулей и единиц. Известно, что один символ может быть неверен. Как вводом одного символа иметь информацию о том, есть ошибка или ее нет?

Такой код называют кодом с общей проверкой на четность. Такую же идею используют при составлении номера банковского счета: последняя цифра счета является проверочной.
  • Расстоянием Хемминга между двумя кодовыми словами называют число символов, в которых они отличаются.
  1. Докажите, что расстояние Хемминга обладает основным свойством расстояний: для него выполняется неравенство треугольника.
  • Кодовое расстояние кода — минимальное расстояние между различными кодовыми словами кода. Ясно, чем больше кодовое расстояние, тем большими исправляющими способностями обладает данный код.
  1. (а) Какое наибольшее количество двоичных последовательностей длины 10 можно выписать, чтобы попарные расстояния между ними были больше 1?
    (б) (Турнир Городов, 2004) Два числа назовем близкими, если их десятичная запись отличается ровно одной цифрой. Какое наибольшее число 10-значных чисел можно выписать, чтобы среди них не было близких чисел?

(а) Ответ: 29. Решение: достаточно выбрать все коды с четным количеством единиц.
(б) Ответ: 900 000 000. Решение. Разобьем все 10-значные числа на группы, в каждую из которых поместим числа, отличающиеся только последней цифрой. В каждой такой группе будет ровно 10 чисел, всего 10-значных чисел 9  109, поэтому количество групп равно (9  109) : 10 = 9  108. Никакие два числа из одной группы не могут быть выбраны, поэтому более 9  108 чисел выбрать нельзя. С другой стороны, в каждой группе есть ровно одно число, сумма цифр которого кратна 10. Выберем все такие числа: никакие два из них не будут соседними.
  1. Докажите: чтобы код исправлял любые комбинации из t (и меньшего числа) оши­бок, необходимо и достаточно, чтобы его кодовое расстояние было больше 2t.
  2. Пусть A1, A2, …, An — попарно ортогональные латинские квадраты размера n  n. Для каждой клетки в столбце x и строке y построим набор (x, y, a1xy, a2xy, …, anxy), где akxy — элемент квадрата Ak в соответствующей клетке. Докажите, что любые два набора различаются не менее чем в n + 1 разряде. Из этого будет следовать, что получен код из n2 элементов длины n + 2, исправляющий [n/2] ошибок.

Числа Стирлинга1


1
1
1
1
1
1
1
1
1
1
1
1
1
1
1

1
2



3
4



5
6



7
8



9
10



1






4






9






16






25





  • Таблица 1. Записываем бесконечный ряд единиц. Убиваем каждую третью единицы. Под оставшимися числами записываем сумму числа сверху и числа слева. В третьем ряду получаются полные квадраты.
  • Таблица 2. Аналогично, вычеркивая каждую четвертую единицу, в четвертой строке получится ряд кубов натуральных чисел.


  • Таблица 3. Проделаем то же самое, вычеркивая числа с номерами, равными треугольным числам.
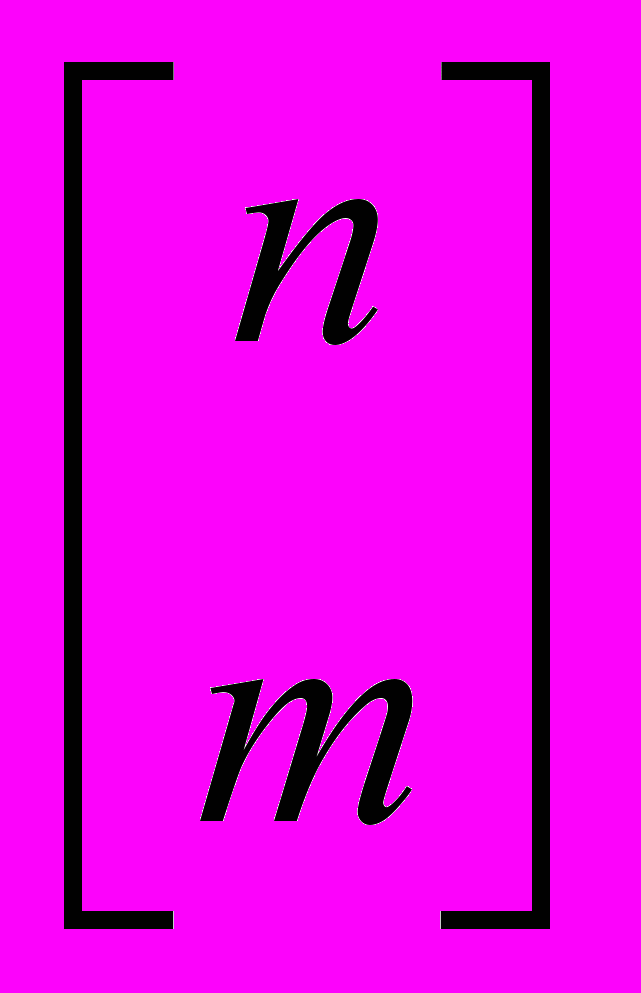  • — количество перестановок на n элементах, которые разлагаются в m циклов (количество способов рассадить n человек за m круглых столов).
  • Из определения следует, что .
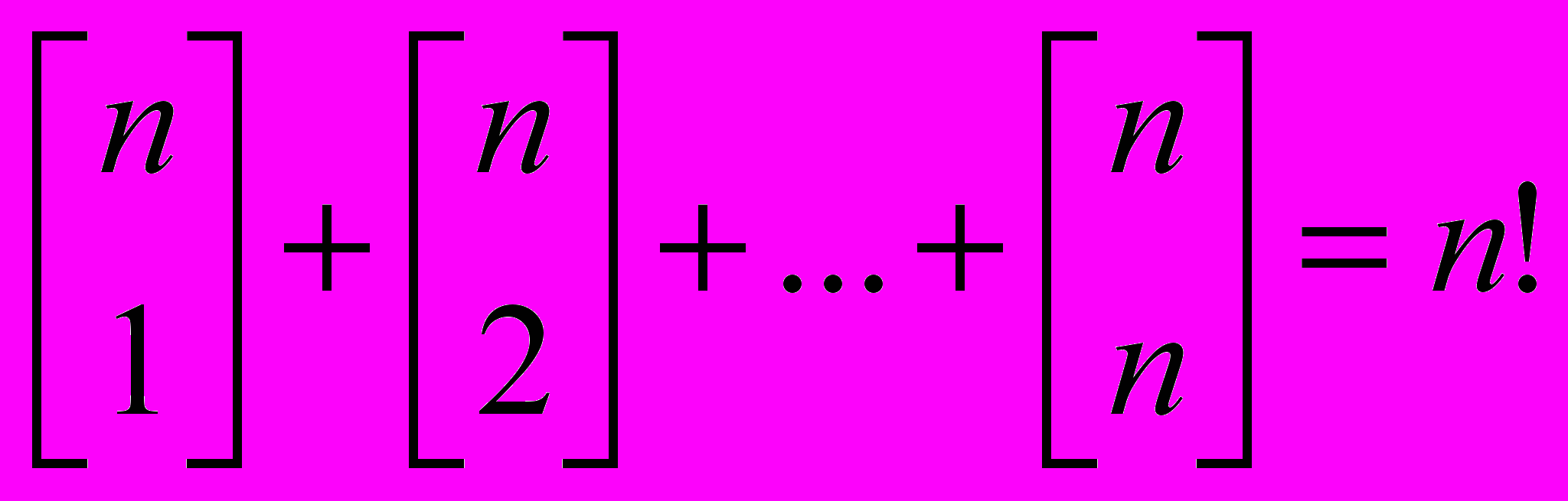  • Элементарные частные случаи: , , .
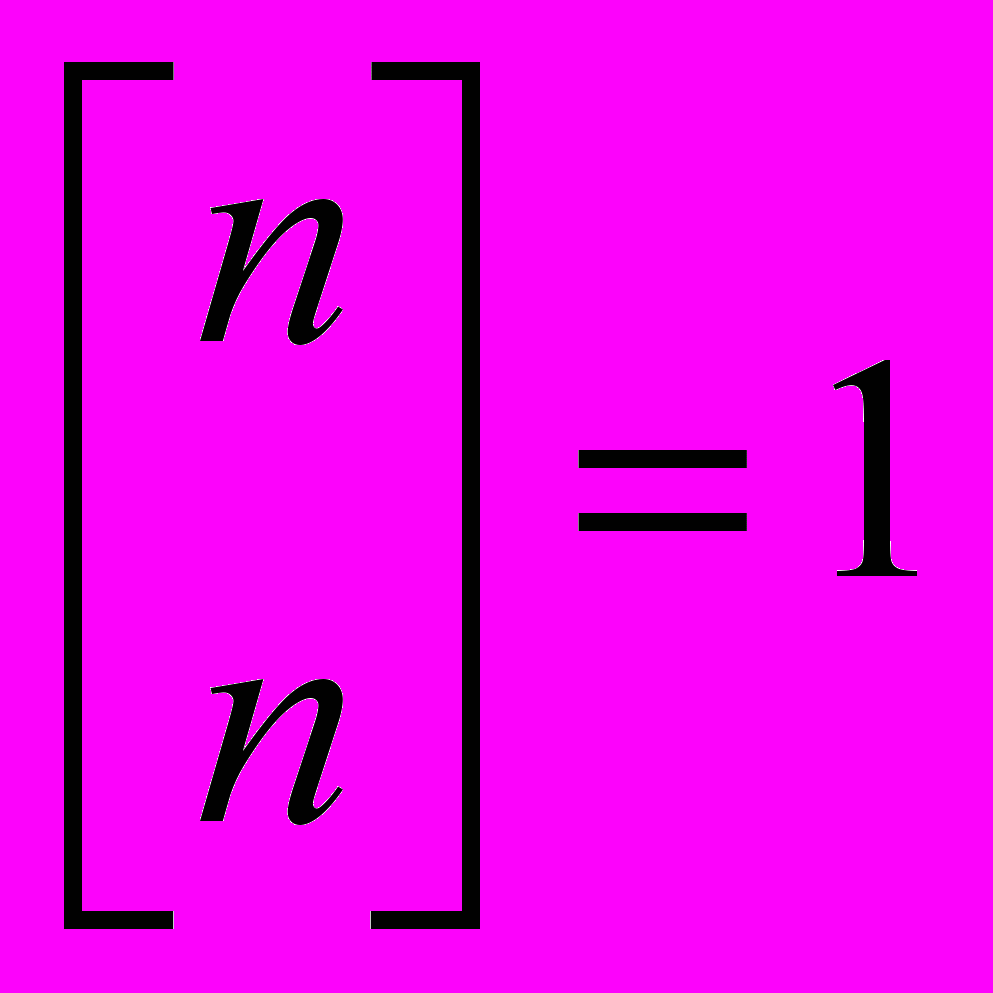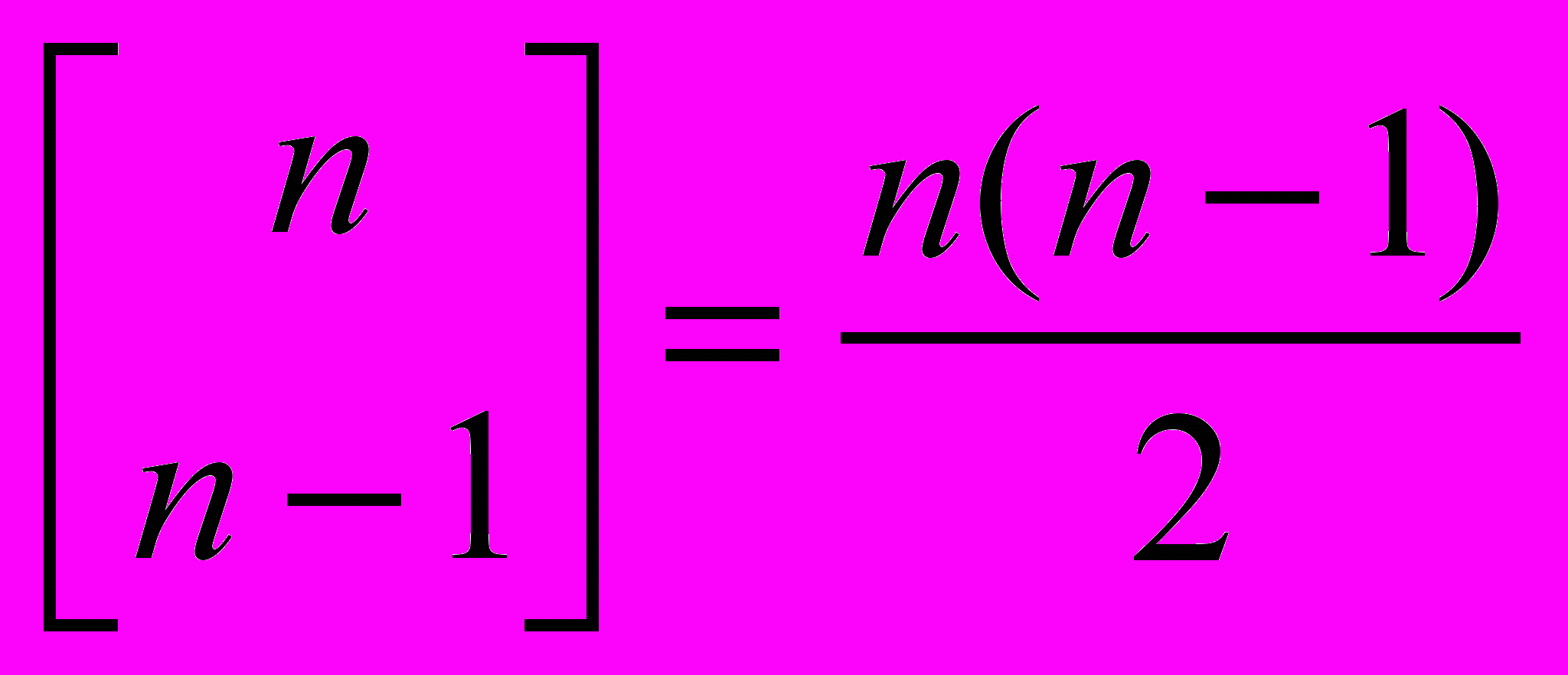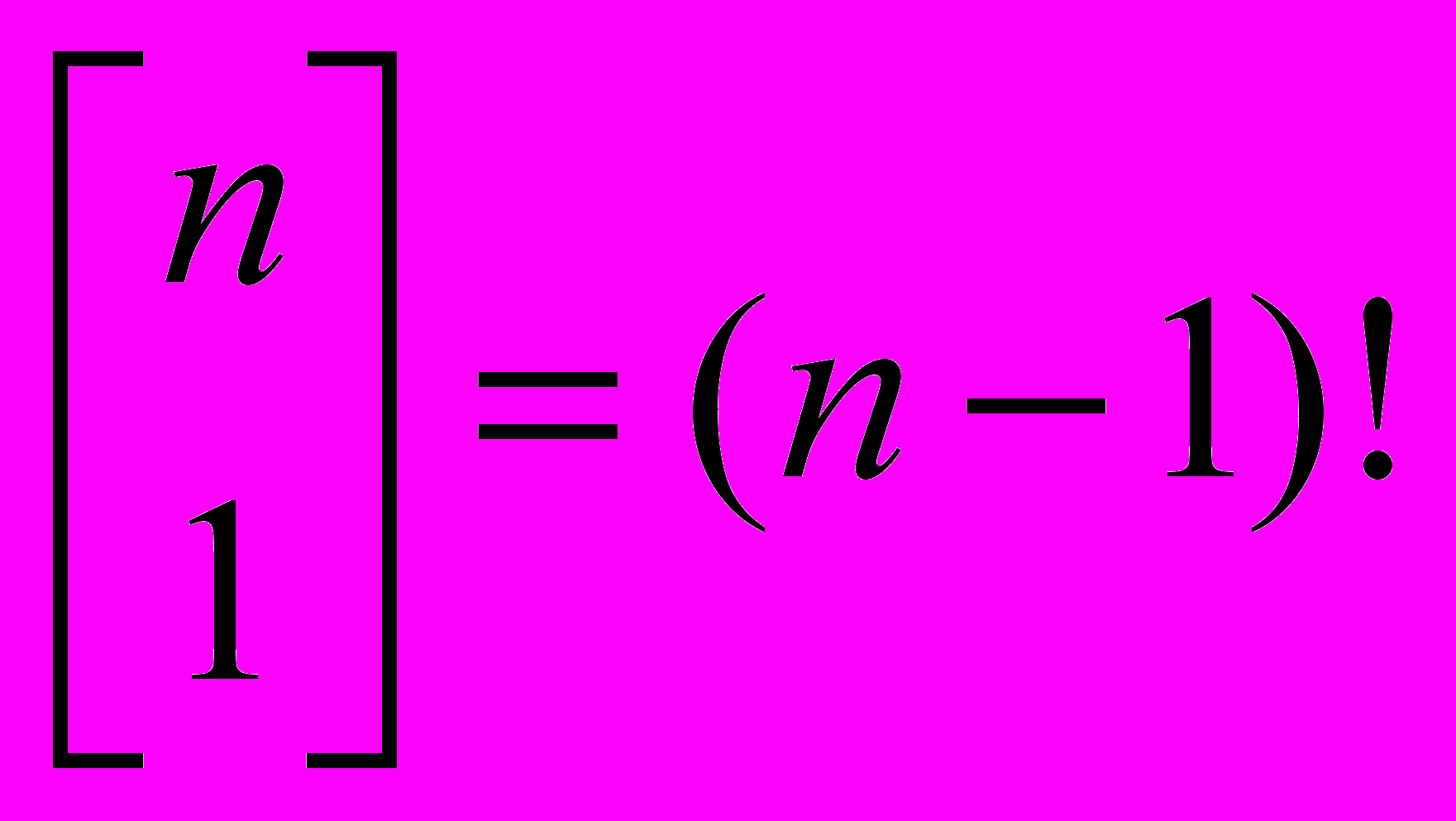  • Заметим, что убитые числа в таблице 3 образуют треугольник чисел Стирлинга.
  • Базовое рекуррентное свойство чисел Стирлинга: .
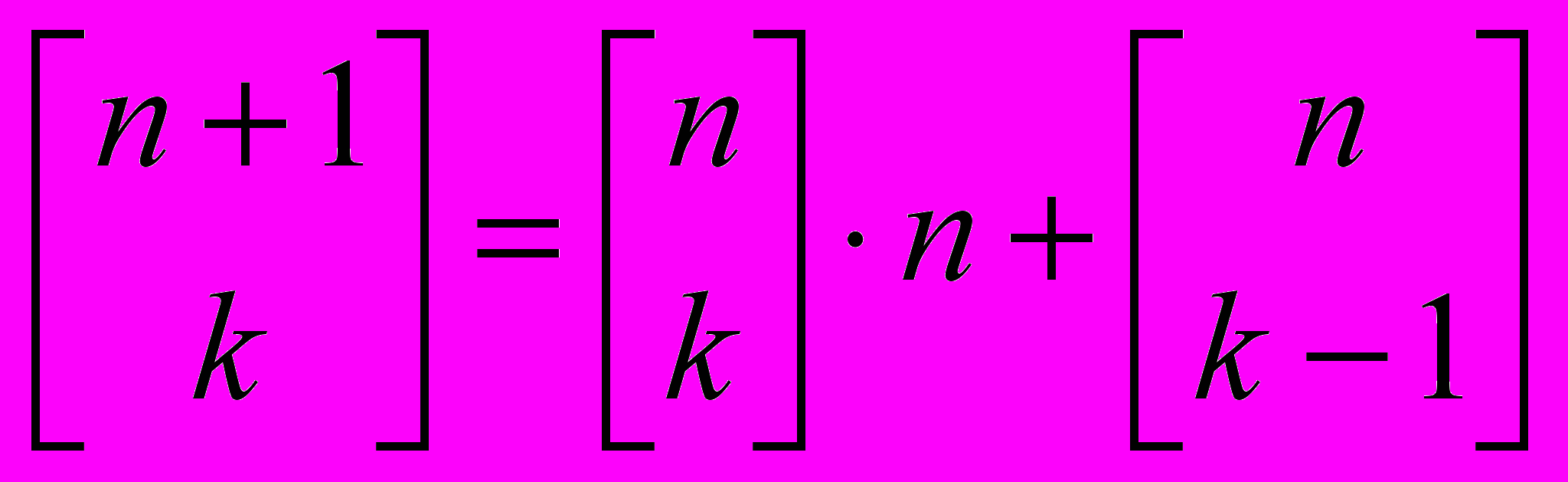  • Пусть 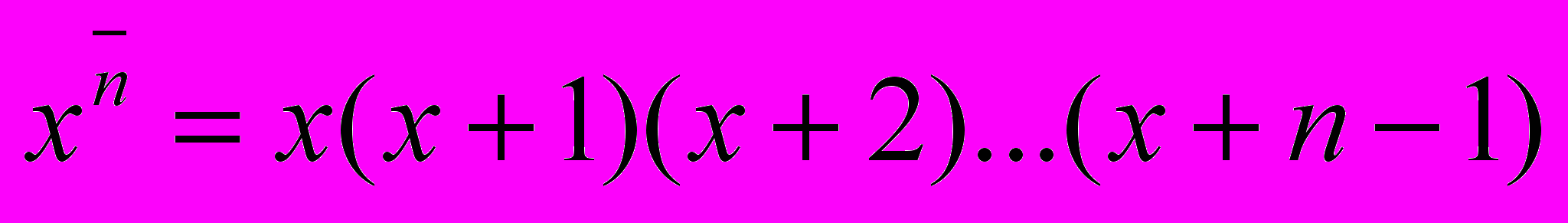. Тогда .
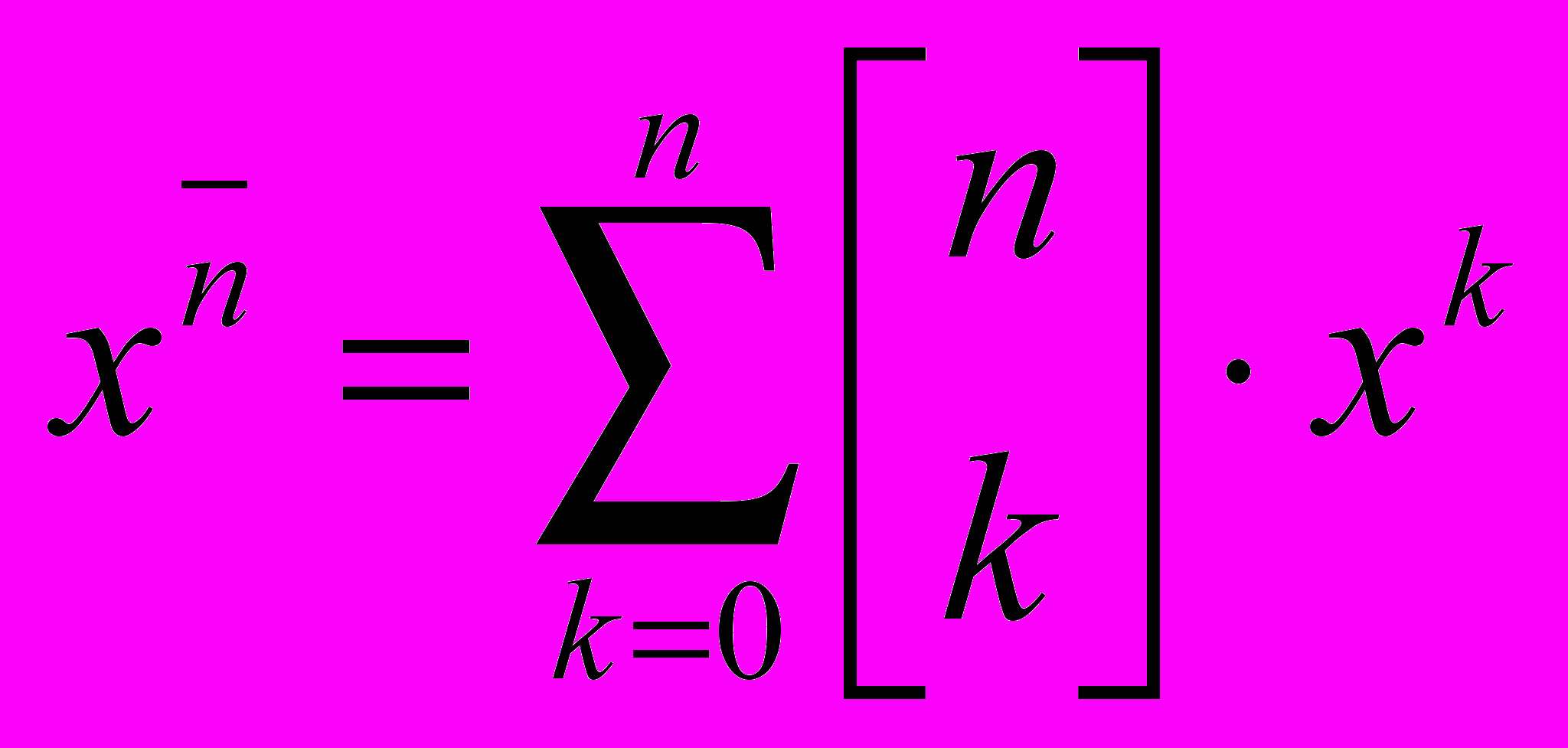    Пусть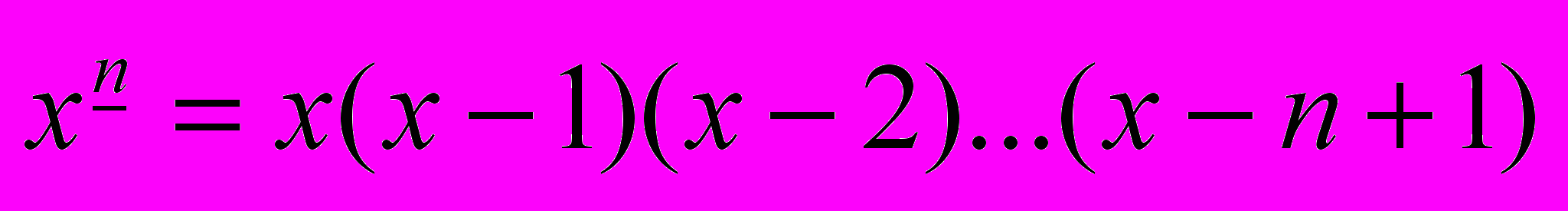 . Тогда .
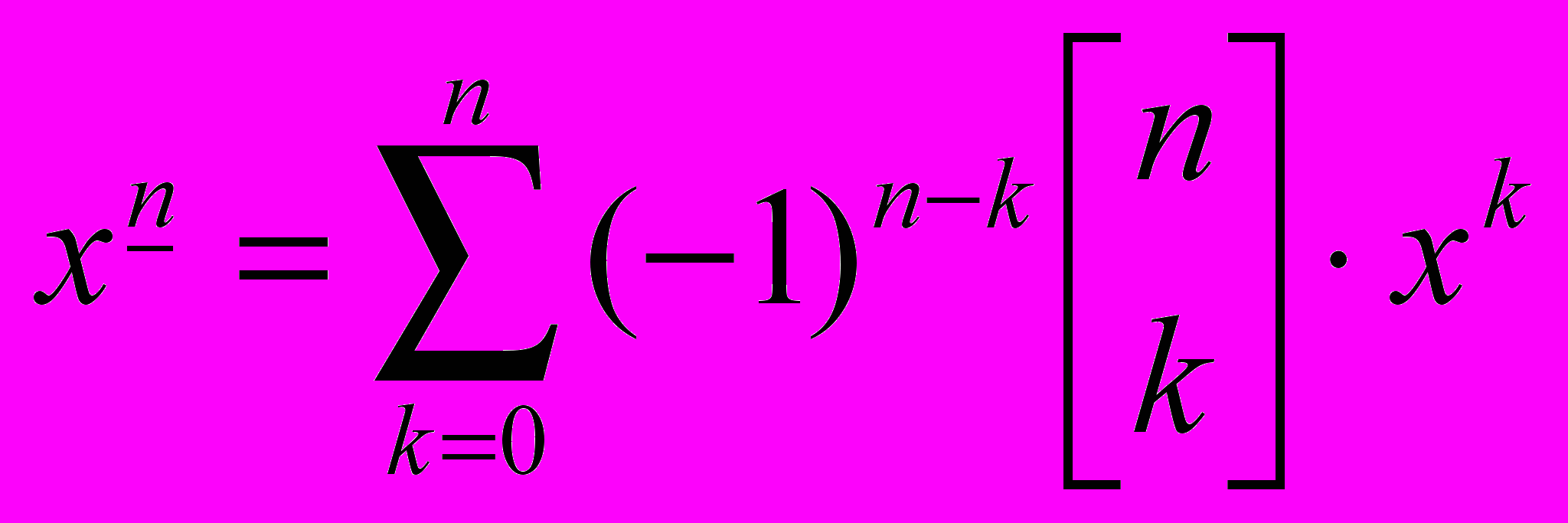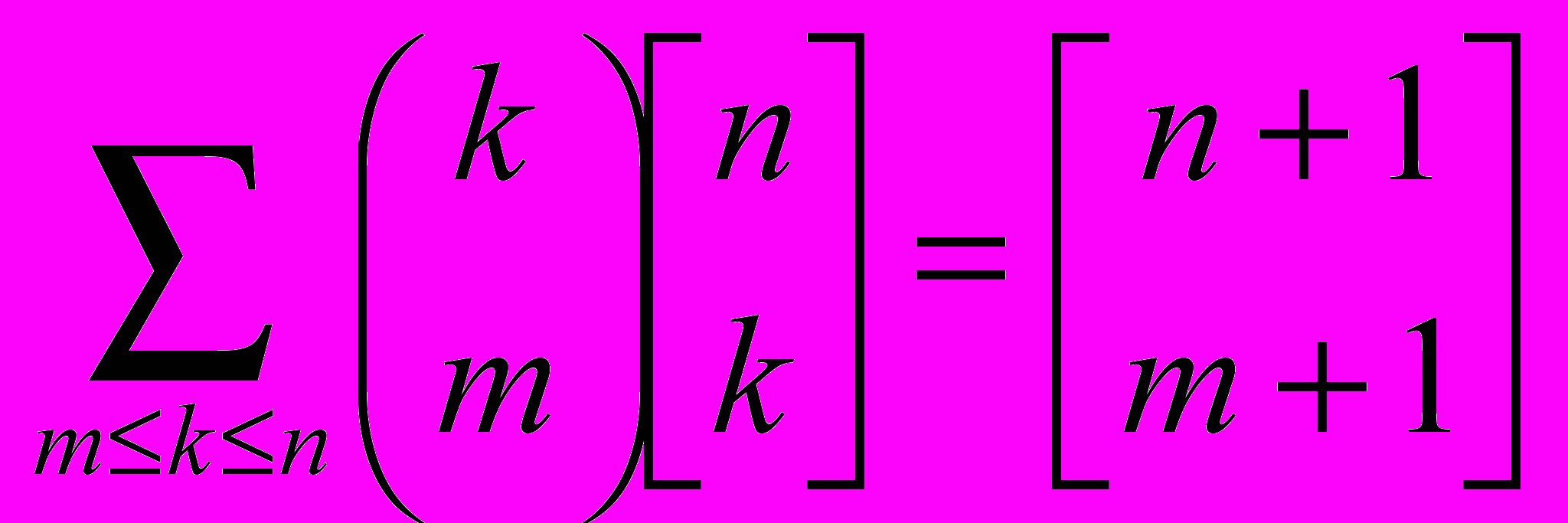  • . Докажем, что .
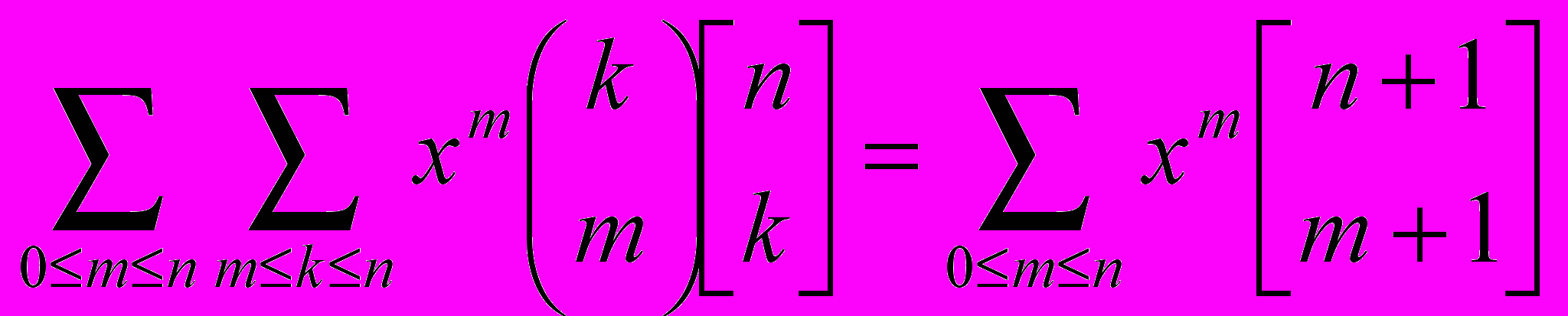    С одной стороны, .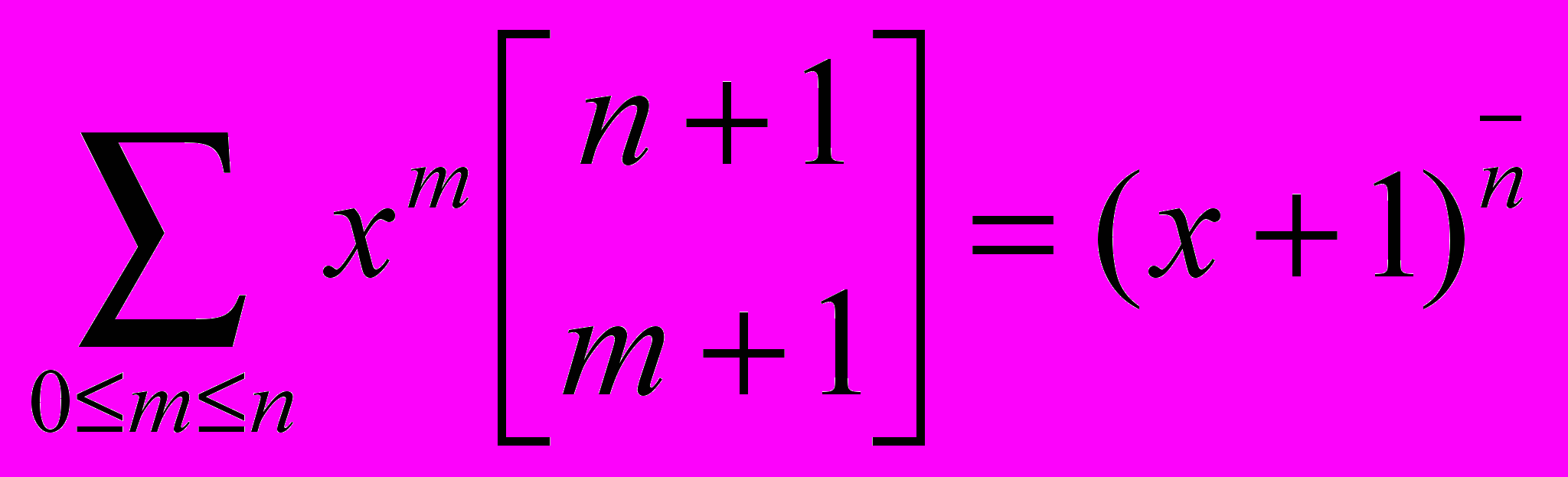
    С другой стороны, .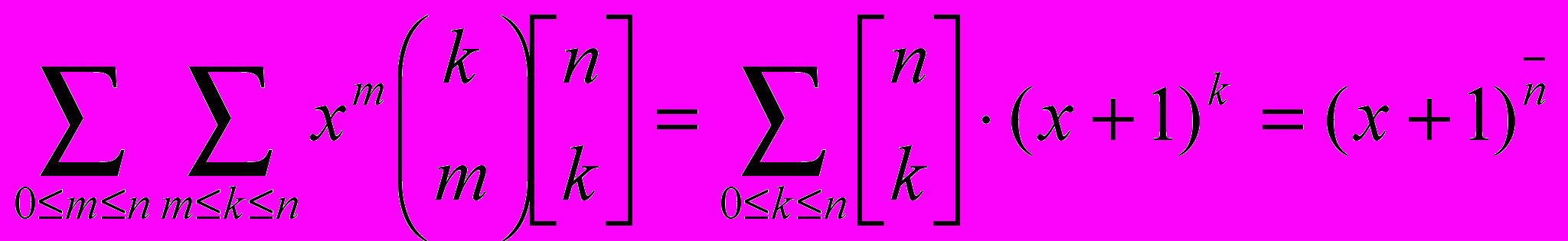
  • Пусть (n + 1) человека надо рассадить за (m + 1) столов. Где-то сядет (n + 1)-ый человек, m столов без этого человека.
    Дано n человек за k столами, m из которых красные, остальные — синие. Красные столы оставляем нетронутыми. Собираем остальных, добавляем (n + 1)-го человека, собираем (как?) из него и остальных стол.

  • 1
    1
    1
    1
    1



    1
    3
    6
    10
    (6,5)



    1
    7
    15
    (6,4)



    1
    15
    (6,3)
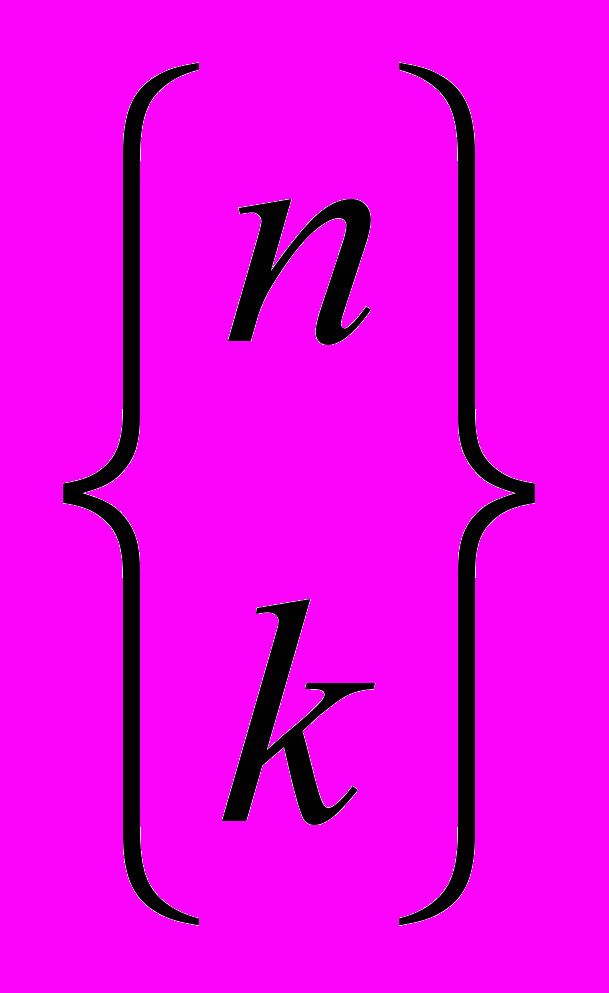    =(n, k)

    1
    (6,2)



    (6,1)





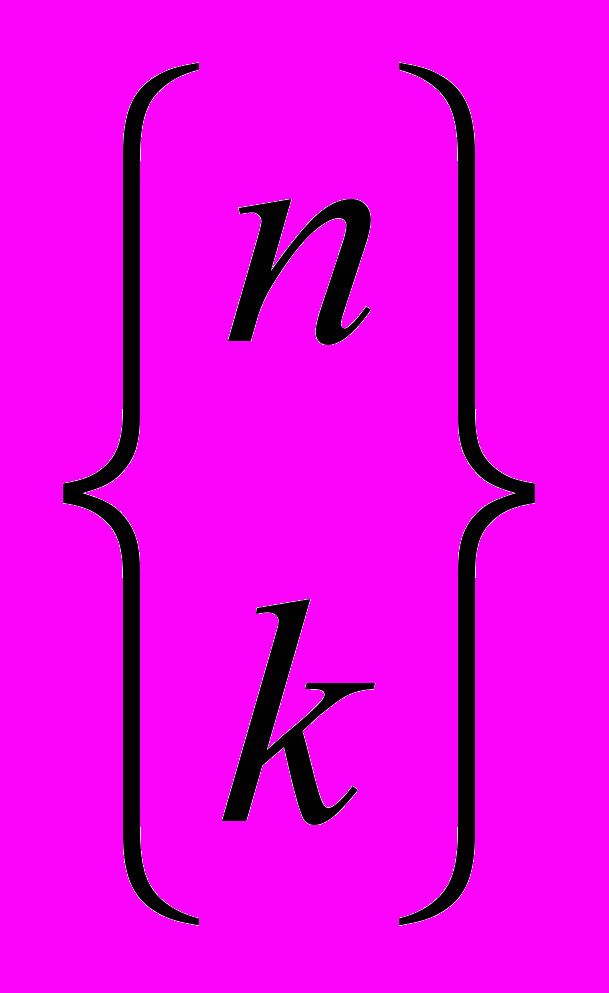    — количество способов разбиения множества из n элементов на k непустых множеств.
  • Найти , , , , , ,.
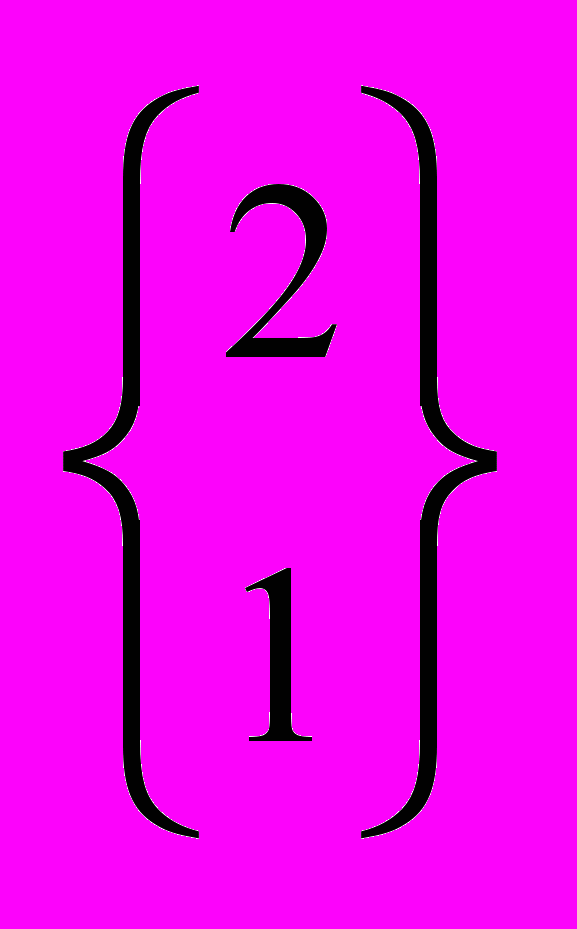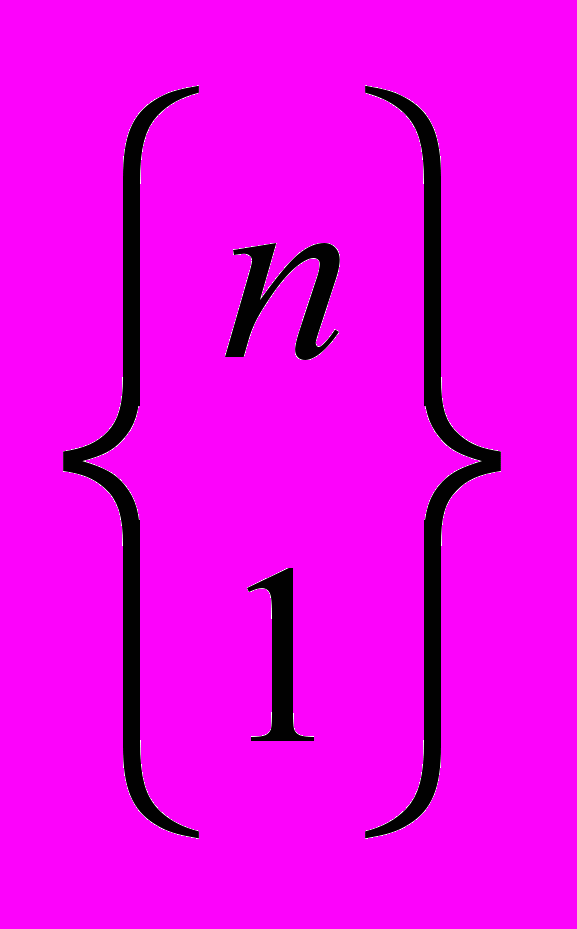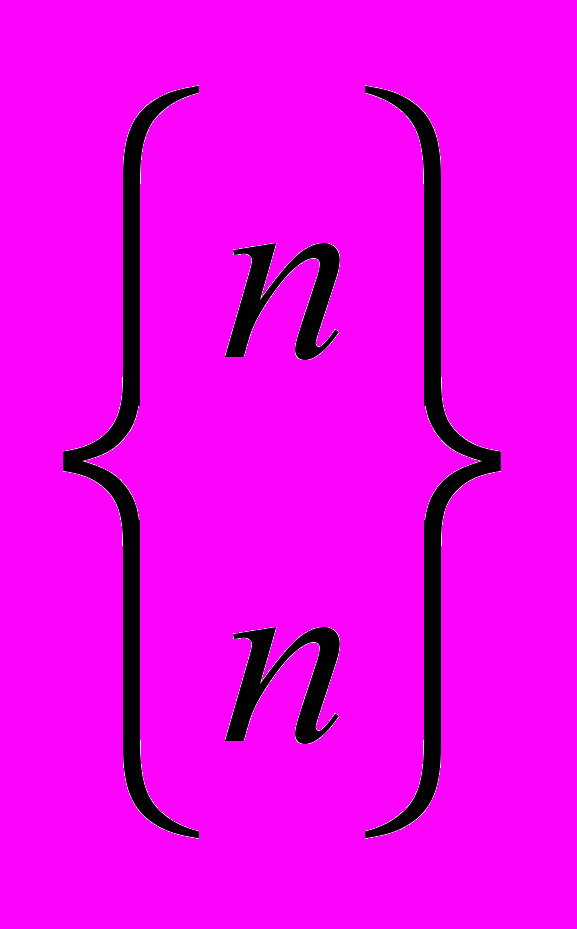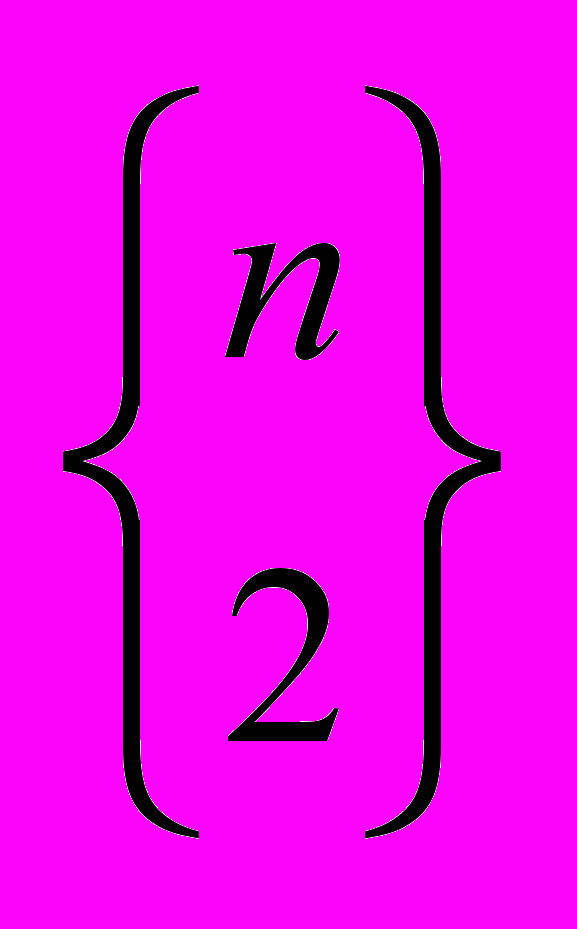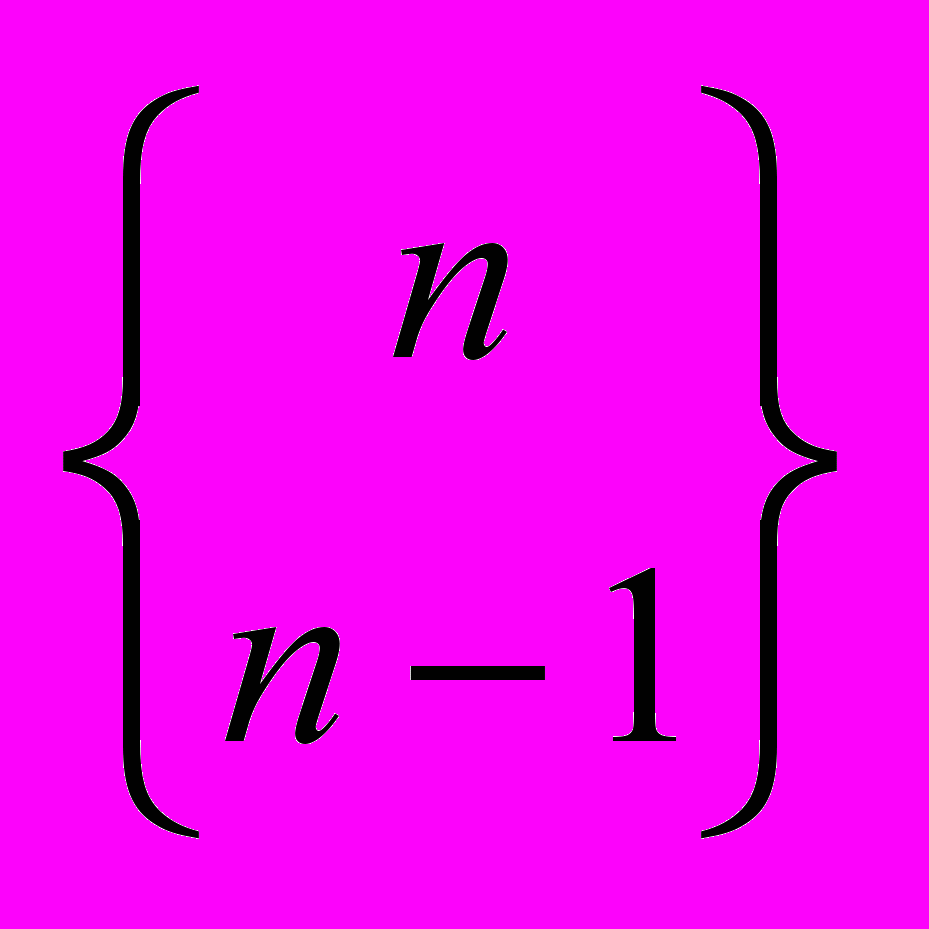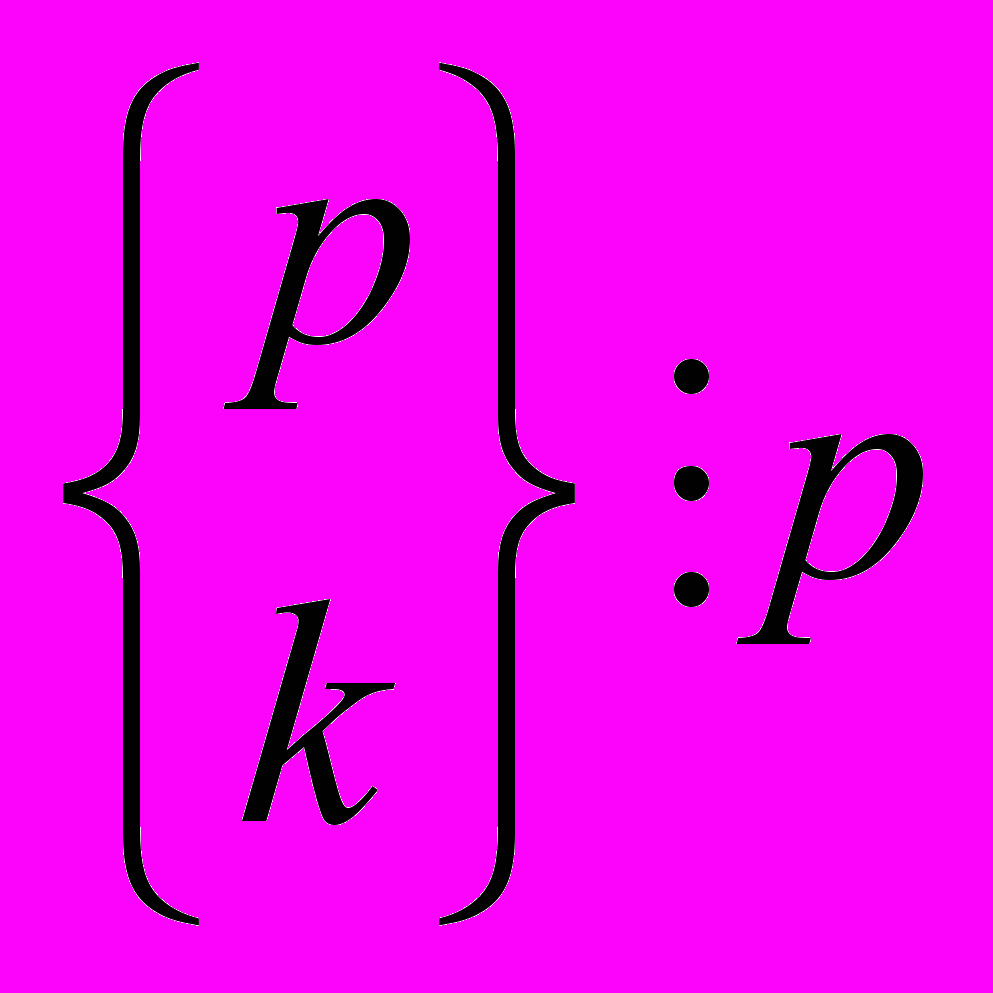  • , если 1 < k < p (утверждение, аналогичное Малой Теореме Ферма).

Указание. Перестановка 1  2  3  …   p  1 делит разбиения на группы по p штук. Аналогично доказывается подобное утверждение для числа сочетаний.
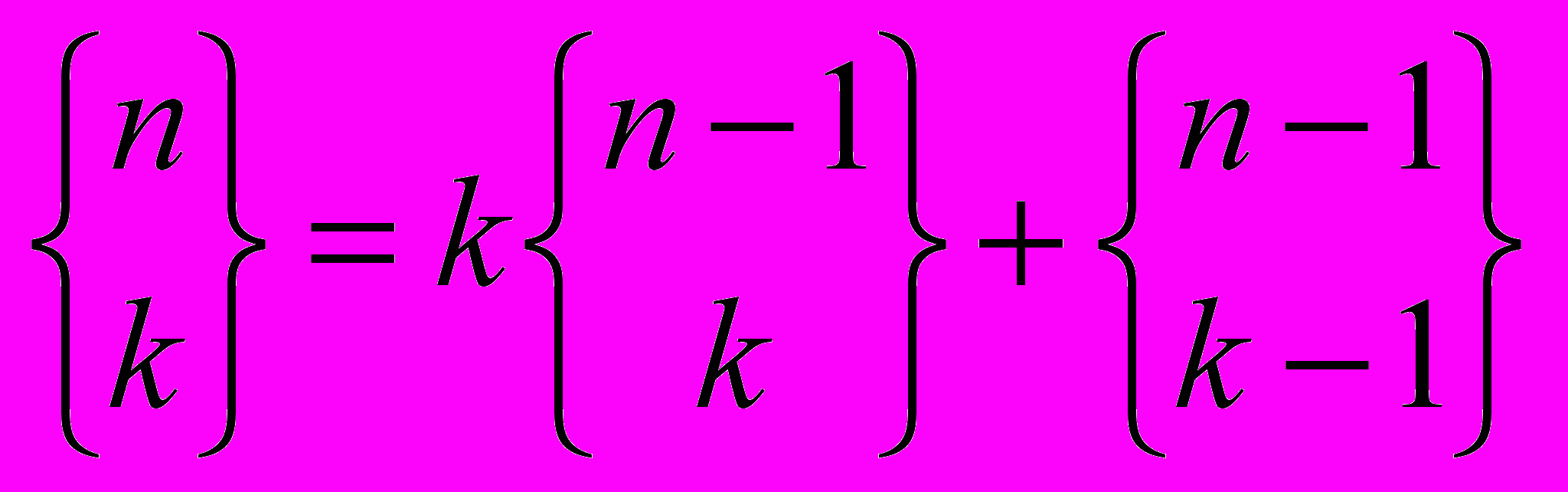  • (n — натуральное число).
  • .

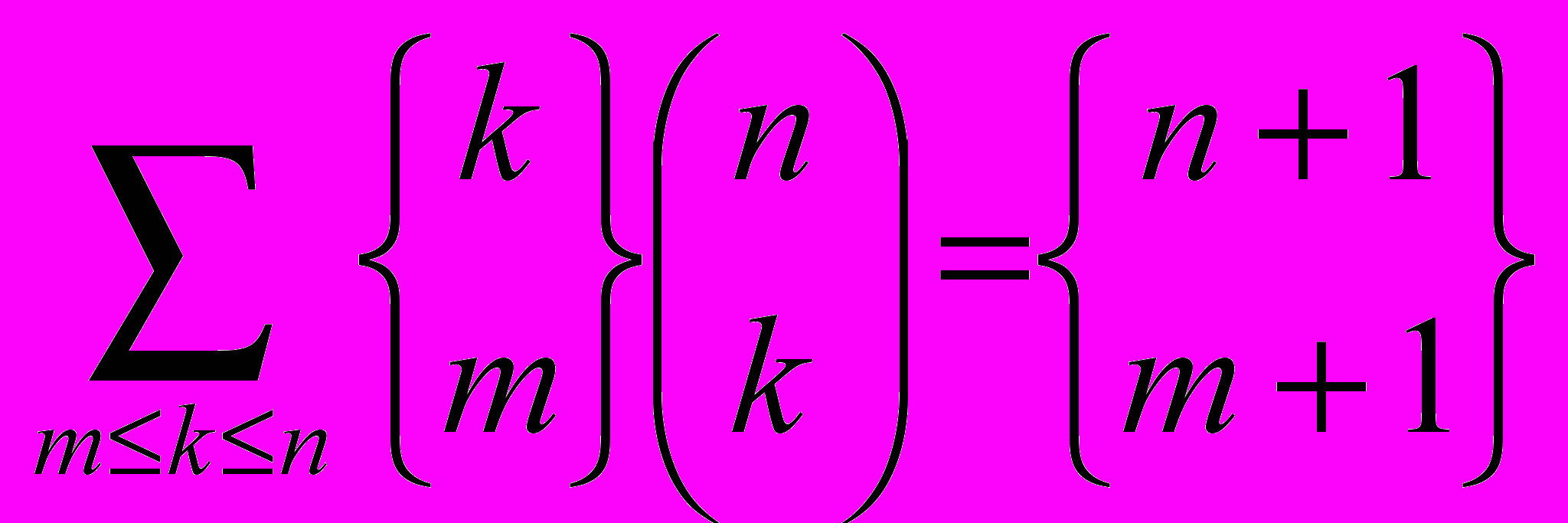Указание. Из n + 1 предметов есть один особый. Выберем k предметов из оставшихся n предметов и разложим их по m мешкам. Остальные положим с особым предметом в отдельный мешок.
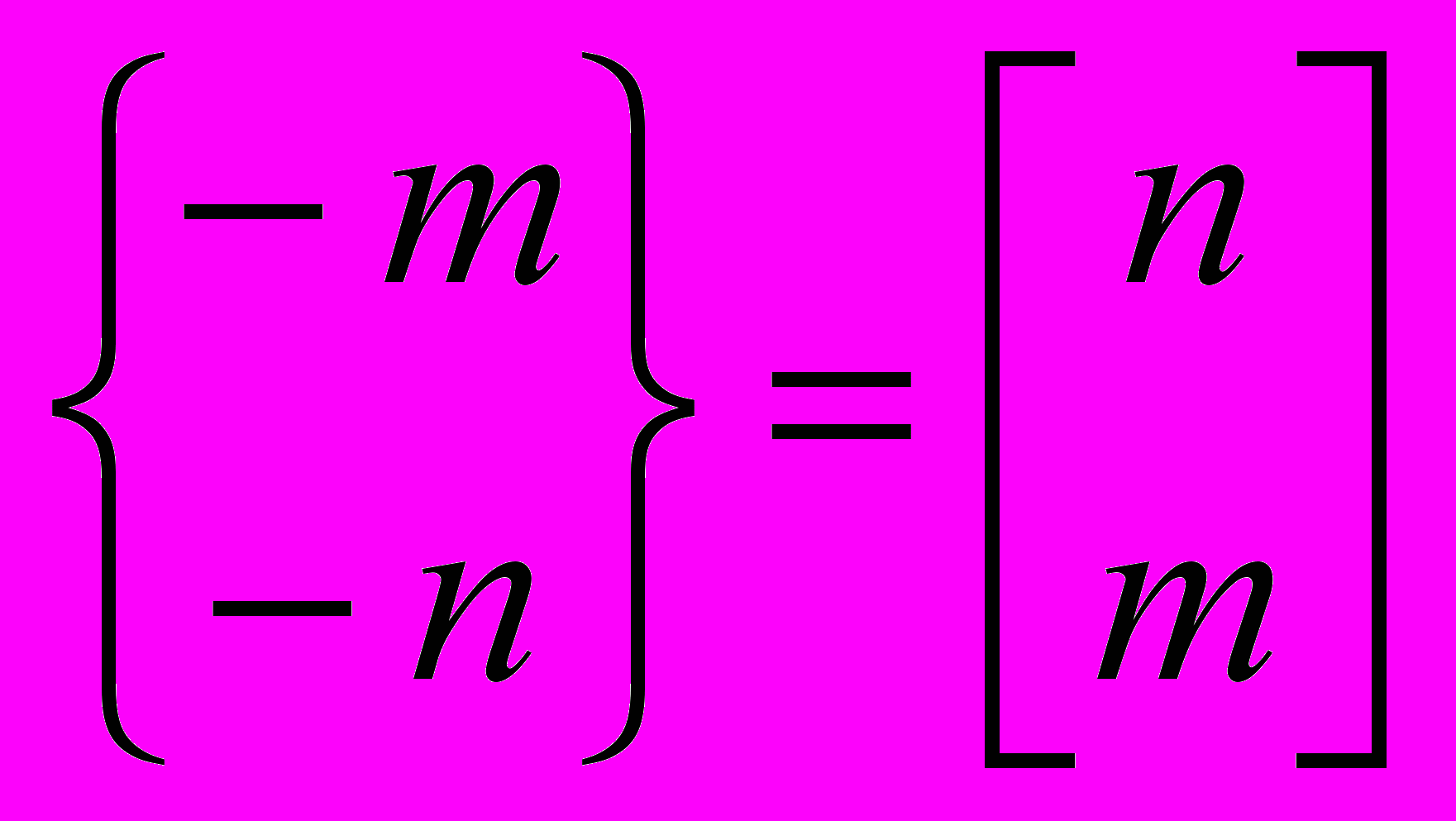  • — определим числа Стирлинга для отрицательных целых чисел. За счет этого рекуррентные формулы для чисел Стирлинга для подмножеств и для циклов (для всех целых чисел) становятся эквивалентными.
  • Заметим следующее:
    ,
    .
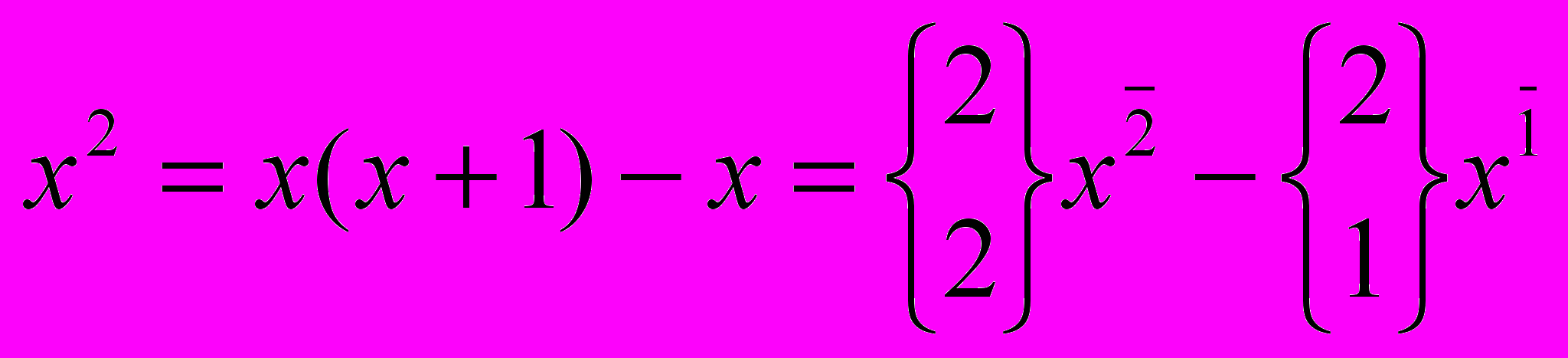    Заменим x  –x: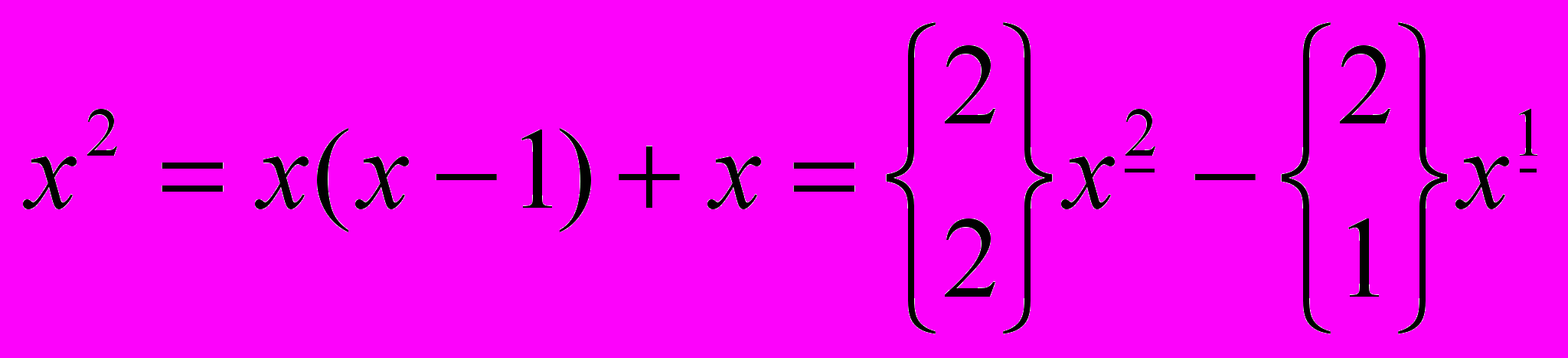
    ,
    .
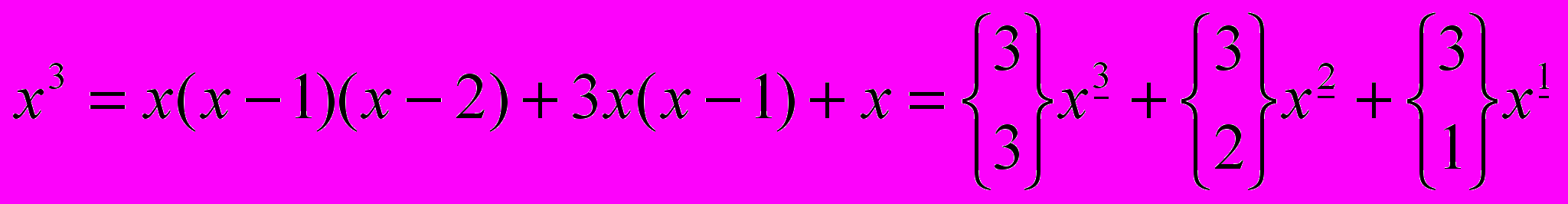    Обобщим: .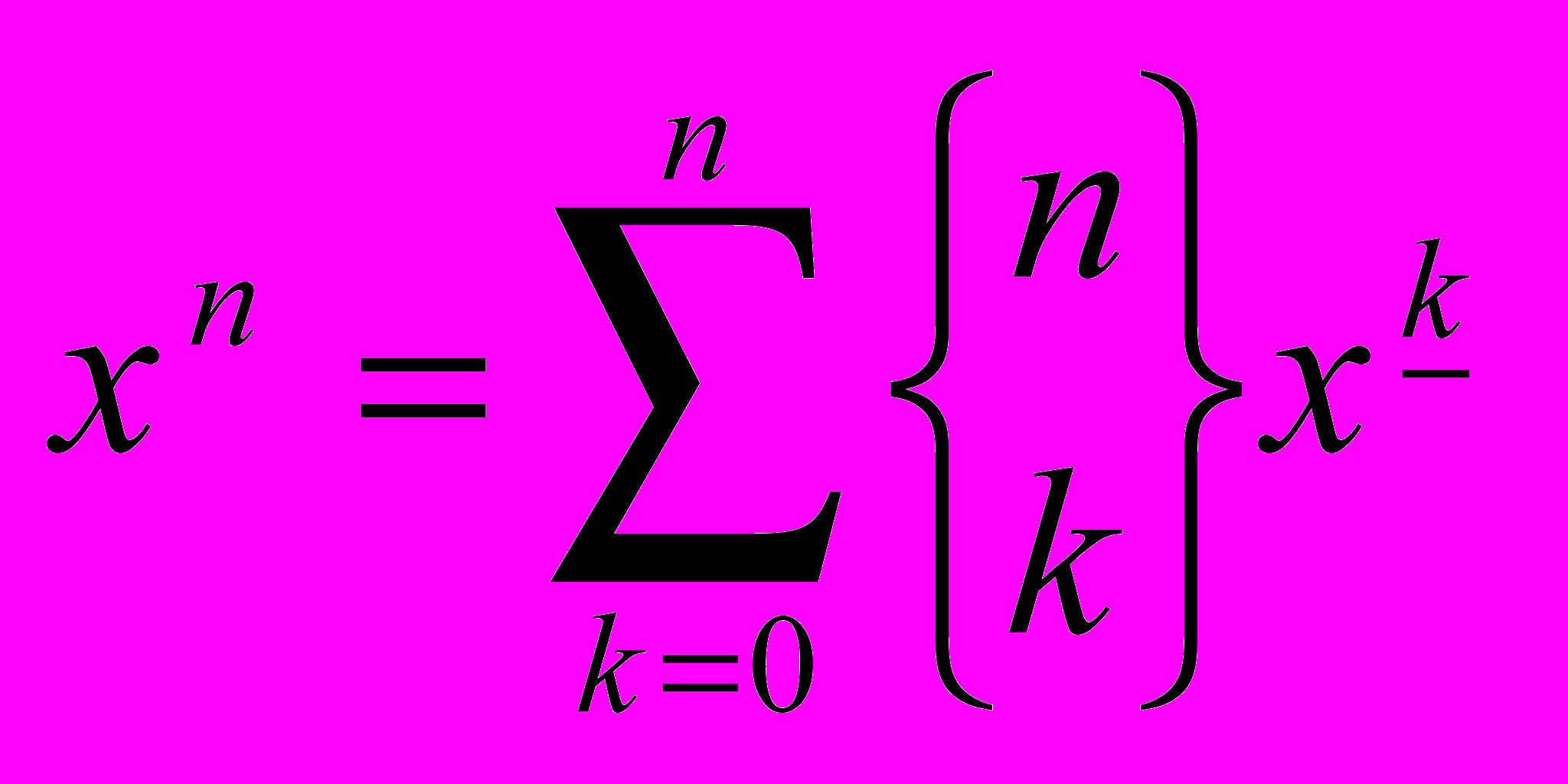
  • Существует комбинаторное доказательство для натуральных значений x.
    Наборов из n чисел от 1 до x всего xn штук.
    С другой стороны, разобьем n мест на k мешков. В первый мешок поместим число x способами, во второй — (x – 1) способом, и так далее.


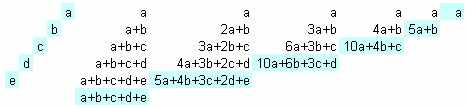
  • Рассматривая подробнее схему, показанную в начале, видим, что коэффициенты при a — биномиальные коэффициенты, при b, c, d и e — так же. Отсюда же следует доказательство тождества.
  • .
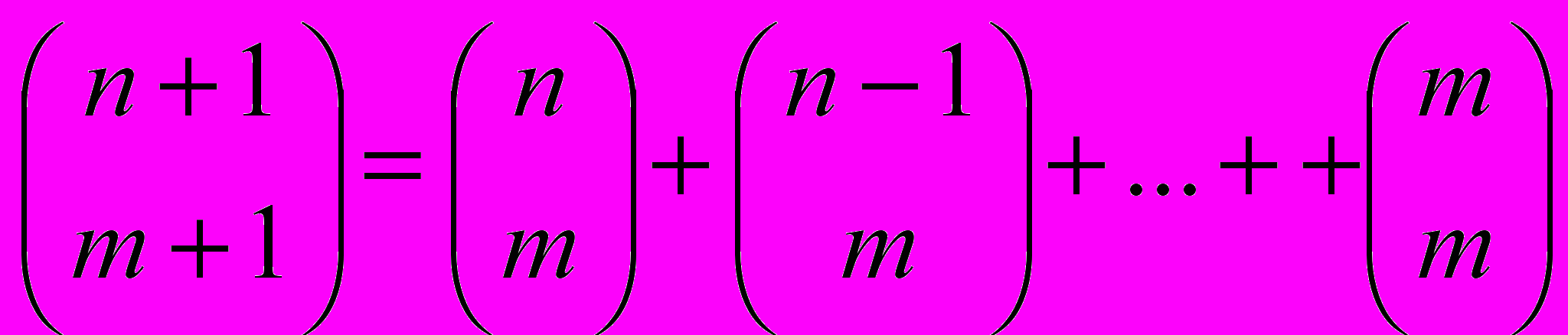    Умножив обе части на m!, получаем .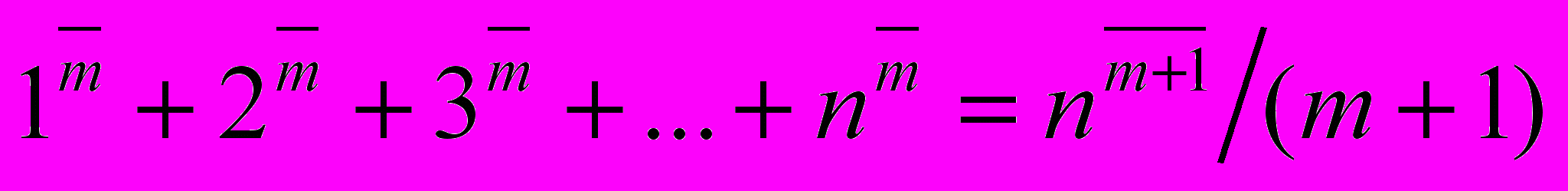
  • .
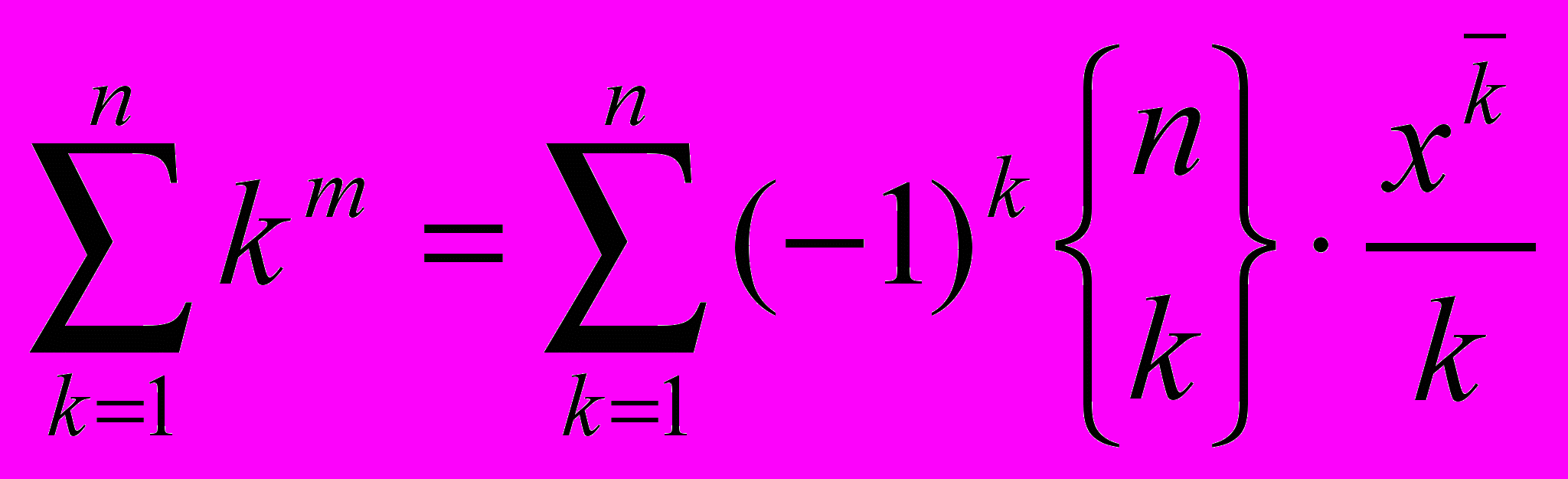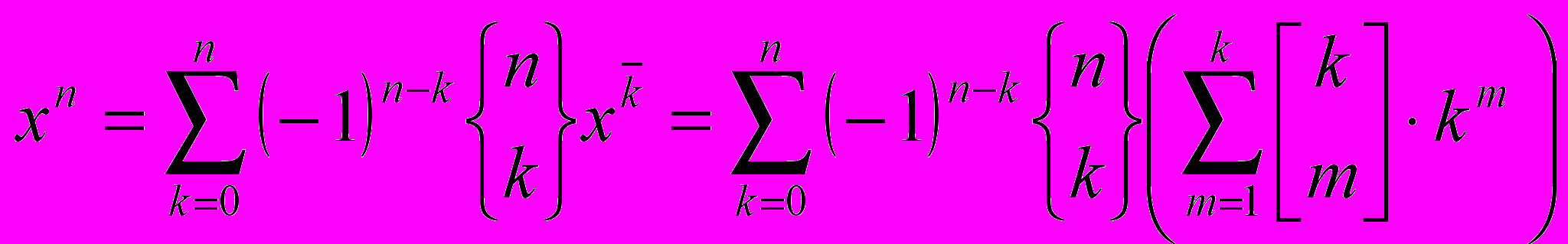  • , откуда .
  • , .
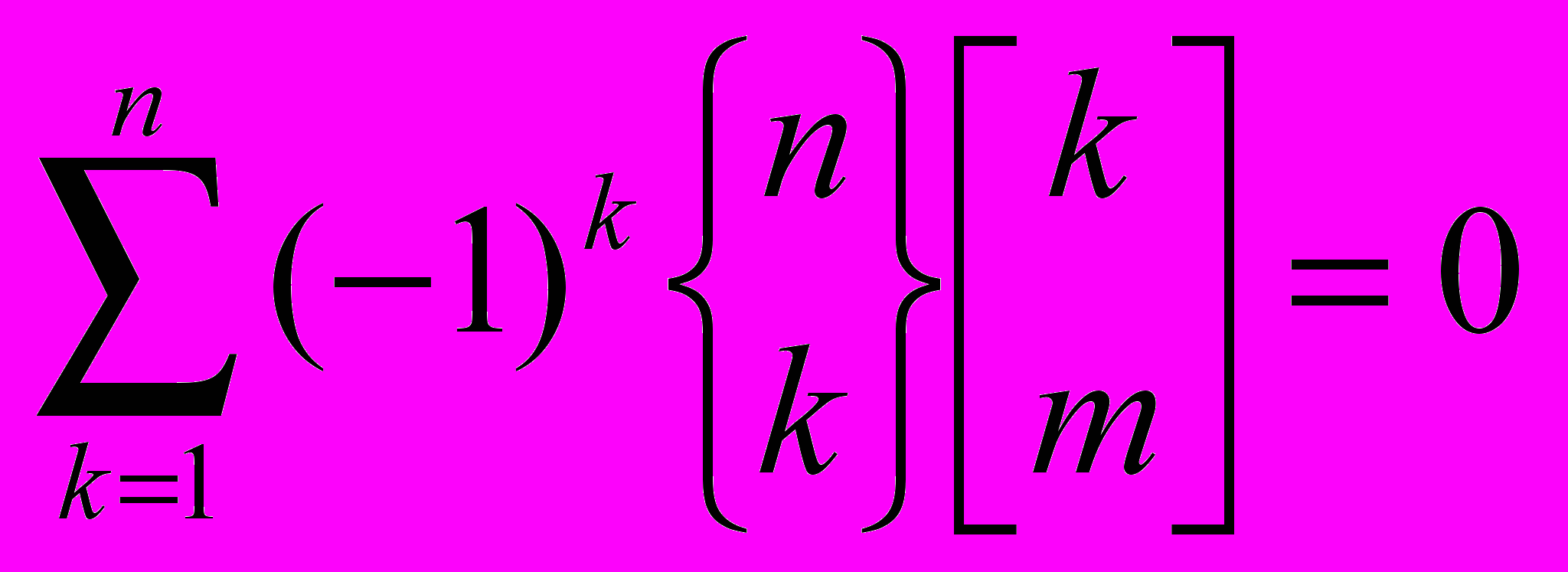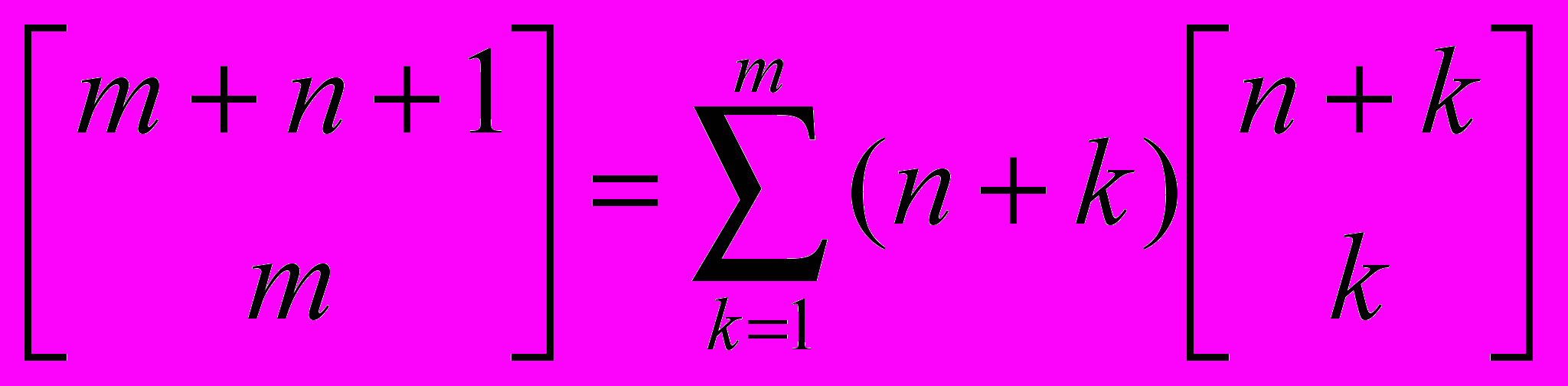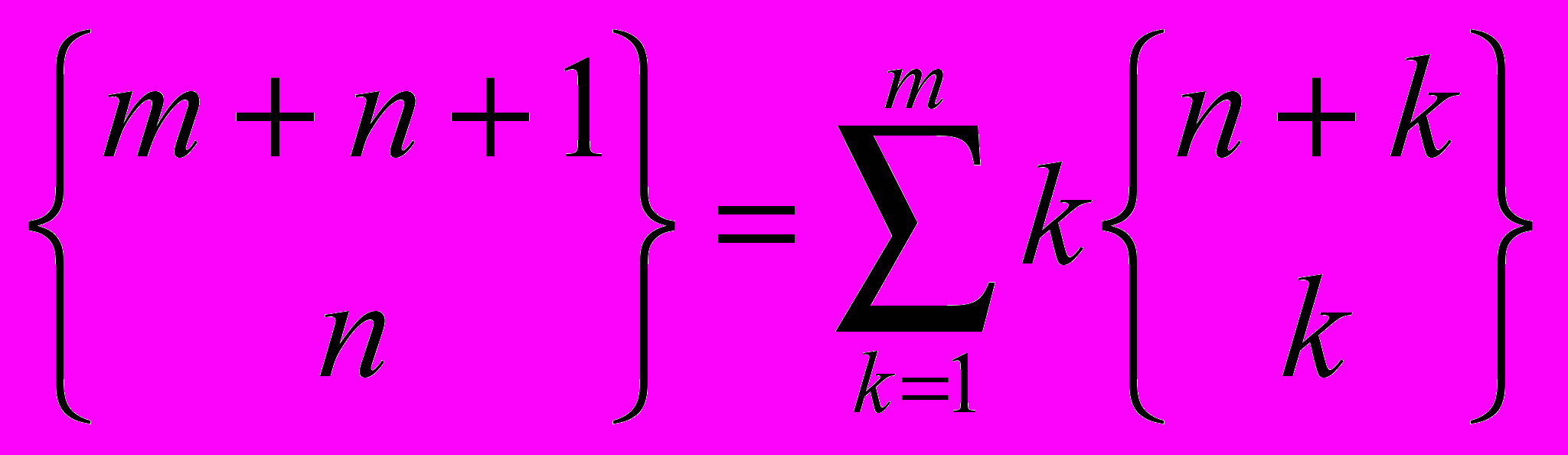    Дайте комбинаторные доказательства этих формул.