Летней Математической Школы, проходившей 11-25 июня 2011 года под Костромой. Всодержание лекционных занятий изложено в опре­де­­лениях, задача

Вид материала

Задача

Содержание Пентагональная теорема Эйлера Разбиение натурального числа N Решение задач Макси-геометрия

Подобный материал:

• Отчет о Летней Школе пул ап день 29 июня, 77.18kb.
• Русской Онтологической Школы в г. Новосибирске, 13-17 июля 2011 года, в том числе лекции, 643.67kb.
• Программа VIII международной летней школы по русской литературе на Карельском перешейке, 53.89kb.
• Вторая- организация профильного обучения в школе, 1770.94kb.
• Конкурс на участие в летней школе " Права человека и медицина", 56.38kb.
• Г. Орел 29 июня 2011 года На основании плана работы Контрольно-счетной палаты, 316.4kb.
• Основная образовательная программа начального общего образования г. Пермь, 2011, 2132.92kb.
• Расписание занятий для студентов, 56.4kb.
• М к. Аммосова Педагогический институт Рабочая программа, 114.38kb.
• Пресс-обзор рынка недвижимости с 22 июня по 28 июня 2011 года, 1403.06kb.

Пентагональная теорема Эйлера

• Судя по переписке, около 1740 г. Эйлер обнаружил, что при разложении бесконечного произведения (1 – x)(1 – x²)(1 – x³)… в степенной ряд получается выражение:
  1 − x − x² + x⁵ + x⁷ − x¹² − x¹⁵ + x²² + x²⁶ − x³⁵ − x⁴⁰ + x⁵¹ + …,
  в котором присутствуют не все степени x и в котором ненулевые коэффициенты равны 1. Эйлер заметил, что все показатели степеней с ненулевыми коэффициентами имеют вид n(3n  1)/2.
  

1. Рассмотрим многочлены P_k(x) = (1 – x)(1 – x²)(1 – x³)…(1 – x^k).
   Докажите, что коэффициенты при x^m, где m = 0, …, k совпадают с коэффициентами при этих степенях в любом многочлене P_n(x), где n > k.
   

Следствие: можно однозначно определить любой коэффициент многочлена
(1 – x)(1 – x²)(1 – x³)….

2. Докажите, что в разложении многочлена P(x) = (1 – x)(1 – x²)(1 – x³)… (до приведения подобных членов) количество одночленов n-ой степени равно числу разбиений числа n на различные натуральные слагаемые.
   

• Разбиение натурального числа N есть представление в N в виде суммы натуральных слагаемых. Представления, различающиеся порядком слагаемых, считаются одинаковыми.
  

3. (а) Пусть m школьников решали задачи: первый решил a₁ задач, второй — a₂ задач, …, m-ый школьник решил a_m задач. Посчитали b₁ — число школьников, решивших по крайней мере одну задачу, b₂ — число школьников, решивших по не менее двух задач, и так далее. Докажите, что a₁ + a₂ + … + a_m = b₁ + b₂ + ….
   (б) Пусть N = a₁ + a₂ + … + a_m. Определим b_k — количество слагаемых, не меньших чем k. Доказать, что N = b₁ + b₂ + ….
   
4. (а) (Эйлер) Пусть Q₀ и Q₁ — количество разбиений натурального числа n на различные слагаемые соответственно с четным и нечетным числом частей.
   Тогда .
   

(б) (Файн) Пусть D₀ и D₁ — количество разбиений натурального числа n на различные слагаемые соответственно с четной и нечетной наибольшей частью.
Тогда .

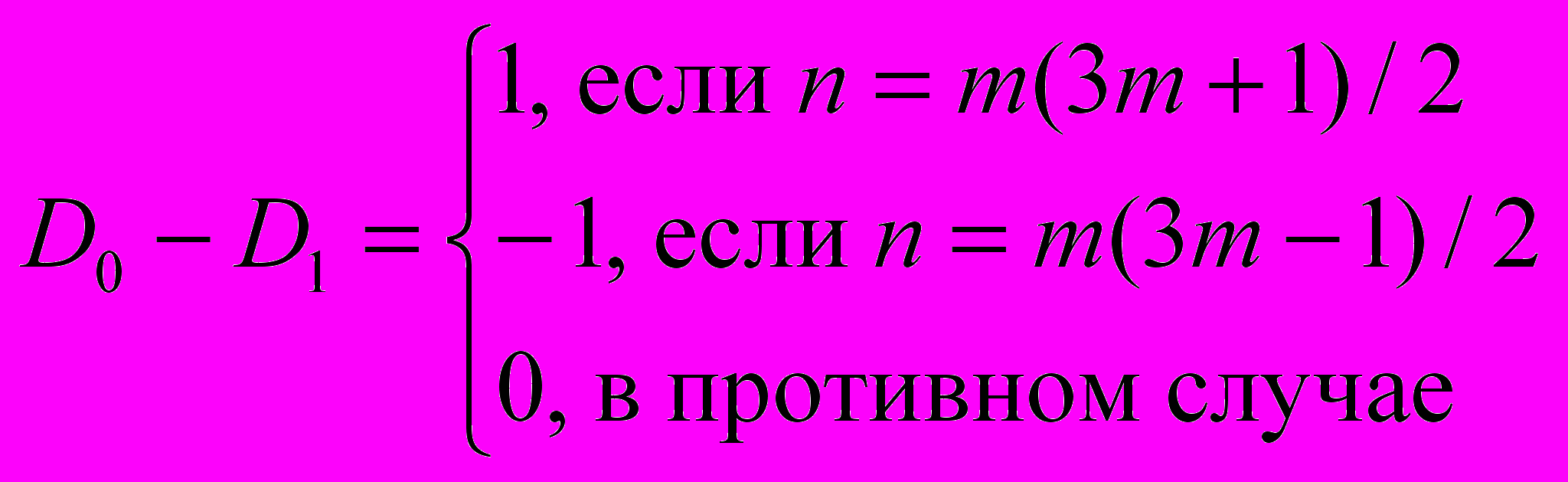Указание (инволюция Франклина).
Для каждого разбиения можно определить A — длину «одноступенчатой лестницы» (заштриховано на рисунке) и B — высоту наименьшего элемента (закрашено на рисунке).
Если A  B, то наименьшим слагаемым «надстроим» лестницу сверху. Если A < B, то снимем верхний слой лестницы и создадим новую наименьшую часть разбиения.
Осталось исследовать, при каких n эта операция не устанавливает взаимнооднозначное соответствие?

Решение задач

Макси-геометрия

1. В треугольнике ABC провели биссектрисы углов A и C. Точки P и Q — основания перпендикуляров, опущенных из вершины B на эти биссектрисы. Докажите, что отрезок PQ параллелен стороне AC.
   

Источник: ММО, 1994, 8 класс, № 3.

2. Докажите, что высота, опущенная на гипотенузу прямоугольного треугольника с углом 15, равна четверти гипотенузы.
   
3. Найдите угол B треугольника ABC, если высота CH равна половине стороны AB, а угол A равен 75.
   
4. Докажите, что длины a и b катетов прямоугольного треугольника с углом 15 удовлетворяют равенству a/b + b/a = 4.
   
5. На сторонах AB и BC треугольника ABC выбраны точки M и N соответственно. Отрезки AN и CM пересекаются в точке O, причем AO = CO. Обязательно ли треугольник ABC равнобедренный, если (а) AM = CN, (б) BM = BN?
   

Источник: РМО, округ, 1992-1993, 9 класс, задача № 3.

6. На стороне AC остроугольного треугольника ABC выбрана точка D. Медиана AM пересекает высоту CH и отрезок BD в точках N и K соответственно. Докажите, что если AK = BK, то AN = 2KM.
   

Источник: РМО, округ, 1992-1993, 10 класс, задача № 1.

7. * Угол B равнобедренного треугольника ABC (AB = BC) равен 80. Точка D внутри треугольника такова, что DAC = 30, DCA = 10. Найдите величину угла BDC.
   
8. Сторона AB трапеции ABCD видна из середины боковой стороны CD под прямым углом. Докажите, что AB = BC + AD.
   
9. (а) Как построить на стороне AB точку F такую, что S_BCE = S_BFE, S_ADE = S_AFE?
   (б) На боковой стороне CD трапеции ABCD отметили середину E. Через точку D провели прямую, параллельную BE, через точку C провели прямую, параллельную AE. Докажите, что эти прямые пересекаются на стороне AB.
   
10. В равнобедренном треугольнике ABC (AB = AC) угол A равен 20. Точка Q лежит на стороне AC таким образом, что ABQ равен 20. Точка P расположена на стороне AB, при этом ACP равен 10.
    Найдите величины следующих углов: (а) PQB; (б) CPQ; (в) APQ.
    
11. В треугольнике ABC угол A равен 15, угол B равен 60. На сторонах AC и AB взяты соответственно точки M и N такие, что AM = BM и MN = NC. Найдите угол MNC.
    

Источник: Квант-2002, Д. Калинин.

12. Внутри квадрата ABCD расположен квадрат KLMN так, что треугольники AKN, BLK, CML, DNM — равносторонние. Докажите, что площадь квадрата KLMN равна сумме площадей треугольников ABK, BCL, CDM, DAN.
    
13. Докажите, что любой квадрат можно разбить на прямоугольные треугольники, в каждом из которых есть угол 15.