Р. С. Гиляревский основы информатики курс лекций
| Вид материала | Курс лекций |
СодержаниеЗакон рассеяния По вертикали |
- С. Н. Постовалов Программирование в системе 1С: Предприятие 7 (компонента "Бухгалтерский, 899.42kb.
- Программа № «Математические основы информатики» (элективный курс) образовательная,, 124.66kb.
- Лекция №11 Сжатие изображений Курс лекций «Алгоритмические основы машинной графики», 54.41kb.
- Основы семейной психопедагогики (курс лекций), 11111.59kb.
- О. В. Свидерская Основы энергосбережения Курс лекций, 2953.76kb.
- Курс лекций введение в профессию "социальный педагог", 4415.45kb.
- Пояснительная записка 3 Содержание разделов и тем 5 Элективный курс «Математические, 106.07kb.
- Курс лекций по дисциплине " основы компьютерных технологий" Часть I. Microsoft Word, 432.92kb.
- Урок на тему «Решение логических задач с помощью электронных таблиц ms excel\ Раздел, 149.53kb.
- Это нескучное делопроизводство, 58.75kb.
Закон рассеяния
Еще одним важным свойством научных публикаций является их рассеяние. Закон рассеяния научных статей в журналах был открыт в 1934 г. С. Бредфордом, который в 1948 г. дал ему следующую формулировку1: "Если научные журналы расположить в порядке убывания числа помещенных в них статей по какому-либо заданному предмету, то в полученном списке можно выделить ядро журналов, посвященных непосредственно этому предмету, и несколько групп или зон, каждая из которых содержит столько же статей, что и ядро. Тогда числа журналов в ядре и в последующих зонах будут относиться как 1 : a : a2 ".
В соответствии с этим законом журналы по продуктивности можно сгруппировать так, чтобы они как бы образовали три зоны. Включенные в каждую такую зону журналы содержали бы одну треть публикаций по данному предмету, помещенных во всех этих журналах. Первая, ядерная зона содержит публикации из небольшого числа самых продуктивных журналов – Т 1. Вторая зона содержит публикации из большего числа журналов средней продуктивности – Т2, а третья зона – из еще большего числа журналов с низкой продуктивностью – ТЗ. Тогда в соответствии с рассматриваемым законом
Т1 : Т2 : ТЗ = 1 : a : a2,
где а является коэффициентом рассеяния, т. е. величиной для данного предмета и времени постоянной.
Для 248 журналов по электрохимии, которые были проанализированы С. Бредфордом, численное значение а составляло примерно 5. В ядерной зоне содержалось 8 самых продуктивных журналов, во второй зоне 8 х 5 = 40 журналов средней продуктивности и в третьей зоне 8 х 25 = 200 журналов. В каждой из этих трех зон содержалось по 220 релевантных публикаций, общее число которых составляло 660. Кривая рассеяния публикаций в соответствии с законом Бредфорда представлена на рис. 8. Другими словами, если совокупность всех публикаций по какому-либо вопросу принять за целое, то в специальных журналах данного профиля (число которых невелико) помещается лишь одна треть этих публикаций.
Вторая треть статей по данному вопросу оказывается опубликованной в значительно большем числе тематически родственных (смежных) журналов. Последняя треть этих публикаций рассеяна в огромном числе периодических изданий, в которых появление статей данной тематики трудно предвидеть, так как эти издания имеют широкий профиль или общенаучный характер.
За годы, прошедшие со времени открытия этого закона, проведены сотни исследований с целью проверить его истинность и найти для него строгое математическое выражение. Они показали, что закон этот выполняется только при определенных условиях, когда предмет или тема четко сформулированы, учитываются все релевантные документы в полном перечне изданий и строго ограничено время выхода этих изданий.

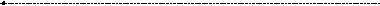


0
s
c
N
A
R (N)
B
По горизонтали: Ранг периодического издания (log e n)
По вертикали: Число релевантных публикаций, R (n)
C
Ядерная зона
Рис. 8. Рассеяние публикаций (по С. Бредфорду)

Последнее условие имеет особый смысл, так как закон этот характеризует рассеяние в определенный момент. Он является частным случаем более общего распределения, описываемого законом Ципфа. Дж. Ципф установил, что если к достаточно большому тексту составить список всех встретившихся в нем слов и расположить их в порядке убывания частоты встречаемости в данном тексте, то для любого слова произведение его порядкового номера (ранга) на эту частоту есть постоянная величина, имеющая одинаковое численное значение в данном тексте. Этому закону подчиняется распределение не только слов во всех языках мира, но и других явлений социального характера: ученых по числу опубликованных ими работ, городов по численности населения, людей по размерам дохода и даже биологических родов по числу входящих в них видов.
Следует отметить, что многие попытки объяснить механизм осуществления закона Бредфорда оказались неубедительными из-за того, что их авторы распространяли этот закон на процессы, происходящие во времени (т. е. в диахронии), тогда как он справедлив только для определенного временного среза (т. е. в синхронии). Закон Бредфорда отражает одно из свойств открытой социальной системы, каковой и является научная литературе по предмету, а именно стабильность ее иерархической структуры.
Некоторое отличие этого закона от ципфовского распределения объясняется спецификой периодических изданий как формы квантования научной литературы. Эти издания обладают большой инерционностью: изменения в их профилях и номенклатуре происходят значительно медленнее, чем в содержании статей, которые непосредственно отражают все процессы в науке и технике.
Закон рассеяния публикаций имеет большое практическое значение. Из него следует, что охват всех публикаций по какой-либо отрасли или предмету не может быть обеспечен, если ограничиться просмотром лишь профильных журналов и журналов по родственной тематике – для этого приходится просматривать значительную часть научно технических журналов. Этот закон учитывается при организации национальных информационных систем. Он позволяет решить ряд практических задач информационной деятельности:
- определять число журналов, которые обеспечивают тот или иной процент всех публикаций по какой-либо отрасли или предмету,
- составлять списки журнальных публикаций по определенной теме с гарантированной степенью полноты,
- оценивать полноту библиографических списков журнальных публикаций,
- комплектовать журнальные фонды при фиксированных ассигнованиях на подписку,
- вычислять длину полок, необходимых для хранения оптимального фонда журналов.
Рассмотренные нами закономерности далеко не исчерпывают всех достижений информатики в изучении средств информационной коммуникации. К ним следует также добавить и результаты исследований последних десятилетий в области социологии массовой коммуникации и информации: распределение типов и видов передач на радио и телевидении, организацию газетных банков данных и информационно-поисковых систем и т. п.
