Лекция №11 Сжатие изображений Курс лекций «Алгоритмические основы машинной графики»

Вид материала

Лекция

Содержание 3. Фрактальное сжатие. 7 2.Изображение как функция. 2.1Разложение в ряд Фурье. 2.2Дискретное косинусное преобразование 2.3Вейвлеты (Wavelets) 2.4S – преобразование. 3.Фрактальное сжатие.

Подобный материал:

• Московского Государственного Университета им. М. В. Ломоносова. Данная лекция, 138.53kb.
• Конспект Лекций Лекция 1 Введение в компьютерную геометрию и графику Основные направления, 1002.69kb.
• Параллельное сжатие больших изображений, 4.6kb.
• Основы построения изображений для www цель обучения, 19.73kb.
• Лекция 12. Возможности машинной графики cad/cals, 196.91kb.
• Реферат по дисциплине Основы программирования и алгоритмические языки на тему : "Архитектурные, 1249.68kb.
• Анализ и сжатие изображений с использованием математической 3d морфологии, 99.2kb.
• Вопросы к циклу лекций по уэф (VIII семестр) Лекция, 55.08kb.
• Основы семейной психопедагогики (курс лекций), 11111.59kb.
• Процедуры графики в языке Turbo Pascal, 62.62kb.

Сжатие изображений 2.

Курс лекций «Алгоритмические основы машинной графики» читается в качестве специального курса на Механико-математическом факультете Московского Государственного Университета им. М.В. Ломоносова.

Содержание

1.Введение.

Так как современные средства получения цифровых изображений позволяют нам получать их с очень высоким разрешением, то вопрос о сохранении и размерах памяти занимаемой такими изображениями стал очень важен. Сократить объём памяти занимаемый изображением можно сжатием этого изображения с потерями либо без них. Сжатие без потерь применимо не только к изображениям, но и к любой другой информации, представленной в цифровом виде. Данная лекция посвящена сжатию изображений с потерями. Сжатие с потерями основывается на особенностях восприятия человеком изображения: наилучшая чувствительность в определённом диапазоне волн цвета, а также способность воспринимать изображение как единое целое, тем самым не замечая мелких искажений.

2.Изображение как функция.

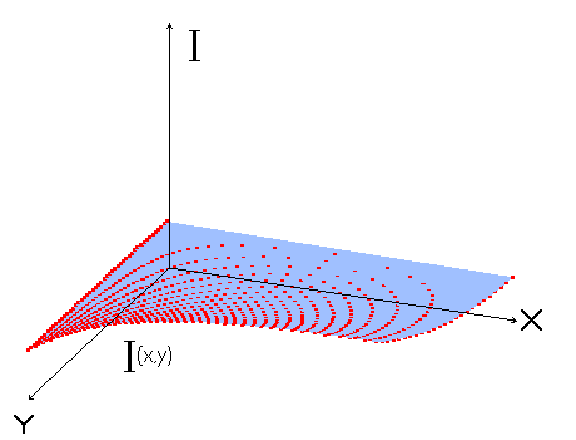
Рисунок 1.Функция Изображения.

Будем рассматривать изображение как целочисленную функцию 2-ух переменных 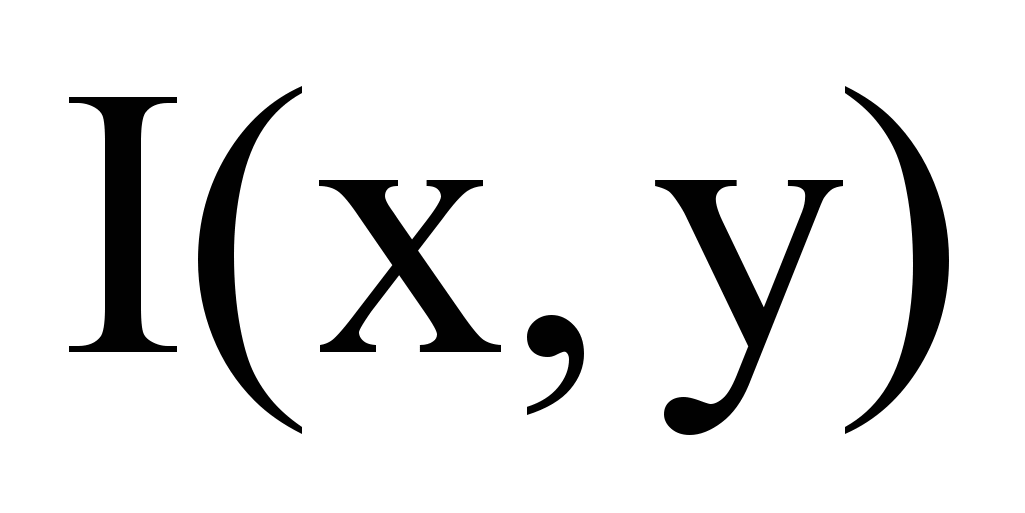, где 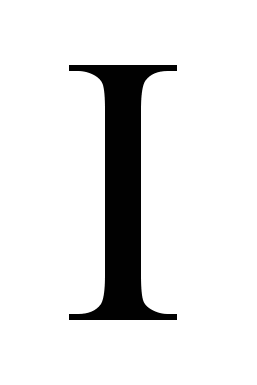значение цвета, либо его номер в палитре, либо, например, интенсивность – это зависит от цветовой модели представления изображения (см. Рисунок 1.Функция Изображения)

Эту функцию можно разложить в ряд:


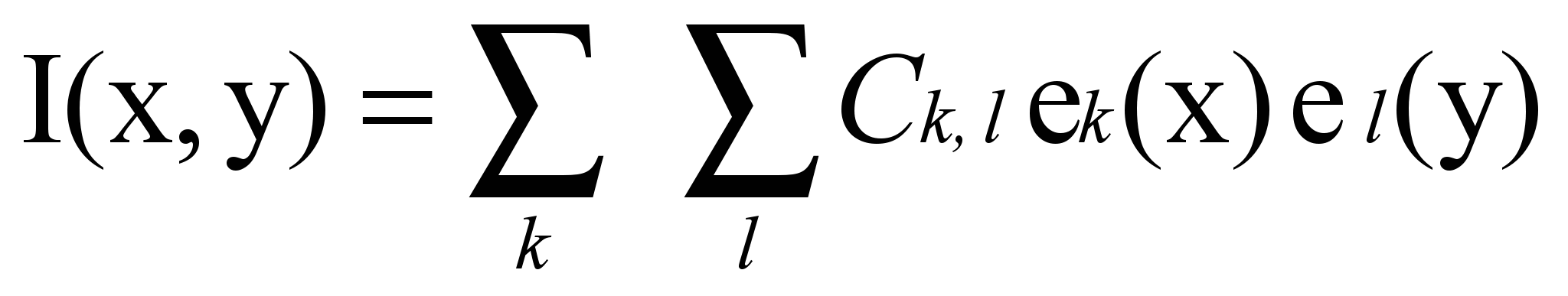
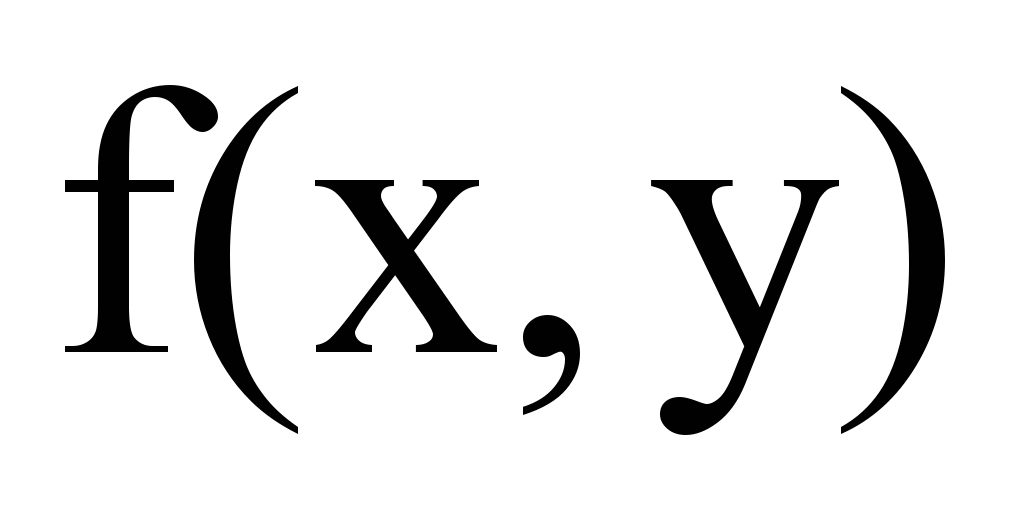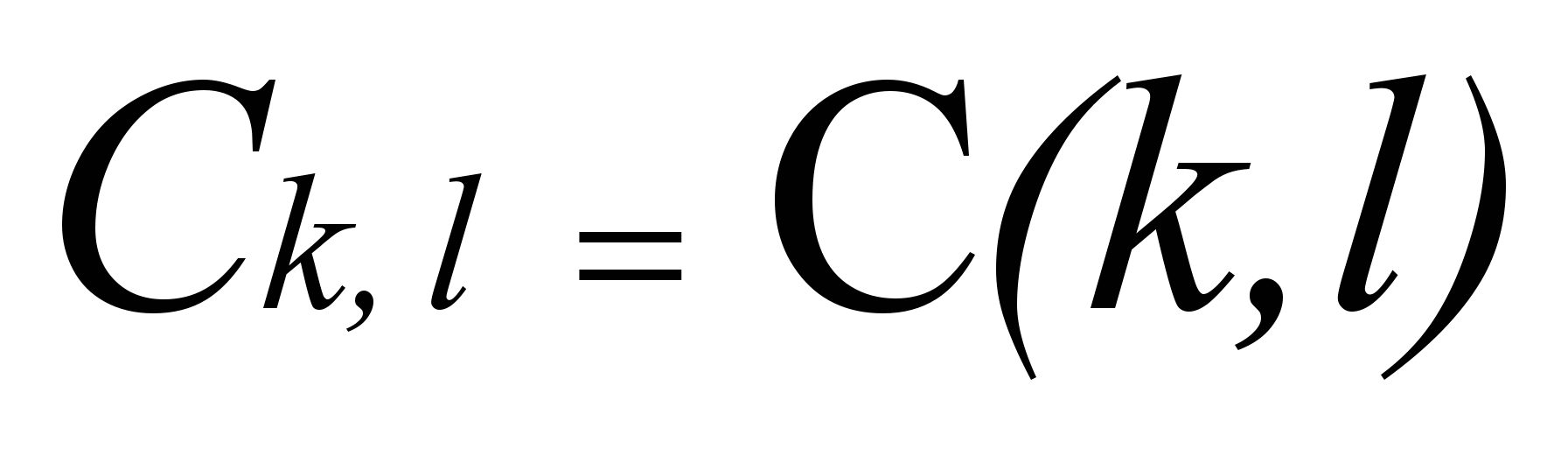Где мы формально заменили на , a 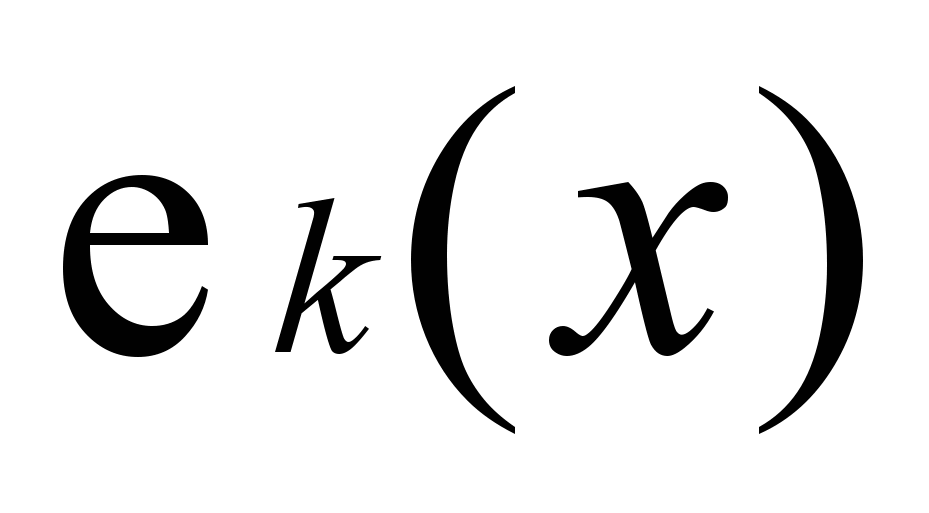, 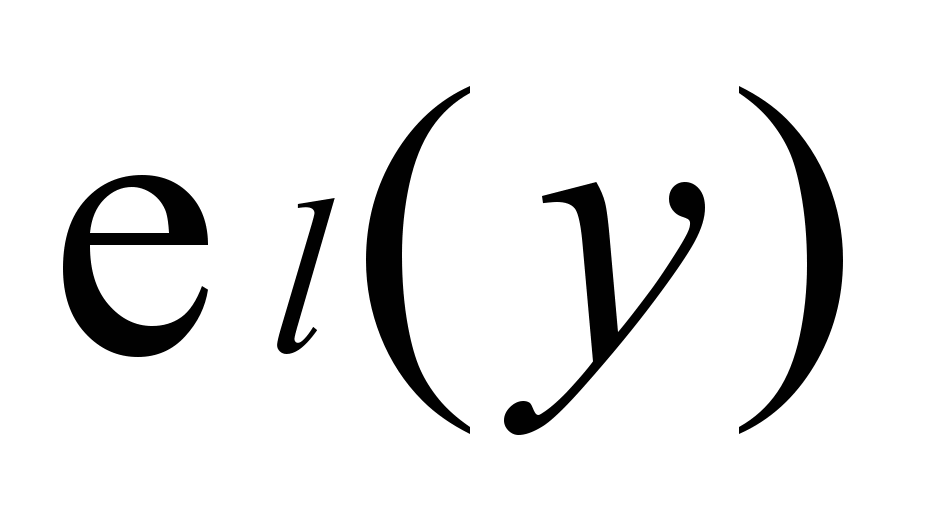– базисные функции.

2.1Разложение в ряд Фурье.

Здесь: 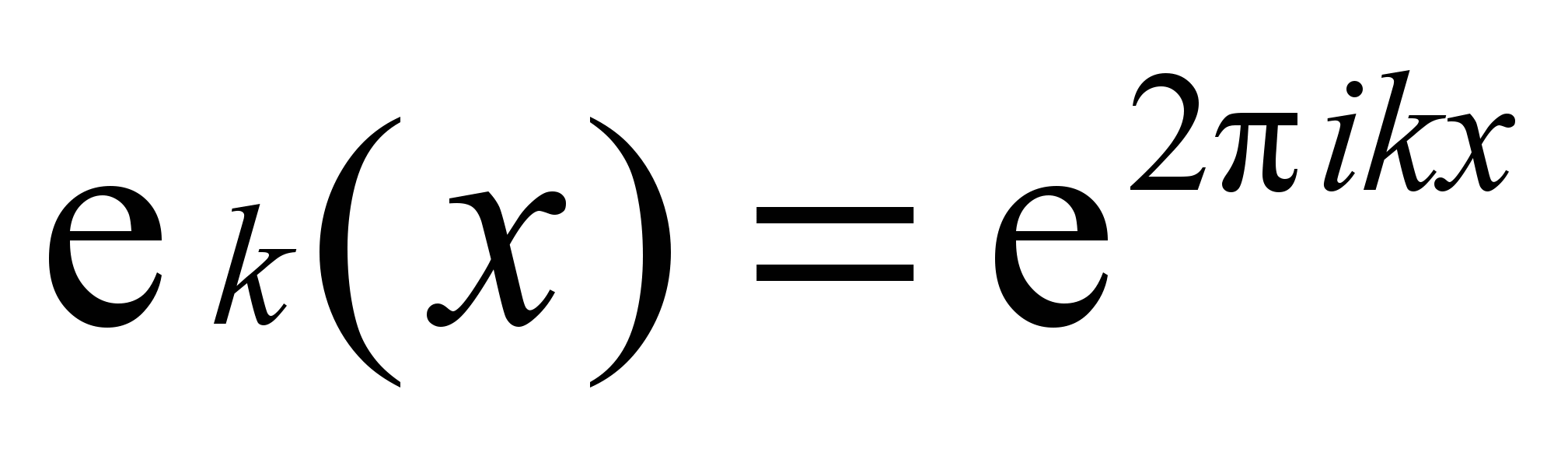, соответственно получим разложение: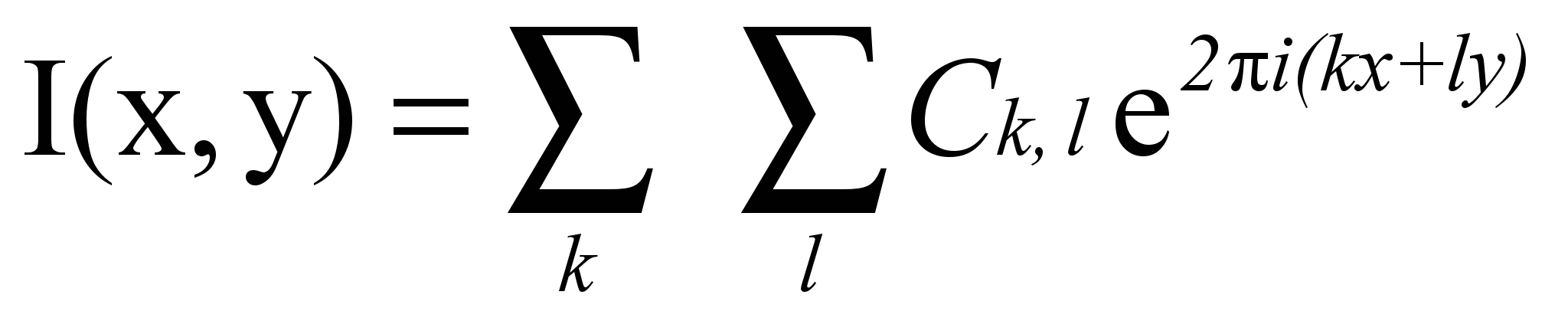

Т.к. 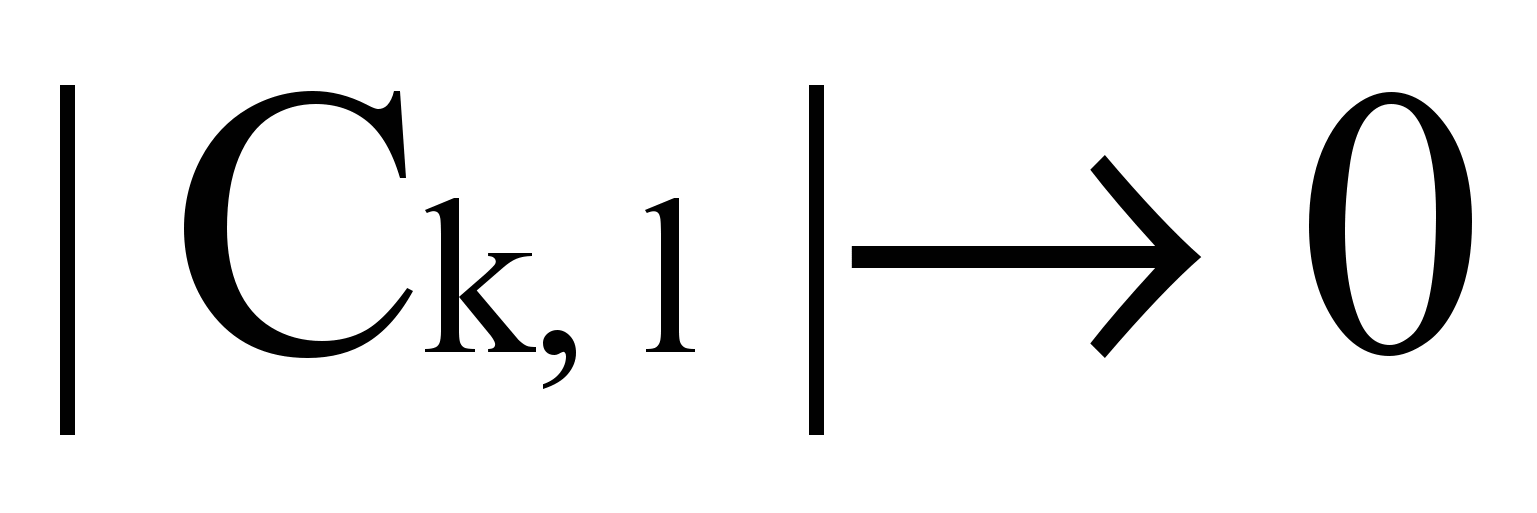, при 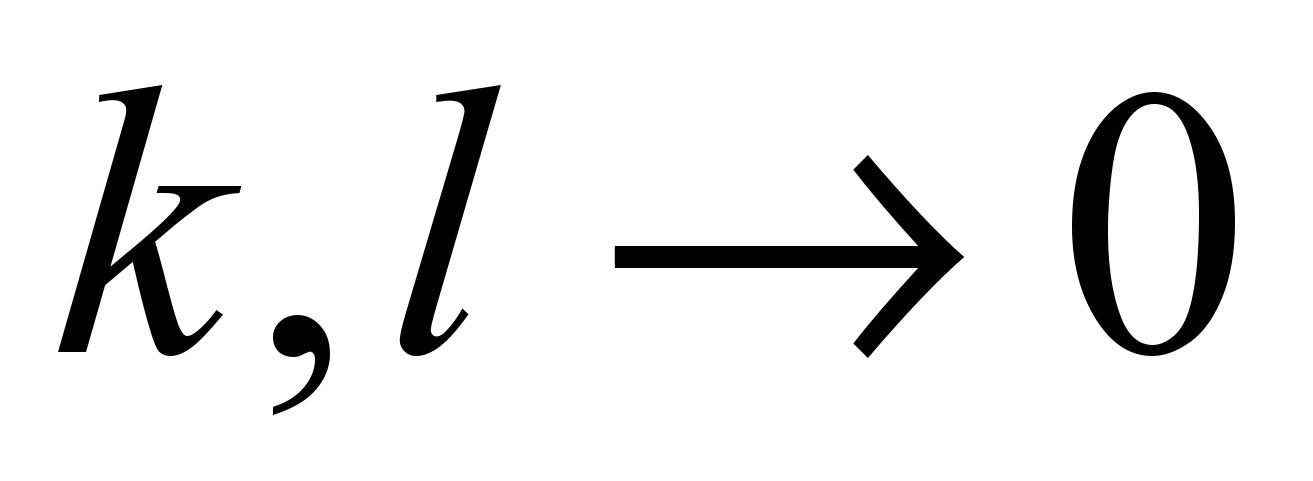можно ограничиться конечным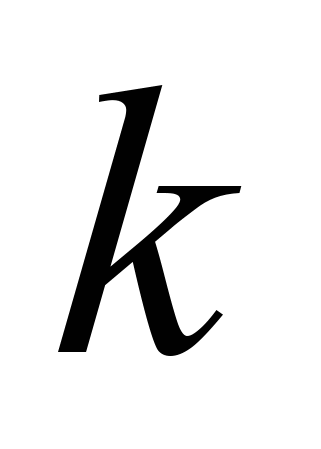и и 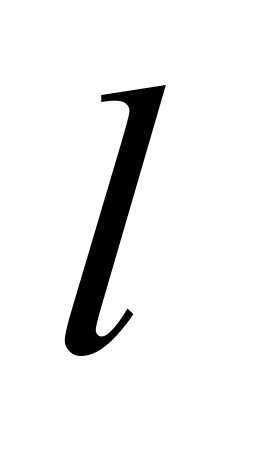. Поскольку это есть разложение в ряд по косинусам и синусам, то так можно судить о периодичности изображения как функции.

Для сжатия изображений практически не используется.

2.2Дискретное косинусное преобразование

В формате JPEG используется дискретное косинусное преобразование (ДКП) (DCT - Discrete Cosine Transform)


Пусть наше изображение квадратное, т.е. размера .

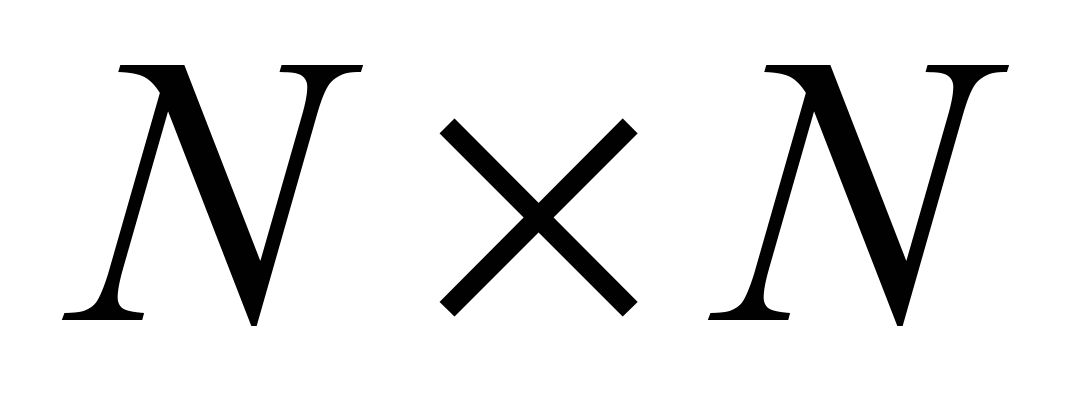Рассмотрим прямое преобразование (Forward):

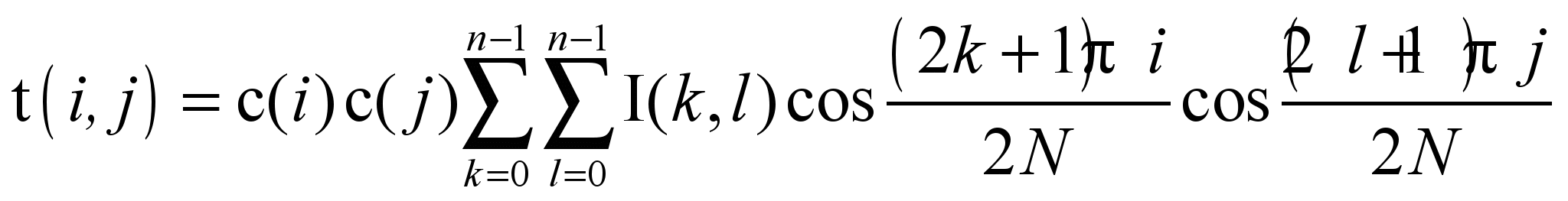, где ,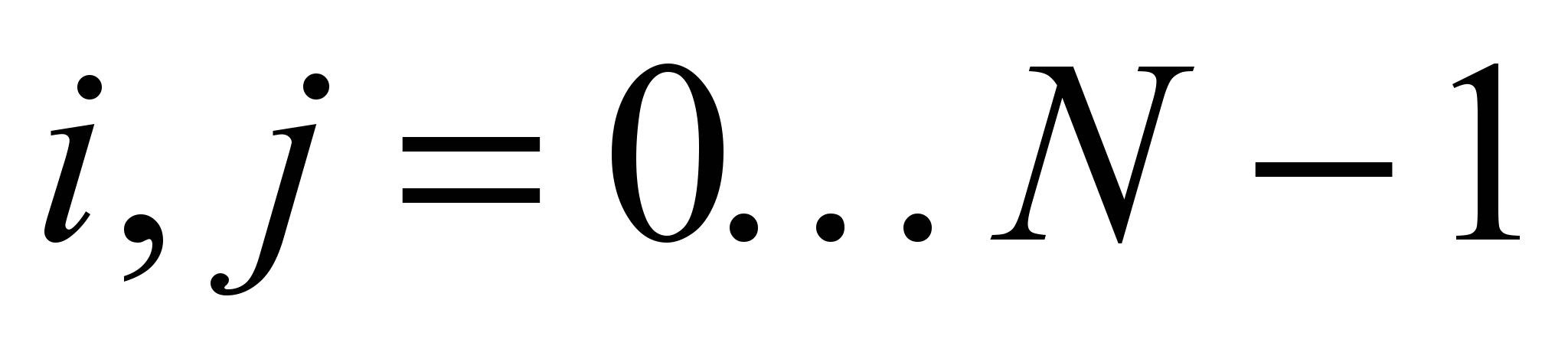


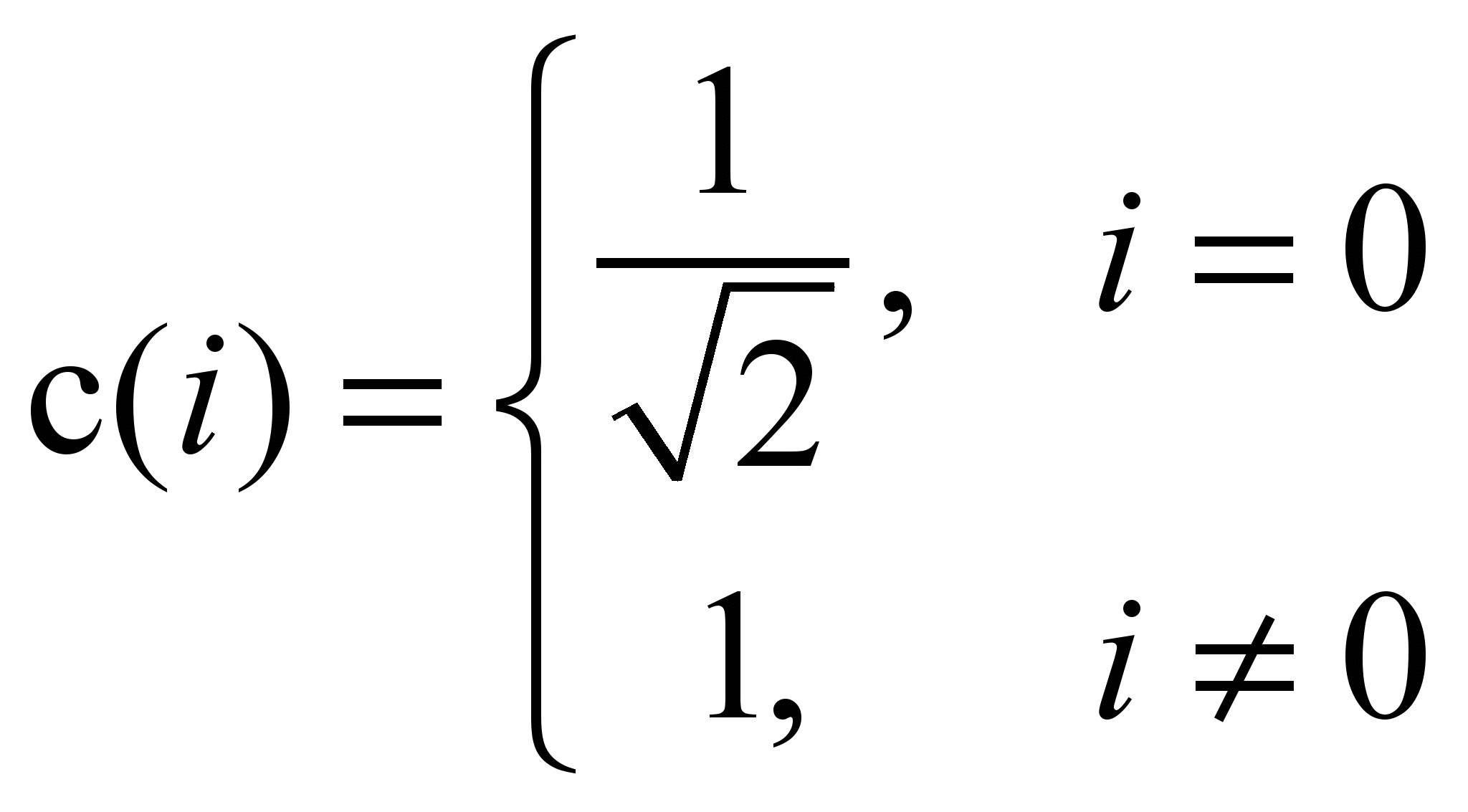
Существует и обратное преобразование (inverse):

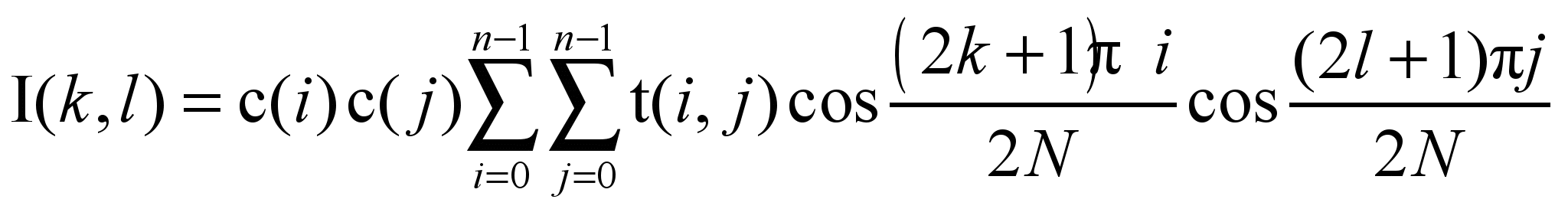,где ,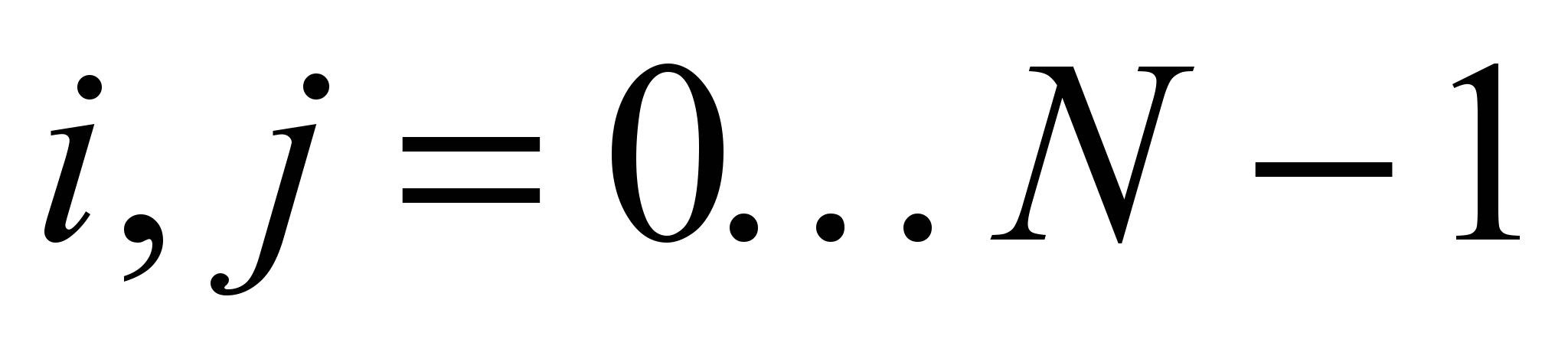

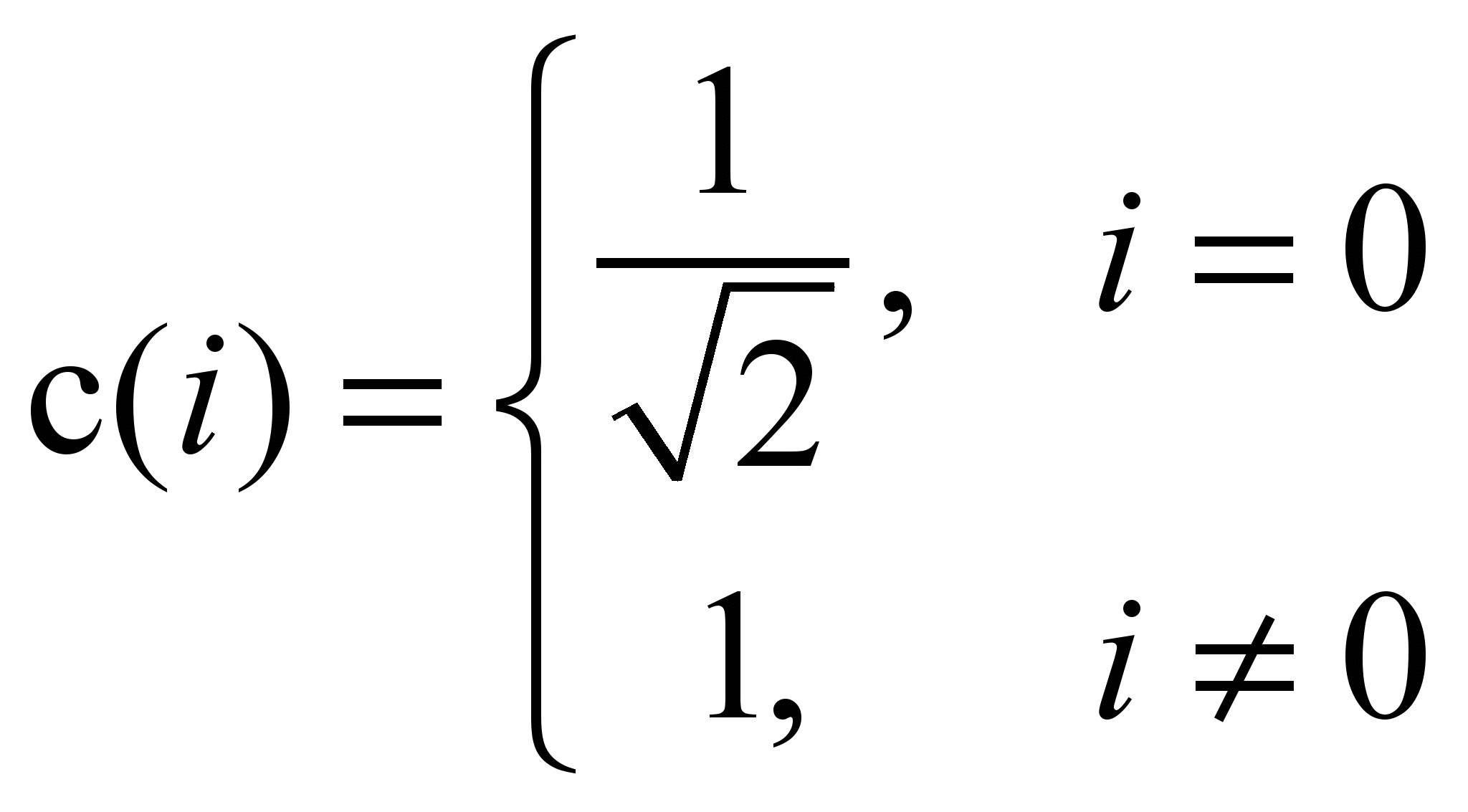
В чём же смысл, если коэффициентов столько же?

Рассмотрим некоторые:

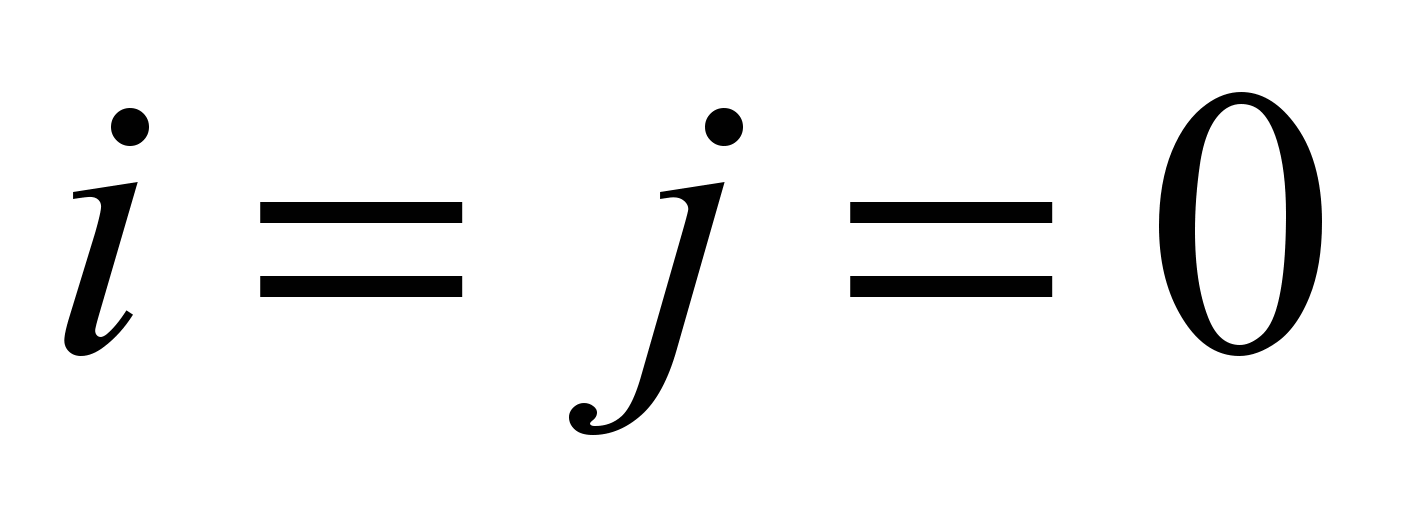
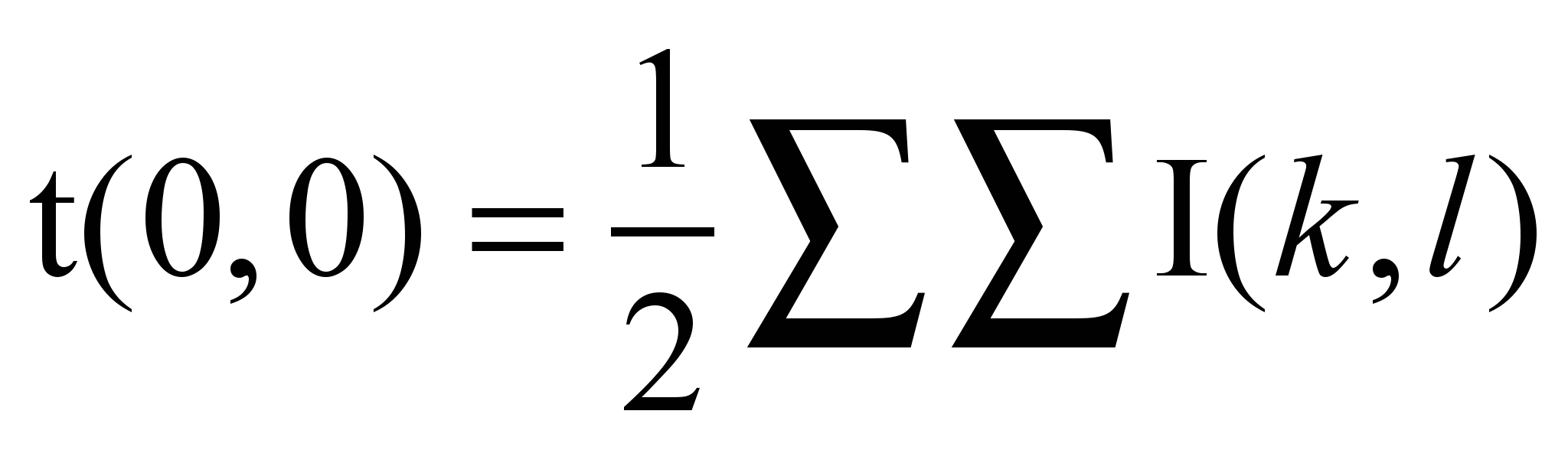- фактически среднее арифметическое изображения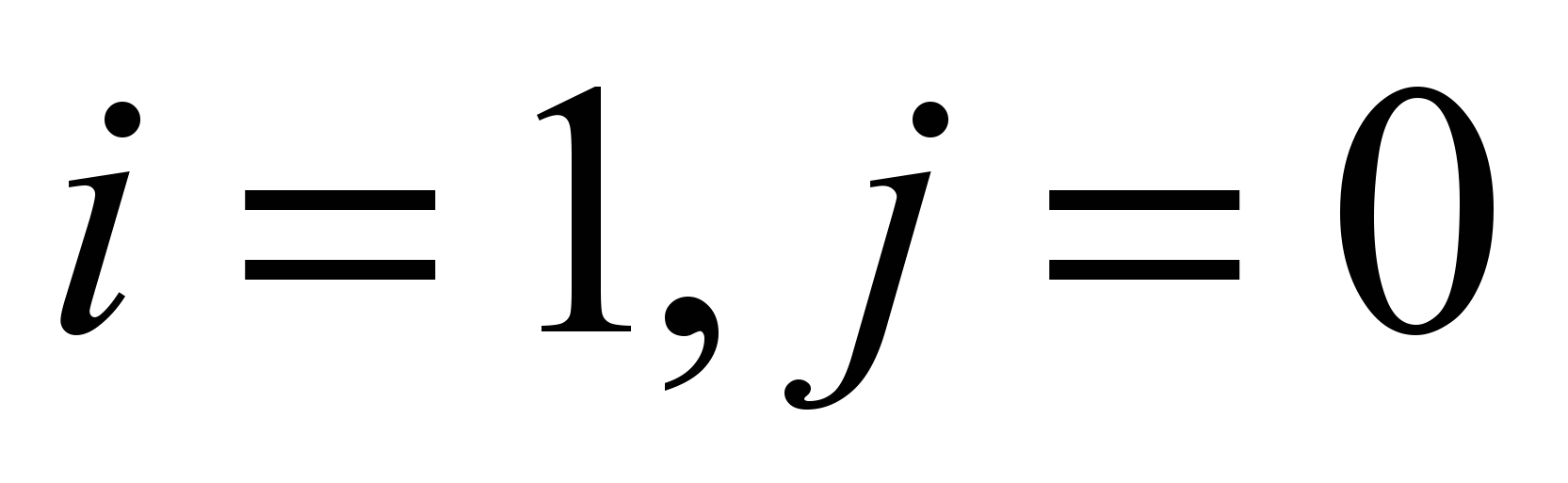

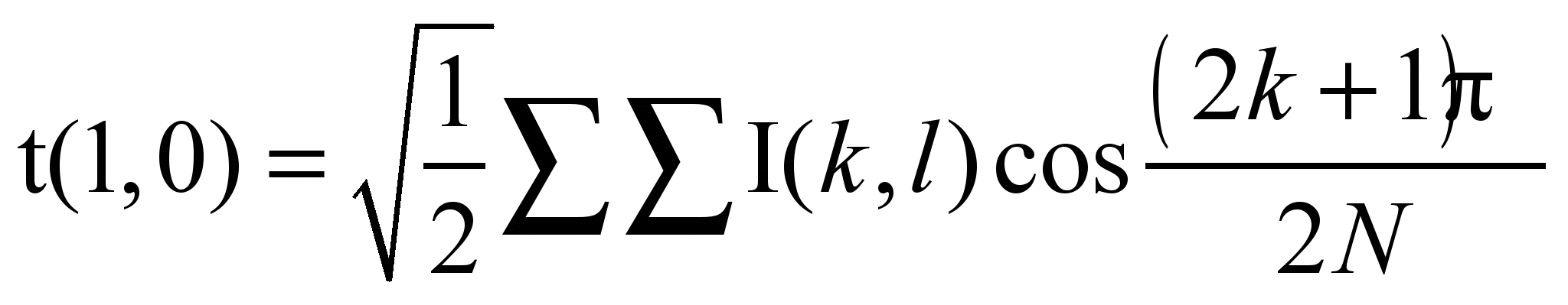- появляется первый косинус (см. Рисунок 2. График при i=1, j=0.)




Рисунок 2. График при i=1, j=0.


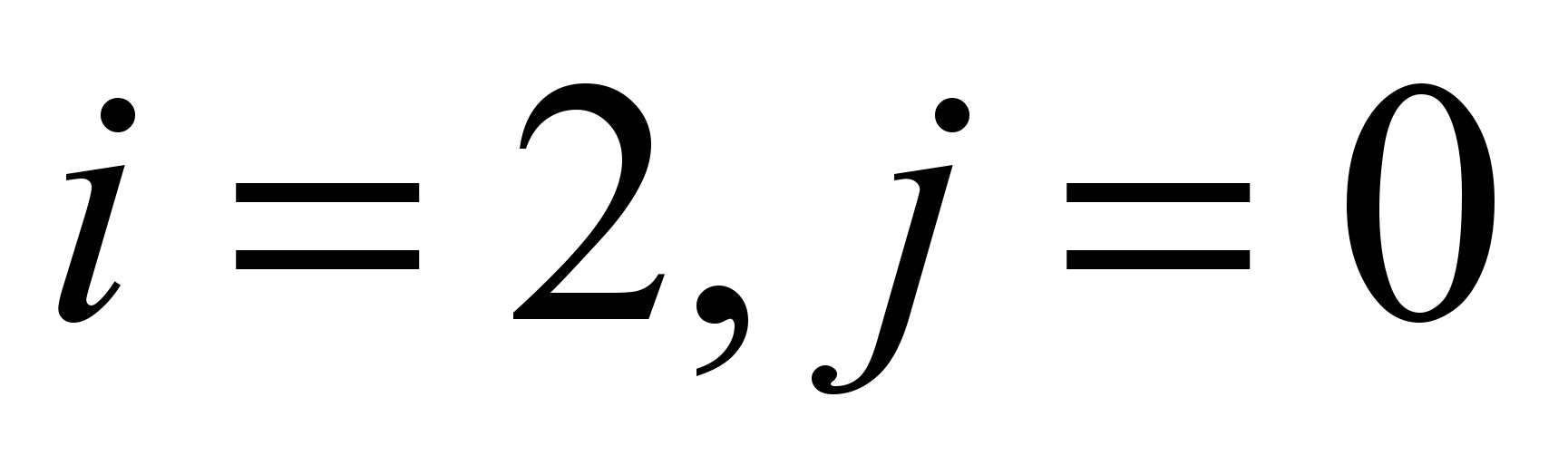
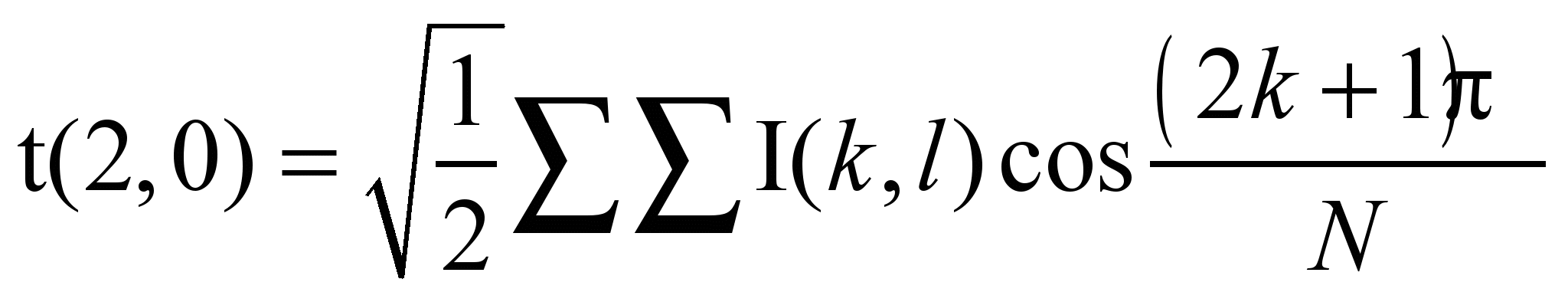(см. Рисунок 3)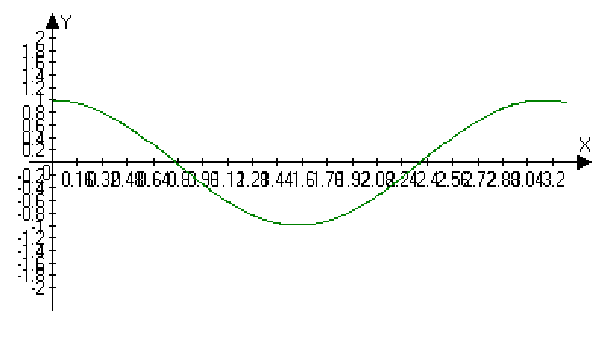



Рисунок 3. График при i=2, j=0.

Можно сделать вывод, что ДКП раскладывает изображение по амплитудам некоторых частот. Таким образом, получится матрица, где будет много коэффициентов близких к нулю.

В формате JPEG, перед тем как применить ДКП, изображение разбивается на блоки размером 8 на 8 пикселей (это становится если задать высокую степень компрессии). Затем к ним применяется ДКП.

Некоторые коэффициенты можно хранить приближённо, т.к. глаз не сможет заметить достаточно маленьких изменений. Операция округления коэффициентов называется квантованием и выполняется по формуле:



Здесь означает покомпонентное умножение плюс взятие целой части.

Таким образом, мы получаем новую матрицу 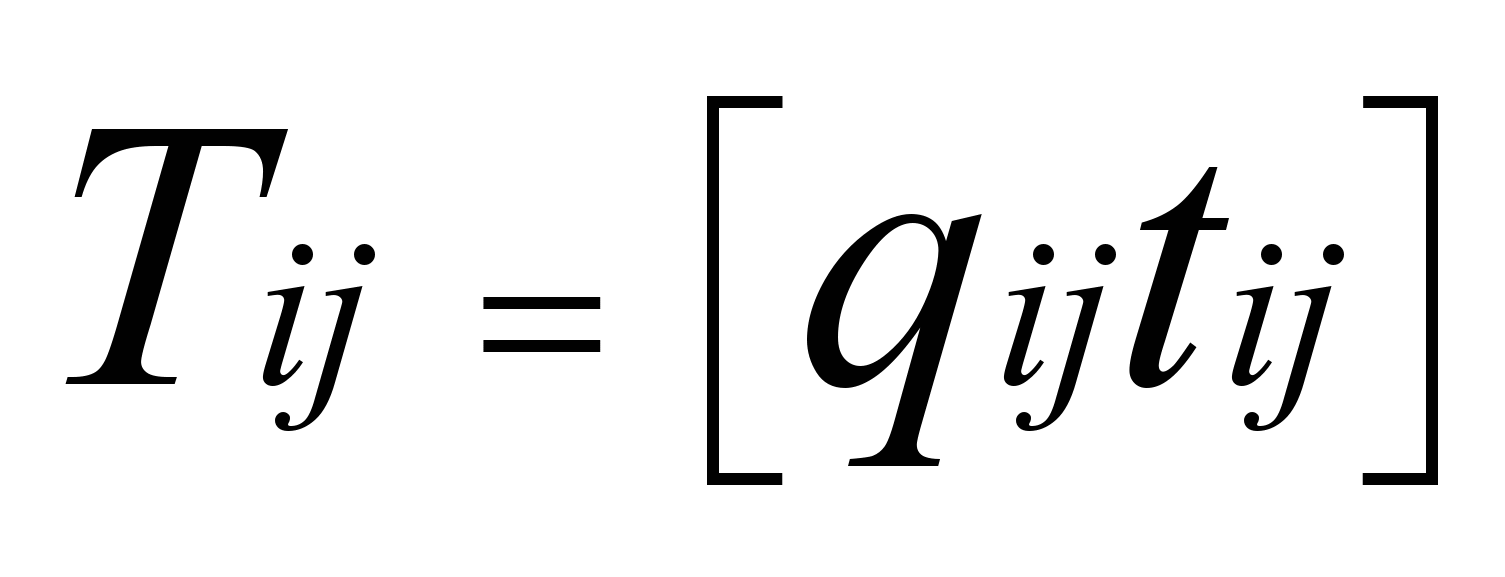, где - коэффициенты после применения ДКП, 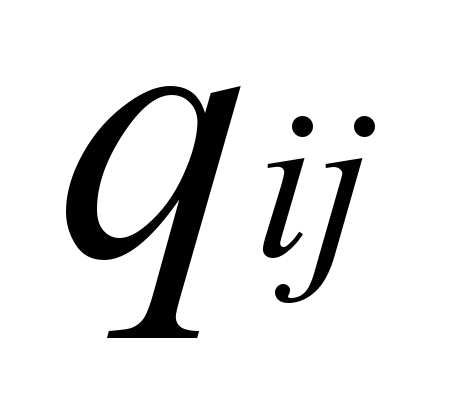- коэффициенты округления ( - означает взятие целой части). Далее применяется зигзагообразный обход матрицы 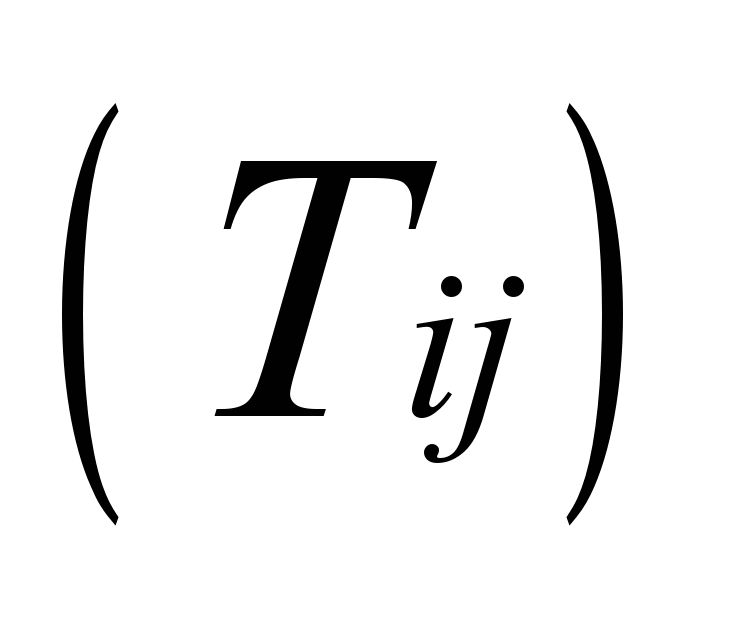для получения длинных последовательностей нулей (см. Рисунок 4. Зигзаг упорядочивание.).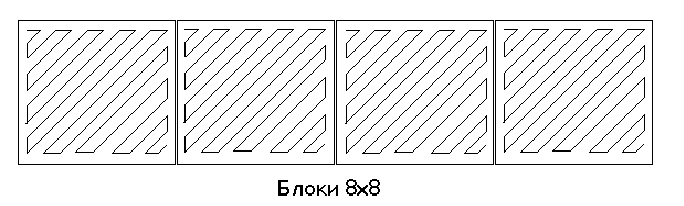



Рисунок 4. Зигзаг упорядочивание.

Затем используется сжатие без потерь сначала RLE, а затем метод Хаффмана с фиксированной таблицей.

Соответственно составим краткую схему алгоритма сжатия применяемого в JPEG:

1. Разбиение изображения на блоки .
   
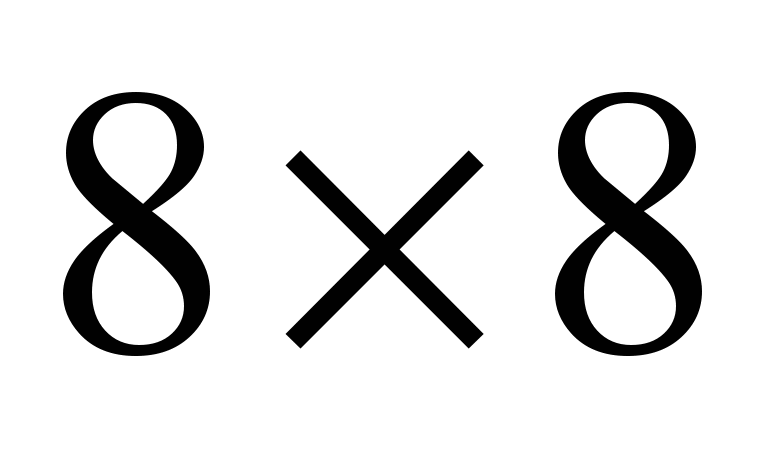2. Применение к ним преобразования(FDCT).
   
3. Квантование.
   
4. Зигзаг упорядочивание.
   
5. RLE+Huffman.
   

Восстановление изображение - этот же алгоритм только в обратном порядке.

2.3Вейвлеты (Wavelets)

Идея в использовании локального всплеска (см. Рисунок 5. Пример локального всплеска.) вместо глобально-периодических функций, т.е.

таких функций 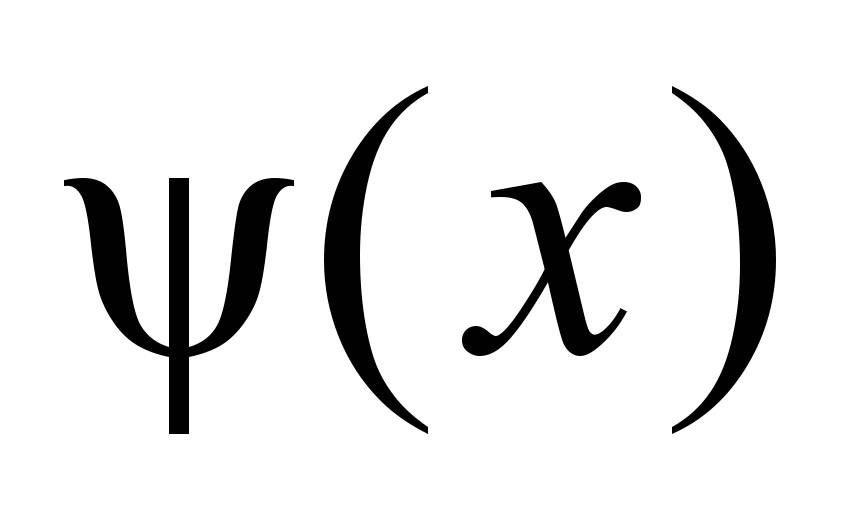, что:



Рисунок 5. Пример локального всплеска.

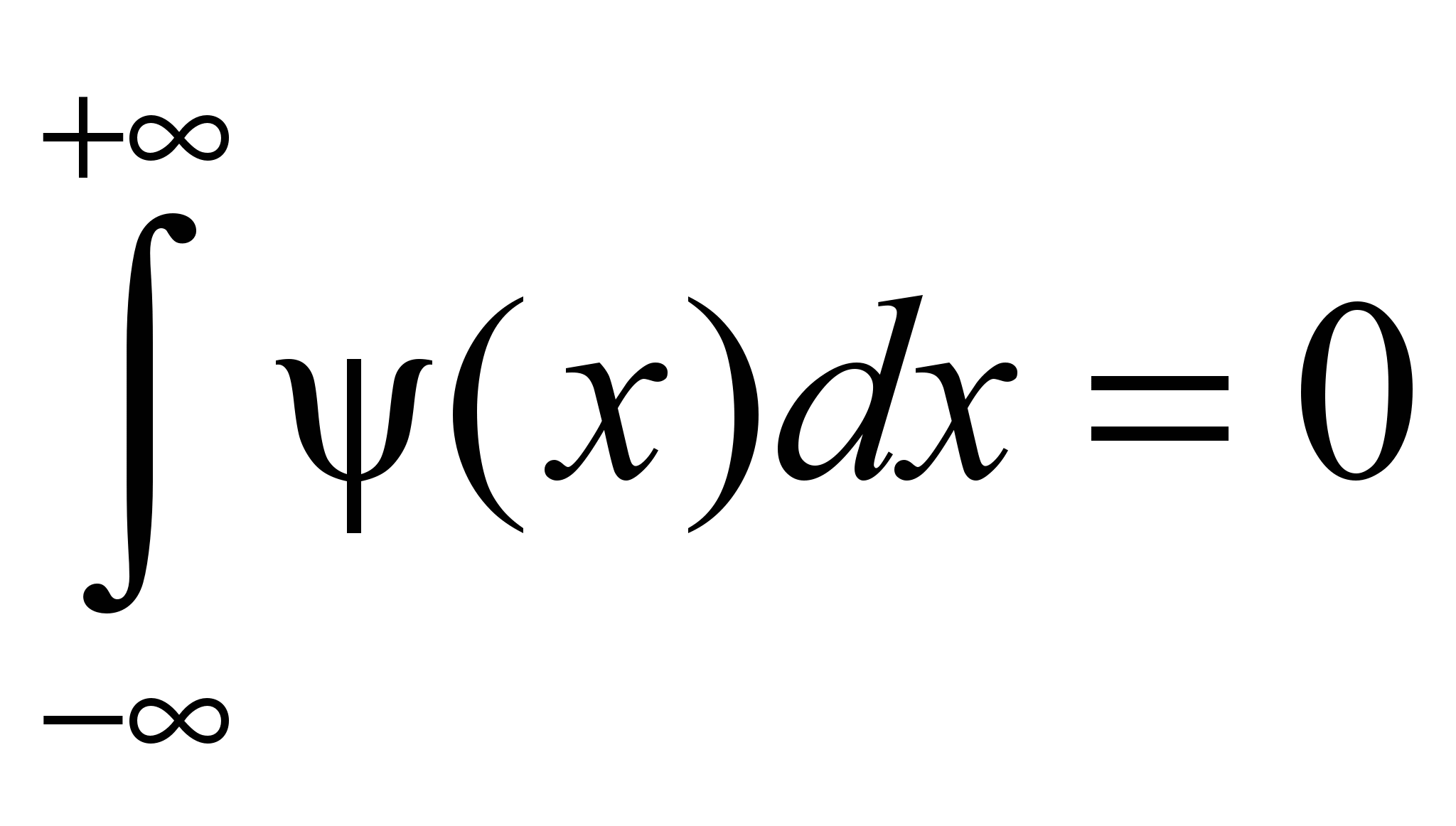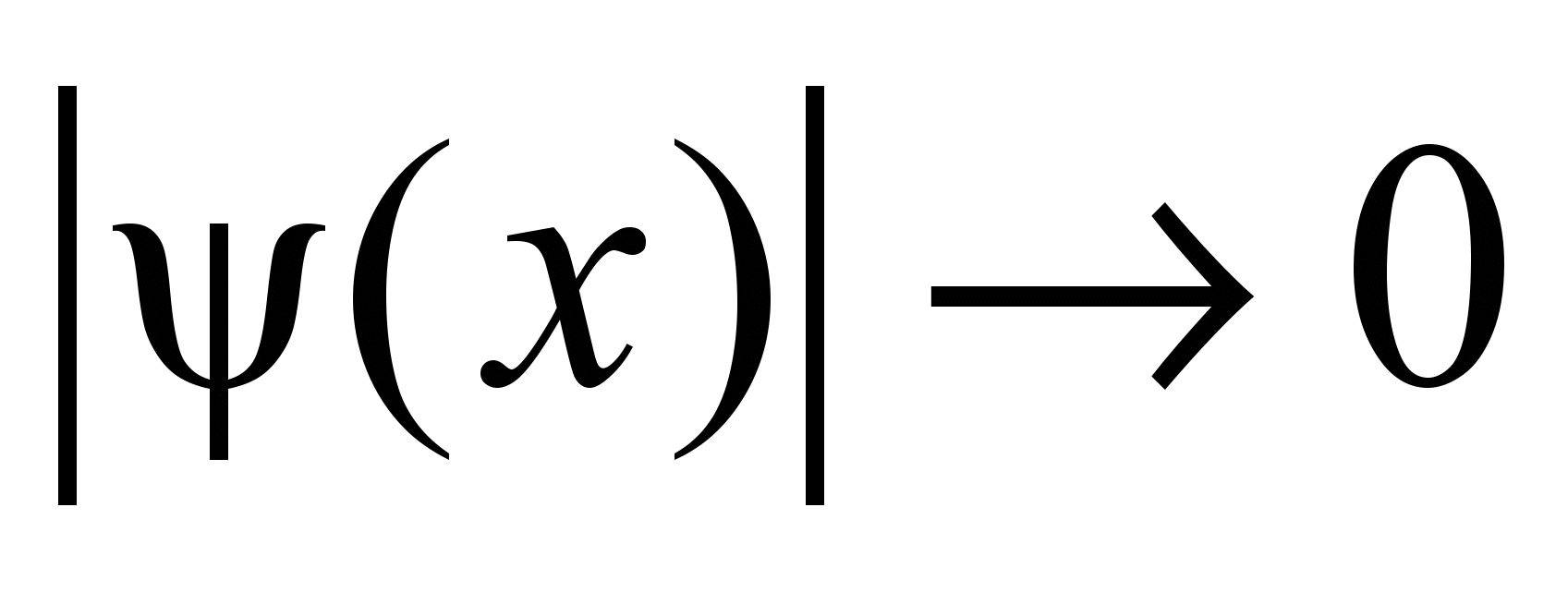и , при .

Рассмотрим пример таких функций - систему Хаара. В общем виде она записывается так:





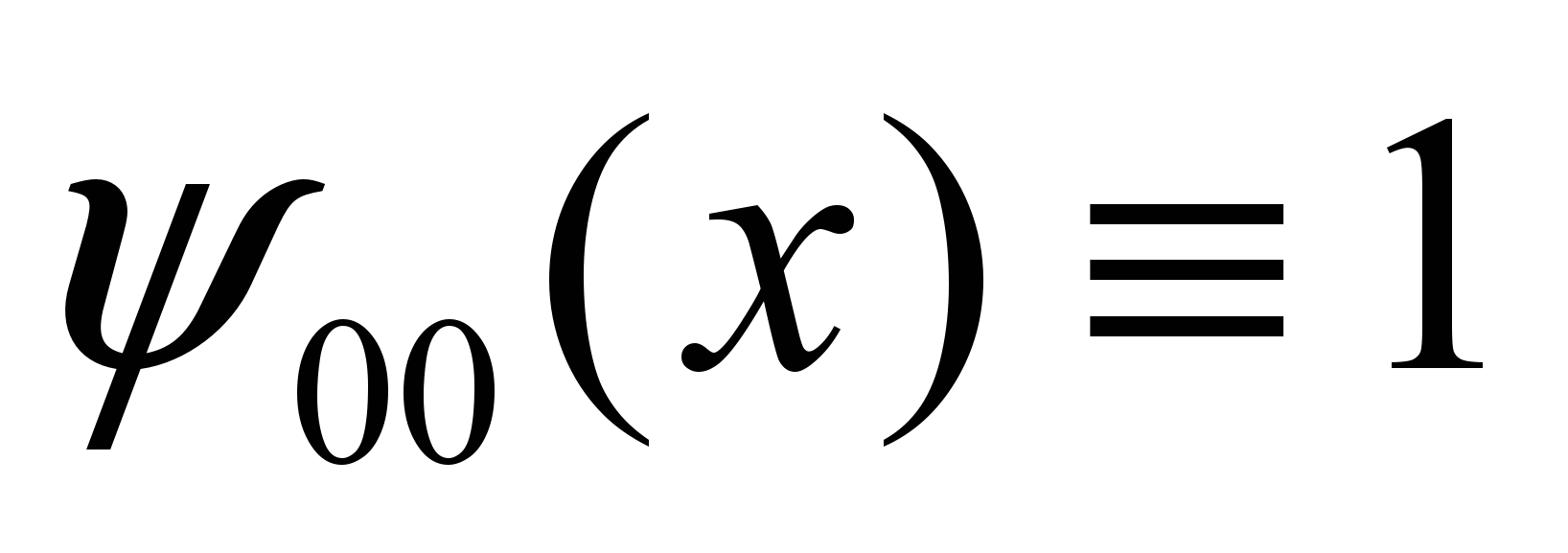
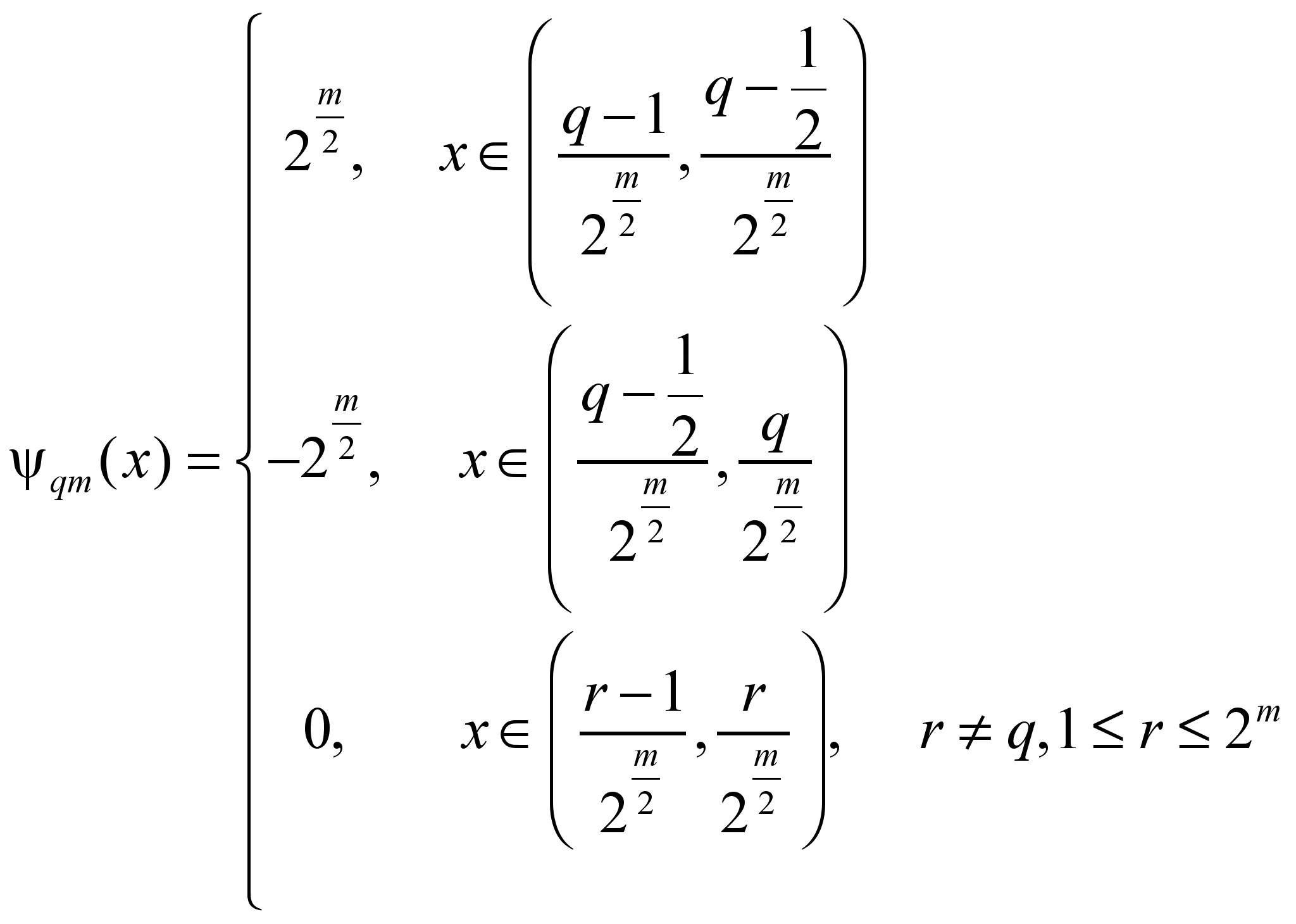
- общий вид обратного



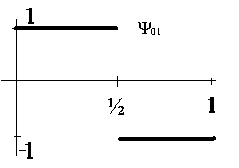
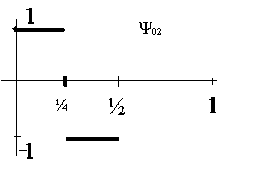
Рисунок 6. 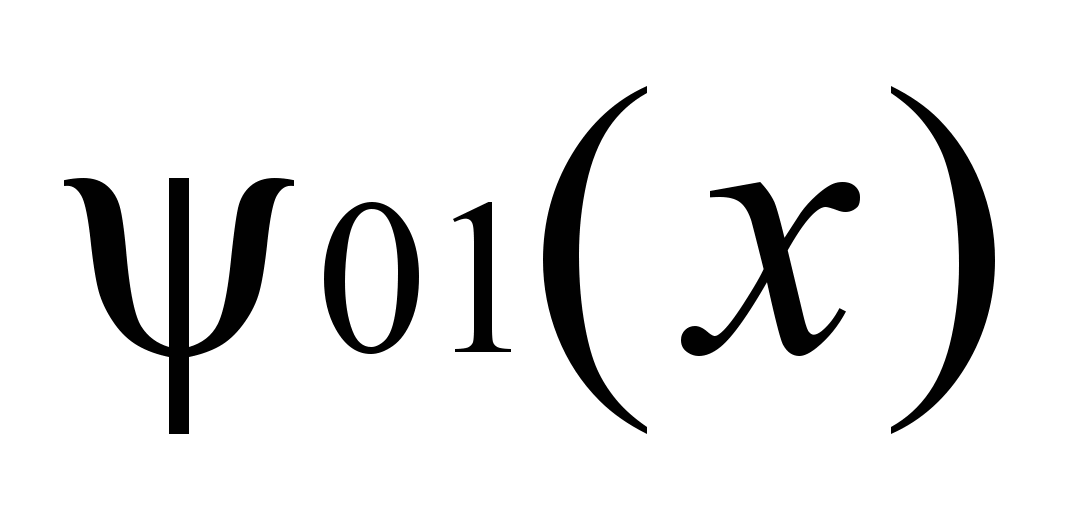Рисунок 7.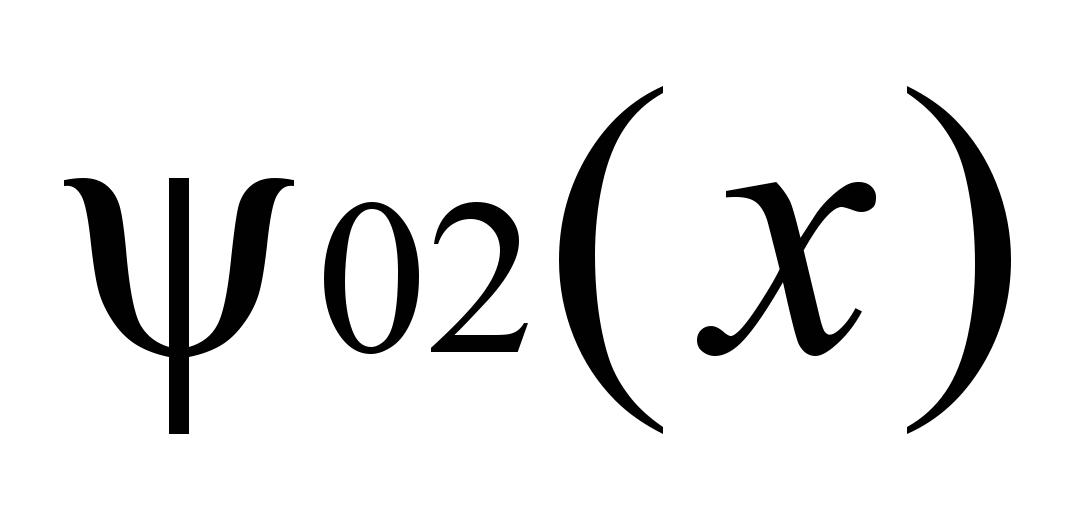

Если преобразование применяется к строке то так (здесь рассматриваем функцию 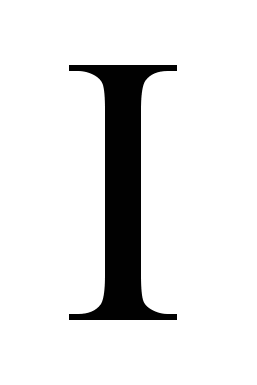, которая определена на отрезке от 0 до 1, который разбит на 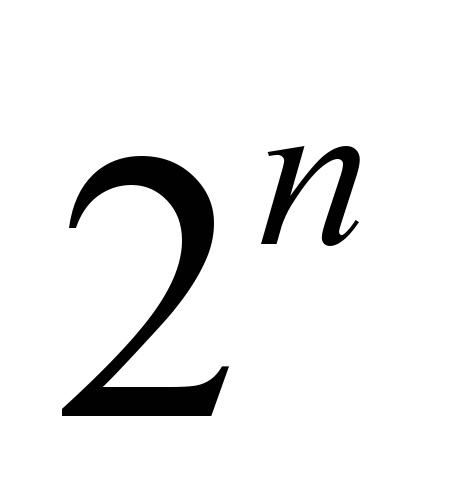частей, см. Рисунок 8. Строка изображения):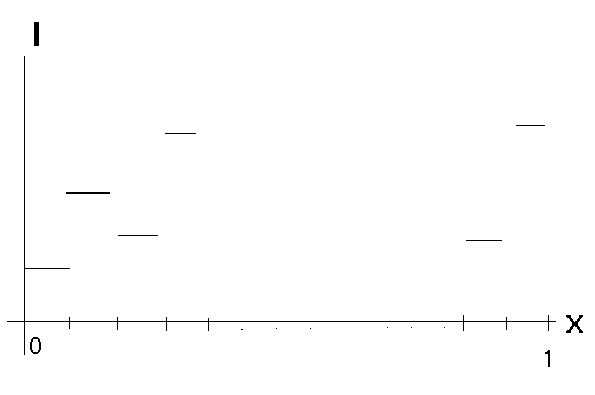



Рисунок 8. Строка изображения



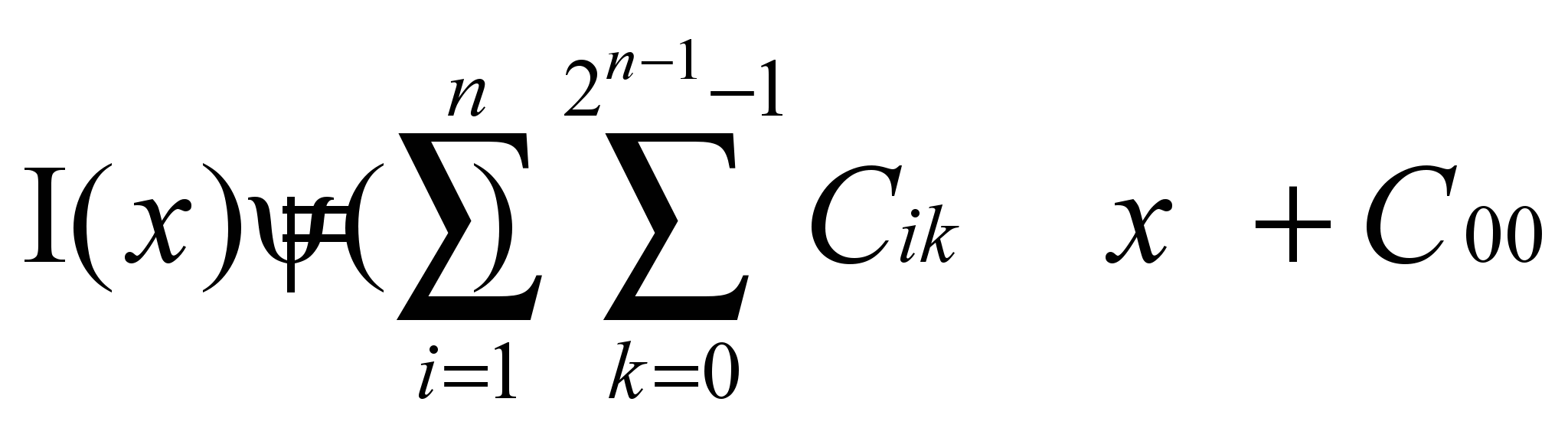
Получается, что мы берём на каждом шаге некоторое среднее значение функции в точке.

2.4S – преобразование.

Рассмотрим строчку изображения 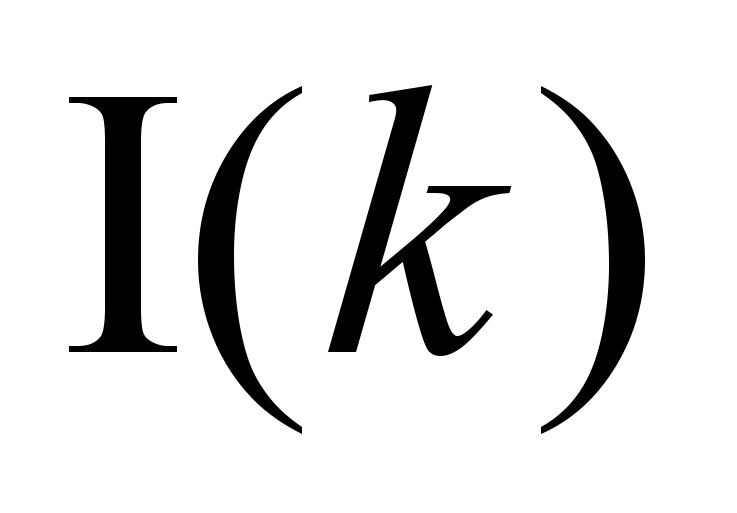и применим к ней преобразование по таким формулам:

,

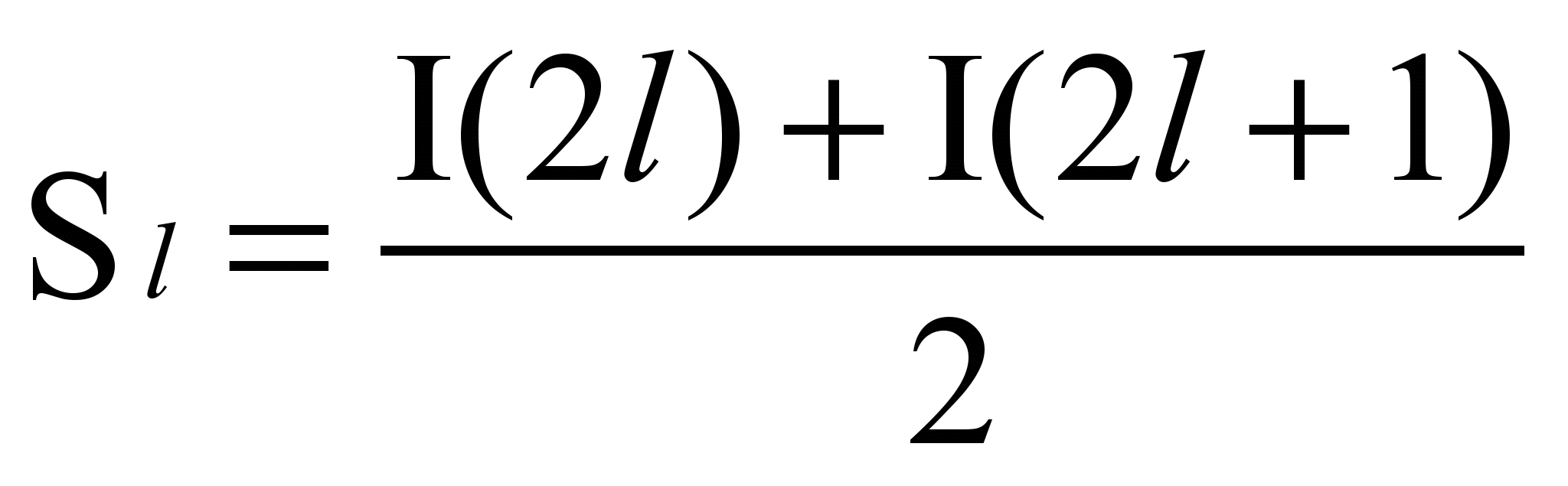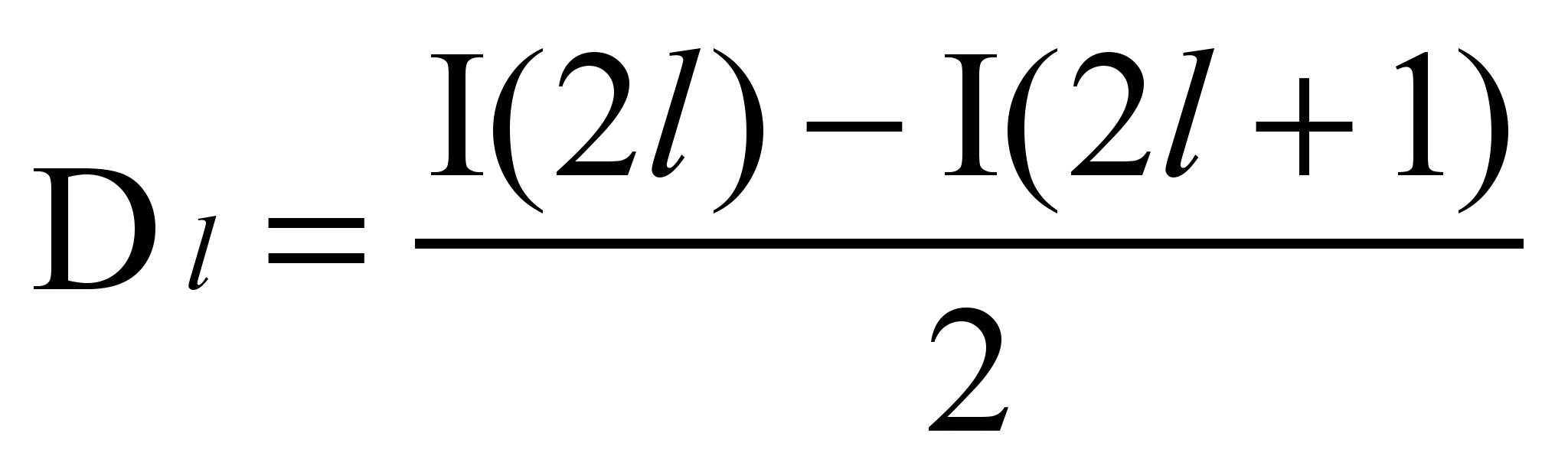
Т.к. делить на два плохо из-за проблем с точностью и скоростью, то обычно применяют другие формулы, а именно:

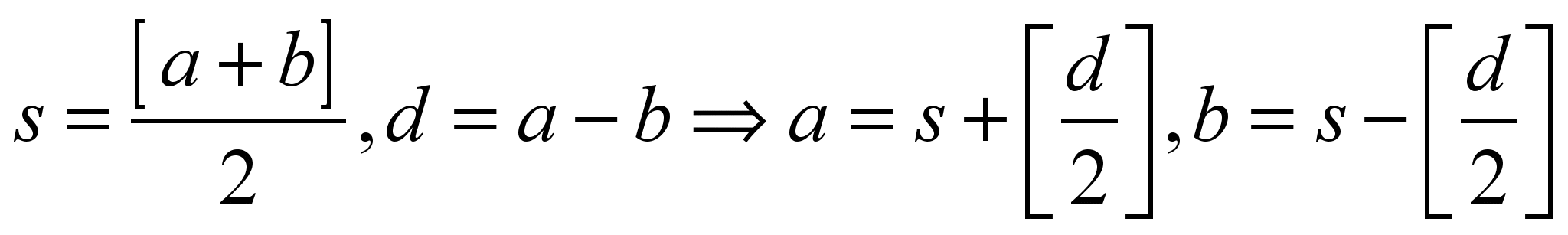, [ ] - означает взятие целой части.

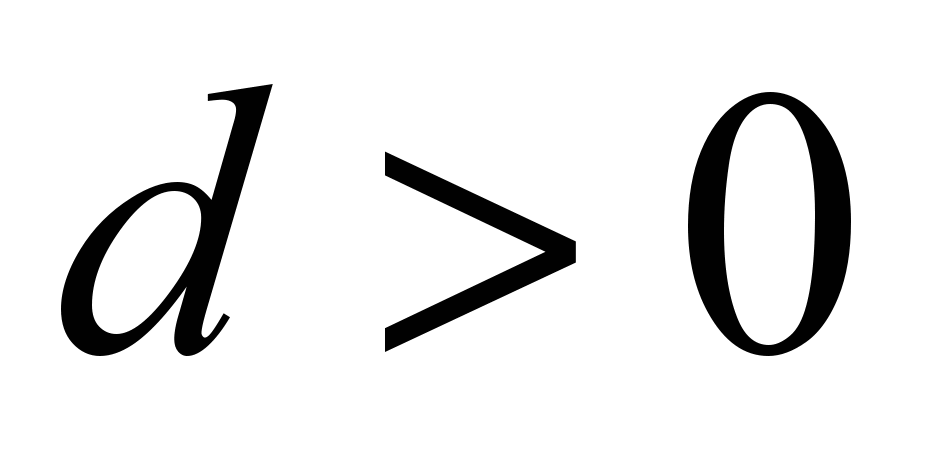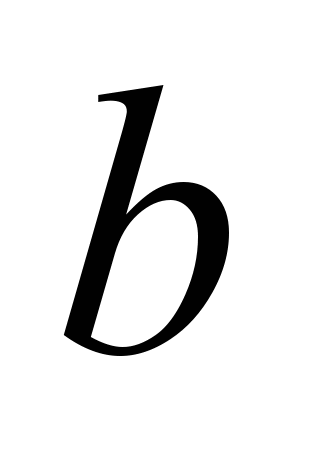если нечётное, то если прибавляем к 1, иначе (если меньше) прибавляем к 1.

В силу того, что обычно соседние пиксели имеют одинаковые значения цвета(например), то разность будет близка к нулю. Такое преобразование можно применить несколько раз. Обычно такое преобразование применяется к некоторой квадратной матрице (нашему изображению) несколько раз. Далее полученные коэффициенты сжимают без потерь методами Хаффмана, арифметическим или SPIHT(Set Partitioning in Hierarchical Trees).



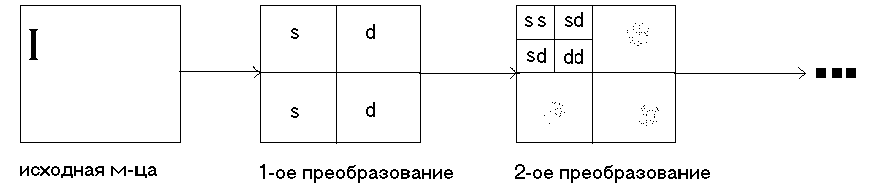
Рисунок 9. S - преобразование.

Метод описанный выше чаще всего используется для сжатия последовательностей изображений, например, в форматах серии MPEG и DivX.

3.Фрактальное сжатие.

Фрактальное сжатие основано на том, что мы представляем изображение в более компактной форме - с помощью коэффициентов системы итерируемых функций ( Iterated Function System(IFS)) Фактически, фрактальная компрессия - это поиск самоподобных областей в изображении и определение для них параметров аффинных преобразований. Получается, что даже для небольших изображений мы получим огромное число перебираемых вариантов. Соответственно современные алгоритмы направлены на уменьшение времени архивации изображения без ухудшения качества изображения. Декомпрессия заключается в необходимости проведения нескольких итераций аффинных преобразований, коэффициенты которых получаем при компрессии. Соответствующий математический аппарат гарантирует нам сходимость изображений, получаемых в ходе итераций, к исходному. Обычно достаточно 16 итераций.

Литература