Московского Государственного Университета им. М. В. Ломоносова. Данная лекция
| Вид материала | Лекция |
- Московский государственный университет им. М. В. Ломоносова московский государственный, 2110.62kb.
- Московского Государственного Лингвистического Университета и Центра международного, 3885.39kb.
- М. В. Ломоносова I. Общие положения Настоящий Регламент, 146.57kb.
- Клименко Алексей Владимирович Образование 2001-2006: Механико-математический факультет, 41.65kb.
- Гаранина Наталья Сергеевна, доцент кафедры стилистики русского языка факультета журналистики, 230.2kb.
- России москва 2007 Общеуниверситетская кафедра истории Московского гуманитарного университета, 1041.61kb.
- Пороховский Анатолий Александрович (д э. н., профессор, заведующий кафедрой политической, 77.75kb.
- Рихтер Андрей Георгиевич, кандидат филологических наук, доцент факультета журналистики, 144.52kb.
- Московский государственный университет им. М. В. Ломоносова, 690.3kb.
- Программа-минимум кандидатского экзамена по специальности 01. 04. 03 «Радиофизика», 172.9kb.
| Алгоритмические основы машинной графики | Лекция № 12 |
Представление объектов в 3D пространстве
Курс лекций «Алгоритмические основы машинной графики» читается в качестве специального курса на Механико-математическом факультете Московского Государственного Университета им. М.В. Ломоносова.
| Данная лекция может содержать ошибки (как логические, так и грамматические). Авторы будут признательны за любые сообщения об ошибках, неточностях, а также за любые комментарии и дополнения, присланные по адресу Denis@fit.com.ru (Денису Иванову). |
Содержание
1. Общие соображения о представлении трехмерных объектов 2
1.1 Введение 2
1.2 Основные типы представлений объектов в 3D пространстве 2
2. Поверхностное представление (Boundary representation, B-rep) 3
2.1 Неявная функция (implicit function) 3
2.2 Параметрическое задание, сплайны, NURBS 4
2.3 Полигональные поверхности 5
2.4 Конструктивная геометрия тел (Constructive Solid Geometry, CSG) 7
3. Объемное представление (Volume representation) 7
3.1 3D растр 8
3.2 Восьмеричное дерево 8
3.3 Двоичное дерево 9
4. Синтез изображений по изображениям (Image-based rendering, immersive imaging) 9
4.1 Общая идея 9
4.2 Lumigraph 10
4.3 Concentric mosaic 11
Литература 12
1.Общие соображения о представлении трехмерных объектов
1.1Введение
Итак, мы хотим научиться работать с трехмерными объектами, наша цель – обработка (в частности, визуализация) 3D объектов и сцен при помощи ЭВМ. Для этого необходимо иметь модели соответствующих объектов в форме, пригодной для такой обработки.
Теоретически нам может потребоваться:
- Свойства тела, связанные с пространством (его положение относительно других тел, геометрическая форма, размер тела и т.д.)
- Информация о материале тела (цвет, текстура, отражательная способность, прозрачность и т.д.)
- Информация, характеризующая взаимодействие объектов (плотность, возможность деформироваться, масса и т.д.)
Этот набор данных может меняться в зависимости от стоящих перед нами задач и конкретных объектов, которые мы хотим представить.
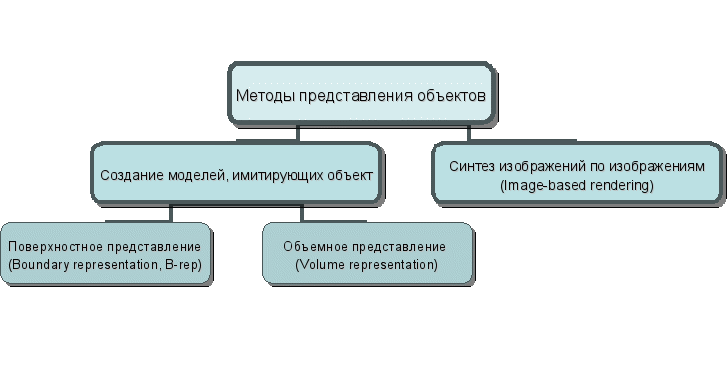
1.2Основные типы представлений объектов в 3D пространстве
Существует две крупные группы подходов для решения такой задачи. В соответствии с первыми, мы создаем отдельную модель, имитирующую наш трехмерный объект, и затем отображаем ее на экран, а в соответствии со вторыми мы синтезируем необходимое нам изображение трехмерных объектов по уже существующим изображениям. Методы первой группы, в свою очередь, делятся на две подгруппы: поверхностное представление (хранится только граница объекта) и объемное представление (хранится информации обо всех точках объекта). Однако, стоит отметить, что метод синтеза изображений по изображениям стоит несколько особняком, так как не позволяет осуществлять ни каких действий, кроме визуализации объектов.
2.Поверхностное представление (Boundary representation, B-rep)
В поверхностном представлении объект создается при помощи набора тонких поверхностей, составляющих его границу. Как правило, поверхностное представление используется в тех областях, где нет необходимости обрабатывать каким-либо образом внутренность тела: дизайнерские проекты, моделирование обводов какого-либо изделия, создание объектов с нестандартными элементами (например, скругление с изменяемым радиусом, винтообразная улитка) и т. д.
Существует несколько основных способов задания границы тела.
2.1Неявная функция (implicit function)
Задание 3D объекта при помощи неявной функции состоит в том, что мы указываем некую функцию
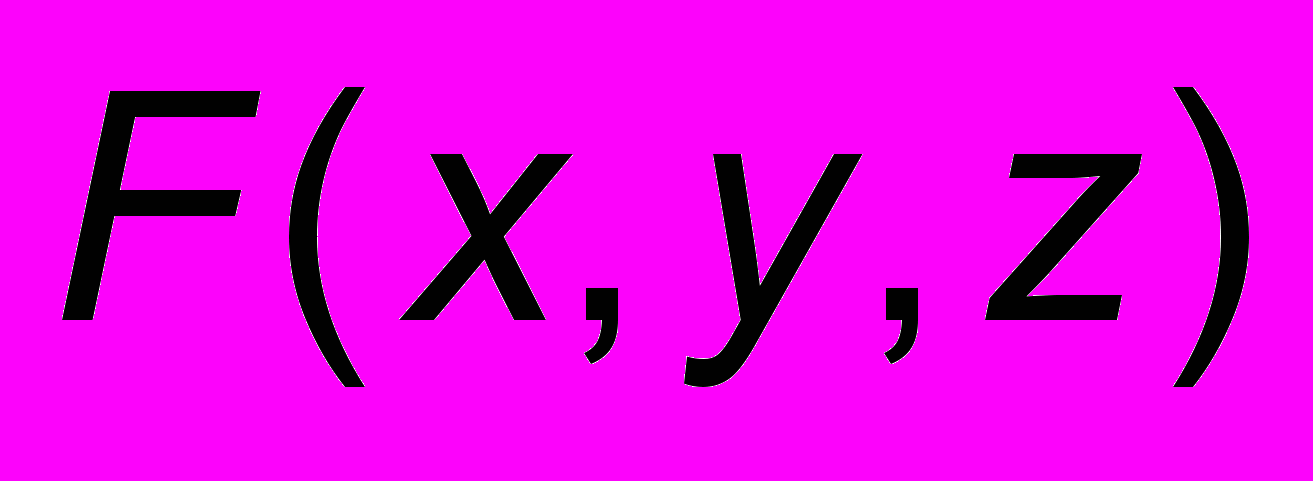 , нулями которой будут точки
, нулями которой будут точки 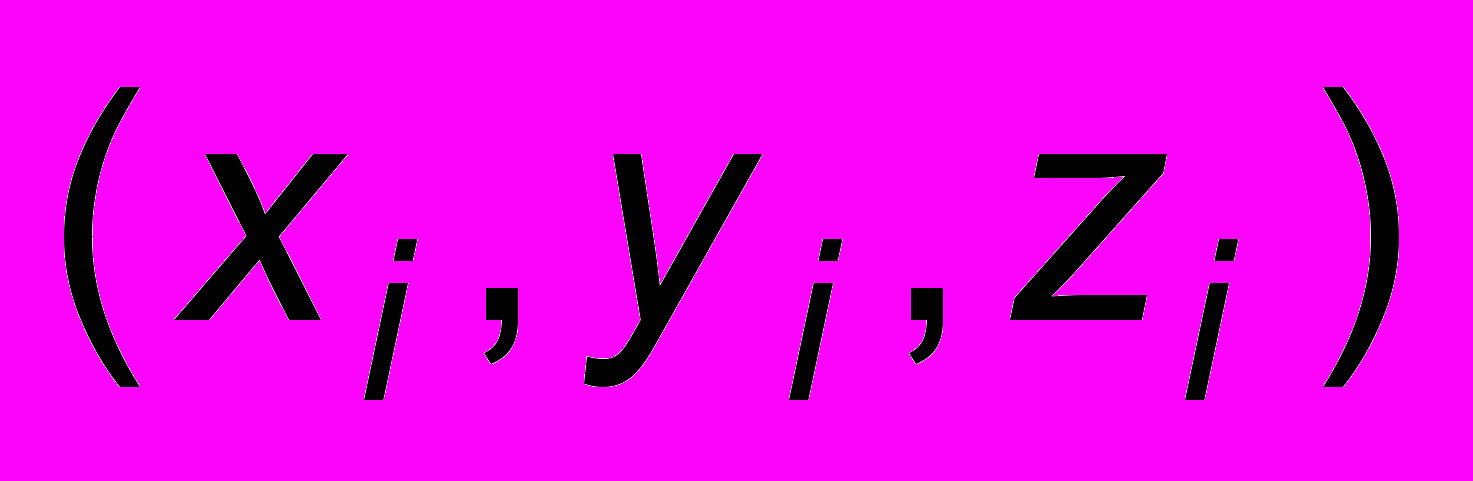 , образующие нашу поверхность, либо дающие ее приближение. Так, например, неявная функция для сферы радиуса
, образующие нашу поверхность, либо дающие ее приближение. Так, например, неявная функция для сферы радиуса 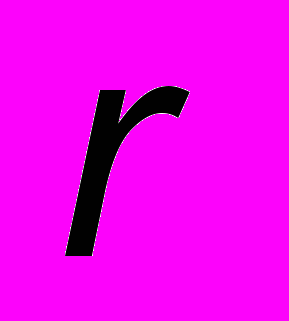 (см. Рис. 1), с центром в точке
(см. Рис. 1), с центром в точке 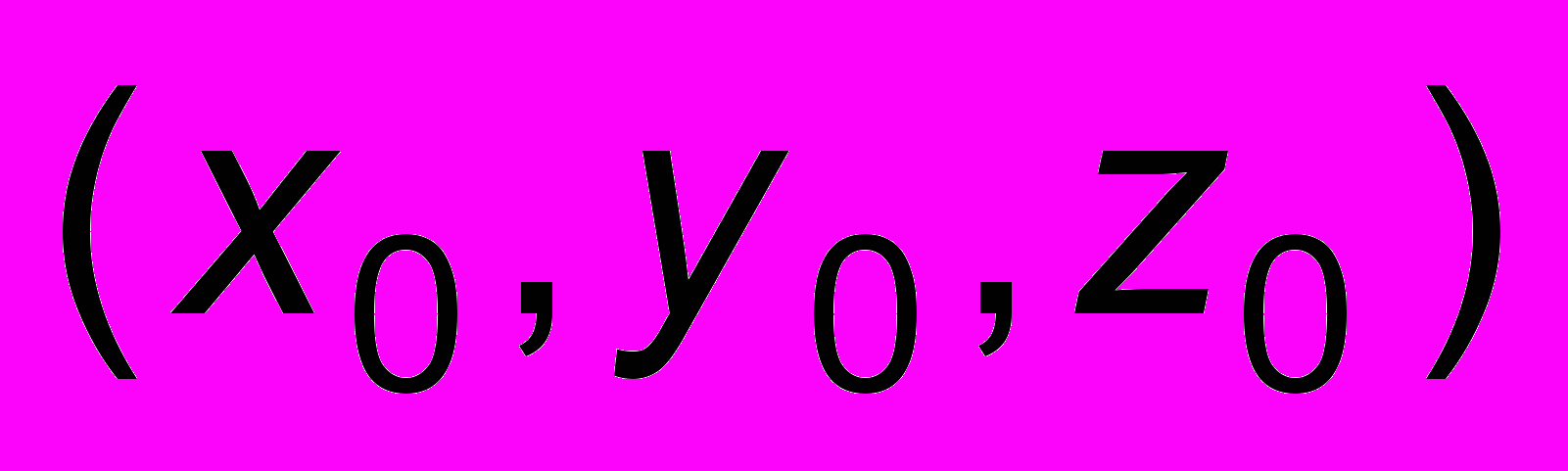 имеет вид:
имеет вид:

Рис. 1. Сфера.
2.2Параметрическое задание, сплайны, NURBS
При параметрическом задании координаты точек поверхности рассматриваются как некие функции от двух параметров, пробегающих некоторый набор значений.

Так, например, параметризация той же сферы (см. Рис. 1) относительно двух углов φ (долгота) и θ (широта) будет иметь вид:

Помимо этого используются различного рода особые параметрические поверхности, например, поверхности Безье, B-сплайны, в частности, NURBS ("Non-Uniform Rational B-Spline", неоднородный рациональный B-сплайн).
Если говорить кратко, то поверхность Безье строится по некоторой топологически прямоугольной сетке в соответствии со следующей формулой (подробнее см. []):
 ,
,где
 и
и 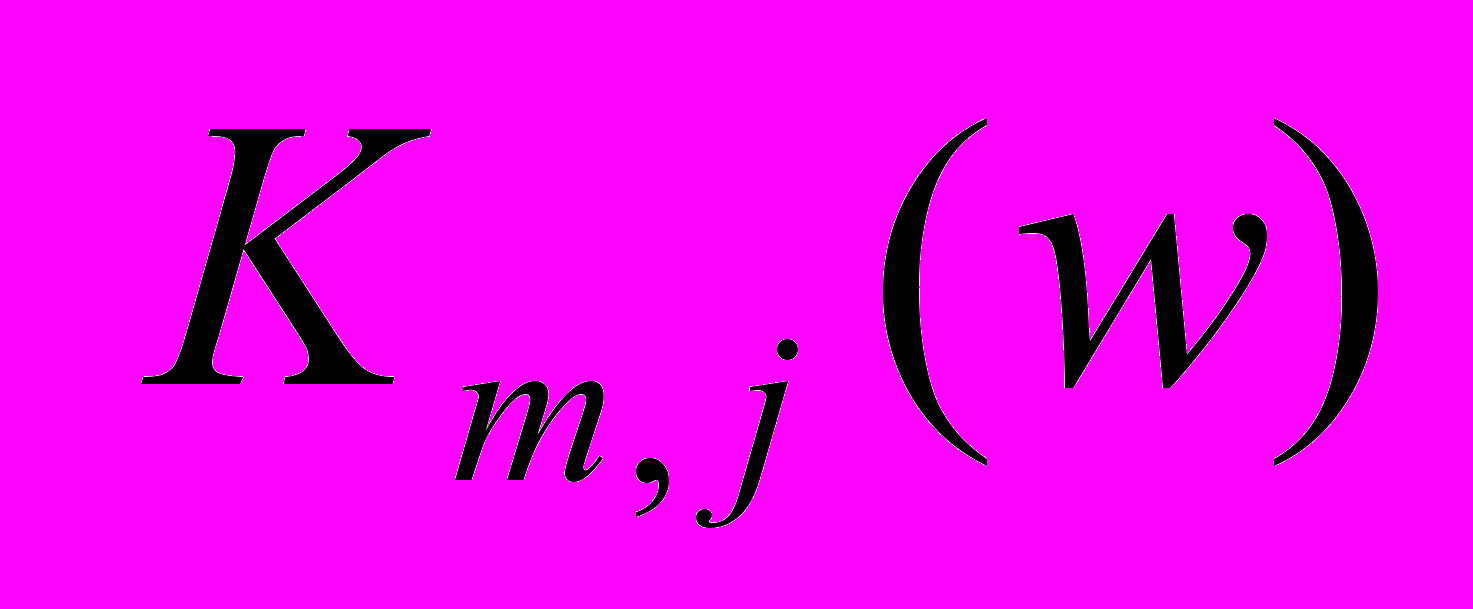 - базисные функции Берштейна в параметрических направлениях
- базисные функции Берштейна в параметрических направлениях  и
и  :
: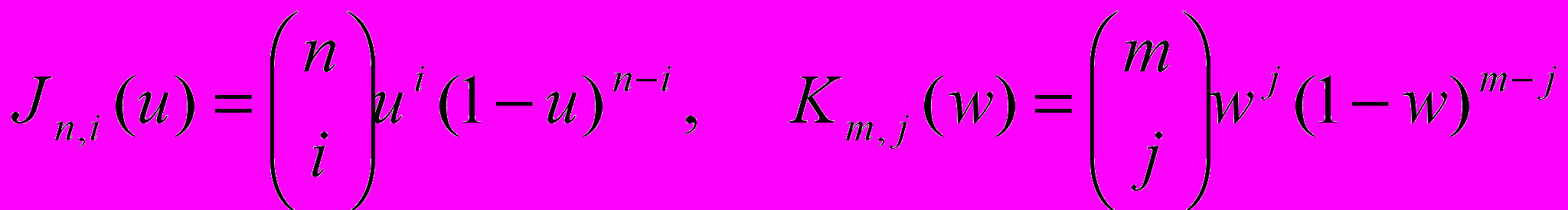
Элементы
 - вершины задающей полигональной сетки. Каждая из граничных кривых поверхности Безье является кривой Безье.
- вершины задающей полигональной сетки. Каждая из граничных кривых поверхности Безье является кривой Безье.B-сплайны строятся в соответствии со следующими формулами:
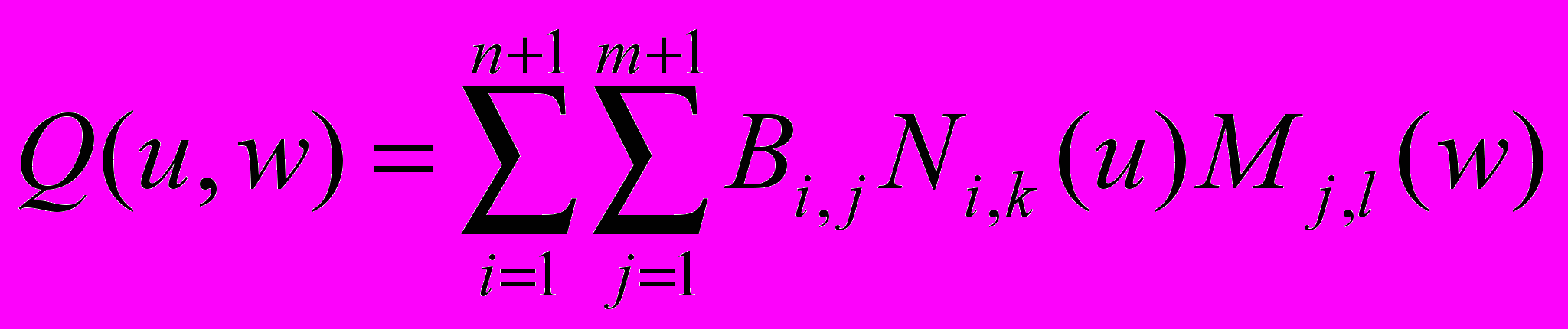 ,
,где
 и
и  - базисные функции B-сплайна в бипараметрических направлениях:
- базисные функции B-сплайна в бипараметрических направлениях: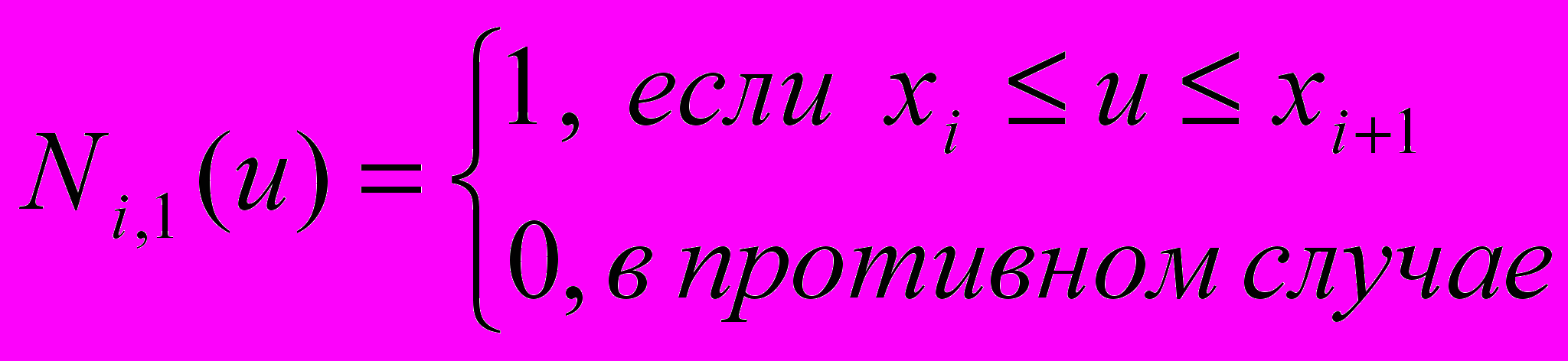

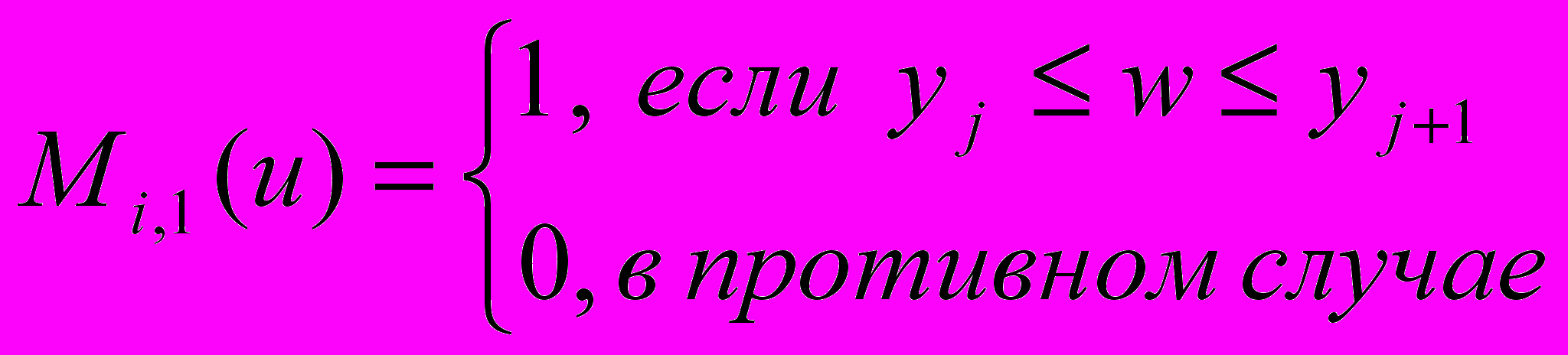

Элементы
 - вершины задающей полигональной сетки,
- вершины задающей полигональной сетки,Эти параметрические поверхности очень широко используются в различных CAD - системах (в России используется термин САПР - системы автоматического проектирования). Так, при помощи них моделируются и рассчитываются обводы автомобилей, формы деталей и т.п.
2.3Полигональные поверхности
При использовании данного метода поверхность (surface) представляется в виде набора некоторых многоугольников (face) в пространстве (см. Рис. 2).

Рис. 2. Триангуляция поверхности.
Часто в качестве многоугольников используются треугольники, в этом случае само разбиение поверхности (приближенное представление треугольниками) называется триангуляцией поверхности. Топология полученной при этом сетки описывается следующим образом:
- Объектами сетки являются вершины, ребра и треугольники (задаваемые тремя вершинами или тремя ребрами), а в более общем случае – face.
- У любой вершины есть свойство валентности (т.е. число многоугольников, содержащих ее).
- Для любого треугольника существует не более одного другого треугольника, инцидентного для первого по фиксированному ребру. Т.е., в частности, не может быть вот такой ситуации:
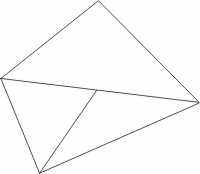
Рис. 3. Нарушение условия об инцидентности.
При таком способе задания мы можем, например, организовать обход в некотором направлении по треугольникам, содержащим фиксированную вершину, просто переходя каждый раз к треугольнику, инцидентному по ребру для предыдущего.
Разумеется, при триангуляции качество получаемой поверхности тем лучше, чем больше треугольников мы будем для этого использовать (см. Рис. 4). Подробнее о триангуляции поверхности см. [].
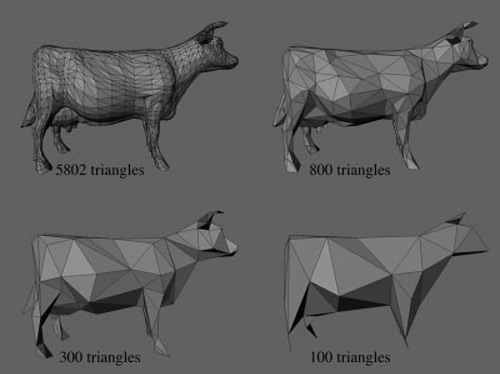
Рис. 4. Зависимость качества изображения от числа треугольников.
2.4Конструктивная геометрия тел (Constructive Solid Geometry, CSG)
Метод конструктивной геометрии тел заключается в том, что мы получаем нужную нам поверхность как результат применения последовательности различных множественных операций (объединения, пересечения, разности и т.д.) к некоторым примитивам (т.е. минимальным объектами для построения). В качестве примитивов могу выступать параллелепипеды, шары, конусы, пирамиды и т.д. Сама поверхность задается при помощи дерева построения (см. Рис. 5).

Рис. 5. Дерево построения.
3.Объемное представление (Volume representation)
Методы объемного представления тел сохраняют информацию о любых, не обязательно видимых, частях тела. Все они, как правило, требуют гораздо больше места для хранения объекта, но как уже было сказано, дают дополнительную информацию об объектах, которая может нам потребоваться. Также эти методы необходимы, когда тела не имеют как таковой границы (например, туман, взвесь в жидкости и т.д.)
3.13D растр
3D растр представляет собой набор кубиков (см. Рис. 6) (voxel’ов, от «volume element») в пространстве. Каждый воксел может иметь некоторое числовое значение, являющееся атрибутом соответствующей точки в пространстве.

Рис. 6. 3D растр.
Данный метод, несмотря на свою простоту, имеет серьезный недостаток: для хранения даже небольшого объекта в приемлемом качестве требуется очень много места. Например, если мы храним кубик с ребром 1024 и выделяем по одному байту (8 бит) на атрибут воксела, то нам потребуется
 Учитывая тот факт, что хранить объект нам, скорее всего, надо будет в оперативной памяти компьютера, применение этого метода в чистом виде становится крайне затруднительным.
Учитывая тот факт, что хранить объект нам, скорее всего, надо будет в оперативной памяти компьютера, применение этого метода в чистом виде становится крайне затруднительным.3.2Восьмеричное дерево
В большинстве случаев в 3D растре есть некоторые области вокселов, имеющих одинаковые атрибуты. Этим можно воспользоваться для того, чтобы сократить объем занимаемого объектом места. Будем хранить растр в виде дерева (см. Рис. 7), вершины которого имеют степень 0 или 8. Сначала проверим, не лежат ли во всех вокселах в растре одинаковые значения, если да, то нам достаточно будет сохранить это значение (p) и обозначить, что дальше дробить кубик не надо, например, положим в вершину это значение p и 0 (обозначение терминальности вершины). Если у нас есть вокселы с разными значениями, то продолжим процесс. А именно, разделим растр на октанты, соответствующие координатным плоскостям. Для каждого октанта снова проверим, не содержит ли он одинаковые вокселы. И т.д. Получим дерево, в вершинах которого лежат 1 (что обозначает, что соответствующий октант не однороден) или 0 и некоторые числа pi, соответствующие значениям всех вокселов в данном октанте.
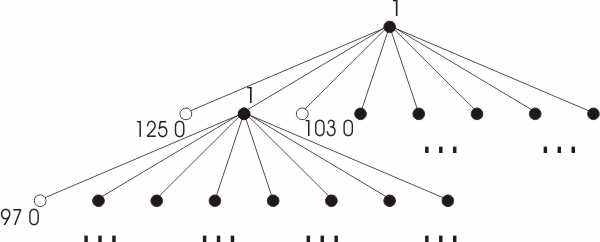
Рис. 7. Восьмеричное дерево 3D растра.
Таким образом, если растр состоит из вокселов, имеющих один и тот же атрибут, то мы сэкономим
 ; если же все воксели различны, то лишнее место, которое мы потратим (на 1 и 0), составит
; если же все воксели различны, то лишнее место, которое мы потратим (на 1 и 0), составит  . Но последняя ситуация встречается крайне редко, поэтому использование восьмеричных деревьев в большинстве случаев позволяет значительно сократить объем памяти для хранения объекта.
. Но последняя ситуация встречается крайне редко, поэтому использование восьмеричных деревьев в большинстве случаев позволяет значительно сократить объем памяти для хранения объекта.3.3Двоичное дерево
Идея построения двоичного дерева полностью аналогична построению восьмеричного дерева. Но в данном случае растр последовательно делится не на октанты, а на половинки: сначала параллельно плоскости OXY, потом OYZ и т.д. Соответственно, аналогично строится дерево, вершины которого имеют степень 0 или 2. Более подробно см. []
4.Синтез изображений по изображениям (Image-based rendering, immersive imaging)
Идея использования синтеза изображений по изображениям состоит в том, что мы генерируем изображение трехмерного объекта на мониторе по набору существующих изображений (например, фотографий). При этом нам не приходится решать, иногда весьма трудоемкую, задачу создания моделей объектов.
4.1Общая идея
Итак, мы хотим генерировать изображение трехмерной сцены по набору изображений. На эту задачу можно посмотреть как на нахождение значений некоторой функции
 (т.е. атрибутов пикселей) от 5 параметров -
(т.е. атрибутов пикселей) от 5 параметров - 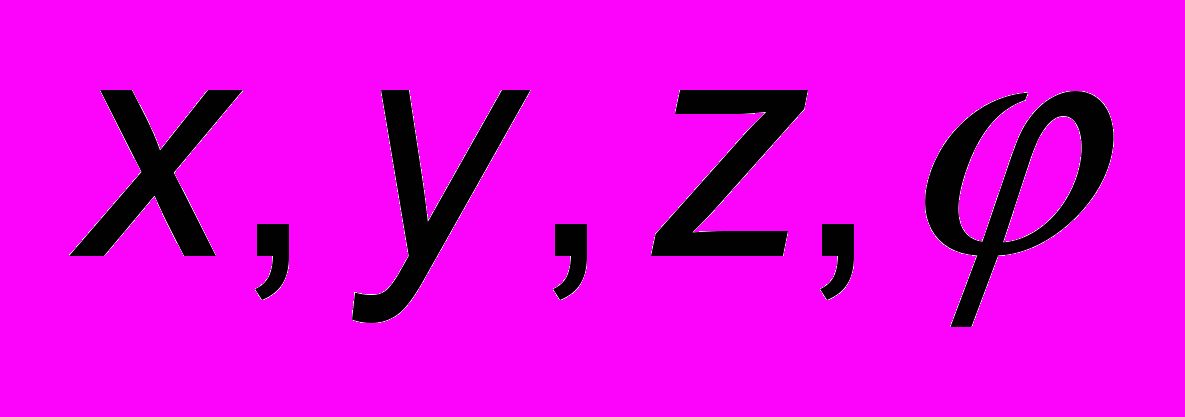 и
и  , где
, где - координаты наблюдателя, а
- координаты наблюдателя, а  и
и - углы, задающие направление луча зрения (см. Рис. 8).
- углы, задающие направление луча зрения (см. Рис. 8).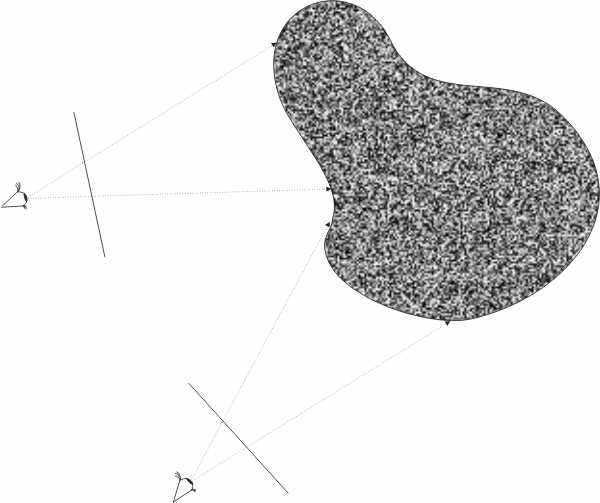
Рис. 8. Определение атрибутов пикселей в зависимости от положения наблюдателя.
Размерность массива данных, которые нам потребуются при таком подходе, составит, таким образом, 5D.
4.2Lumigraph
В том случае, если мы знаем, что наблюдатель не может находиться за некоторой линией, можно сократить необходимый нам объем данных. А именно: сфотографировать объект вдоль этой линии (на всех уровнях по вертикали), а затем в качестве значений пикселя, соответствующего некоторому лучу зрения, будем брать значение, соответствующее ближайшему лучу камеры (см. Рис. 9).
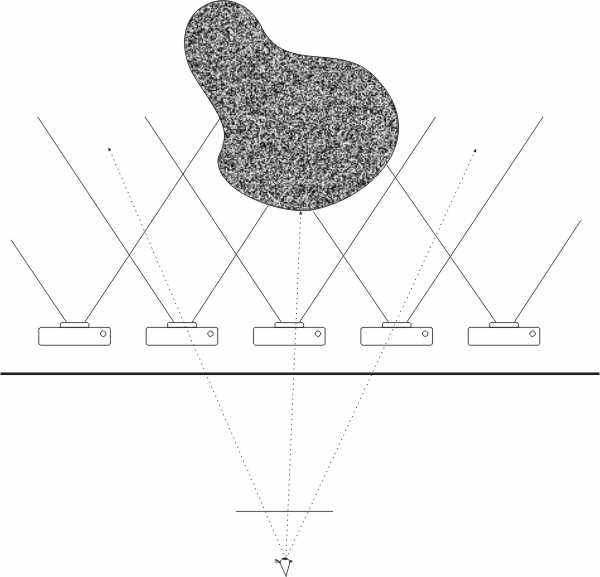
Рис. 9. Lumigraph.
Размерность массива данных в этом случае будет составлять 4D (2D на положение камеры и 2D на изображение от каждой камеры).
4.3Concentric mosaic
Данный метод состоит в следующем: пусть нам необходимо получить вид некоторой комнаты изнутри. Сделаем в центре комнаты набор вертикальных линейных (т.е. шириной в 1 пиксель) снимков во всех направлениях. Затем сделаем аналогичные снимки из точек концентрических окружностей по касательным направлениям (см. Рис. 10) (как по часовой стрелке, так и против; на рисунке показано только одно направление).

Рис. 10. Concentric mosaic.
В качестве значений пикселя, соответствующего некоторому лучу зрения, будем брать значение, соответствующее ближайшему касательному лучу. В этом случае размерность массива данных составит 3D (по 1D на радиус окружности, угол и само изображение).
Литература
- Д. Роджерс, Дж. Адамс. Математические основы машинной графики. М, изд-во «МИР», 2001.
- Steve Seitz, Paul Heckbert, Andy Witkin, Joel Welling, Jessica Hodgins. Implicit Surfaces and Polygons. ссылка скрыта
- Алексей Игнатенко. Геометрическое моделирование сплошных тел. ссылка скрыта
| © Группа Компьютерной Графики, 2002 Лаборатория Вычислительных Методов, Мех-мат МГУ | Стр. из |
