А. М. Мубараков

Вид материала

Содержание

4.6.4 Фотохимическое действие света. Основные фотохимические законы. Основы фотографии
Ф. При прохождении через фольгу α -частицы отклонялись от первоначального направления движения на различные углы θ. Микроскоп М

Подобный материал:

1 ... 35 36 37 38 39 40 41 42 ... 48

4.6.4 Фотохимическое действие света. Основные фотохимические законы. Основы фотографии

Под действием света могут происходить самые разнообразные химические реакции. В основе химического (а также биохимического) действия света лежит явление взаимодействия света с веществом. В зависимости от конкретного объекта поглощение света может вызвать то или иное действие. В основе так называемого первого закона фотохимии лежат как раз эти положения. Исходя из них, первый закон фотохимии, можно сформулировать так: фотохимическая реакция может быть вызвана только поглощенным молекулой светом. Если поглощения не произошло, то химическая реакция невозможна. Этот закон носит название закона эквивалентности.

Второй закон фотохимии связан с именем А. Эйнштейна (его иногда называют законом Эйнштейна). Согласно этому закону, поглощение света не обязательно заканчивается фотохимической реакцией, однако если это происходит, то для химического изменения каждой молекулы требуется только один фотон. Этот закон математически можно выразить формулой n = ηN, где N — число поглощенных фотонов, п — число молекул (атомов), претерпевших химическую реакцию, η - квантовый выход (эффективность) фотохимической реакции, величина различная в различных процессах.

Химические реакции, протекающие под влиянием света, носят название фотохимических реакций. Примером фотохимической реакции может служить разложение под влиянием света аммиака NH₃ на азот и водород или бромистого серебра AgBr — на серебро и бром. Под влиянием света протекают также реакции образования более сложных молекул, например молекул НС1 из молекул водорода и хлора. Эта последняя реакция протекает настолько бурно, что сопровождается взрывом. Существуют также фотохимические процессы, сводящиеся к полимеризации вещества, т. е. к образованию многоатомных молекул из атомов исходного вещества. Большую роль играют фотохимические реакции в биологии, например, разложение углекислоты под действием света в зеленых частях растений, что было впервые выяснено К. А. Тимирязевым.

Фотохимические процессы подчиняются следующему количественному закону: масса фотохимически прореагировавшего вещества пропорциональна количеству поглощенной световой энергии. Если обозначить через W мощность поглощенного света и через t — время освещения, то закон запишется в виде m=kWt, где k — коэффициент пропорциональности, зависящий от природы происходящей фотохимической реакции. Численно коэффициент k равен массе прореагировавшего вещества, приходящейся на единицу поглощенной световой энергии.

Фотохимический процесс может сопровождаться вторичными реакциями, вызванными химической активностью продуктов, возникающих в результате фотохимического превращения. Закон, сформулированный нашей последней формулой, относится лишь к первичному фотохимическому процессу.

Изучение первичных фотохимических процессов показало, что они протекают в соответствии с фотонной природой света: каждому поглощенному фотону hν соответствует превращение одной молекулы. Этот закон был впервые проверен на фотохимической реакции разложения бромистого водорода НВr под влиянием монохроматического света. Измерения показали, что на каждую порцию поглощенного света hν приходится разложение одной молекулы. Таким образом, реакция протекает согласно уравнению: 2HBr + 2hν = Н₂ + Br₂. Так как на превращение одной молекулы требуется некоторая минимальная работа А, то энергия фотона hν должна удовлетворять условию: hν ≥А, откуда вытекает существование длинноволновой границы фотохимического процесса: если частота света ν =<ν₀ = A/h то фотохимическая реакция не протекает. Для каждой данной фотохимической реакции v0 имеет свое значение. Большинство фотохимических реакций протекает под влиянием лишь ультрафиолетовых лучей. Последнее условие необходимо, чтобы фотохимическая реакция могла протекать, но оно еще не является достаточным: необходимо, чтобы свет данной частоты поглощался молекулой. Если вещество прозрачно для света данной частоты, то этот свет не может вызывать химического превращения.

Опыт, однако, показывает, что в некоторых случаях, возможно осуществить фотохимическую реакцию и в области частот v, для которых вещество прозрачно, если прибавить второе вещество («сенсибилизатор»), поглощающее свет. Такого рода фотохимические реакции называются сенсибилизированными.

На фотохимическом процессе основана фотография. Как известно, современный фотографический процесс ведется с помощью светочувствительной эмульсии, нанесенной тонким слоем на стекло (фотопластинка) или целлулоидовую пленку (фотопленка). Эмульсия состоит из микроскопических кристаллов бромистого серебра, взвешенных в желатине. Первичный фотохимический процесс сводится к разложению под влиянием света бромистого серебра и выделению металлического серебра в виде отдельных очень мелких частичек. При длительном освещении число этих частичек может оказаться настолько значительным, что эмульсия заметно потемнеет. При обычной же длительности освещения число выделившихся частичек серебра невелико и они не дают заметного поглощения света. Поэтому под влиянием первичного фотохимического действия возникает лишь так называемое скрытое изображение. Фотопластинка, на которой в результате действия света возникло скрытое изображение, подвергается вторичной химической обработке - проявлению. Под влиянием соответствующих химических реактивов (проявителя) вызывается восстановление металлического серебра, там. где имелись «затравки» из отдельных частиц серебра. В результате металлическое серебро выделяется преимущественно в тех местах, которые были подвергнуты действию света, и таким образом возникает негатив. Когда проявление закончено, остаток неразложенного бромистого серебра удаляется с помощью раствора гипосульфита (Na₂Sa0₃).

4.7 Развитие квантовых представлений об атоме

4.7.1 Опыты Резерфорда по рассеянию альфа-частиц. Планетарно-ядерная модель атома

В первой четверти 20-го века было установлено, что атом состоит из положительно заряженного ядра и окружающей его электронной оболочки. Линейные размеры ядра порядка 10^-13— 10^-12 см. Размеры самого атома, определяемые электронной оболочкой, примерно в 10⁵раз больше. Однако почти вся масса атома (не менее 99,95 %) сосредоточена в ядре. Это связано с тем, что ядро состоит из «тяжелых» протонов и нейтронов, а электронная оболочка — из одних только «легких» электронов (m_p = 1836,15m_e, m_n = 1838,68m_e). Число электронов в оболочке нейтрального атома равно заряду ядра, если за единицу принять элементарный заряд (т. е. заряд электрона по абсолютной величине). Но электронная оболочка может терять или приобретать электроны. Тогда атом становится электрически заряженным, т. е. превращается в ион.

Химические свойства атома определяются электронной оболочкой, точнее, её наружными электронами. Они сравнительно слабо связаны с атомом и более подвержены любым воздействиям. Напротив, протоны и нейтроны прочно связаны внутри ядра. Чтобы воздействовать на ядро, нужны силы, в миллионы раз превосходящие те силы, которые достаточны для отрыва наружных электронов атома. Экспериментальное доказательство этой модели атома было дано Резерфордом в 1911 г. Под руководством Резерфорда опыт осуществлялся следующим образом (рисунок - 4.66).

Выделяемый отверстием узкий пучок α-частиц, испускаемых радиоактивным веществом Р, падал на тонкую металлическую фольгу Ф. При прохождении через фольгу α -частицы отклонялись от первоначального направления движения на различные углы θ. Микроскоп М и экран Э можно было вращать вокруг оси, проходящей через центр рассеивающей фольги, и устанавливать таким образом под любым углом θ. Весь прибор помещался в откачанный кожух, чтобы устранить рассеяние α-частиц за счет столкновений с молекулами воздуха. При ударе о флуоресцирующий экран из сернистого цинка α-частица оставляла на нем вспышку (сцинтилляцию). И экспериментаторы производили подсчет таких сцинтилляций. В эксперименте подавляющее число α-частиц рассеивалось на небольшие углы порядка 1—3°. Однако наблюдались также отдельные α-частицы, отклоняющиеся на очень большие углы,

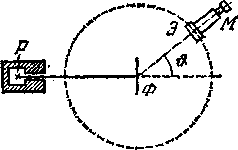Рисунок - 4.66

доходившие до 150°. Относительное число таких частиц было ничтожно мало. Например, при прохождении через платиновую фольгу пучка α-частиц от RaC из 8000 падающих частиц в среднем только одна частица отклонялась на угол, превышавший 90°. Но и этого было бы слишком много, если бы большие отклонения возникали в результате накопления множества случайных отклонений.

Резерфорд сделал вывод, что каждое большое отклонение появляется в результате единичного акта взаимодействия какого-то, практически точечного, силового центра с близко пролетающей положительно заряженной α-частицей. Таким силовым центром и является положительно заряженное ядро атома. Резерфорд предположил, что электроны в атоме движутся вокруг ядра по круговым и эллиптическим орбитам, как планеты округ Солнца, т.е. предложил планетарно-ядерную модель строения тома. Схема этой модели (на примере атома водорода) изображена на рисунке - 4.67. Электрон удерживается на орбите кулоновской силой F_K притяжения к ядру, которая обеспечивает центростремительное ускорение. Согласно такой планетарной (ядерной) модели, весь положительный заряд атома и почти вся его масса сосредоточены в атомном ядре. Вокруг ядра с большой скоростью движутся электроны, образуя электронную оболочку атома.

Поскольку α-частицы взаимодействуют с атомным ядром кулоновской силой, угол θ - рассеяния α-частиц зависит и от заряда ядро Z_e, и от расстояния р (взятого по перпендикуляру) от ядра до первоначальной траектории α-частицы (рисунок - 4.68). Это


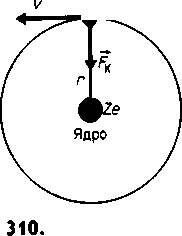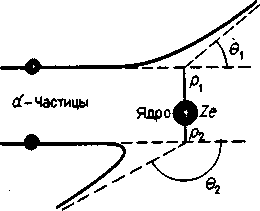Рисунок - 4.67	Рисунок - 4.68

расстояние Резерфорд назвал прицельным. Исходя из того, что прицельное расстояние может принимать любые значения, Резерфорд, используя методы математической статистики (теории вероятности), вывел формулу, описывающую распределение частиц по углу рассеяния θ (формула Резерфорда):

N_θ = N₀nd(Ze²/m_αv_α²)²1/ sin⁴(θ/2)

(4.78),

где N_θ — число α-частиц, рассеянных на угол θ в пределах единичного телесного угла; N₀ — число α-частиц, падающих на поверхность единичной площади, перпендикулярную первоначальному

направлению их движения; n — концентрация атомов вещества фольги; d — толщина фольги; m_а и v_a — масса и скорость частицы.

В 1913 г. сотрудники Резерфорда произвели проверку этой формулы путем подсчета сцинтилляций, наблюдавшихся под разными углами θ за одинаковые промежутки времени и доказали ее совпадаемость с теоретическими данными.

В основе теории периодичности свойств атомов элементов лежат два принципа:

1) принцип Паули, который гласит: в атоме (или в какой-либо другой квантовой системе) не может быть двух электронов, обладающих одинаковой совокупностью квантовых чисел. Иными словами, в одном и том же состоянии не могут находиться одновременно два электрона, они должны отличаться хотя бы по одному из четырех показателей, описывающих его состояние. Принцип Паули дает объяснение периодической повторяемости свойств атомов;

2) принцип минимума энергии: при данном числе электронов в атоме осуществляется состояние с минимальной энергией.

Принцип минимума энергии является естественным требованием с точки зрения устойчивости атома: если данное состояние не является состоянием минимальной энергии, то атом может под влиянием лишь внутренних причин перейти в состояние с меньшей энергией и в конце концов должно осуществиться состояние с минимальной энергией. Принцип Паули учитывает квантовые свойства возможных состояний атома.

Все количество электронов в атоме закономерно распределяется в соответствии с ядерно-планетарной моделью атомов по оболочкам, с учетом выделенных принципов. Схема заполнения строится по принципу, когда, каждый вновь присоединяющийся электрон связывается в состояния в пределах, допускающих принципом Паули значениями. Когда заполнение оболочки закончено, образуется устойчивая электронная конфигурация, соответствующая электронной конфигурации данного элемента. После этого начинает заполняться следующая оболочка, атома следующего элемента. Процесс происходит следующим образом.

Состояние электрона в кулоновском поле ядра характеризуется четырьмя квантовыми числами:

1) главным квантовым числом: n=1, 2, 3, ;

2) орбитальным квантовым числом: l = 0, 1, 2, n-1;

3) магнитным квантовым числом: m_l= -l, -l+1, l-1, l (всего 2l +1 значений);

4) спином: m_s =+½,-½.

Совокупность электронов, обладающих одним и тем же главным квантовым числом (n), образует оболочку атома (таблица - 4.2). Различные оболочки атома обозначаются большими буквами К, L, М, N, О и т. д. по схеме указанной в таблице- 4.2.

Таблица - 4.2 Схема распределения электронов по оболочкам атома

Главное квантовое число, n	1	2	3	4	5
Обозначение оболочки	К	L	М	N	О

Состояния орбитального движения электронов характеризуются буквами s, p, d, f и т. д. по схеме, указанной в таблице – 4.3.

Совокупность электронов с одним и тем же значением l образуют подоболочку.

Таблица – 4.3 Схема распределения электронов по подоболочкам атома

Орбитальное квантовое число, l	0	1	2	3	4
Обозначение орбитального состояния	s	р	d	/	g

Число электронов, которое может находиться на той или иной оболочке с учетом принципа Паули при данных п и l равно 2 (2l + 1). Главное квантовое число п определяет энергию электронов в атоме , которая увеличивается с увеличением п. Минимальной энергией обладают электроны на К-оболочке (п =1), затем на L-оболочке (п = 2) и т. д. Это означает, что оболочки К, L, М, должны заполняться последовательно, начиная с К. Однако, необходимо выяснить в какой последовательности заполняются состояния s, p, d, f . и т. д. в пределах каждой оболочки. Учет того факта, что при взаимодействии между электронами их энергия увеличивается с увеличением I (при данном п), при построении идеальной схемы принимается, что заполнение оболочки начинается с l_mi_n = 0 и заканчивается l_mах = п - 1. При данном l, m_l принимает (2l +1) значений, а при каждом m_l величина m_s принимает два значения. При данном значении п величина l принимает п значений от 0 до п -1. Таким образом, максимальное число электронов, которые могут находиться в состоянии, соответствующее главному квантовому числу п,, можно рассчитать по формуле

(4.79),

т. е. на данной оболочке может находиться не больше 2n2 электронов.

Химические и физические свойства элементов определяются внешними (валентными) электронами. Поскольку при заполнении очередной оболочки повторяется порядок заполнения предыдущей оболочки, это означает, что химические свойства элементов от оболочки к оболочке меняются периодически: заполнение каждой оболочки начинается со щелочного металла и заканчивается благородным газом. Поэтому можно сказать, что элементы, образующиеся при заполнении оболочки, составляют период системы Менделеева. Число элементов в последовательных периодах идеальной схемы заполнения оболочек должно быть по расчету 2, 8, 18, 32, 50. В действительности, в реальной периодической системе Менделеева число элементов в последовательных периодах равно 2, 8, 8, 18, 18, 32. Таким образом, построение периодической системы элементов существенно отличается от идеальной схемы заполнения оболочек. Причина различия между реальной и идеальной схемами заполнения оболочек состоит в том, что предпосылки, при которых была построена идеальная схема, для большинства элементов не соблюдаются. Взаимодействием электронов между собой и отклонением законов ядерного взаимодействия от кулоновского типа пренебрегать нельзя. Более полный учет взаимодействия электронов позволяет полностью объяснить периодическую повторяемость свойств атомов.

Blog

Содержание

4.6.4 Фотохимическое действие света. Основные фотохимические законы. Основы фотографии