А. М. Мубараков

Вид материала

Содержание

4.4.3 Оптические свойства одноосных кристаллов. Интерференция поляризованных лучей

Подобный материал:

1 ... 32 33 34 35 36 37 38 39 ... 48

4.4.3 Оптические свойства одноосных кристаллов. Интерференция поляризованных лучей

Простейшими оптическими свойствами обладают оптически одноосные кристаллы, которые к тому же имеют наибольшее практическое значение. Поэтому имеет смысл особо выделить этот простейший частный случай.

Оптически одноосными называются кристаллы, свойства которых обладают симметрией вращения относительно некоторого направления, называемого оптической осью кристалла.

1. Разложим электрические векторы Е и D, на составляющие Е_║ и D_║, вдоль оптической оси и составляющие Е_┴ и D_┴, перпендикулярные к ней. Тогда

D_║= ε_║ Е_║ и D_┴, = ε_┴Е_┴, где ε_║ и ε_┴— постоянные, называемые продольной и поперечной диэлектрическими проницаемостями кристалла. К оптически одноосным кристаллам относятся все кристаллы тетрагональной, гексагональной и ромбоэдрической систем. Плоскость, в которой лежат оптическая ось кристалла и нормаль N к фронту волны, называется главным сечением кристалла. Главное сечение — это не какая-то определенная плоскость, а целое семейство параллельных плоскостей.

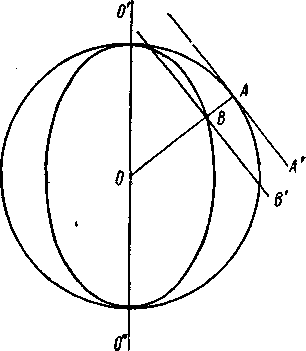Рисунок - 4.52.

Рассмотрим теперь два частных случая.

Случай 1. Вектор D перпендикулярен к главному сечению кристалла. В этом случае D == D_┴, а потому D = ε_┴Е. Кристалл ведет себя как изотропная среда с диэлектрической проницаемостью ε┴. Для нее D = ε_┴Е из уравнений Максвелла получаем D = -с/v H, H =с/v E или ε_┴Е = с/v H, H =-с/v E, откуда v = v_┴= v₀c/√ ε_┴.

Таким образом, если электрический вектор перпендикулярен к главному сечению, то скорость волны не зависит от направления ее распространения. Такая волна называется обыкновенной.

Случай 2. Вектор D лежит в главном сечении. Так как вектор Е лежит также в главном сечении (рисунок 160), то Е = E_n + E_D, где E_n— составляющая этого вектора вдоль n, a E_D — вдоль D. Из векторного произведения [nE] составляющая E_n выпадает. Поэтому формулу для H из уравнений Максвелла можно записать в виде H = с/v [nED]. Очевидно E_D = ED/D = (Е_║D_║+ Е_┴D_┴ )/D = (D_║2ε_║+D_┴2ε_┴)/D или E_D = D (sin²α/ ε_║+ cos2α/ ε_┴) = D(n_┴2/ ε_║+ n_║2/ ε_┴), где α — угол между оптической осью и волновой нормалью.

Если ввести обозначение 1/ε = (n_┴2/ ε_║+ n_║2/ ε_┴), то получится D = εЕD, и мы придем к соотношениям εЕD = с/v H, H =с/v ED, формально тождественным с соотношениями, полученными раньше. Роль величины ε_┴ теперь играет величина ε, определяемая полученным только что выражением для нее. Поэтому нормальная скорость волны будет определяться выражением v = c/√ ε = c√ (n_┴2/ ε_║+ n_║2/ ε_┴. Она меняется с изменением направления волновой нормали n. По этой причине волну, электрический вектор которой лежит в главном сечении кристалла, называют необыкновенной.

Термин «оптическая ось» был введен для обозначения такой прямой, вдоль которой обе волны в кристалле распространяются с одинаковыми скоростями. Если таких прямых в кристалле две, кристалл называется оптически двуосным. Если оптические оси совпадают между собой, сливаясь в одну прямую, кристалл и называется оптически одноосным.

2. Так как уравнения Максвелла в кристаллах линейны и однородны, то в общем случае, волна, вступающая в кристалл из изотропной среды, разделяется внутри кристалла на две линейно поляризованные волны: обыкновенную, вектор электрической индукции которой перпендикулярен к главному сечению, и необыкновенную с вектором электрической индукции, лежащим в главном сечении. Эти волны распространяются в кристалле в различных направлениях и с различными скоростями. В направлении оптической оси скорости обеих волн совпадают, так что в этом направлении может распространяться волна любой поляризации.

К обеим волнам применимы все рассуждения, которыми мы пользовались при выводе геометрических законов отражения и преломления. Но в кристаллах они относятся к волновым нормалям, а не к световым лучам. Волновые нормали отраженной и обеих преломленных волн лежат в плоскости падения. Их направления формально подчиняются закону Снеллиуса sinφ/sin ψ_┴ = n_┴, sinφ/sin ψ_║ = n_║, где n_┴ и n_║— показатели преломления обыкновенной и необыкновенной волн, т. е. n_┴= с/v_┴ = n₀ , n_║= с/v_║ = (n_┴2/ ε_║+ n_║2/ ε_┴)-1/2. Из них n_┴ = n₀ не зависит, а n_║: зависит от угла падения. Постоянная n_v называется обыкновенным показателем преломления кристалла. Когда необыкновенная волна распространяется перпендикулярно к оптической оси (n_┴= 1, n_║ = 0), n_║= √ε_║ = n_е. Величину п_е называют необыкновенным показателем преломления кристалла. Ее нельзя смешивать с показателем преломления n_║ необыкновенной волны. Величина n_еесть постоянная, а n_║ — функция направления распространения волны. Величины совпадают, когда волна распространяется перпендикулярно к оптической оси.

3. Теперь легко понять происхождение двойного лучепреломления. Допустим, что плоская волна падает на плоскопараллельную пластинку из одноосного кристалла. При преломлении на первой поверхности пластинки волна внутри кристалла разделится на обыкновенную и необыкновенную. Эти волны поляризованы во взаимно перпендикулярных плоскостях и распространяются внутри пластинки в разных направлениях и с разными скоростями. Волновые нормали обеих волн лежат в плоскости падения. Обыкновенный луч, поскольку его направление совпадает с направлением волновой нормали, также лежит в плоскости падения. Но необыкновенный луч, вообще говоря, выходит из этой плоскости. В случае двуосных кристаллов деление на обыкновенную и необыкновенную волны теряет смысл — внутри кристалла обе волны «необыкновенные». При преломлении волновые нормали обеих волн, конечно, остаются в плоскости падения, однако оба луча, вообще говоря, выходят из нее. Если падающая волна ограничена диафрагмой, то в пластинке получатся два пучка света, которые при достаточной толщине пластинки окажутся разделенными пространственно. При преломлении на второй границе пластинки из нее выйдут два пучка света, параллельные падающему лучу. Они будут линейно поляризованы во взаимно перпендикулярных плоскостях. Если падающий свет естественный, то всегда выйдут два пучка. Если же падающий свет линейно поляризован в плоскости главного сечения или перпендикулярно к ней, то двойного преломления не получится — из пластинки выйдет только один пучок с сохранением исходной поляризации.

Двойное преломление возникает и при нормальном падении света на пластинку. В этом случае, преломление испытывает необыкновенный луч, хотя волновые нормали и волновые фронты не преломляются. Обыкновенный пучок лучей преломления не испытывает. Необыкновенный луч в пластинке отклоняется, но по выходе из нее снова идет в первоначальном направлении.

Лучи, обыкновенный и необыкновенный, возникающие при двойном лучепреломлении из естественного света, не когерентны. Лучи же, обыкновенный и необыкновенный, возникающие из одного и того же поляризованного луча, когерентны. Если колебания в двух таких лучах привести с помощью поляризационного прибора к одной плоскости, то лучи будут интерферировать обычным образом. Если колебания в двух когерентных плоско поляризованных лучах происходят во взаимно перпендикулярных направлениях, то они, складываясь, как два взаимно перпендикулярных колебания, возбуждают колебания эллиптического характера.

Световые волны, электрический вектор в которых меняется со временем так, что его конец описывает эллипс, называются эллиптически поляризованными. В частном случае, эллипс может превратиться в круг, и тогда мы имеем дело со светом, поляризованным по кругу. Магнитный вектор в волне всегда перпендикулярен электрическому вектору и в волнах рассматриваемого типа также меняется со временем таким образом, что его конец описывает эллипс или круг.

Рассмотрим случай возникновения эллиптических волн подробнее. При нормальном падении пучка лучей на пластинку из одноосного кристалла, оптическая ось в которой параллельна преломляющей поверхности, обыкновенный и необыкновенный лучи идут по одному направлению, но с разными скоростями. Пусть на такую пластинку падает плоско поляризованный луч, плоскость поляризации которого составляет с плоскостью главного сечения пластинки угол, отличный от нуля и от π/2. Тогда в пластинке возникнут оба луча, обыкновенный и необыкновенный, и они будут когерентны. В момент их возникновения в пластинке разность фаз между ними равна нулю, но она будет возрастать по мере проникновения лучей в пластинку. Разность между коэффициентами преломления n0- nе и чем больше толщина кристалла l. Если толщину пластинки подобрать так, чтобы ∆ = kπ, где k — целое число, то оба луча, выйдя из пластинки, снова дадут плоско поляризованный луч. При k, равном четному числу, его плоскость поляризации совпадает с плоскостью поляризации луча, падающего на пластинку; при k нечетном плоскость поляризации вышедшего из пластинки луча окажется повернутой на π/2 по отношению к плоскости поляризации луча, падающего на пластинку (рисунок - 4.53). При всех иных значениях разности фаз Δ колебания обоих лучей, вышедших из пластинки, складываясь, дадут эллиптическое колебание. Если ∆ = 2k+1)π/2 то оси эллипса совпадут с направлениями колебаний в обыкновенном и необыкновенном лучах (рисунок - 4.54). Наименьшая толщина пластинки, способной превратить плоскополяризованный луч в луч, поляризованный по кругу (∆ = π/2), определится равенством π/2 = 2πl/λ (n₀- n_е), откуда получаем: l = λ/ 4(n₀- n_е )


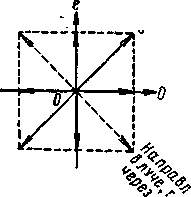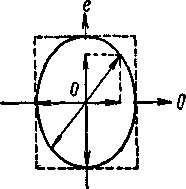Рисунок - 4.53	Рисунок - 4.54

Такая пластинка даст разность хода между обыкновенным и необыкновенным лучами, равную λ/4, поэтому она сокращенно называется пластинкой в четверть волны. Очевидно, что пластинка в четверть волны даст разность хода между обоими лучами, равную λ/4, лишь для света данной длины волны λ. Для света других длин волн она даст разность хода, несколько отличную от λ/4, как из-за прямой зависимости l от λ, так и из-за зависимости от λ разности коэффициентов преломления (n₀- n_е). Очевидно, что наряду с пластинкой в четверть волны, можно изготовить и пластинку «в полдлины волны», т. е. такую пластинку, которая вносит между обыкновенным и необыкновенным лучами разность хода λ/2, чему соответствует разность фаз π. Такая пластинка может употребляться для поворачивания плоскости поляризации плоско поляризованного света на π/2. Как указано, с помощью пластинки λ/4 из плоскополяризованного луча можно получить луч, поляризованный эллиптически или по кругу; обратно, из эллиптически поляризованного или поляризованного по кругу луча с помощью пластинки λ/4 можно получить свет, плоско поляризованный. Этим обстоятельством пользуются, чтобы отличить свет, поляризованный эллиптически, от частично поляризованного, или свет, поляризованный по кругу, от естественного.

Указанный анализ эллиптически поляризованного света можно произвести с помощью пластинки λ/4 в том случае, когда эллиптическая поляризация возникает в результате сложения двух взаимно перпендикулярных колебаний разной амплитуды с разностью фаз π/2. Если же эллиптическая поляризация возникает в результате сложения двух взаимно перпендикулярных колебаний с разностью фаз ∆≠π/2, то для превращения такого света в плоско поляризованный надо ввести такую добавочную разность фаз ∆', которая в сумме с ∆ дала бы разность фаз, равную π (или 2kπ). В этих случаях вместо пластинки λ/4 употребляются приборы, носящие название компенсаторов, которые позволяют получить любое значение разности фаз.

4.5 Виды излучения

4.5.1 Основные законы теплового излучения. Абсолютно черное тело. Пирометрия

Прежде чем перейти к изложению основных законов теплового излучения, ознакомимся с некоторыми необходимыми понятиями.

Излучательная способность. Мощность излучения с единицы площади поверхности тела в единичном интервале частот называется излучательной способностью тела. Если мощность излучения в интервале частот от v до v + dv с единицы площади обозначить через dЕ_v.v+dvто излучательная способность может быть записана в виде

R(v, Т)= dЕ_v.v+dvdv /υ

(4.63).

Поскольку излучательная способность зависит кроме температуры также и от частоты, то ее называют спектральной плотностью поверхностного излучения.

Поглощательная способность. Под поглощательной способностью тела понимается отношение количества поглощенной поверхностью тела энергии в интервале частот v, v + dv к общему количеству падающего излучения в том же интервале частот:

A(υ, T) = dЕ_погл_v_._v₊_dv/ dЕ_пад_v_._vdv

(4.64).

Тела, способные поглощать все падающее на них излучение произвольной длины волны при любой температуре, называются абсолютно черными телами. Для абсолютно черных тел A(v,T) = 1 при всех длинах волн и при любой температуре.

В природе не существует абсолютно черных тел. Но можно найти тела, очень близкие по своим свойствам к абсолютно черным телам (сажа, черный бархат). Полость с маленьким отверстием на поверхности и идеально отражающими внутренними стенками, непроницаемыми для электромагнитных волн, ведет себя как абсолютно черное тело (рисунок - 4.55). Действительно, если на поверхности стенок полости открыть отверстие размером меньше 0,1 диаметра полости, то вошедшее через это отверстие в полость излучение претерпевает многократное отражение и рассеяние от внутренней поверхности стенок, в результате чего падающее излучение всех длин волн «полностью поглощается». На таком принципе устроена, например, щетка из стальных полированных иголок, расположенных, как показано на рисунке - 4.56, будет сильно поглощать свет, ибо луч, попавший между иголками, претерпит многократное отражение от иголок, прежде чем выйти наружу.

В 1859 г. Кирхгоф установил количественную связь между излучательной и поглощательной способностями тел. Согласно этому закону, отношение излучательной и поглощательной способностей тел является универсальной для всех тел функцией частоты и температуры:

Е(v, T)/A(v, T)=f{v,T)

(4.65).

Функция f(v,T), называемая функцией Кирхгофа, не зависит от природы тел. Если излучательную способность абсолютно черных тел


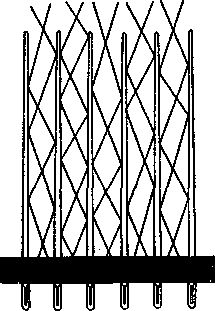Рисунок - 4.55	Рисунок - 4.56

обозначить через r(v, Т), то, поскольку A(v, Т) = 1, получим

Е(v, T)/A(v, T) = r (v, T)/1=f{v,T)

(4.66),

т. е. r(v,T) = f(v, T). Следовательно, универсальная функция Кирхгофа есть не что иное, как излучательная способность абсолютно черного тела и закон Кирхгофа можно переписать в виде

Е(v, T)/A(v, Т) = ε(v,T)

(4.67),

т. е. для всех тел отношение излучательной способности к поглощательной равно излучательной способности абсолютно черного тела при той же температуре и частоте. Данный вывод представляет собой закон Кирхгофа для теплового излучения.

В 1879 г. Стефан и Больцман — теоретически анализируя экспериментальные результаты излучений абсолютно черного тела, установили, что интегральная (просуммированная по всем частотам) излучательная способность тел прямо пропорциональна четвертой степени абсолютной температуры:

R(v, T)= aT⁴

(4.68),

где a— постоянная величина. Это выражение получило название закон Стефана — Больцмана. На основе опытных данных был определен коэффициент пропорциональности: а = 5,672 10-8 Bт/м •К4. Закон Стефана—Больцмана, хотя и определяет вид зависимости интегральной излучательной способности абсолютно черного тела от температуры, но не дает никаких сведений о частотной зависимости энергии излучения, т. е. остается неизвестным явный вид универсальной функции Кирхгофа.

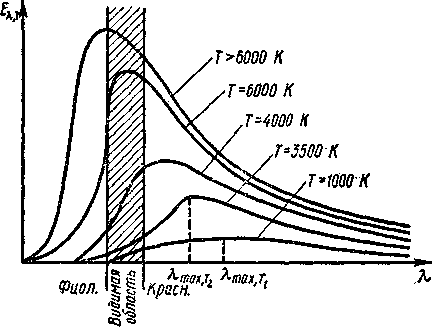
Важным шагом вперед в указанном направлении является закон Вина. Экспериментально было найдено, что распределение энергии в спектре абсолютно черного тела имеет максимум при определенной длине волны λ (рисунок - 4.57). В 1887 г он установил важную закономерность, определяющую положение этого максимума в спектре излучения в зависимости от абсолютной температуры черного тела:

λ_max = b/T

(4.68.1).

При повышении температуры длина волны, на которую приходится максимум спектральной излучательности, смещается в сторону меньших длин волн (рисунок - 4.58). Поэтому данный закон Вина называют законом смещения Вина. Само значение максимальной спектральной излучательности абсолютно черного тела, нагретого до температуры Т, можно найти по формуле:

ε(υ, T)max =CT⁵

(4.69),

где C – постоянная (C = 1,3 10^-5 Вт/м³К⁵ ).

Данное соотношение иногда называют вторым законом Вина.

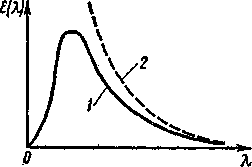
Во всех разобранных выше случаях подход к изучению теплового излучения был термодинамическим. Рэлей, в отличие от своих предшественников, впервые применил методы статистической физики к описанию явлений теплового излучения. Эта формула носит название формулы Рэлея—Джинса. На рисунке 4.57 показаны экспериментальное спектральное распределение энергии излучения абсолютно черного тела при постоянной температуре (сплошная кривая 1) и теоретическая кривая Рэлея — Джинса (пунктирная кривая 2).

Пользуясь законом равномерного распределения энергии равновесной системы по степеням свободы и учитывая, что на каждую колебательную степень свободы в классической физике приходится энергия, равная kT, Рэлей получил следующее выражение для излучательной способности абсолютно черного тела:ε(υ, T)~υkT, где k — постоянная Больцмана. Используя идею Рэлея, Джинс провел точные вычисления и, определив коэффициенты пропорциональности, нашел, что

ε(υ, T) = ((2πv²/с²)kT⁵

(4.70).

В рамках классической физики не удается, как это мы видели,


Рисунок - 4.57	Рисунок - 4.58

описать теоретически всю экспериментальную кривую; другими словами, невозможно определить явный вид функции Кирхгофа при любой температуре и частоте. Эта задача в начале нашего века (1900 г.) была успешно решена М. Планком. Ему удалось подобрать эмпирическое выражение, которое блестяще согласовалось с экспериментальными данными при любой частоте и температуре:

ε(υ, T) = ((2πħv³/с²) 1/(е^hυ/kT- 1)

(4.71),

где h—постоянная Планка, равная 6,625*10-34 Дж с.

Эта формула хорошо описывает cплошную кривую 2 на рисунке 4.57. Поскольку формула Планка справедлива при любых частотах и температурах, то из нее должны следовать все известные законы теплового излучения.

Законы теплового излучения положили начало методам измерения температуры нагретых тел. Существуют различные приборы для измерения температуры нагретых тел (термометры расширения, электрические термометры сопротивления, термопары и т. д.). Однако для сильно нагретых тел (свыше 2000°С) эти методы измерения температуры непригодны. Кроме того, эти методы совершенно неприменимы, если раскаленные тела, температуру которых необходимо определить, чрезвычайно удалены от наблюдателя (например, Солнце, звезды). В этом, а также и в других случаях в качестве термометрического фактора можно использовать тепловое излучение.

Методы измерения высоких температур на основе законов теплового излучения (зависимость спектральной и интегральной излучательной способностей от температуры тел) называются оптической пирометрией. В зависимости от того, какой тепловой закон используется при измерении температуры нагретых тел, различают три температуры — радиационную, цветовую и яркостную. Если измерять интегральную излучательную способность абсолютно черного тела, то температуру тела можно определить, исходя из закона Стефана— Больцмана: R(v, T)= aT⁴.

Как известно, нечерные тела не подчиняются закону Стефана— Больцмана. Определенная таким образом температура нечерного тела называется его радиационной температурой. Пирометр, определяющий радиационную температуру, называется радиационным пирометром. Схема радиационного пирометра показана на рисунке - 4.59. Оптическая система пирометра позволяет сфокусировать резкое изображение удаленного источника И на приемнике П так, чтобы изображение обязательно перекрыло всю пластинку приемника. При этом условии энергия излучения источника, падающая в единицу времени на приемник, не будет зависеть от расстояния между источником и приемником. Тогда температура нагрева пластинки приемника и термоэлектродвижущая сила в цепи батареи термопар зависят только от интегральной излучательной способности R(Т) тела, температуру которого определяем. Шкала милливольтметра, включенного в цепь термопар, градуируется по излучению абсолютно черного тела в градусах. Следовательно, вышеописанный пирометр позволит определить радиационную температуру произвольного нечерного тела,

При известном распределении энергии излучения в спектре абсолютно черного тела можно определить температуру по другому закону теплового излучения - закону смещения Вина, по расположению максимума излучательной способности: T = b/λ_max. Вычисленная таким способом средняя температура называется цветовой температурой. К сожалению, из-за неприменимости закона смещения Вина к нечерным телам подобное определение температуры нельзя считать универсальным. Цветовая температура обычно выше истинной температуры тел.

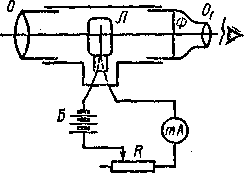
Кроме условно принятых цветовой и радиационной температур тел используется также понятие яркостной температуры. Под яркостной температурой понимается такая температура абсолютно черного тела, при которой его излучательная способность для определенной длины волны равна излучательной способности рассматриваемого тела. Яркостную температуру можно определить с помощью пирометра с исчезающей нитью, схема которого дана на рисунке - 4.60. Принцип действия указанного пирометра заключается в следующем. С помощью объектива О изображение светящейся поверхности нагретого тела, температуру которого хотим определить, совмещается с плоскостью нити накала лампы Л. Яркость накала нити регулируется с помощью реостата R. Нить и изображение нити наблюдаются через окуляр О₁ Светофильтр Ф, расположенный перед окуляром, пропускает узкую полосу длин волн в области λ₀ =6600 A. С помощью реостата подбирается .такое значение силы тока I, при котором излучательная способность нити накала лампы становится равной излучательной способности наблюдаемого тела. При удовлетворении этого условия нить не будет видна на фоне светящейся поверхности тела, т. е. нить как бы исчезает.


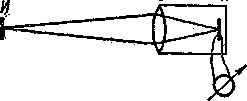Рисунок - 4.59..	Рисунок - 4. 60

Если миллиамперметр заранее проградуировать в градусах по излучению абсолютно черного тела, то, очевидно, он покажет яркостную температуру.

Blog

Содержание

4.4.3 Оптические свойства одноосных кристаллов. Интерференция поляризованных лучей