Т. С. Рамазанов доктор физико-математических наук, профессор, Казну им. Аль-Фараби, г. Алматы; > С. К. Тлеукенов доктор физико-математических наук, профессор, пгу им. С. Торайгырова, г. Павлодар; > А. М. Мубараков

Вид материала

Учебник

Содержание 3.5.2 Постоянные магниты Взаимодействие магнитных полюсов. Взаимодействие токов. Действие тока на магнит. Действие магнита на ток. 3.6.2 Ток смещения. Вихревое электрическое поле Уравнения Максвелла D направлен от обкладки В В и его производной по времени dB/dt. Первую пару уравнений Максвелла 3.6.3 Энергия магнитного поля токов L, в котором сила тока возрастает от нуля до некоторого конечного значения I V, то плотность магнитной энергии

Подобный материал:

• Титульный лист программы Форма обучения по дисциплине ф со пгу 18. 3/37 (Syllabus), 349.17kb.
• Б. А. – доктор юридических наук, профессор Казну им аль-Фараби, 209.21kb.
• Карпухин В. Б., доктор физико-математических наук, профессор кафедры «Высшая и прикладная, 263.95kb.
• А. М. Мубараков доктор пед наук, профессор. Н. Э. Пфейфер доктор пед наук, профессор, 1066.25kb.
• Веселаго Виктор Георгиевич, доктор физико-математических наук, профессор мфти, область, 30.58kb.
• Практических: 0 Лабораторных, 16.69kb.
• Практических: 34 Лабораторных, 24.5kb.
• Практических: 0 Лабораторных, 16.63kb.
• Практических: 34 Лабораторных, 20.05kb.
• Практических: 0 Лабораторных, 18.53kb.

3.5.2 Постоянные магниты

Возможность иметь в ферромагнитных веществах остаточное намагничение позволяет осуществить постоянные магниты, т. е. такие тела, которые без поддержания в них электрического тока за счет каких-либо внешних источников возбуждают в окружающем пространстве магнитное поле. Постоянные магниты готовятся из ферромагнетиков с большим остаточным намагничением и большой коэрцитивной силой.

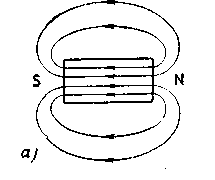
Поле прямого магнита имеет сходство с полем соленоида (рисунок - 3.42). Линии напряженности нам кажутся выходящими из одного конца магнита, называемого северным, и входящими в его другой конец (южный). Разница между магнитом и соленоидом заключается лишь в том, что в случае соленоида мы можем проследить ход линий напряженности и внутри самого соленоида и убедиться, что каждая линия образует замкнутую кривую. В случае постоянного магнита мы не можем непосредственно установить ход линий напряженности внутри тела магнита.

Рисунок - 3.42

Поле постоянного магнита в отличие от поля соленоида или тока вообще является не вихревым, а потенциальным, подобным электростатическому полю электрического заряда. Циркуляция вектора напряженности магнитного поля постоянного магнита равна нулю, как и циркуляция вектора напряженности кулоновского электростатического поля. Силовые линии внутри постоянного магнита направлены, так же как и вне его, от северного полюса к южному (рисунок - 3.43). Поле постоянного магнита представляет собой поле диполя.

Любой ферромагнетик, будучи помещен в магнитное поле, намагничивается в той или иной степени и становится магнитом с двумя полюсами. Если магнитное поле создано током, например током в соленоиде, то оно является вихревым, намагниченные этим полем ферромагнетики создают поле, которое можно считать потенциальным, поэтому результирующее поле носит смешанный характер. На рисунке - 343, а, б, в показаны поля постоянного магнита, соленоида и соленоида с ферромагнитным сердечником.

Качество материала для постоянного магнита определяется его остаточной индукцией я коэрцитивной силой. Так как постоянные магниты всегда используются для создания внешнего магнитного поля, они не могут быть замкнутыми, поэтому в них существует размагничивающее поле, уменьшающее остаточную индукцию.

Наилучшими материалами для постоянных магнитов являются такие, у которых спинка петли гистерезиса имеет форму, близкую к прямоугольной. Большая коэрцитивная сила необходима для того, чтобы магнит был устойчив к случайным внешним магнитным полям. Для повышения устойчивости магнита его подвергают так называемому старению, которое заключается в том, что магнит подвергается воздействию переменного магнитного поля небольшой частоты и амплитуды или нагреванию до 100° С. При этом его остаточная индукция B_d несколько уменьшается, но в дальнейшем она почти не меняется.

Рисунок - 3.43

Среда, магнит, токи находятся в сложном взаимодействии между собой.

а) Взаимодействие магнитных полюсов. Возьмем два постоянных магнита; допустим, что длина каждого из них так велика, что можно пренебречь действием второго полюса и рассматривать взаимодействие этих магнитов как взаимодействие уединенных магнитных полюсов. Взаимодействие таких полюсов, при помещении магнитов в среду с магнитной проницаемостью μ, уменьшается в μ раз.

б) Взаимодействие токов. Оно определяется формулой Ампера. Сила взаимодействия зависит от магнитной проницаемости среды, увеличиваясь при помещении токов в сплошной однородный магнетик в μ раз.

в) Действие тока на магнит. Рассмотрим действие тока на магнит, которые находятся в магнитной среде с проницаемостью μ. Действие тока на магнит определяется полем тока В, которое от среды не зависит, и полем В′ которое создается магнитной средой внутри магнита. Если магнит намагничен до насыщения, то внутри его проницаемость μ. стремится к единице. Если при этом магнит длинный и ориентирован по полю, то ввиду отсутствия в этом случае собственного размагничивающего поля напряженность поля внутри магнита будет такая же, как и в вакууме, следовательно, действие тока на магнит в данном случае не зависит от среды. Если магнит не бесконечной длины, то в нем существует размагничивающее поле В₀, и тогда поле в нем не равно полю в вакууме и действие тока на такой магнит будет сложным образом зависеть от формы магнита. То же будет и в том случае, когда магнит намагничен не до насыщения. Проницаемость вещества магнита больше единицы, поэтому внутреннее поле В′ определяется магнитными свойствами как среды, так и самого магнита; простого общего закона взаимодействия в этом случае дать нельзя.

г) Действие магнита на ток. В вакууме это действие определяется формулой F = IBl sin a, так как μ = 1; при заполнении пространства однородным магнетиком индукция В увеличивается в μ раз, но напряженность поля, созданного полюсом постоянного магнита, уменьшается в μ раз, следовательно, сила действия магнита на ток останется неизменной: действие магнита на ток не зависит от среды.

Возможности магнетиков, явления связанные с ними, имеют широкое применение в науке и технике. Наиболее распространенными такими устройствами, являются моторы и генераторы различных конструкций.

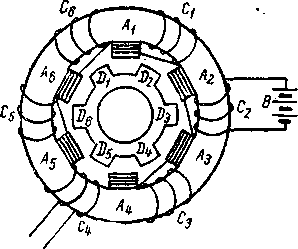
Генераторы представляют собой машины, служащие.для получения токов путем использования явления электромагнитной индукции. Простейшей такой машиной переменного тока является рамка, образованная одним витком провода, вращающаяся в поле постоянного магнита. На практике пользуются, конечно, не одной рамкой, а значительным числом витков провода, намотанных на барабан (ротор). В технике также употребляются машины с неподвижными обмотками и электромагнитами вместо постоянных магнитов. Схема такой машины представлена на рисунке - 3.44. Катушки, в которых индуцируется ток, намотаны на выступы А₁, A₂, A₃, железного сердечника. Сердечник намагничивается током, текущим по обмоткам C₁, C₂, С₃, от небольшого постороннего источника тока В. Вращающаяся часть машины (ротор) имеет вид кольца с зубцами D_1, D₂, D₃ При вращении ротора зубцы перемещаются относительно выступов А₁, A₂, A₃, и таким образом то более, то менее замыкают магнитную цепь между соседними выступами. В результате меняется поток магнитной индукции через катушки, намотанные на выступы А₁, A₂, и в них индуцируется ток.

Наряду с указанными генераторами переменного тока возможно построение генераторов постоянного тока. Если концы вращающейся рамки соединить с двумя изолированными друг от друга полукольцами (коллектором) (рисунок - 3.45), то щетки а и в будут попеременно касаться то одного, то другого полукольца, и во внешней цепи потечет ток все время в одном направлении, лишь меняющий свою силу. Употребляя вместо одной рамки систему обмоток, концы которых присоединены к отдельным секциям сложного коллектора, можно получить постоянный ток, сила которого лишь слегка пульсировать со временем. Магнитное поле во всех сколько-нибудь значительных по размеру генераторе постоянного тока создается электромагнитом, причем обычно используется так называемый принцип самовозбуждения, сводящийся к тому, что электромагнит питается током, возбуждаемым в самой генераторе.

Рисунок - 3.44	Рисунок - 3.45

Современные генераторы и электромоторы представляют собой машины с весьма высоким к. п. д., достигающим для больших машин 95°/₀. Неизбежные вредные потери на трение, джоулево тепло, токи Фуко и гистерезис удается снизить до 5%.

Для многих технических и лабораторных целей бывает необходимо иметь более высокие э. д. с, чтобы передавать электрическую энергию на дальние расстояния.

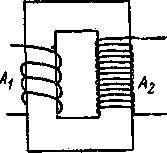
В случае переменного тока повышение э. д.с. (или, как говорят в технике, „напряжения") легко осуществляется с помощью повышающих трансформаторов. Трансформатор в простейшем виде (рисунок - 3.46) состоит из двух обмоток, намотанных на общий замкнутый железный сердечник. Первичная обмотка А₁ состоит из небольшого числа витков толстого провода, вторичная обмотка А₂,— из большого числа витков более тонкого провода. Первичный ток, проходящий через обмотку I₁, создает переменный поток магнитной индукции Ф₁, который целиком сосредоточен лишь внутри сердечника и, следовательно, практически полностью пронизывает витки вторичной обмотки.

При разомкнутой вторичной обмотке первичная обмотка является частью цепи с некоторым омическим и индуктивным сопротивлением. Если считать омическое сопротивление столь малым, что его ролью можно пренебречь, то э д. с. ε_i действующая в первичной обмотке, численно равна и противоположна по знаку возникающей в ней э. д. с. самоиндукции ε_si :ε₁ = - ε_si. В каждом витке первичной обмотки возникает э. д. с. самоиндукции, равная — - dФ/dt, откуда ε_si = - N₁ dФ/dt, где N₁— число витков первичной обмотки. Отсюда для э. д. с. ε₁, действующей в первичной обмотке, получаем:

ε1 = N1 dФ/dt

(3.116).

Так как тот же поток Ф пронизывает вторичную обмотку, то в каждом ее витке возникает э. д. с. индукции — dФ/dt , всего во вторичной обмотке возникает э. д. с. ε₂: ε₂ = N₂ dФ/dt, где N₂ — число витков во вторичной обмотке. Сравнивая выражения два последних выражения, получим, что э. д. с. индукции, возникающая во вторичной обмотке, равна:

ε2 = -(N2/N1) ε1

(3.117).

Таким образом, трансформатор повышает э. д. с. в отношении числа витков вторичной обмотки к числу витков в первичной обмотке. Знак минус указывает, что э. д. с. в первичной и вторичной обмотках противоположны по фазе.

Обычно у трансформаторов, при разомкнутой вторичной обмотке, коэффициент самоиндукции первичной обмотки велик. Это ведет к большому значению индуктивного сопротивления первичной обмотки. Благодаря этому при разомкнутой вторичной обмотке, ток I_t в первичной обмотке слаб. Значение этого тока носит название холостого тока. При замыкании вторичной цепи в ней индуцируется ток, создающий свое магнитное поле, компенсирующее, по правилу Ленца, магнитное поле первичной обмотки. Это ведет к уменьшению индуктивного сопротивления первичной обмотки и возрастанию тока /₁ Таким образом, мощность потребляемая в первичной цепи, зависит от мощности, которая берется во вторичной цепи.

Вредные потери в трансформаторе идут на выделение ленц-джоулева тепла в обмотках, на утечку линий магнитной индукции, на токи Фуко в сердечнике и на работу перемагничения, обусловленную гистерезисом сердечника. Для уменьшения роли двух последних причин сердечники трансформаторов делают из наиболее мягких сортов железа и притом из отдельных полос листового железа, разделенных изолирующими слоями. В больших современных трансформаторах потери удается снизить до 2% от общей мощности, и, таким образом, их к. п. д. достигает 98%.

Всякий трансформатор, работающий как повышающий, может быть использован и как понижающий трансформатор, для чего нужно первичный ток пускать через более тонкую обмотку с большим числом витков. Тогда в другой обмотке возникает такой ток, что сила тока будет больше, а э. д. с. меньше, чем в первой обмотке. Обычно ток высокого „напряжения", переданный по проводам от станции, у потребителя снова понижается с помощью понижающего трансформатора до более низкого «напряжения».

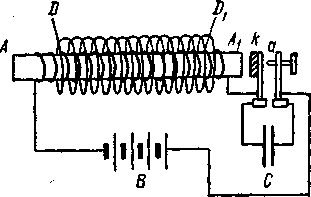
Кроме указанных технических применений, трансформаторы находят широкое применение в лабораторной технике (как повышающие, так и понижающие). В зависимости от предъявляемых требований, лабораторным трансформаторам придают весьма различную конструкцию. Для получения высоких э. д. с, при небольших мощностях, пользуются так называемой индукционной катушкой. Она состоит из двух цилиндрических соленоидов, надетых на общий железный незамкнутый сердечник (рисунок - 3.47). Первичной обмоткой является обмотка внутреннего соленоида AA_lt делаемая из сравнительно небольшого числа витков толстой проволоки. Вторичной обмоткой служит обмотка внешнего соленоида DD_U делаемая из весьма большого числа витков очень тонкой проволоки. Обычно первичную обмотку питают от источника постоянного тока, например от батареи аккумуляторов В. Для того чтобы первичная обмотка создавала переменное магнитное поле, ток в ней периодически прерывают и замыкают. Замыкание и размыкание производится с помощью автоматического прерывателя.

Рисунок - 3.46	Рисунок - 3.47

Простейшим прерывателем является молоточек, который состоит из пружинки с железной насадкой k (рисунок – 3.47). Когда ток начинает идти по первичной обмотке, сердечник катушки намагничивается и притягивает к себе пружину. В результате цепь размыкается в месте контакта между пружинкой k и штифтом а. Чтобы при разрыве контакта не образовывалась интенсивная искра, между k и а включается конденсатор С. Тогда ток от батареи В, при разрыве цепи, идет на заряжение конденсатора, и искра не образуется. Ток в первичной обмотке, прерываемый молоточком или другим механическим приспособлением, не является синусоидальным переменным током.

Если вторичную обмотку замкнуть накоротко, то в ней пойдет переменный ток несимметричной формы, но количества электричества, переносимые в обоих направлениях, будут одинаковы. Если же во вторичной цепи оставить значительный искровой промежуток, то э. д. с, возникающая при замыкании, может оказаться недостаточной для пробоя. Тогда, искра возникает лишь при размыканиях первичной цепи, и во вторичной цепи будет идти прерывистый ток, но каждый раз одного направления.

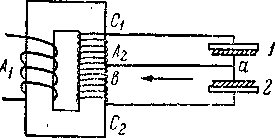
Благодаря удобству генерирования и передачи переменные токи получили исключительно широкое техническое применение. Однако для потребления во многих случаях нужен постоянный ток, поэтому современная техника пользуется различными приемами выпрямления переменного тока. Пользуясь трансформатором и двумя выпрямителями, можно произвести эффективное выпрямление переменного тока. На рисунке - 3.48 A₁ представляет собой первичную обмотку трансформатора, включенного в цепь переменного тока, А₂ — его вторичную обмотку. Два выпрямителя 1 и 2 присоединены к концам вторичной обмотки. От средней части вторичной обмотки сделан отвод bа. Тогда в одну половину периода переменного тока работает часть С₁b вторичной обмотки, и ток проходит через выпрямитель 1. Во вторую половину периода работает часть обмотки C₂b, и ток проходит через выпрямитель 2. В участке цепи аb ток идет все время одного направления.

Рисунок - 3.48

Для измерения переменных токов непригодны магнитоэлектрические приборы с подвижной рамкой, так как направление поворота рамки меняется с изменением направления тока. Для измерения переменных токов пригодны электродинамические приборы с двумя катушками и электромагнитные приборы, в которых в катушку втягивается кусок железа. В последних приборах втягиваемый стерженек должен изготов­ляться из сорта железа, обладающего возможно малым гистерезисом. Кроме того, переменные токи могут измеряться с помощью так называемых индукционных (электродинамических) приборов. Принцип действия этих приборов следующий (рисунок - 3.49): переменный ток, сила которого измеряется, проходит по обмотке Ф электромагнита и возбуждает между его полюсами переменное магнитное поле. Подвижная часть прибора D представляет собою пластинку, расположенную, по отношению к этому переменному магнитному полю так, что она лишь частично экранирует ноле. В пластинке возникают индукционные токи Фуко, на которые магнитное поле действует с силами, стремящимися выдвинуть пластинку из пределов поля. В результате пластинка поворачивается и поворачивает соединенную с ней стрелку. Постоянный магнит М служит для успокоения колебания пластинки.

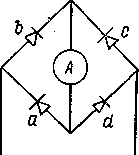
Наконец, переменные токи можно измерять и с помощью магнитоэлектрических приборов с подвижной рамкой, если к ним добавить выпрямители. Для этой цели обычно применяются твердые выпрямители (купроксы). На рисунке - 3.50 представлена схема включения амперметра А в цепь переменного тока с помощью четырех купроксов а, Ь, с, d, обеспечивающих прохождение тока через амперметр А в одном направлении.

Рисунок - 3.49	Рисунок - 3.50

Сопротивление R и самоиндукция L играют роль шунта.


3.6 Электромагнитная индукция

3.6.1 Явления электромагнитной индукции. Закон Фарадея. Токи Фуко

Индукцию электрических токов пытались обнаружить после установления А. Ампером основных электродинамических законов. Однако только в 1831 г. М. Фарадею после многочисленных опытов удалось открыть явление электромагнитной индукции. Оказалось, что в отличие от электростатической индукции, где заряд даже в случае неподвижных проводников вызывает появление индуцированных зарядов на соседних проводниках, индукция токов наблюдается только при движении проводников с током или других источников магнитного поля, а также при изменении тока в проводнике. Основные опыты Фарадея заключались в следующем:

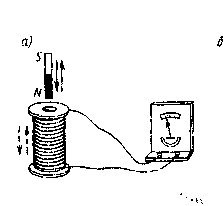
1-й опыт. Концы катушки присоединяются к гальванометру, затем внутрь катушки достаточно быстро вставляется постоянный магнит (рисунке - 3.51,а). В момент перемещения магнита и приемного контура гальванометр показывает отброс стрелки. Направления отклонения стрелки при вдвигании и выдвигании магнита противоположны. Отброс стрелки тем больше, чем быстрее двигается магнит.

2-й опыт. Одна катушка помещается внутри другой. Концы одной из катушек присоединяются к гальванометру, через вторую катушку пропускается ток. В момент включения или выключения тока, увеличения или уменьшения его, производимого с помощью реостата или при движении катушек одной относительно другой (рисунок - 3.51,б), наблюдается отброс стрелки гальванометра. При включении тока, его увеличении или сближении катушек, стрелка отклоняется в одну сторону, при выключении тока, уменьшении его или удалении катушек, стрелка отклоняется в другую сторону.

Рисунок - 3.51

3-й опыт. Катушка изготовляется из нескольких десятков витков мягкой проволоки. Сжимая или растягивая катушку, можно изменять ее площадь. Если перед катушкой поместить магнит, концы катушки присоединить к гальванометру, то при сжатии или растяжении катушки (изменении ее площади) гальванометр покажет наличие токов противоположных направлений. Данный эффект хорошо проявляется в опыте, схема которого представлена на рисунке - 3.52. Приемный контур в виде рамки, замкнутой на гальванометр, помещают в однородное магнитное поле. Если рамка движется поступательно, не пересекая линий магнитной индукции (рисунок - 3.52, а), индукционный ток в ней не возникает. Если же рамка вращается, пересекая линии индукции (рисунок - 3.52, 6), в ней возникает индукционный ток.

Из этих опытов Фарадей заключил, что индукционный ток возникает тогда, когда проводник пересекается магнитными силовыми линиями. Во всех экспериментах 1, 2 и 3 происходит изменение магнитного потока охватываемого приемным контуром. При этом в приемном контуре возникает индукционный ток, который существует все время, пока изменяется магнитный поток. Известно, что условием существования электрического тока в замкнутой цепи является наличие в этой цепи электродвижущей силы (э.д.с.). Возникающая при изменении магнитного потока, э.д.с., получила название э.д.с. индукции.

Следовательно, при изменении магнитного потока, охватываемого контуром проводника, в замкнутом контуре возникает э.д.с. индукции, которая создает в нем индукционный ток, продолжающийся все время, пока изменяется магнитный поток. Это явление называют электромагнитной индукцией.

Рисунок - 3.52

Установленная зависимость количественно замерялась с помощью отброса стрелки гальванометра и позволила установить зависимость между электродвижущей силой ε_i, индуцированной в катушке, и скоростью пересечения проводника магнитными силовыми линиями в таком виде

εi = - dФ/dt

(3.118).

Следовательно, э.д.с. индукции пропорциональна первой производной от магнитного потока по времени и выражает собой основной закон электромагнитной индукции Фарадея. Знак минус в этих формулах ставят согласно правилу Ленца: индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей. Направление индукционного тока в этом проводнике определяется с помощью правила правой руки: если расположить правую руку так, чтобы линии индукции магнитного поля входили в ладонь, а отогнутый под прямым углом большой палец совпадал с направлением движения проводника, то четыре вытянутых пальца покажут направление индукционного тока.

Электрический ток, текущий в любом контуре, создает пронизывающий этот контур магнитный поток Ψ. При изменениях I изменяется также и Ψ, вследствие чего в самом же контуре индуцируется э. д. с. Это явление называется самоиндукцией.В соответствии с законом Био — Савара- Лапласа магнитная индукция В пропорциональна силе тока, вызвавшего поле. Отсюда вытекает, что ток / в контуре и создаваемый им полный магнитный поток Ψ через контур пропорциональны друг другу:

Ψ = LI

(3.119).

Коэффициент пропорциональности L между силой тока и полным магнитным потоком называется индуктивностью контура. Индуктивность L зависит от геометрии контура (т. е. его формы и размеров), а также от магнитных свойств (от μ) окружающей контур среды. Вычислим индуктивность соленоида. Возьмем соленоид такой длины, чтобы его можно было практически считать бесконечным. При протекании по нему тока I внутри соленоида возбуждается однородное поле, индукция которого равна В — р,0ил/ Поток через каждый из витков равен Ψ = BS, а полный магнитный поток, сцепленный с соленоидом,

Ψ = NФ = nlBS = μ0μn2lSI

(3.120),

где l —длина соленоида (которая предполагается очень большой), S — площадь поперечного сечения, п — число витков на единицу длины (произведение nl дает полное число витков N). Индуктивность очень длинного соленоида будет иметь выражение

L = μ0μn2lS= μ0μn2V,

(3.121),

где V = lS — объем соленоида. При изменениях силы тока в контуре возникает э.д. с. самоиндукции S_s, равная

εsi = - dΨ/dt = d(LI)dt = - LdI/dt

(3.122).

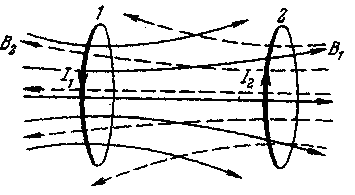
Возьмем два контура 1 и 2, расположенные близко друг к другу (рисунок - 3.53). Если в контуре 1 течет ток силы I₁ он создает через контур 2 пропорциональный I₁ полный магнитный поток Ψ₂ =L₂₁I₁ (поле, создающее этот поток, изображено на рисунке сплошными линиями). При изменениях тока I₂ в контуре 2 индуцируется э. д. с.

εs2 =- L21dI1/dt

(3.123).

Аналогично, при протекании в контуре 2 тока силой I₂ возникает сцепленный с контуром 1 поток Ψ₁ =L₁₂I₂ (поле, создающее этот поток, изображено на рисунке пунктирными линиями). При изменениях I₂ в контуре 1 индуцируется э.д.с.

εs1 =- L12dI2/dt

(3.124).

Контуры 1и 2 называются связанными, а явление возникновения э. д. с. в одном из контуров при изменениях силы тока в другом называется взаимной индукцией (рисунок - 3.54). Коэффициенты пропорциональности L₁₂ и L₂₁ называются взаимной индуктивностью контуров. Соответствующий расчет дает, что в отсутствие ферромагнетиков эти коэффициенты всегда равны друг другу: L₁₂= L₂₁. Их величина зависит от формы, размеров и взаимного расположения контуров, а также от магнитной проницаемости окружающей контуры среды.

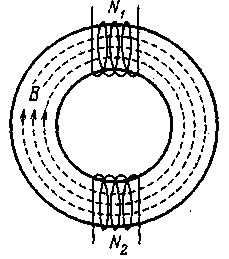Рисунок - 3.53	Рисунок - 3.54

Индукционные токи могут возбуждаться и в сплошных массивных проводника,. которые нельзя рассматривать как линейные контуры. В этом случае их называют токами Фуко и вихревыми токами. Электрическое сопротивление массивного проводника мало, поэтому токи Фуко могут достигать очень большой силы. В соответствии с правилом Ленца токи Фуко выбирают внутри проводника такие пути и направления, чтобы своим действием возможно сильнее противиться причине, которая их вызывает. Поэтому движущиеся в сильном магнитном поле хорошие проводники испытывают сильное торможение, обусловленное взаимодействием токов Фуко с магнитным полем. Этим пользуются для демпфирования (успокоения) подвижных частей гальванометров, сейсмографов и других приборов. Тормозящим действием токов Фуко пользуются для устройства магнитных успокоителей, демпферов Например, если под качающейся в горизонтальной плоскости магнитной стрелкой расположить массивную медную пластину, то токи Фуко, возбужденные в этой пластине, будут тормозить («успокаивать», «тушить») колебания стрелки (рисунок - 3.55). Магнитные успокоители такого рода часто применяют в гальванометрах, сейсмографах и других приборах.

Преимущество такого устройства состоит в том, что торможение возникает лишь при движении пластинки и исчезает, когда пластинка неподвижна. Поэтому электромагнитный успокоитель совершенно не препятствует точному приходу системы в положение равновесия.

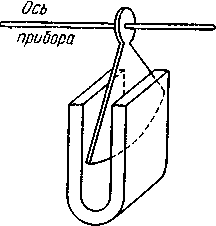Рисунок - 3.55

Тепловое действие токов Фуко используется в индукционных печах. Такая печь представляет собой катушку, питаемую высокочастотным током большой силы. Если поместить внутрь катушки я проводящее тело, в нем возникнут интенсивные вихревые токи, которые могут разогреть тело до плавления. Таким способом осуществляют плавление металлов в вакууме, что позволяет получать материалы исключительно высокой чистоты. С помощью токов Фуко осуществляется также прогрев внутренних металлических частей вакуумных установок для их обезгаживания.

Во многих случаях токи Фуко бывают нежелательными, и приходится принимать для борьбы с ними специальные меры. Так, например, чтобы предотвратить потери энергии на нагревание токами Фуко сердечников трансформаторов, эти сердечники набирают из тонких пластин, разделенных изолирующими прослойками. Пластины располагаются так, чтобы возможные направления токов Фуко были к ним перпендикулярными. Появление ферритов (полупроводниковых магнитных материалов с большим электрическим сопротивлением) сделало возможным изготовление сердечников сплошными.

Токи Фуко, возникающие в проводах, по которым текут переменные токи, направлены так, что ослабляют ток внутри провода и усиливают вблизи поверхности. В результате быстропеременный ток оказывается распределенным по сечению провода неравномерно — он как бы вытесняется на поверхность проводника. Это явление называется скин-эффектом или поверхностным эффектом. Из-за скин-эффекта внутренняя часть проводников в высокочастотных цепях оказывается бесполезной. Поэтому в высокочастотных цепях применяют проводники в виде трубок.

В массивном проводнике, передвигаемом в магнитном поле, вследствие токов Фуко выделяется большое количество тепла. Во избежание этих потерь на нагревание вихревыми токами якори динамо-машин и сердечники трансформаторов делают не из сплошного железа, а из тонких пластин или же проволок с изолирующими прослойками, перпендикулярными к возможным направлениям токов Фуко. Для уменьшения потерь на токи Фуко при изготовлении трансформаторных сердечников часто применяют так называемое легированное железо, содержащее от 2 до 4% кремния. Эта примесь кремния почти не влияет на магнитные свойства железа, но значительно понижает его электропроводность, что соответственно снижает силу токов Фуко. Интенсивным выделением тепла при большой величине токов Фуко пользуются в электрометаллургии для плавки металла, помещаемого в переменное магнитное поле (металл, подлежащий плавке, загружают в полость индукционной печи; обмотку этой печи питают мощным переменным током, имеющим частоту 500—2000 герц, а в лабораторных установках — десятки и сотни тысяч герц; в таких печах, применяемых для выработки высококачественных сплавов, при мощности в 600 кВт тонна металла плавится 40-50 мин.).

3.6.2 Ток смещения. Вихревое электрическое поле Уравнения Максвелла

Рассмотрим подробнее процессы, происходящие при прохождении переменного тока по цепи, содержащей конденсатор. В случае постоянного тока, как мы видели, линии тока всегда замкнуты. Не так обстоит дело для переменного тока В диэлектрике между пластинами конденсатора заряды не могут перемещаться, в результате чего линии тока подходящие к пластине конденсатора обрываются у ее поверхности. Ток проводимости, текущий по проводнику соединяющему обкладки конденсатора оказывается разомкнутым. Пусть в некоторый момент левая обкладка плоского конденсатора А имеет положительный заряд, расположенный на ее поверхности с плотностью +σ, а правая — отрицательный заряд, расположенный с плотностью –σ (рисунок - 3.56). При разряде конденсатора через проводник, соединяющий обкладки, течет ток от левой обкладки к правой. Численное значение плотности этого тока i внутри обкладки получим, взяв производную по времени от плотности заряда:

j = dσ/dt

(3.125).

Ток такой плотности оттекает от левой обкладки А.

Рассмотрим теперь, что происходит в пространстве между пластинами конденсатора. Если ограничиться переменными токами не слишком большой частоты, то можно легко определить изменение электрического поля между обкладками.

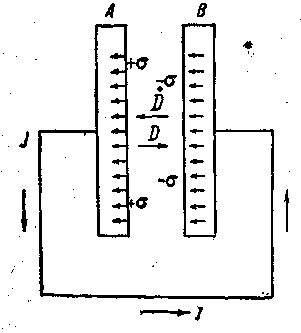Рисунок - 3.56

Действительно, в этом случае мгновенное значение поля внутри конденсатора можно вычислить по мгновенным значениям поверхностных плотностей зарядов. Значение вектора электрической индукции D между обкладками конденсатора численно равно:

D = ε0εσ

(3.126).

Взяв производную по времени от правой и левой частей этого равенства, получим:

dD/dt = σ/dt

(3.127).

В рассматриваемом случае вектор D направлен от обкладки В к обкладке А. Действительно, при разряде конденсатора поле между его пластинами убывает, откуда следует, что производная по времени dD/dt отрицательна, т. е, вектор dD/dt направлен в сторону, противоположную вектору D. Вектор же электрической индукции D направлен между пластинами слева направо. Отсюда приходим к выводу: внутри пластины А налево направлены линии вектора плотности тока проводимости j, в пространстве же между пластинами в том же направлении идут линии вектора dD/dt. Таким образом, линии плотности тока j и линии вектора D, равны друг другу:

j = dD/dt

(3.128).

Тогда оказывается: линии плотности тока проводимости j внутри проводящей пластины непрерывно переходят в линии вектора i_см между пластинами. Максвелл, впервые введший в рассмотрение величину i_см назвал ее плотностью тока смещения.

Таким образом, непрерывность линий тока формально оказывается восстановленной, если плотности тока проводимости i в проводниках сопоставлять в- диэлектриках плотность тока смещения i_см, определяемого меняющимся по времени электрическим полем. Однако в действительности дело идет не только о формальной аналогии между током проводимости и током смещения. Дальнейшее развитие учения об электромагнитных явлениях показало, что ток смещения описывает некоторые реальные свойства электромагнитного поля. Согласно гипотезе, высказанной Максвеллом, ток смещения создает в пространстве, его окружающем, магнитное поле такое же, как и магнитное поле эквивалентного тока проводимости. Эта гипотеза полностью подтверждена многочисленными опытными проверками. Следует при этом иметь в виду, что ток смещения эквивалентен току проводимости только в отношении способности образовывать магнитное поле. Во всех других отношениях ток смещения не может быть уподоблен току проводимости; например, при прохождении тока смещения не выделяется джоулево тепло.

Наряду с током проводимости и током смещения Максвелл ввел в рассмотрение полный ток, плотность и которого определяется как геометрическая сумма плотности тока проводимости и плотности тока смещения:

i = iпр + iсм

(3.129).

Полный ток, как можно показать, является всегда замкнутым. Замкнутость полного тока вытекает из следующих простых рассуждений: в проводнике, соединяющем обкладки, полный ток можно считать равным току проводимости. Между обкладками полный ток равен току смещения; так как у поверхности обкладок, плотности тока смещения и тока проводимости одинаковы и одинаково направлены, то полный ток у поверхностей не терпит изменений.

Таким образом, мы приходим к следствию: всякое меняющееся со временем электрическое поле связано с наличием магнитного поля. Дальнейшие рассуждения показывают, что и переменное магнитное поле, в свою очередь, обусловливает образование электрического поля.

Пусть переменное по времени магнитное поле характеризуется вектором индукции В и его производной по времени dB/dt. Предположим, что в этом поле находится неподвижный замкнутый проводящий контур. Тогда в силу переменности вектора магнитной индукции В поток магнитной индукции Ф через площадь, ограниченную этим контуром, будет меняться, и в контуре возникает э. д. с. индукции ε_i.

Рассмотрим случай электромагнитной индукции, когда проволочный контур, в котором индуцируется ток, неподвижен, а изменения магнитного потока обусловлены изменениями магнитного поля. Возникновение индукционного тока свидетельствует о том, что изменения магнитного поля вызывают появление в контуре сторонних сил, действующих на носители тока. Эти сторонние силы не связаны ни с химическими, ни с тепловыми процессами в проводе; они также не могут быть магнитными силами, потому что такие силы работы над зарядами не совершают. Остается заключить, что индукционный ток обусловлен возникающим в проводе электрическим полем. Обозначим напряженность этого поля Е_В (это обозначение, равно как и применяемое в дальнейшем обозначение Е_q является вспомогательным; указывающая на источник этих полей Электродвижущая сила равна циркуляции вектора Е_В по данному контуру: ε_i- = ∫Е_В dl. Подстановка в формулу ε_i- = —dФ/dt полученного выражения для ε_i, и выражения ∫BdS для Ф приводит к соотношению ∫Е_В dl = -d(∫BdS)/dt (интеграл в правой части равенства берется по произвольной поверхности, опирающейся на контур). Поскольку контур и поверхность неподвижны, операции дифференцирования по времени и интегрирования по поверхности можно поменять местами:

∫ЕВ dl = -∫d(BdS)/dt

(3.130).

Следовательно, мы приходим к заключению, что наличие переменного во времени магнитного поля обусловливает возникновение в области расположения проводника электрической силы. Максвелл, обобщая этот результат, высказал положение, что электрическое поле возникает во всех точках пространства, в которых имеется меняющееся со временем магнитное поле, независимо от того, есть в них проводник или нет. Согласно представлениям Максвелла, проводник, в котором появляется э. д. с, служит только тем объектом, в котором электрические силы себя проявляют. Таким образом, мы можем резюмировать: всякое меняющееся со временем магнитное поле связано с наличием электрического поля.

Практически мы всегда имеем такие переменные магнитные поля, при которых переменен не только вектор магнитной индукции В, но и его производная по времени В. Но в этом случае будет возникать и переменное электрическое поле. Отсюда, вообще говоря, пространство, заполненное переменным магнитным полем, одновременно заполнено и переменным электрическим полем. Оба переменных поля — электрическое и магнитное, связаны друг с другом, и образуют единое электромагнитное поле, которое имеет вихревое свойство.

Рассмотрим вначале вихревой характер магнитного поля. Магнитное поле, создаваемое током смещения, рассчитывается по тем же самым формулам, по которым рассчитывается магнитное поле тока проводимости, лишь с заменой в них плотности тока проводимости плотностью тока смещения. В магнитном поле токов смещения линии магнитной напряженности имеют тот же вид, что и вблизи аналогичных токов проводимости, т. е. они всегда замкнуты и охватывают линии тока. Магнитные линии напряженности вблизи i_см образуют концентрические окружности тем меньшего радиуса, чем ближе они к i_см. Электрическое поле, создаваемое переменным магнитным полем тоже носит вихревой характер. Таким образом, электрическое поле, создаваемое переменным магнитным полем, носит вихревой характер. Его линии напряженности всегда замкнуты. Этим оно отличается от электростатического поля неподвижных зарядов, линии напряженности которого, как мы это не раз отмечали, не замкнуты: они начинаются на одних зарядах и кончаются на других. Циркуляция вектора ∫Е_qdl = 0, что свидетельствует о потенциальном характере этого поля: линии напряженности начинаются и заканчиваются на электрических зарядах.

Для электрического поля, созданного переменным магнитным полем выполняется соотношение ∫Е_В dl ≠ 0. Это говорит о том, что поле индуцированное магнитным полем имеет вихревой характер, не имеет ни начала , ни конца: линии индукции замкнуты вокруг проводника с током.

Таким образом, электрическое поле может быть как потенциальным (Е_q), так и вихревым (Е_В). С учетом этого, последнее полученное соотношение можем записать в более общем виде следующим образом

∫Е dl = -∫d(BdS)/dt = -∫(dB)/dt) dS

(3.131).

Это уравнение является одним из основных в электромагнитной теории Максвелла. Оно свидетельствует о том, что раздельное рассмотрение электрических и магнитных полей имеет лишь относительный смысл: они связаны между собой, порождают друг друга. Действительно, электрическое поле создается системой неподвижных зарядов. Однако если заряды неподвижны относительно некоторой инерциальной системы отсчета, то относительно других инерциальных систем эти заряды движутся и, следовательно, порождают не только электрическое, но и магнитное поле. Неподвижный провод с постоянным током создает в каждой точке пространства постоянное магнитное поле. Однако относительно других инерциальных систем этот провод находится в движении. Создаваемое им магнитное поле в любой точке пространства будет меняться и, следовательно, порождать вихревое электрическое поле. Таким образом, поле, которое относительно некоторой системы отсчета оказывается «чисто» электрическим или «чисто» магнитным, относительно других систем отсчета будет представлять собой совокупность электрического и магнитного полей.

Открытие тока смещения позволило Максвеллу создать единую теорию электрических и магнитных явлений. Эта теория объяснила все известные в то время экспериментальные факты и предсказала ряд новых явлений, существование которых подтвердилось впо­следствии. Основным следствием теории Максвелла был вывод о существовании электромагнитных волн, распространяющихся со скоростью света. Теоретическое исследование свойств этих волн привело Максвелла к созданию электромагнитной теории света.

Основу теории образуют уравнения Максвелла. В учении об электромагнетизме эти уравнения играют такую же роль, как законы Ньютона в механике или основные законы (начала) в термодинамике.

Первую пару уравнений Максвелла образуют уравнения

∫Edl= —d/dt ∫(BdS)

(3.132),

∫(BdS) = 0

(3.133).

Вторую пару уравнений Максвелла образуют

∫Hdl =∫ jdS+d/dt(∫DdS)

(3.134),

∫DdS= ∫ρdV

(3.135).

Соотношения (3.132) - (3.135) представляют собой уравнения Максвелла в интегральной форме.

Этого количества уравнений мало для однозначного расчета полей, поэтому необходимо их дополнить уравнениями, связывающими D и j с Е, а также Н с В. Эти уравнения имеют вид

D=ε0εE

(3.136),

В = μ0μH

(3.137),

j = σЕ

(3.138).

Совокупность этих уравнений образует основу электродинамики покоящихся сред.

3.6.3 Энергия магнитного поля токов

При протекании по проводам постоянного тока вся мощность, развиваемая источником э. д. с., идет на выделение джоулевого тепла. Не так обстоит дело при непостоянных, возрастающих или убывающих токах. При возрастании тока в контуре возникает, как мы видели, ток самоиндукции, направленный против тока, возбуждающего э.д.с. В результате, сила тока будет меньше, причем только часть работы, совершаемой внешней э. д. с, пойдет на выделение джоулева тепла. Наоборот, при падении силы тока в контуре возникает э. д. с. самоиндукции того же направления, что внешняя, ток оказывается сильнее, в цепи выделяется больше джоулева тепла, чем должно было бы выделиться при дайной внешней э. д. с. Очевидно, что лишняя работа, затрачиваемая при возрастании тока, могла пойти лишь на создание какого-то вида энергии, которая затем, при убывании силы тока, выделилась обратно в цепи. Так как с усилением тока усиливается и создаваемое им магнитное поле, то, очевидно, что эта возникающая энергия является энергией магнитного поля.

Для подсчета магнитной энергии рассмотрим контур с самоиндукцией L, в котором сила тока возрастает от нуля до некоторого конечного значения I. При возрастании тока в контуре возникает э. д. с. самоиндукции ε_s. Работа против этой э. д. с. и идет на образование энергии магнитного поля. Если в данный момент сила тока в цепи равна I, то мощность, развиваемая э. д. с. самоиндукции, равна Iε_s а следовательно, работа, совершаемая за малый промежуток времени dt, равна:

dA = Iεsdt

(3.139).

Э. д. с. самоиндукции ε_s численно равна dФ/dt, где dФ—поток индукции, пронизывающий рассматриваемый контур. Отсюда элементарная работа dA за время dt численно равна dA = I dФ. При постоянном коэффициенте самоиндукции dФ = Ldl, и выражение для элементарной работы dA можно переписать в виде: dA = ILdI. Проинтегрировав это выражение по I в пределах от первоначального значения I до нуля, получим работу, совершаемую в цепи за время, в течение которого происходит исчезновение магнитного поля:

A = ∫dA = ∫ILdI = LI2/2

(3.140).

Совершение этой работы сопровождается исчезновением магнитного поля, которое первоначально существовало в окружающем пространстве. Таким образом, приходим к выводу, что проводник с индуктивностью L, по которому течет ток I, обладает энергией

W = LI2/2

(3.141).

Формуле можно придать такой вид, что она представит энергию как функцию величин, характеризующих магнитное поле в окружающем пространстве. Проведем это преобразование для магнитного поля внутри длинного соленоида. Индуктивность соленоида равен:

L = μ0μn2V

(3.142),

где V — объем соленоида, п — число витков, приходящихся на единицу длины, и μ — магнитная проницаемость среды. Кроме того, сила тока I и индукция В магнитного поля внутри соленоида связаны соотношением: I = B/μ₀μ. Подставляя эти значения L и I в формулу для энергии, найдем:

W= В2V/2μ0μ

(3.143).

Так как магнитное поле можно считать сосредоточенным только внутри соленоида, т. е. в объеме V, то плотность магнитной энергии:

w = W/V = В2/2μ0μ = BH/2

(3.144).