Т. С. Рамазанов доктор физико-математических наук, профессор, Казну им. Аль-Фараби, г. Алматы; > С. К. Тлеукенов доктор физико-математических наук, профессор, пгу им. С. Торайгырова, г. Павлодар; > А. М. Мубараков

Вид материала

Учебник

Содержание 3.1.4 Потенциал электростатического поля. Работа и энергия заряда в электрическом поле E = — dφ/dl = -gradφ С конденсатора подразумевают величину отношения заряда q Плоский конденсатор. S — площадь одной пластины конденсатора, то заряд конденсатора q = σS,.

Подобный материал:

• Титульный лист программы Форма обучения по дисциплине ф со пгу 18. 3/37 (Syllabus), 349.17kb.
• Б. А. – доктор юридических наук, профессор Казну им аль-Фараби, 209.21kb.
• Карпухин В. Б., доктор физико-математических наук, профессор кафедры «Высшая и прикладная, 263.95kb.
• А. М. Мубараков доктор пед наук, профессор. Н. Э. Пфейфер доктор пед наук, профессор, 1066.25kb.
• Веселаго Виктор Георгиевич, доктор физико-математических наук, профессор мфти, область, 30.58kb.
• Практических: 0 Лабораторных, 16.69kb.
• Практических: 34 Лабораторных, 24.5kb.
• Практических: 0 Лабораторных, 16.63kb.
• Практических: 34 Лабораторных, 20.05kb.
• Практических: 0 Лабораторных, 18.53kb.

3.1.4 Потенциал электростатического поля. Работа и энергия заряда в электрическом поле

Электрическое поле неподвижных зарядов называют также электростатическим, Поэтому энергия электростатического поля в той или иной точке зависит от положения точки и является потенциальной энергией.

Пусть пробный электрический заряд q₀ находится в электростатическом поле. Такой заряд под действием сил поля может прийти в движение. При перемещении этого заряда полем совершается работа. Как известно, работа консервативных сил совершается за счет убыли потенциальной энергии. Поэтому работу сил электростатического поля можно представить как разность потенциальных энергий, которыми обладает точечный заряд q₀ в начальной и конечной точках своего перемещения в поле заряда q: A = (1/4πε₀) (q₀q)/ εr₁ - (1/4πε₀) (q₀q)/ εr₂ = Eп₁ – Еп₂, откуда следует, что потенциальная энергия заряда q в поле заряда q₀ равна E_п = q₀q /4πε₀ εr + C. Она определяется не однозначно, а с точностью до произвольной постоянной С. Если считать, что при удалении заряда в бесконечность (r→∞) потенциальная энергия обращается в нуль (E_п = 0), то С = 0 и потенциальная энергия заряда q, находящегося в поле заряда Q на расстоянии r от него, равна

Eп = q q0/4πε0 εr.

(3.17).

Для одноименных зарядов q₀q>0 и потенциальная энергия их взаимодействия (отталкивания) положительна, для разноименных зарядов q₀q <0 и потенциальная энергия их взаимодействия (притяжения) отрицательна.

Если поле создается системой п точечных зарядов q₁, q₂, , q_n, то работа электростатических сил, совершаемая над зарядом q₀, равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности. Поэтому потенциальная энергия E_п заряда q₀, находящегося в этом поле, равна сумме его потенциальных энергий E_пi, создаваемых каждым из зарядов в отдельности: E_п = ∑ E_пi = q₀∑q_i/4πε₀ εr_i. Из этой формулы вытекает, что если поле создается несколькими зарядами, то потенциал поля системы зарядов равен алгебраической сумме потенциалов полей этих зарядов:

φ = ∑ φi =∑qi/4πε0 εri.

(3.18).

Пусть заряд q в данной точке поля обладает потенциальной энергией Е_п. В различных точках поля потенциальная энергия данного заряда может быть различна, она зависит как от свойств поля, так и от величины заряда. Но если в одну и ту же точку поля помещать разные заряды потенциальная энергия которых соответственно равна Е_п1, Е_п2;.. .; Е_пi и взять отношение Е_п к q, то получается постоянная величина, не зависящая от величины заряда. Это отношение взято в качестве энергетической характеристики поля и называется потенциалом поля. Следовательно, потенциал данной точки поля определяется формулой

φ = Еп/q

(3.19).

Итак, потенциал φ какой-либо точки электростатического поля равен потенциальной энергии: приходящейся на единицу пробного заряда, помещенного в эту точку. Следовательно, потенциал поля есть величина, равная отношению потенциальной энергии заряда к величине заряда, помещенного в данную точку электростатического поля. Если напряженность поля есть силовая характеристика и является вектором, то потенциал— энергетическая характеристика поля и величина скалярная.

Потенциал φ в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку. Из полученной формулы следует, что потенциал поля, создаваемого точечным зарядом q, равен

φ = q/4πε0 εr

(3.20)

Система из двух точечных зарядов +q_x и -q₂, находящихся па расстоянии b друг от друга, называется диполем. Такую систему в физике рассматривают потому, что центры положительных и отрицательных зарядов молекул многих веществ можно представить смещенными друг относительно друга. Представление о диполях часто позволяет с известным приближением описать взаимодействие молекул различных веществ. Модель дипольного строения вещества лежит в основе теории диэлектриков.

Величину произведения плеча на значение одного из зарядов, образующих диполь, называют электрическим моментом диполя: p = qb. Электрический момент представляет собой вектор, длина которого изображает величину момента, а направление совпадает с осью диполя от отрицательного заряда к положительному заряду. Пользуясь рисунком- 3.10, произведем расчет поля диполя. По принципу суперпозиции, потенциал поля диполя в точке наблюдения равен

φ = q/4πε0 ε (1/r2 -1/r1) =( q/4πε0 ε)* (r1-r2)/r2* r1

(3.21)

где r₂ и r₁ — расстояния от положительного и отрицательного зарядов диполя до точки наблюдения. Пусть точка наблюдения выбрана так, что длина b«r намного меньше расстояний r₂ и r₁. В этом случае можно положить, что r₁ - r₂≈ bcosα; r_2* r₁ ≈ r², и предыдущую формулу можно переписать так: φ = qbcosα/ r²=p cosα/ r², где α— угол между направлением момента диполя и направлением к точке наблюдения, проведенным из диполя. Зная зависимость φ(r,) можно определить напряженность поля по соответствующим формулам.

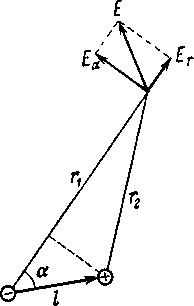Рисунок - 3.10

Чтобы определить величину напряженности поля Е в той же точке, найдем сначала величины составляющих напряженности поля в направлении радиуса Е_r и перпендикулярно к нему Е_α (рисунок - 3.10).

Е = √ Е2r+ Еα2

(3.22).

Величины же составляющих легко найдутся по формуле, выражающей связь между напряженностью и потенциалом поля:

Еr = - dφ/db

(3.23).

Применяя эту формулу к вычислению Е_r находим, что db = dr, α = const, и, cледовательно, Е_r = - d/dr(p cosα/ r²) = 2p cosα / r².

При вычислении Е_α, учтем, что при перемещении на величину db, в направлении, перпендикулярном к радиусу, r = const, а угол α изменится на величину db =r dα.

Тогда Е_α = - dφ/dl =- 1/r (dφ/dα) = - 1/r [d(p cosα)/r²]dα = 2p sinα / r², и далее, Е = √ Е²_r+ Е_α² = p/r²√ 4cos²α + sin²α = p/r²√ 3cos²α + 1.

На одинаковом расстоянии от центра диполя наибольшее значение напряженности поля будет на оси диполя, когда cos²α =1, а наименьшее — в направлении, перпендикулярном к оси, когда cos² α = 0. Следовательно,

Emax = 2p/r2, Emin = p/r2 = Emax /2

(3.24).

Нетрудно увидеть, что ось диполя является осью симметрии поля. Напряженность и потенциал поля диполя убывают обратно пропорционально целым степеням расстояния, причем показатели степени оказываются большими на единицу, чем для соответствующих величин точечного заряда.

Работа, совершаемая силами электростатического поля при перемещении заряда q из точки 1 в точку 2, может быть представлена какA₁₂ = - q ∆ Е, или

A = q (φ2 — φ1).

(3.25).

Как видно, работа, совершаемая электростатическими силами при перемещении электрического заряда из одной точки электрического поля в другую, равна произведению величины электрического заряда на разность потенциалов в этих точках поля. Полученная формула есть одно из основных соотношений электростатики, из которого следует, что работа электростатического поля по перемещению заряда между двумя точками не зависит от формы пути, а является функциями положения начальных и конечных точек перемещения. Физический смысл имеет понятие разность потенциалов, но считается, что электрическое поле в бесконечности имеет нулевой потенциал φ_∞ = 0. Поэтому, когда говорят о потенциале точки, условно принимается за уровень отсчета потенциал бесконечно удаленной точки с φ_∞=0. Этим свойством электростатического поля пользуются при рассмотрении многих задач электростатики, например, при определении потенциала точечного заряда.

Пусть работа поля при бесконечно малом перемещении dr = dl cosα равна dA, тогда для вычисления работы электрических сил на конечном пути l необходимо взять интеграл вида А = ∫dA. Элементарная работа электрических сил при бесконечно малом перемещении dr заряда q (рисунок - 3.11) равна

dA = Eqdl cos α,

(3.26),

где α—угол между напряженностью поля и направлением элементарного смещения. Величина Ecos α = Е_l, есть проекция

Рисунок - 3.11

напряженности поля на направление dl. Таким образом, dA = qE_l dl. Если электрический заряд перемещается по произвольному замкнутому контуру так, что начало пути, совпадает с его концом, то результирующая работа электрических сил равна нулю (разность потенциалов равна нулю): А=0.Поэтому для замкнутого контура q ∫ E_ldl = 0;так как q≠0, то

∫Eldl = 0

(3.27).

Величина ∫E_ldl называется циркуляцией вектора напряженности поля. Таким образом, циркуляция вектора напряженности электростатического поля по произвольному контуру равна нулю. Силовое поле, обладающее таким свойством, называется потенциальным, а силы поля – консервативным.

Если в одну точку пространства приходят электрические поля из разных источников, то вследствие свойства суперпозиции электрических полей результирующий потенциал φ в данной точке будет равен алгебраической сумме потенциалов φ₁,φ₂ , ,φ_n. создаваемых отдельными зарядами:

φ = φ1+φ2 + +φn = ∑φi

(3.28).

В электрическом поле можно сформировать поверхность так, чтобы все ее точки имели бы один и тот же потенциал. Такие поверхности называются поверхностями равного потенциала или эквипотенциальными поверхностями.

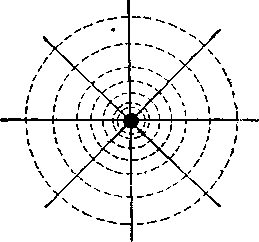
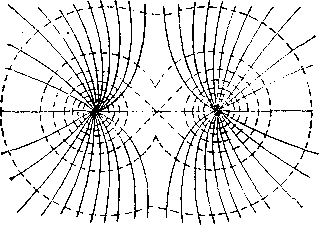
Пользуясь эквипотенциальными поверхностями, можно электрические поля изобразить графически, подобно тому, как это делается с помощью силовых линий. Так как все точки эквипотенциальной поверхности имеют одинаковый потенциал, то работа перемещения заряда вдоль поверхности равна нулю. Это значит, что электрические силы, действующие на заряд, всегда направлены по нормалям к поверхности равного потенциала. Отсюда следует, что силовые линии всегда перпендикулярны к эквипотенциальным поверхностям. На рисунке - 3.12 изображены эквипотенциальные поверхности и силовые линии: а) - точечного заряда, б) – двух одноименных зарядов, в) – эквипотенциальные линии электрического поля тела произвольной формы.

а)	б)	в)
Рисунок - 3.12

Эквипотенциальные линии на графике можно проводить с произвольной густотой, но обычно их проводят на картах полей так, чтобы они соответствовали одинаковым приращениям потенциала, например 1, 2, 3 и т. д. вольт. В этом случае быстрота изменений потенциала в направлении силовых линий будет обратно пропорциональна расстоянию между соседними эквипотенциальными линиями. Поэтому густота эквипотенциальных линий пропорциональна напряженности поля. Таким образом, по картине расположения эквипотенциальных поверхностей и расположении силовых линий. всегда можно составить представление об электрическом поле.

Установим теперь соотношение между потенциалом и напряженностью. Существование такой связи следует из того факта, что работа электрических сил, выражаемых через напряженность, вместе с тем выражается и через разность потенциалов точек поля. Как явствует из предыдущего, электрическое поле может быть охарактеризовано различными величинами:— векторной величиной—напряженностью и скалярной величиной—потенциалом. Установим связь между этими характеристиками поля. Искомую связь получим, сравнивая выражения работы через напряженность и через потенциал поля: dA = qEdl и dA = —dЕ = —qdφ. Приравнивая оба выражения для работы и сокращая на q, получим: E dl = —dφ. Отсюда

E = — dφ/dl = -gradφ

(3.29).

Эту мысль выражают следующим образом: напряженность поля равна градиенту потенциала, взятому с обратным знаком. Знак минус означает, что потенциал убывает при перемещении в направлении силовой линии, и, таким образом, напряженность поля измеряется изменением потенциала, приходящимся на единицу длины в направлении силовой линии, т. е. в направлении наиболее значительного уменьшения потенциала. Из формулы связи между потенциалом и напряженностью электростатического поля определяется единица измерения напряженности в СИ: В/м.


3.2 Электрическое поле в диэлектриках

3.2.1 Электроемкость проводников, конденсаторы

Опытом установлено, чем больше заряд, сообщаемый проводнику, тем больше его потенциал, т.е. заряд проводника пропорционален его потенциалу q = CU. Постоянная. С есть величина, характерная для каждого проводника при данных внешних условиях и называемая его электрической емкостью:

C = q/U

(3.30).

Численно емкость равна количеству электричества, на которое нужно изменить заряд проводника, чтобы его потенциал изменился на единицу. Если форма и размеры проводника не меняются и если при этом остаются неизменными внешние условия (не изменяется среда, в которой находится проводник, не изменяется расположение окружающих предметов), то и емкость остается величиной постоянной. Это показывает, что емкость зависит от формы и размеров, но не зависит от материала проводника.

Из электростатики мы установили, что потенциал уединенного шара радиуса R в среде с диэлектрической проницаемостью ε, равен

φ = q/4πε0εR

(3.31).

Сравнивая с формулой, определяющей емкость, находим, что емкость шара равна

С = 4πε0εR.

(3.32)

Таким образом, емкость уединенного проводящего шара пропорционален его радиусу. Расчеты по полученной формуле показывают, что емкостью 1 Фарад должен обладать шар радиусом R = С/4πε₀ε ≈ 9_*10⁶ км, что примерно в 1400 раз больше радиуса Земли. Следовательно Фарад, очень крупная единица измерения. Поэтому в обычной жизни допускается оперирование долями Фарад – пикофарад (10^-12 Ф), нанофарад (10^-9 Ф) и т.д.

В различных электротехнических и радиотехнических устройствах часто необходимы значительные электроемкости, которые образуются из системы проводников. Система проводников, предназначенных для образования значительной емкости, называется конденсатором, а сближенные проводники, образующие конденсатор, называются обкладками конденсатора.

Под емкостью С конденсатора подразумевают величину отношения заряда q одного знака, накопленного в конденсаторе к разности потенциалов ∆φ между обкладками:

C = q/∆φ

(3.33).

Эта величина, как и емкость уединенного проводника, зависит лишь от геометрических факторов и величины диэлектрической постоянной изолирующей прослойки между обкладками конденсатора. Исследуем емкости таких конденсаторов.

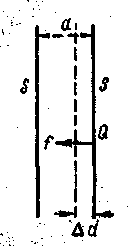
Плоский конденсатор. Плоский конденсатор состоит из двух параллельных пластин (рисунок 3.13,а), расположенных друг от друга на расстоянии d, малом по сравнению с их собственными размерами. Пространство между пластинами конденсатора заполнено диэлектриком. По определению емкость конденсатора C = q/∆φ .

Выразим емкость плоского конденсатора через величины, характеризующие его размеры. Так как размеры пластин велики по сравнению с расстоянием между ними, то ∆φ поля между пластинами такая же, как и в случае двух бесконечных плоскостей, несущих равные по численному значению заряды противоположных знаков.

Если σ — поверхностная плотность зарядов на этих пластинах, a S — площадь одной пластины конденсатора, то заряд конденсатора q = σS,. При наличии диэлектрика между обкладками разность потенциалов между ними можно рассчитать как для системы двух заряженных пластин:

∆φ = σd/ε0ε

(3.34).

Подставим в формулу емкости и получим выражение емкости плоского конденсатора:

C = q/∆φ = σS/ σd/ε0ε = ε0ε S/d

(3.35).

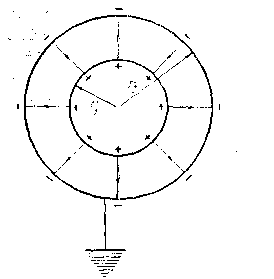
Сферический конденсатор. Сферический конденсатор состоит из двух концентрических шаровых обкладок, разделенных сферическим слоем диэлектрика. Если внутренней обкладке такого конденсатора сообщить заряд +q, то на внешней заземленной обкладке образуется наведенный заряд -q ((рисунок – 3.13,б).).

Поле сферического конденсатора сосредоточено между его обкладками и таково, как если бы заряд был сосредоточен в центре сферы. Поэтому потенциалы обкладок равны: φ₁ = q/εr₁, φ₂ = q/εr₂. Поэтому разность потенциалов между обкладками конденсатора равен φ₁ – φ₂ = q/ε(1/r₁ - 1/r₂) = q (r₁ - r₂)/ εr₁r₂. что позволяет найти электроемкость сферического конденсатора

C = q/∆φ = εr1r2 /(r1 - r2)

(3.36).

Если d = (r₂ — r₁₎« r₁ то r ₂≈ r₁≈ r и C = εr²/ d. Умножая числитель и знаменатель на 4π, и отмечая, что 4πr² есть площадь поверхности сферической обкладки, получим

C = εS/4πd

(3.37).

Таким образом, при малой величине зазора по сравнению с радиусом сферы выражение для емкости сферического и плоского конденсатора совпадают. Если внешний радиус сферического конденсатора гораздо больше внутреннего радиуса, то формула (3.37) упрощается:

C = εr1

(3.38),

т.е., в этом она равна емкости уединенного шара радиуса r₁.

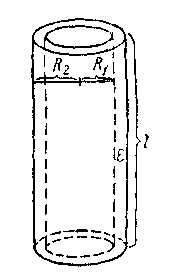
Цилиндрический конденсатор. Цилиндрический конденсатор состоит из двух цилиндрических обкладок, имеющих общую ось и разделенных цилиндрическим слоем диэлектрика (рисунок 3.13,в).

а)	б)	в)
Рисунок - 3.13

Если внутреннюю обкладку такого конденсатора зарядить (при внешней заземленной обкладке), то, пренебрегая краевыми эффектами, его поле можно считать радиально-симметричным и сосредоточенным между цилиндрическими обкладками. Напряженность поля между обкладками конденсатора создается только зарядом на внутреннем цилиндре и в точке на расстоянии r от оси цилиндра равна: Е = 2τ/εr, где τ - линейная плотность зарядов. Изменение потенциала на участке dr связано соотношением: - dφ/dr = E, откуда dφ = -E dr = -( 2τ/εr) dr. Разность потенциалов между обкладками (φ₂ – φ₁) получим, интегрируя это выражение в пределах от R₁ до R₂: φ₂ – φ₁ = - ∫( 2τ/εr) dr = - 2τ/εr ln(R₂/R₁). Следовательно, емкость цилиндрического конденсатора

С = q/(φ1 – φ2) = εl/2ln(R2/R1)

(3.39),

где R₂ и R₁ — радиусы цилиндров.

Емкость подземных и одножильных кабелей может вычисляться по формуле цилиндрического конденсатора, при этом роль внутренней обкладки играет металлическая жила, роль внешней обкладки — броня.

Величину емкости можно менять, соединяя конденсаторы в батареи различным образом.

При параллельном соединении конденсаторов (рисунок - 3.14, а) общим для всех конденсаторов является напряжение U, поэтому U = U₁ = U₂ = U₃ ; Суммарный заряд батареи равен q = q₁+q₂+q₃+ . Поэтому емкость батареи равна С =q/U = q₁/U+q₂/U+q₃/U + . Но q₁/U = С₁, q₂/U = С₂, q₃/U = С₃ и т.д. Так что

С= С1+С2+ С3+ = ∑Ci,

(3.40),

т.е. емкость батареи при параллельном соединении конденсаторов равна сумме емкостей отдельных конденсаторов. Очевидно, в этом случае допустимое рабочее напряжение определяется соответствующим напряжением одного конденсатора.

При последовательном соединении конденсаторов (рисунок - 3.14, б) одинаковым для всех конденсаторов, благодаря явлению индукции, будет заряд q, равный полному заряду батареи: q = q₁=q₂=q₃= . Напряжение же батареи определяется суммой напряжений на отдельных конденсаторах: U = = U₁ + U₂ + U₃+ ; Поэтому для всей батареи справедливо: q/C = q /С₁+ q /C₂+ q/C₃+ или

1/C = 1 /С1+ 1 /C2+ 1/C3+ = ∑1/Ci.

(3.41).

При последовательном соединении конденсаторов суммируются обратные величины емкостей. Т. е. при последовательном соединении п одинаковых конденсаторов емкость батареи в п раз меньше емкости одного конденсатора, во столько же раз напряжение на каждом конденсаторе меньше напряжения батареи.

Комбинируя оба типа соединений, можно получить смешанные батареи с разнообразными данными (рисунок - 3.14, в).

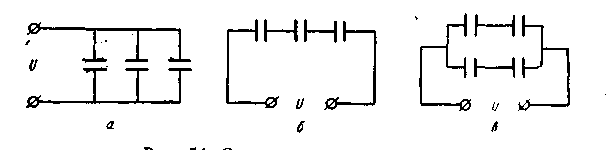Рисунок - 3.14

Для расчета емкости при таком соединении можно сначала подсчитать емкость отдельных групп конденсаторов, представляющих батареи с параллельным или последовательным соединением, а затем каждую из них мысленно заменить одним конденсатором соответственной емкости.