Популяризаторские работы по Русской логике представлены на сайте
| Вид материала | Изложение |
Содержание1.2. Алгоритм «Селигер» (решение системы логических уравнений) 1.3. Решение системы логических уравнений. Алгоритм «НИИДАР» решения системы логических уравнений. |
- Программа и описание курса Лекция «Андеррайтинг владельцев бизнеса» Специфика работы, 74.06kb.
- Которая была проведена с участием редакции сайта «Политучеба», 830.24kb.
- Оценка программы Вданной лекции ( шаг 2 ) представлены литературные источники и базы, 308.47kb.
- Анализ методической работы мбоу «сош №15» за 2010 2011 учебный год, 197.04kb.
- Курсовая работа, 193.69kb.
- Удк 519. 816 Способ представления термов в логике предикатов первого порядка. Алгоритм, 184.64kb.
- Техническое задание мбоу толстомысенской сош №7: «Варианты учебных планов подростковой, 160.12kb.
- М. М. Розенталь принципы диалектической логики глава V понятие в диалектической логике, 1324.47kb.
- Интернет, как информационно-образовательная среда, 70.95kb.
- Доклады и тезисы представлены в авторской редакции. Сподробными материалами конференции, 2528.5kb.
1.2. Алгоритм «Селигер» (решение системы логических уравнений)
1. Привести систему уравнений к нулевому виду (исходная система).
2. Заполнить карту Карно нулями в соответствии с термами левых частей исходной системы уравнений, а в оставшиеся клетки вписать единицы. Эти единичные термы представляют собой СДНФ полной единицы системы.
3. Произвести минимизацию совокупности единичных термов. Полученное соотношение представляет МДНФ уравнения полной единицы системы.
4. Построить сокращённую (только для единичных термов) таблицу истинности уравнения полной единицы и выписать из неё все значения входных и выходных переменных в виде частных таблиц истинности для искомых функций.
5. Произвести минимизацию искомых функций.
Алгоритм «Селигер» предполагает не только графическую, но и аналитическую минимизацию методом обобщённых кодов . Для систем уравнений с числом аргументов не более 10 графический метод эффективнее. Минимизация в трёхзначной и комплементарной логиках для двоичных аргументов несущественно отличается от минимизации в двузначной : нужно лишь проводить раздельное склеивание по i, j, 1 или 0.
Пример 3
Рассмотрим 2-ю задачу Порецкого.
Относительно белья в комоде известны 2 положения:
1) часть его состояла из крупных предметов, всё же остальное было тонким, причём часть этого последнего была поношена, прочая часть дёшево стоила;
2) всё бельё не тонкое, а также всё бельё не новое, но дорогое, принадлежало или к такому тонкому белью, которое не было ни крупно, ни дорого, или же к такому крупному белью, которое частью было ново, частью же, будучи тонким, было дёшево.
Узнать, какое бельё было поношено: крупное или мелкое.
Решение.
Пусть а - тонкое, b - крупное, с - дорогое, d - новое бельё. Тогда имеем следующую систему уравнний ( по-Порецкому):
1. b + a(d’ + c’) = 1
2. (a’ + d’c) = ab’c’ + b(d + ac’)
В соответствии с алгоритмом «Селигер» получим:
1. a’b’ + b’cd = 0
2. a’b’ + a’d’ + cd’ + 0
Нулевые термы системы уравнений занесём в карту Карно, откуда получим функцию полной единицы. По полученному соотношению строим сокращённую таблицу истинности и выписываем из неё значения b и d в виде таблицы, из которой получаем логическую функцию. Из этой функции следует, что d не зависит от b, что совпадает с результатом Порецкого.
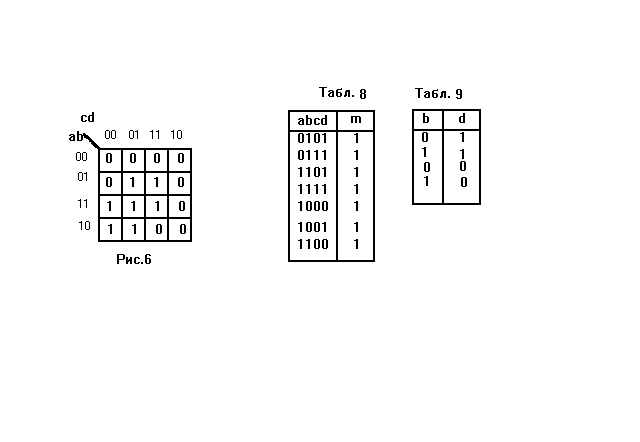
1.3. Решение системы логических уравнений.
В некоторых случаях требуется найти решение системы логических уравнений в обычном понимании, т. е. найти все варианты комбинаций переменных, удовлетворяющие заданным уравнениям. В отличие от обычных линейных алгебраических систем уравнений, имеющих один единственный вариант решения, логическая система уравнений имеет множество решений.
Пример.
Дана система логических уравнений:
abc = 0;
a+b = 1;
b+c = 1.
Найти a,b,c.
Решение.
Полная единица системы
M = (abc)’ & (a+b) & (b+c) = a’b+bc’+ab’c.
Развернув МДНФ системы в СДНФ, получаем 4 различных варианта решения системы:
| Номер варианта | a | b | c |
| 1 | 0 | 1 | 1 |
| 2 | 0 | 1 | 0 |
| 3 | 1 | 0 | 1 |
| 4 | 1 | 1 | 0 |
Каждая строчка таблицы соответствует одному логическому слагаемому (конституенте единицы) в СДНФ. Подставляя любой из вариантов решения в систему, убеждается в корректности метода.
Пример.
Дана система логических уравнений:
a+b+c = 1
bcd = 0
c+d+e = 1
def = 0
a+e+f = 1
aef = 0
Найти a, b, c, d, e, f.
Решение.
M = (a+b+c) & (bcd)’ & (c+d+e) & (def)’ & (a+e+f) & (aef)’.
В этом случае система имеет 29 вариантов решения.
Алгоритм «НИИДАР» решения системы логических уравнений.
1. Привести систему уравнений к нулевому виду (исходная система).
2. Заполнить карту Карно нулями в соответствии с термами левых частей исходной системы уравнений, а в оставшиеся клетки вписать единицы. Эти единичные термы представляют собой СДНФ полной единицы системы.
3. По СДНФ системы находятся все варианты решения, причём каждая конституента единицы соответствует одному варианту решения системы.
Кстати, решая уравнения по алгоритму «Селигер», мы попутно находим и все варианты решений относительно переменных системы. Например, во второй задаче Порецкого получены 7 вариантов решения системы логических уравнений для 4-х переменных. В алгебраической системе уравнений количество уравнений точно соответствует количеству переменных, в логической системе такое соответствие не обязательно.
