Geum.ru

Популяризаторские работы по Русской логике представлены на сайте

Вид материалаИзложение

Содержание


1.4. Равносильные преобразования.
1.5. Отыскание обратных функций.
Подобный материал:
1   ...   13   14   15   16   17   18   19   20   ...   29

1.4. Равносильные преобразования.



При решении логических уравнений иногда возникает необходимость в равносильных преобразованиях. Эта проблема рассмотрена в [7] и решена путём введения понятий парного и непарного индивидов. Однако, чёткое определение этих понятий отсутствует.

Докажем раносильность преобразований с помощью традиционных методов. Пусть х, у - логические функции, для которых справедливо уравнение х = у, приведённое через эквивалентность к виду.

( х = у ) = ху + х’у’

Требуется найти парный индивид z , т.е. такую функцию, добавление (удаление) которой к обеим частям равенства х=у не нарушало бы его равносильности. Это требование записывается в виде уравнения.

x + z = у + z

Но полученное выражение через формулу эквивалентности приводится к виду:

(x+z=у+z) = (x+z)(у+z)+(x+z)’(у+z)’ =

= xу+x’у’+z = (х=у)+z

Откуда следует, что z должен принадлежать исходному равенству, и парным индивидом для исходного уравнения х=у может быть любой терм уравнения или их комбинация, т.е. в данном случае парными индивидами являются термы ху, х’у’, xу+х’у’.

х = у

х +ху = у + ху

х + х’у’ = у + x’у’

x + ху + x’у’ = у + xу + х’у’


Пример 4.

Пусть х+а = у+b . Найти парные термы (индивиды).

Решение.

Развернём исходное уравнение на основе формулы эквивалентности :

(x+a=у+b)=(х+а)(у+b)+(х+а)’(у+b)’ = xу+ау+bx+ab+a’b’x’у’

Из (20) соледует, что парными термами являются ху, ау, bx, ab, a’b’x’у’ и все их комбинации, которые более наглядно можно представить на карте Карно.



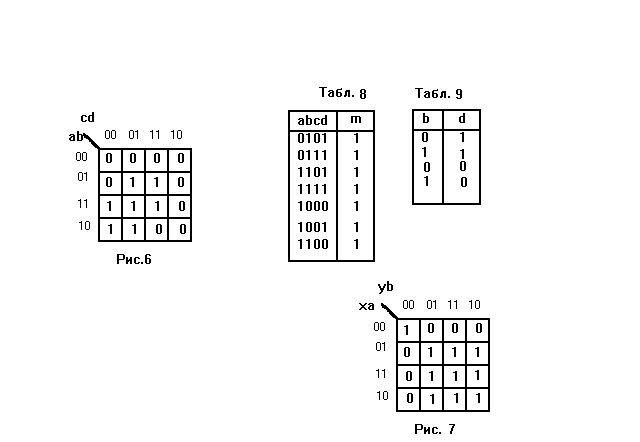
Любой набор термов из единичных фигур покрытия [7] карты Карно может быть парным индивидом. Определим общее количество парных индивидов n. Пусть u - количество переменных, входящих в уравнение f1=f2. Тогда количество конституент единицы k определится следующими соотношениями.

Для чётного u: k = 1 + [2(u/2) - 1]2

Для нечётного u: k = 1+(2[(u+1)/2]-1)

Эти соотношения легко выводятся из анализа карты Карно для уравнения х+а = у+b .Общее количество парных индивидов равно сумме биноминальных коэффициентов для бинома степени k без единицы:

n = 2k - 1

На основе метода, заложенного в алгоритме «Селигер», можно вывести соотношения для операций, обратных конъюнкции и дизъюнкции. Поскольку эти операции часто называются соответственно логическими умножением и сложением, то логично обратным операциям присвоить имена логического деления и логического вычитания. Впервые формулы для логического частного и логической разности для троичной логики получены Н.П.Брусенцовым[7].

Если логическое уравнение вида z=f(x1, x2, x3 .....xi .....xn) решается относительно одной из своих переменных, например, отыскивается обратная функция x1=fi(z, x2, x3 .....xi ..... xn), то можно воспользоваться более простым алгоритмом «Селигер-С» решения задачи.

Алгоритм «Селигер-С».

1. Построить таблицу истинности для уравнения z=f(x1, x2 ..... xn).

2. По исходной таблице истиннсти построить таблицу истинности для обратной функции вида x1=fi(z, x2 ......xn) простой перестановкой столбцов z и х1.

3. По полученной таблице истинности построить обратную функцию x1=fi(z, x2, ..... xn) и провести её минимизацию.

Простота алгоритма «Селигер-С» обусловлена тем, что наличие уравнения z=f(x1, x2 ..... xn) автоматически представляет полную единицу системы М=F(x1, x2 ..... xn,z). Для этого достаточно к столбцам (x1, x2 ..... xn) присоединить столбец z.

Пример 5.

Дано: z = xу , v = x + у.

Найти: у = z/x , у = v-x .

Решение.

На основе формулы эквивалентности преобразуем исходную формулу z=xу. Тогда получим M=(z=xу) = zxу + z’(x’+у’). В соответствии с пп.4, 5 алгоритма «Селигер» получим у = xz+ix’z’+jx’z.

На основе формулы эквивалентности преобразуем исходную формулу v=x+у. Тогда получим M=(v=xу) = vx+vу + v’x’у’. В соответствии с пп.4, 5 алгоритма «Селигер» получим y = vx’+ivx+jv’x.

Решим ту же задачу посредством алгоритма «Селигер-С». Исходные уравнения представим в виде таблицы истинности. Тогда в соответствии с п.2 алгоритма «Селигер-С» построим частные таблицы истинности для у= z/x и у=v-x.


Xy
z
v

00
0
0

01
0
1

10
0
1

11
1
1




Xz
y=z/x

00
i

01
j

10
0

11
1




Xv
y=v-x

00
0

01
1

10
j

11
i


В соответствии с п.3 алгоритма «Селигер-С проведём минимизацию искомых функций в трёхзначной и комплементарной логиках.





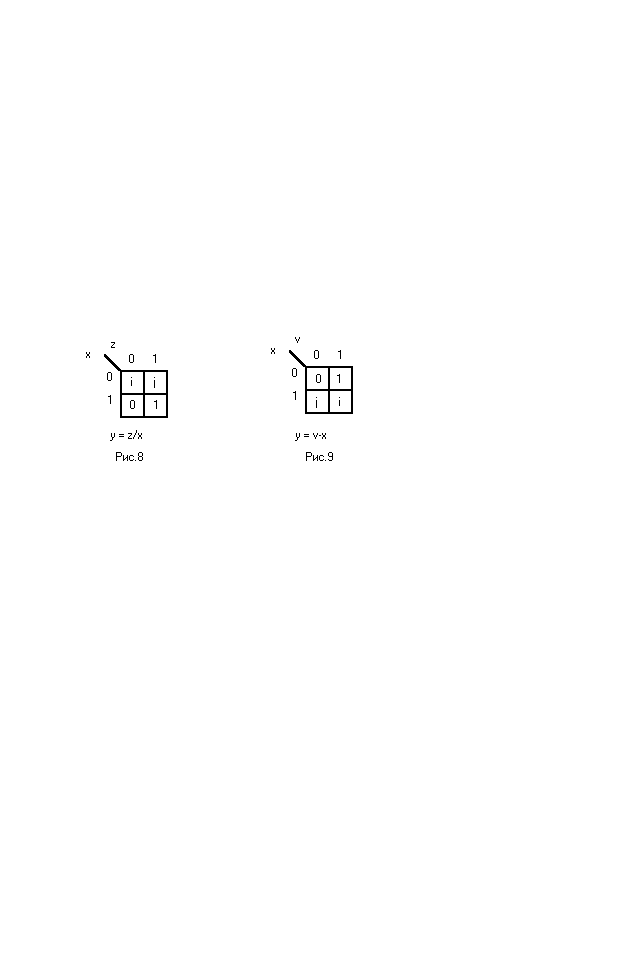
Для комплементарной логики получим:

у = z/x = xz + ix’z’ + jx’z

у = u-x = x’v + ixv + ixv’

Для трёхзначной логики уравнения имеют вид:

у = z/x = xz + ix’

у = v-x = x’v + ix

Однозначным и более строгим решением являются уравнения комплементарной логики. Как и следовало ожидать, алгоритмы «Селигер» и «Селигер-С» дали одинаковые результаты.


Пример 5.

Дана система логических уравнений :

ax = bc

bx = ac

Найти х.

Решение .

Напрашивается простой и “очевидный” метод решения: сложить левые и правые части уравнений и сократить на общий множитель. В результате получим (a+b)x = (a+b)c. Откуда x = c, a = b. Ответ настораживает, тем более, что что решение противоречит принципу отыскания парных индивидов, поэтому проверим его на основе разработанных алгоритмов.

. Действительно, сложить левые и правые части уравнений мы имеем право на основании правила (9П) Порецкого[46,стр,376]. Кстати, заодно и проверим это правило:

(9П) (e=c)  (e+b=c+b) = ec’+e’c+(e+b)(c+b)+(e+b)’(c+b)’ = ec’+e’c+ec+b+e’b’c’ = 1;

Да, Порецкий не ошибся. Но в нашем примере несколько иная ситуация: нам нужно доказать, что (a=b)(c=d)  ((a+c) = (b+d)). Это соотношение также легко доказывается, дополнительно подтверждая правоту Порецкого. Однако относительно сокращения на общий множитель великий русский логик нам ничего не сообщил. А так хочется это сделать, тем более что всё очевидно, и обычная алгебра нам не запрещает подобные операции. Проверим допустимость сокращения на общий множитель с помощью алгоритма “Импульс”:

(cx=cy)  (x=y) = cx(cy)’+(cx)’cy+xy+x’y’ = cxy’+cx’y+xy+x’y’  1.

Оказывается, что алгебра логики не разрешает нам этакие вольности

По алгоритму “Селигер” :

M = (ax = bc)( bx = ac)

M’ = (ax  bc) + ( bx  ac) = ab’x+ac’x+a’bc+bcx’+a’bx+bc’x+acx’+ab’c.

После занесения M’в карту Карно получим

M = a’b’+abcx+c’x’.

Откуда решение системы логических уравнений в соответствии с алгоритмом «Селигер» примет вид:

x = abc+ia’b’+jc(ab’+a’b).

a = bcx+ic’x’+jb(cx’+c’x).

Заданная система уравнений может быть представлена графически при помощи скалярных диаграмм . Скалярные диаграммы построены по рабочим наборам таблицы истинности для М.

A


B


C


X




















Скалярные диаграммы дают полное представление о системе уравнений. Более того, эти диаграммы наглядно демонстрируют связи между всеми переменными. Например, из них легко просматриваются троичные соотношения

x = abc+ia’b’

a = bcx+ic’x’.

Подтвердим корректность метода на решении более прозрачной задачи.


Пример 6.


Дана система логических уравнений:

x = y

u = v

Найти решение системы в виде y(x,u,v).

Решение.

M = (x = y)(u = v) = (xy + x’y’)(uv + u’v’) = u’v’(x’y’ + xy)+uv(x’y’ + xy)

По алгоритму «Селигер» получим

y(x,u,v) = x(u = v)+j(u  v)

Для перехода к y(x) достаточно в таблице истинности для полной единицы М вынести столбец значений y в графу функций и произвести синтез y(x) по вышеизложенным алгоритмам, либо присвоить избыточным переменным в формуле y(x,u,v) = x(u = v)+j(u  v) значение 1. В результате мы подтвердим исходное уравнение системы y(x) = x. Аналогично можно показать,что u(v) = v.

1.5. Отыскание обратных функций.


Используя алгоритм «Селигер» или «Селигер-С», можно получить полную систему обратных функций для двоичной логики. В таблице приведена полная система функций двоичной логики.


xy
z0
z1
z2
z3
z4
z5
z6
z7
z8
z9
z10
z11
z12
z13
z14
z15

00
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1

01
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1

10
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1

11
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1


Перестановкой столбцов у и z исходной таблицы строим таблицу истинности для полной системы обратных функций.


xz
y0
y1
y2
y3
y4
y5
y6
y7
y8
y9
y10
y11
y12
y13
y14
y15

00
I
i
i
i
0
0
0
0
1
1
1
1
j
j
j
j

01
J
j
j
j
1
1
1
1
0
0
0
0
i
i
i
i

10
I
0
1
j
i
0
1
j
i
0
1
j
i
0
1
j

11
J
1
0
i
j
1
0
i
j
1
0
i
j
1
0
i


Из таблицы обратных функций получаем полную симметричную систему обратных функций y = f1(x,z),а по алгоритму «Селигер» – y = f2(x):

у0 = iz’+jz y0 = j

у1 = xz+ix’z’+jx’z y1 = x+jx’

у2 = xz’+ix’z’+jx’z y2 = jx’

у3 = i(xz+x’z’)+j(xz’+x’z) y3 = ix+jx’

у4 = x’z+ixz’+jxz y4 = x’+jx

у5 = z y5 = 1

у6 = xz’+x’z y6 = x’

у7 = x’z+ixz+jxz’ y7 = x’+ix

у8 = x’z’+ixz’+jxz y8 = jx

у9 = xz+x’z’ y9 = x

у10= z’ y10 = 0

у11= x’z’+ixz+jxz’ y11 = ix

у12= i(xz’+x’z)+j(xz+x’z’) y12 = ix’+jx

у13= xz+ix’z+jx’z’ y13 = x+ix’ - импликация

у14= xz’+ix’z+jx’z’ y14 = ix’

у15= iz+jz’ y15 = i

Для троичной логики получим более простые выражения.

у0 = iz’ y0 = 0

у1 = xz+ix’z’ y1 = x

у2 = xz’+ix’z’ y2 = 0

у3 = i(xz+x’z’) y3 = ix

у4 = x’z+ixz’ y4 = x’

у5 = z y5 = 1

у6 = xz’+x’z y6 = x’

у7 = x’z+ixz y7 = x’+ix

у8 = x’z’+ixz’ y8 = j0

y9 = xz+x’z’ y9 = x

у10= z’ y10 = 0

у11= x’z’+ixz y11 = ix

у12= i(xz’+x’z) y12 = ix’

у13= xz+ix’z’ y13 = x+ix’ - импликация

у14= xz’+ix’z y14 = ix’

у15= iz y15 = i


Кстати, переход от левой системы уравнений к правой легко выполняется простой заменой z на 1 и z’ на 0. Аналогичные результаты мы получим, если таблицу прямых функций заменим скалярными диаграммами, а из них по алгоритму ТВАТ выведем соотношения y = f(x). Самой примечательной из полученных функций является y13 = x+ix’ – импликация. Из этого выражения легко просматривается физический смысл импликации: из истинности x следует истинность y.

Решая 1-ю задачу Порецкого, мы заметили аналогию между рекурсивным вхождением функции и комплементарным значением i. Резонно предположить, что такая аналогия существует между комплементарным j и рекурсивным значением инверсии функции. Проверим это предположение на полученных одноаргументных функциях и убедимся в их обратимости с помощью формулы эквивалентности.


0) (y = j)  (y = y')

M = (y=y') = yy'+y'y = 0

1) (y = x+jx')  (y = x+x'y') = (y = x+y')

M = (y=x+y') = y(x+y')+y'(x+y')' = xy+y'x'y = xy

2) y = jx'  x'y'

M = (y=x'y') = yx'y'+y'(x'y')' = y'(x+y) = xy'

3) y = ix+jx'  xy+x'y'

M = (y=xy+x'y') = y(xy+x'y')+y'(xy'+x'y) = xy+xy' = x

4) y = x'+jx  x'+xy' = x'+y'

M = (y=x'+y') = y(x'+y')+y'(x'+y')' = x'y

5) y = 1

M = (y=1) = y&1+y'&0 = y

6) y = x'

M = (y=x') = xy'+x'y

7) y = x'+ix  x'+xy = x'+y

M = (y=x'+y) = y(x'+y)+y'(x'+y)' = y+xy' = x+y

8) y = jx  xy'

M = (y=xy') = yxy'+y'(xy')' = x'y'

9) y = x

M = (y=x) = x'y'+xy

10)y = 0

M = (y=0) = y&0+y'&1 = y'

11)y = ix  xy

M = (y=xy) = yxy+y'(xy)' = xy+y' = x+y'

12)y = ix'+jx  x'y+xy'

M = (y=x'y+xy')=y(x'y+xy')+y'(x'y'+xy)=x'y+x'y' = x'

13)y = x+ix'  x+x'y = x+y

M = (y=x+y) = y(x+y)+y'(x+y)' = y+x'y' = x'+y

14)y = ix'  x'y

M = (y=x'y) = yx'y+y'(x'y)' = x'y+y' = x'+y'

15)y=i  y

M = (y=y) = y&y+y'&y' = y+y' = 1

После обращения были получены все 16 прямых функций от двух аргументов без какого-либо искажения. Это подтверждает правильность всех алгоритмов решения логических уравнений и корректность комплементарной логики.

Четырёхзначные обратные функции необходимо использовать тогда, когда остро стоит вопрос диагностирования или контроля цифрового устройства. Во всех остальных случаях вполне достаточно троичной логики. Вычислим все обратные функции для троичного основания. По таблице истинности для полной системы обратных функций построим скалярные диаграммы, по ним с помощью карт Карно проведём синтез каждой функции отдельно.

Y0


xz
y0

00
0

00
1

10
0

10
1


X



Z


Y







x

i -


i -

z


0


1

0 1

Из карты Карто и скалярных диаграмм видно, что

Y0 = i.


Y1


xz
y1

00
0

00
1

10
0

11
1



X



Z


Y










x

i -


0 1

z


0


1

0 1

Из карты Карто и скалярных диаграмм видно, что

Y1 = z+ix’.


Y2


xz
y2

00
0

00
1

11
0

10
1



X



Z


Y













x

i -


1 0

z


0


1

0 1

Из карты Карто и скалярных диаграмм видно, что

Y2 = xz’+ix’.


Y3


xz
y3

00
0

00
1

11
0

11
1



X




Z


Y










x

i -


- i

z


0


1

0 1

Из карты Карто и скалярных диаграмм видно, что

Y3 = i.


Y4


xz
y4

00
0

01
1

10
0

10
1



X




Z


Y










x

0 1


i -

z


0


1

0 1

Из карты Карто и скалярных диаграмм видно, что

Y4 = z+ix.


Y5


xz
y5

00
0

01
1

10
0

11
1



X




Z


Y













x

0 1


0 1

z


0


1

0 1

Из карты Карто и скалярных диаграмм видно, что

Y5 = z.


Y6


xz
y6

00
0

01
1

11
0

10
1



X



Z


Y













x

0 1


1 0

z


0


1

0 1

Из карты Карто и скалярных диаграмм видно, что

Y6 = x’z+xz’.


Y7


xz
y7

00
0

01
1

11
0

11
1



X




Z


Y













x

0 1


- i

z


0


1

0 1

Из карты Карто и скалярных диаграмм видно, что

Y7 = x’z+ix.


Y8


xz
y8

01
0

00
1

10
0

10
1



X



Z


Y













x

1 0


i -

z


0


1

0 1

Из карты Карто и скалярных диаграмм видно, что

Y8 = x’z’+ix.


Y9


xz
y9

01
0

00
1

10
0

11
1



X




Z


Y













x

1 0


0 1

z


0


1

0 1

Из карты Карто и скалярных диаграмм видно, что

Y9 = x’z’+xz.


Y10


xz
y10

01
0

00
1

11
0

10
1



X




Z


Y














1 0


1 0

x

z


0


1

0 1




Из карты Карто и скалярных диаграмм видно, что

Y10 = z’.


Y11


xz
y11

01
0

00
1

11
0

11
1



X




Z


Y













x

1 0


- i

z


0


1

0 1




Из карты Карто и скалярных диаграмм видно, что

Y11 = z’+ix.


Y12


xz
y12

01
0

01
1

10
0

10
1



X




Z


Y










x

- i


i -

z


0


1

0 1




Из карты Карто и скалярных диаграмм видно, что

Y12 = i.


Y13


xz
y13

01
0

01
1

10
0

11
1



X




Z


Y










x

- i


0 1

z


0


1

0 1




Из карты Карто и скалярных диаграмм видно, что

Y13 = xz+ix’.


Y14


xz
y14

01
0

01
1

11
0

10
1



X




Z


Y













x

- i


1 0

z


0


1

0 1




Из карты Карто и скалярных диаграмм видно, что

Y14 = z’+ix’.


Y15


xz
y15

01
0

01
1

11
0

11
1



X




Z


Y










x

- i


- i

z


0


1

0 1




Из карты Карто и скалярных диаграмм видно, что

Y15 = i.


В алгебре множеств, т.е. всё в той же алгебре логики, существует функция вычитания множеств. Если заданы два множества Х и Y, то их разность мнемонически обозначается как Х\Y. Однако нигде не приводится аналитическое представление для этой мнемоники. Поскольку для двух логических переменных существуют 16 функций, то, очевидно, мы получим 16 различных реализаций для X\Y.

Для f(x,y) нарисуем скалярные диаграммы, а по ним проведём синтез X\Y. Для f0(x,y) = 0 эти диаграммы вырождаются в вертикальную линию со штрихами X,Y. Разность X\Y = 0.

Для f1(x,y) = xy получим следующие диаграммы:

X


Y








Откуда X\Y = Y\X = 0.

Для f2(x,y) = xy’

X


Y








X\Y = x.


В случае f3(x,y) = x имеем

X


Y








X\Y = y’.


Если f4(x,y) = x’y, то получим

X


Y








Y\X = y.

Для f5(x,y) = y синтез выглядит так:

X


Y








Y\X = x’.


При f6(x,y) = xy’+x’y получим

X


Y








X\Y = x, Y\X = y.


Если f7(x,y) = x+y, то в результате синтеза имеем

X


Y








X\Y = y’, Y\X = x’.

Для f8(x,y) = x’y’ получим

X


Y








X\Y = Y\X = 0.

При f9(x,y) = x’y’+xy имеем

X


Y








X\Y = Y\X = 0.

В случае f10(x,y) = y’ диаграммы выглядят так:


X


Y








X\Y = x.


Для f11(x,y) = xy’ получим

X


Y








X\Y = xy’.


При f12(x,y) = x’ имеем

X


Y








Y\X = y.


В случае f13(x,y) = x’+y диаграммы представлены так:

X


Y








Y\X = x’y.


Для f14(x,y) = x’+y’ синтез представлен так:

X


Y








X\Y = x, Y\X = y.

При f15(x,y) = 1 имеем

X


Y








X\Y = xy’, Y\X = x’y.


Заключение.

1. Простота метода, заложенного в алгоритме «Селигер», позволяет решать логические уравнения от большого числа переменных.

2. Минимизация функций в 3-значной и комплементарной логиках для двоичных аргументов несущественно отличается от традиционных методов двузначной логики.

3. Парные термы для равносильных преобразований определяются набором термов, полученных на основе применения формулы эквивалентности к исходному логическому уравнению.

4. Применение метода при выводе обратных логических функций показало, что однозначное решение для двоичных аргументов может быть получено лишь в комплементарной логике.

5.Впервые получены все 16 обратных логических функций для двух аргументов.

6. Комплементарная логика при аппаратной реализации позволяет значительно упростить решение проблемы самодиагностирования вычислительной техники: например появление j на любом выходе может свидетельствовать о сбое или отказе.