А. И. Тимофеев логика и основы аргументации учебное пособие

Вид материала

Содержание

3.6. Отношения между суждениями. Логический квадрат
3.7. Модальность суждений
4. Основные формально-логические законы
4.2. Закон тождества
4.3. Закон непротиворечия
4.4. Закон исключенного третьего
4.5. Закон достаточного основания

Подобный материал:

1 2 3 4 5 6 7 8 9 10 11

3. 5. Сложные суждения

Сложным называется суждение, имеющее в своем составе два и более простых суждения, или, иначе говоря, оно имеет два и более субъекта или предиката. Сложные суждения рассматриваются в логике только с точки зрения их истинностных значений, которые зависят от истинностных значений простых суждений и от типа связи простых суждений в сложное. Можно выделить пять основных типов связи двух простых суждений:

1) конъюнктивная связь, образующаяся с помощью логического союза и;

2) соединительно-разделительная дизъюнктивная связь, образующаяся с помощью логического союза или;

3) исключительно-разделительная дизъюнктивная связь, образующаяся с помощью логического союза либо...либо;

4) импликативная, или условная связь, образующаяся с помощью логического союза если...то... ;

5) эквивалентная связь, образующаяся с помощью логического союза если и только если.

Эти типы связи простых суждений отражаются соответствующими логическими связками – конъюнкцией, дизъюнкцией, строгой дизъюнкцией, импликацией и эквиваленцией. Логические связки обычно обозначают символами: Л, V, VV, Й, є, соответственно. Следует заметить, что для обозначения этих логических связок используются и другие символы.

Тип связи выявляется при анализе предложения, которым выражено сложное суждение. Например, суждение “Эрмитаж и Русский музей находятся в Санкт-Петербурге” содержит утверждение о двух музеях, а, точнее, два утверждения: “Эрмитаж находится в Санкт-Петербурге”, “Русский музей находится в Санкт-Петербурге” – и при этом предполагается их одновременная истинность. Значит, мы имеем сложное, состоящее из двух простых, конъюнктивное суждение, логическую форму которого можно записать так: (A Л B), где A, B обозначают указанные простые суждения, а Л– конъюнкцию.

Устанавливают истинностные значения сложных суждений при помощи истинностных таблиц. Для их построения нужно знать определения перечисленных логических связок: конъюнкции, слабой дизъюнкции, строгой дизъюнкции, импликации и эквиваленции.

Какими бы ни были суждения А и В, если они принимают значения, выписанные в двух левых столбцах приведенной далее таблицы, то суждения, образованные связыванием их L, V, VV, Й, є, принимают значения, выписанные, соответственно, в пяти правых столбцах:

Буква “и” означает истинно, буква “л” – ложно.

3.6. Отношения между суждениями. Логический квадрат

Установление отношений между суждениями предполагает выяснение таких вопросов: могут ли быть эти суждения вместе истинными, могут ли они быть вместе ложными, обусловливает ли истинность одного истинность другого и т. п. , иначе говоря, отношения между суждениями устанавливают по их истинностным значениям.

Все указанные отношения делятся на две группы: совместимости и несовместимости. Суждения называются совместимыми, если они могут одновременно быть истинными, и несовместимыми, если они не могут быть одновременно истинными.

Между простыми категорическими суждениями можно устанавливать отношения только в случае, если они имеют одинаковые субъект и предикат, а различаются по количеству и (или) качеству. Отношения между ними определяют по “логическому квадрату”. “Логический квадрат” предложен в XI веке византийским логиком Михаилом Пселлом. “Логический квадрат” – наглядная схема, облегчающая запоминание характера отношений между общеутвердительными (А), частноутвердительными (I), общеотрицательными (E) и частноотрицательными (O) суждениями.

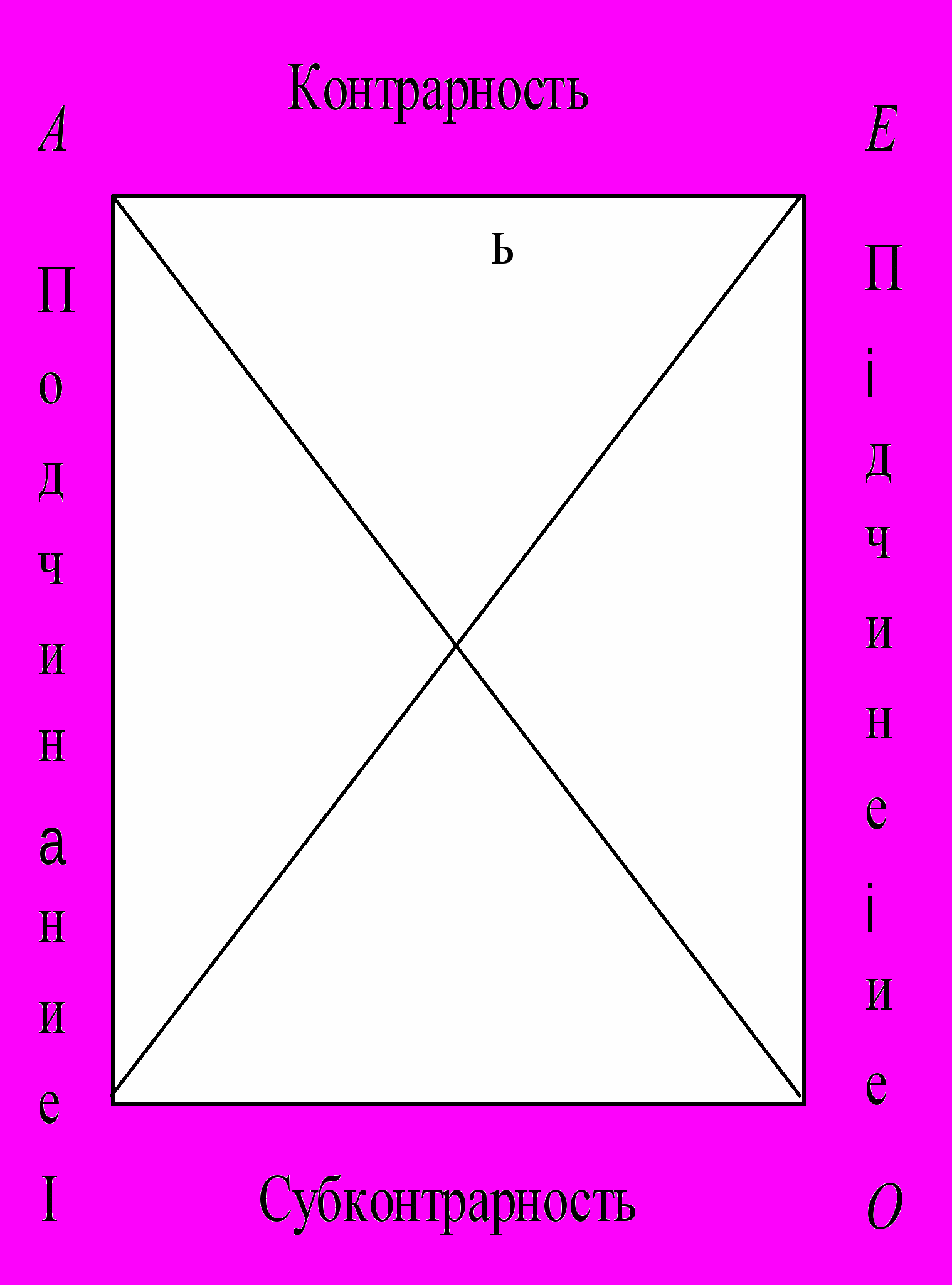
1. В отношениях контрадикторности находятся суждения A и O, E и I, они различаются по качеству и количеству. Из двух противоречащих суждений одно непременно истинно, другое – ложно. Оба противоречащих суждения не могут быть одновременно истинными и не могут быть одновременно ложными.

2. В отношениях контрарности находятся суждения A и E, они различаются по качеству, но не по количеству. Два противных суждения не могут быть одновременно истинными, но могут быть одновременно ложными.

3. В отношениях подчинения находятся суждения A и I, O и E, они различаются по количеству, но не по качеству. Из истинности подчиняющего суждения следует истинность подчиненного. Но из истинности подчиненного необходимо не следует истинность подчиняющего. Тем самым это отношение не определено. Из ложности подчиняющего суждения необходимо не следует ложность подчиненного суждения. Тем самым это отношение не определено. Из ложности подчиненного суждения необходимо следует ложность подчиняющего.

4. В отношениях субконтрарности находятся суждения I и O различные по качеству, но не по количеству. Их отношения истинности и ложности непосредственно не определены. Если I истинно, то E ложно и так как E ложно, то O может быть как истинным, так и ложным. Если I ложно, то E истинно и, значит, O истинно. Итак, если одно из двух подпротивных суждений ложно, то другое истинно. Оба субконтрарные суждения не могут быть одновременно ложными, но могут быть одновременно истинными.

Отношения между суждениями, представленными в “логическом квадрате”, можно записать в виде следующей таблицы:

Буква “и” означает истинно, буква “л” – ложно, буква “н” – не определено.

3.7. Модальность суждений

Модальностью суждения называется оценка того, что в нем утверждается или отрицается с той или иной точки зрения. Модальная оценка выражается с помощью понятий “необходимо”, “возможно”, “доказуемо”, “разрешено”, “запрещено” и т. п. Эти оценочные понятия называют модальными операторами.

O предмете S можно просто сказать, что он имеет свойство P. Но можно, сверх того, уточнить, является ли эта связь S и P необходимой или же она случайна, хорошо ли, что S есть P, или это плохо, доказано, что S есть P, или это не доказано и т. д.

Результатами таких уточнений будут модальные суждения разных типов. Общая их форма: M (S есть P) или M (S не есть P). Вместо M в эту форму могут подставляться различные модальные операторы, определяющие тип связи субъекта и предиката. Например, из немодального суждения “Цирконий – металл” можно образовать модальные суждения “Возможно, что цирконий – металл”, “Хорошо, что цирконий – металл”, “Доказано, что цирконий – металл” и т. д. Одно и то же суждение может стать объектом нескольких последовательных модальных оценок с одной или разных точек зрения (“Хорошо, что доказано, что цирконий – металл”).

Истинность модального суждения зависит от истинности того суждения, которое стоит под модальным оператором, и от модальности, т. е. оценки, которая этому суждению дается.

Если оценка дается с точки зрения законов природы или логики (“необходимо”, “возможно”, “невозможно), модальность называется алетической; если с точки зрения норм права (“обязательно”, “разрешено”, “запрещено”) – деонтической; если с точки зрения познания (“доказано”, “проблематично”, “опровергнуто”) – эпистемической. Существуют и многие другие виды модальностей.

В алетической группе выделяют фактическую и логическую модальности. Первая – характеризует суждение с точки зрения законов природы, а вторая – с точки зрения законов логики. Для их различения модальные операторы уточняют: “логически необходимо”, “фактически возможно” и т. п. Существуют отношения между логическими и фактическими модальностями:

1) если верно, что суждение логически необходимо, то оно фактически необходимо, но наоборот неверно;

2) если верно, что суждение фактически возможно, то оно логически возможно, но не наоборот;

3) если верно, что суждение логически невозможно, то оно фактически невозможно, но не наоборот.

Для деонтической модальности философской основой ее понимания является аксиология (от греч. axios – ценность и logos – слово, понятие). Это – учение о ценностях, философская теория общезначимых принципов, определяющих направленность человеческой деятельности, мотивацию человеческих поступков. Возникновение понятия ценности в конце XVIII века было связано с пересмотром традиционного обоснования этики, характерного для античности и средних веков и предполагавшего тождество бытия и блага. Согласно этому обоснованию, добро имеет абсолютное основание своего бытия в боге, зло никаких оснований бытия не имеет. Пересмотр этого фундаментального для западноевропейской культуры принципа был начат И. Кантом. Он противопоставил сферу нравственности (свободы), а, значит, и блага, сфере природы (необходимости), а, значит, и бытию. Тем самым благо перестало непосредственно иметь и бытийный статус. Оно стало пониматься в виде ценности. Ценности сами по себе не имеют бытия, у них есть только значимость: они суть требования, обращенные к человеческой воле, цели, поставленные перед ней.

Логический аспект теории ценностей изучает логика оценок. Она изучает логическую структуру и логические связи оценочных суждений. В этой логике все виды оценок обычно делятся на абсолютные и сравнительные оценки. Абсолютные оценки выражают с помощью слов: “хорошо” (добро), “плохо” (зло) и (оценочно) “безразлично”. Сравнительные оценки формулируются в суждениях с оценочными словами “лучше”, “хуже”, “равноценно”, “предпочитается” и т. д. В обыденном языке для правильного понимания оценок важную роль играет контекст, в котором они формулируются.

Обычно оценочные суждения, выражающие оценочные отношения, противопоставляют истинностным суждениям. В случае истинностного отношения отправным пунктом сопоставления суждения и объекта является последний; суждение выступает как его описание и, если оно соответствует объекту, то оно истинно. В случае ценностного отношения исходным является суждение, выражающее некий образец, стандарт. Соответствие ему объекта характеризуется с помощью оценки. Позитивно ценным является объект, соответствующий высказанному о нем суждению, отвечающий предъявленным к нему требованиям. Например, сопоставляются какой-то дом и его план. Можно, приняв за исходное дом, сказать, что план, соответствующий дому, является истинным. Но можно, приняв за исходное план, сказать, что дом, отвечающий плану, является хорошим, т. е. таким, каким он должен быть.

Нормы – это частный случай оценок, а именно групповые оценки, поддерживаемые угрозой наказания. Нормативные суждения исследуются деонтической логикой (от греч. deon – долг, правильность). Эта отрасль логики рассматривает логическую структуру и логические связи нормативных суждений. Анализируя рассуждения, посылками и заключениями которых служат такие суждения, деонтическая логика отделяет необоснованные схемы рассуждений от обоснованных и систематизирует последние. Нормативные понятия “обязательно”, “разрешено”, “запрещено” определяются в терминах абсолютных оценочных понятий: “Обязательно А” равносильно “А является позитивно ценным и хорошим, поэтому уклонение от А ведет к наказанию”. Если учитываются условия приложения нормы, то возникает ее относительность, и она приобретает вид “Обязательно (разрешено, запрещено) А в условиях В”.

Понятия “обязательно”, “разрешено”, “запрещено” считаются взаимно определимыми: обязательно то, от чего не разрешается воздерживаться, т. е. обязательно все, что запрещено не делать; разрешено то, от выполнения чего не обязательно воздерживаться, т. е. разрешено все, что не запрещено; запрещено то, от чего обязательно следует воздерживаться, т. е. запрещено все, что не является разрешенным. Безразлично действие, не являющееся ни обязательным, ни запрещенным, или, что то же самое, действие, которое разрешено выполнять и разрешено не выполнять.

Область норм крайне широка; между нормами и тем, что ими не является, нет явной границы. Самым общим образом нормы можно разделить на правила (правила игры, грамматики, математики, ритуала и т. п. ); предписания (законы государства, команды и т. п. ); технические нормы, говорящие о том, что должно быть сделано для достижения определенного результата. Помимо этих основных групп к нормам относят также обычаи (“Принято, чтобы младшие приветствовали старших первыми”), моральные принципы (“Не будь завистлив”) и правила идеала (“Солдат должен быть стойким”).

Все нормы независимо от конкретного содержания имеют одну и ту же структуру. Каждая норма включает в себя четыре “элемента”: содержание – действие, являющееся объектом нормативного регулирования; характер – норма обязывает, разрешает или запрещает это действие; условия приложения – обстоятельства, в которых должно или не должно выполняться это действие; субъект – лицо или группа лиц, которым адресована норма.

В деонтической логике имеют место закон деонтической непротиворечивости (выполнение действия и воздержание от него не могут быть вместе обязательными), закон деонтической полноты (всякое действие или обязательно, или безразлично, или запрещено).

Эпистемическая модальность характеризует суждение с точки зрения способов обоснования его истинности и степени этой обоснованности. Истинность суждений может быть объективно или субъективно обоснована. Суждение, истинность которого объективно обоснована, является знанием. Суждение, истинность которого обоснована, субъективно является убеждением (верой).

Одна из первых логик знания была сформулирована австрийским логиком К. Геделем (1906 – 1978). Исходным термином ее является “доказуемо”. В числе ее законов положения: если высказывание доказуемо, то оно истинно (доказать можно только истину, доказательства лжи не существует); логические следствия доказуемого также являются доказуемыми; если нечто доказуемо, то доказуемо, что оно доказуемо; логическое противоречие недоказуемо и т. п.

В логике убеждений в качестве исходного обычно принимается понятие “убежден” (“верит”), через него определяются понятия “сомневается” и “отвергает”. Это происходит следующим образом. Субъект сомневается в чем-то, если он не убежден ни в этом, ни в противоположном. Субъект отвергает нечто, если только он убежден в противоположном. Среди принципов логики убеждения наиболее значимы четыре положения:

Субъект убежден, что первое и второе, если он убежден, что первое и убежден, что второе (субъект верит, что Марс и Луна – планеты, если он верит, что Марс – планета и что Луна – планета).

Нельзя одновременно верить и сомневаться, быть убежденным и отвергать, сомневаться и отвергать.

Субъект или убежден в чем-то, или сомневается в этом, или отвергает это.

Невозможно быть убежденным в чем-либо и противоположном одновременно.

Контрольные вопросы

Что такое суждение и в какой языковой форме оно выражается?
Какие бывают виды простых суждений?
Какова структура атрибутивных суждений?
Какие бывают виды сложных суждений?
Каковы условия истинности сложных суждений?
В чем состоят основные отличия модальных суждений от категорических?
На какие виды делятся суждения по качеству и количеству?
Как делятся суждения по объединенной классификации?
Что такое распределенность терминов суждения?
Как распределены термины в суждениях A, E, I, O?
Какие простые суждения называются совместимыми, а какие несовместимыми?

4. ОСНОВНЫЕ ФОРМАЛЬНО-ЛОГИЧЕСКИЕ ЗАКОНЫ

4.1. Общая характеристика формально-логических законов

Закон мышления – это внутренняя, необходимая связь между мыслями. Наиболее простые и вместе с тем необходимые связи между мыслями выражаются с помощью основных формально-логических законов, подчинение которым обусловливает определенность, последовательность, непротиворечивость и обоснованность мышления. Они представляют собой ряд таких исходных общих положений, аксиом, с помощью которых обосновываются отдельные правила мышления. Положения эти должны соблюдаться во всякой правильной мысли, поэтому они и называются основными законами мышления.

Формальная логика рассматривает четыре основных закона: тождества, непротиворечия, исключенного третьего, достаточного основания. Эти законы считаются основными, так как они выражают наиболее общие свойства всякого правильного мышления и имеют всеобщий и необходимый характер. Без соблюдения этих законов правильное мышление вообще невозможно.

4.2. Закон тождества

Закон тождества формулируется следующим образом: в процессе рассуждения по поводу какого-либо объекта нашей мысли необходимо иметь в виду один и тот же объект, его нельзя подменять другим объектом.

Закон тождества обозначается формулой А есть А, где А обозначает любую мысль.

Закон тождества утверждает равенство объекта мысли самому себе. Но тождественность нельзя путать с неизменностью. Объект может меняться, развиваться, но в пределах своего понятия, т. е. сущность меняться не должна. Например, конкретный человек меняется в течение своей жизни, но остается при всех изменениях данным лицом. Таким образом, закон тождества выражает относительно неизменное, что остается в объекте во всех его выраженных, осознаваемых изменениях, пока этот объект продолжает мыслиться как нечто, равное себе самому.

Из закона тождества вытекает, что нельзя отождествлять разные мысли и, наоборот, тождественные мысли принимать за нетождественные. Требуя определенности мысли, он направлен против такого существенного недостатка, встречающегося в мышлении отдельных людей, как расплывчатость, неконкретность рассуждений. Определенность – это одна из коренных общечеловеческих черт правильного мышления. Мышление, которое лишено этой черты, теряет всякий смысл.

Закон тождества формулирует требование: прежде чем начинать обсуждение какого-либо вопроса, необходимо ясно установить точное, определенное, устойчивое, конкретное, относительно тождественное содержание его, а затем в ходе обсуждения все время, пока не изменится предмет обсуждения, твердо держаться основных определений этого содержания, не перескакивать с одного определенного понятия на другое, не подменять данное содержание другим, не смешивать разные понятия, не допускать двусмысленности.

Неопределенность, неустойчивость, двусмысленность может быть результатом поверхностного изучения действительности. Но чаще закон тождества нарушается преднамеренно. Делается это в тех случаях, когда хотят исказить истинное положение дел. Это, конечно, не значит, что одно только соблюдение требований закона тождества неприменно приведет к истинному выводу в умозаключении. Соблюдение требований закона тождества – только одно из условий получения правильного вывода.

4.3. Закон непротиворечия

Закон непротиворечия формулируется следующим образом: не могут быть одновременно истинными две противоположные мысли об одном и том же предмете, взятом в одно и то же время и в одном и том же отношении.

Закон непротиворечия обозначается формулой А не есть не-А.

Закон непротиворечия непосредственно связан с законом тождества. Если закон тождества говорит об определенном равенстве объекта мысли самому себе, то закон непротиворечия указывает, что “этот” объект мысли необходимо должен отличаться от всех других объектов. Тем самым закон непротиворечия имеет свое собственное содержание. Оно выражается в следующем: одному и тому же объекту в одно и то же время и в одном и том же смысле нельзя приписывать противоположные признаки. Если одному и тому же объекту приписываются противоположные признаки, то один из них, во всяком случае, приписан ложно. Например, если А означает, что бумага белая, то она в то же время и в том же смысле не может иметь какое-то другое, противоположное определение, т. е. быть черной или синей, или красной.

Для того чтобы правильно пользоваться этим законом, надо хорошо уяснить все условия его применимости. Закон гласит: две противоположные мысли, высказанные по одному и тому же вопросу, не могут быть сразу обе истинными в одно и то же время и в одном и том же отношении или смысле. Между тем некоторые начинающие изучение логики делают серьезную ошибку, считая, что вообще, безотносительно ко времени и разному смыслу суждений, нельзя об одном и том же предмете высказывать две противоположные мысли. На самом деле, мы нисколько не нарушим закон непротиворечия, если утвердительное и отрицательное суждения будут относиться к разным периодам времени или будут применяться нами в разных отношениях.

Аристотель, сформулировавший этот закон, говорил, что он является недоказуемым, непосредственно очевидным основоположением. Он его обосновывал “от противного”, показывая, что непринятие этого закона ведет к абсурду. Если бы закон непротиворечия не действовал, то все было бы единым, и одну вещь невозможно было бы отличить от другой. Следовательно, не было бы ложных суждений, все было бы истинным.

4.4. Закон исключенного третьего

Закон исключенного третьего формулируется следующим образом: два суждения с противоречащими предикатами не могут быть одновременно ложными, одно из них необходимо истинно, третье суждение исключено.

Закон исключенного третьего обозначается формулой А есть или В, или не-В.

Смысл этой формулы следующий. Каков бы ни был предмет нашей мысли (А), предмет этот либо обладает известным свойством (В), либо не обладает им. Невозможно, чтобы ложным было как то, что предмет А обладает свойством В, так и то, что предмет этим свойством не обладает. Истина обязательно находится в одном из двух противоречащих суждений. Никакое третье суждение об отношении А к В и не-В не может быть истинным. Следовательно, здесь имеет место дихотомия, согласно которой, если одно из двух истинно, то другое ложно, и наоборот.

Закон исключенного третьего и закон непротиворечия связаны между собой. Оба они не допускают существования противоречивых мыслей. Но между ними есть и различия. Закон непротиворечия выражает отношение между противоположными суждениями. Например: “Эта бумага белая”. – “Эта бумага черная”. Закон исключенного третьего выражает отношение между противоречащими суждениями. Например: “Эта бумага белая”. – “Эта бумага не белая”. В силу этого, в случае действия закона непротиворечия оба суждения не могут быть одновременно истинными, но могут быть одновременно ложными, а истинным будет третье суждение – “Эта бумага красная”. В случае действия закона исключенного третьего обе мысли не могут быть одновременно ложными, одна из них будет необходимо истинной.

При применении закона исключенного третьего следует учитывать, что когда одно из суждений что-либо утверждает относительно единичного предмета или явления, а другое суждение это же самое отрицает относительно этого же предмета или явления, взятого в одно и то же время и в одном и том же отношении, то такими суждениями будут, например, следующие: “Нева впадает в Балтийское море” и “Нева не впадает в Балтийское море. ” Оба эти суждения не могут быть одновременно ни истинными, ни ложными. Одно из них истинное, а другое – ложное, и невозможно никакое третье, среднее суждение.

Если же противоречащие по форме суждения относятся не к единичному предмету, а к классу предметов, когда что-либо утверждается или отрицается относительно каждого предмета данного класса и это же отрицается относительно каждого предмета данного класса, то отношения истинности между ними устанавливаются по правилам “логического квадрата”. Допустим, мы имеем два таких суждения: “Все предприятия нашего района уплатили налоги” и “Все предприятия нашего района не уплатили налоги”. В данном случае из ложности одного суждения необходимо не следует истинность противного суждения. Истинным может быть, например, третье суждение: “Некоторые предприятия нашего района уплатили налоги”.

Когда одно из суждений что-либо утверждает относительно всего класса предметов или явлений, а другое суждение это же отрицает относительно части предметов или явлений этого же класса, тогда одно из таких суждений будет обязательно истинно, другое – будет ложным, а третьего не дано. Например: “Все рыбы дышат жабрами” и “Некоторые рыбы не дышат жабрами”. Оба эти суждение не могут быть одновременно ни истинными, ни ложными.

4.5. Закон достаточного основания

Закон достаточного основания формулируется следующим образом: всякая мысль может быть признана истинной только тогда, когда она имеет достаточное основание, всякая мысль должна быть обоснованной.

Закон достаточного основания обозначается формулой А есть потому, что есть В.

Под достаточным основанием имеется в виду мысль, которая, если признать ее истинной, обязывает признать истинной и другую, вытекающую из нее мысль. Если признание одного утверждения истинным обязывает признать истинным и другое утверждение, то данное утверждение является достаточным основанием другого утверждения. Например, некто утверждает: “Иванов – прекрасный адвокат”. Можно спросить: “Какое основание есть для этого утверждения?” Если ответ будет гласить: “Иванов выиграл почти все процессы, в которых он участвовал”, то это может являться достаточным основанием. Следует отметить, что формального критерия достаточности основания не существует.

Закон достаточного основания является логическим выражением в нашем сознании объективно существующей причинной обусловленности явлений действительности. Но отношение основания и следствия, составляющее содержание закона достаточного основания, не следует смешивать с отношением причины и действия. Отношение между основанием и следствием есть отношение между нашими субъективными утверждениями, нашими мыслями. Тогда как отношение причины и действия есть связь явлений, событий объективного мира.

Поскольку мысль, которая служит основанием, сама, в свою очередь, должна быть обоснована, постольку можно говорить о теоретически бесконечном регрессе оснований. (Регрессивное доказательство – это такое доказательство, в котором ход рассуждений идет от следствий к основаниям.) На практике пределом обоснования может являться очевидность (факт), аксиома, закон.

Контрольные вопросы

Что такое законы мышления?
Каково отличие законов мышления от законов природы?
Как формулируется закон тождества?
В чем состоят различия закона непротиворечия и закона исключенного третьего?
В чем различие между причиной и основанием?
Что служит пределом обоснования в юридической практике?

Blog

А. И. Тимофеев логика и основы аргументации учебное пособие

Содержание