Учебно-методический комплекс учебной дисциплины

Вид материала

Учебно-методический комплекс

Содержание Тест – это кратковременное измерение или испытание, проводимое для определения способностей или состояния человека. Тесты интелл Тесты креативности Тесты личностные Уровень шкал Уровень значимости Цель в педагогическом исследовании Эксперт – специалист, проводящий экспертизу. Эмпирическая функция распределения Сервис выбрать команду Надстройки Описательная статистика

Подобный материал:

• Учебно-методический комплекс учебной дисциплины «комплексный анализ хозяйственной деятельности», 1158.91kb.
• Назарова Вероника Сергеевна учебно-методический комплекс, 2456.13kb.
• Учебно-методический комплекс учебной дисциплины «Муниципальное управление» по специальности, 359.71kb.
• Учебно-методический комплекс учебной дисциплины история политических и правовых учений, 431.59kb.
• Учебно-методический комплекс дисциплины. Иркутск 2008 Учебно методический комплекс, 329.2kb.
• Учебно-методический комплекс дисциплины. Иркутск 2008 Учебно методический комплекс, 115.23kb.
• Учебно-методический комплекс дисциплины. Иркутск 2008 Учебно-методический комплекс, 195.41kb.
• Учебно-методический комплекс дисциплины. Иркутск 2008 Учебно методический комплекс, 102.02kb.
• Учебно-методический комплекс дисциплины. Иркутск 2008 Учебно-методический комплекс, 250.7kb.
• Учебно-методический комплекс дисциплины. Иркутск 2008 Учебно-методический комплекс, 183.52kb.

Тема исследования – лаконичная формулировка исследования.

Тест – это кратковременное измерение или испытание, проводимое для определения способностей или состояния человека.

Тесты интеллекта – это методики психодиагностики, ориентированные на выявление умственного потенциала индивида.

Тесты креативности – это методики для изучения и оценки творческих особенностей личности.

Тесты критериально-ориентированные – это методики, направленные на выявление уровня владения знаниями и навыкам умственных действий, которые необходимы и достаточны для выполнения определенных классов учебных или профессиональных заданий.

Тесты личностные – это методы психодиагностики, с помощью которых измеряют различные стороны личности индивида.

Тесты проективные – это совокупность методик целостного изучения личности, основанного на психологической интерпретации результатов проекции.

Тестирование – исследовательский метод, который позволяет выявить уровень знаний, умений и навыков, а также способностей м других качеств личности путем анализа способов выполнения испытуемыми ряда специальных заданий.

Уровень шкал – с их помощью обозначают измеряемые свойства переменной. Различают четыре типа в возрастающей последовательности:

• Номинальные шкалы (значения переменной – это различные названия, имя или пол, к примеру);
  
• Порядковые – выражения поставлены в определенной последовательности (отлично, хорошо, удовлетворительно);
  
• Интервальные – деление шалы производиться, например, по годам (1951, 1952, 1953) или десятилетиям (1940, 1950, 1960);
  
• Относительные – дополнительно к интервальной шкале подставляется ноль.
  

Уровень значимости – максимальное значение вероятности появления события.

Факт – явление или достоверно зафиксированные связи между явлениями и событиями, истинность познания которых может быть научно доказана.

Формализация – такое уточнение содержания представления, которое делает возможным и целесообразным использование математических средств исследования.

Цель в педагогическом исследовании– образ потребного (желаемого) будущего, предвосхищение результатов преобразований образовательной системы или ее элементов в интересах человека, общества и государства.

Шкала – представляет собой числовую сис­тему, в которой отношения между различными свойствами объектов выражаются свойствами числового ряда.

Шкалирование – это определение состояний (стадий, уровней) объекта диагностики по изучаемому предмету.

Эксперимент – исследовательский метод, который заключается в том, чтобы путем активного вмешательства создать исследовательскую ситуацию и сделать доступным и возможным изучение психических процессов через их проявления и регистрацию соответствующих изменений в поведении человека.

Эксперт – специалист, проводящий экспертизу.

Эмпирическая функция распределения – называется функция, значение которой в точке х равно накопленной частоте.

Приложение

ОТВЕТЫ

Ответы на тест к модулю №1

1. В.

2. 1 – Е, 2 – Г, 3 – В, 4 – Д, 5 – Б, 6 – Ж, 7 – 3, 8 – А.

3. 1 – Б, 2 – В, 3 – А.

4. Передовой, новаторский, модифицирующий.

5. А, Б, В.

Ответы на тест к модулю № 2

1. Б.
   
2. 3 – А, 1 – Б, 2 – В.
   
3. А.
   
4. А.
   
5. А – 4), Б – 1), Г – 3), В – 2).
   

Ответы на итоговый тест

1. А, В, Е, Д.
   
2. А.
   
3. Б.
   
4. 1), 4), 6), 13).
   
5. Б.
   
6. Б.
   
7. В.
   
8. А.
   
9. Б.
   
10. А.
    
11. Б.
    
12. А.
    
13. Б.
    
14. Д.
    
15. Б.
    
16. В.
    
17. Б.
    
18. Б.
    
19. В.
    
20. Б.
    
21. В.
    
22. В.
    
23. С
    
24. В.
    
25. 2), 6), 8), 13).
    
26. Г.
    
27. Д.
    

Примеры решения задач

Пример 1.

Пусть имеется выборка значений некоторого признака X объемом n=50:

9,19	11,9	9,46	12,2	6,39
11,5	10,9	9,11	13,1	6,97
10,7	5,82	12,1	11,7	9,03
12,6	8,89	12,5	10,4	6,84
13	9,32	9,33	11,5	8,29
12,3	8,3	11	9,02	10,5
7,46	8,76	10,1	9,23	11,7
8,92	8,01	9,61	7,16	7,05
8,8	15,5	13,7	12	12,1
11,6	12,3	15	10,6	9,53

Требуется, разбивая ее на 6групп, составить:

1). Интервальный вариационный ряд и построить гистограмму частот;

2). Дискретный вариационный ряд и построить полигон частот.

Решение.

1. 
   Вводим данные в диапазон А1:A50, выделяем его и отсортируем по возрастанию.
   
2. Из полученного ряда находим min=А1=5,82 и max=А50=15,5 значения (можно воспользоваться функциями МИН и МАКС).
   

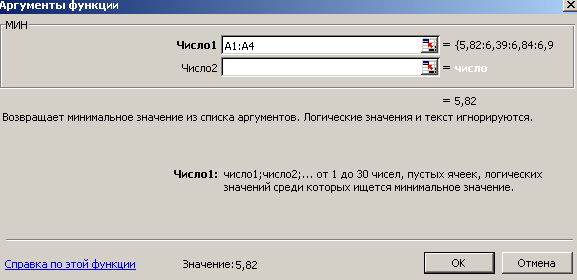
3. По формуле =А50-А1 найдем размах выборки, 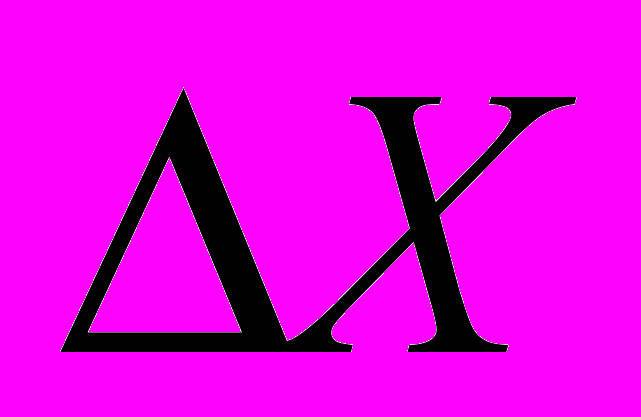=9,68
   
4. Оцениваем шаг 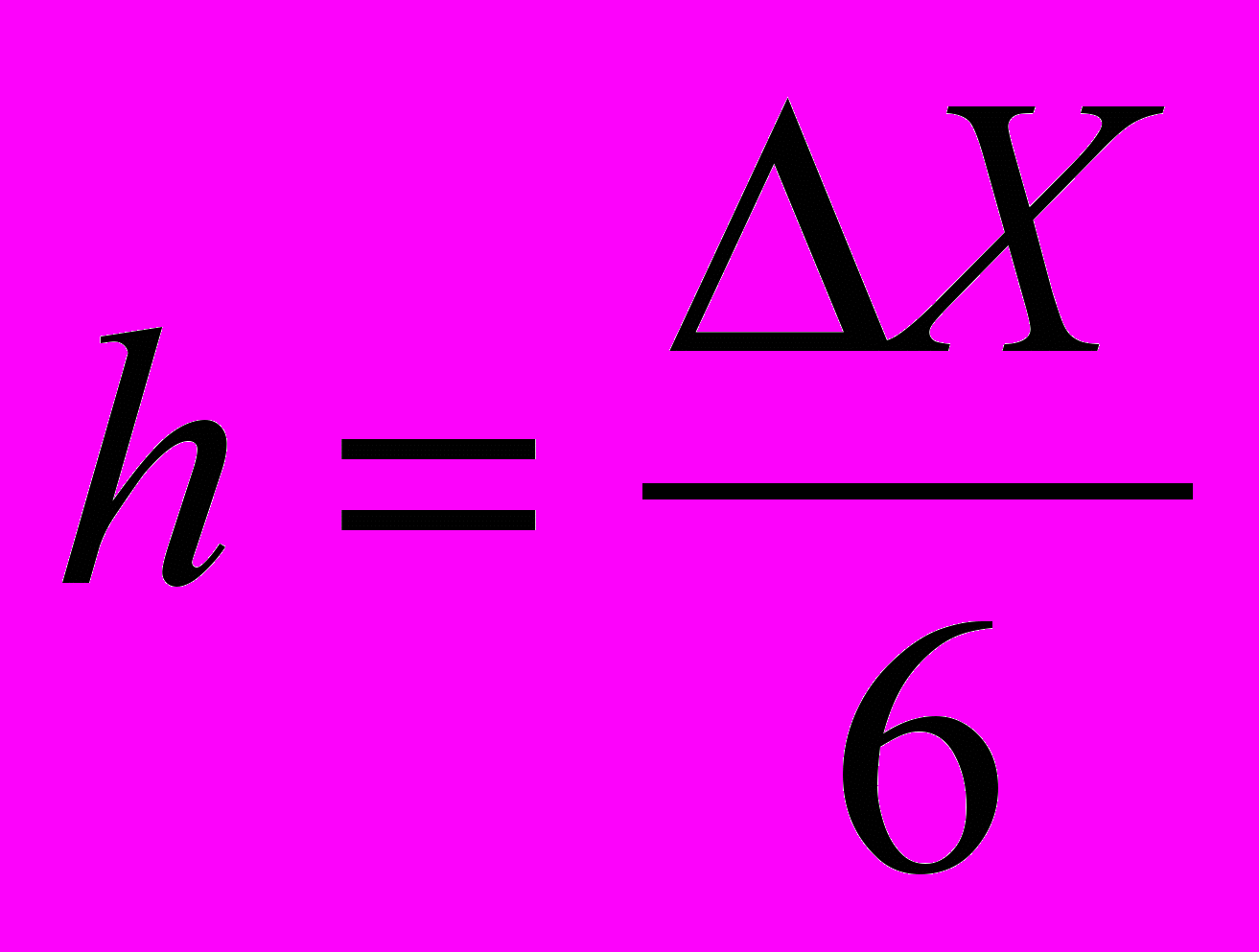, получаем 1,613333. Округляем в большую сторону и принимаем h=1,7.
   
5. По формуле
   

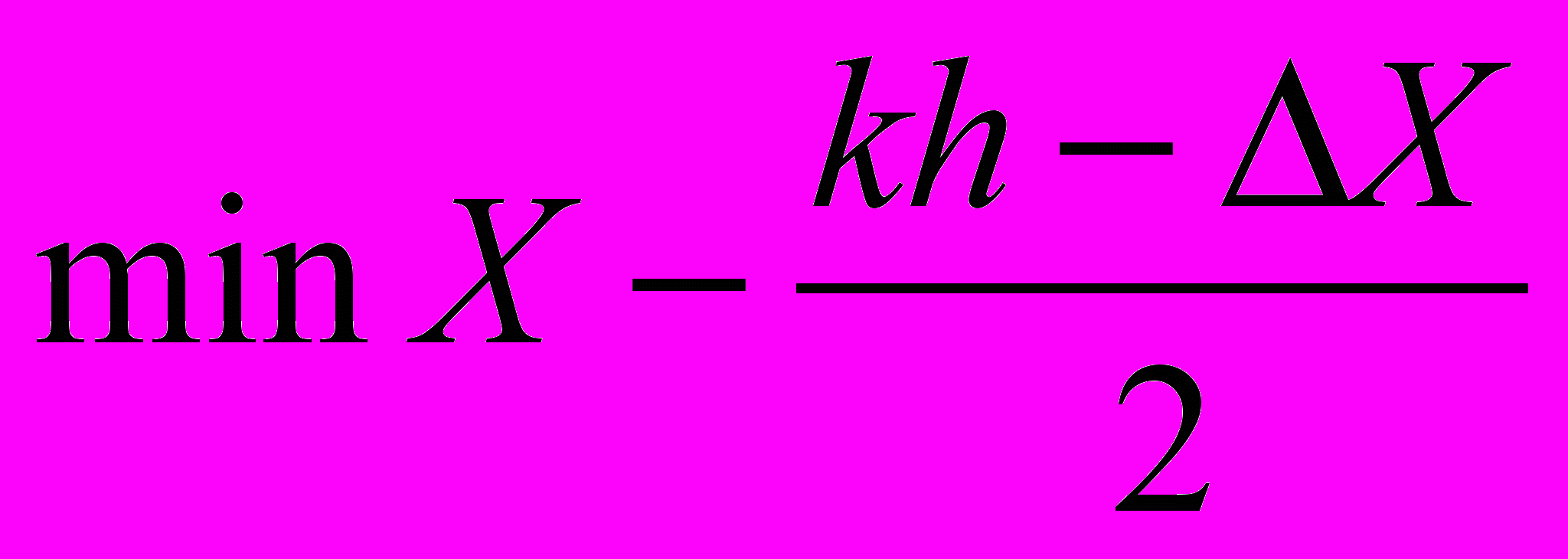
Оцениваем крайнее левое значение первого интервала, что дает 5,56. Округлим до 5,6 (округлить можно: 5,6+6*1,7=15,8>15,5).

6. В диапазоне B1:B7 задаем арифметическую прогрессию, с первым членом 5,6, разностью (шагом) 1,7, предельным значением 15,8:
   

7. C помощью встроенной функции СЧЕТЕСЛИ подсчитываем число вариантов, принадлежащих промежутку (5,6, 7,3] и записываем результат в ячейку C1:
   

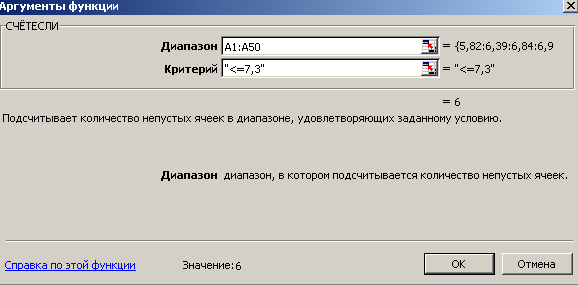
8. Аналогично подсчитываем и записываем в ячейку С2 число вариантов, принадлежащих промежутку (5,6, 9]. Продолжая вычисления, приходим к последовательности:
   

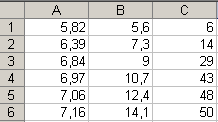
9. Вводим в ячейку D1 формулу =(B1+B2)/2 и копированием ее, задаем в диапазоне D1:D6 середины интервалов. В ячейку E1 вводим 6, а в ячейку E2- формулу =С2-С1. Копируя ее в ячейки Е3: Е6, получаем последовательность частот:
   

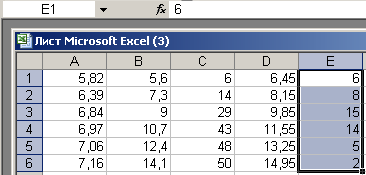
Т. о., интервальный вариационный ряд выборки записывается в виде:

(5,6 ; 7,3)	(7,3; 9)	(9; 10,7)	(10,7; 12,4)	(12,4; 14,1)	(14,1; 15,8)
6	8	15	14	5	2

Дискретный вариационный ряд задан в диапазоне D1:E6.

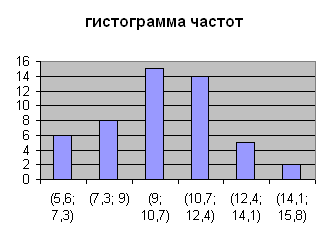
10. С помощью графического редактора «Мастера диаграмм» проводим построение гистограммы частот диапазона E1:E6.
    

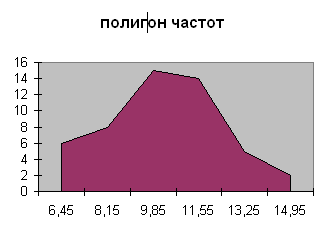
11. Полигон частот строим командами Диаграмма Нестандартные Гистограмма/Область:
    

В командах ДиаграммаНестандартныеГрафики (2 оси) он имеет классический вид: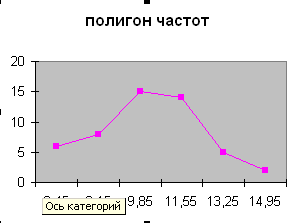



Пример 2. Найти моду для следующих значений выборки: 10; 14; 5; 6; 10; 12; 13.

1. 
   Откройте новую рабочую таблицу. Введите соответствующие значения в ячейки A1:A7.
   
2. Установите курсор в свободную ячейку. На панели инструментов нажмите кнопку Вставка функции (f_x). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию МОДА, после чего нажмите ОК.
   

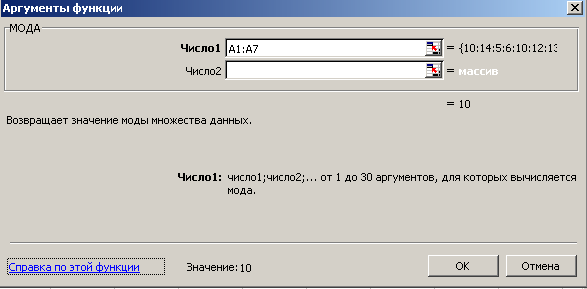
Ответ: 10.

Пример3. Рассматриваются данные, полученные в экспериментальной группе до и после проведения эксперимента. Ниже приведены баллы тестирования.

до	после рекламы
162	135
156	126
144	115
137	140
125	121
145	112
151	130

Требуется найти средние значения и стандартные отклонения этих данных

Решение

1. 
   Для проведения статистического анализа, прежде всего, необходимо ввести данные в рабочую таблицу. Откройте новую рабочую таблицу. Введите в ячейку А1 слово до, затем в ячейки А2:А8 — соответствующие значения числа, В ячейку В1 введите слова после, а в В2:В8 — значения чисел, заметим, что рассматриваемые группы данных со статистической точки зрения являются выборками.
   
2. Для определения среднего значения в контрольной группе необходимо установить табличный курсор в свободную ячейку (А9). На панели инструментов нажмите кнопку Вставка функции (f_x). В появившемся диалоговом окне Мастер функций вы­берите категорию Статистические и функцию СРЗНАЧ, после чего нажмите кнопку ОК.
   Появившееся диалоговое окно СРЗНАЧ за серое поле мышью отодвиньте вправо на 1-2 см от данных (при нажатой левой кнопке). Указателем мыши введите диапазон данных контрольной группы для определения среднего значения (А2:А8). Нажмите кнопку ОК. В ячейке А9 появится среднее значение выборки — 145,714.
   

Для ячейки В9 среднее значение вычисляется аналогично.

3. Для определения стандартного откло­нения в контрольной группе необходимо установить табличный курсор в свободную ячейку (А10). На панели инструментов нажмите кнопку Вставка функции
(f_x). В появившемся диалоговом окне Мастер функций выберите категорию Стати­стические и функцию СТАНДОТКЛОН, после чего нажмите кнопку ОК. Появившееся диалоговое окно СТАНДОТКЛОН за серое поле мышью отодвиньте вправо на 1 -2 см от данных (при нажатой левой кнопке). Указателем мыши введите диапазон данных контрольной группы для определения стандартного отклонения (А2:А8). Нажмите кнопку ОК. Получим стандартное отклонение выборки — 12,298. Существует правило, согласно которому при отсутствии ар­тефактов данные должны лежать в диапазоне М + З (в примере 145,7+36,9).

Стандартное отклонение для столбца В ячейки В10 находится аналогично и равно — 10,277.

Пример 4. Сколькими способами можно расставить на полке 3 выбранных книги из 5 книг, имеющихся в наличии?

Решение

1. 
   Установим курсор в свободную ячейку, например А1.
   
2. Воспользуемся функцией ПЕРЕСТ, нажав на панели инструментов кнопку Вставка функций (fx) и в категории Статистические выбирем функцию ПЕРЕСТ. Нажимаем на кнопку ОК.
   
3. В открывшемся диалоговом окне в поле Число вводим – 5, в рабочее поле Выбранное число вводим 3. Нажимаем на кнопку ОК.
   

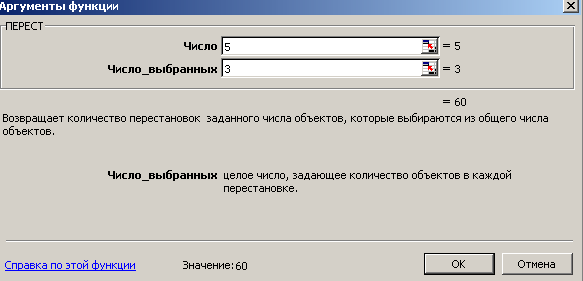
4. В ячейке А1 получим искомое число размещений - 60.
   

Таким образом, 3 книги из 5 имеющихся можно выбрать и расставить на полке шестьюдесятью способами.

Пример 5. Построить диаграмму стандартного нормального интегрального рас­пределения.

Решение

1. 
   В ячейку А1 вводим символ случайной величины х, а в ячейку В1 — символ функции стандартного нормального распределения вероятности — Ф (х).
   
2. Вводим в диапазон А2:А14 значения х от -3 до 3 с шагом 0,5. Для этого в ячейку А2 вводим левую границу диапазона (-3), а в ячейку A3 левую границу плюс шаг (-2,5). Выделяем блок А2:АЗ. Затем за правый нижний угол протягиваем мышью до ячейки А14 (при нажатой левой кнопке).
   
3. Устанавливаем табличный курсор в ячейку В2 и для получения значения вероятности воспользуемся специальной функцией — нажимаем на панели инстру­ментов кнопку Вставка функции (fx).
   
4. В появившемся диалоговом окне Мастер функций-шаг 1 из 2 слева в поле Категория указаны виды функций. Выбираем Статистическая. Справа в поле Функция выбираем функцию НОРМСТРАСП. Нажимаем на кнопку ОК.
   
5. Появляется диалоговое окно НОРМСТРАСП. В рабочее иоле z вводим значение x для которого строится распределение (в примере адрес ячейки А2 щелчком мыши на этой ячейке). Нажимаем на кнопку ОК.
   

В ячейке В2 появляется вероятности р = 0,00135.

Указателем мыши за правый нижний угол табличного курсора протягиванием (при нажатой левой кнопке мыши) из ячейки В2 до В14 копируем функцию НОРМСТРАС в диапазон ВЗ:В14.

По полученным данным строим искомую диаграмму нормальной функции рас­пределения. Щелчком указателя мыши на кнопке на панели инструментов вызы­ваем Мастер диаграмм, В появившемся диалоговом окне выбираем тип диаграммы График, вид — левый верхний. После нажатия кнопки Далее указываем диапазон данных — В1:В14 (с помощью мыши). Проверяем положение переключателя Ряды в: столбцах. Выбираем вкладку Ряд и с помощью мыши вводим диапазон подписей оси Х: А2:А14. Нажав на кнопку Далее, вводим названия осей X и У: :х и Ф(х), соот­ветственно. Нажимаем на кнопку Готово.

Получен график стандартизованной нормальной функции распределения.



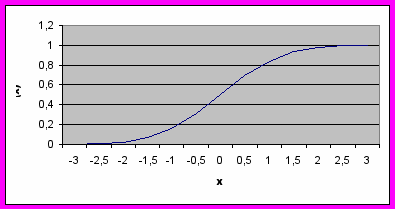
Пример 6. Найти верхнюю и нижнюю квартили для нормальной функции плот­ности вероятности f (х) при М = 24,3 и 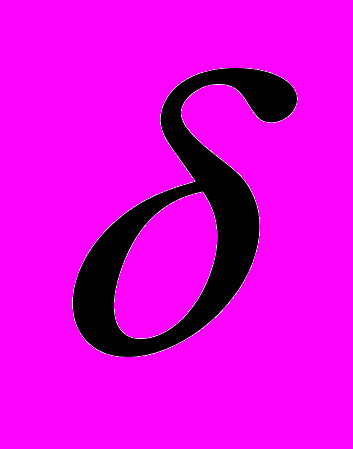= 1,5.

Решение

1. 
   Устанавливаем табличный курсор в ячейку А1 и для получения значения верх­ней квартили воспользуемся специальной функцией: НОРМОБР — нажимаем на панели инструментов кнопку Вставка функции (fx).
   
2. В появившемся диалоговом окне Мастер функций-шаг 1 из 2 слева в поле Категрия указаны виды функций. Выбираем Статистическая. Справа в поле Функция выбираем функцию НОРМОБР. Нажимаем на кнопку ОК.
   
3. Появляется диалоговое окно НОРМОБР. В рабочее поле Вероятность вводим значение вероятности верхней квартили — 0,75 (с клавиатуры). В рабочее поле Среднее вводим с клавиатуры значение математического ожидания М (в примере — 24,3). В рабочее поле Стандартное_откл вводим с клавиатуры значение среднеквадратического отклонения 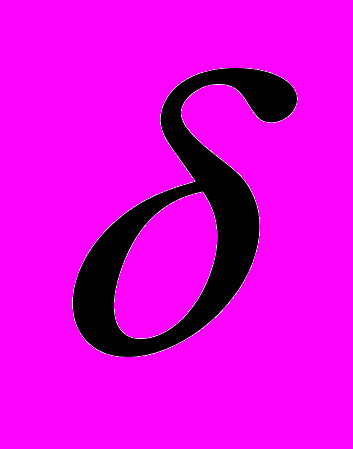(в примере — 1,5). Нажимаем на кнопку ОК.
   
4. В ячейке А1 появляется значение верхней квартили 25,31174.
   

Устанавливаем табличный курсор в ячейку А2 и для получения значения нижней квартили повторяем пункты 1-4. За исключением того, что в п. 3 в рабочее поле Вероятность вводим значение вероятности нижней квартили - 0,25.

В ячейке А2 появляется значение нижней квартили 23,28826.

Таким образом, верхняя и нижняя квартили для нормальной функции плотно­сти вероятности f(x) при М=24,3 и 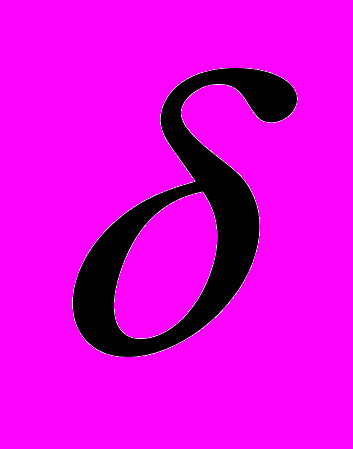=1,5 соответственно равны 25,31174 и 23,28826.

Пример 7. Предприятие получило 1000 мониторов. Вероятность того, что при перевозке монитор окажется поврежденным, равна 0,003. Найти вероятность того, что предприятие получит поврежденных мониторов: 1). ровно два; 2). менее двух; 3). более двух; 4). хотя бы один.

Решение.

Так как n = 1000 велико, а p = 0, 003 мало, то применима формула Пуассона

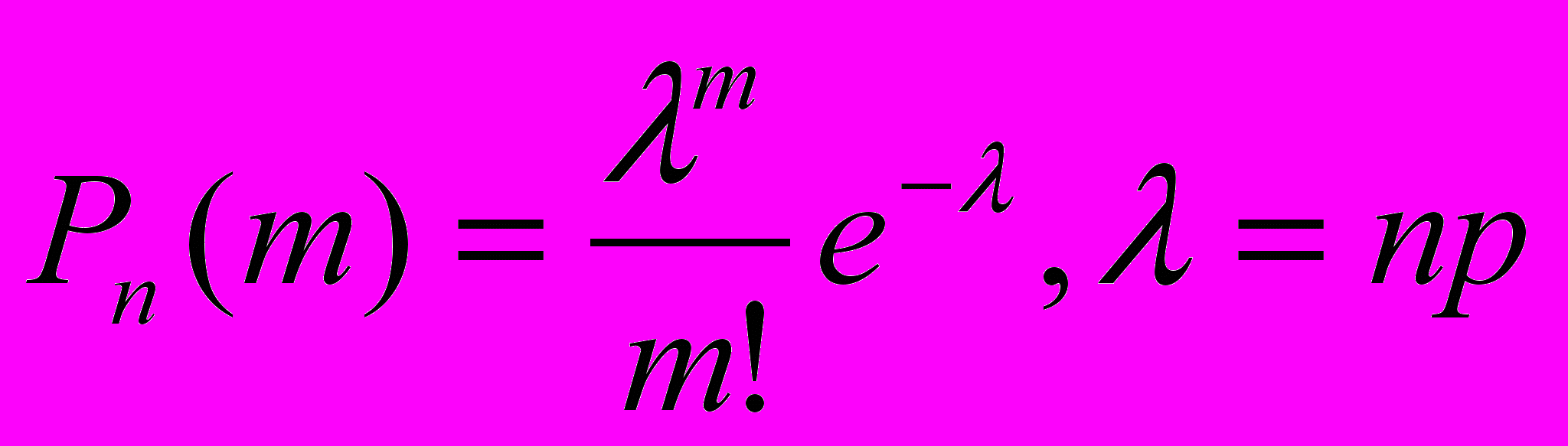, в которой 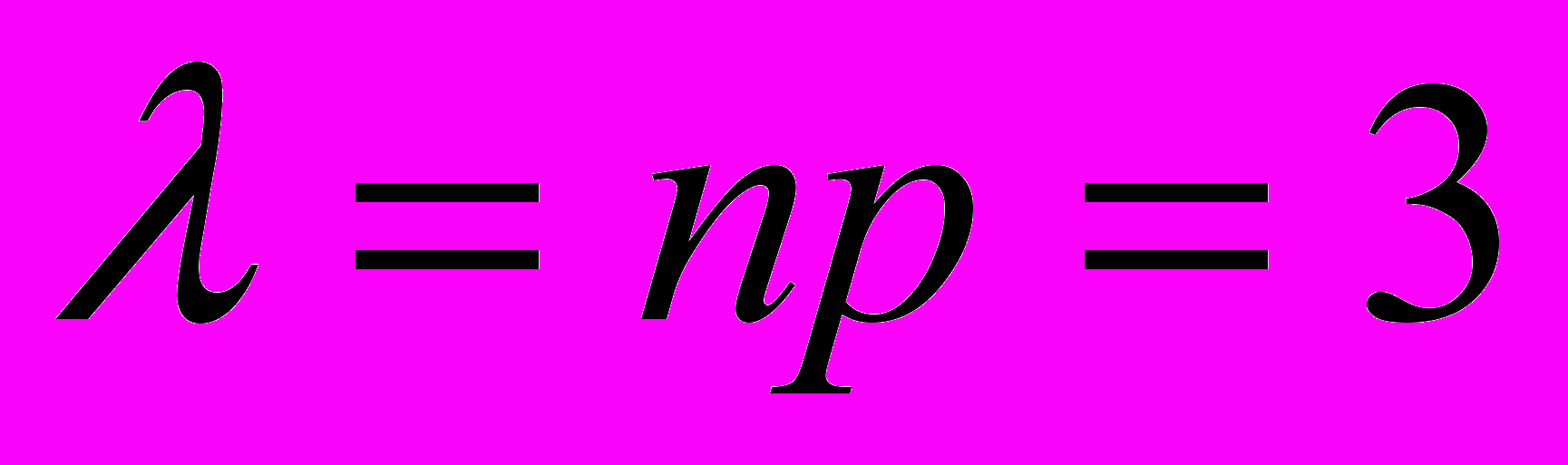. Найдем по ней вероятности, с которыми принимаются значения 0, 1, 2.

1. 
   Вводим их в диапазон А1:A3.
   
2. Выделяем ячейку В1, открываем диалоговое окно ПУАССОН и задаем данные:
   

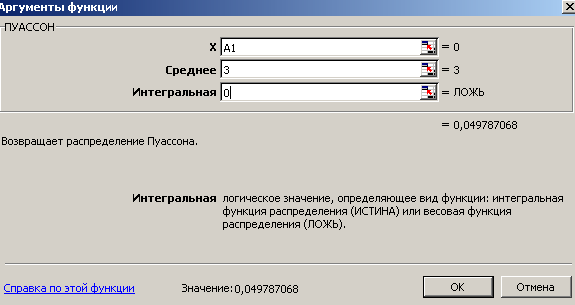
3. Нажимаем ОК и копируем формулу в ячейки В2, В3. Ответ на первый вопрос находится в ячейке В3.
   
4. С помощью кнопки fx находим сумму трех полученных значений.
   
5. Формула =b1+b2, которую запишем в С1, дает ответ на вопрос. Формулой =1- b4 ячейки С2 получаем ответ на третий вопрос. Последняя величина находится по формуле = 1 – b1, ее помещаем в С3. В результате фрагмент таблицы с решением задачи принимает вид:
   

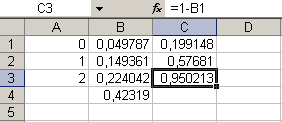
Ответ: Р(2)=0,224042.


Пример 8. Проверить соответствие выборочных данных: 64, 57,63,62, 58,61,63,60,60,61,65,62,62,60,64,61,59,59,63,61,62,58,58,63,61,59,62,60,59,65,60,58,61,60,63,63,58,60,59,60,59,61,62,62,63,62,57,61,58,60,64,60,59,61,64, нормальному закону распределения.

Решение

1. 
   Постройте эмпирическое распределение веса студентов.
   
2. Найдите теоретические частоты нормального распределения. Для этого пред­варительно необходимо найти среднее значение и стандартное отклонение вы­борки.
   

В ячейке I13 найдите среднее значение (СРЗНАЧ ) для данных из диапазона А2:Е12 (60,855). В ячейке J13 с помощью функции СТАНДОТКЛОН най­дите стандартное отклонение для этих же данных (2,05). В ячейки К1 и К2 введите название столбца — Теоретические частости, Затем с помощью функции НОРМРАСП найдите теоретические частости. Установите курсор в ячейку К4, вызовите указанную функцию и заполните ее рабочие поля: х — G4; Среднее — $1$13; Стандартное_откл — $J$13, Интегральный — 0. Получим в ячейке К4 - 0,033. Далее протя­гиванием скопируйте содержимое ячейки К4 в диапазон ячеек К5:К12. Затем в ячей­ки L1 и L2 введите название нового столбца — Теоретические частоты. Установите курсор в ячейку L4 и введите формулу =Н$13*К4. Далее скопи­руйте содержимое ячейки L4 в диапазон ячеек L5: L12.

	G	H	I	J	K	L
1	Вес, кг	Абсолют. частоты	Относит. частоты	Накопленные частоты	Теоретич. частости	Теоретич. частоты
2
3
4	57	2	0,036	0,036	0,033	1,823
5	58	6	0,109	0,145	0,074	4,059
6	59	7	0,127	0,273	0,129	7,109
7	60	10	0,182	0,455	0,178	9,814
8	61	9	0,164	0,618	0,194	10,679
9	62	8	0,145	0,764	0,167	9,158
10	63	7	0,127	0,891	0,113	6,189
11	64	4	0,073	0,964	0,059	3,297
12	65	2	0,036	1,000	0,025	1,384

3. С помощью функции ХИ2ТЕСТ определите соответствие данных нормальному закону распределения. Для этого установите табличный курсор в свободную ячейку L13. На панели инструментов Стандартная -> Вставка функ­ции (f_x). Выберите категорию Статистические -> ХИ2ТЕСТ-> ОК. Указате­лем мыши в рабочие поля введите фактический Н4:Н12 и ожидаемые L4:L12 ди­апазоны частот. ОК. В ячейке L13 появится значение вероятности того, что выборочные данные соответствуют нормальному закону распределения — 0,9842.

4. Поскольку полученная вероятность соответствия экспериментальных данных р = 0,98 много больше, чем уровень значимости 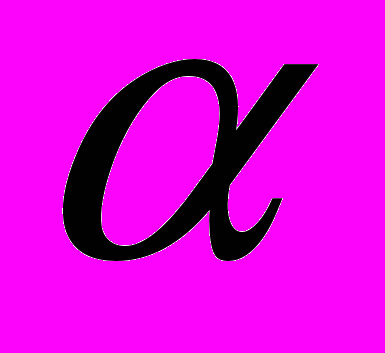= 0,05, то можно утверждать, что нулевая гипотеза не может быть отвергнута и, следовательно, данные не противоречат нормальному закону распределения. Более того, поскольку по­лученная вероятность р = 0,98 близка к 1, можно говорить о высокой степени вероятности того, что экспериментальные данные соответствуют нормально­му закону.

Приме 9. Пусть после окончания двух институтов экономического профиля трудоустроилось по специальности из первого института 90 человек, а из второго 60 (обе группы молодых специалистов включали по 100 человек).

Решение

1. Принимается нулевая гипотеза, что выборки принадлежат к одной генераль­ной совокупности.

2. 
   Определяется ожидаемое значение результата (среднее значение между выборками): (60 + 90)/2 = 75, то есть мы ожидали, что разницы между группами нет, и в обоих случаях должно было трудоустроиться по 75 человек.
   
3. Затем вычисляется значение вероятности того, что изучаемые события (трудоустройство в обеих выборках) произошли случайным образом. Для этого введите данные в рабочую таблицу: 90 — в ячейку Е1, 60 — в F1, 75 — в E2,F2 Табличный курсор установите в свободную ячейку (ЕЗ). На панели инстру­ментов нажмите кнопку Вставка функции (f_x). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию ХИ2ТЕСТ, после чего нажмите кнопку ОК. Появившееся диалоговое окно ХИ2ТЕСТ за серое поле мышью отодвиньте вправо на 1-2 см от данных (при нажатой левой кнопке). Указателем мыши введите диапазон данных наблюдавшегося количества трудоустроившихся в поле Фактический интервал (E1:F1). В поле Ожидаемый интер­вал введите диапазон данных предполагаемого количества трудоустроившихся (E2 :F2). Нажмите кнопку ОК. В ячейке ЕЗ появится значение вероятности —0,014306.
   
4. Поскольку величина вероятности случайного появления анализируемых вы­борок (0,0143) меньше уровня значимости (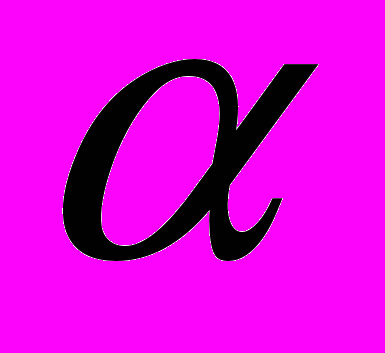= 0,05), то нулевая гипотеза от­вергается. Следовательно, различия между выборками не могут быть случай­ными и выборки считаются достоверно отличающимися друг от друга. Поэтому на основании применения критерия хи-квадрат можно сделать вывод о том, что в двух группах выпускников выявлены достоверные отличия по успешно­сти трудоустройства (р < 0,05), что, по-видимому, явилось результатом более высокой репутации выпускников первого института.
   

Пример 10. Найти основные выборочные характеристики для выборки 10; 14; 5; 6; 10; 12; 13.

Решение.

Для работы с несколькими выборками и углубленного анализа данных, в пакете Excel имеется инструмент Пакет анализа, который может использоваться для решения задач статистической обработки выборочных данных.

Для того, чтобы установить раздел Анализ данных, необходимо выполнить следующее:

• в меню Сервис выбрать команду Надстройки;
  
• в открывшемся списке установить флажок Пакет анализа.
  

Для нахождения основных выборочных характеристик используется процедура Описательная статистика, которая дает информацию о центральной тенденции и изменчивости входных данных. При ее использовании могут быть получены числовые характеристики нескольких рядов данных, каждому ряду будет соответствовать свой столбец (или строка, в зависимости от ввода данных) статистики. Для использования процедуры необходимо:

• произвести команду Сервис Анализ данных;
  
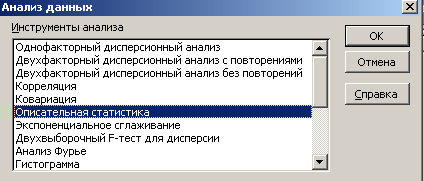
• в списке Инструменты анализа выбрать строку Описательная статистика ОК.
  

• в открывшемся диалоговом окне отметить параметр «Итоговая статистика» ОК.
  

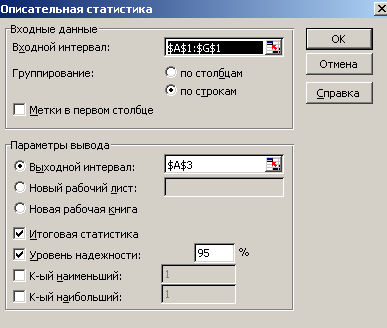
В результате будет получен полный список числовых характеристик выборки.