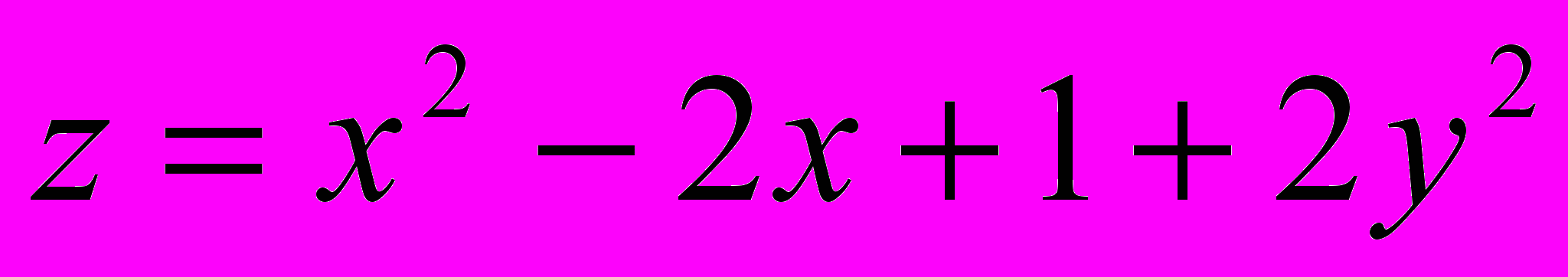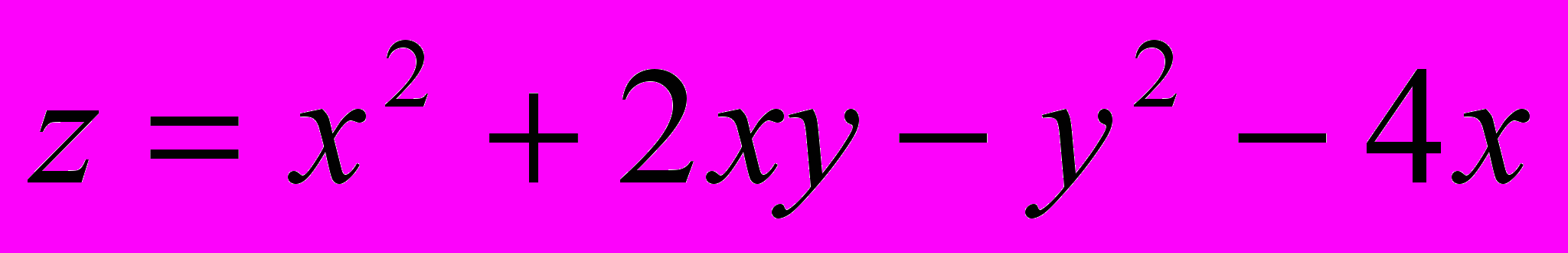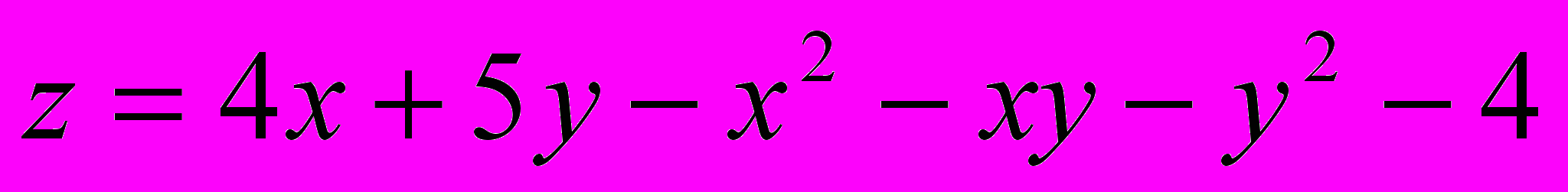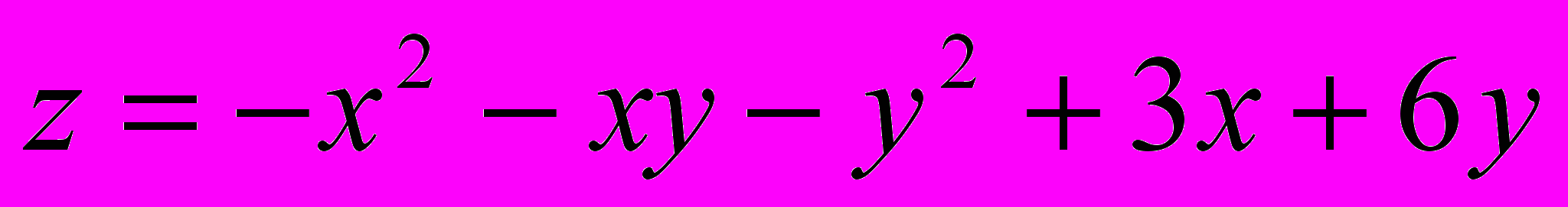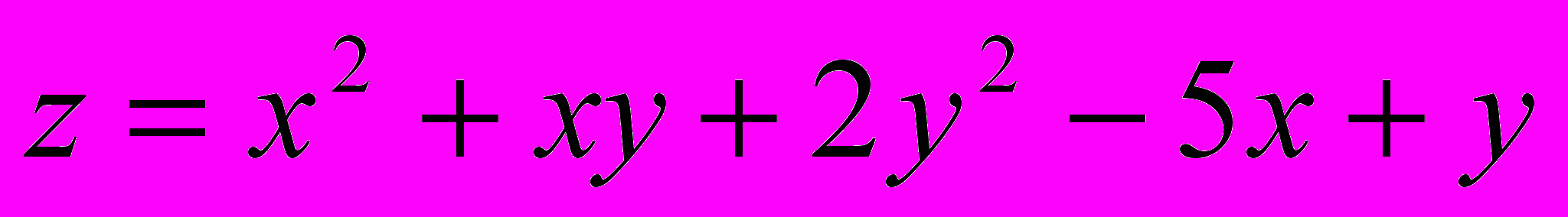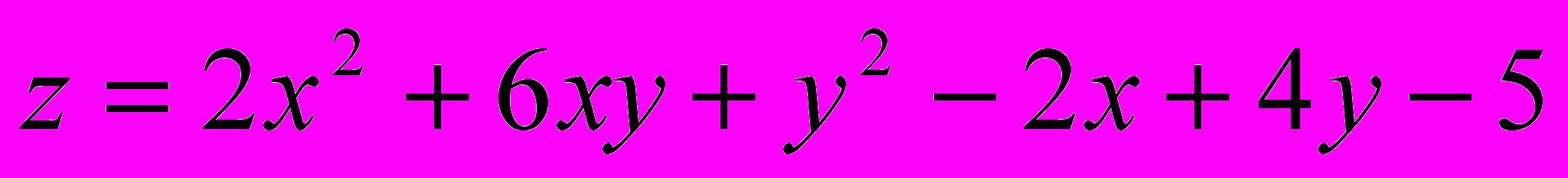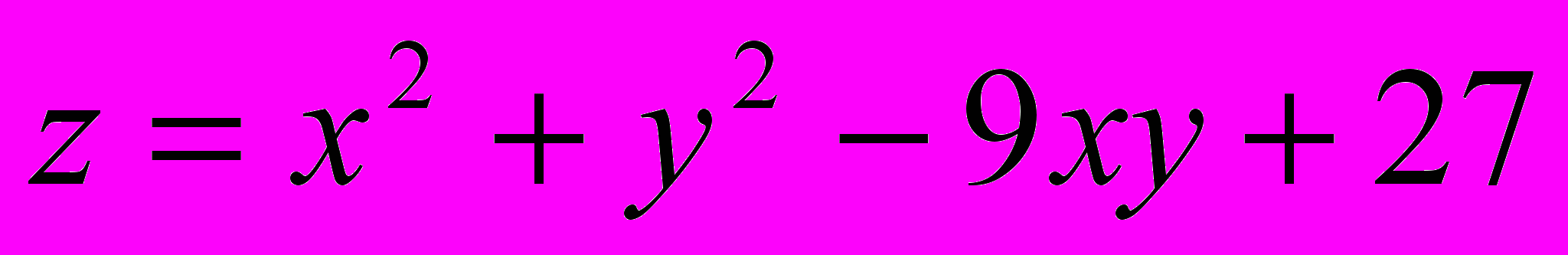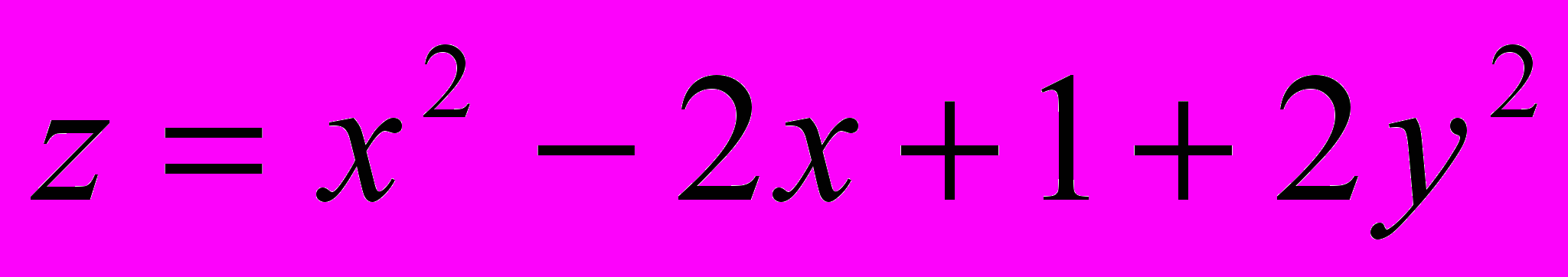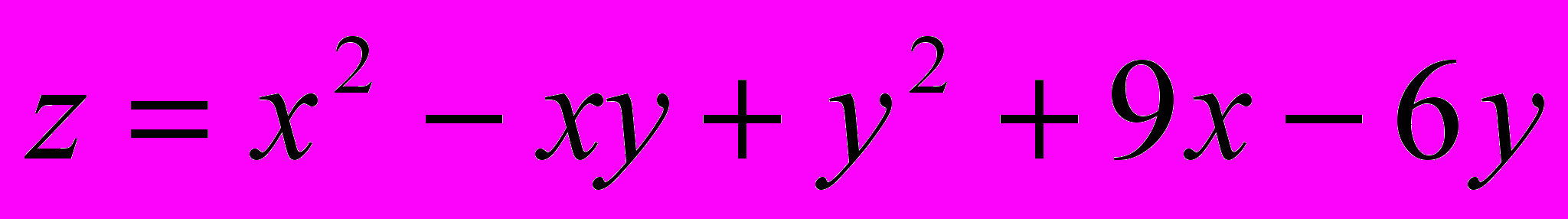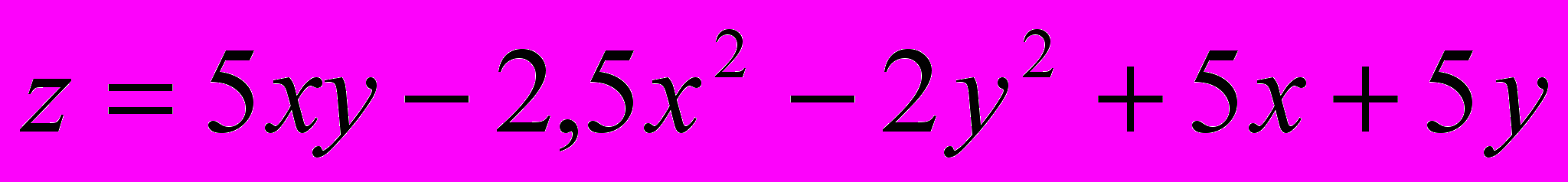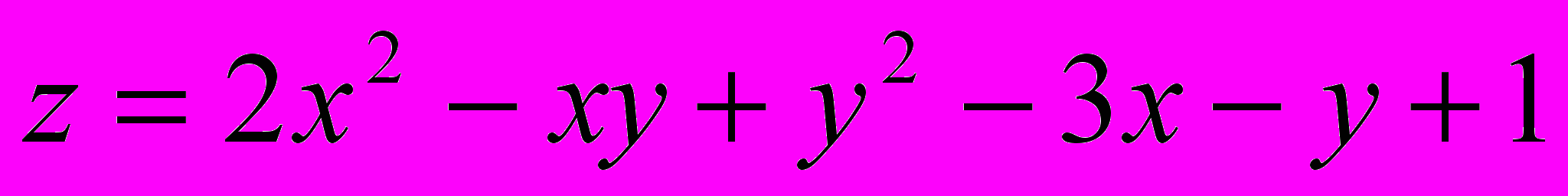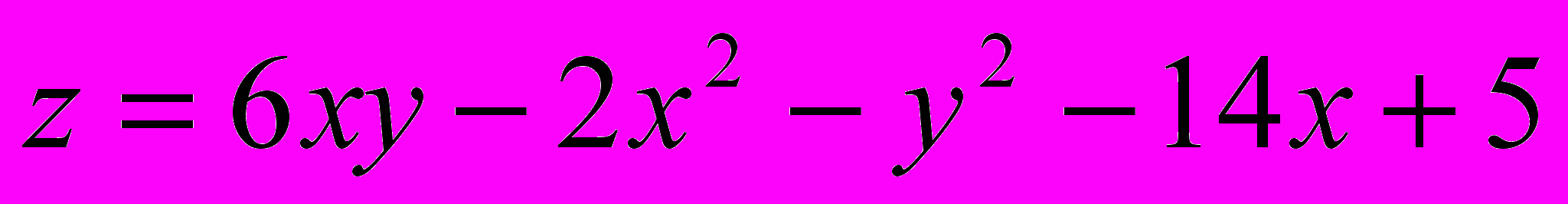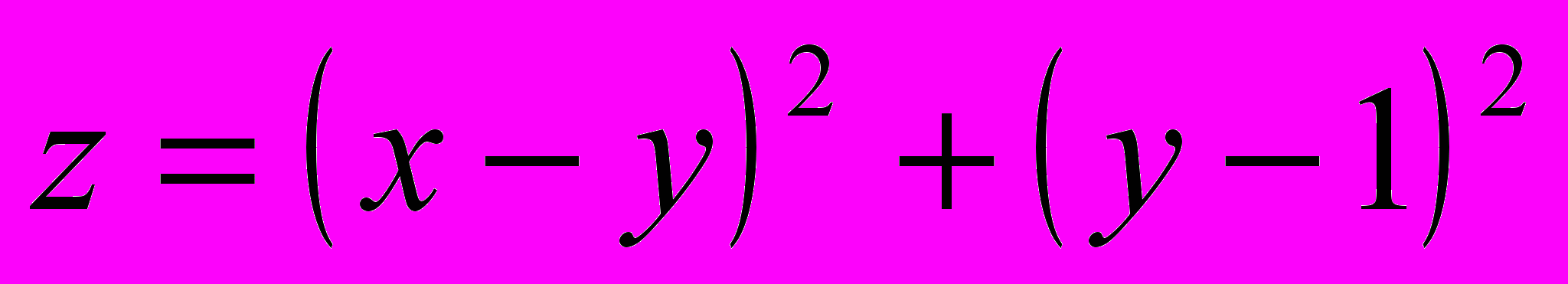Geum.ru

Методические указания и контрольные задания для студентов заочного отделения инженерного факультета Вологда-Молочное

Вид материалаМетодические указания

Содержание


Контрольная работа № 3
Таблица 1. (предпоследняя цифра вашего шифра нечётная
Таблица 2. (предпоследняя цифра вашего шифра чётная
Рекомендуемая литература
Справочный материал
Основные алгебраические тождества
Контрольная работа №
Необходимое условие экстремума
Достаточное условие экстремума
Контрольная работа № 4
Подобный материал:
  1   2

Министерство сельского хозяйства Российской Федерации


ФГОУ ВПО «Вологодская государственная молочнохозяйственная
академия имени Н.В. Верещагина»

Кафедра высшей математики и физики



МАТЕМАТИКА


Методические указания и контрольные задания

для студентов заочного отделения

инженерного факультета


Вологда–Молочное

2010


ПОРЯДОК ВЫПОЛНЕНИЯ

КОНТРОЛЬНЫХ РАБОТ


Настоящее пособие содержит 4 контрольные работы по высшей математике и методические указания по выполнению каждой из работ.

На первом курсе студенты-заочники выполняют работы 1 и 2, на втором курсе – работы 3 и 4.

Перед выполнением каждой контрольной работы студент должен изучить соответствующие разделы рекомендуемой литературы и может воспользоваться решениями типовых примеров, содержащихся в данных методических указаниях.

В начале пособия приведён справочный материал, который включает в себя формулы, табличные значения и т.п., используемые при решении задач.

Каждая контрольная работа выполняется в отдельной тетради. На внешней обложке студент должен указать свои фамилию, имя, отчество, учебный шифр, дисциплину, номер контрольной работы, курс, факультет, специальность (пример оформления титульного листа представлен далее). Работа сдаётся на кафедру и там регистрируется. Решения всех задач и пояснения к ним должны быть достаточно подробными. Все вычисления необходимо делать полностью. В работе должны быть поля для замечаний проверяющего преподавателя.

Во время сессии студент должен быть готов (по требованию преподавателя) давать пояснения к предъявленным решениям контрольных работ.

Контрольные работы сдаются по прибытии на сессию. В случае незачёта работа возвращается для внесения исправлений. Оформить исправленные задания нужно в той же тетради и сдать на повторную проверку в кратчайший срок. Если есть затруднения при решении какого-либо задания, то, приехав на сессию, обратитесь для получения консультации к преподавателям, ведущим занятия по дисциплине.

Студент выполняет тот вариант контрольных работ, который совпадает с последней цифрой его учебного шифра (номер зачётки). При этом если предпоследняя цифра учебного шифра – нечётное число (1, 3, 5, 7, 9), то номера задач для соответствующего варианта даны в таблице 1; если же предпоследняя цифра учебного шифра – чётное число или ноль (2, 4, 6, 8, 0), то номера задач для соответствующего варианта даны в таблице 2.


Пример оформления титульного листа (в печатном или рукописном виде).




Министерство сельского хозяйства Российской Федерации

ФГОУ ВПО «Вологодская государственная молочнохозяйственная

академия имени Н.В. Верещагина»


Инженерный факультет

Специальность:

Заочное отделение

Кафедра высшей математики и физики


^ Контрольная работа № 3

по дисциплине «Математика»


Выполнил

студент 1 курса: Соколов Н. А.

шифр 0837012


Проверил:


Вологда-Молочное

2011


^ Таблица 1. (предпоследняя цифра вашего шифра нечётная)


Номер

варианта
Первый курс
Второй курс

Работа

№ 1
Работа

№ 2
Работа

№ 3
Работа

№ 4

1







1, 21, 41
1, 21, 41,

61

2







2, 22, 42
2, 22, 42,

62

3







3, 23, 43
3, 23, 43,

63

4







4, 24, 44

4, 24, 44,

64

5







5, 25, 45
5, 25, 45,

65

6







6, 26, 46
6, 26, 46,

66

7







7, 27, 47
7, 27, 47,

67

8







8, 28, 48


8, 28, 48,

68

9







9, 29, 49
9, 29, 49,

69

0







10, 30, 50
10, 30, 50,

70



^ Таблица 2. (предпоследняя цифра вашего шифра чётная)


Номер

варианта
Первый курс
Второй курс

Работа

№ 1
Работа

№ 2
Работа

№ 3
Работа

№ 4

1






11, 31, 51


11, 31, 51,

71

2






12, 32, 52
12, 32, 52,

72

3






13, 33, 53
13, 33, 53,

73

4






14, 34, 54
14, 34, 54,

74

5






15, 35, 55
15, 35, 55,

75

6






16, 36, 56
16, 36, 56,

76

7






17, 37, 57
17, 37, 57,

77

8






18, 38, 58
18, 38, 58,

78

9






19, 39, 59
19, 39, 59,

79

0






20, 40, 60


20, 40, 60,

80



^ РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА


Основная
  1. Выгодский М.Я. Справочник по высшей математике.– Любое издание.
  2. Минорский В.П. Сборник задач по высшей математике. – М.: Физматлит, 2003.
  3. Письменный Д.Т. Конспект лекций по высшей математике. - М.: Айрис-пресс, 2004.


Дополнительная
  1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. – М.: Издательский дом «ОНИКС 21 век»: Мир и Образование, 2002.
  2. Шипачев В.С. Высшая математика. – М.: Высшая школа, 2003.


В дальнейшем ссылки на литературные источники будут указываться номерами в квадратных скобках, например, 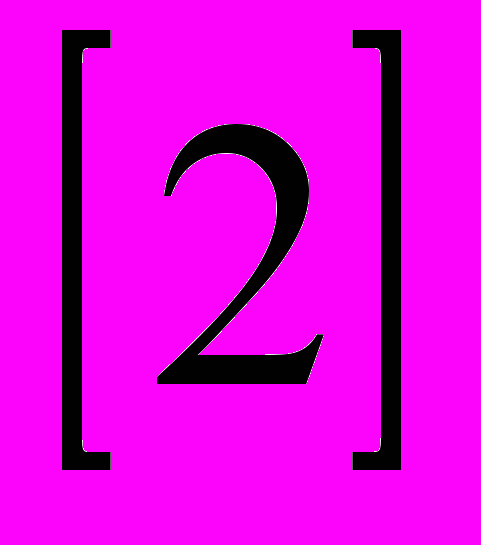. Номер в скобках соответствует номеру источника в данном списке.


^ СПРАВОЧНЫЙ МАТЕРИАЛ


В данном разделе содержатся основные формулы, табличные значения и т.п., необходимые для самостоятельного выполнения заданий.

^ Основные алгебраические тождества


  1. Разность квадратов:

.
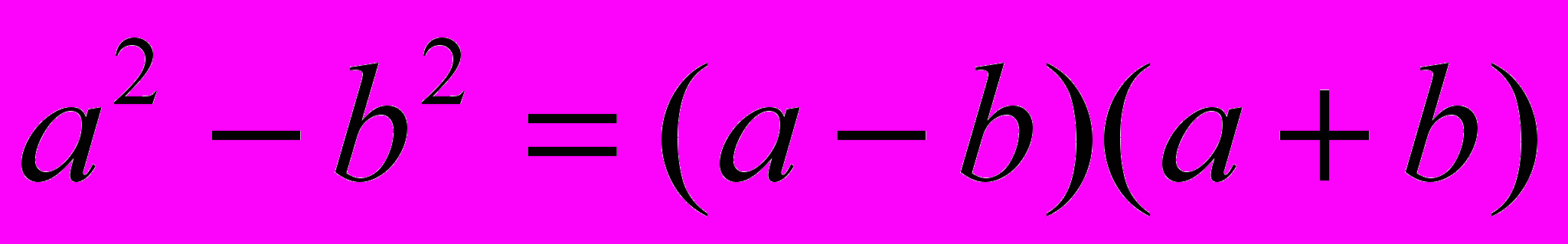  1. Квадрат суммы (разности):

.
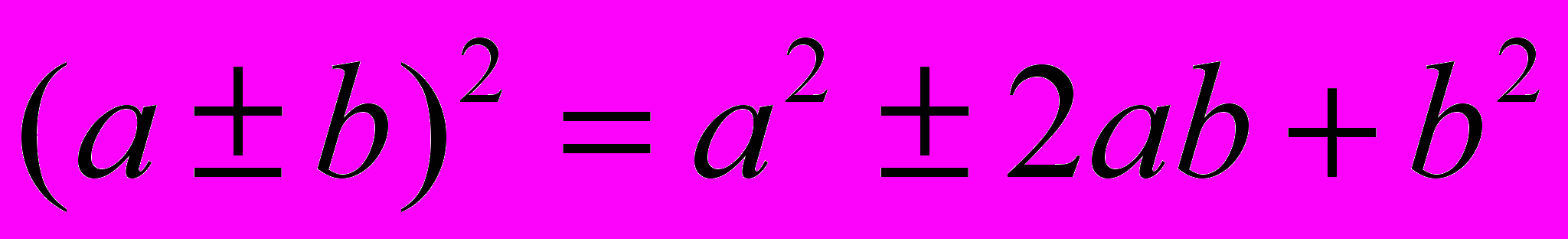  1. Куб суммы (разности):

.
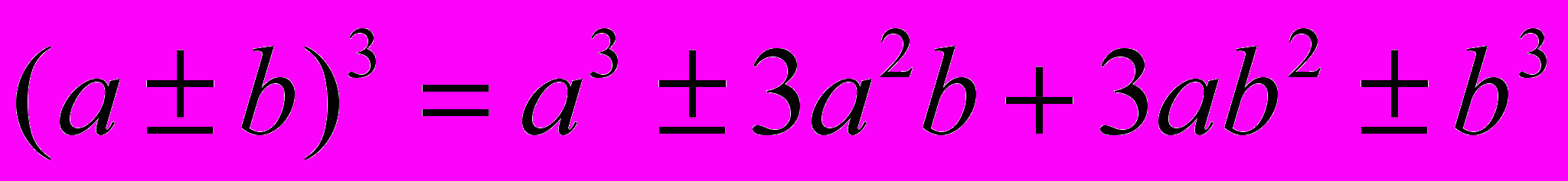  1. Сумма (разность) кубов:

.
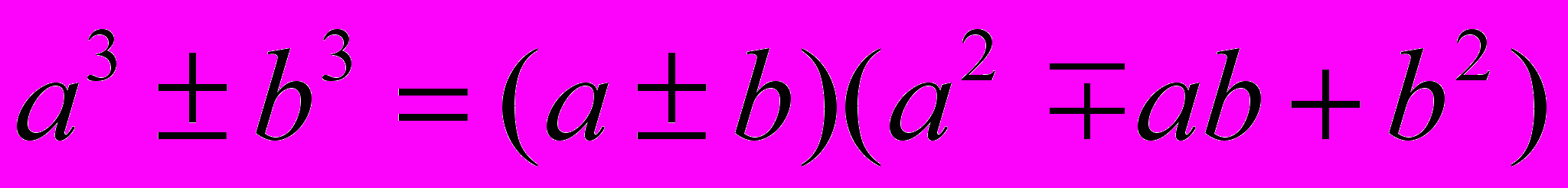  1. Разложение на множители квадратного трехчлена:

,

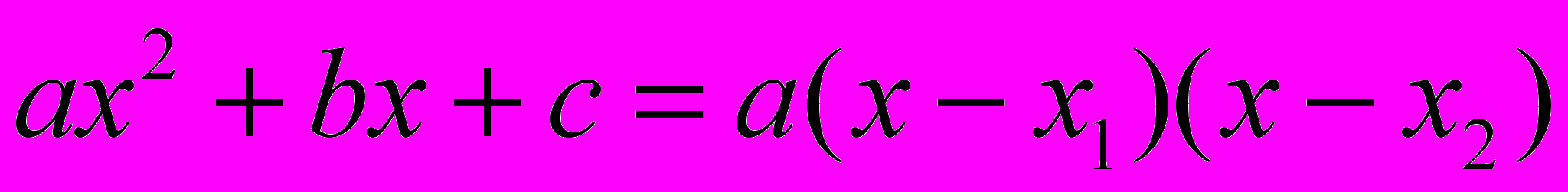где 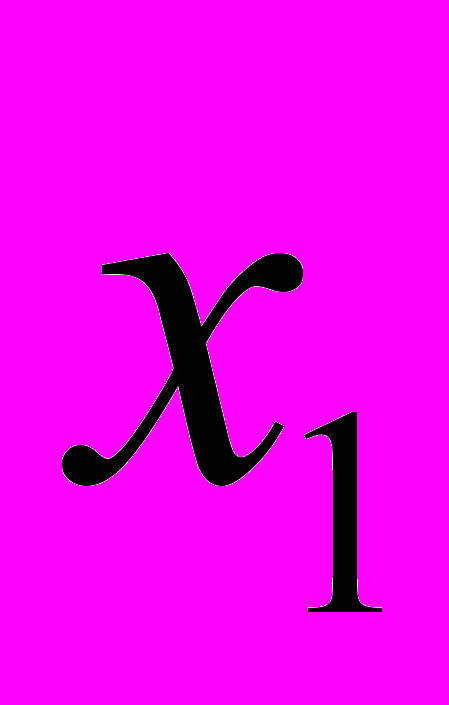и 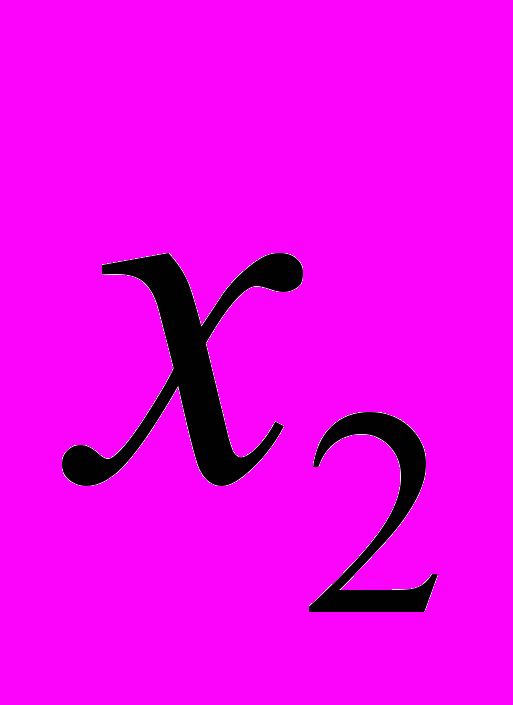— корни квадратного трехчлена, вычисляемые по формулам:

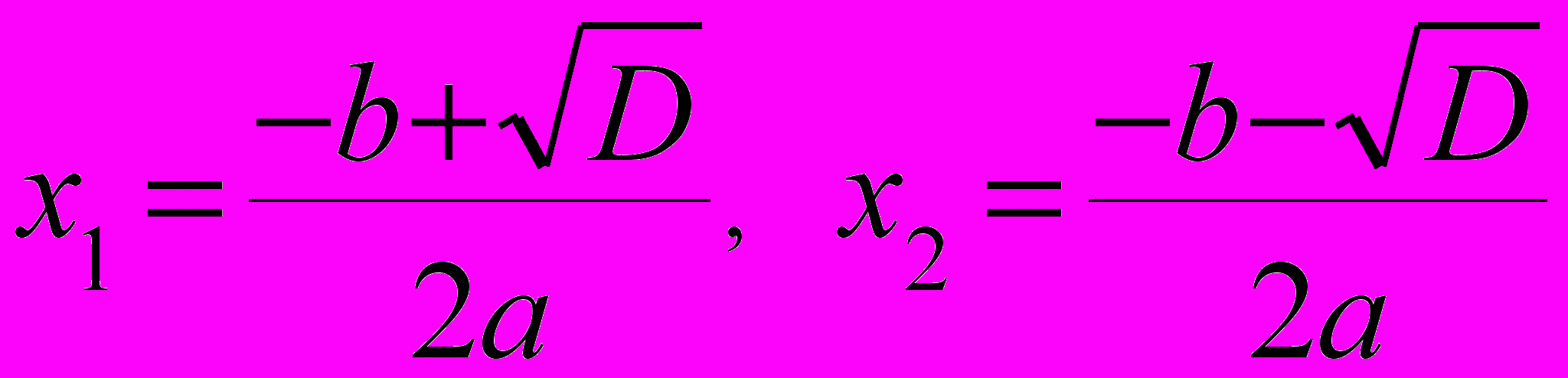, где .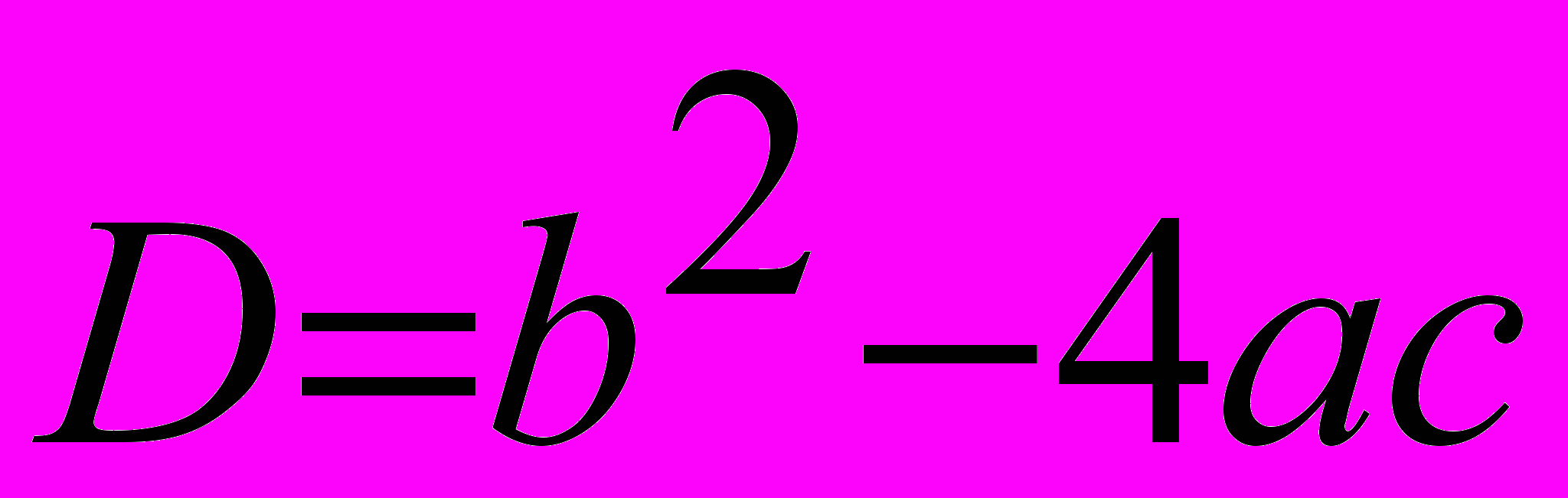


Основные тригонометрические формулы

1. ;

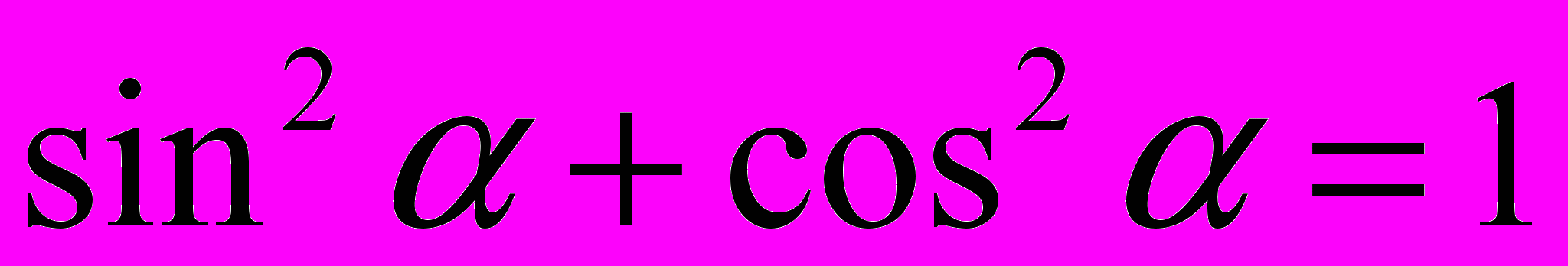2. ;

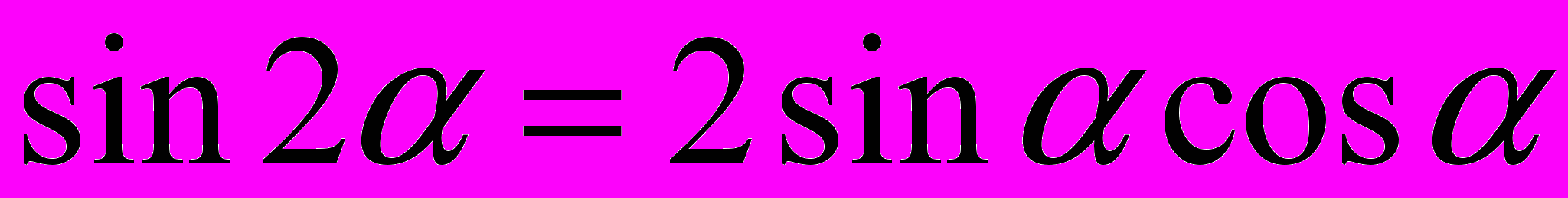3. ;

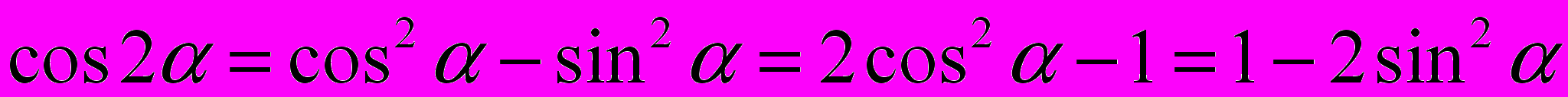4. ;

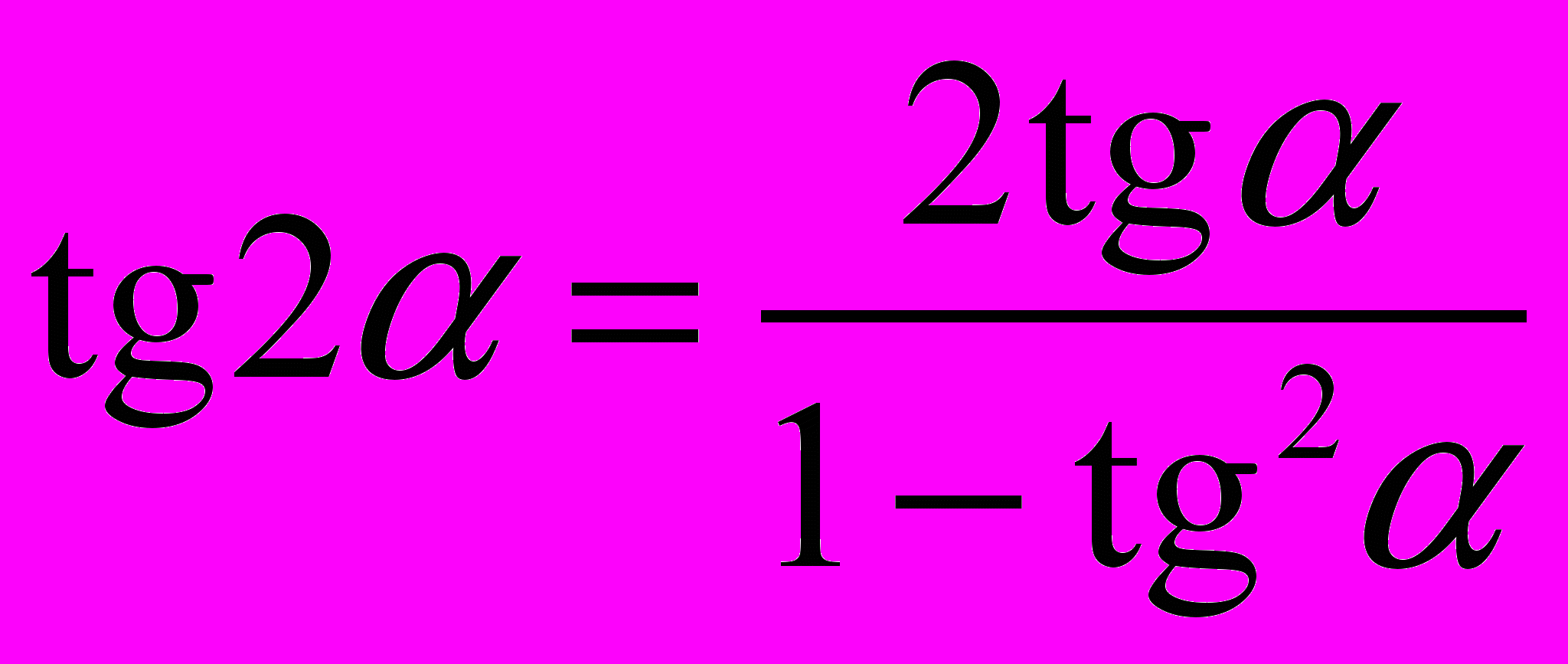5. ;

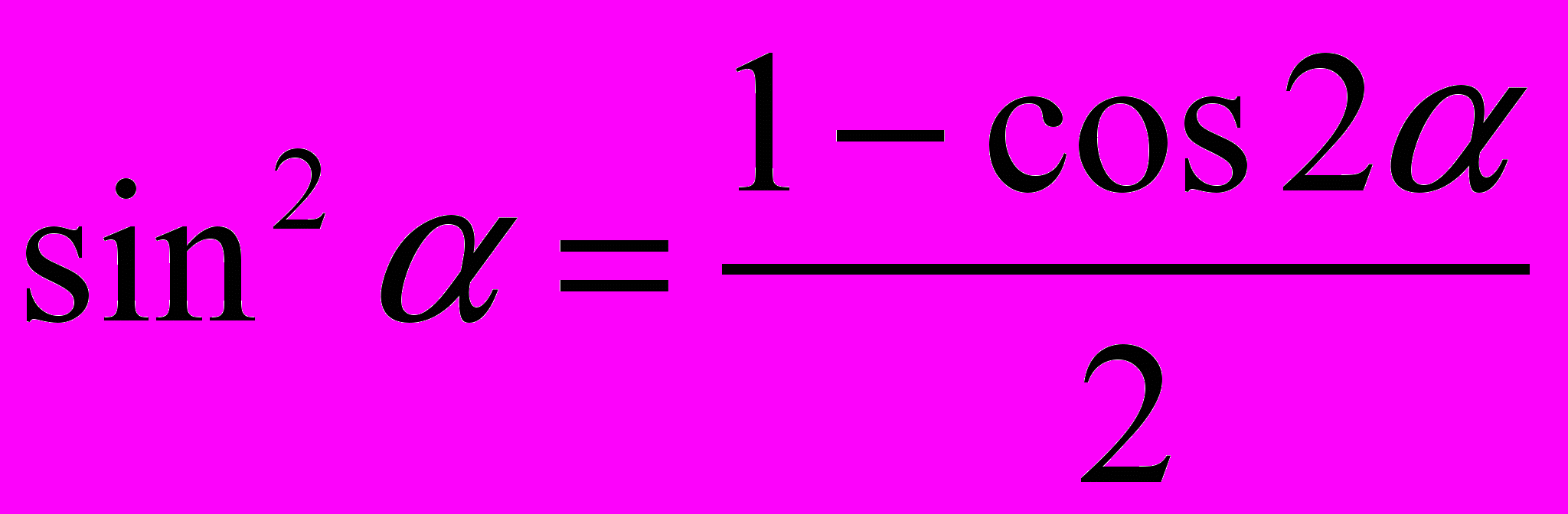6. ;

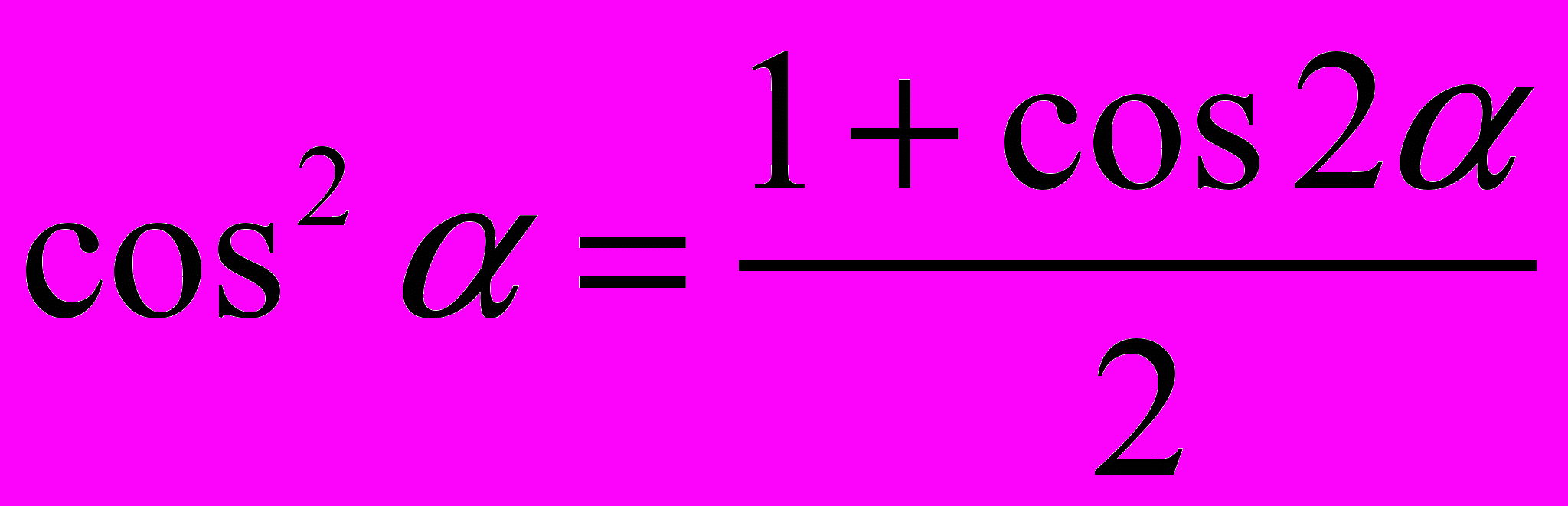7. ;

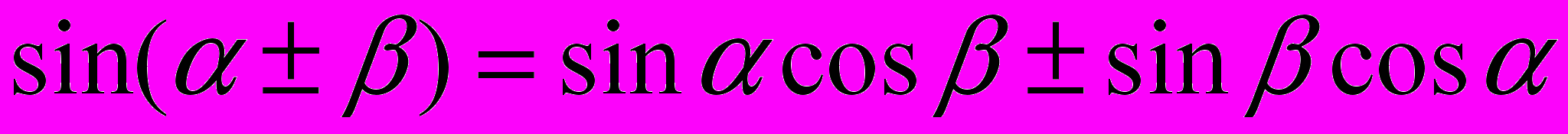8. ;

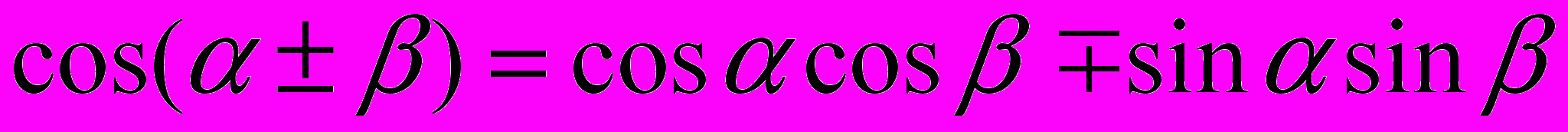9. ;

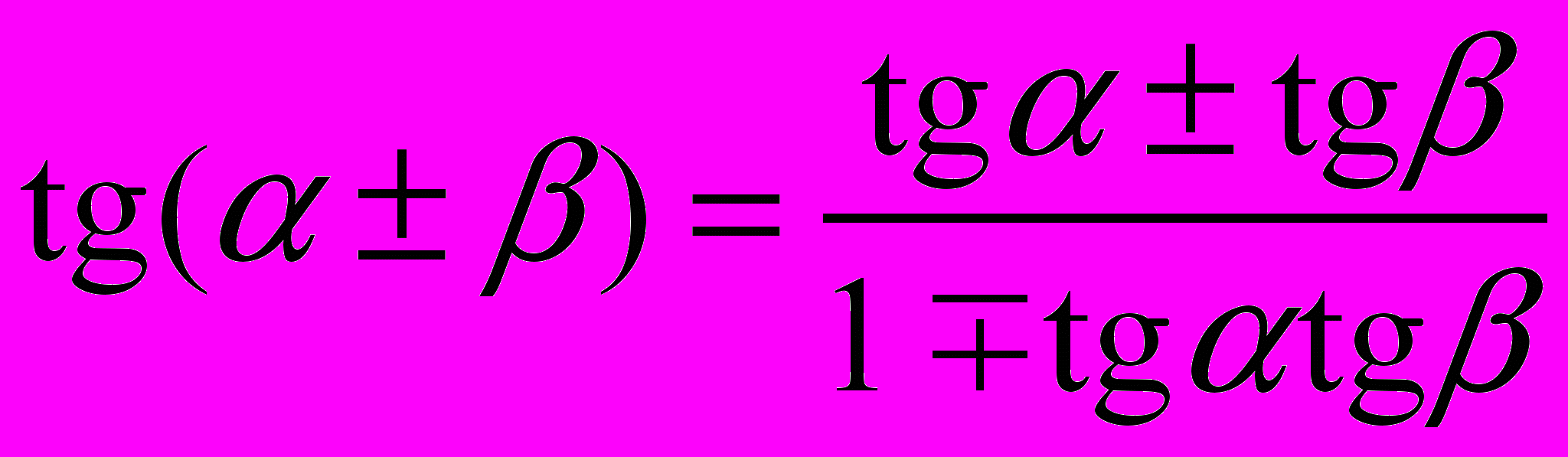10. ;

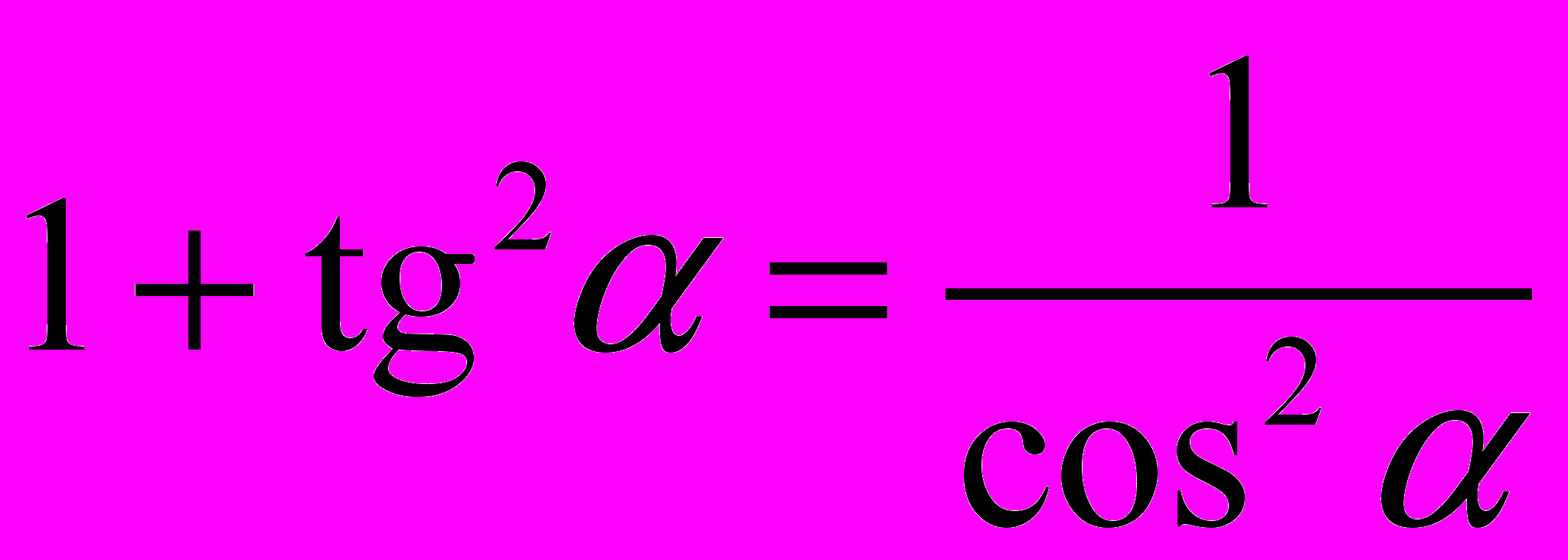11. ;

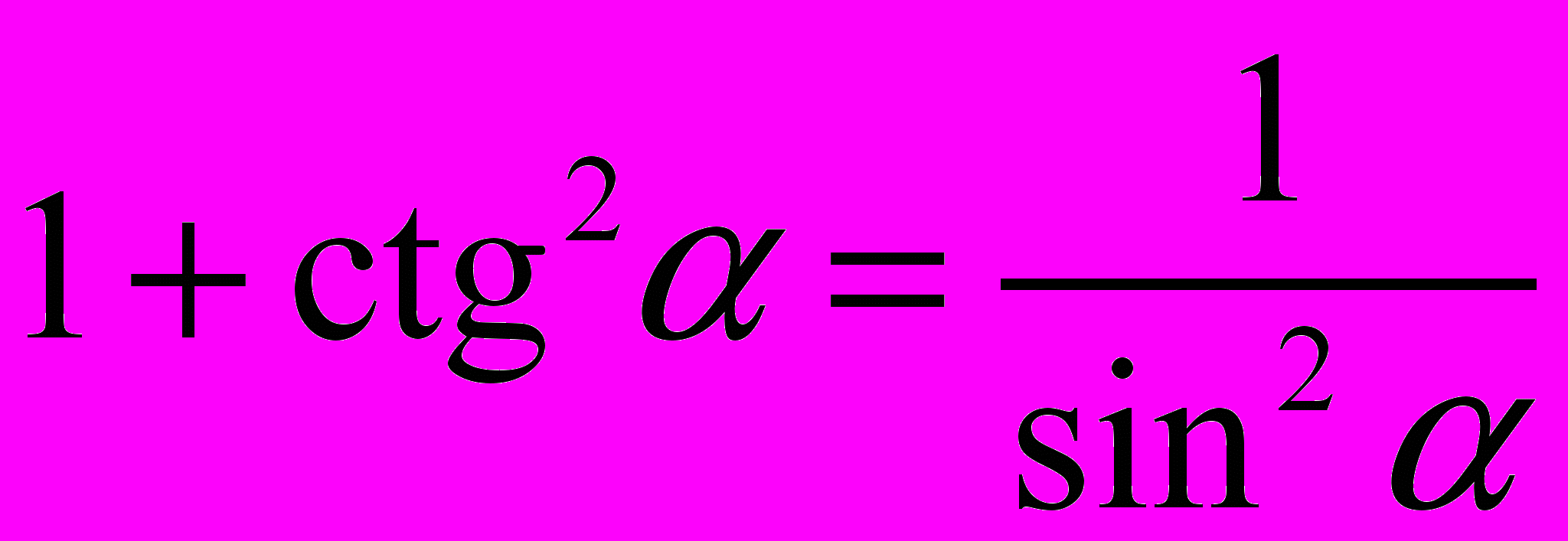12. ;

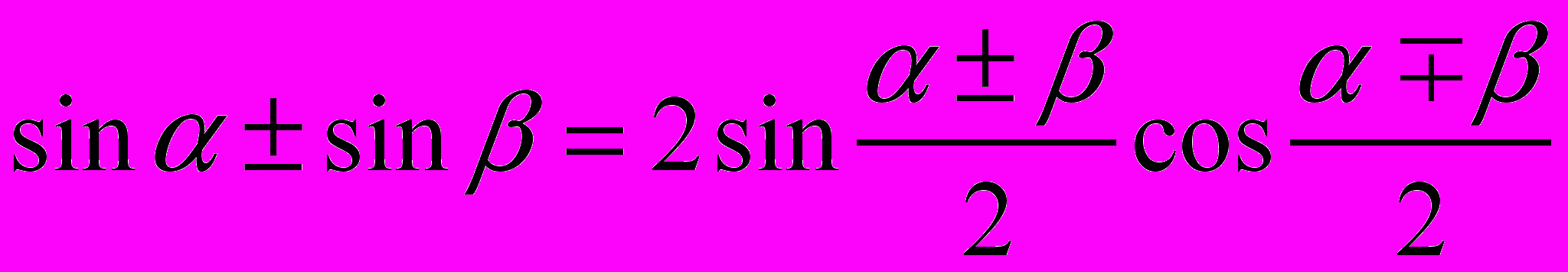13. ;

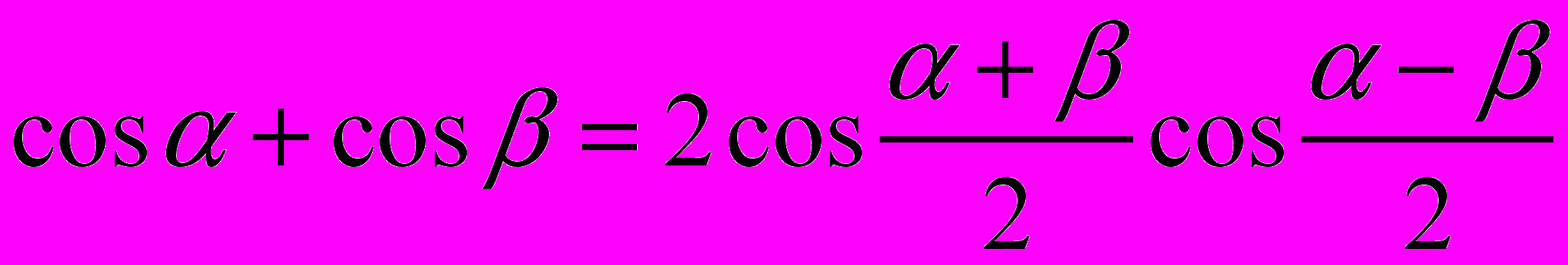14. ;

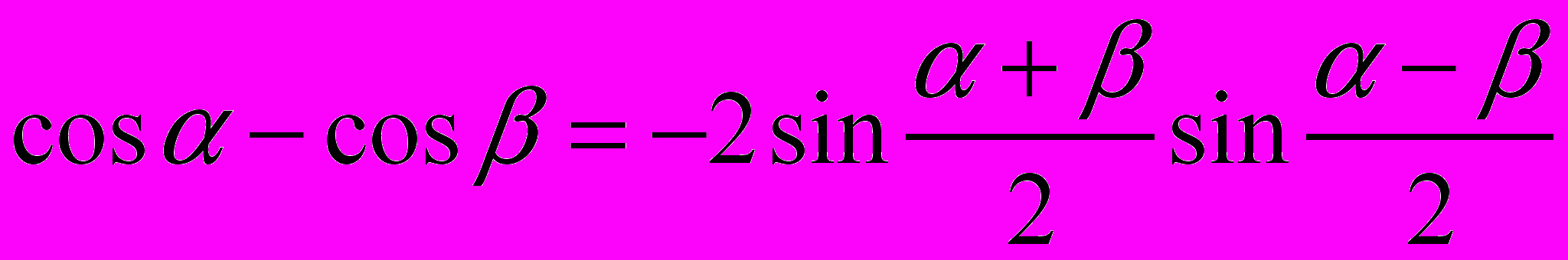15. ;

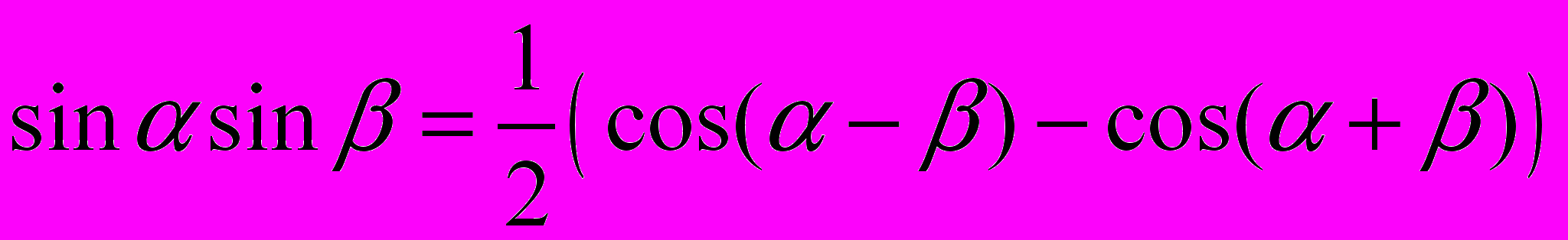16. ;

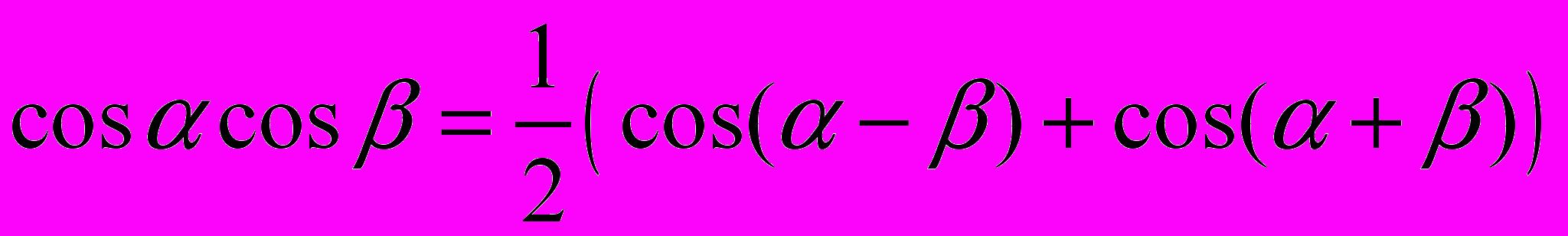17. ;

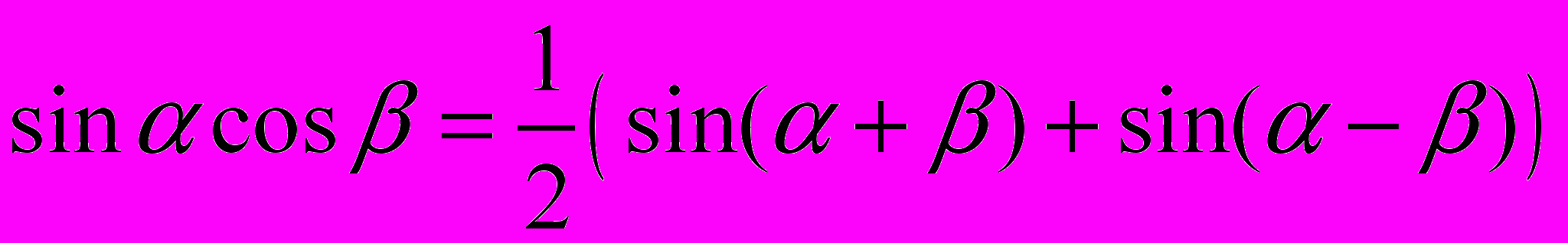18. ;

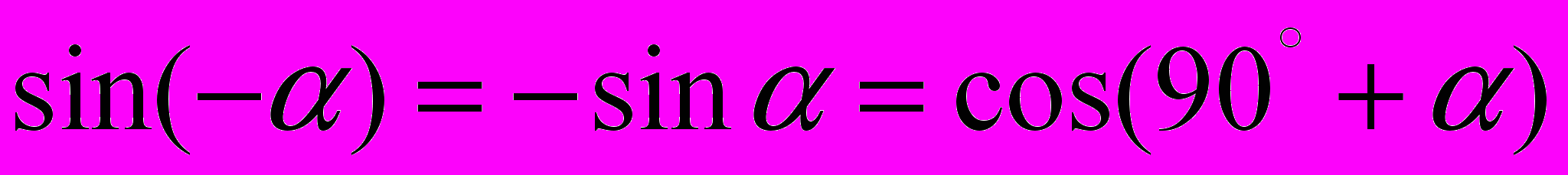19. ;

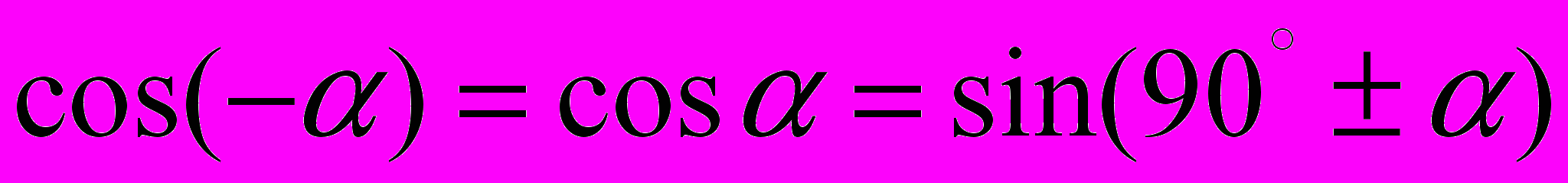20. ;

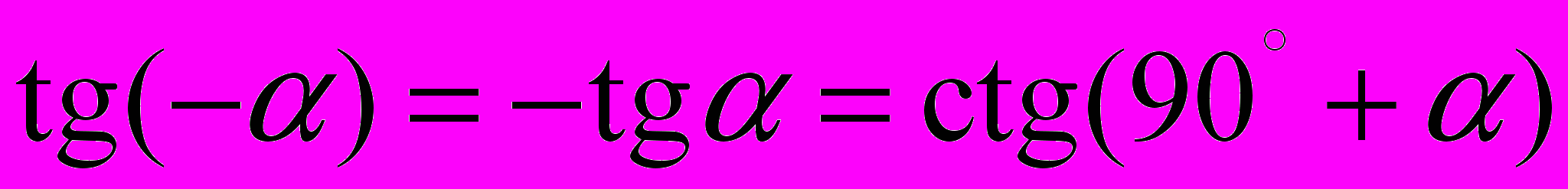21. ;

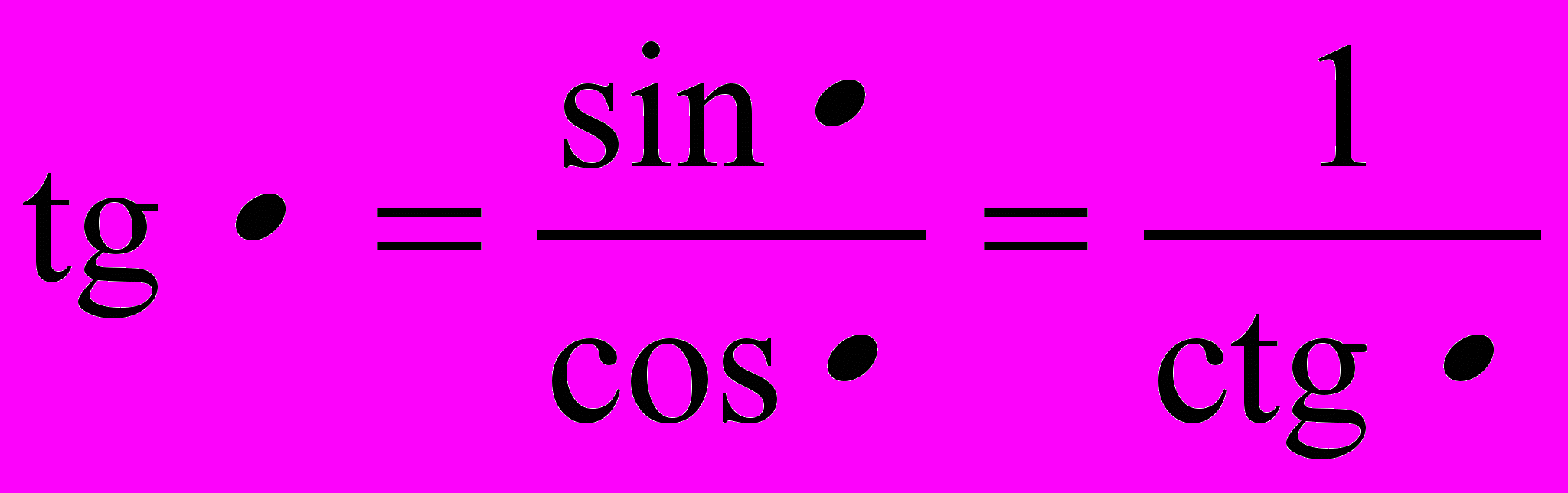22. .


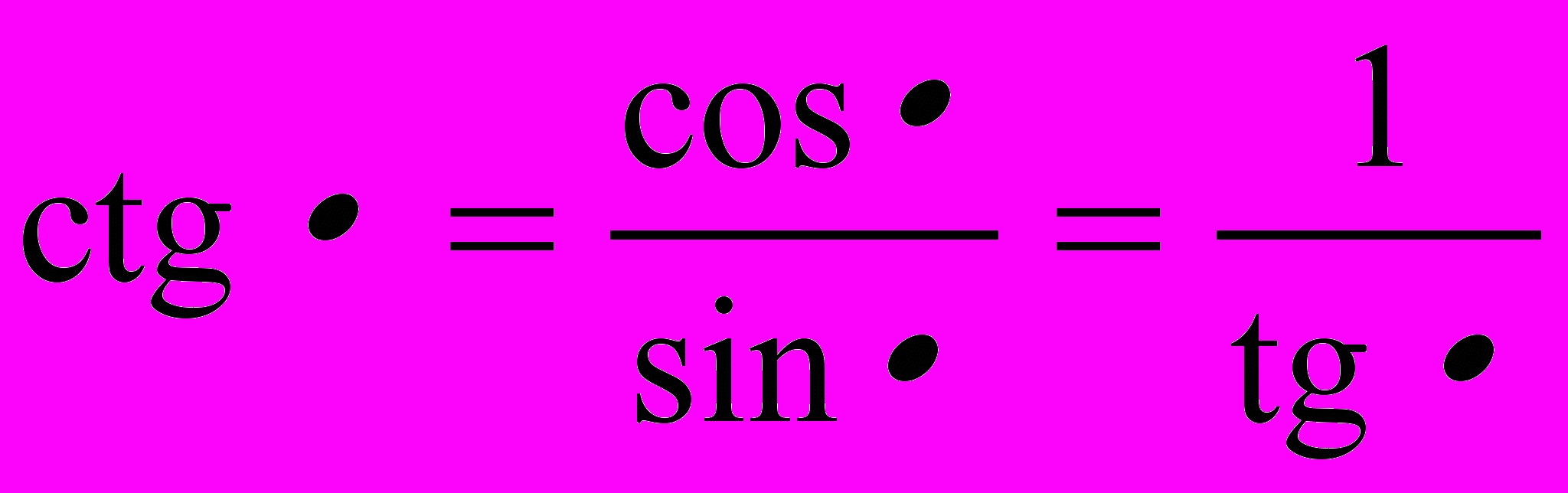Таблица 3 – Значения тригонометрических функций некоторых углов


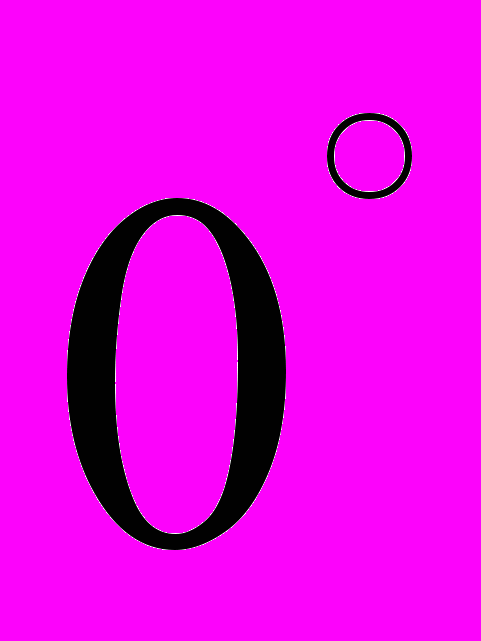0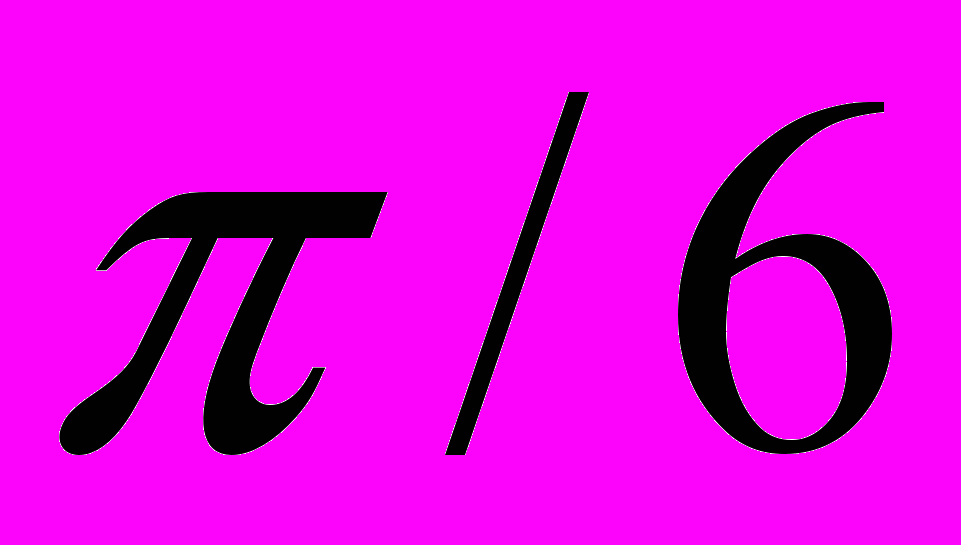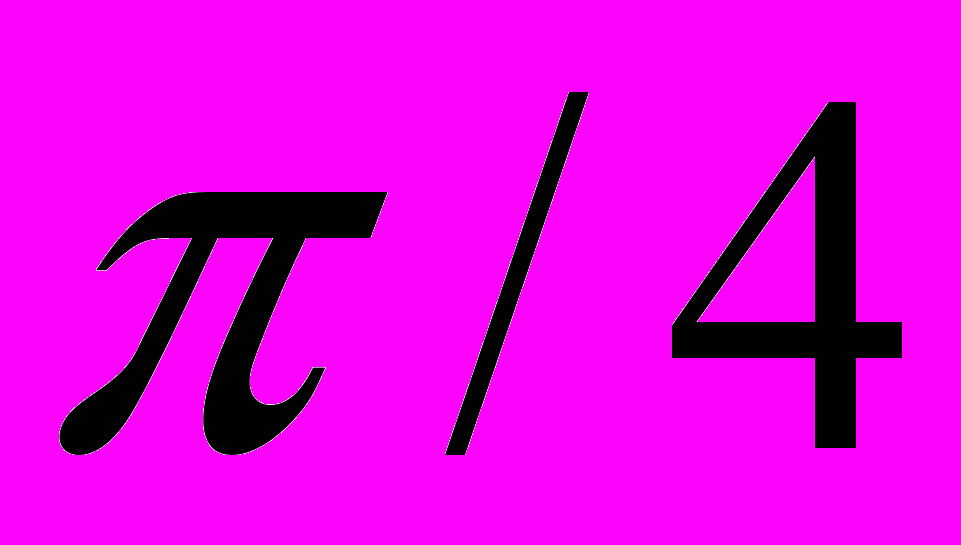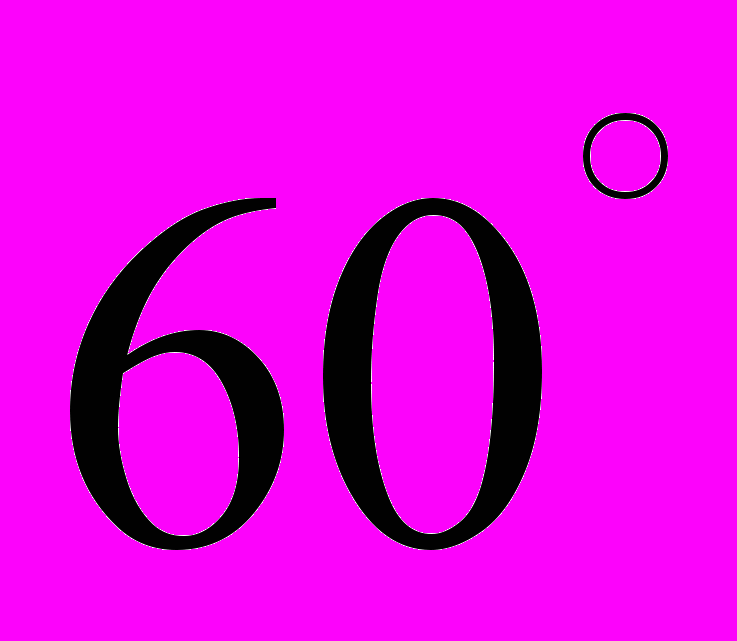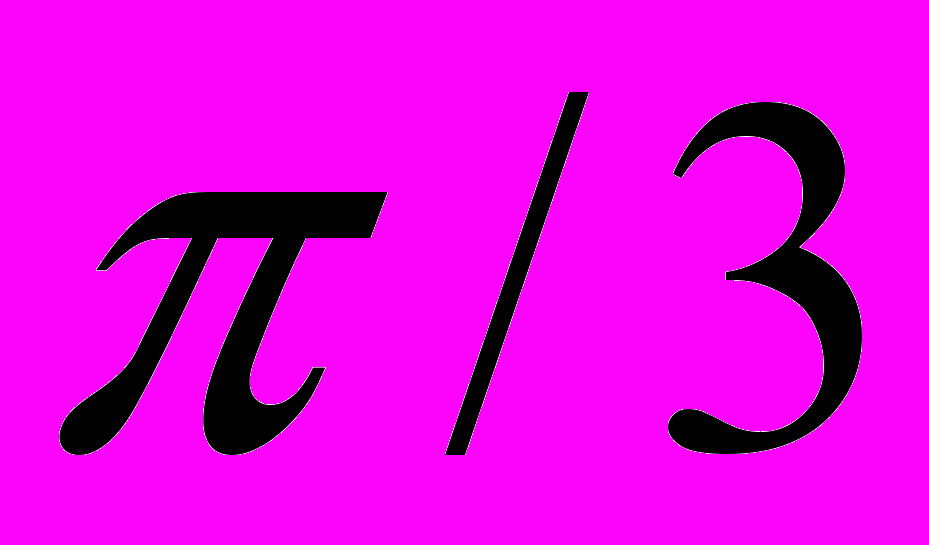


















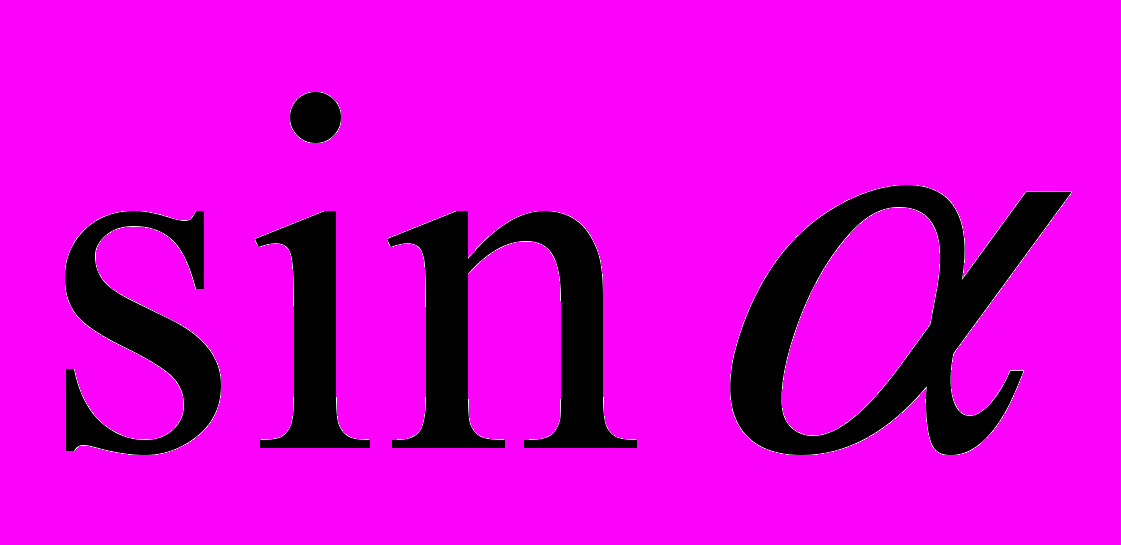0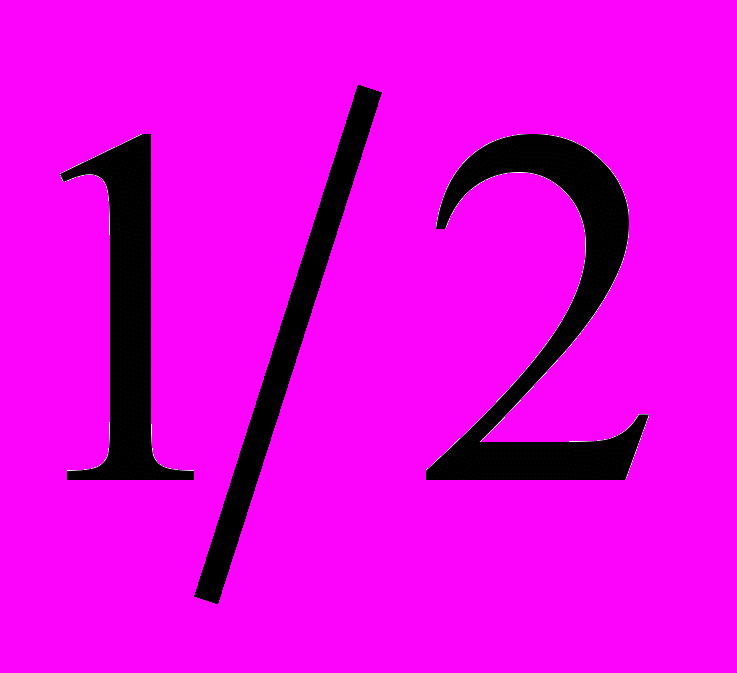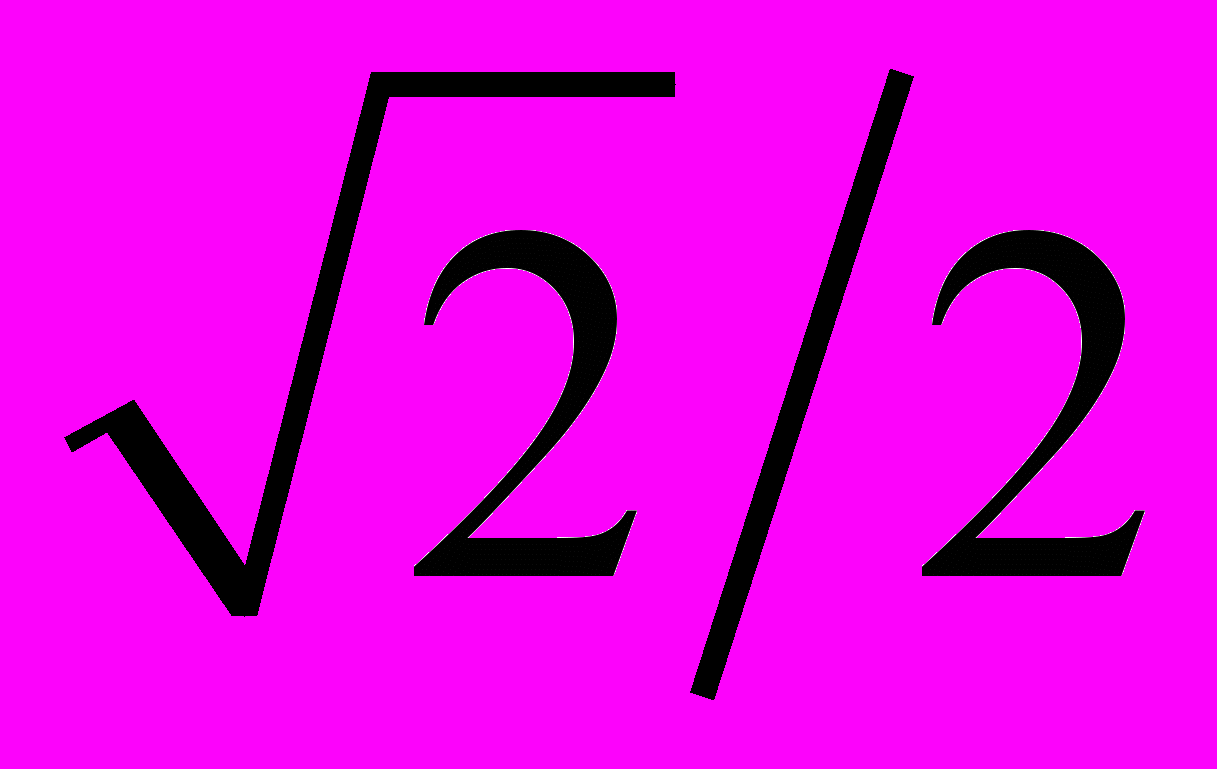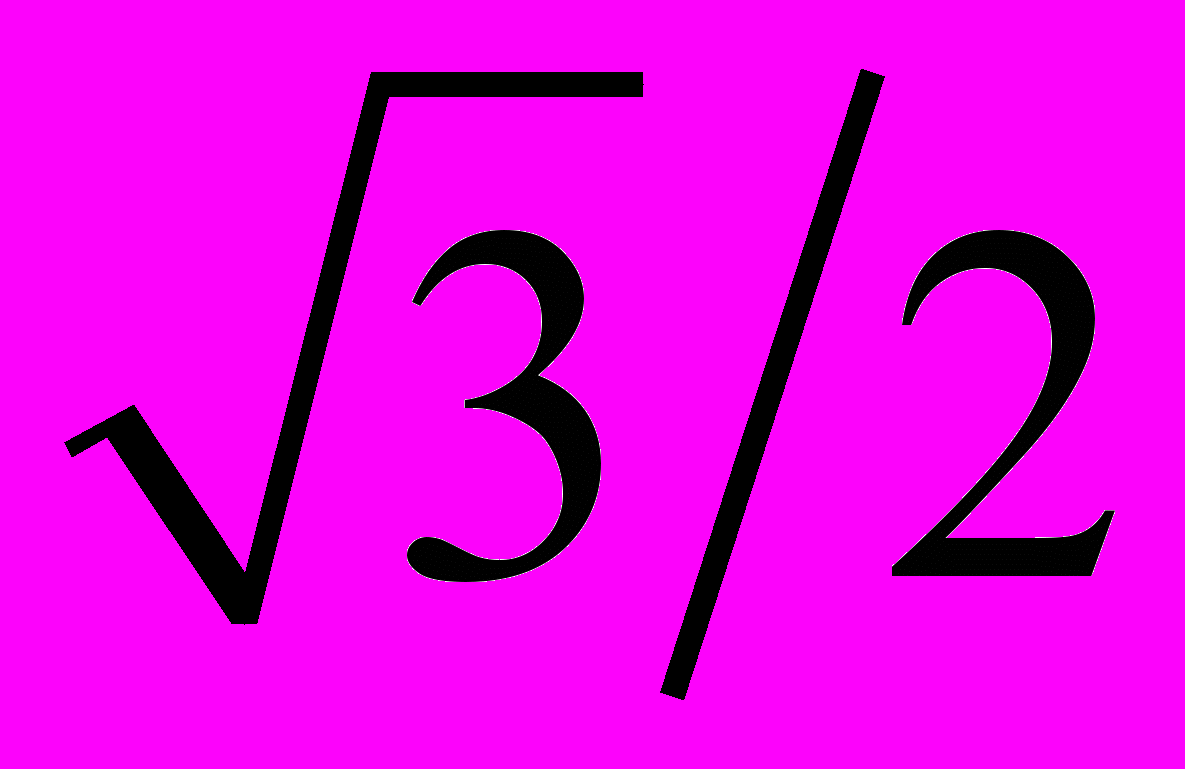






1



1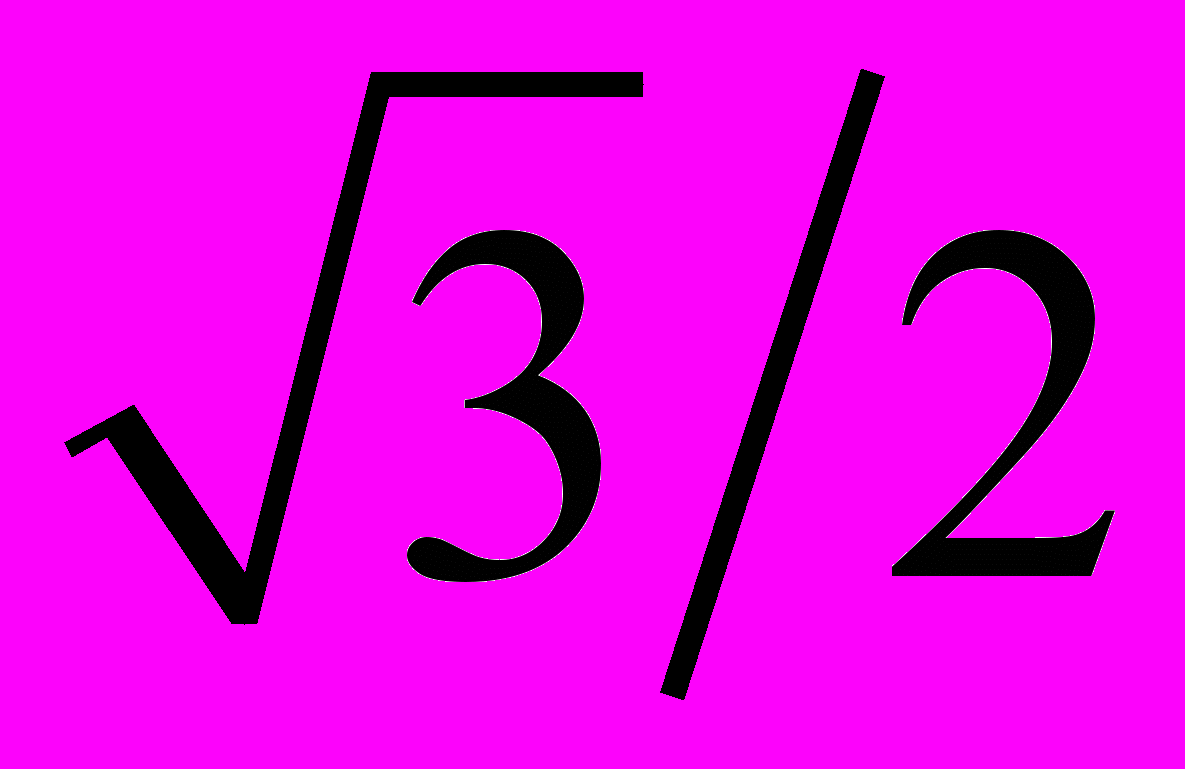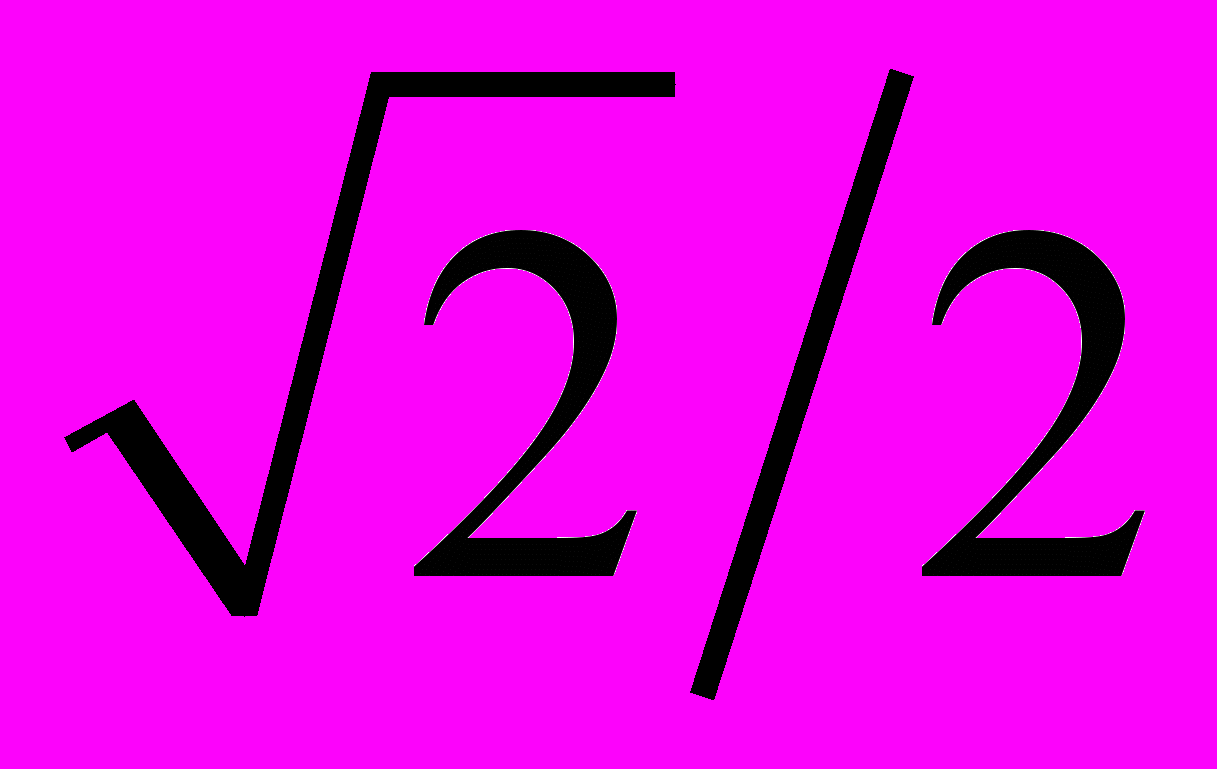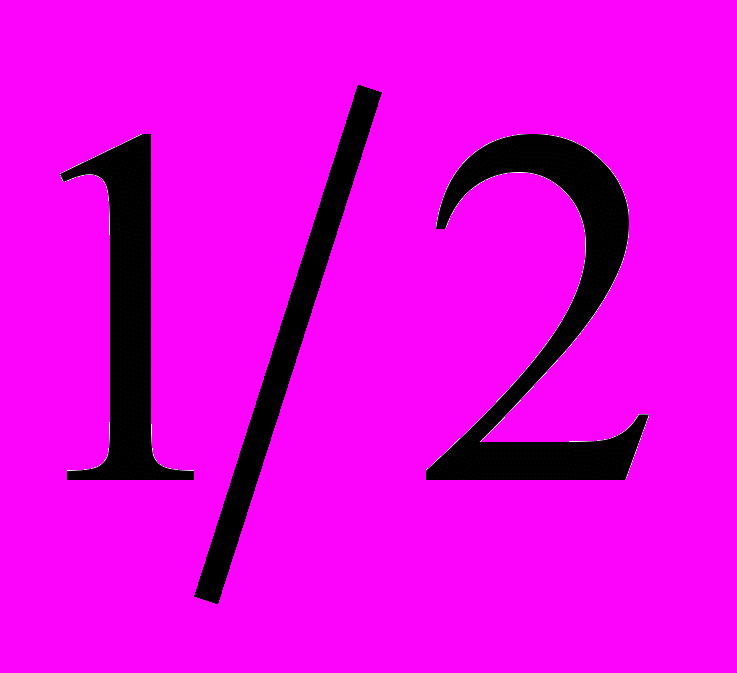






0



0


1










1


0































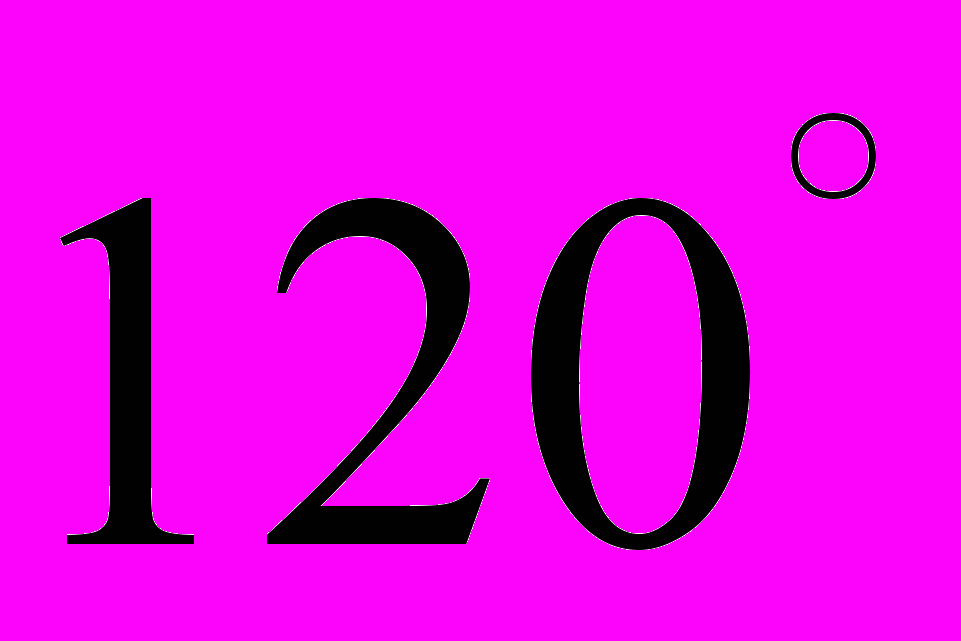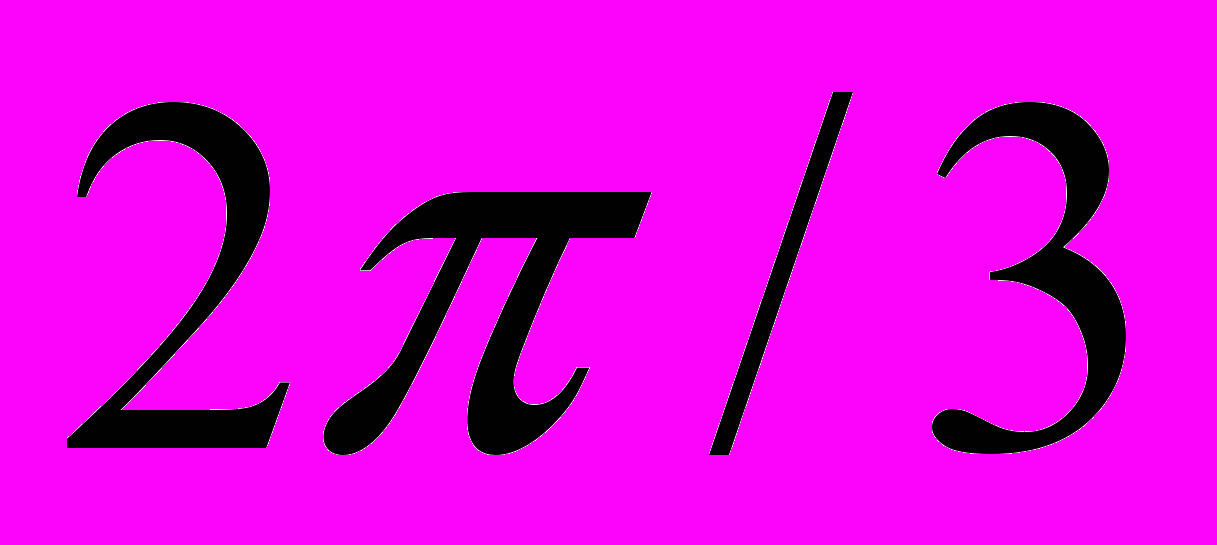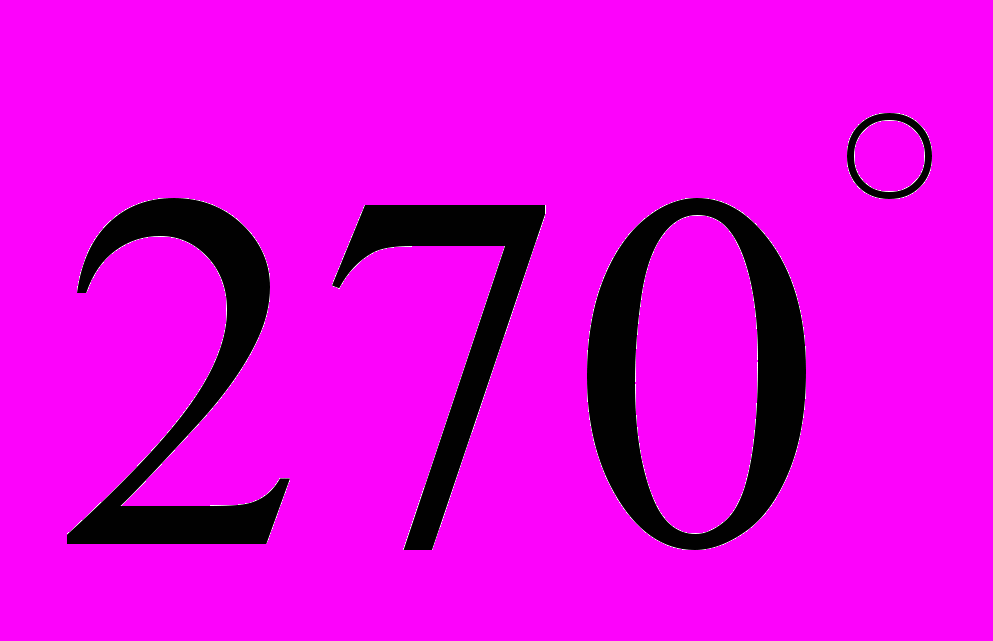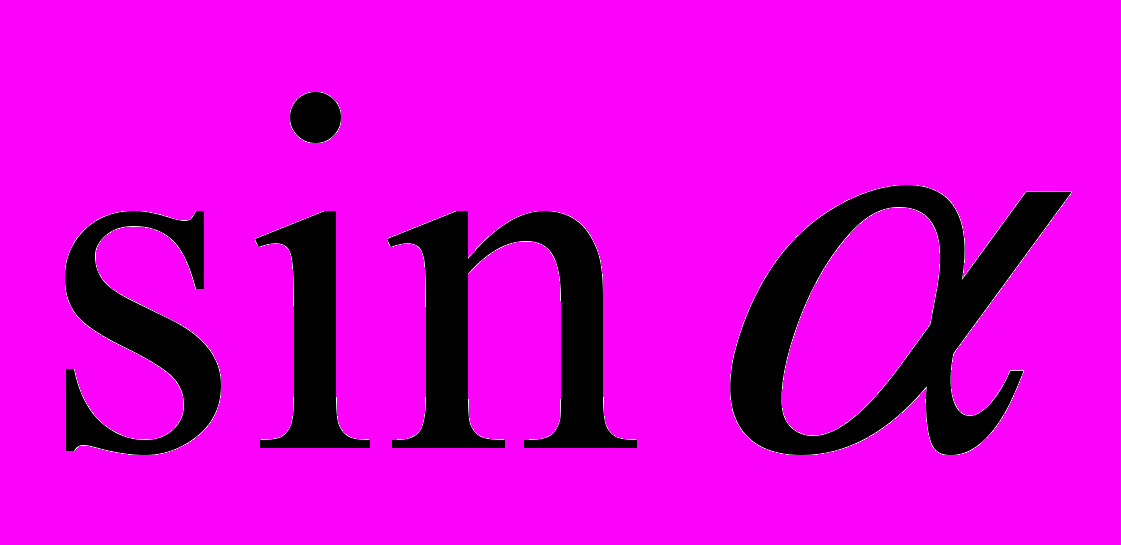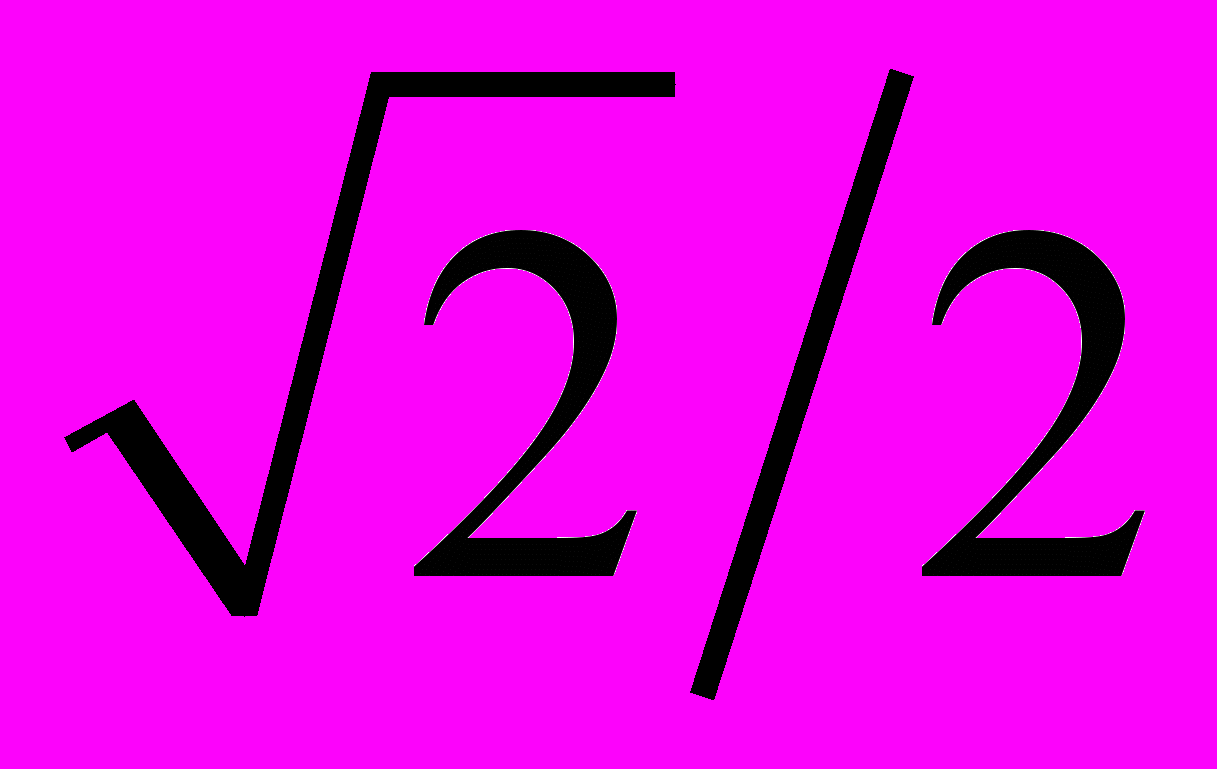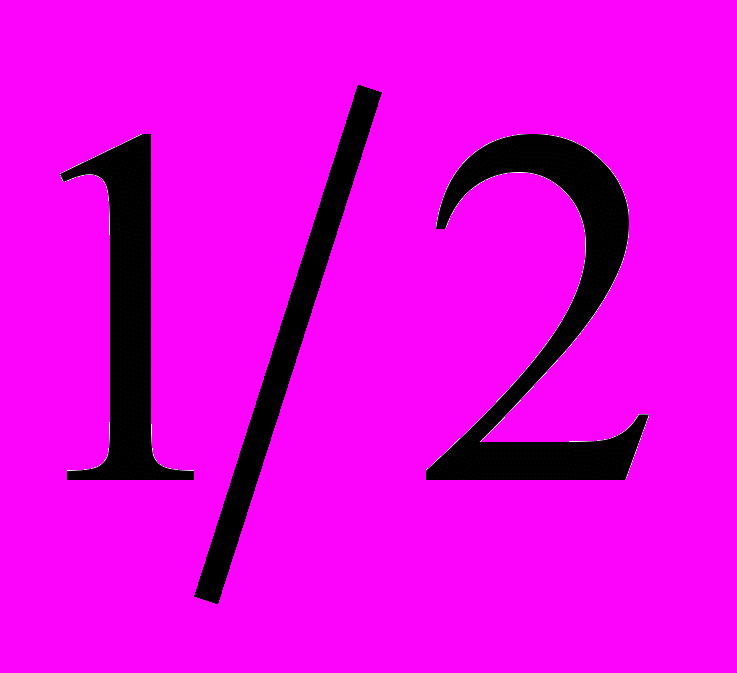0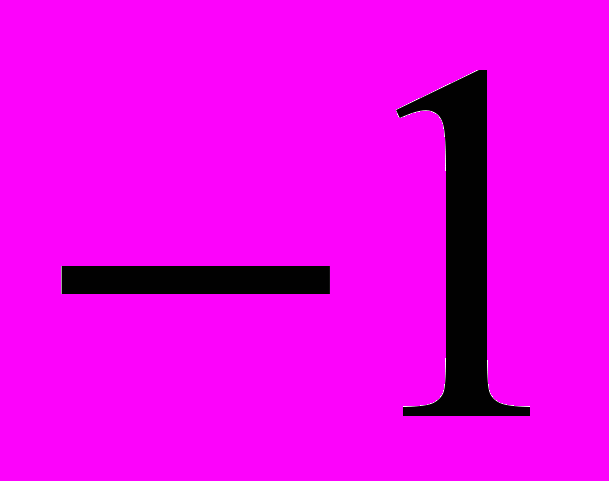












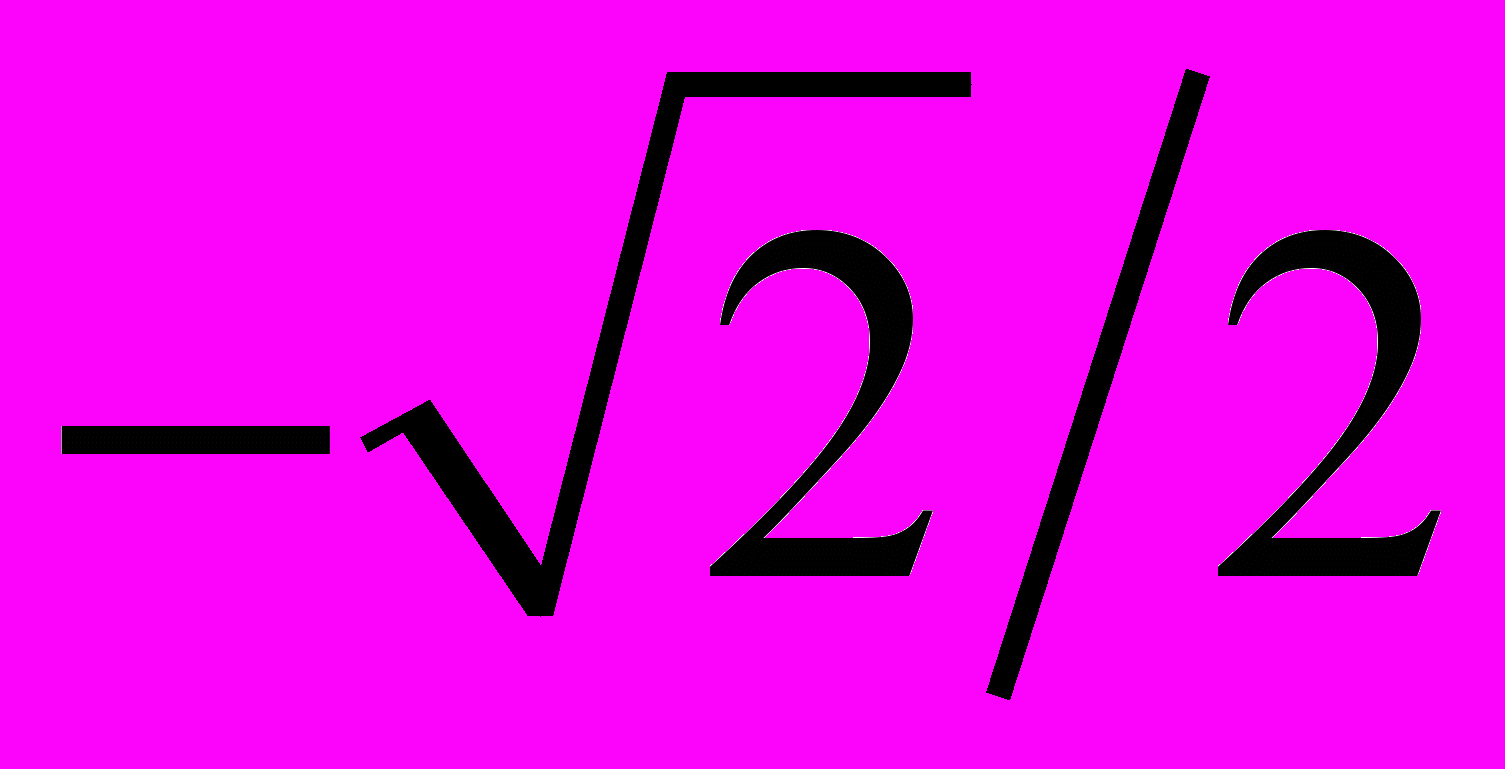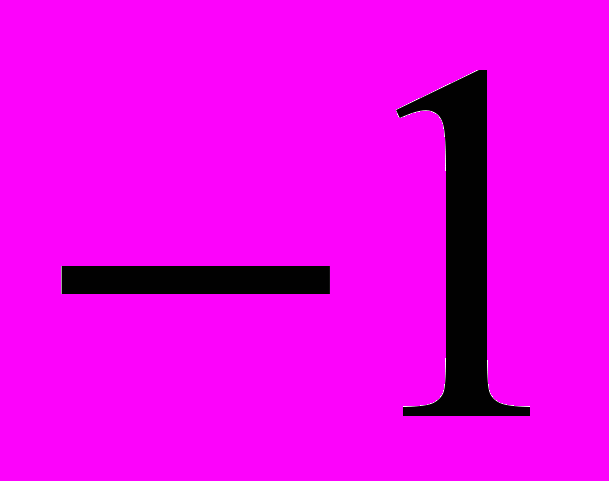0









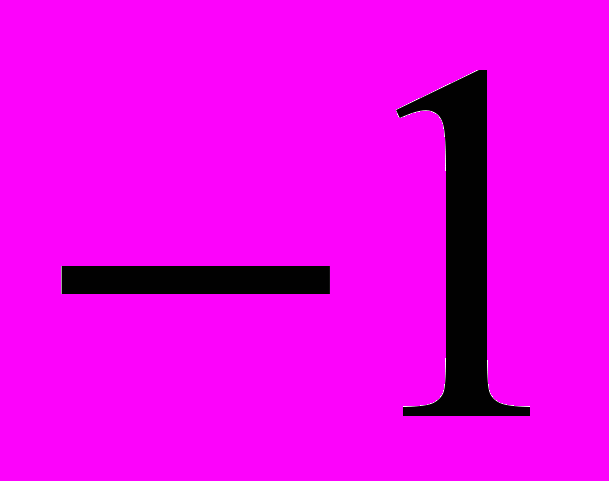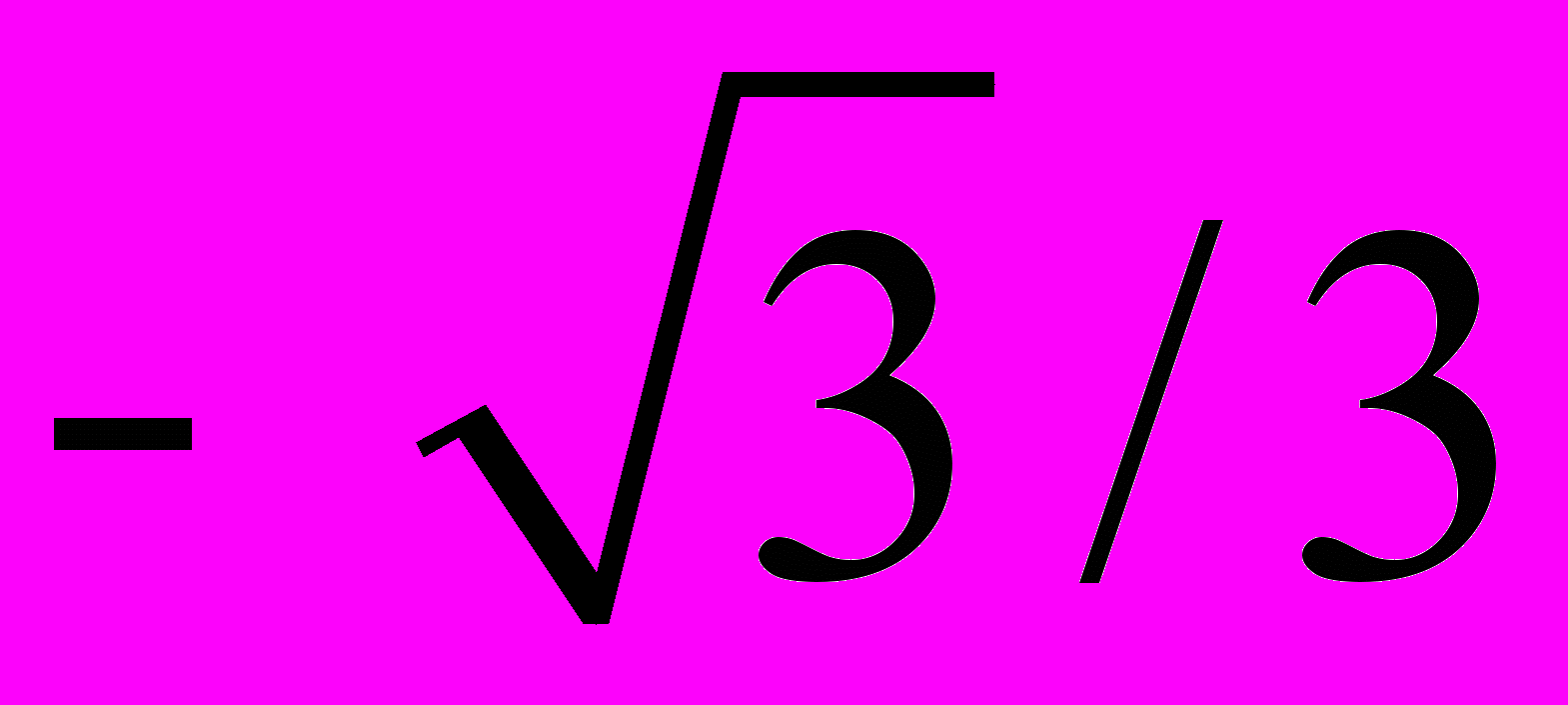0












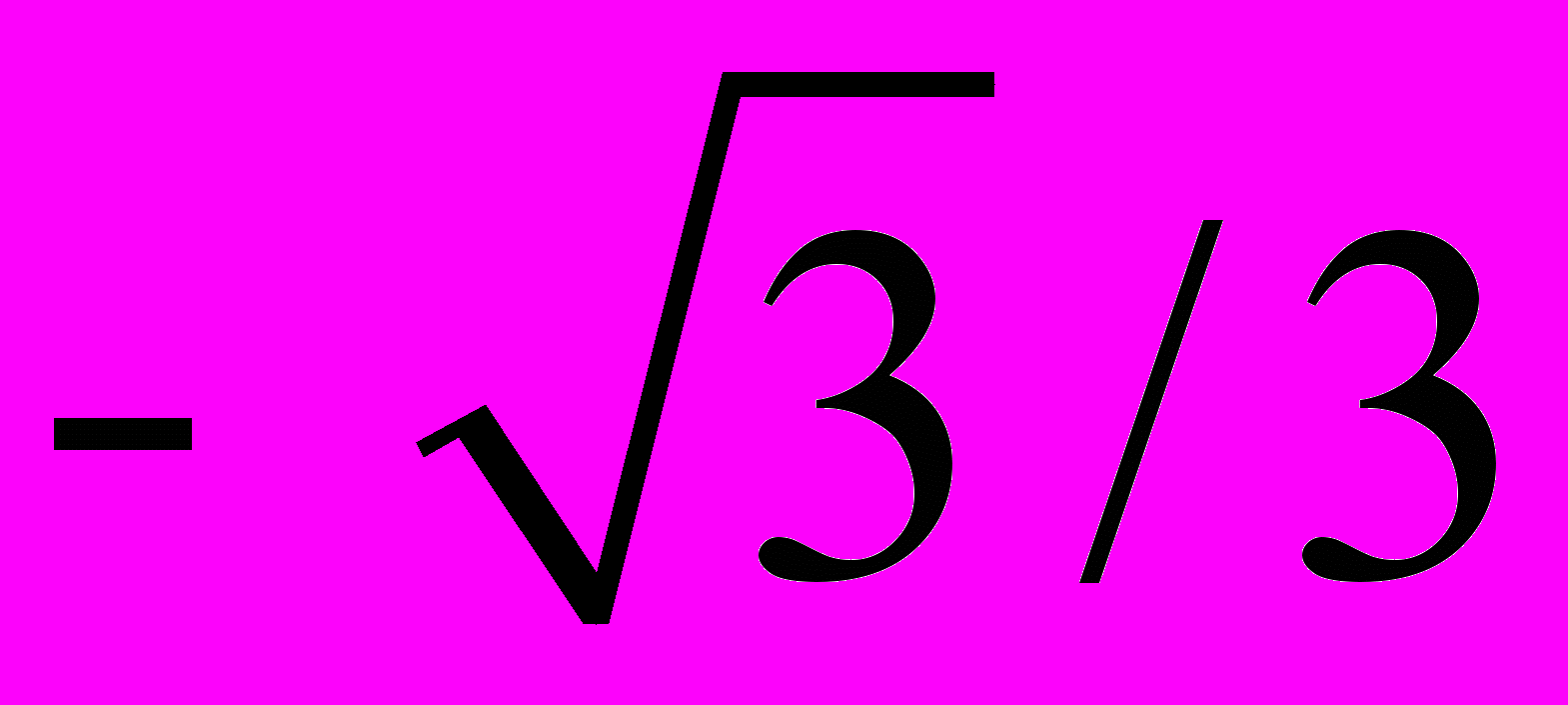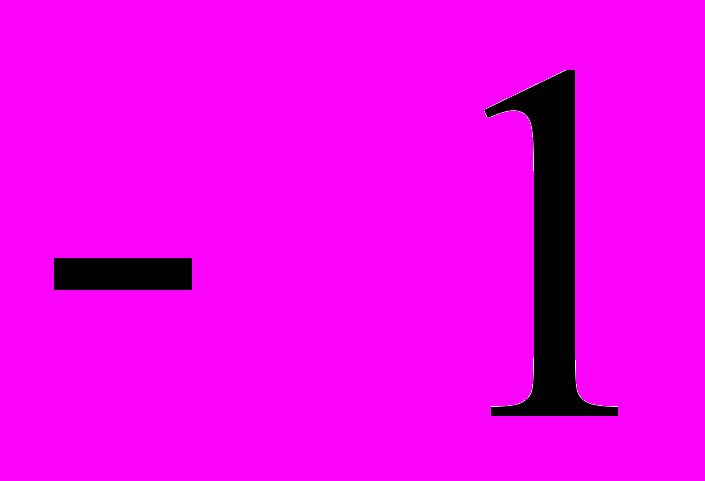0



^ КОНТРОЛЬНАЯ РАБОТА № 3


Тема 1.

Функции многих независимых переменных.


В задачах 1-20 найти частные производные первого и второго порядка, градиент функции в точке 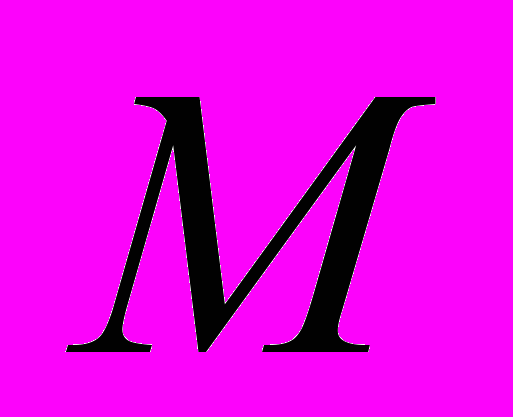и производную функции в точке 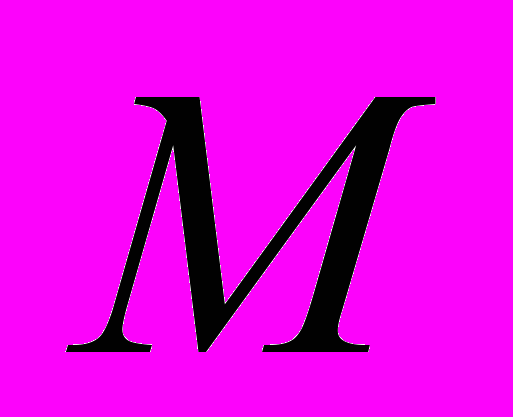в направлении, составляющем угол с положительным направлением оси .
  1. , ,
  2. , ,
  3. , ,
  4. , ,
  5. , ,
  6. , ,
  7. , ,
  8. , ,
  9. , ,
  10. , ,
  11. , ,
  12. , ,
  13. , ,
  14. , ,
  15. , ,
  16. , ,
  17. , ,
  18. , ,
  19. , ,
  20. , ,




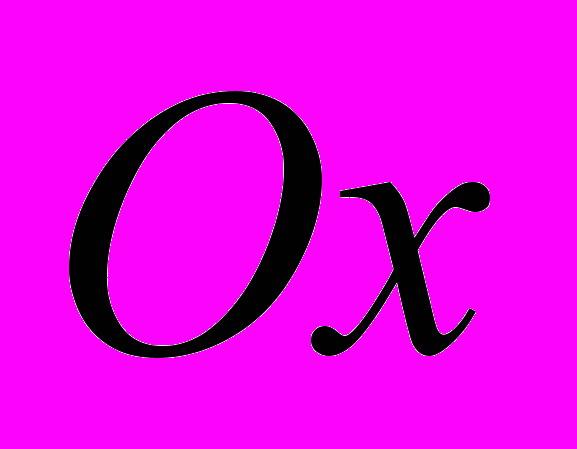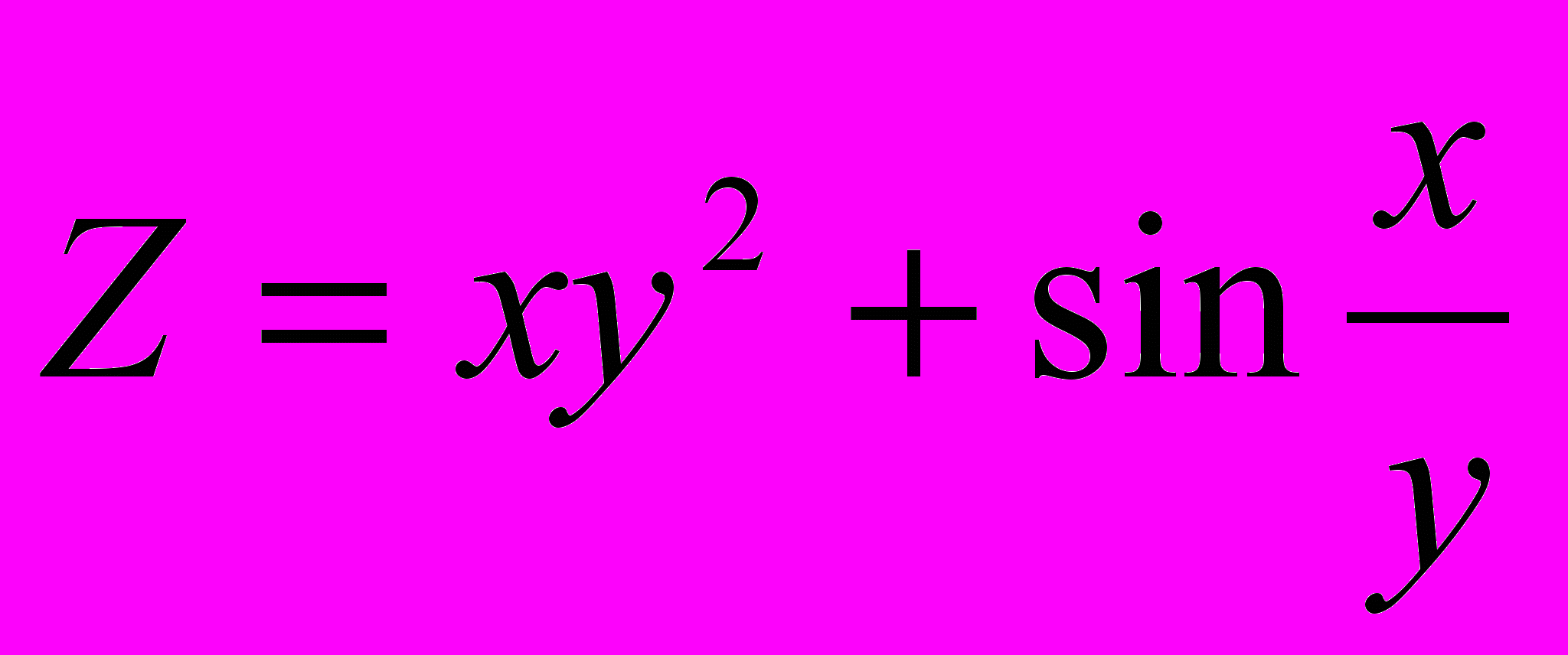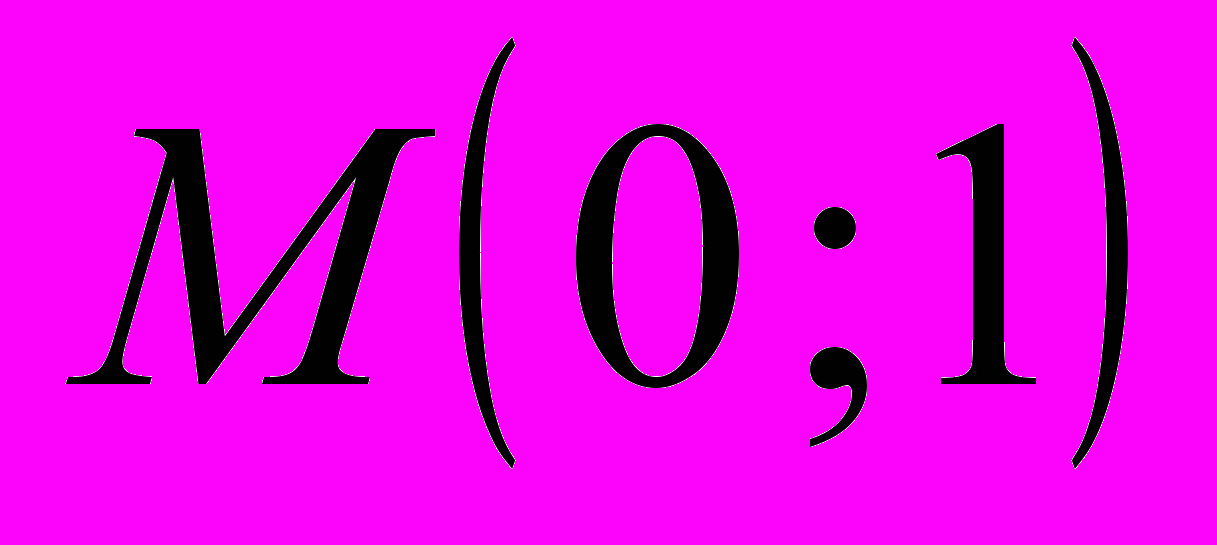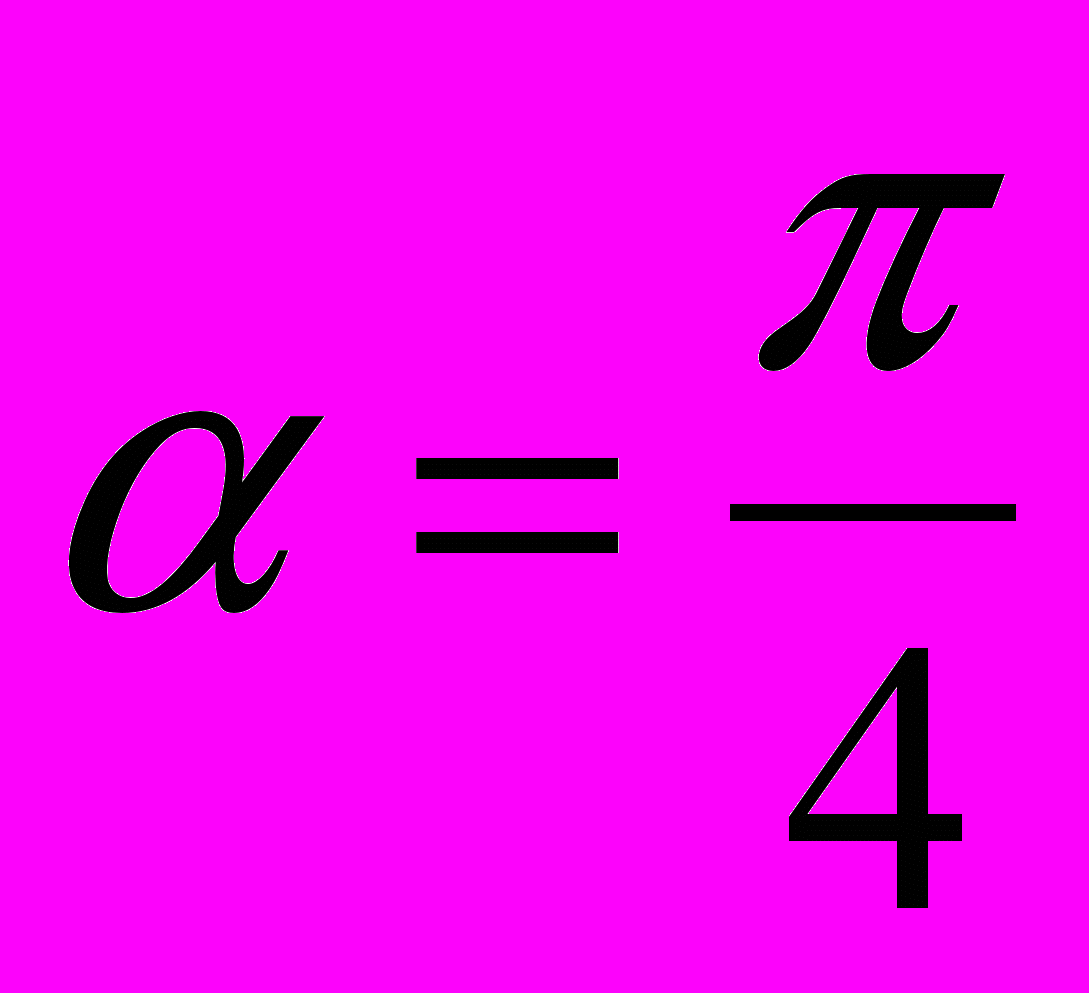
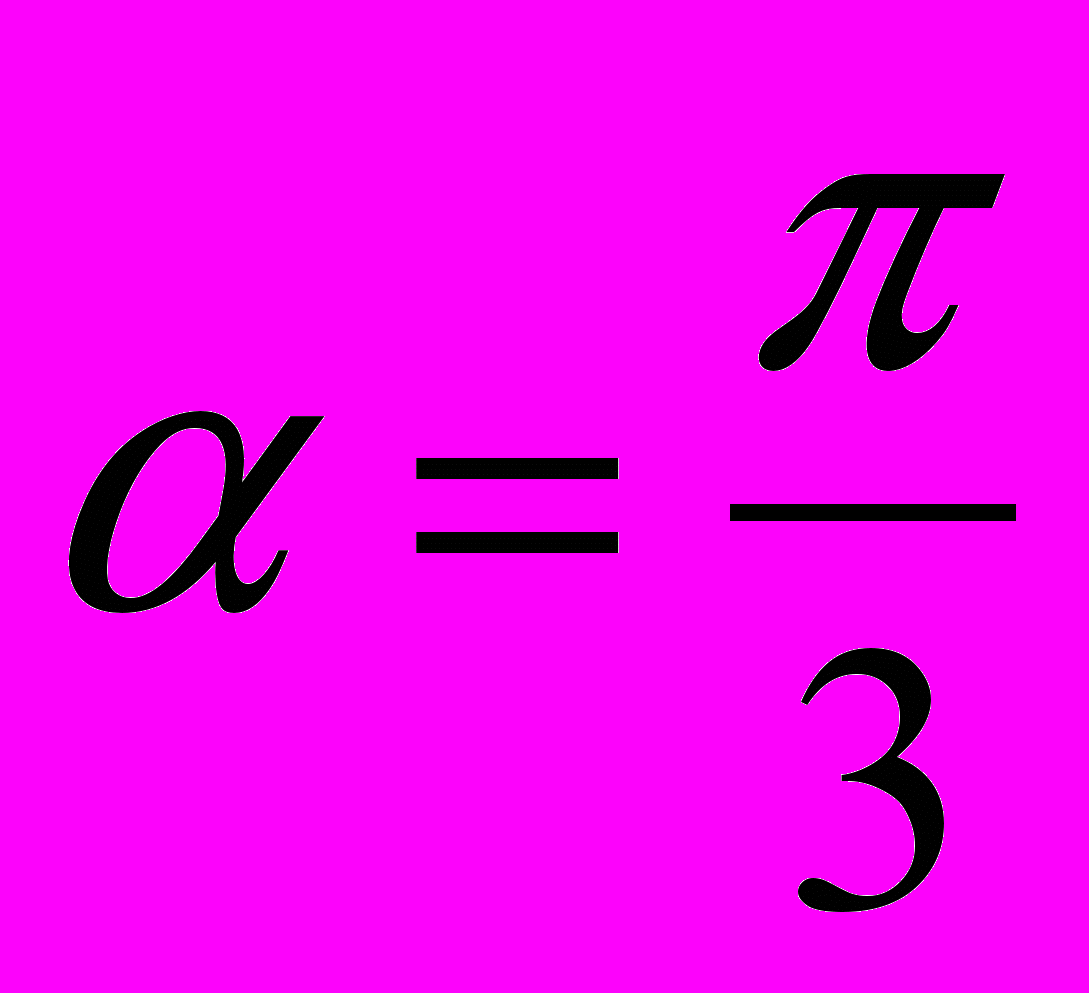
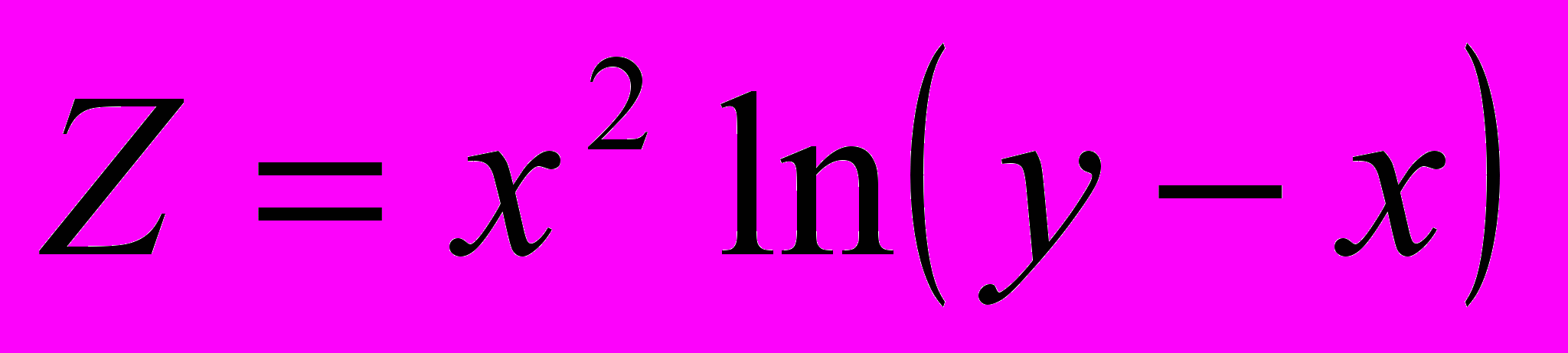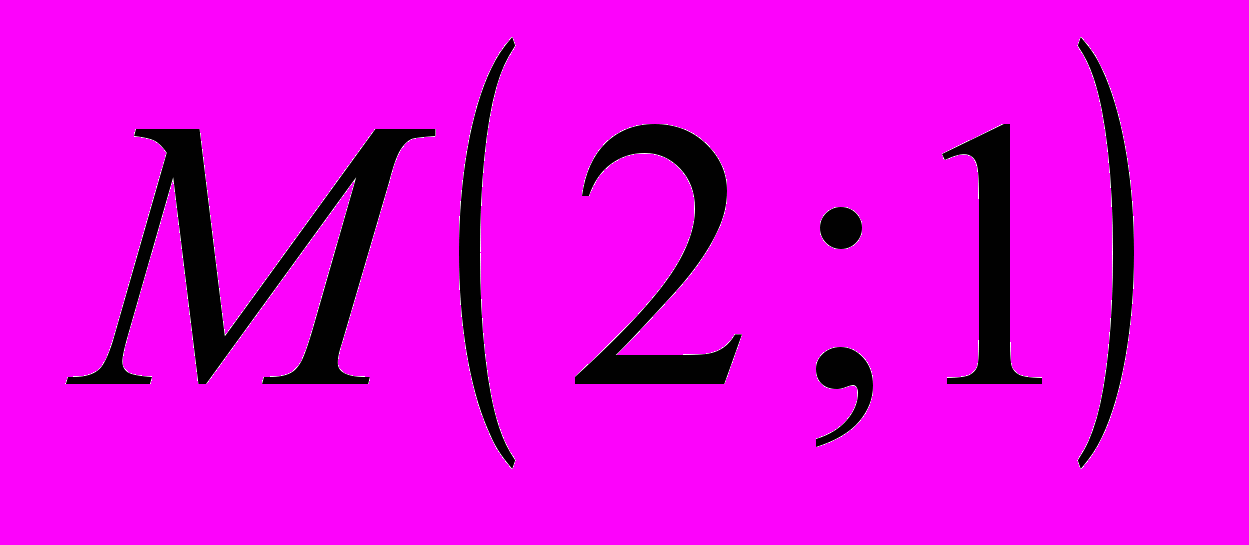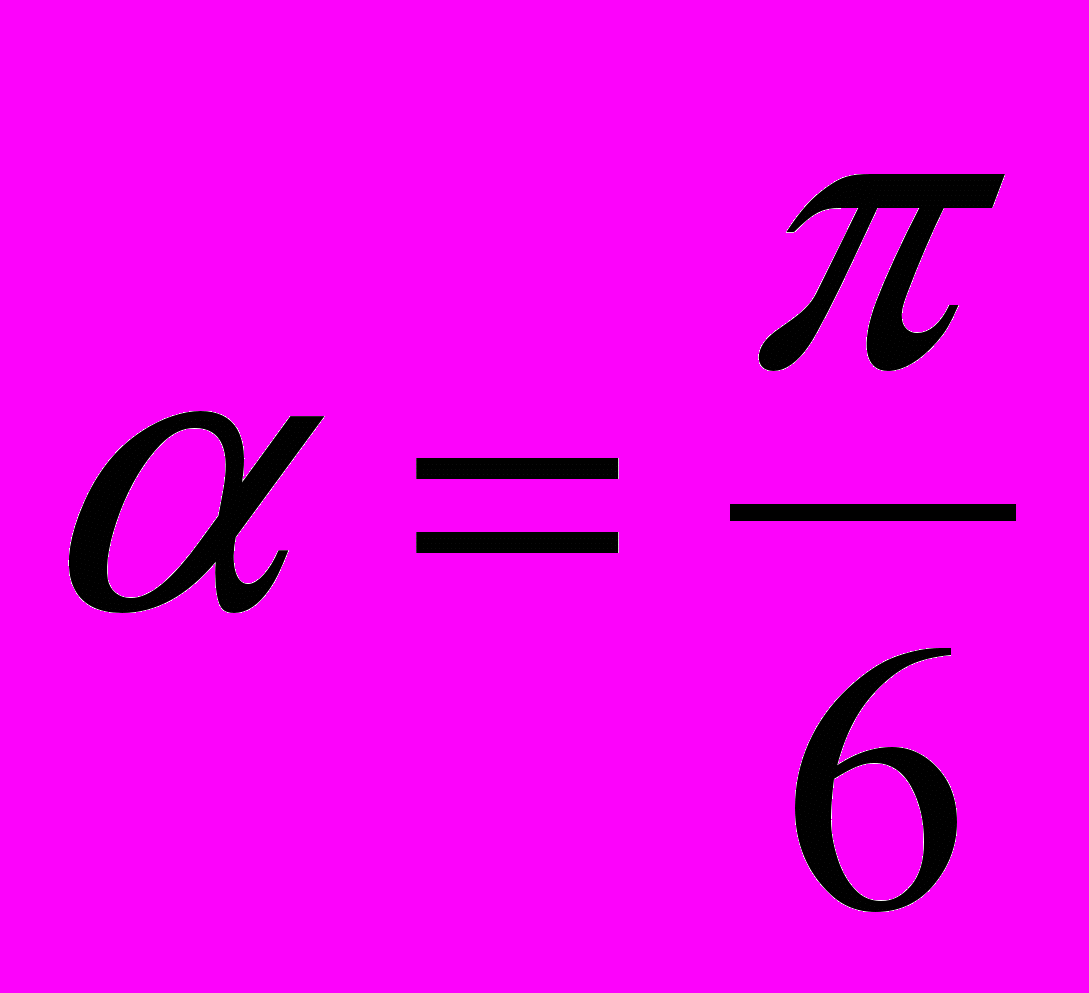
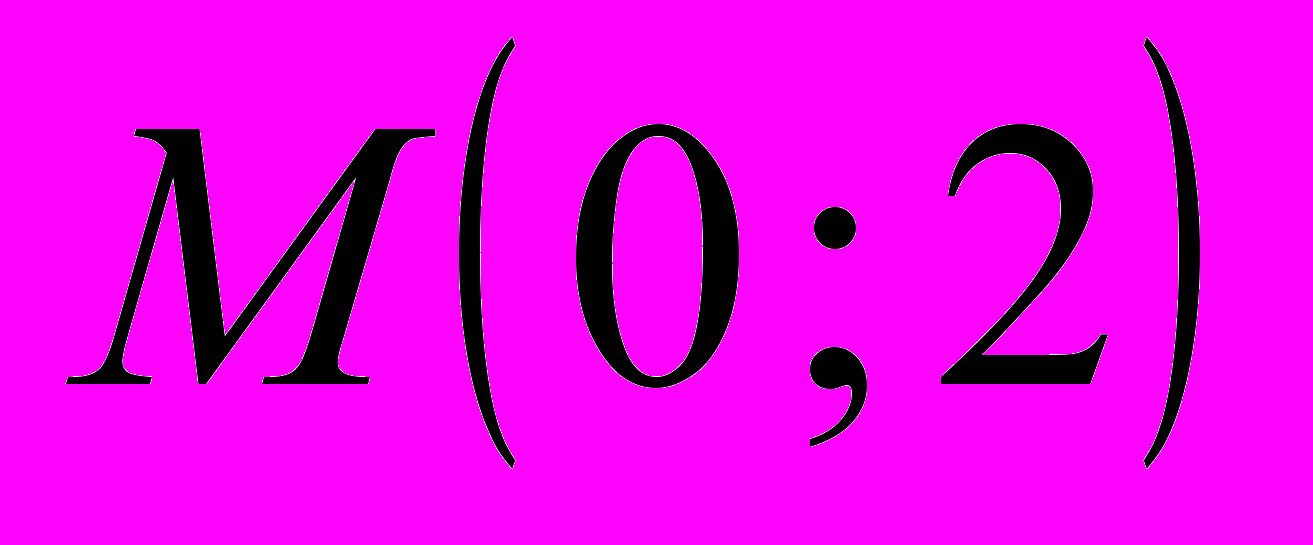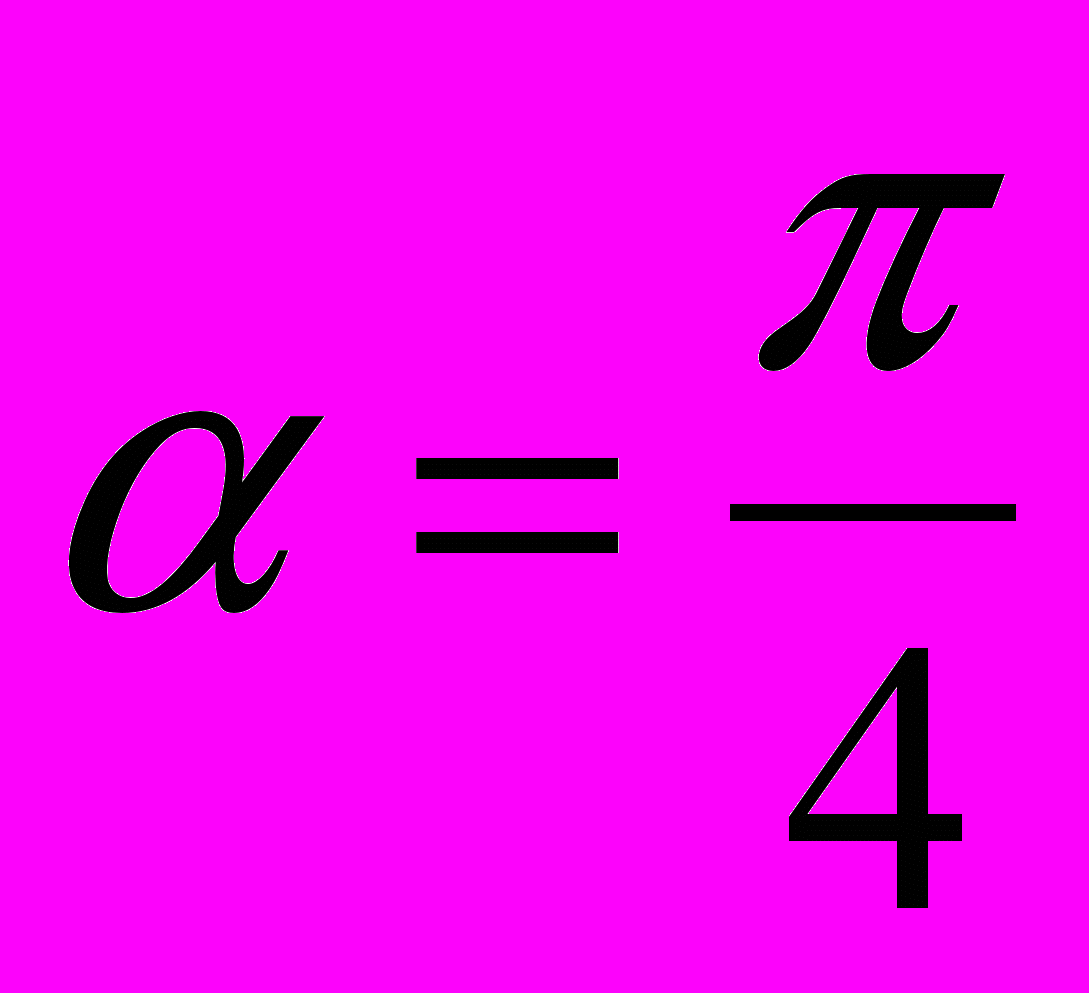
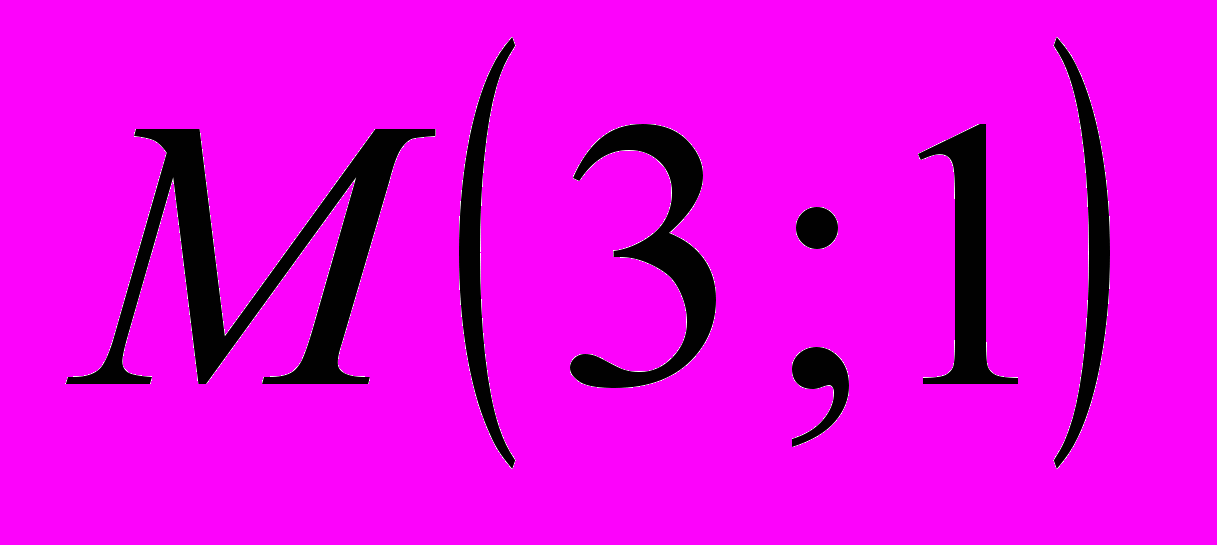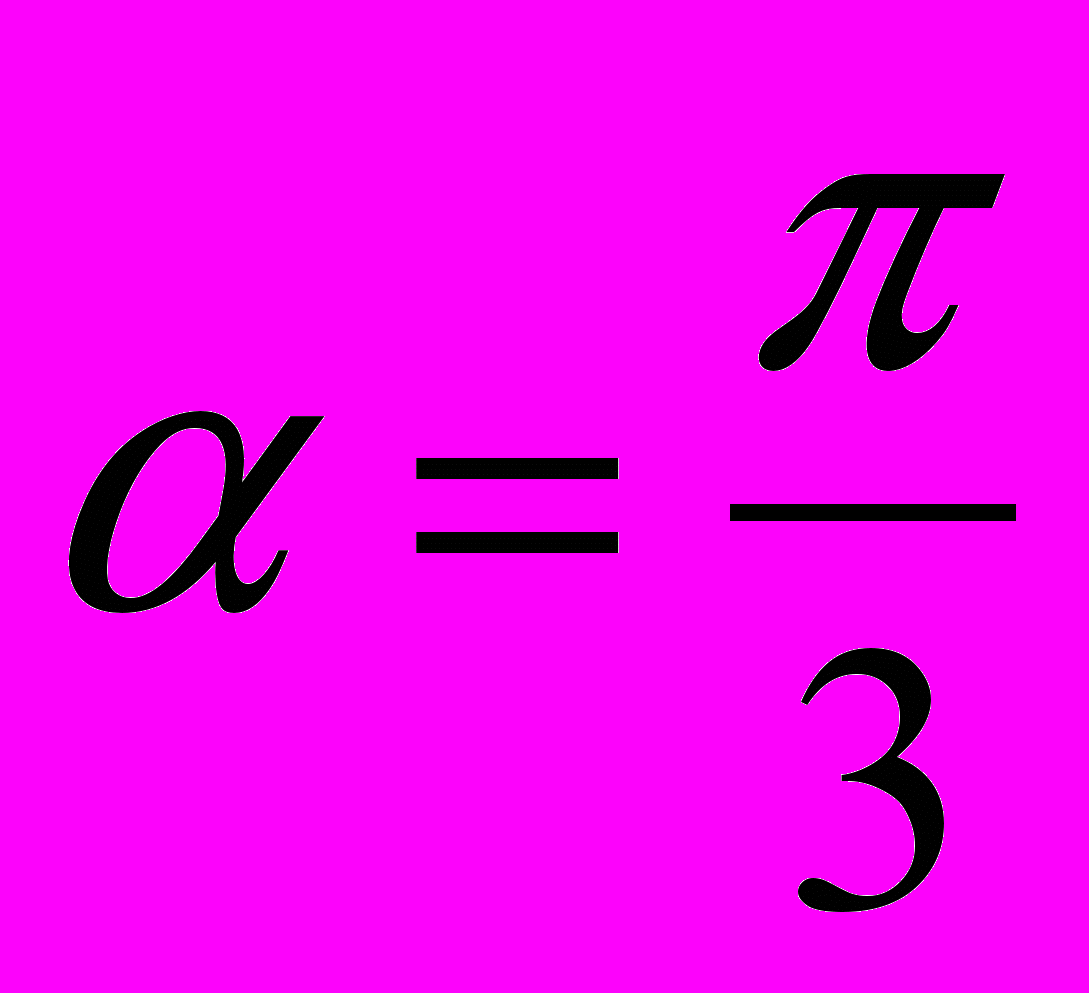
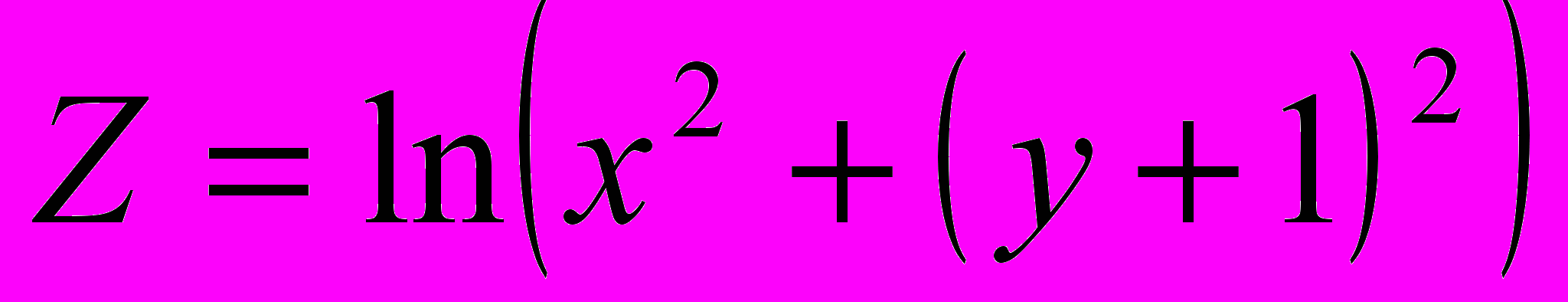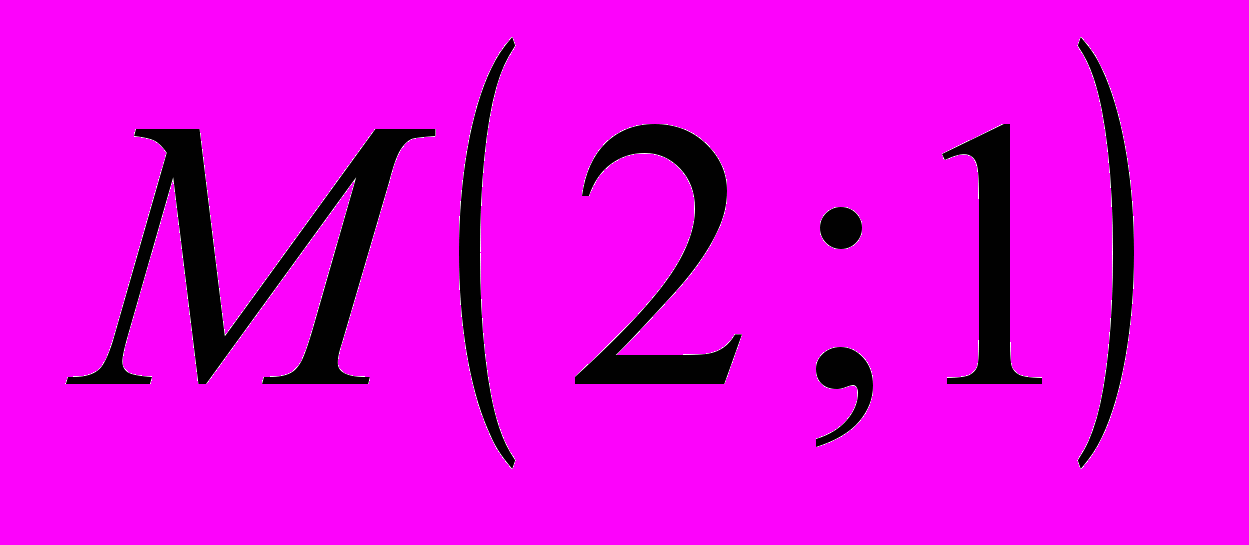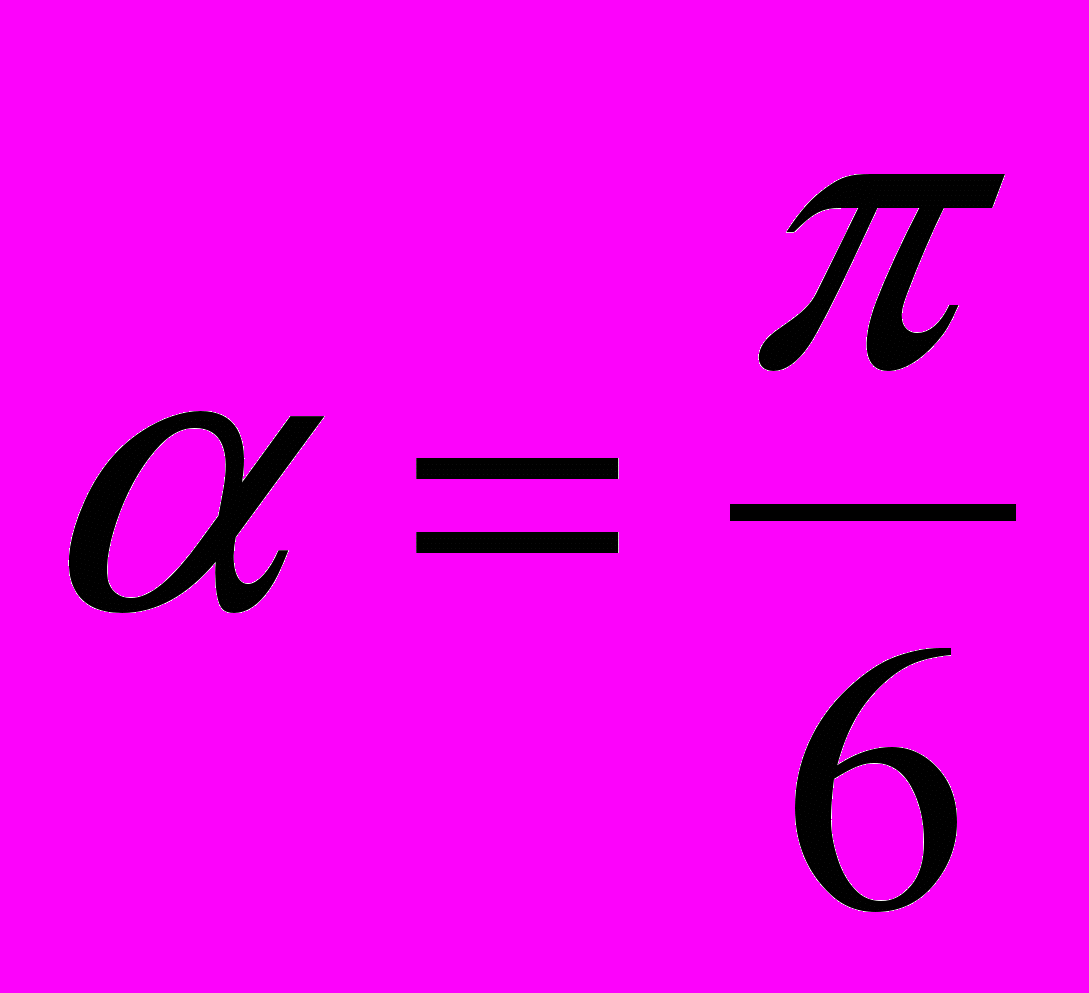
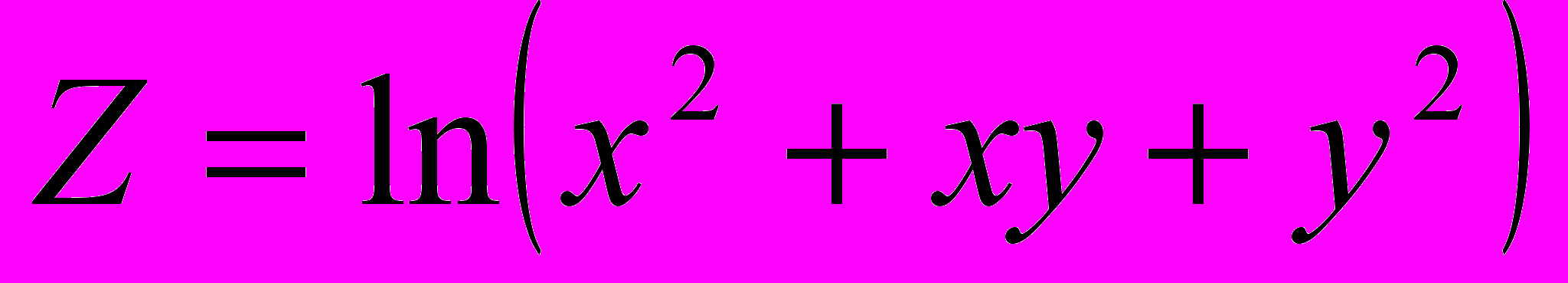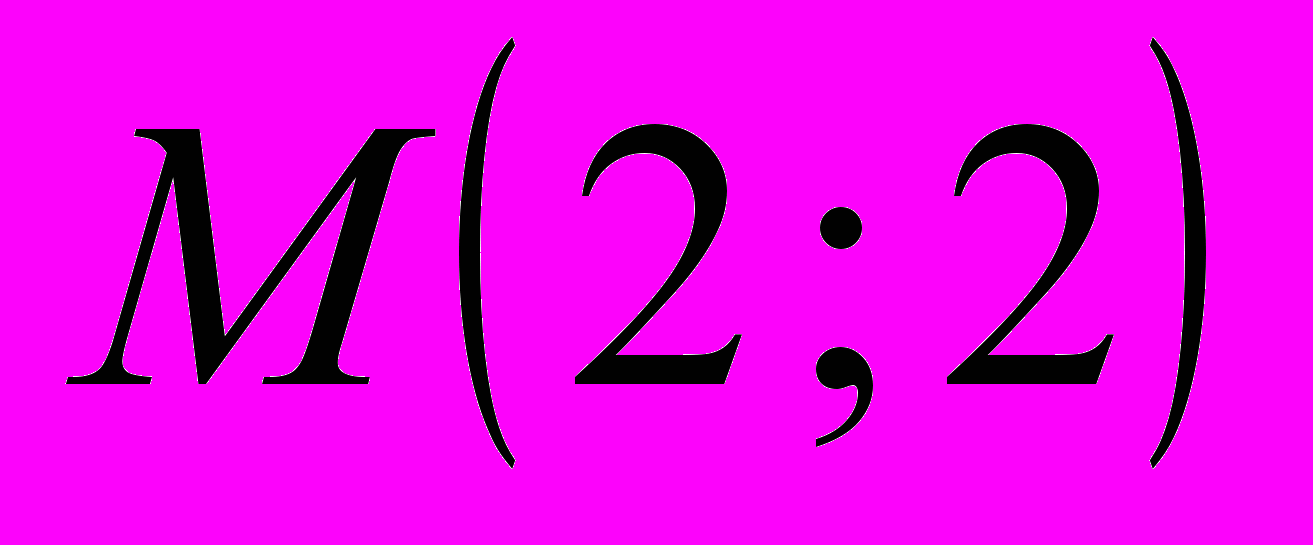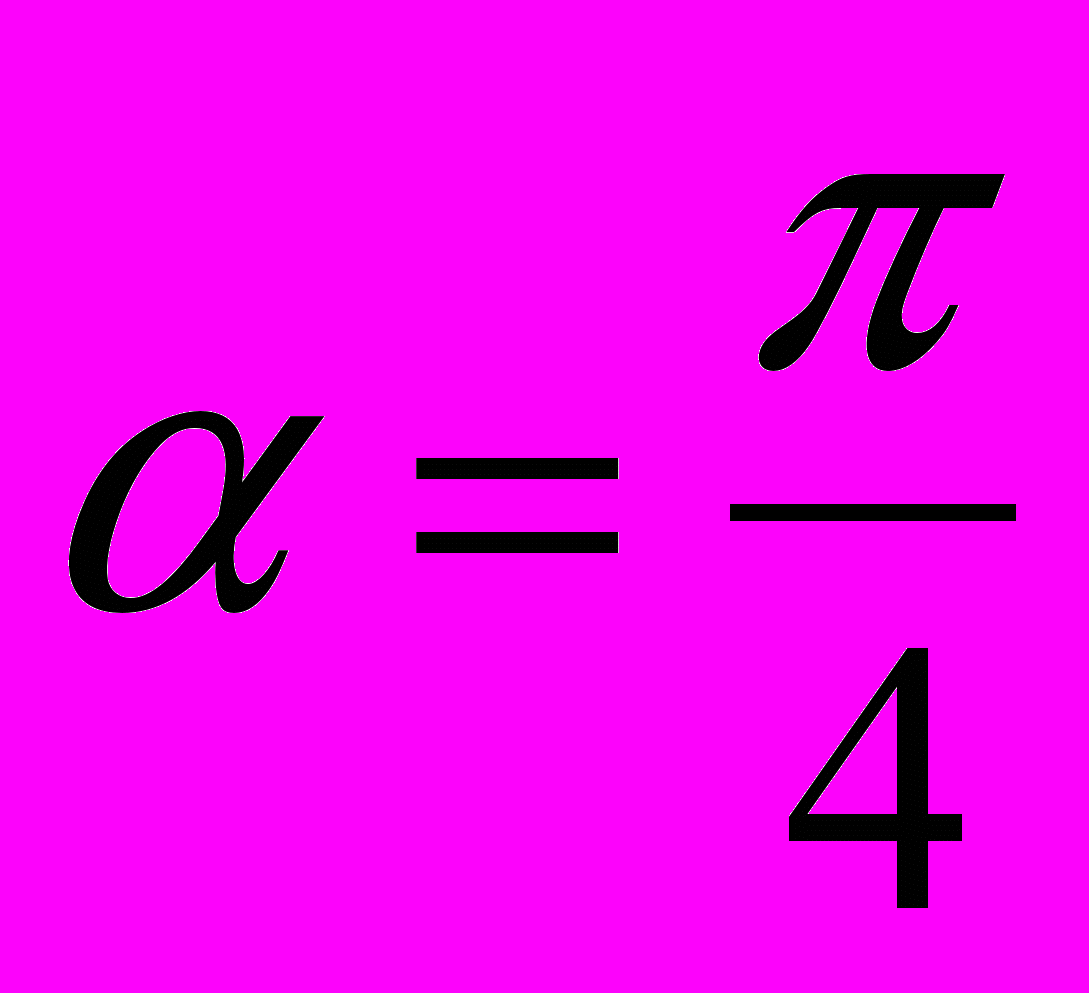
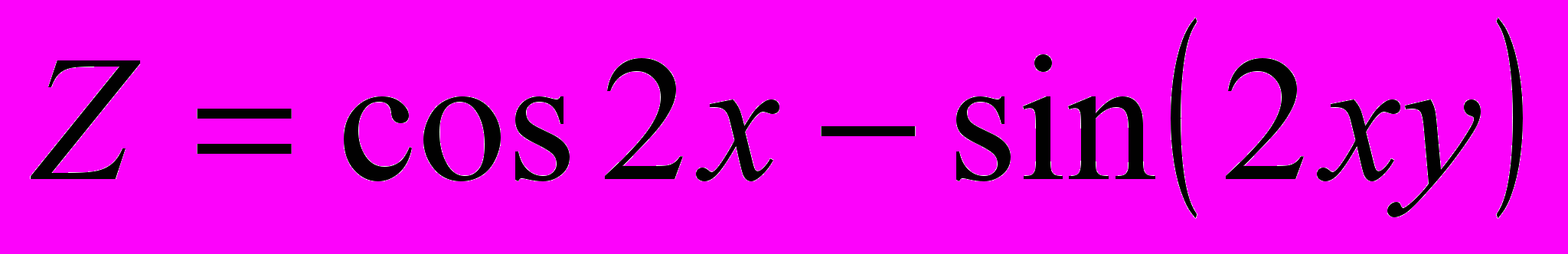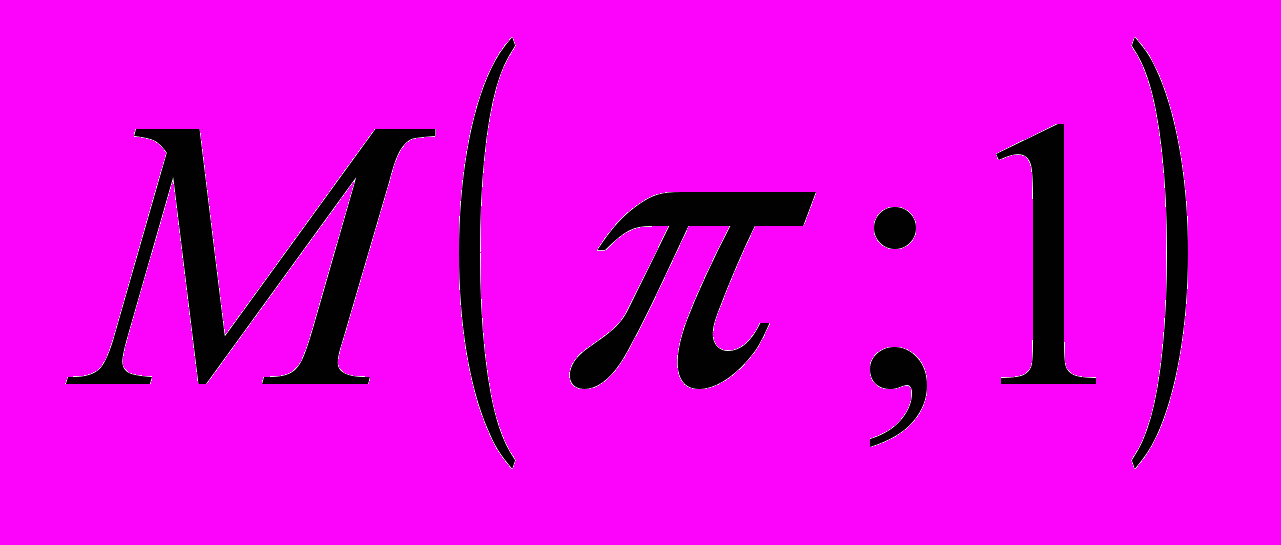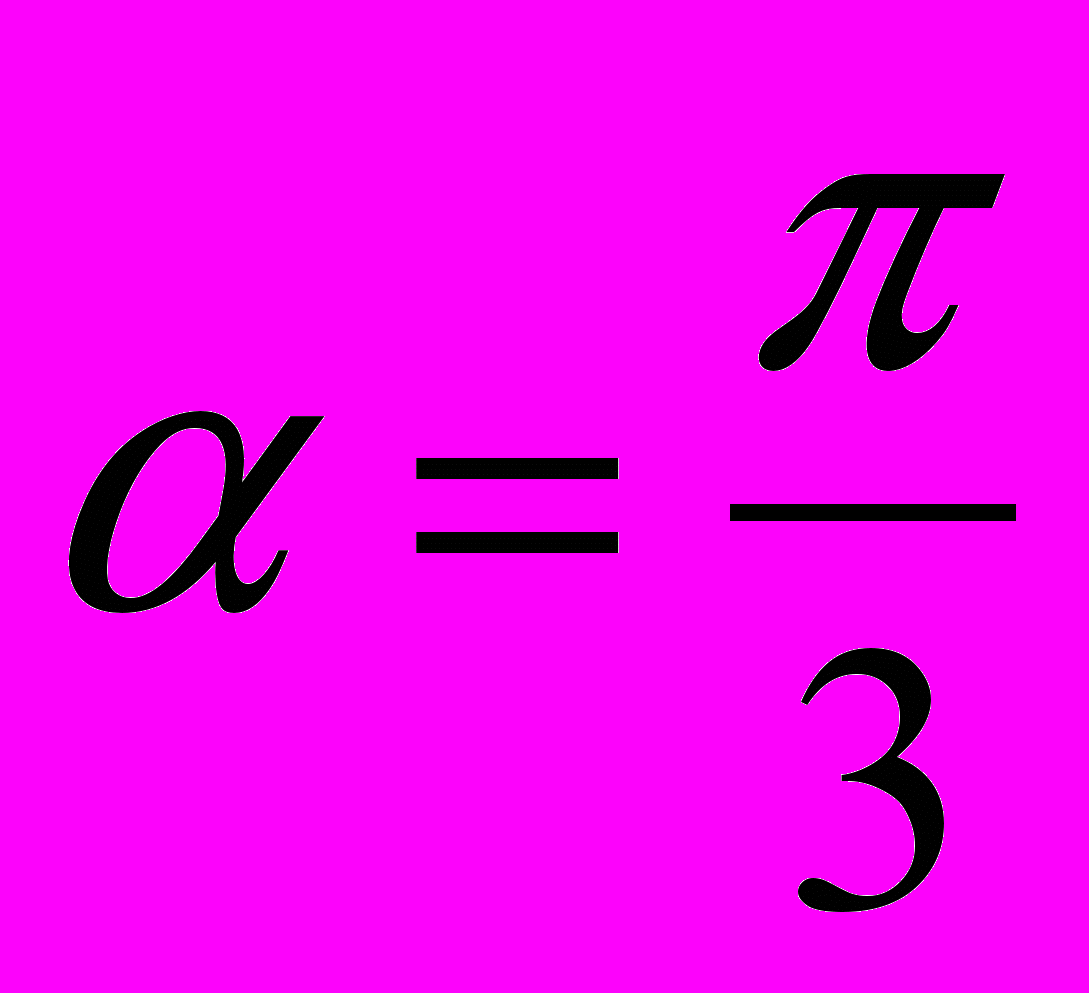
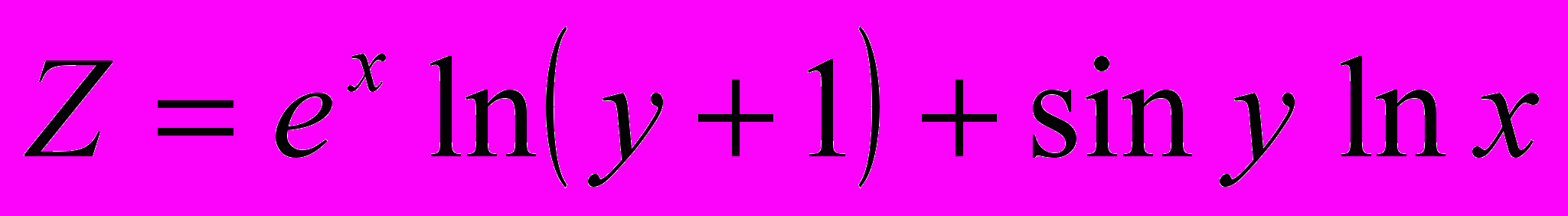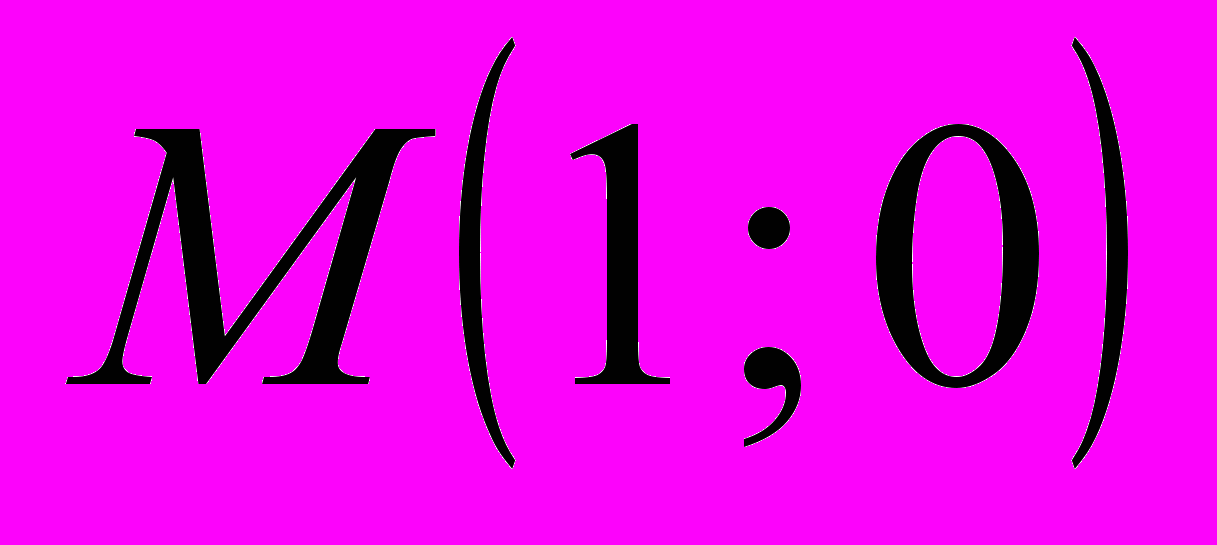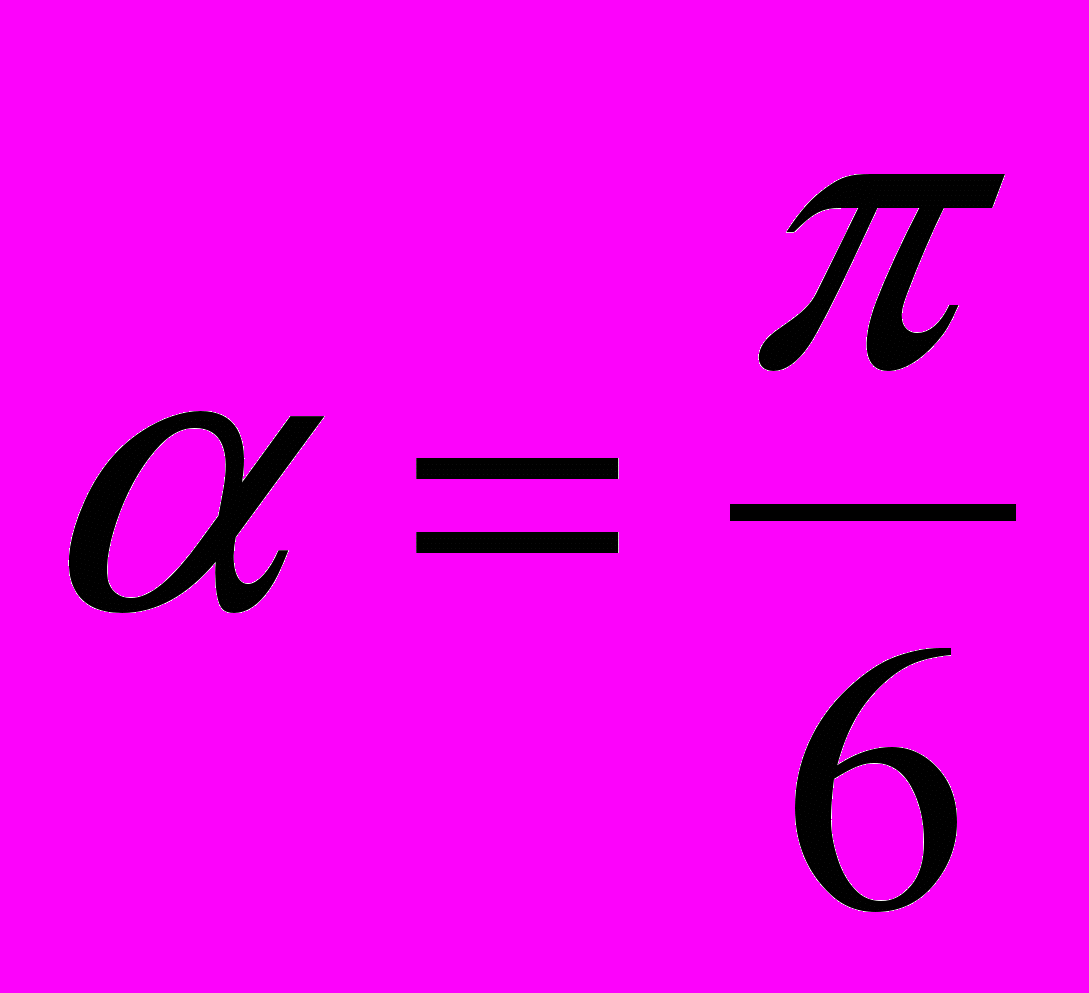
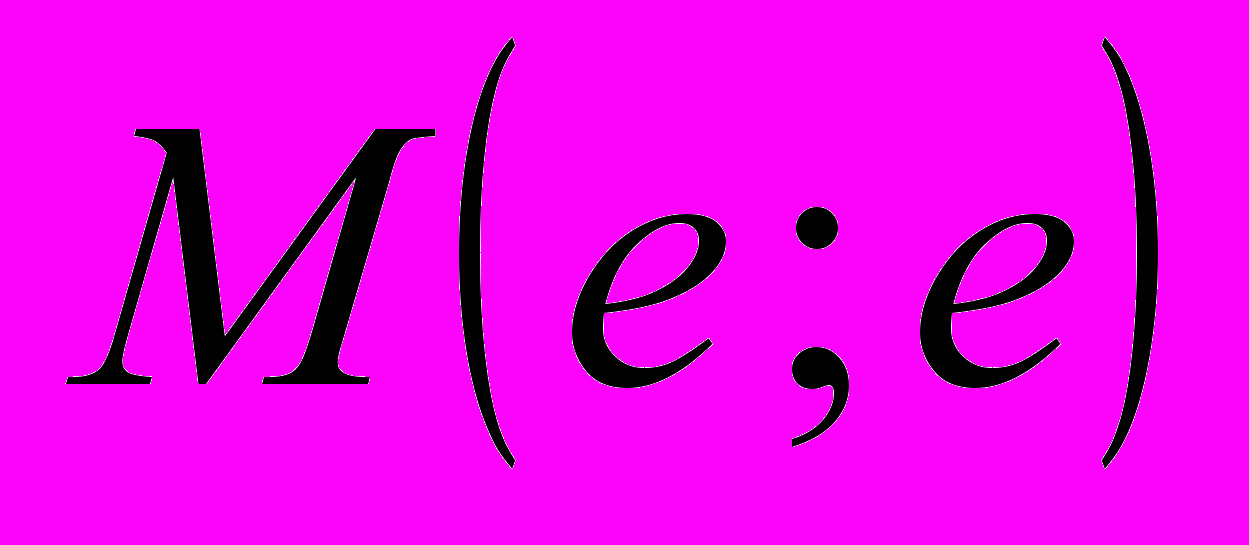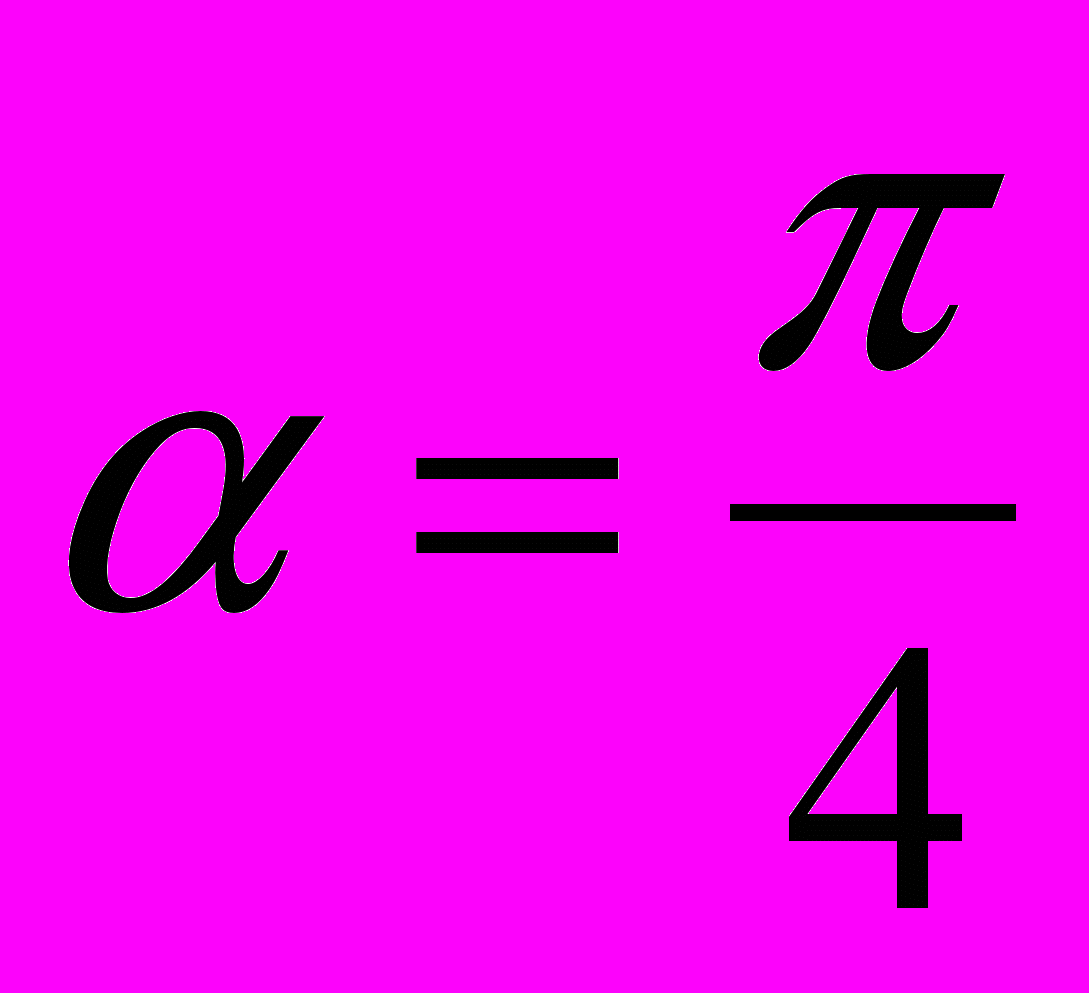
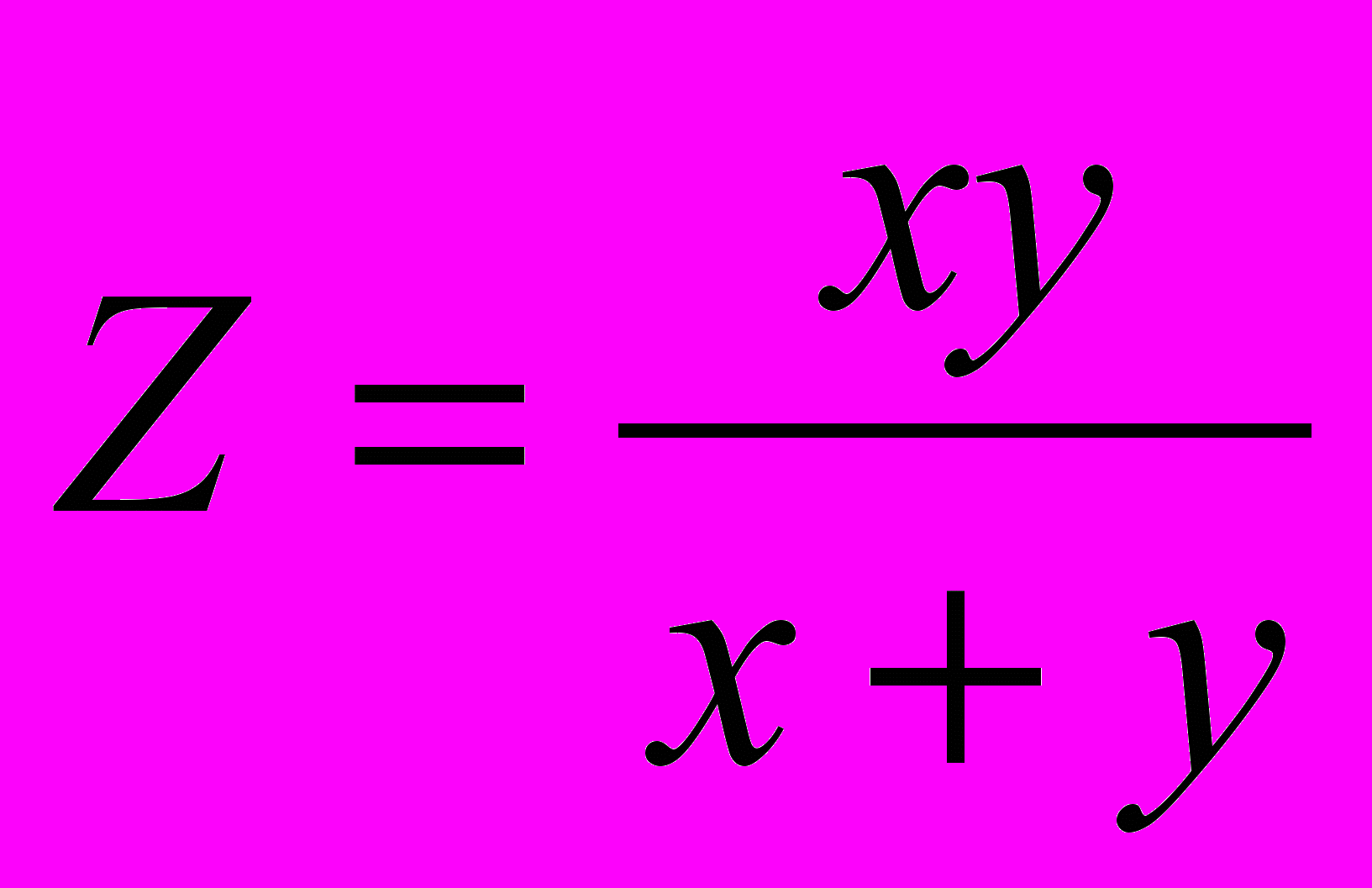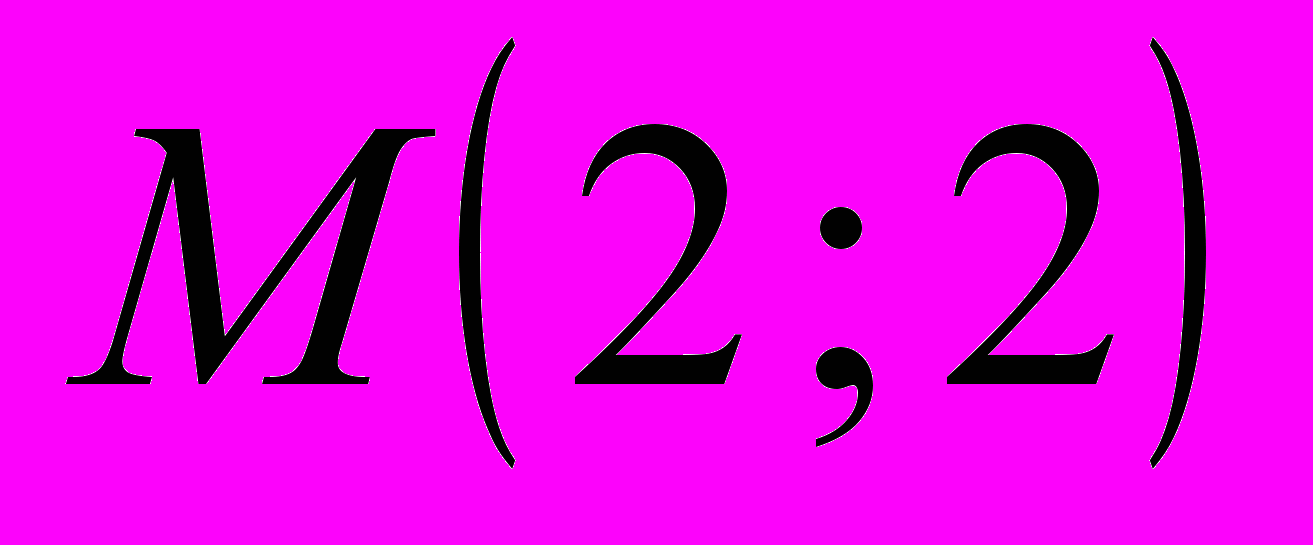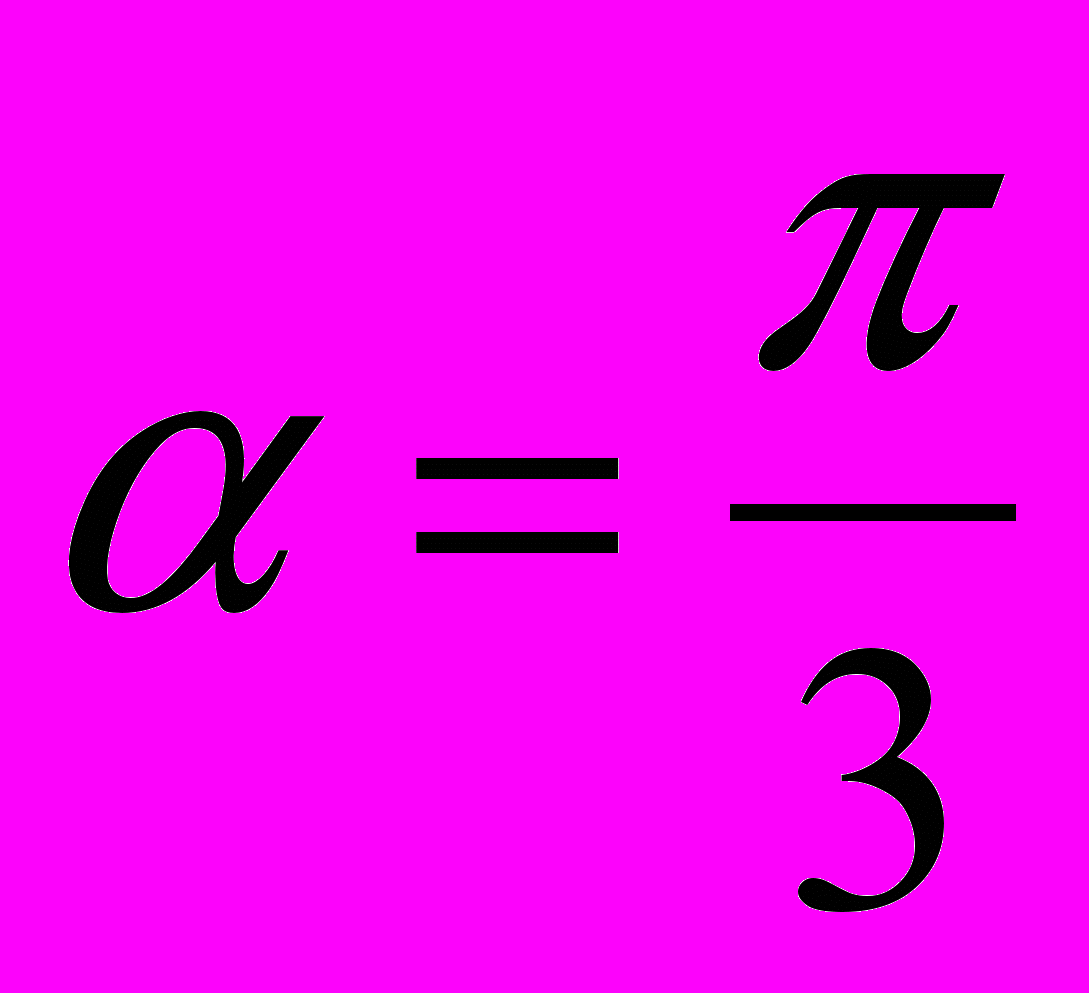
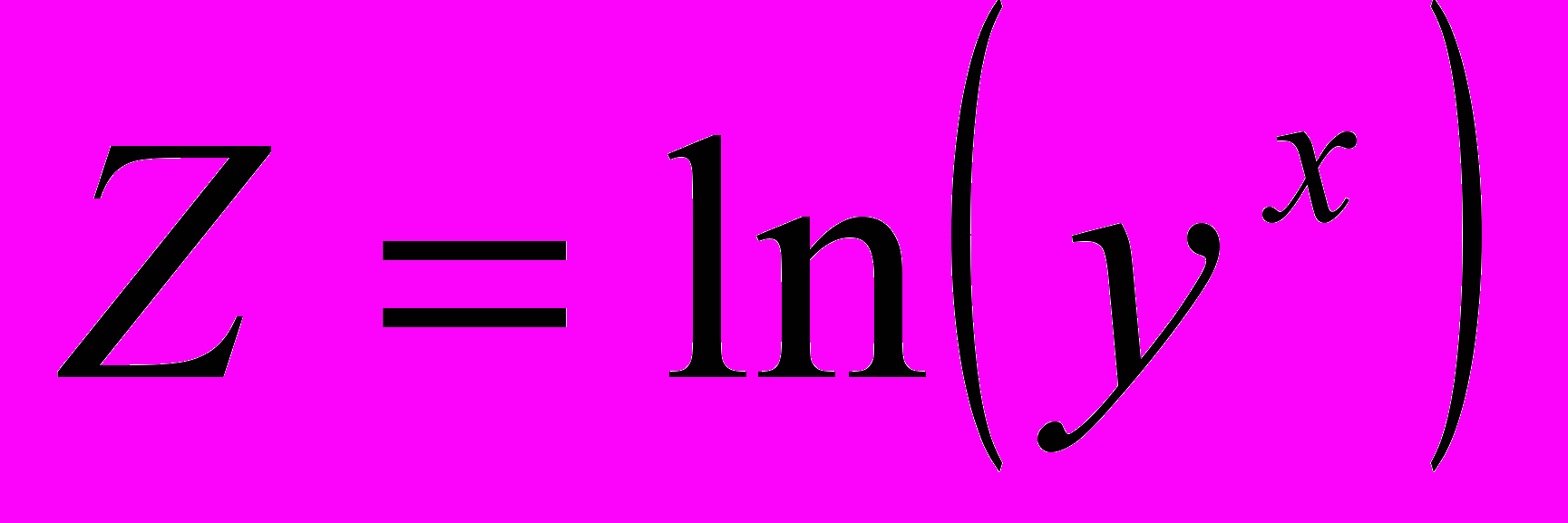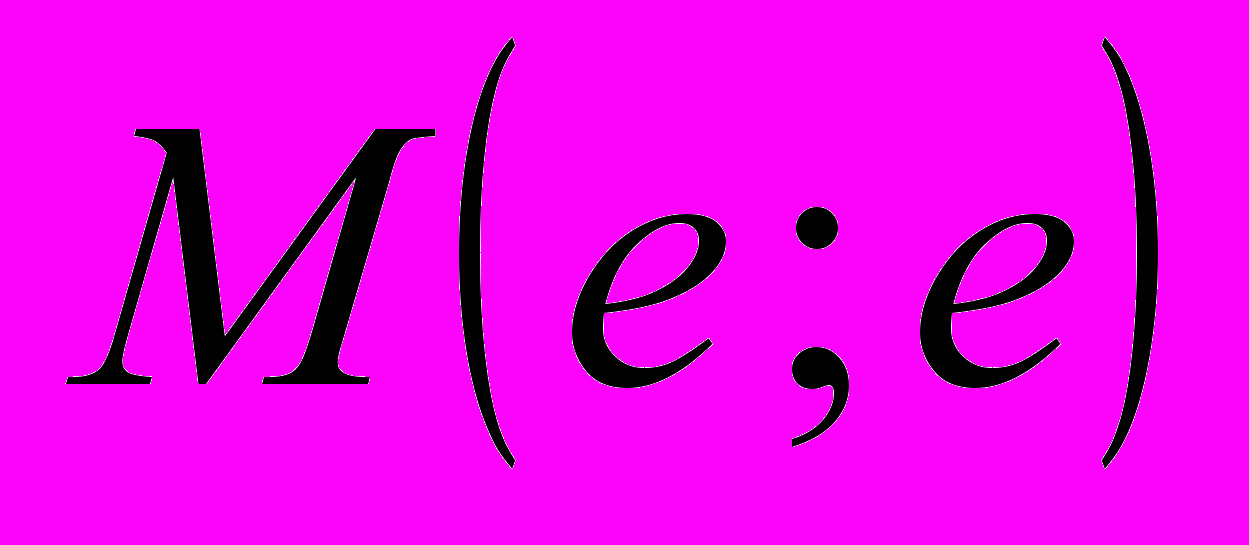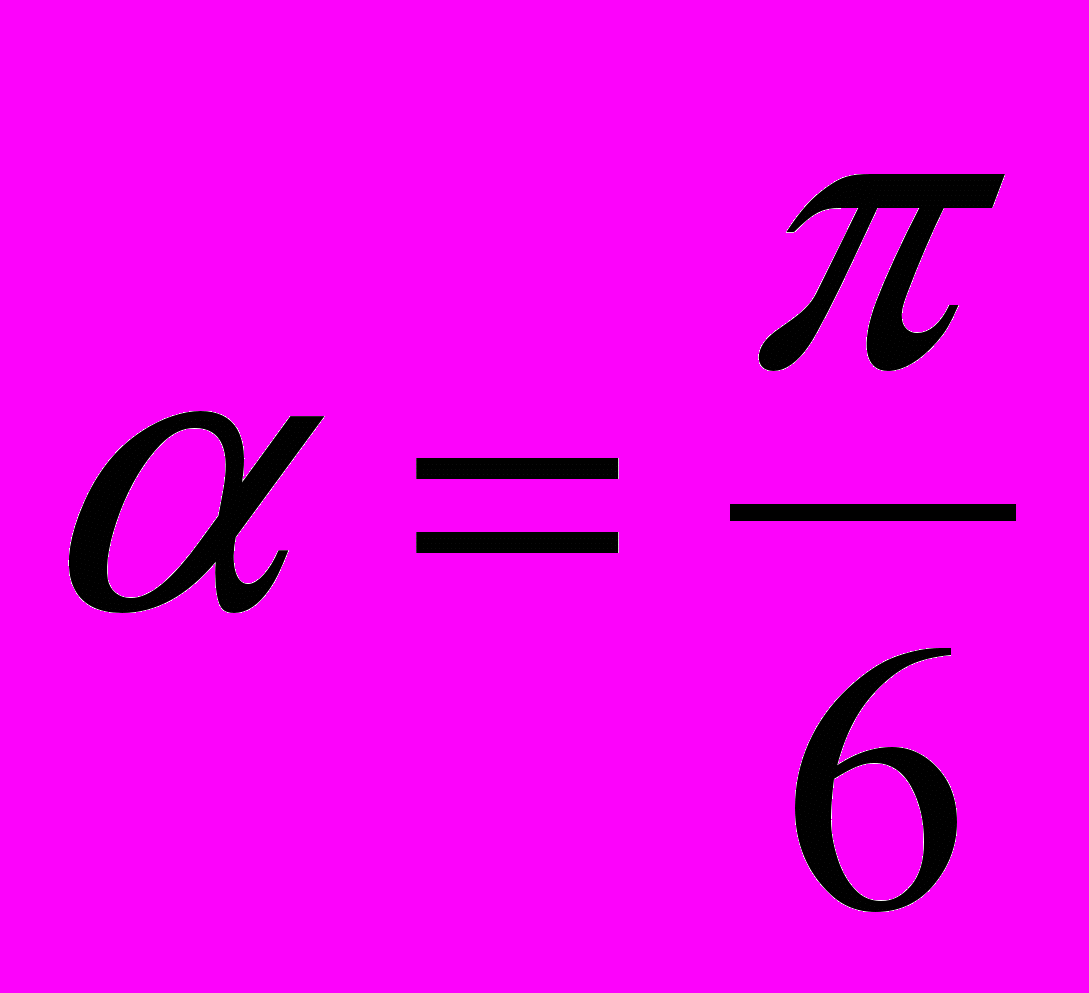
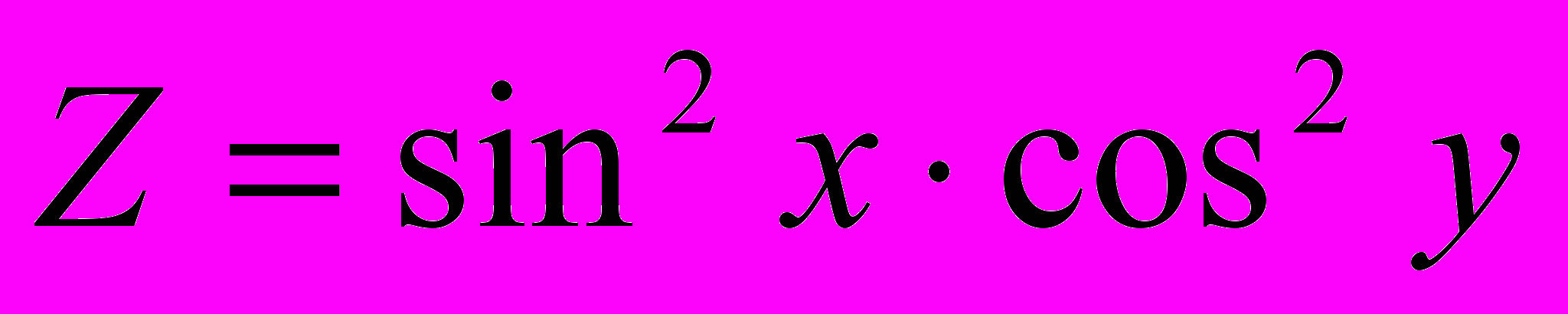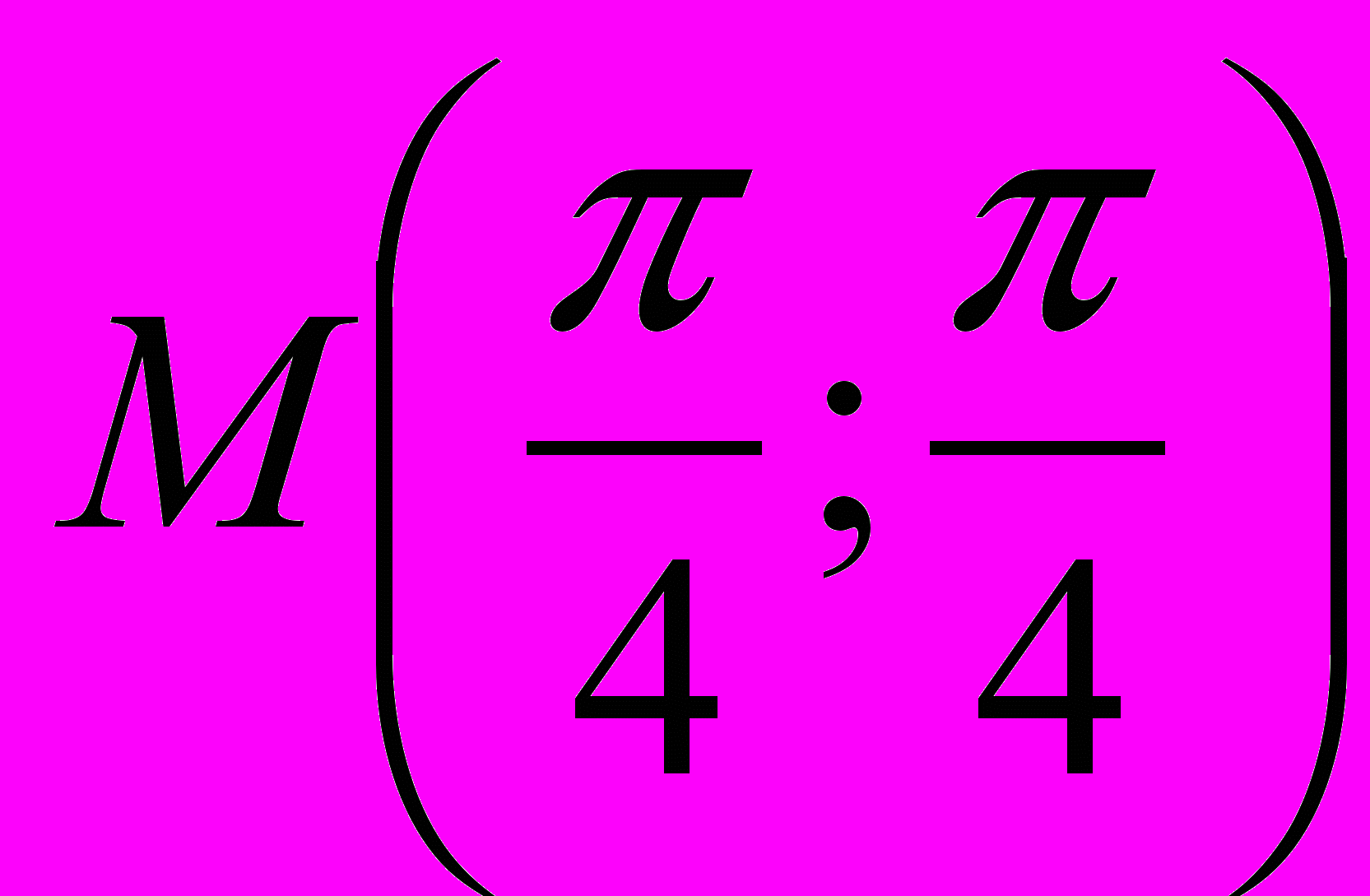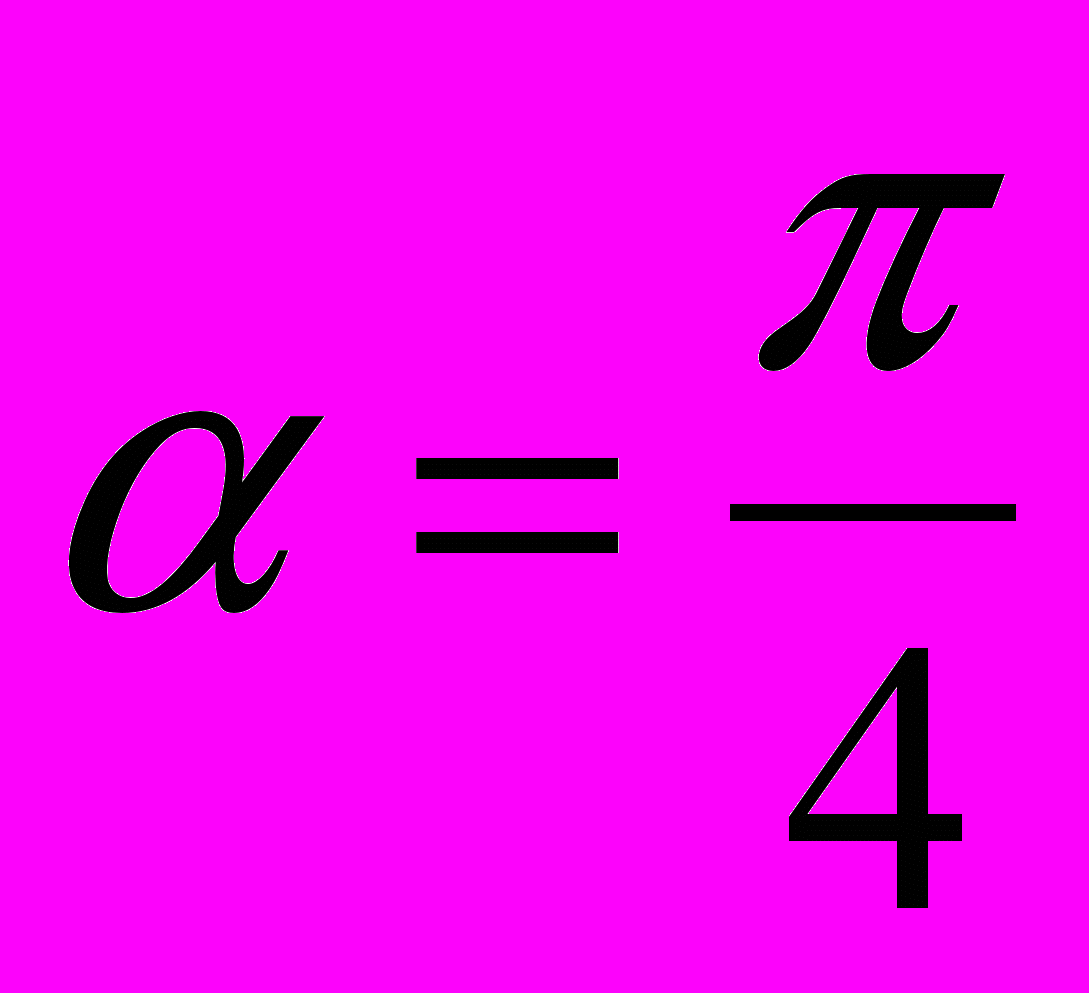
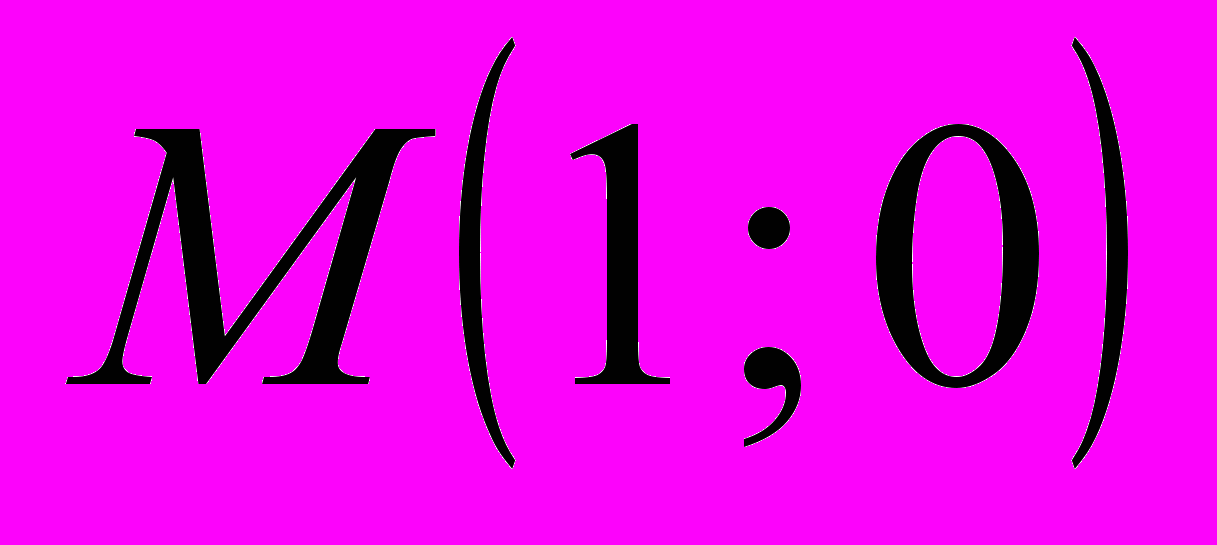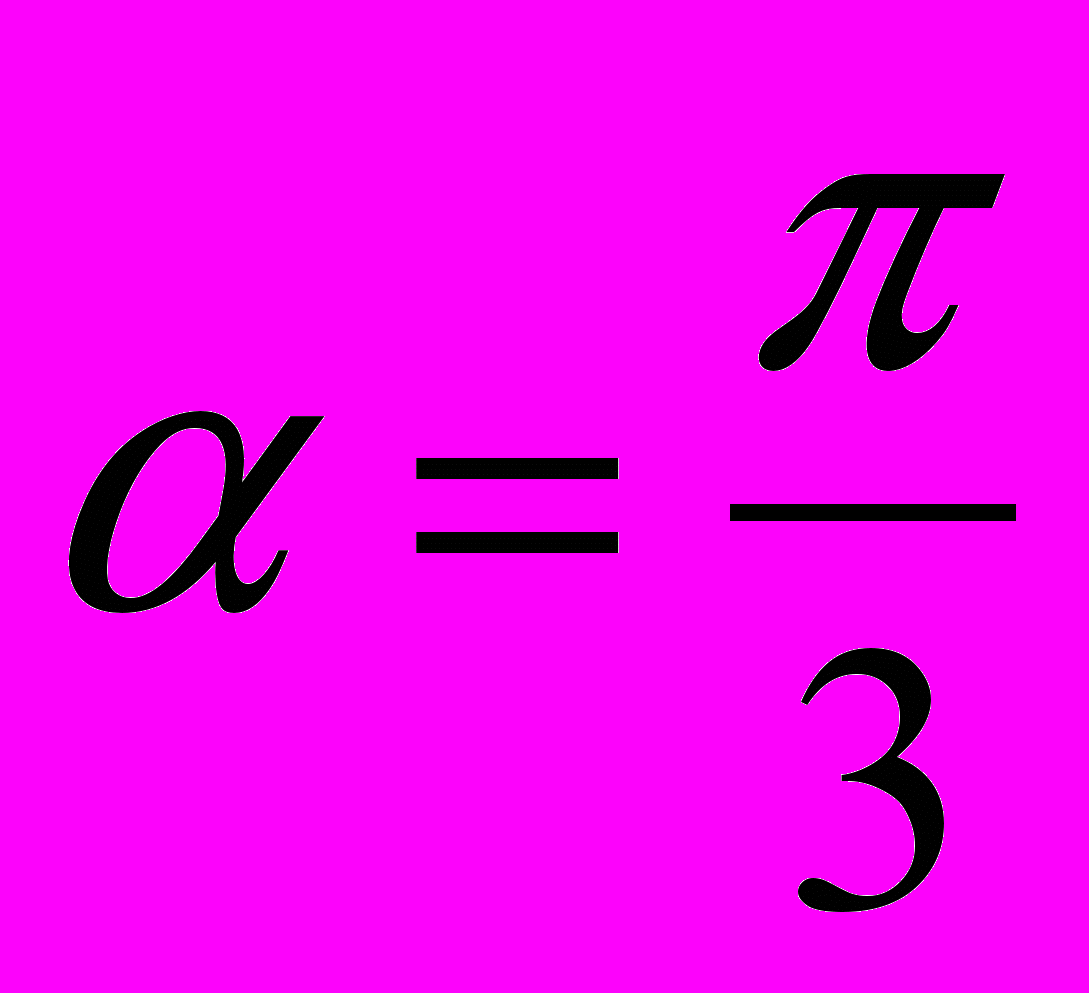
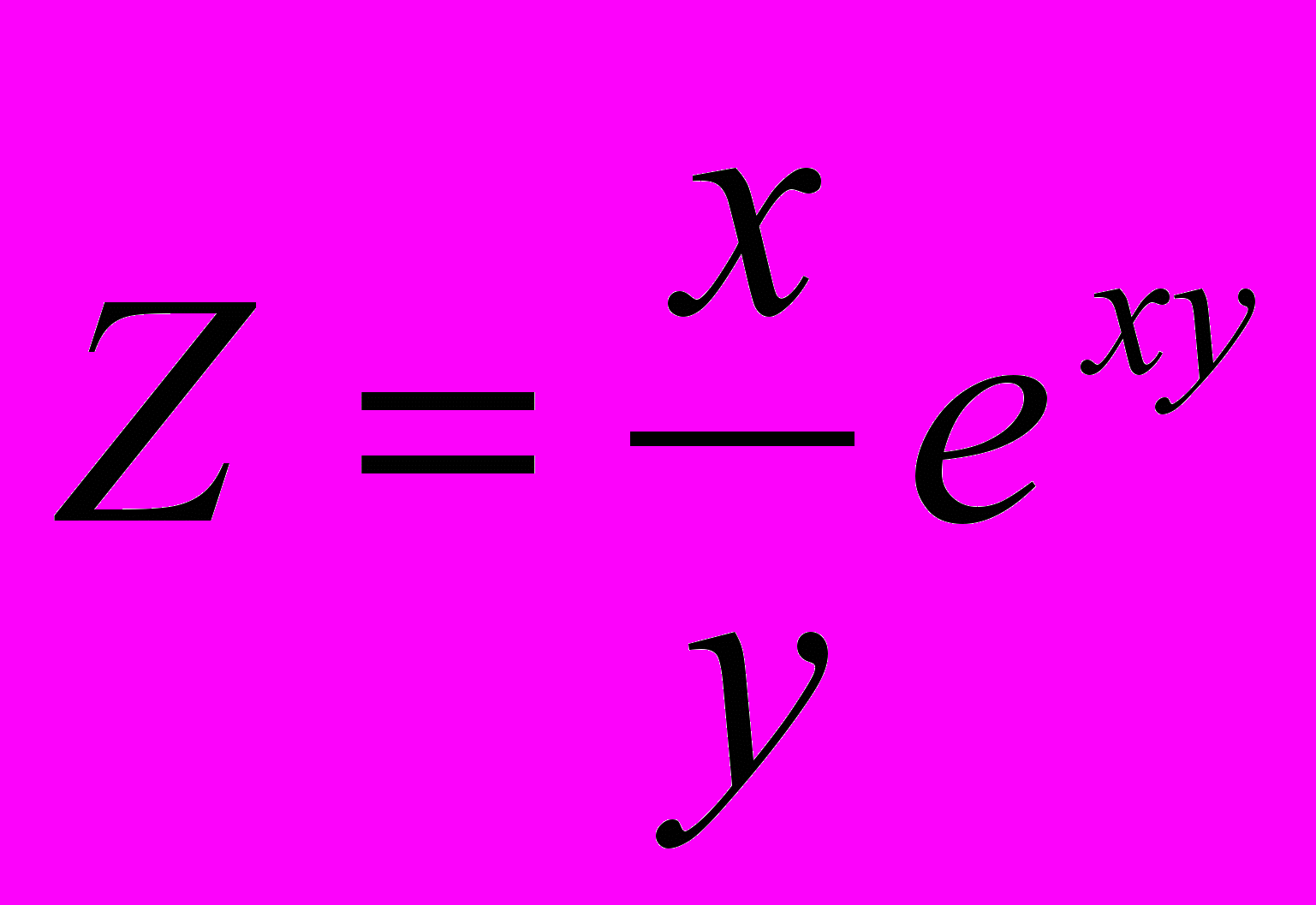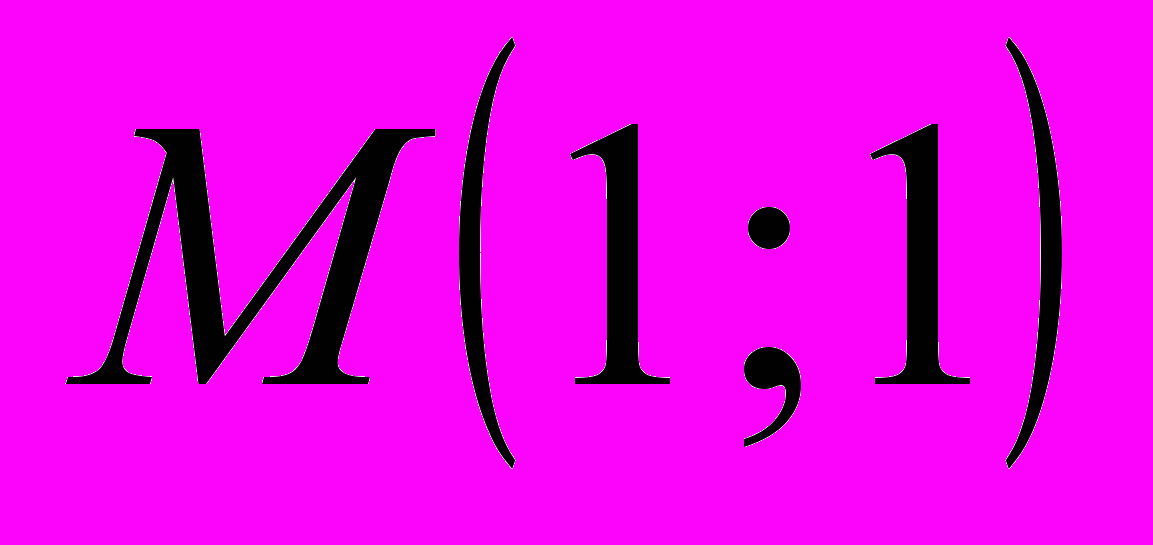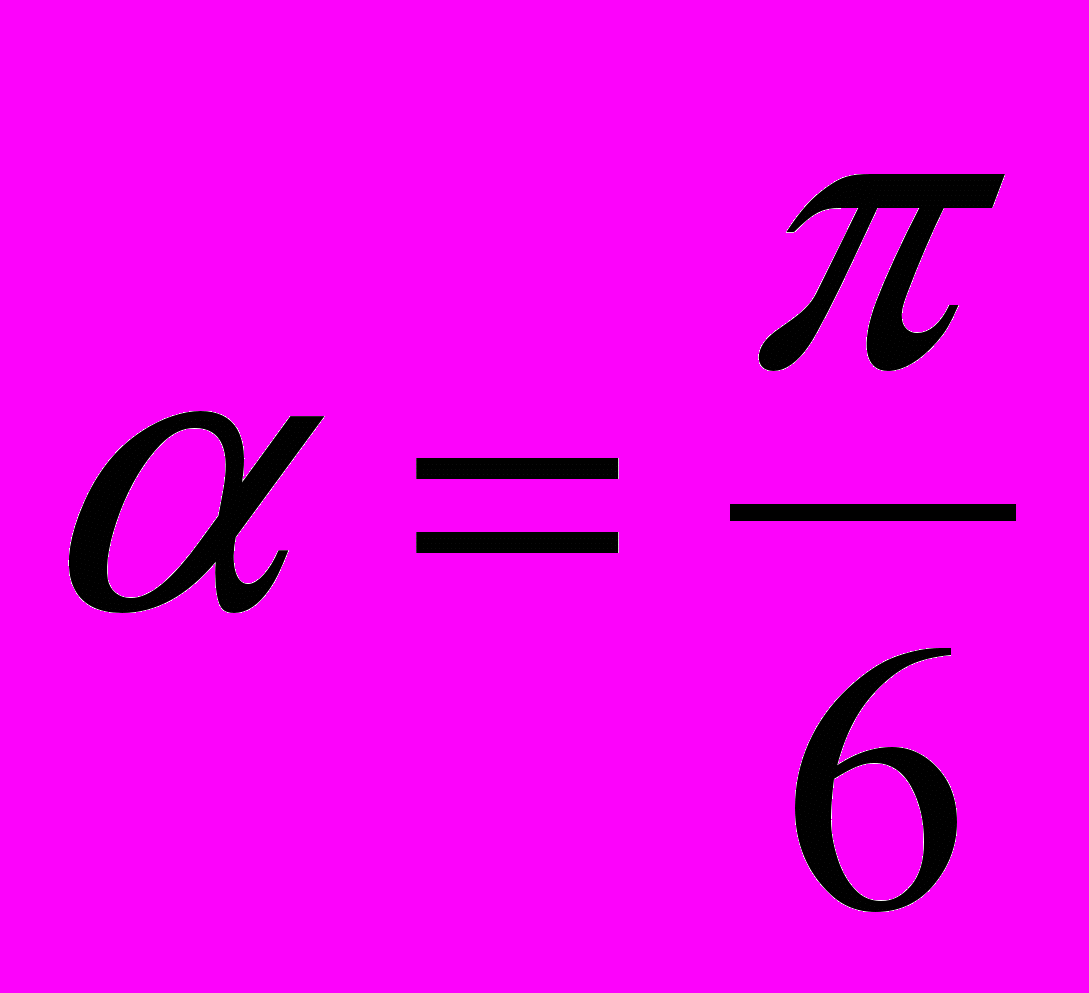
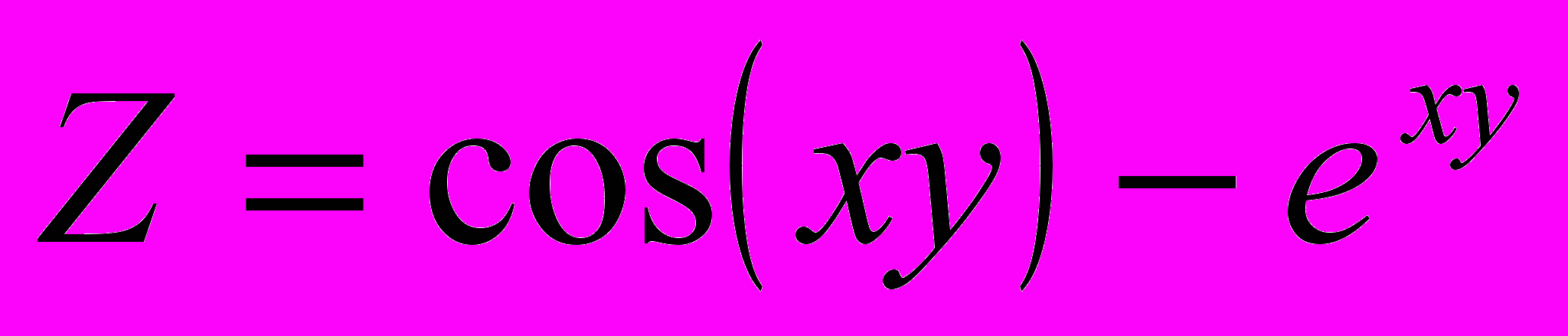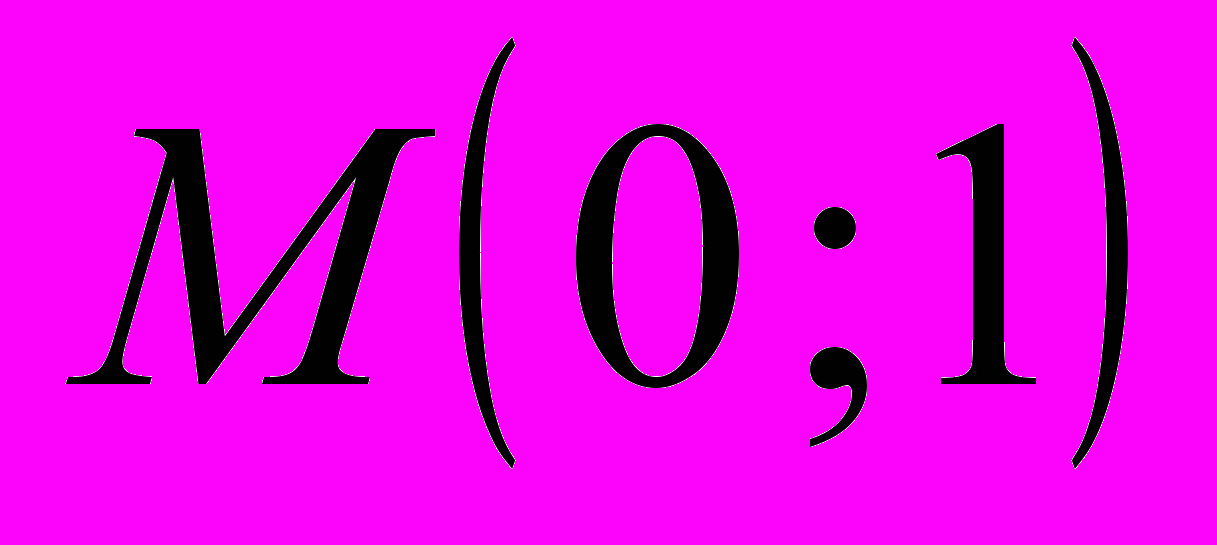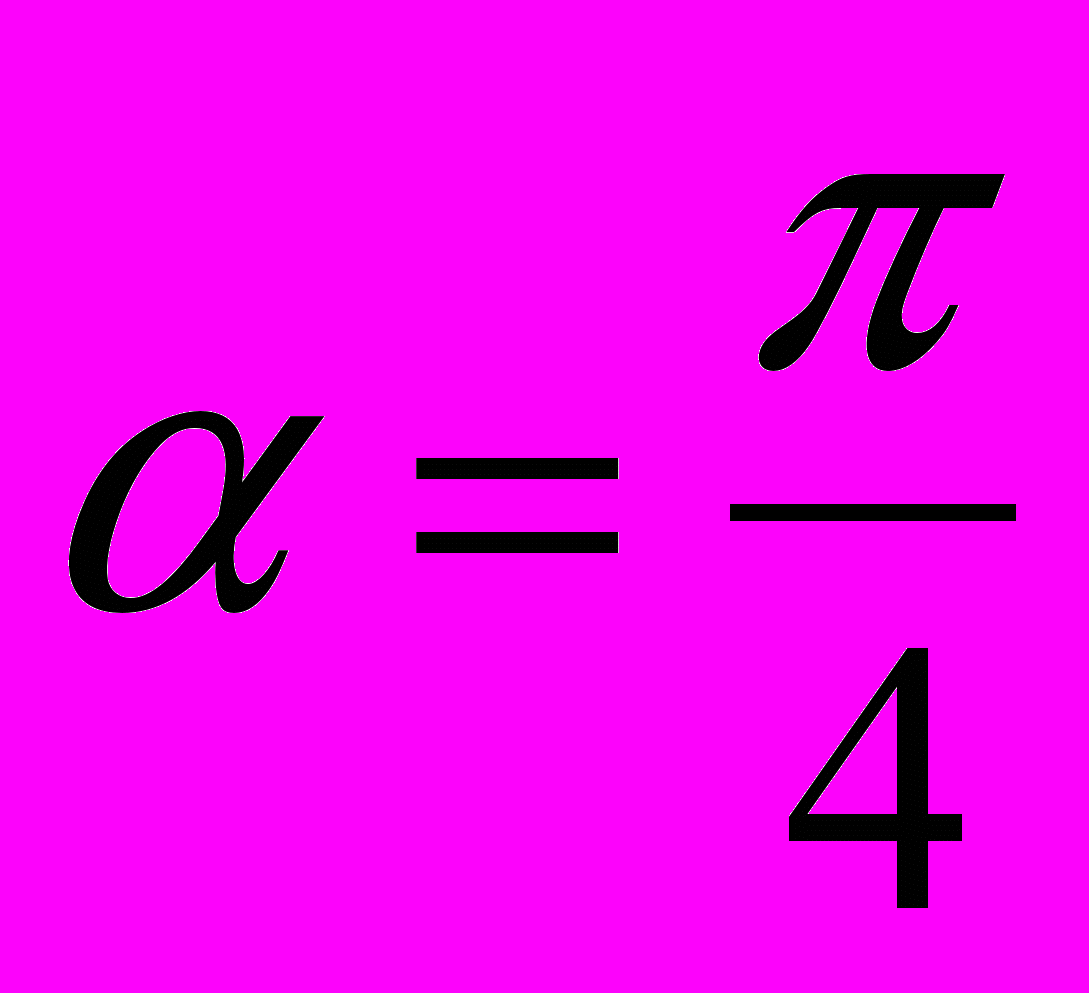
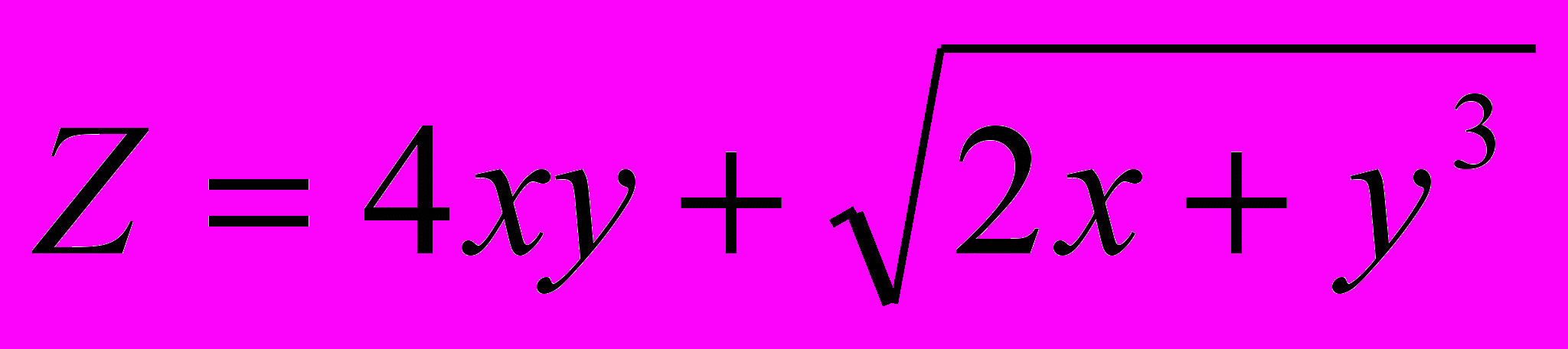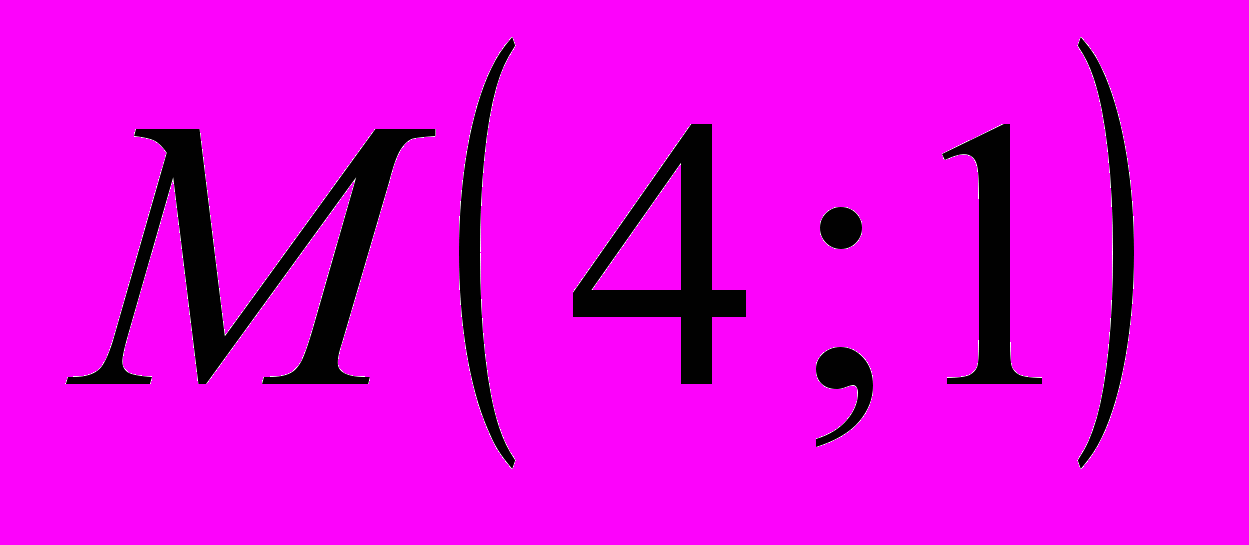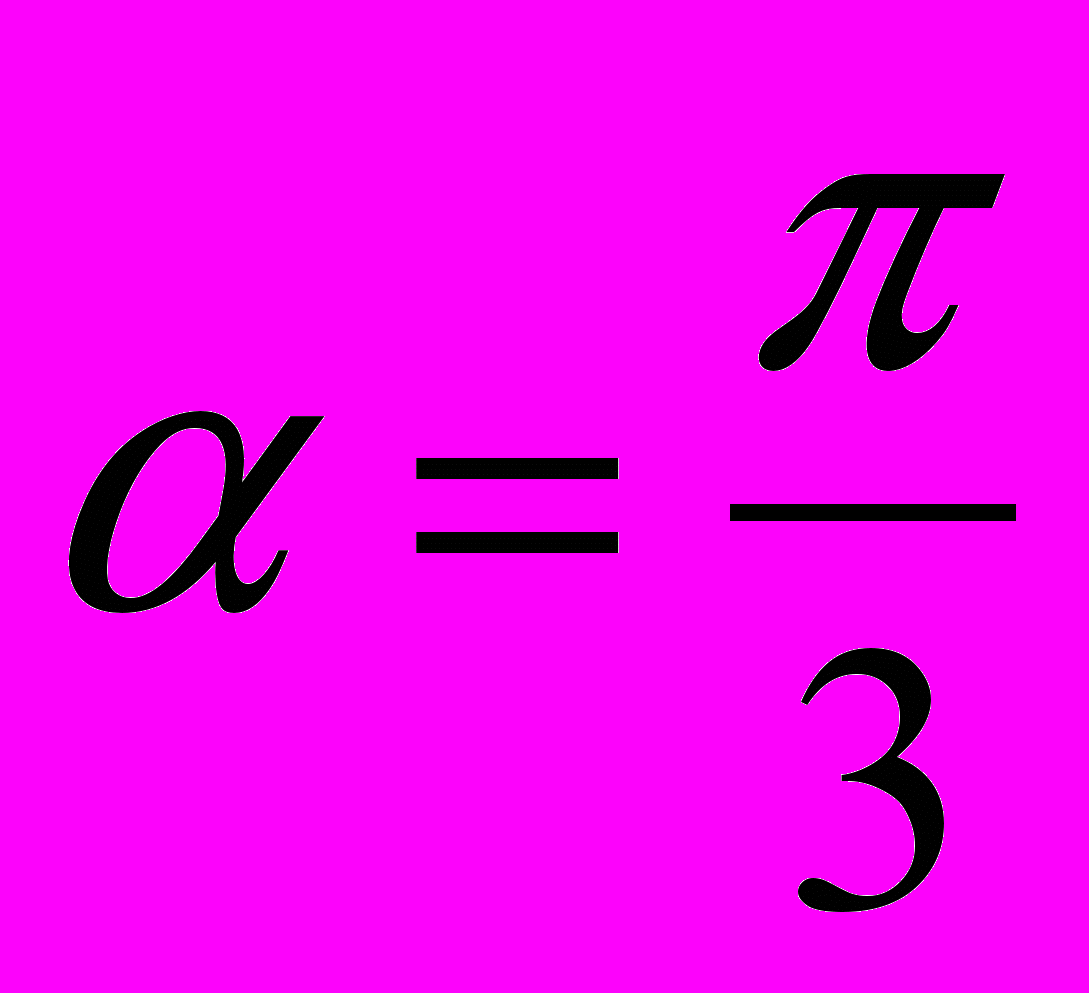
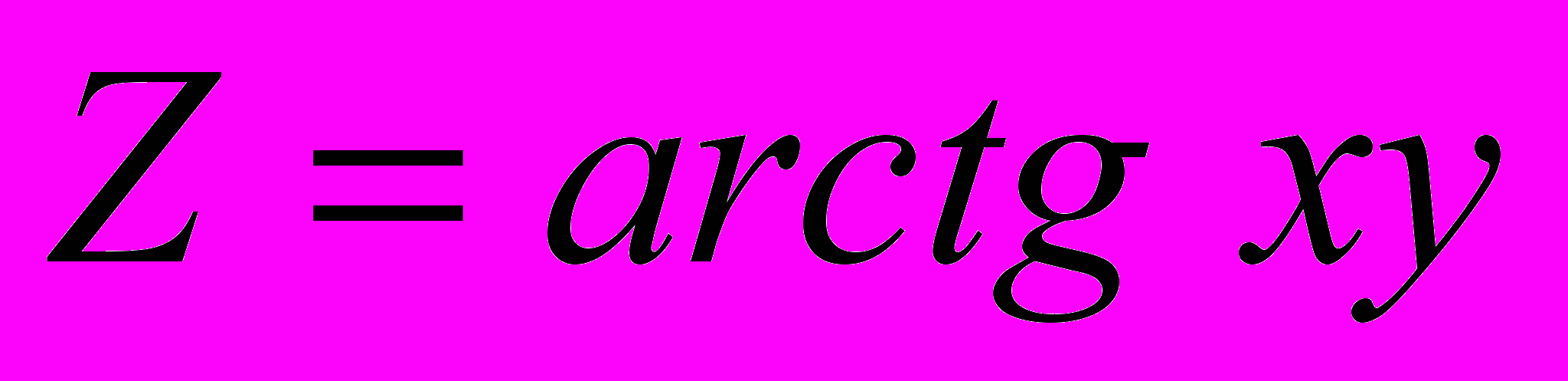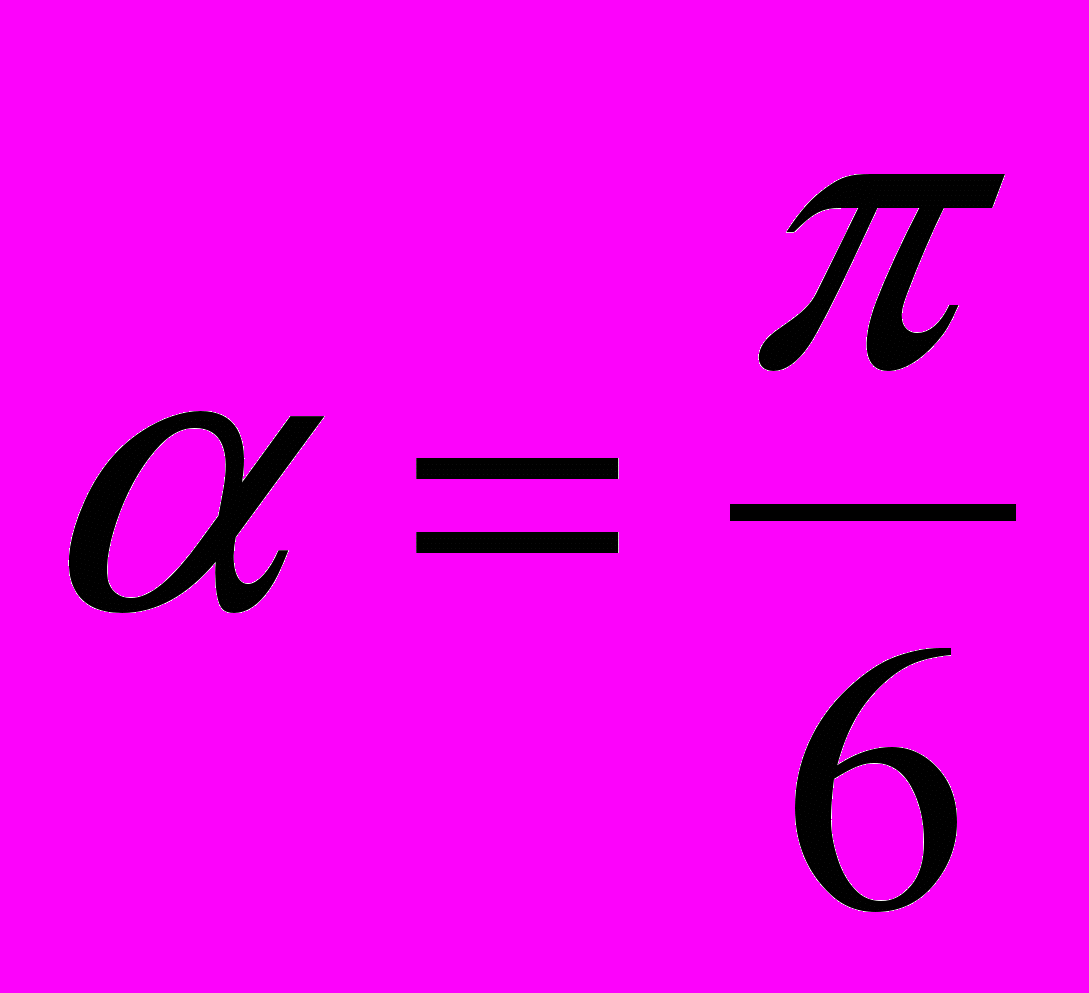
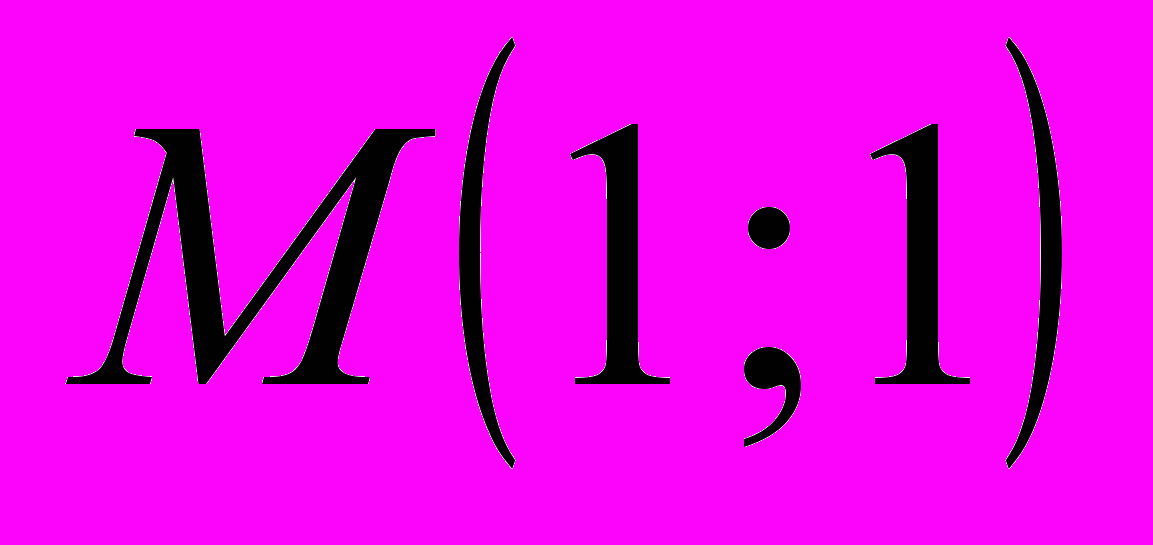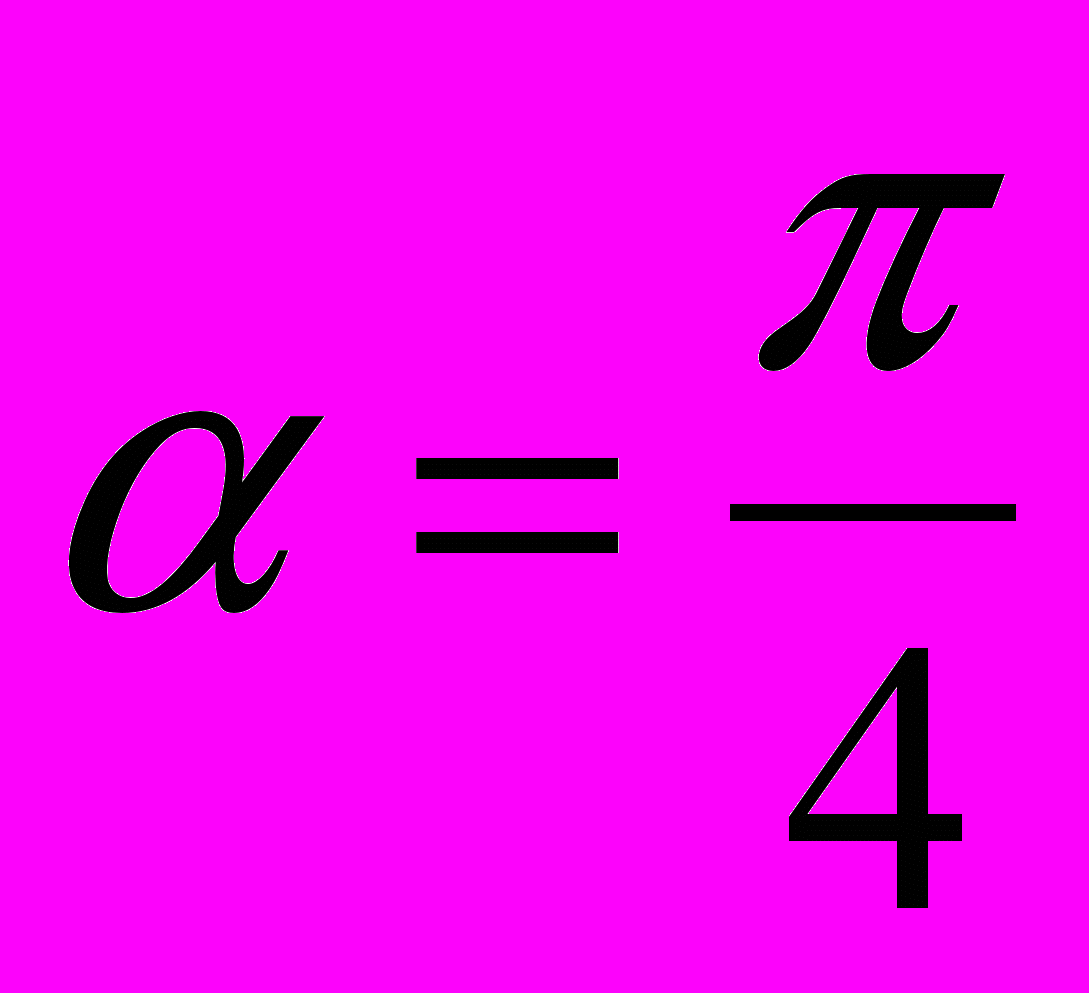
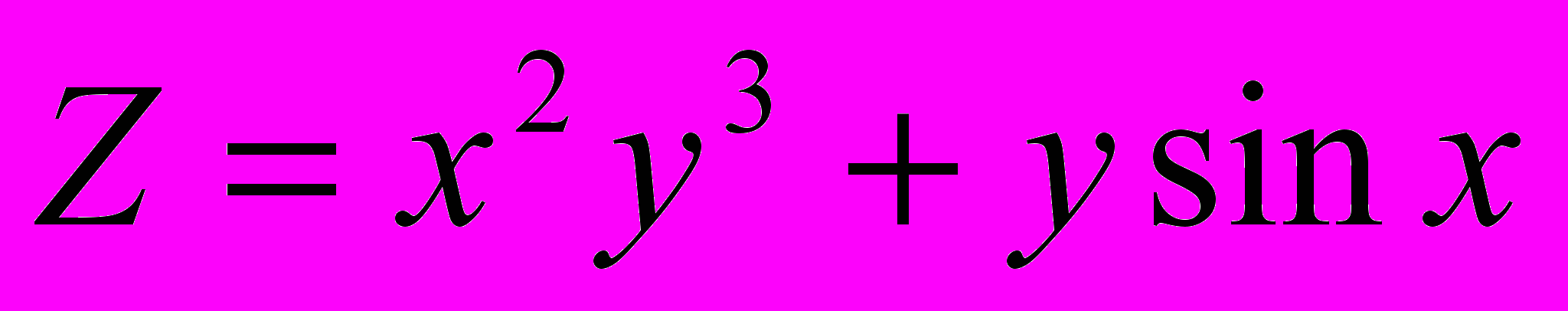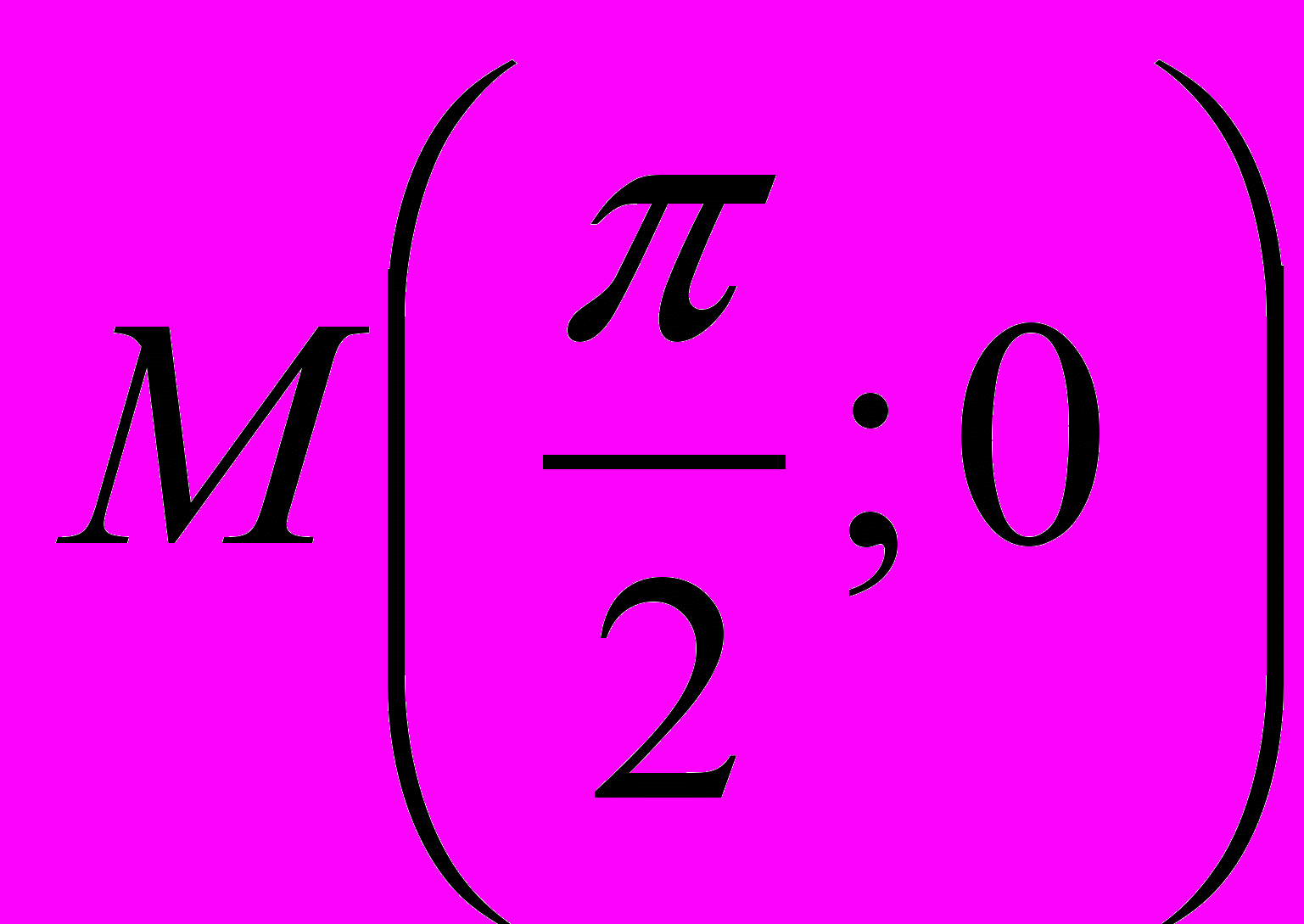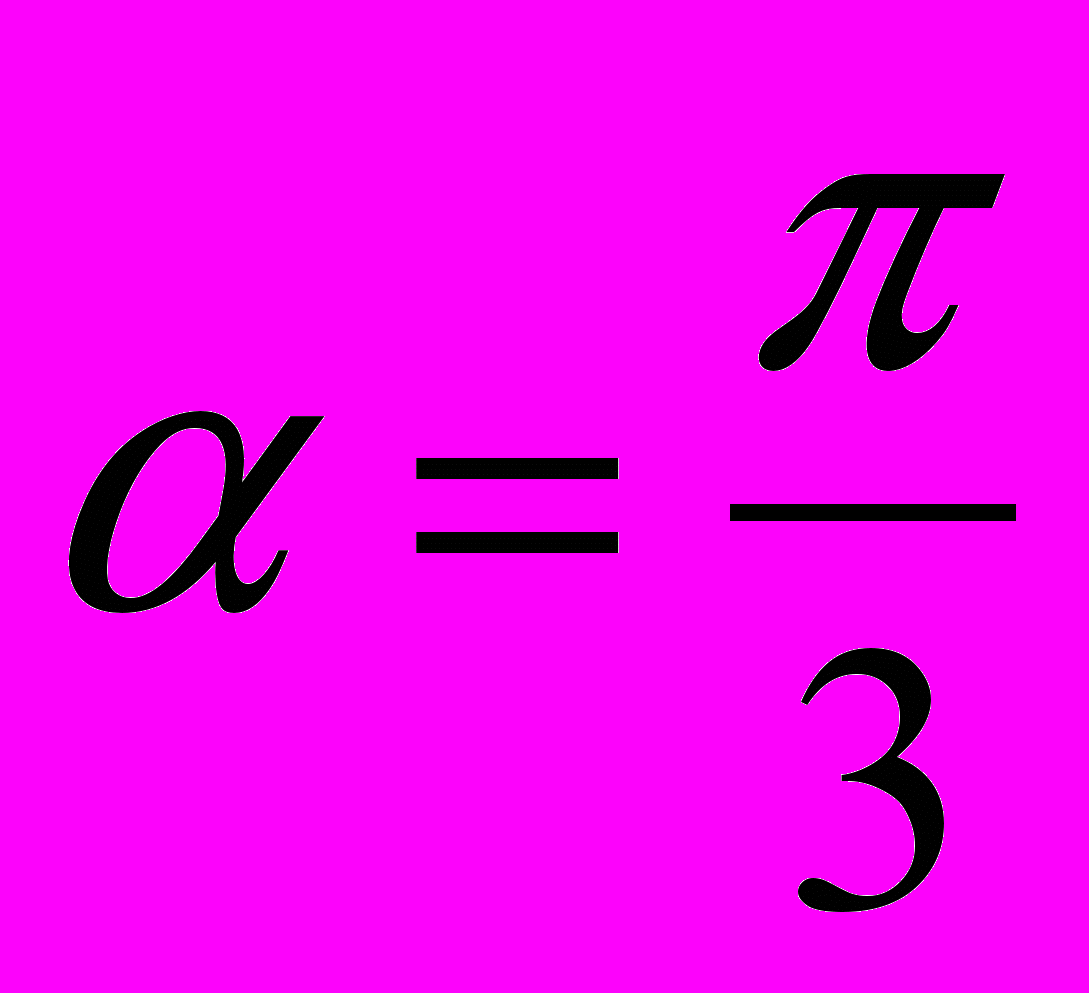
Решение типового примера.

Пусть , , .

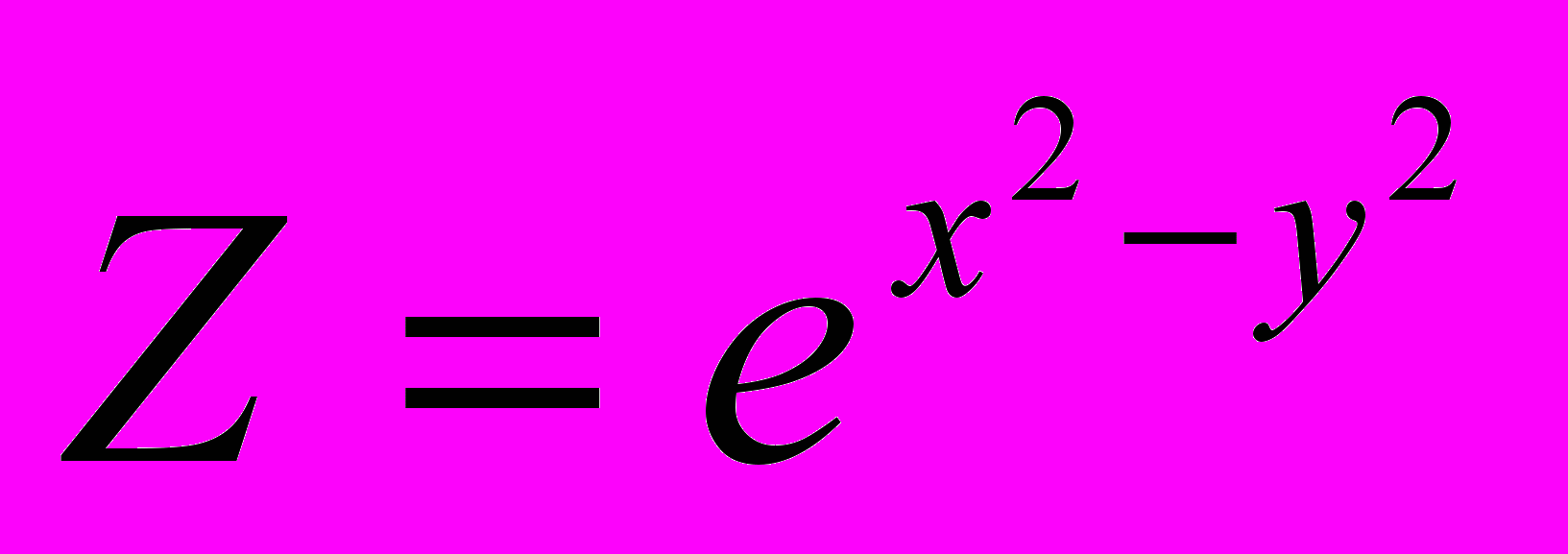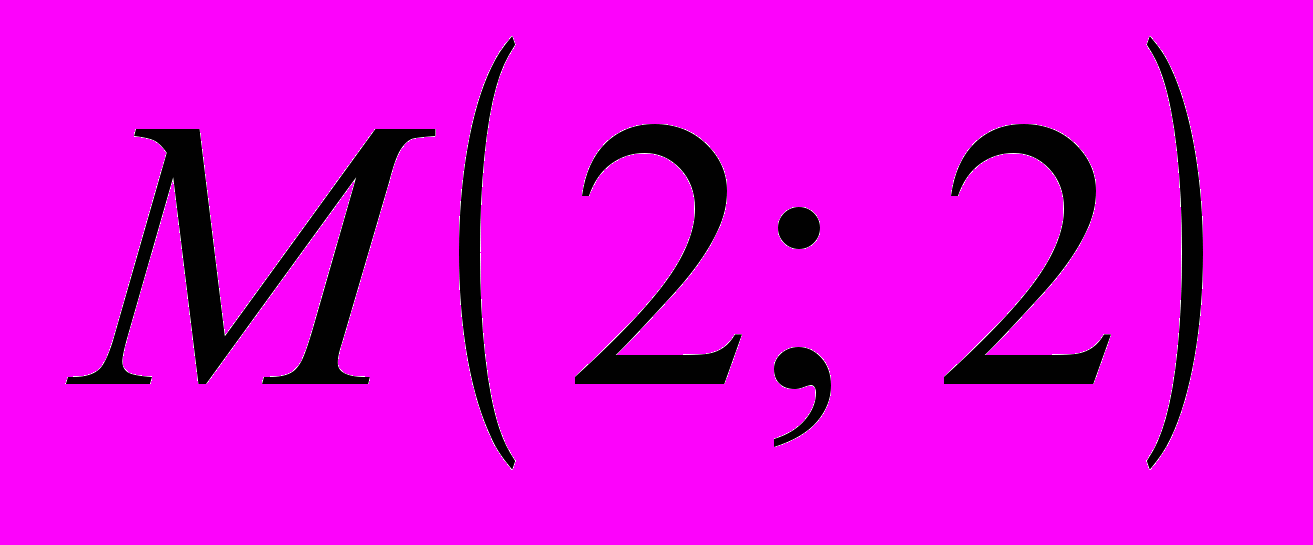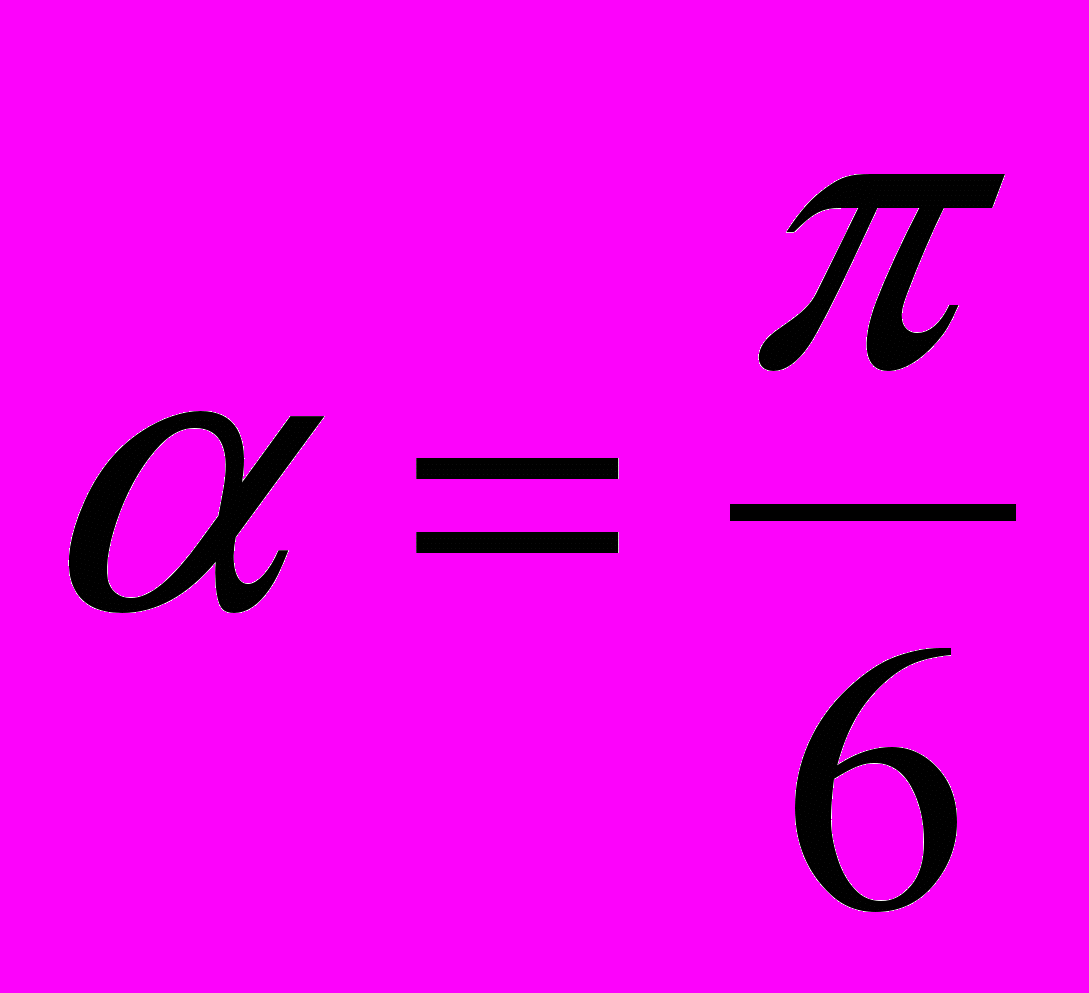При вычислении частной производной функции Z по переменной x (обозначается 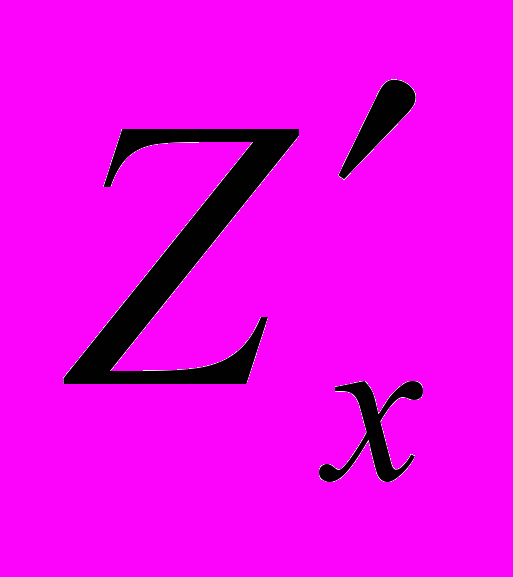или 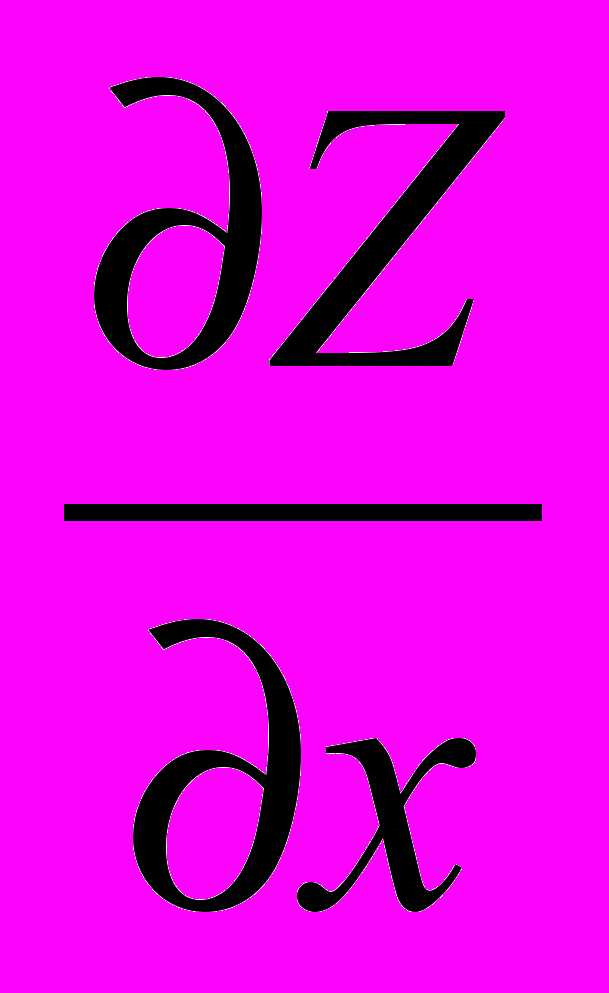), переменную 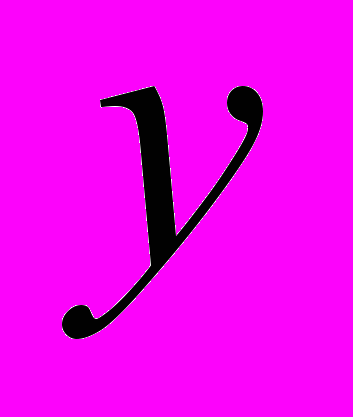рассматриваем как постоянную величину. В остальном пользуемся теми же правилами и формулами, что и при дифференцировании функций одной переменной. Получим:

.

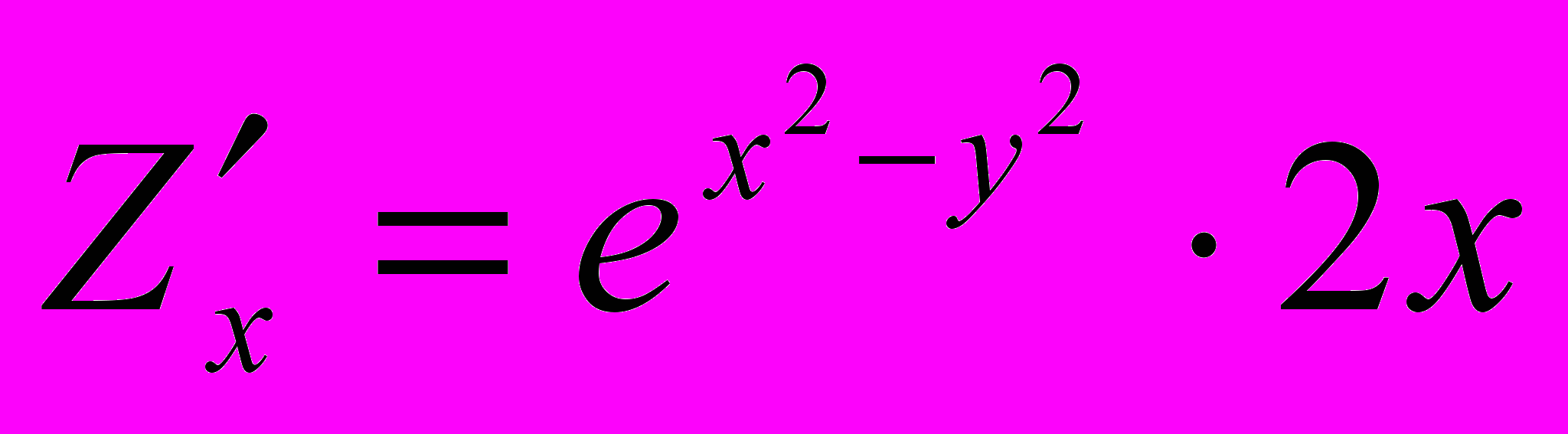При вычислении частной производной функции Z по переменной y (обозначается 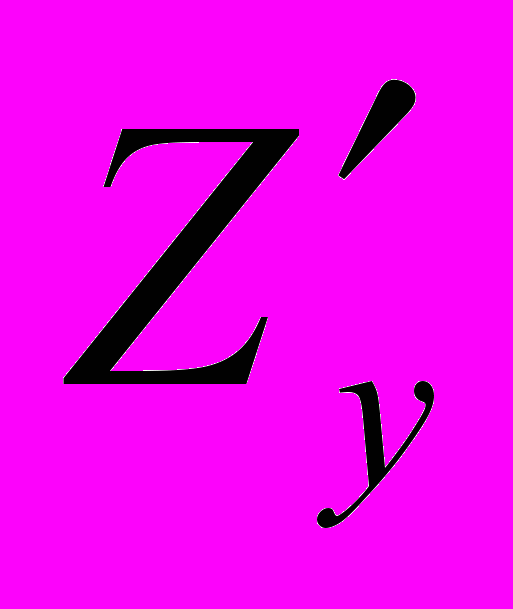или 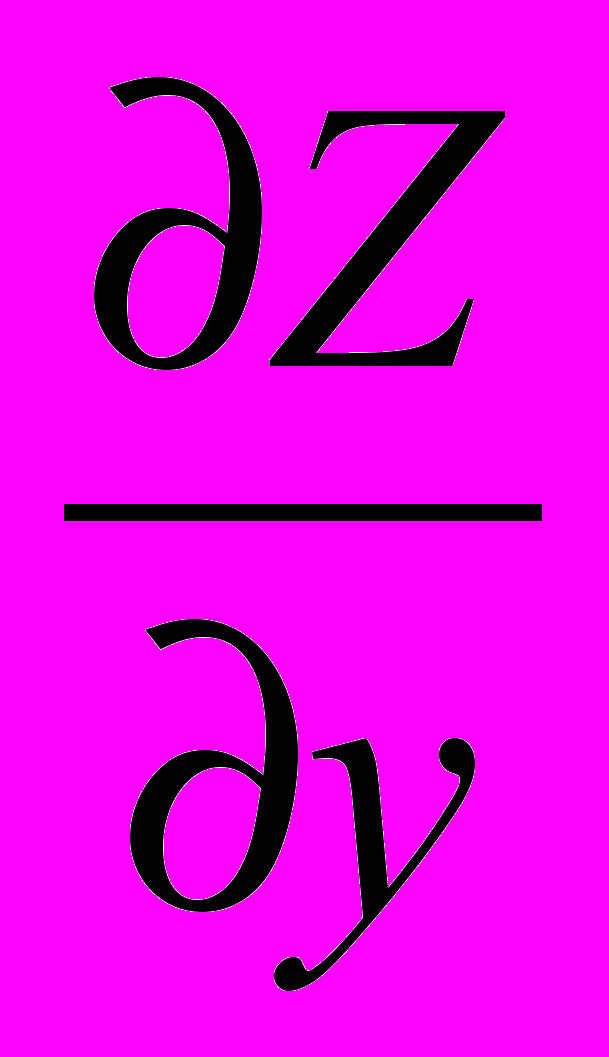), переменную 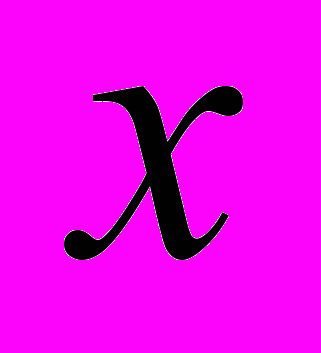рассматриваем как постоянную величину. Поэтому:

.

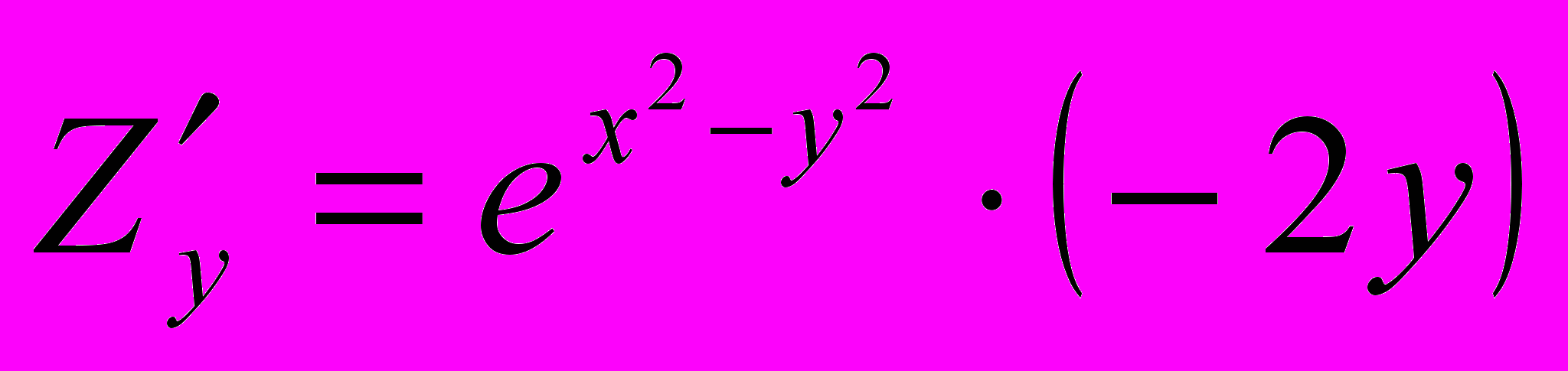Частные производные второго порядка обозначаются и вычисляются по следующим формулам:

Вторая производная по переменной : ==.

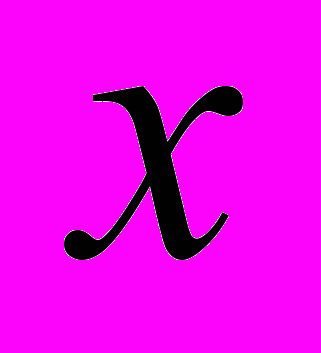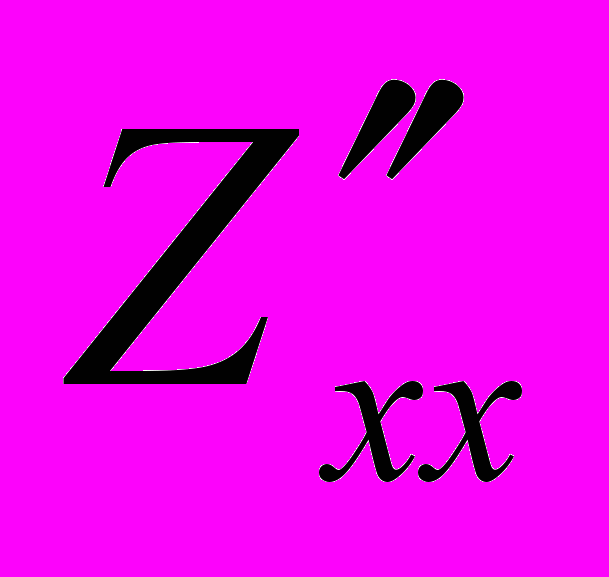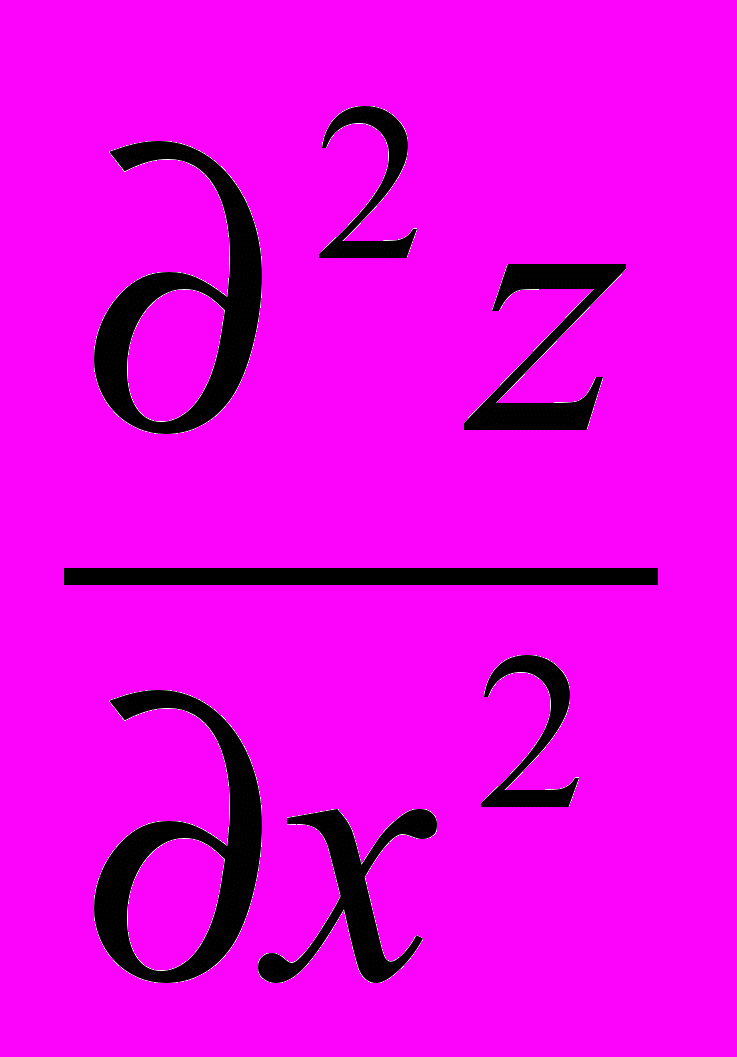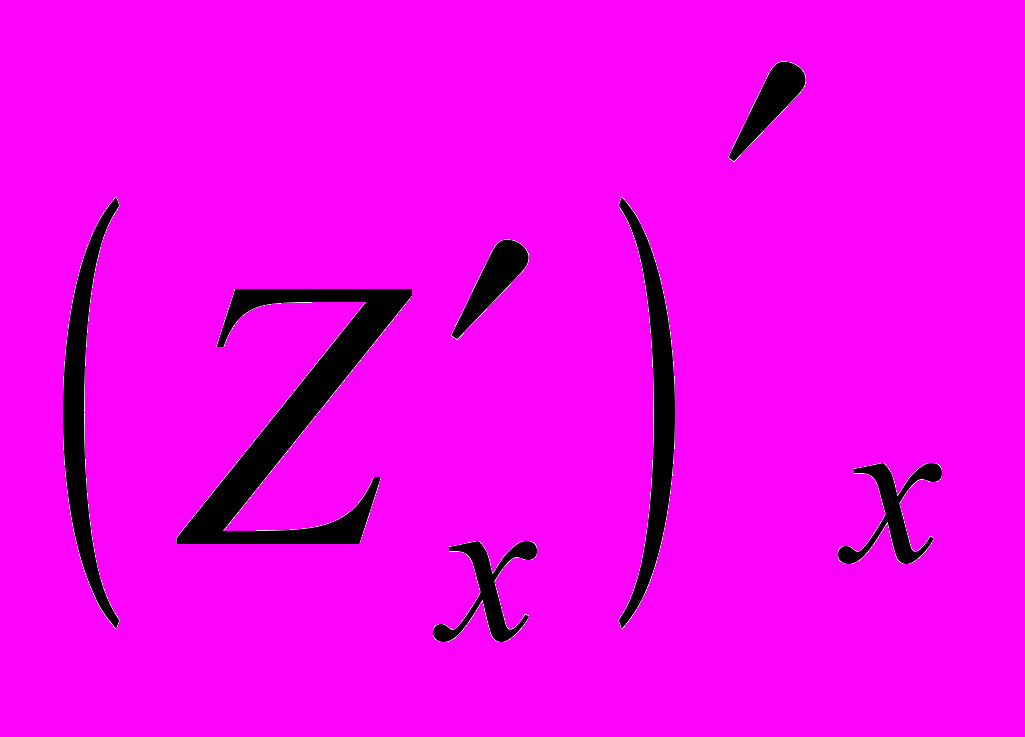Вторая производная по переменной : ==.


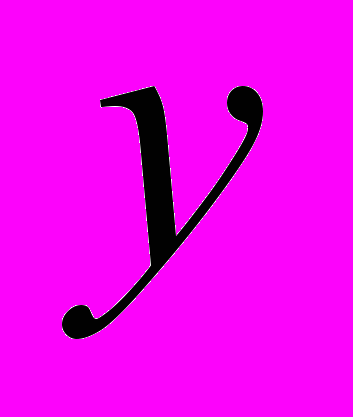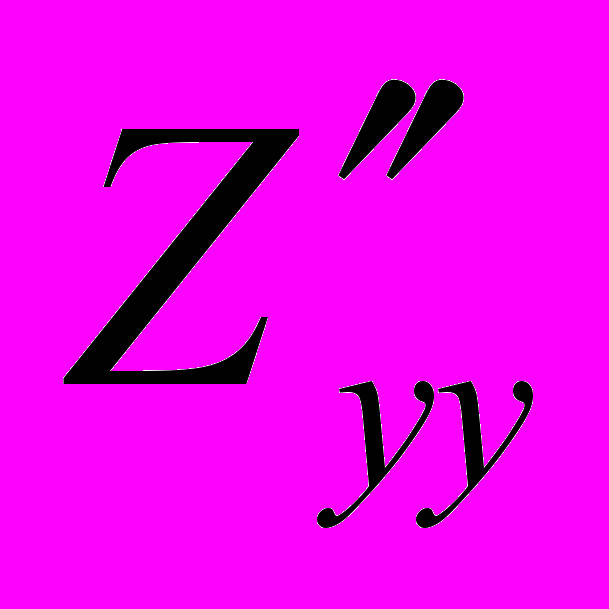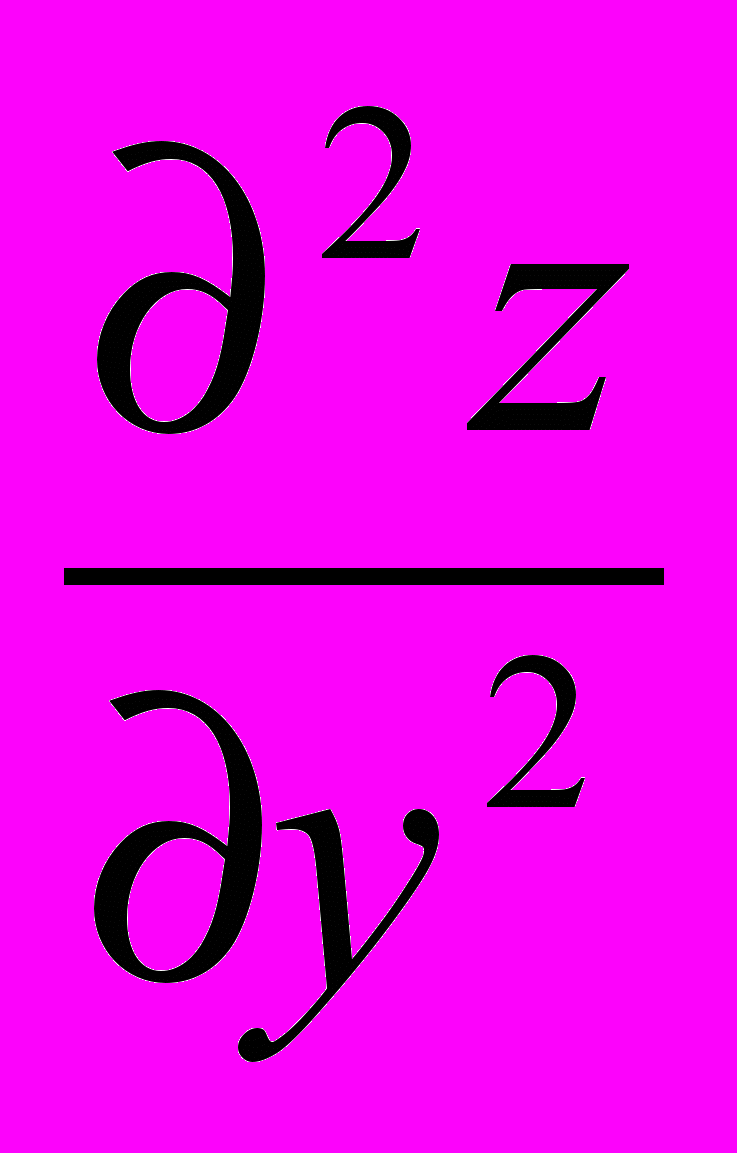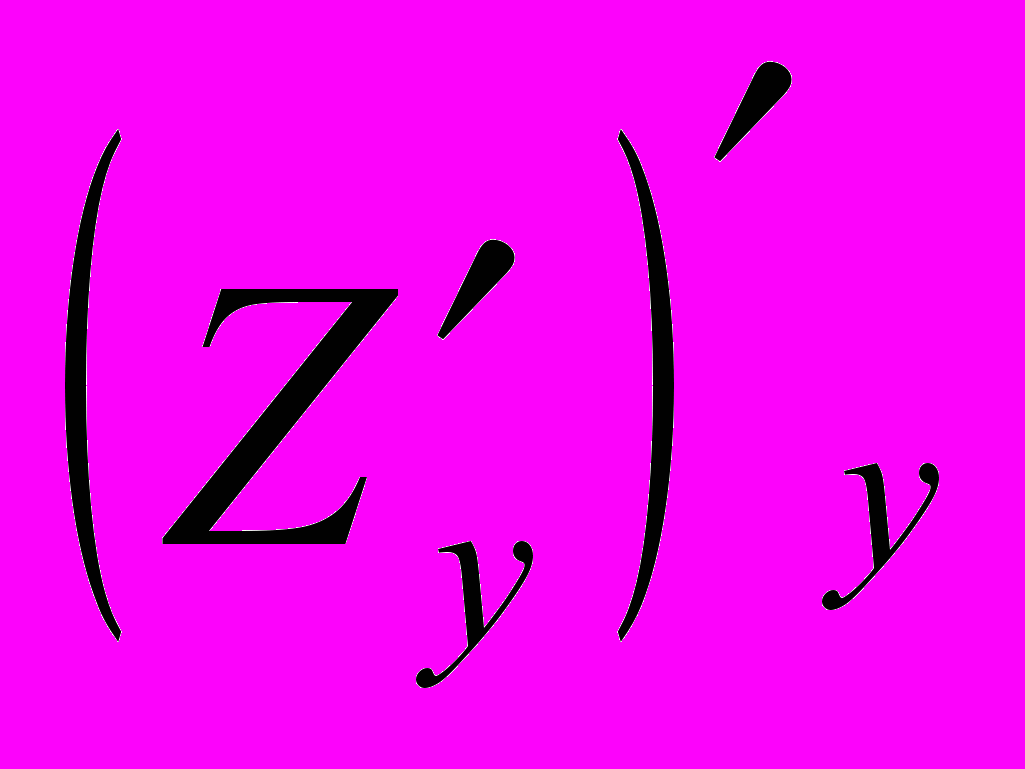Вторая производная по переменным , : ==.

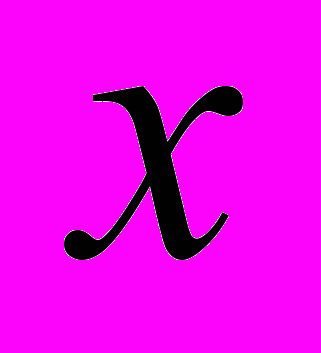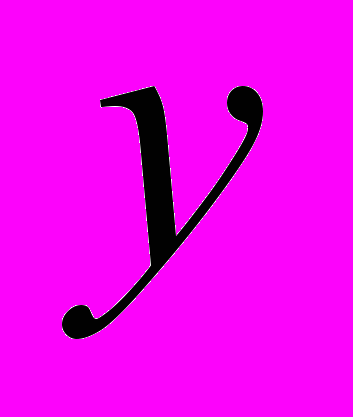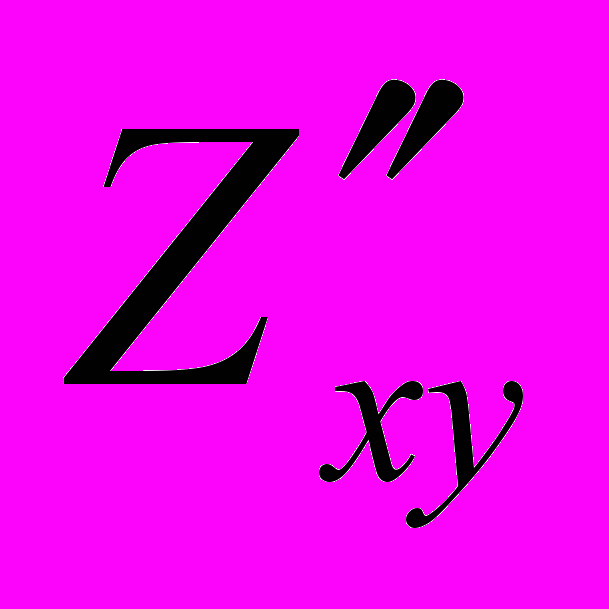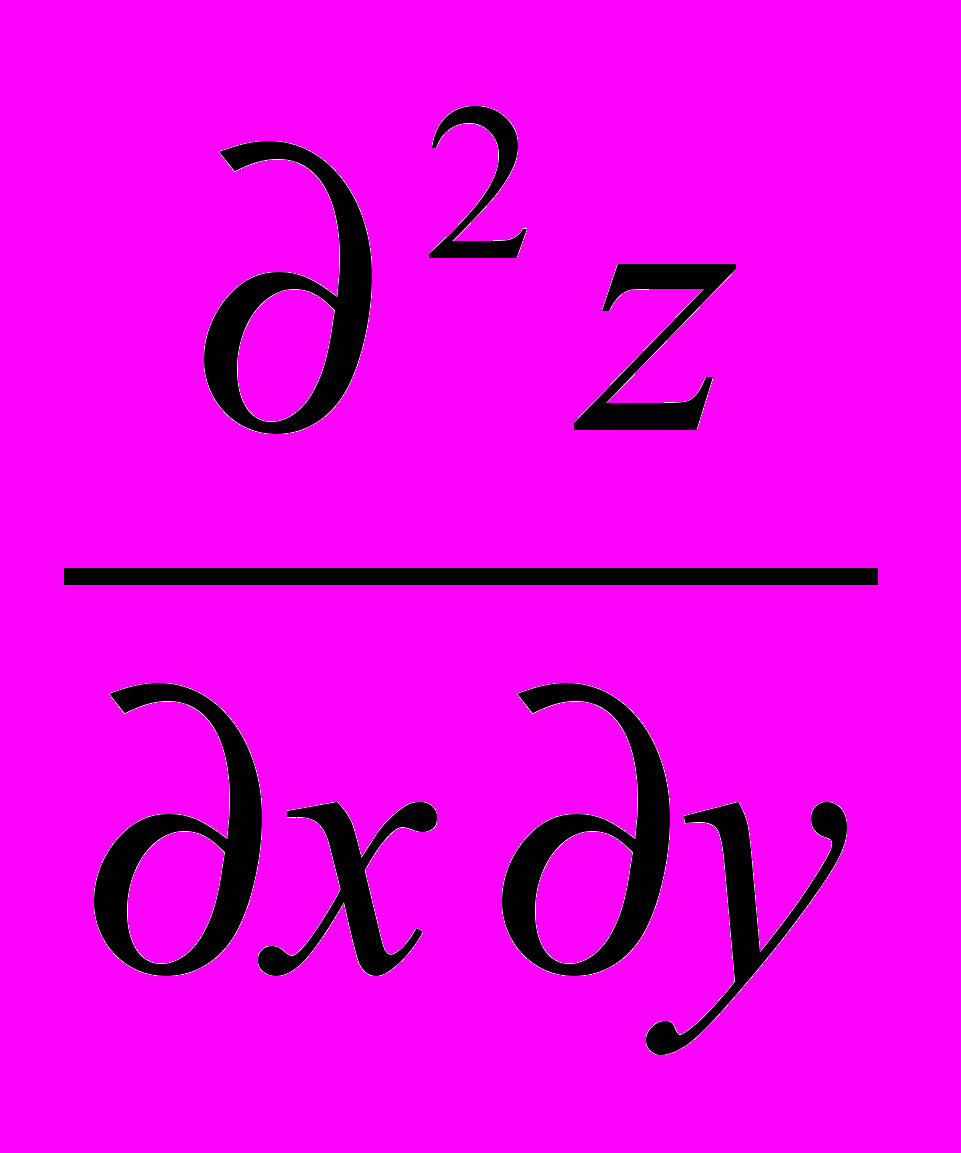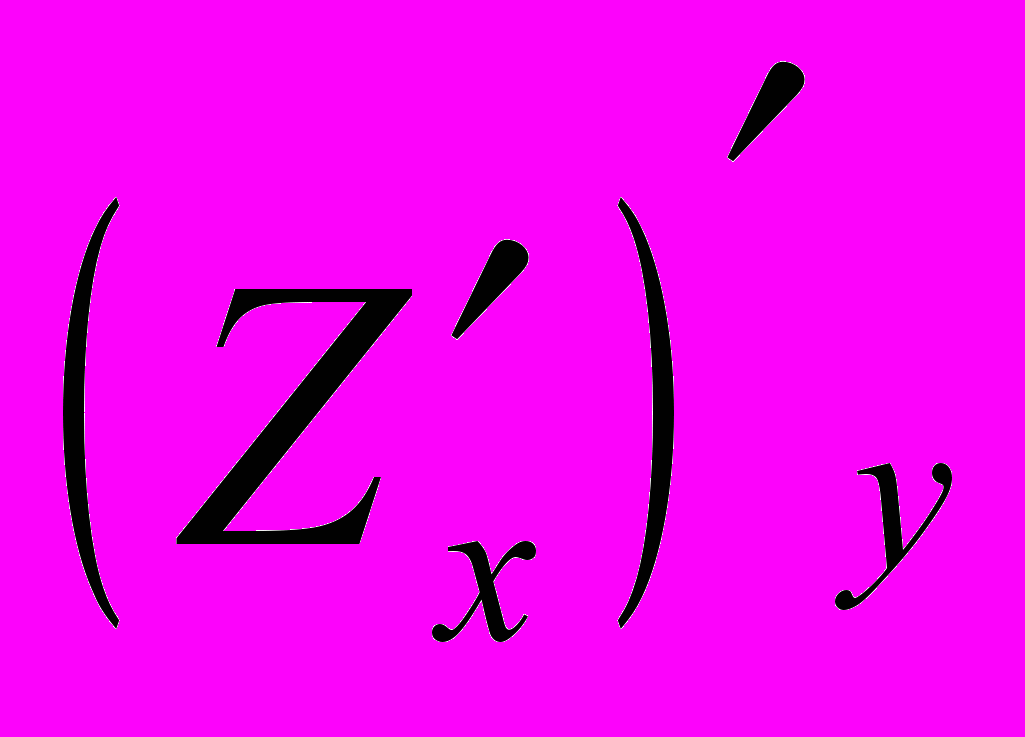Вычислим частные производные второго порядка.

.




.

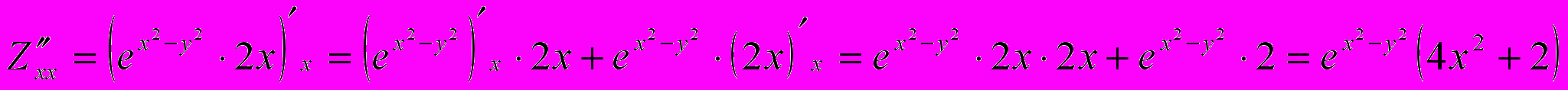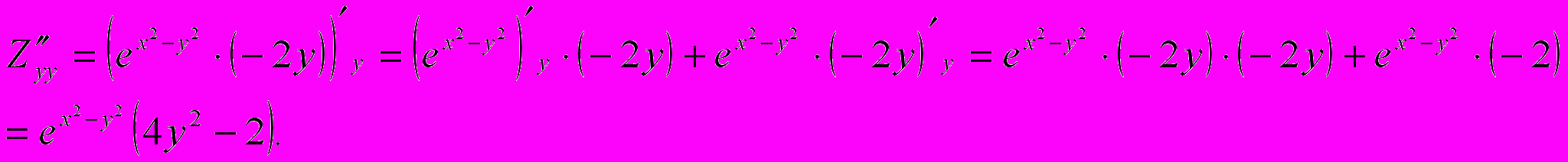
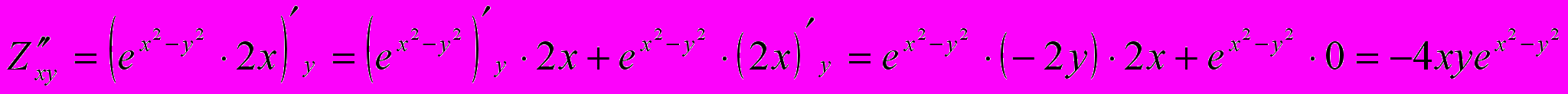Градиентом функции Z в точке М называется вектор, координатами которого являются значения частных производных первого порядка в точке М, т. е.


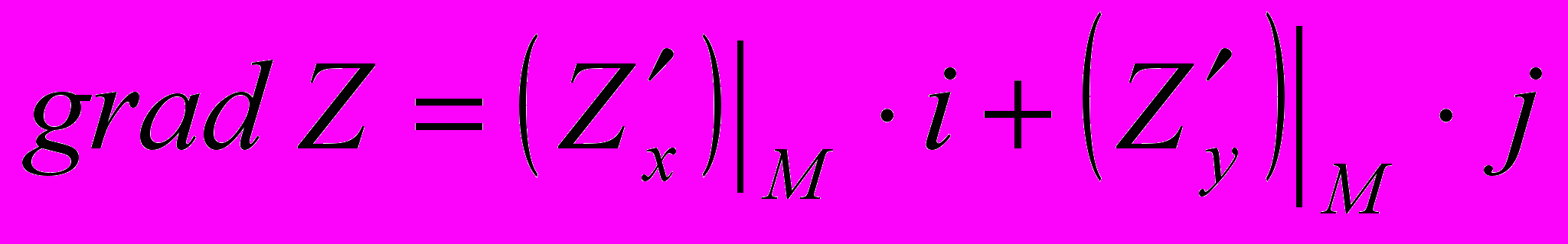(30)


или .

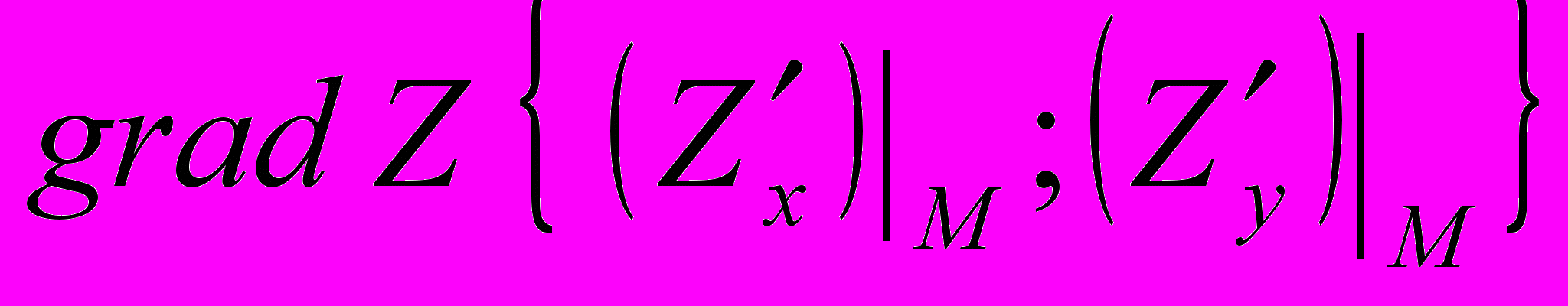В найденные значения производных первого порядка подставляем координаты точки .

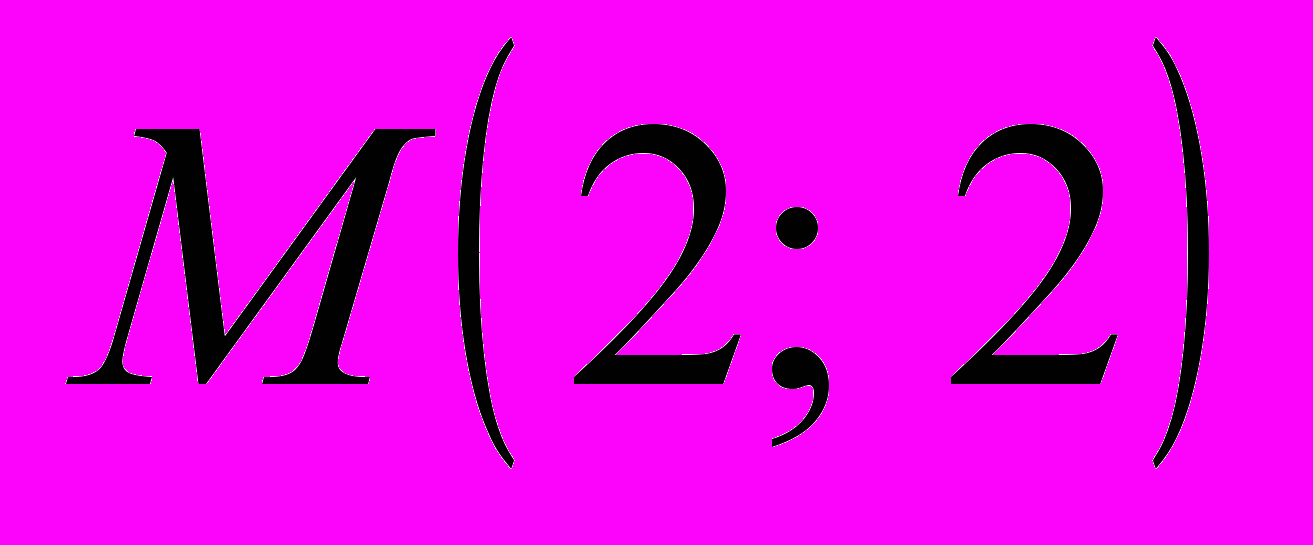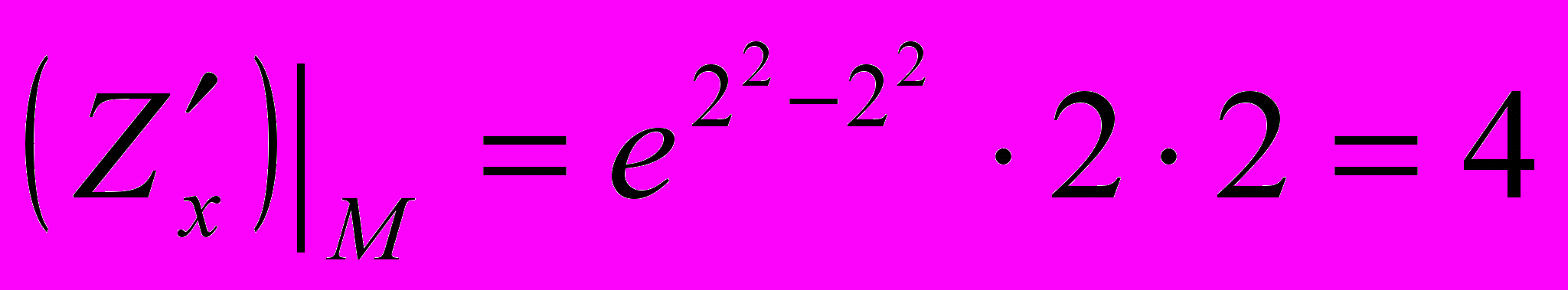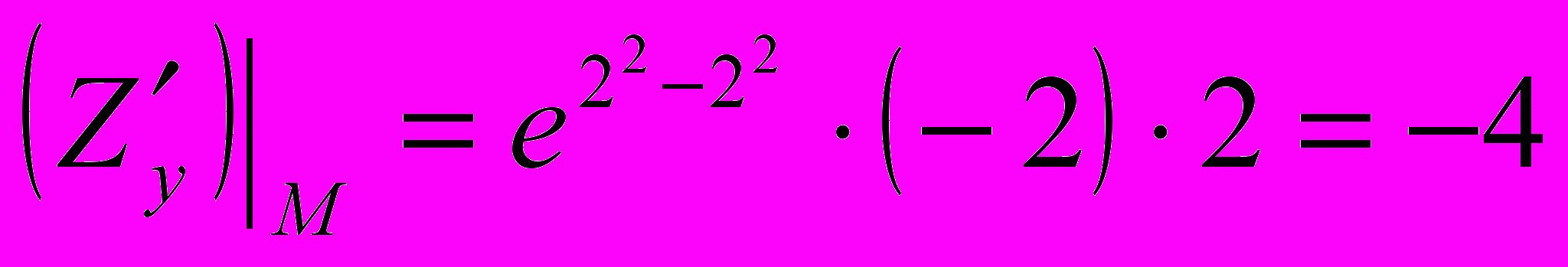, , значит, .

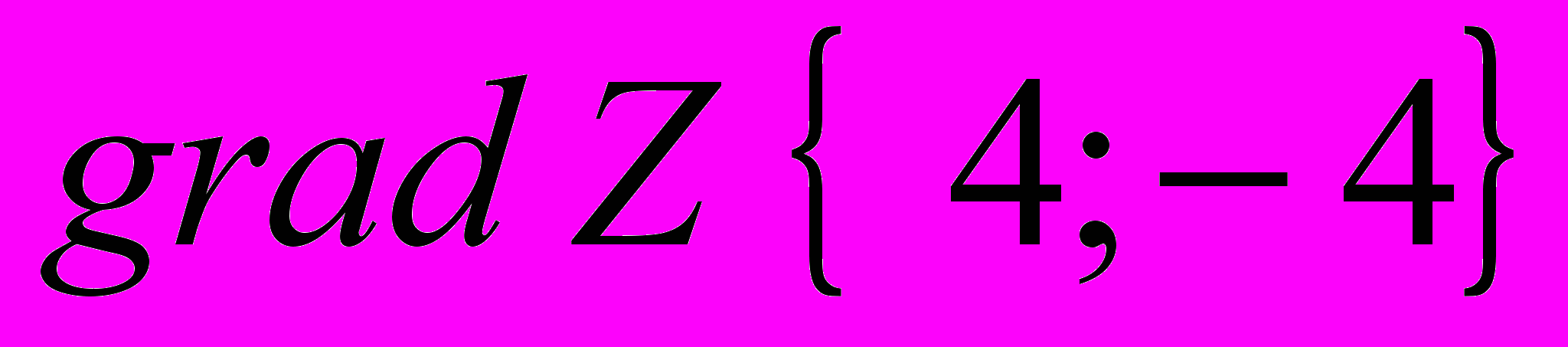Производная в направлении вектора , составляющего угол с положительным направлением оси вычисляется по формул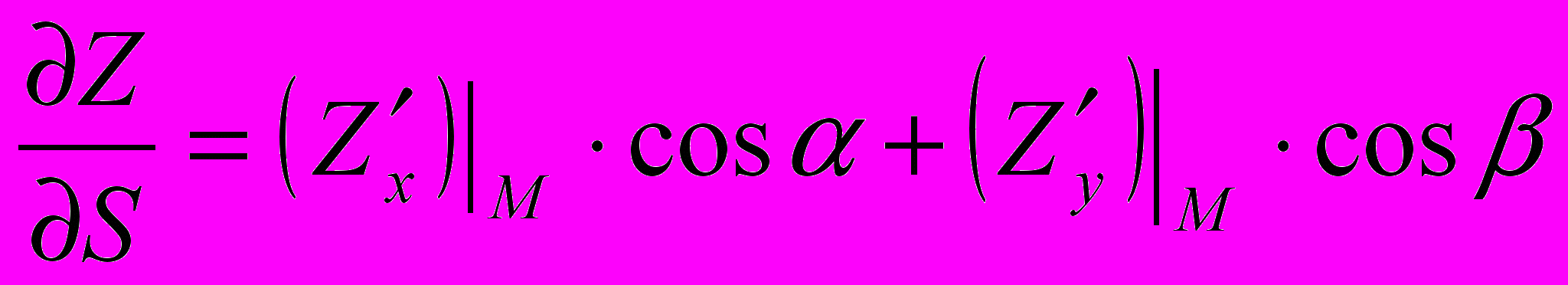е:


, где 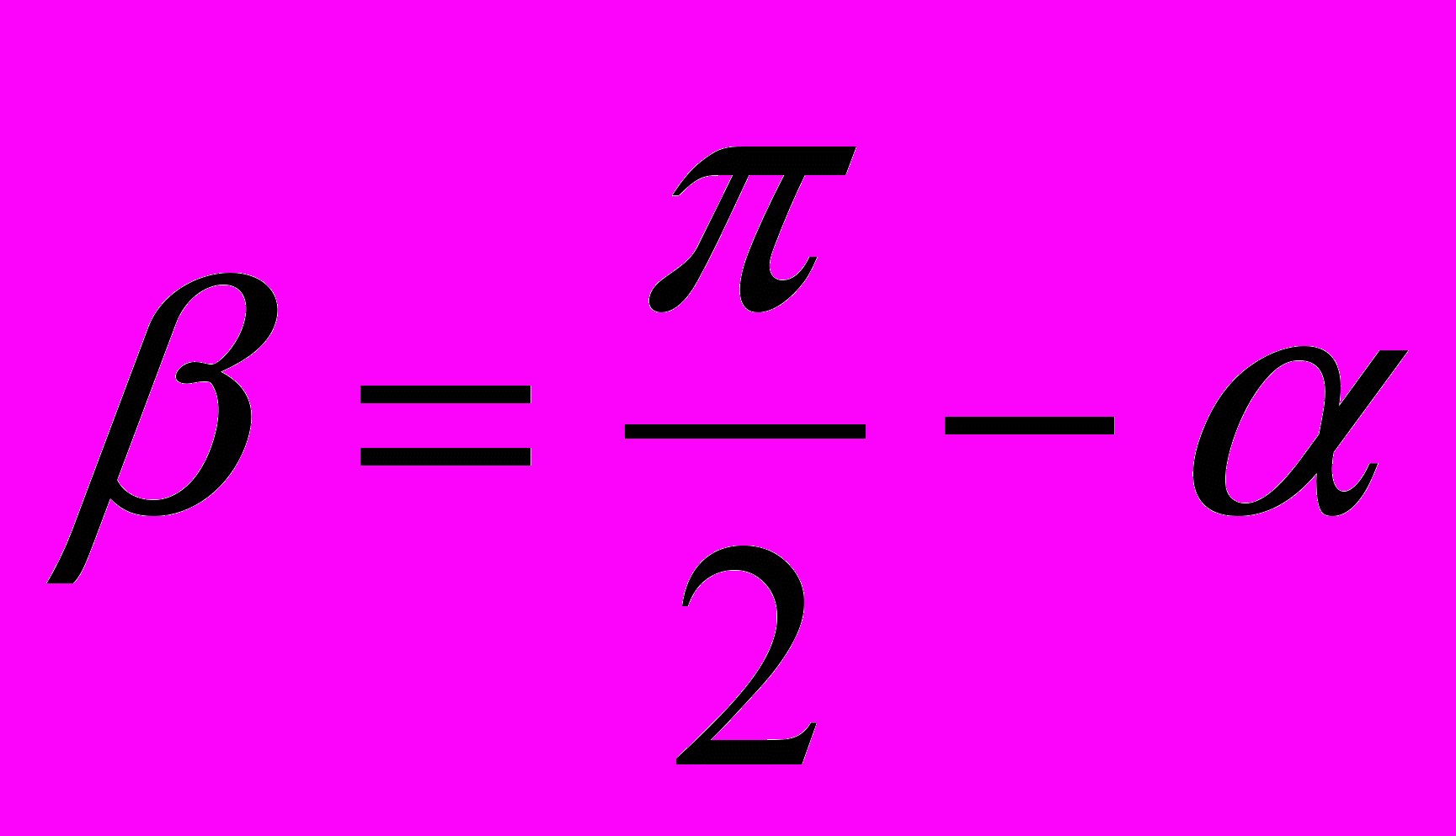. (31)


В нашем случае .


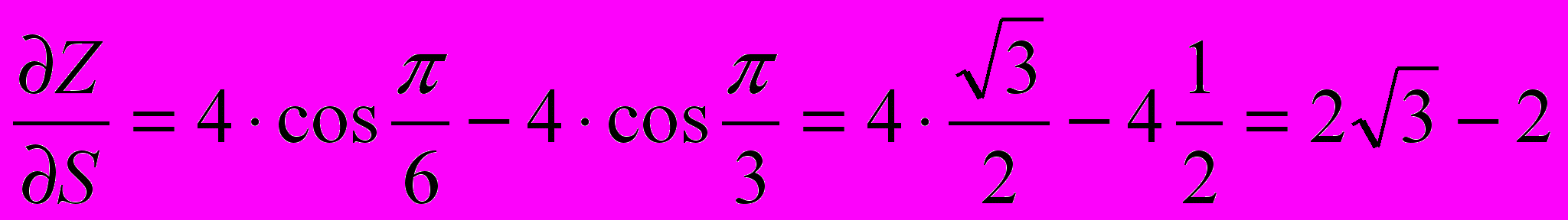В задачах 21- 40 исследовать данную функцию на экстремум:






















Решение типового примера.

Найти экстремум функции .


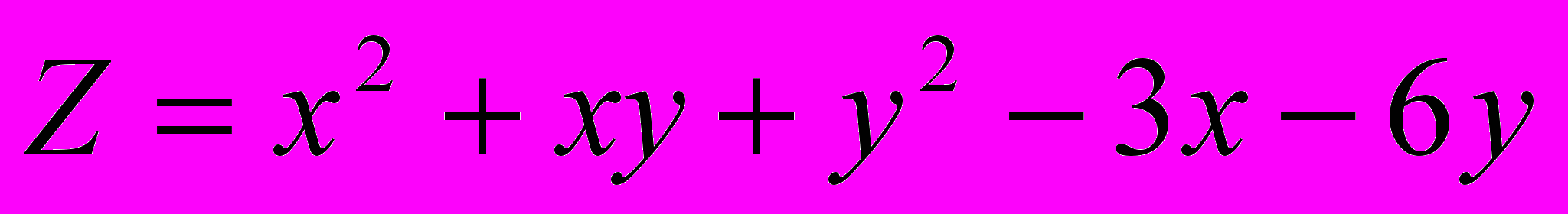^ Необходимое условие экстремума: Если в точке 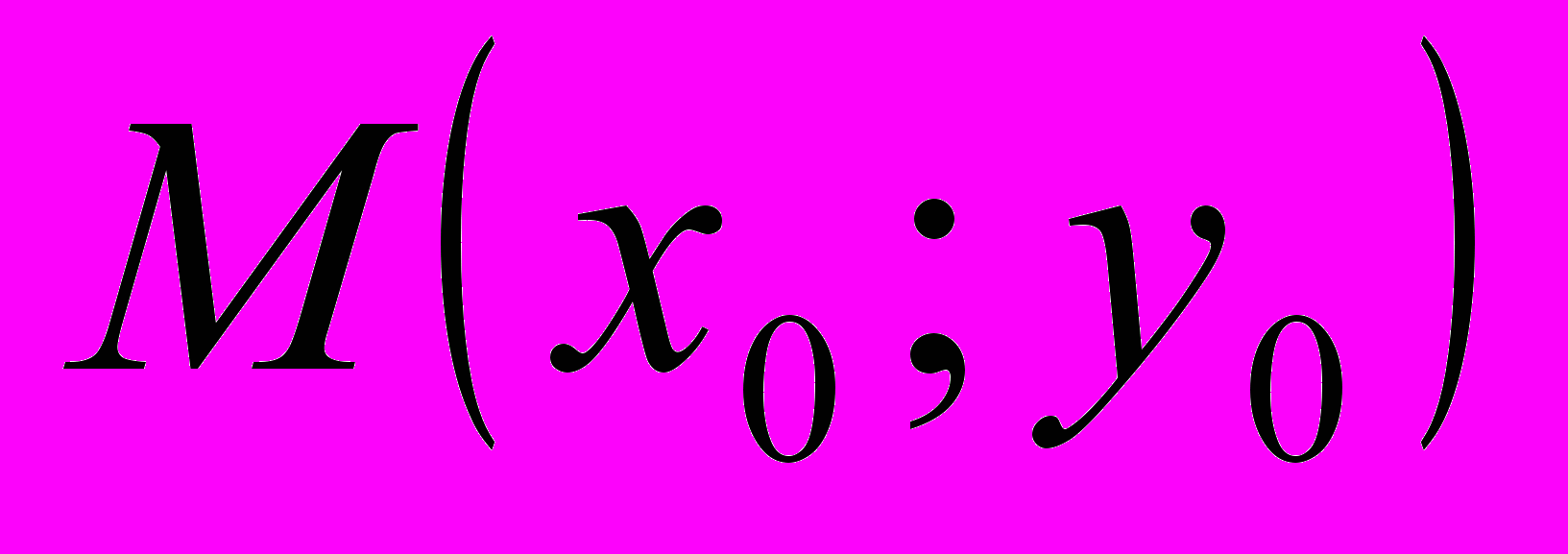дифференцируемая функция 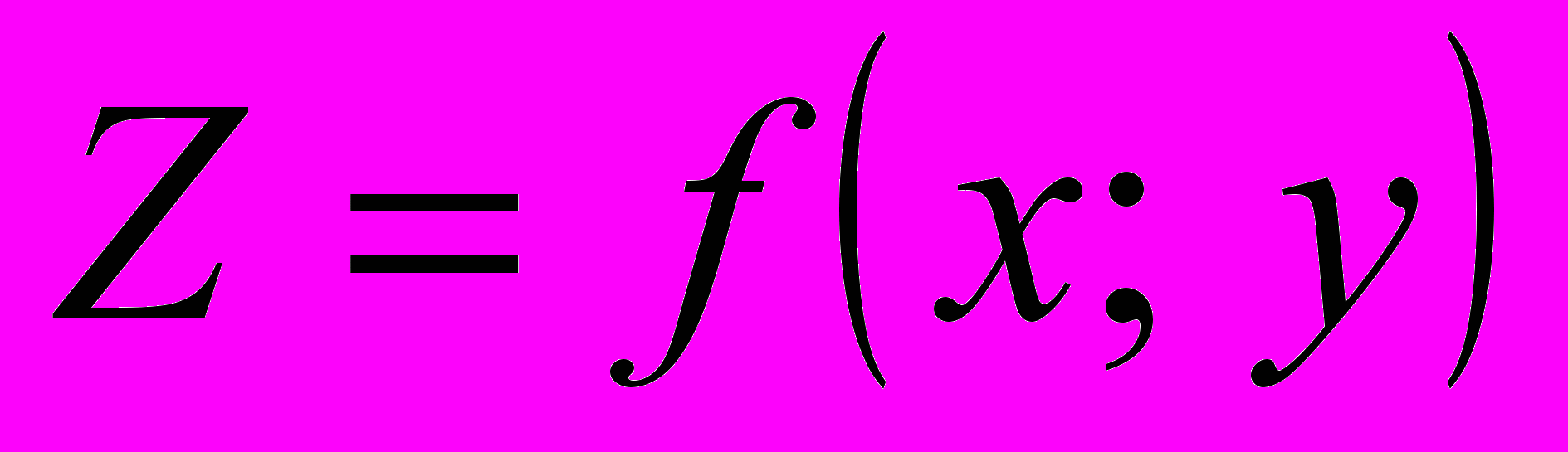имеет экстремум, то её частные производные в этой точке равны нулю, то есть 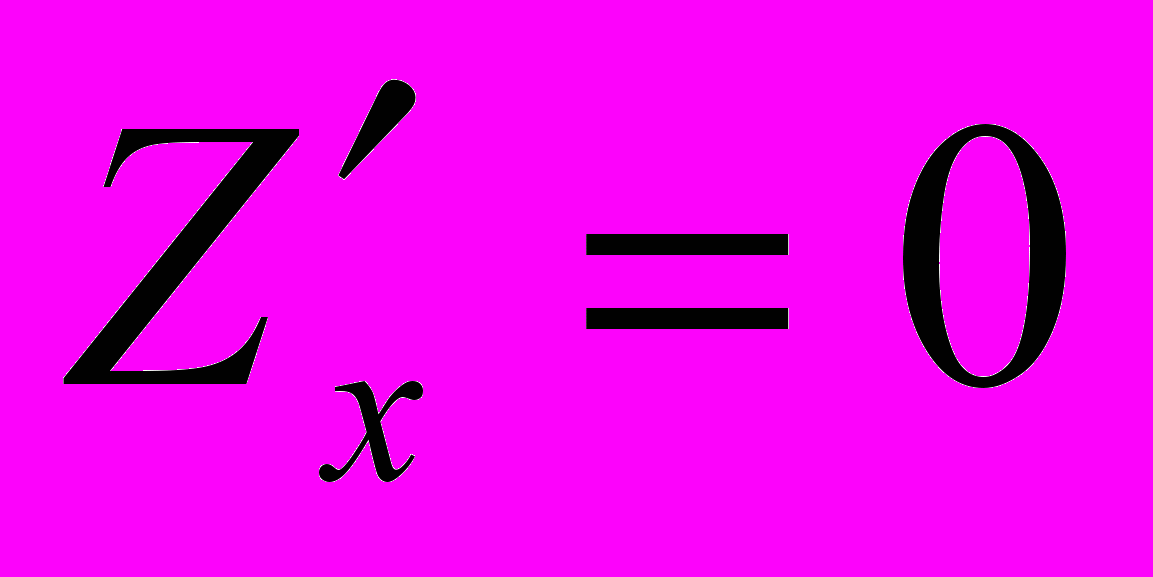и .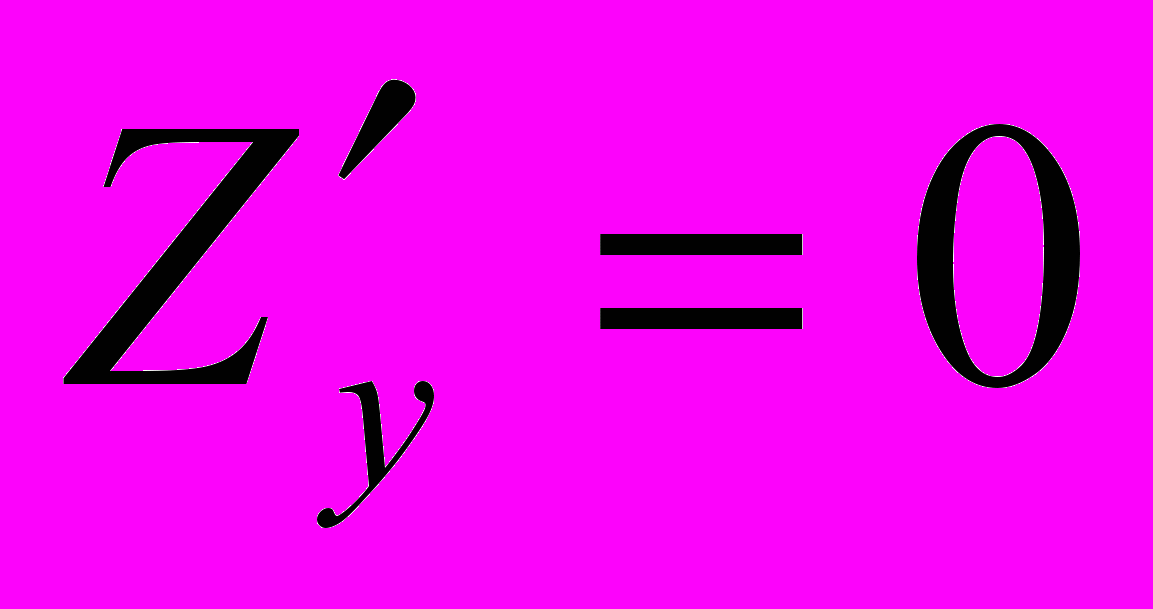

Точки, в которых частные производные равны нулю, называются стационарными точками. Не всякая стационарная точка является точкой экстремума.


^ Достаточное условие экстремума: Пусть 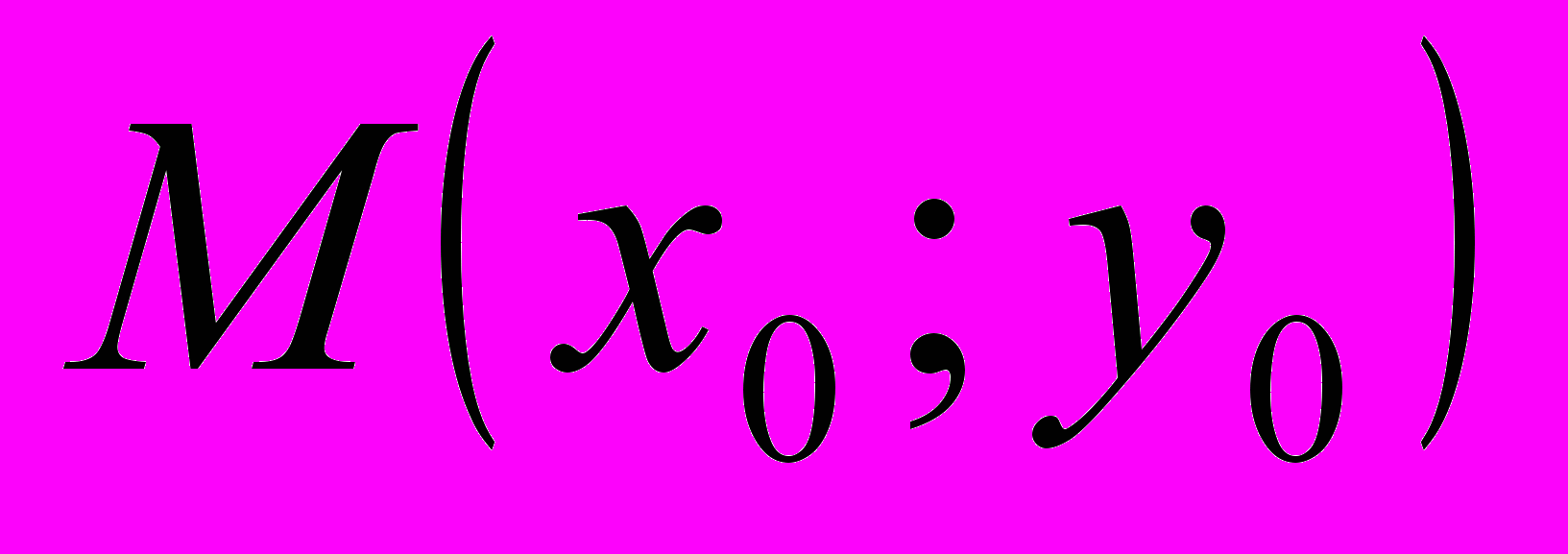- стационарная точка функции 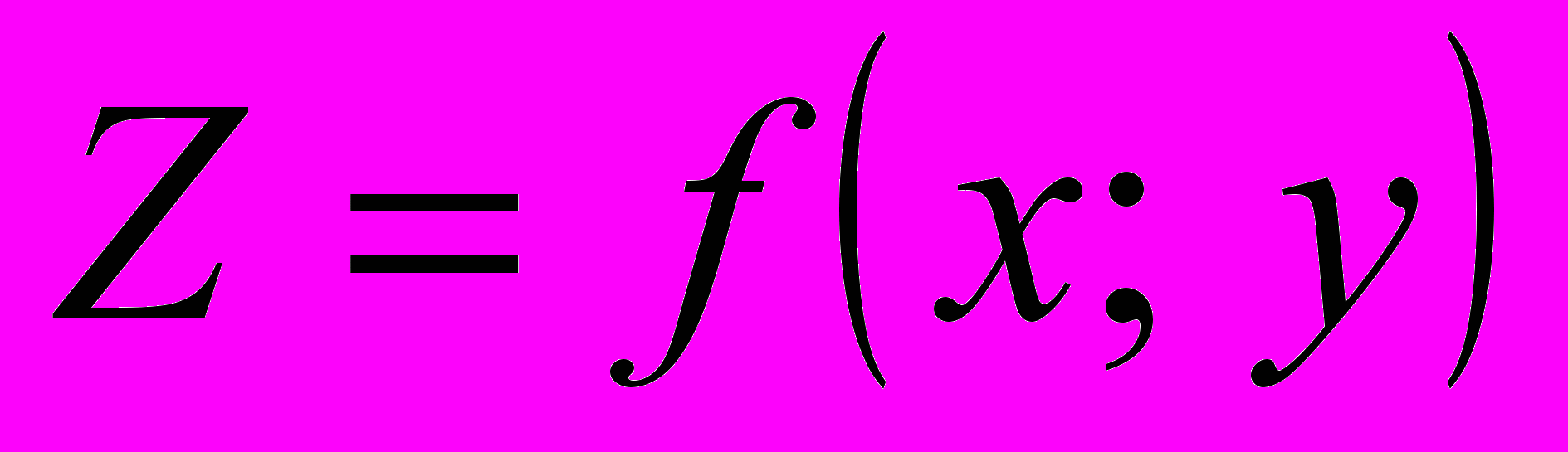. Обозначим , , .

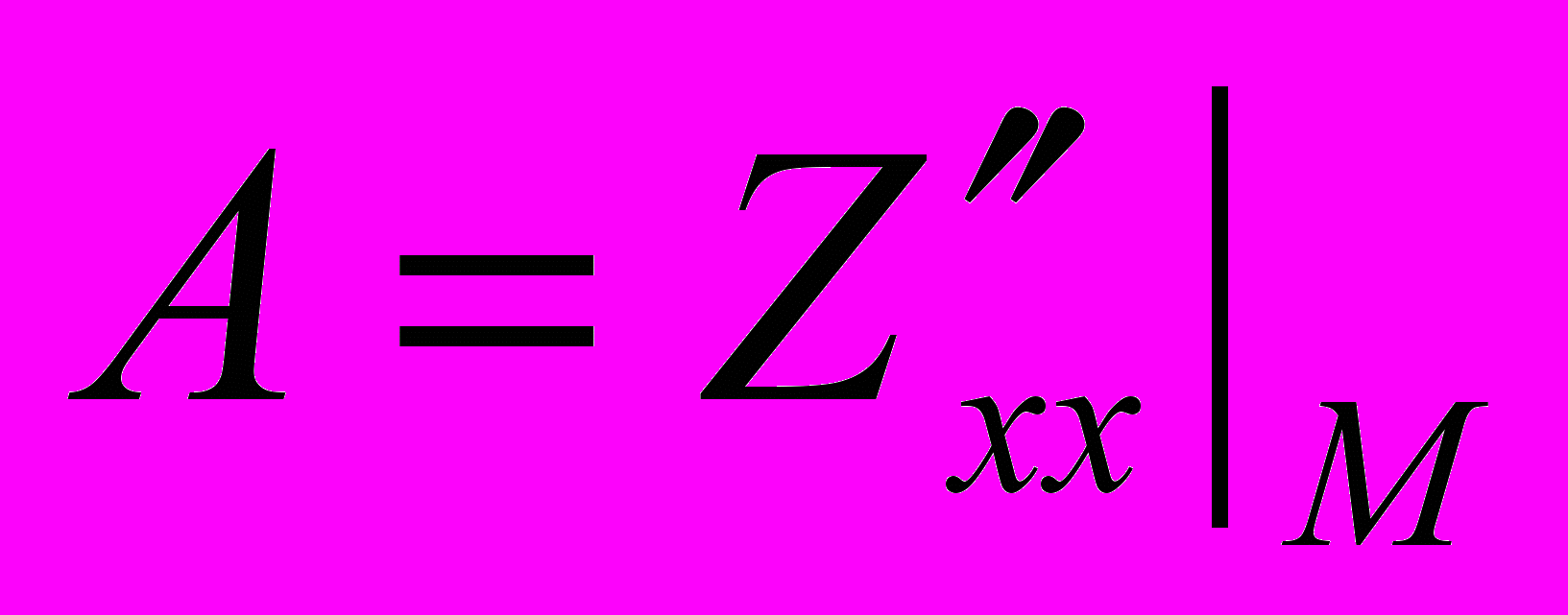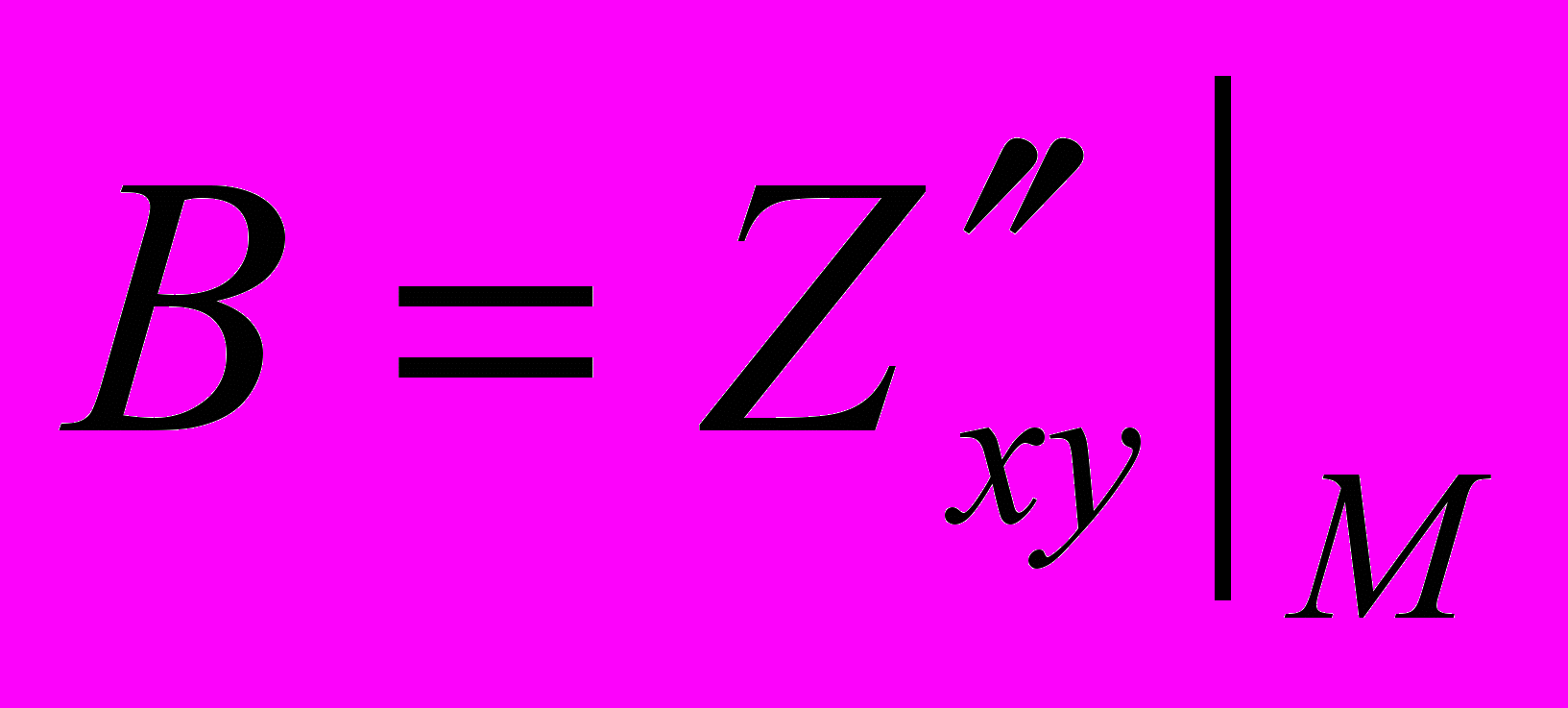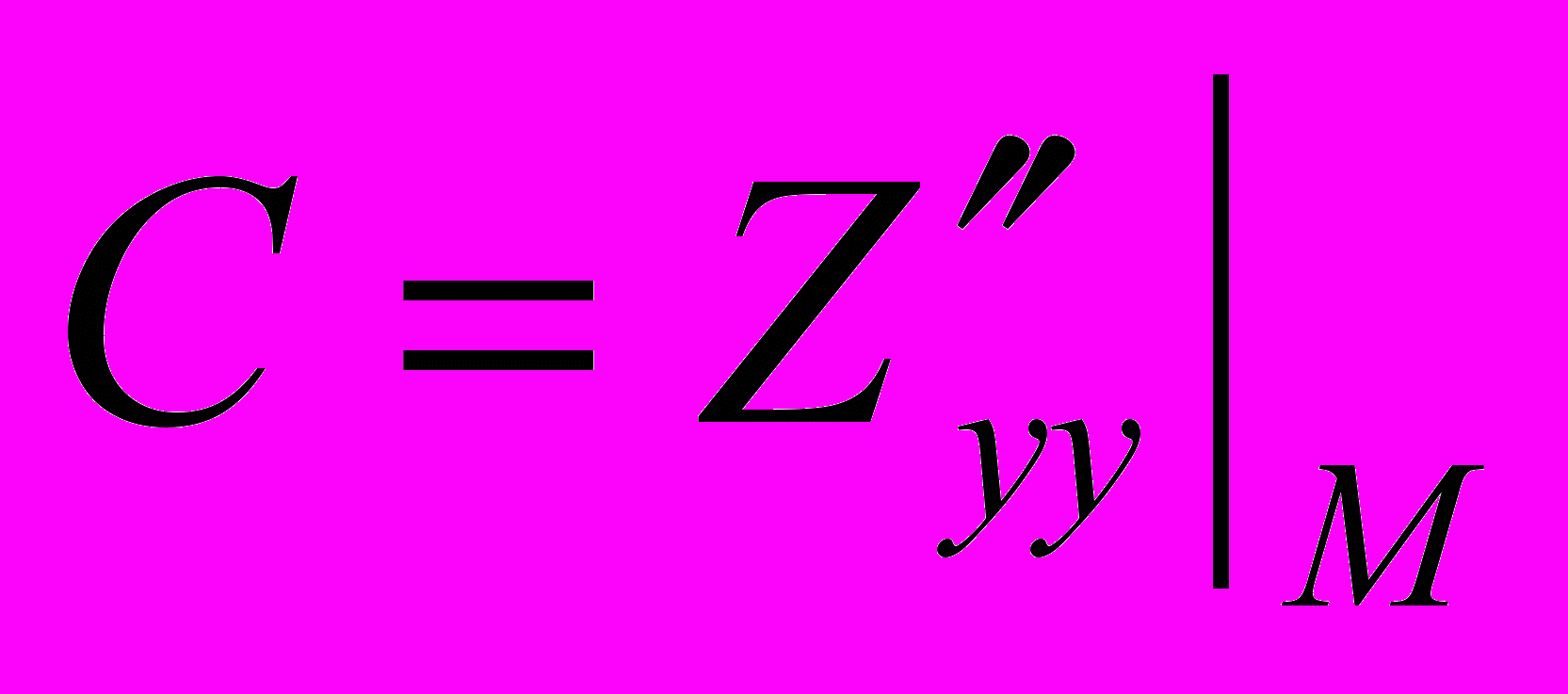Составляем 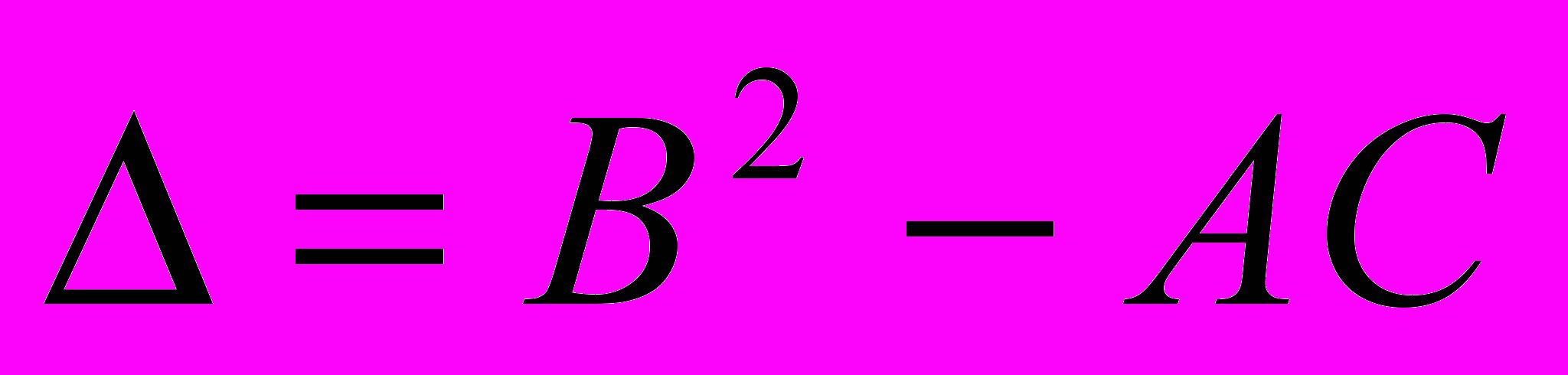. Тогда:

если 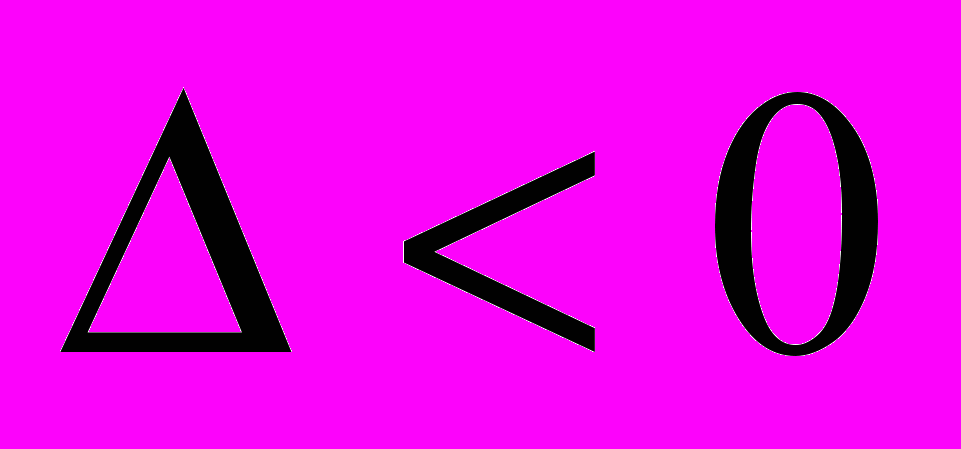, то функция имеет в точке 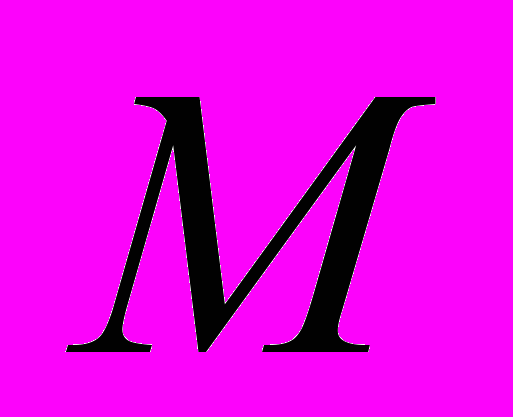экстремум, а именно максимум, если 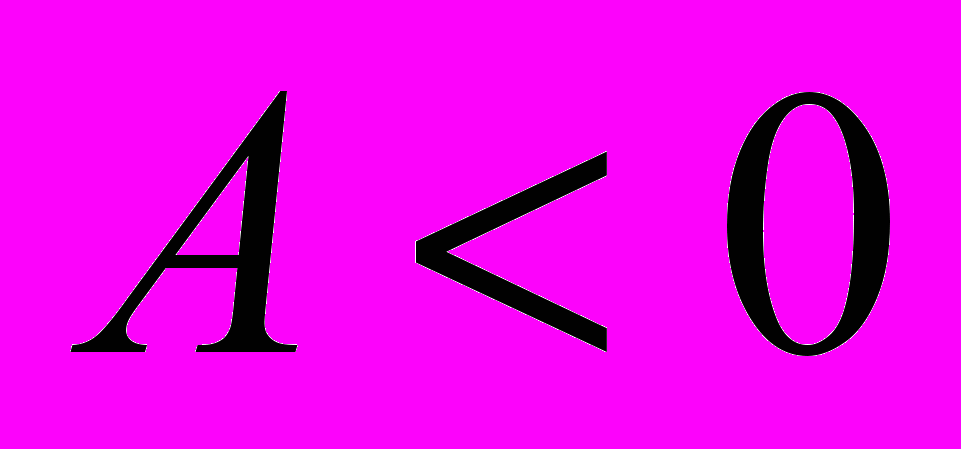и минимум при ;

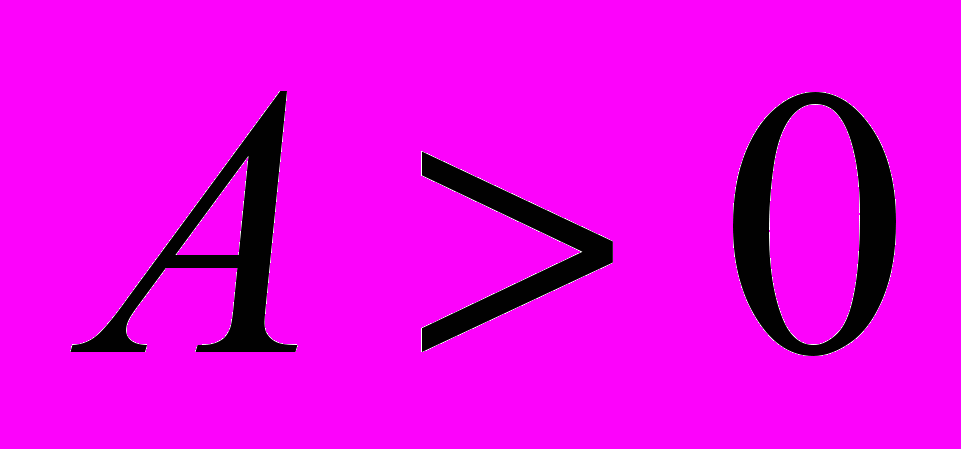если 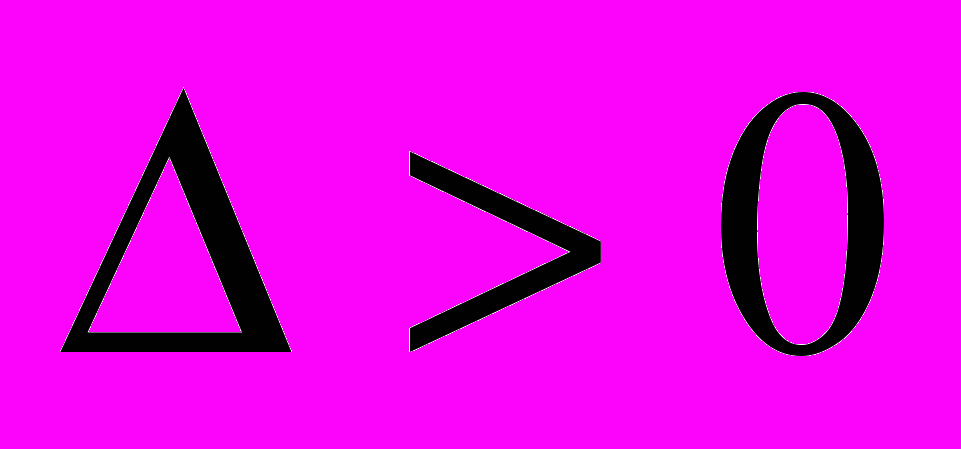, то в точке 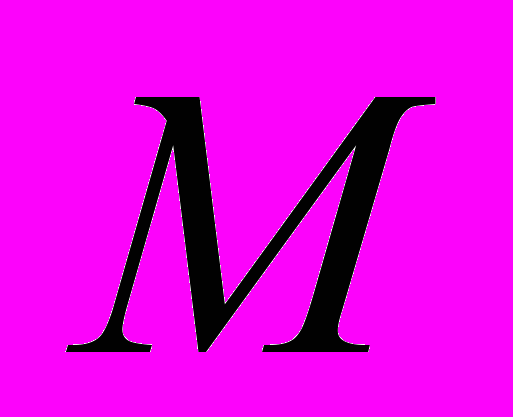экстремума нет;

если 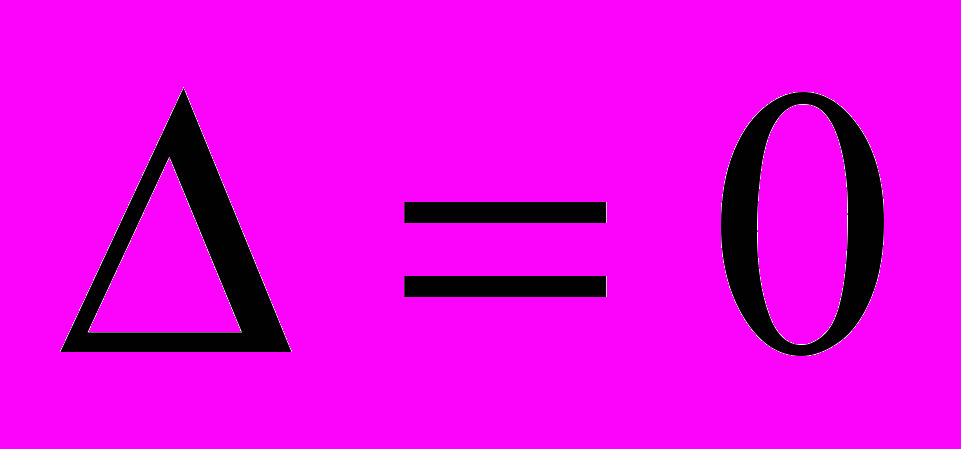, то экстремум в точке может быть, может не быть. Необходимы дополнительные исследования.


Находим частные производные первого порядка: 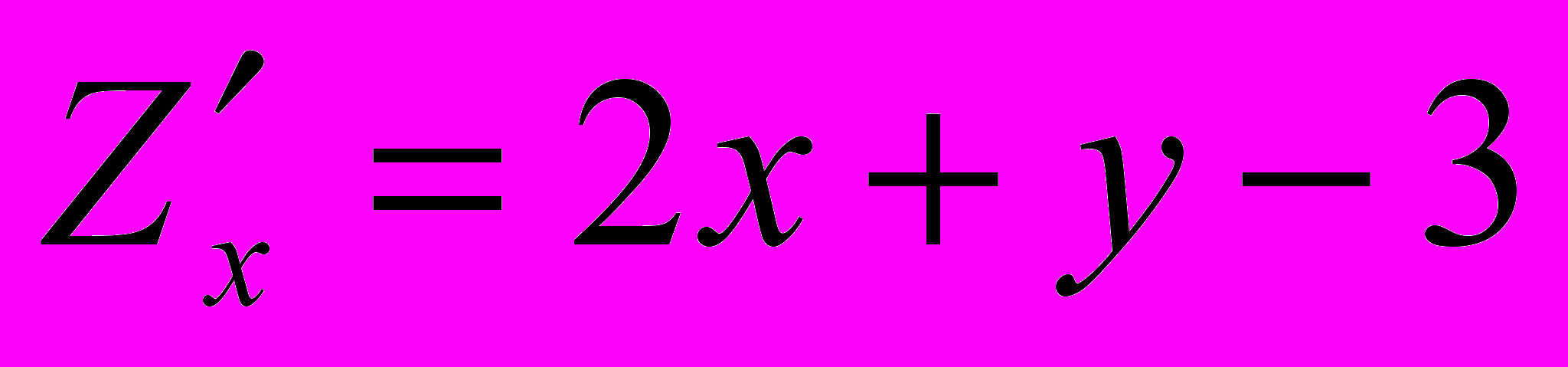, 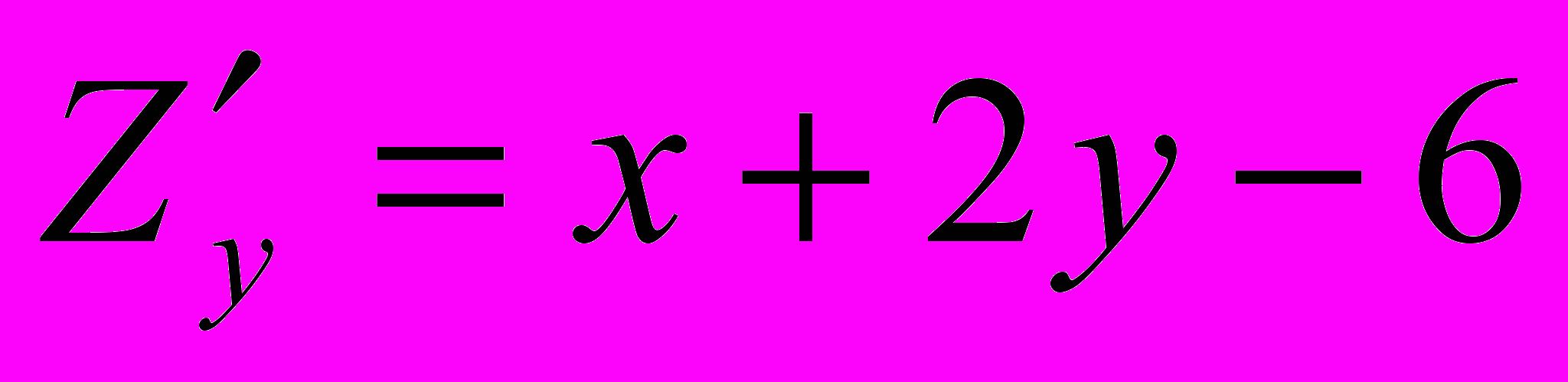. Воспользовавшись необходимым условием экстремума, находим стационарные точки:

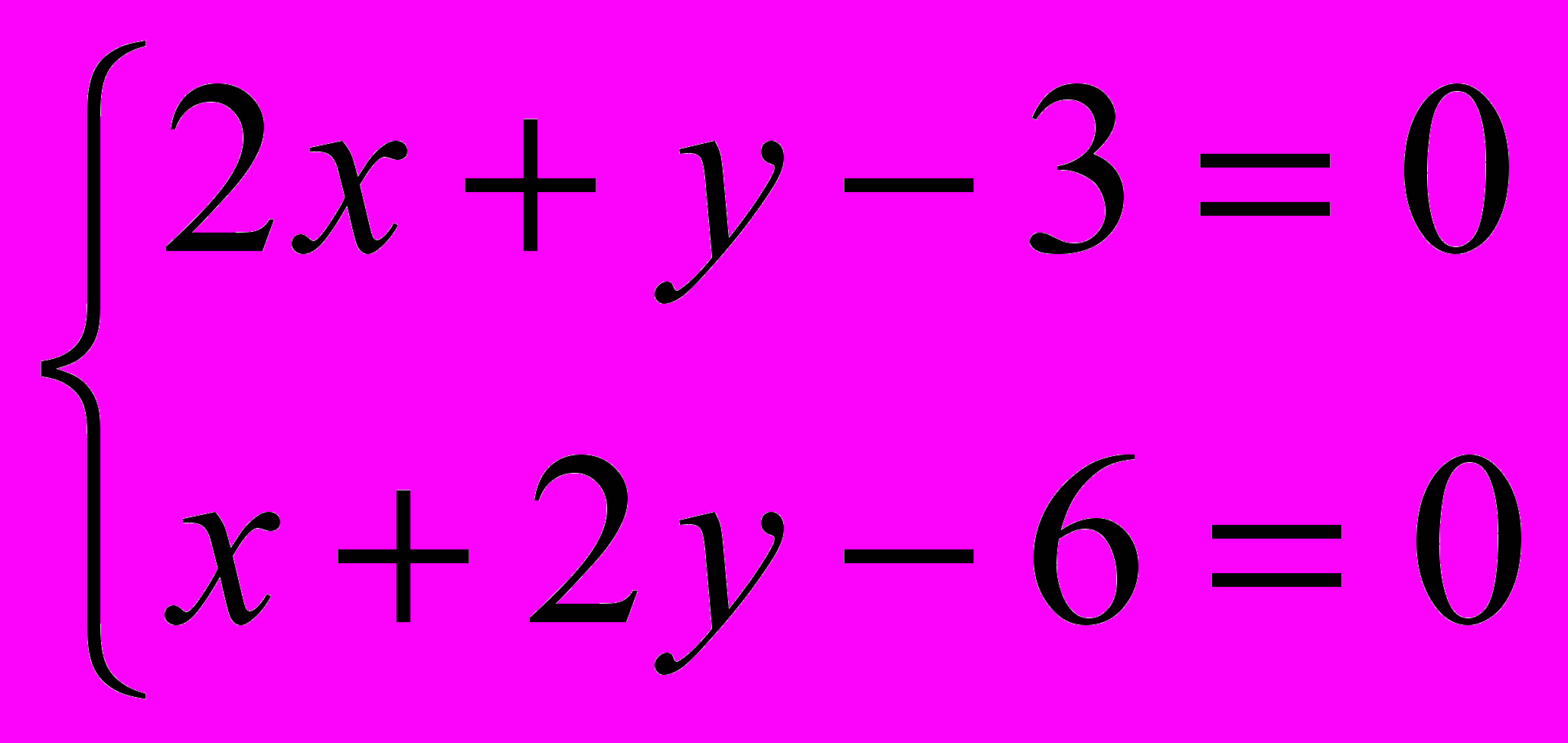, откуда , , .

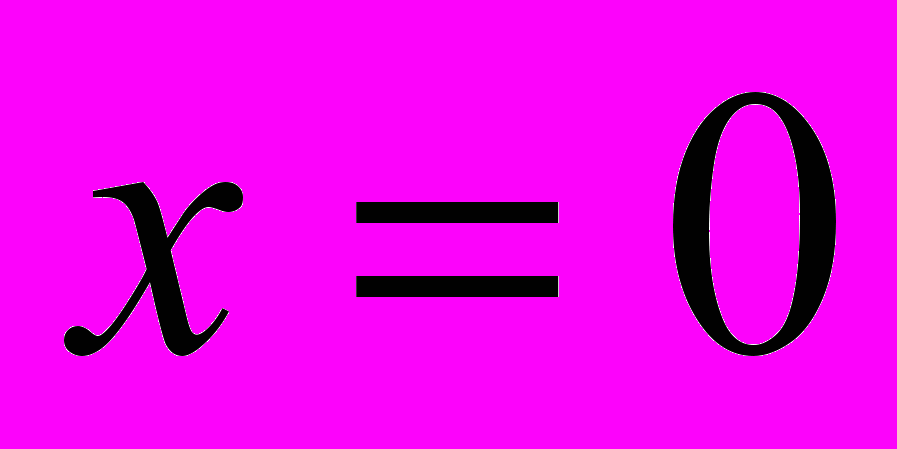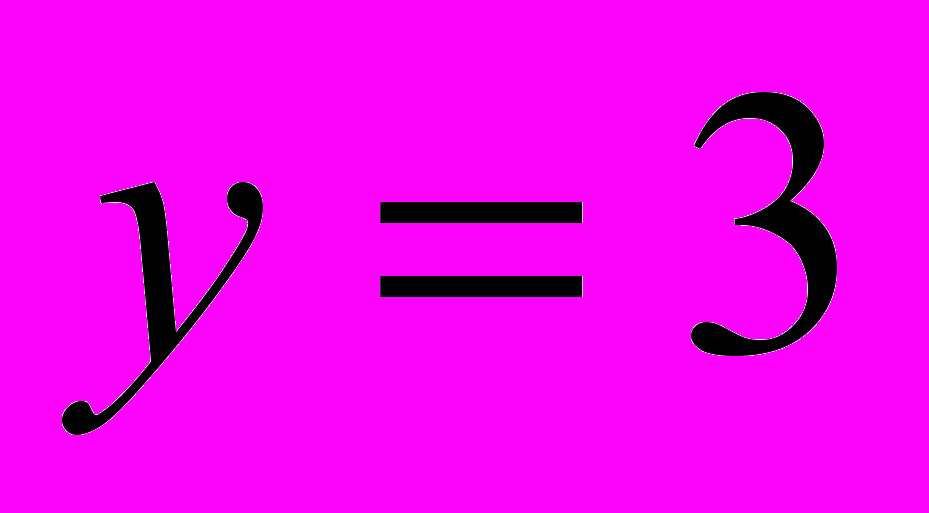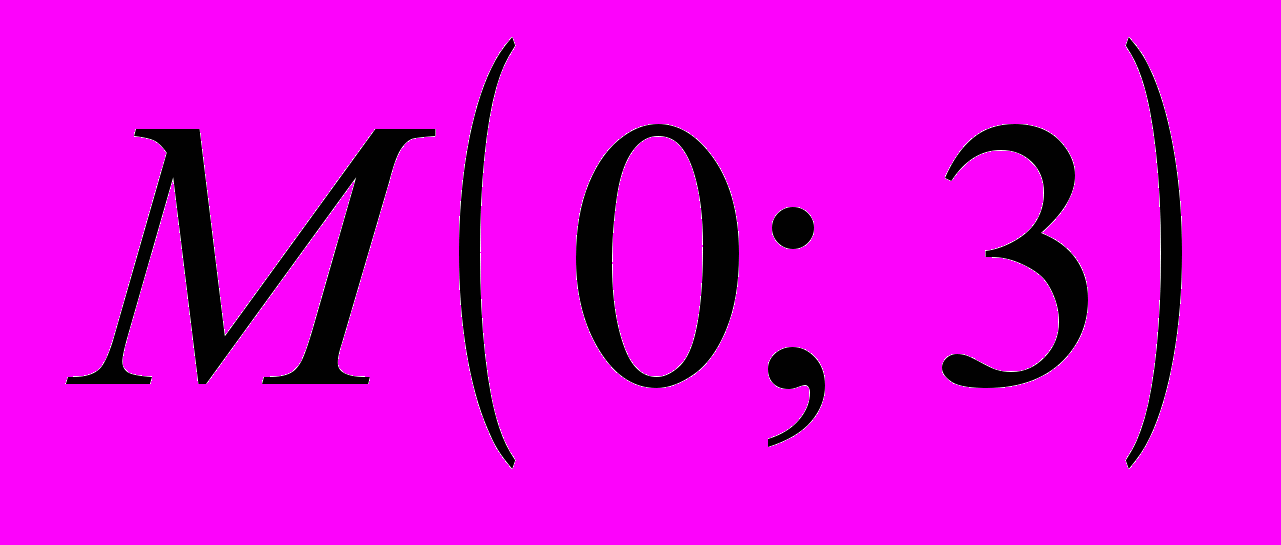Находим значения частных производных второго порядка в точке М:

; ;

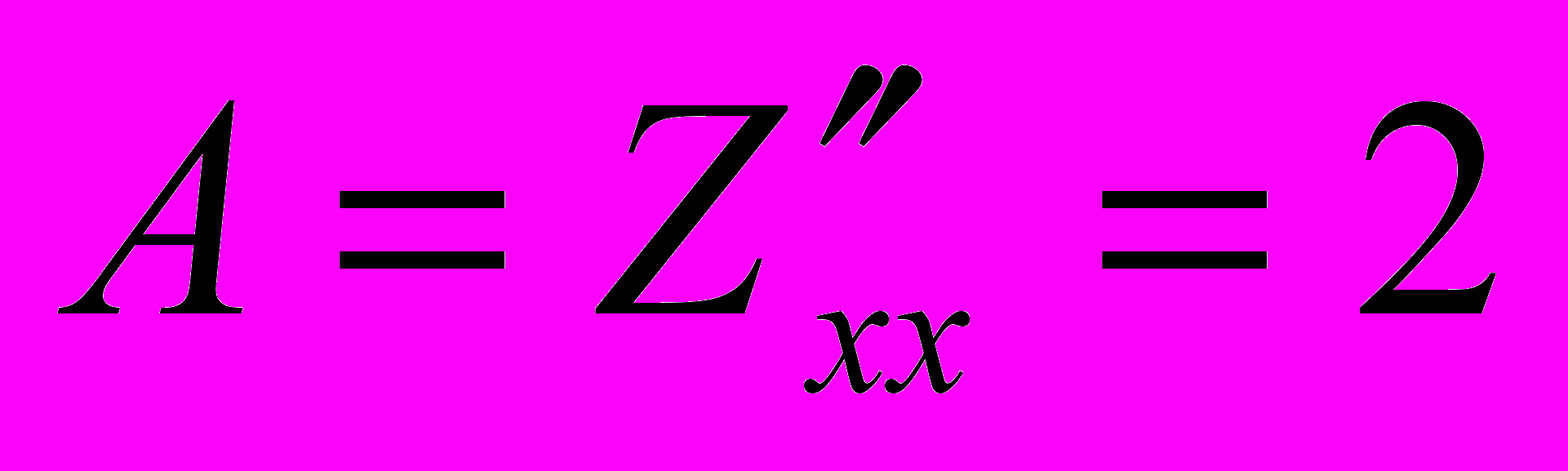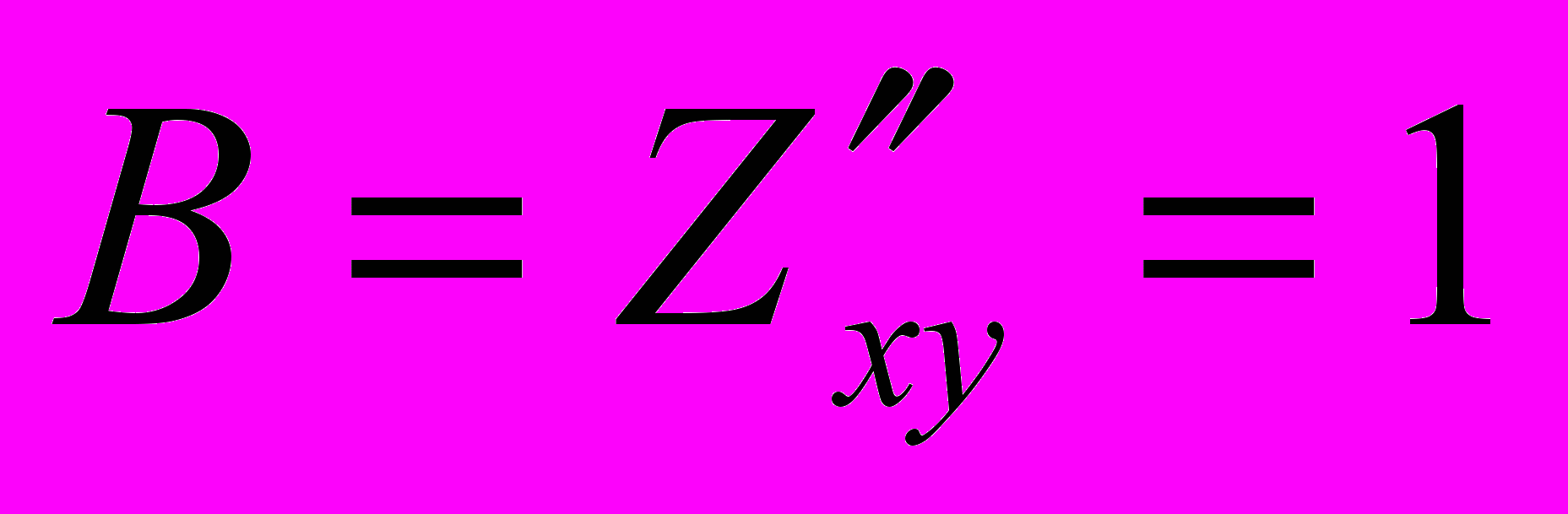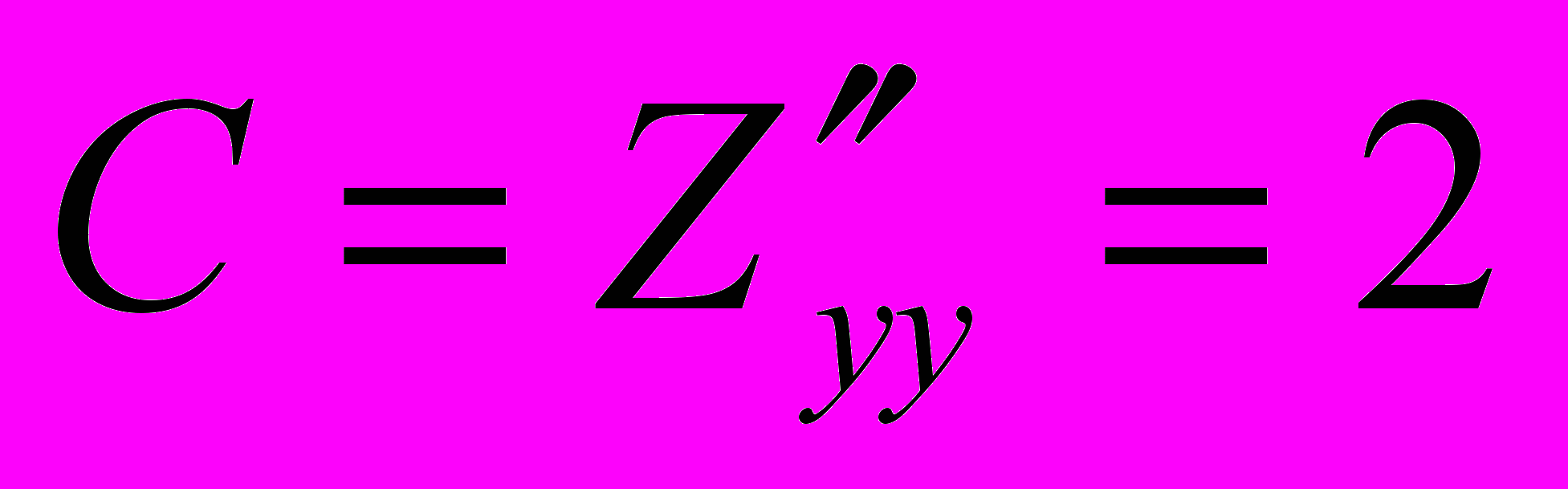
Составляем .

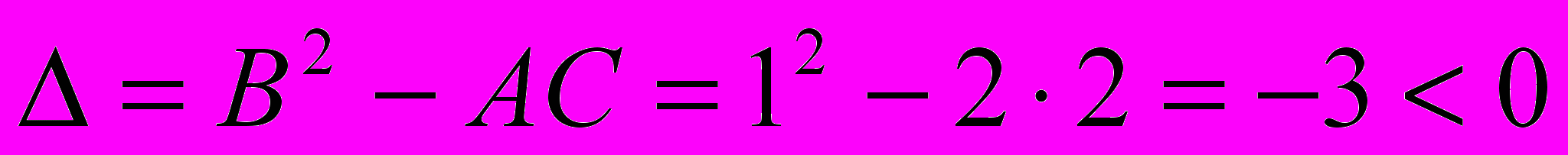Так как 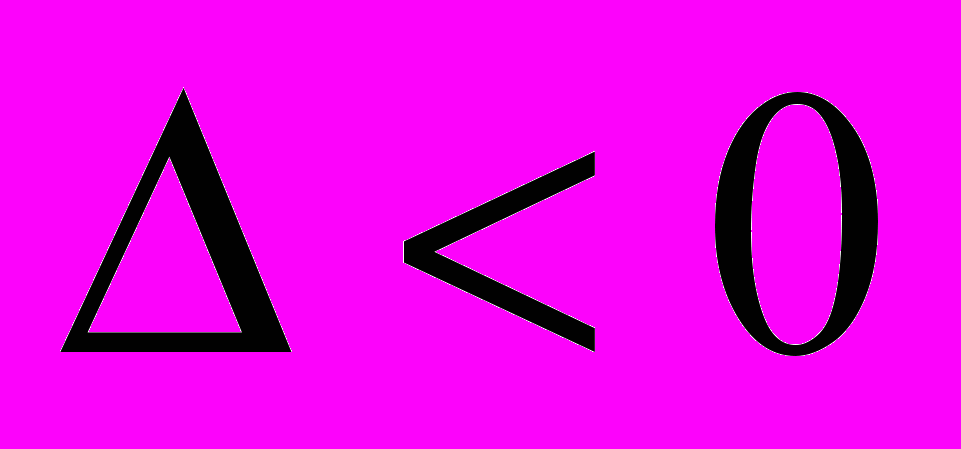и 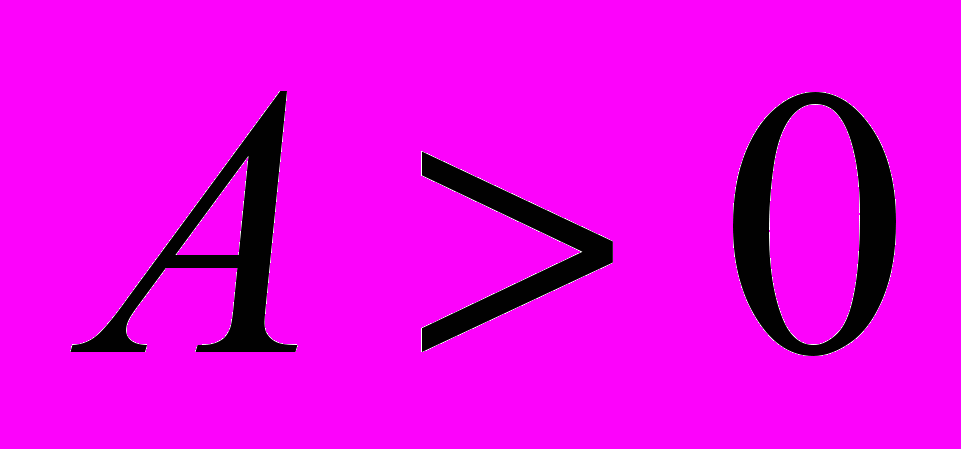, делаем вывод о наличии минимума в точке 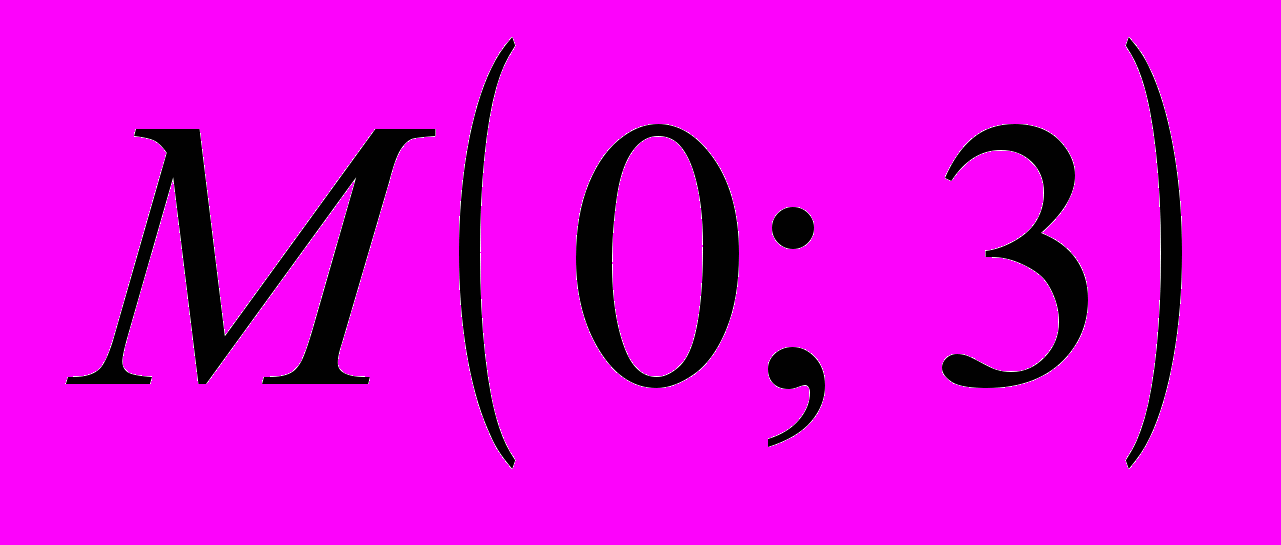. Значение функции в этой точке .


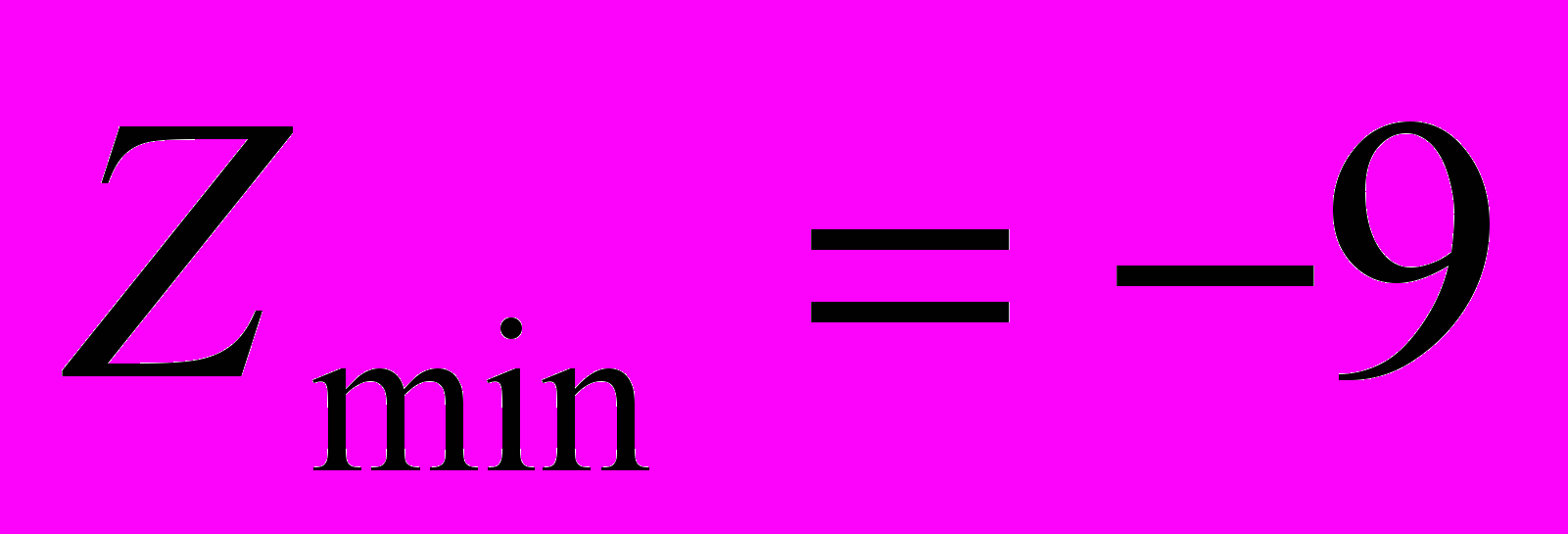Тема 2.

Кратные и криволинейные интегралы.


В задачах 41- 60 с помощью двойного интеграла вычислить координаты центра тяжести фигуры, ограниченной данными линиями (поверхностную плотность считать равной единице).
  1. ; .
  2. ; .
  3. ; .
  4. ; .
  5. ; .
  6. ; .
  7. ; .
  8. ; .
  9. ; .
  10. ; .
  11. ; .
  12. ; .
  13. ; .
  14. ; .
  15. ; .
  16. ; .
  17. ; .
  18. ; .
  19. ; .
  20. ; .


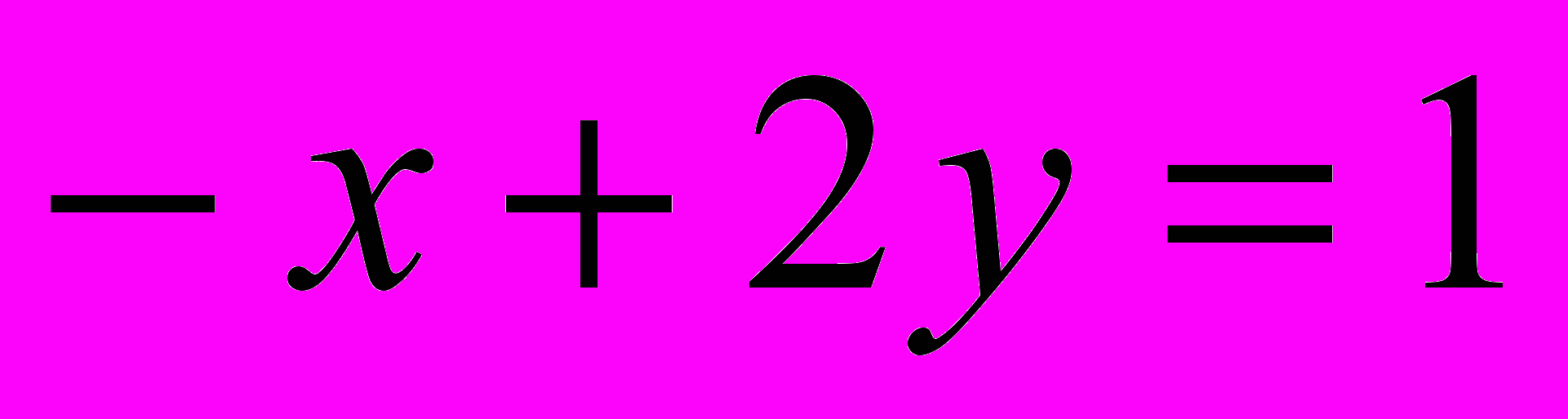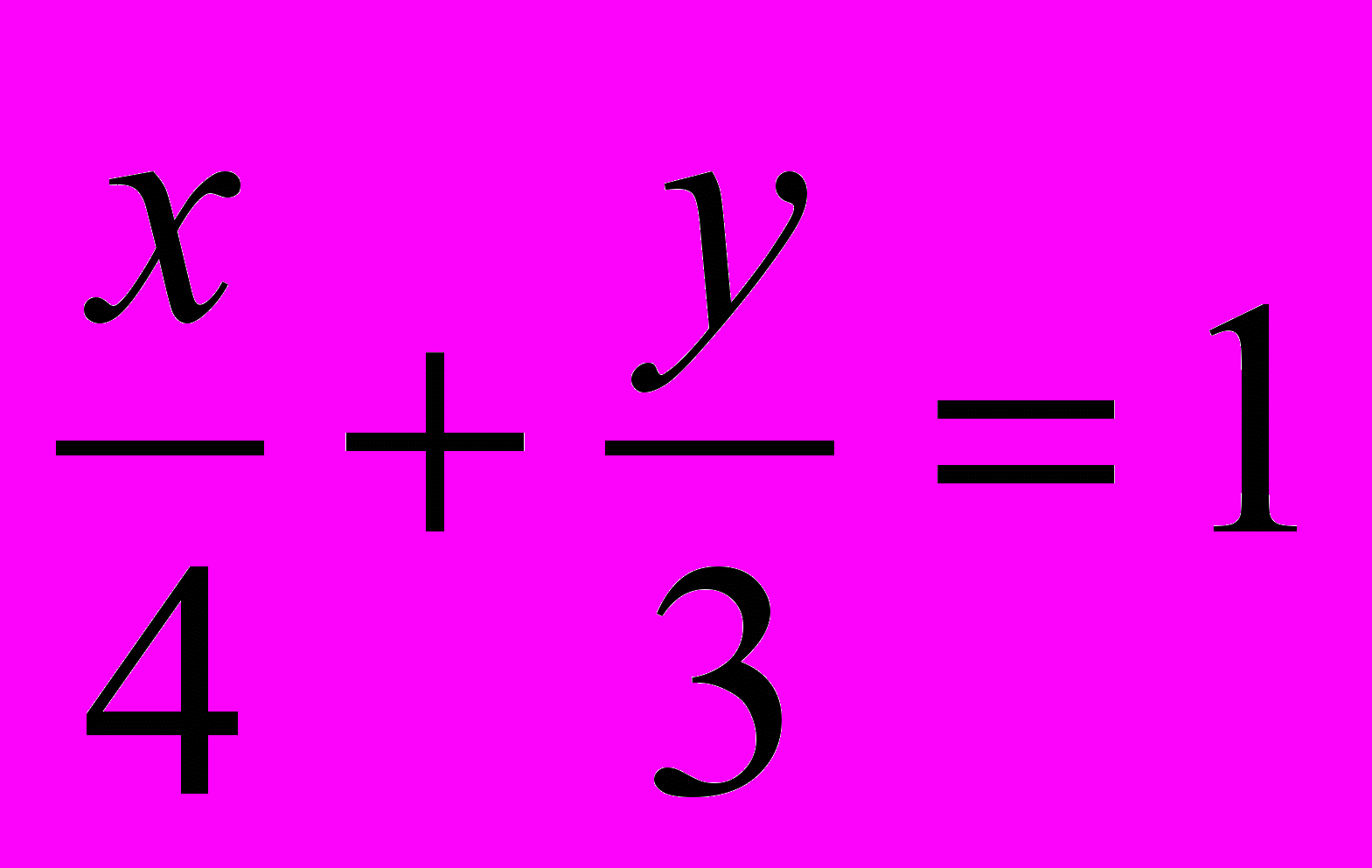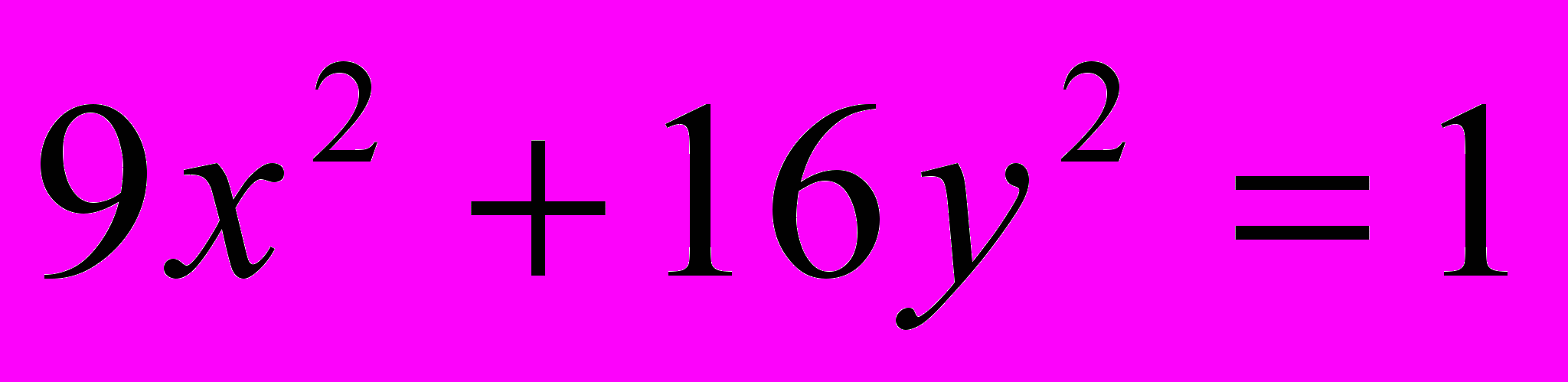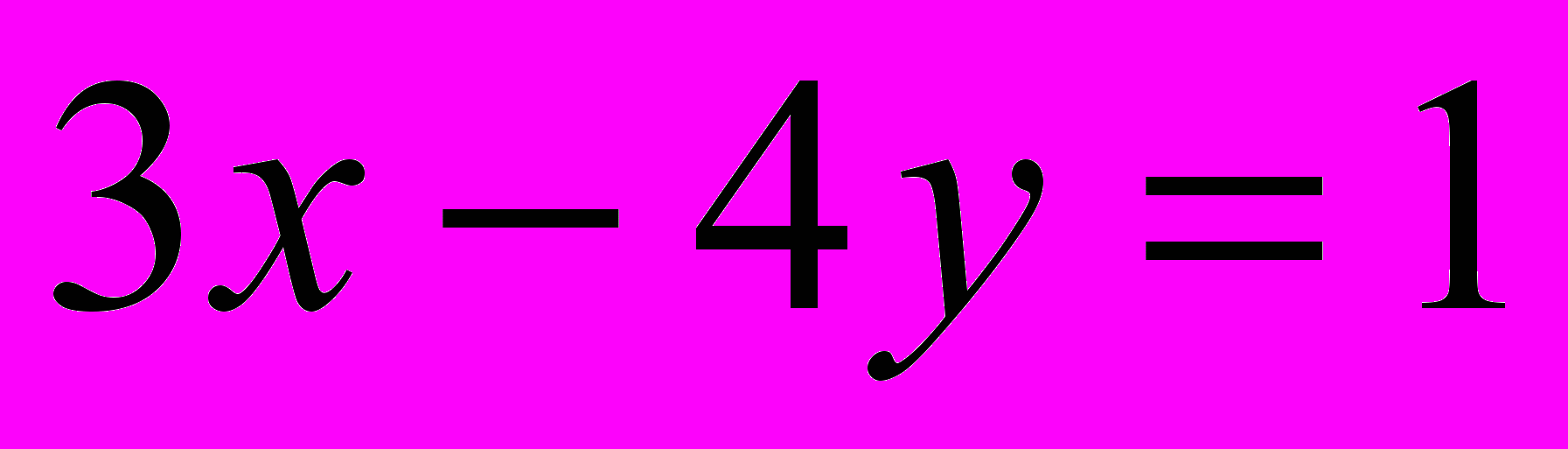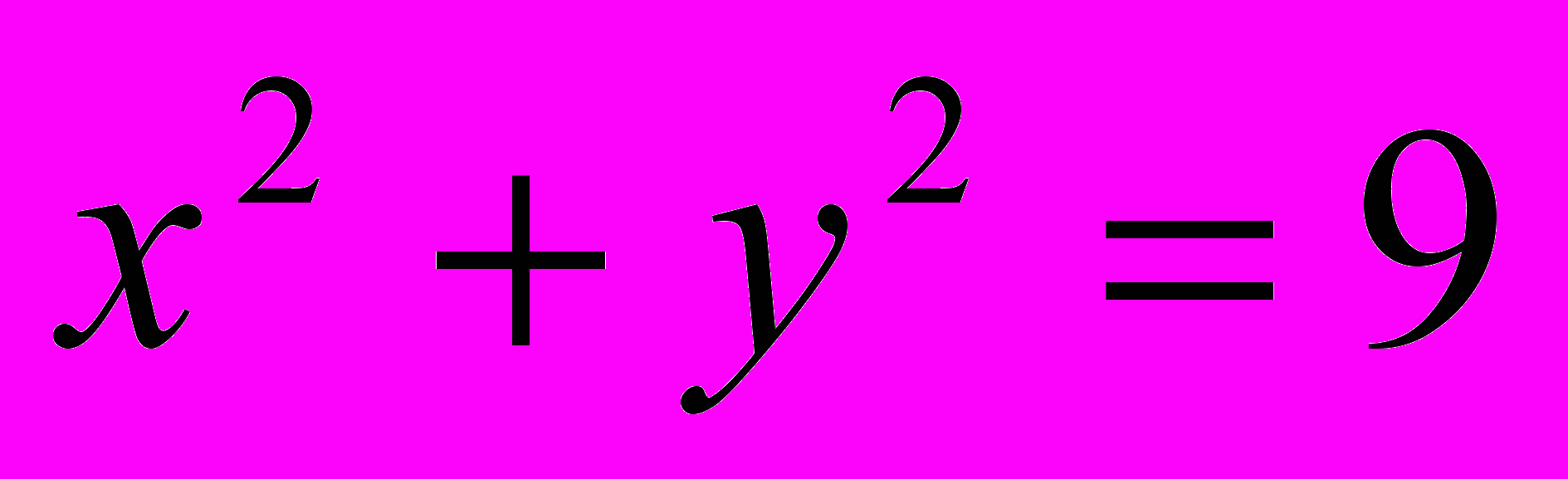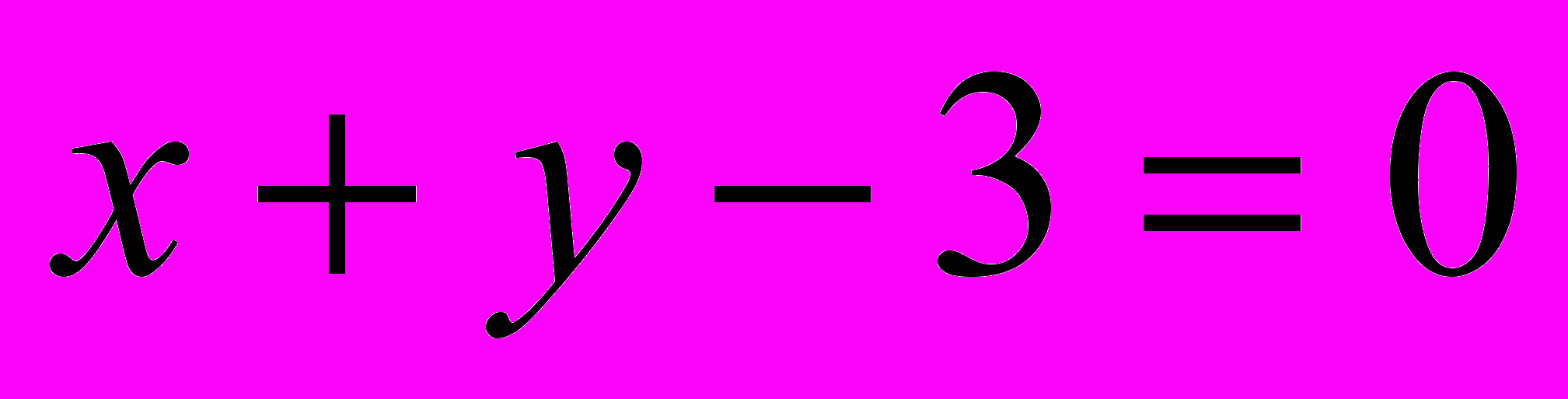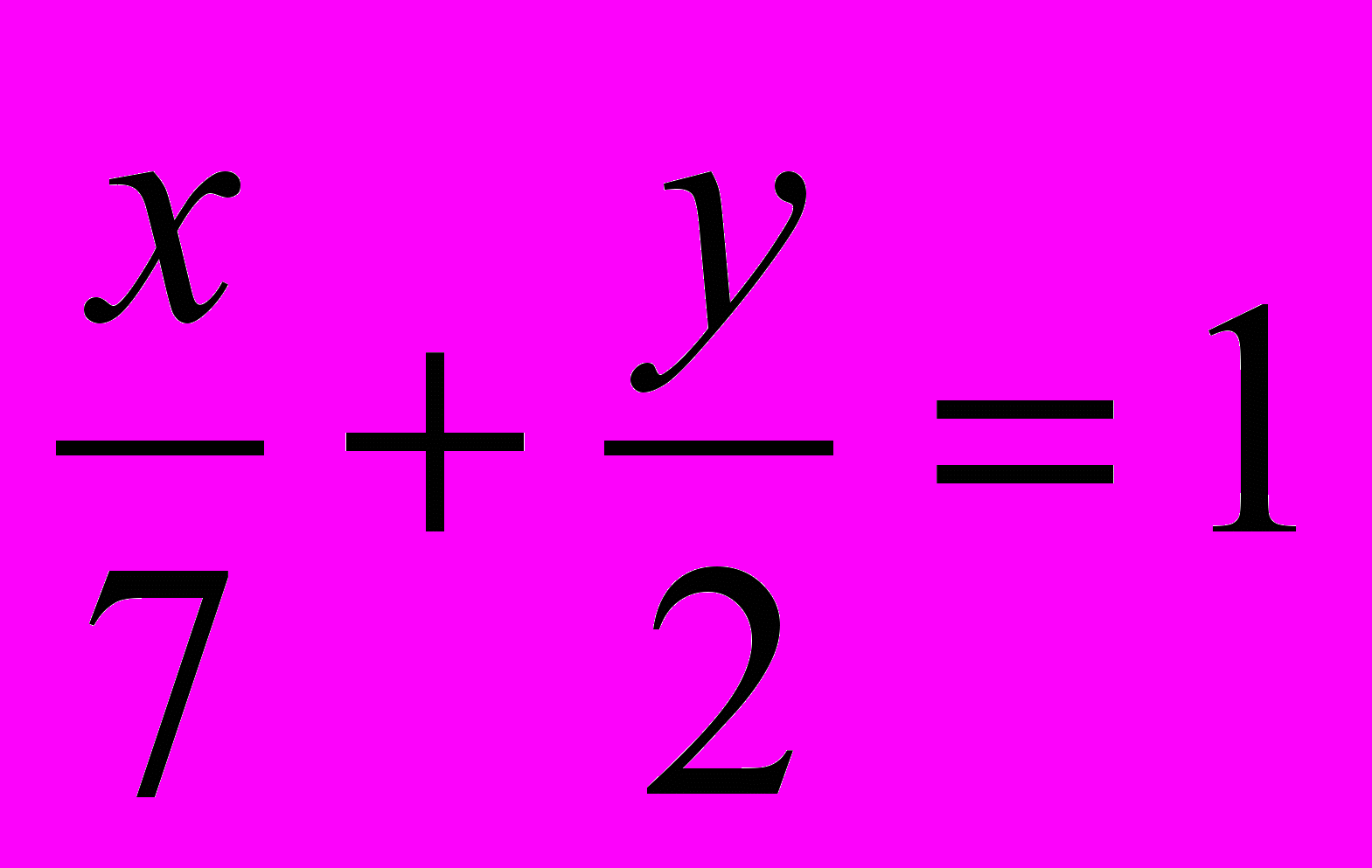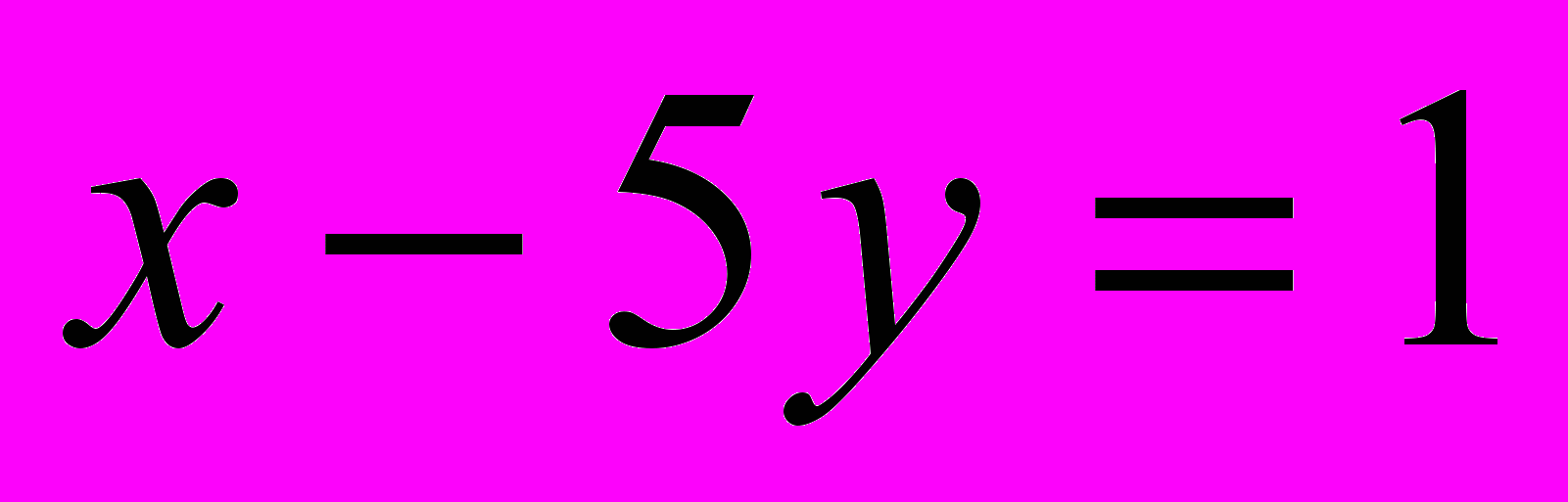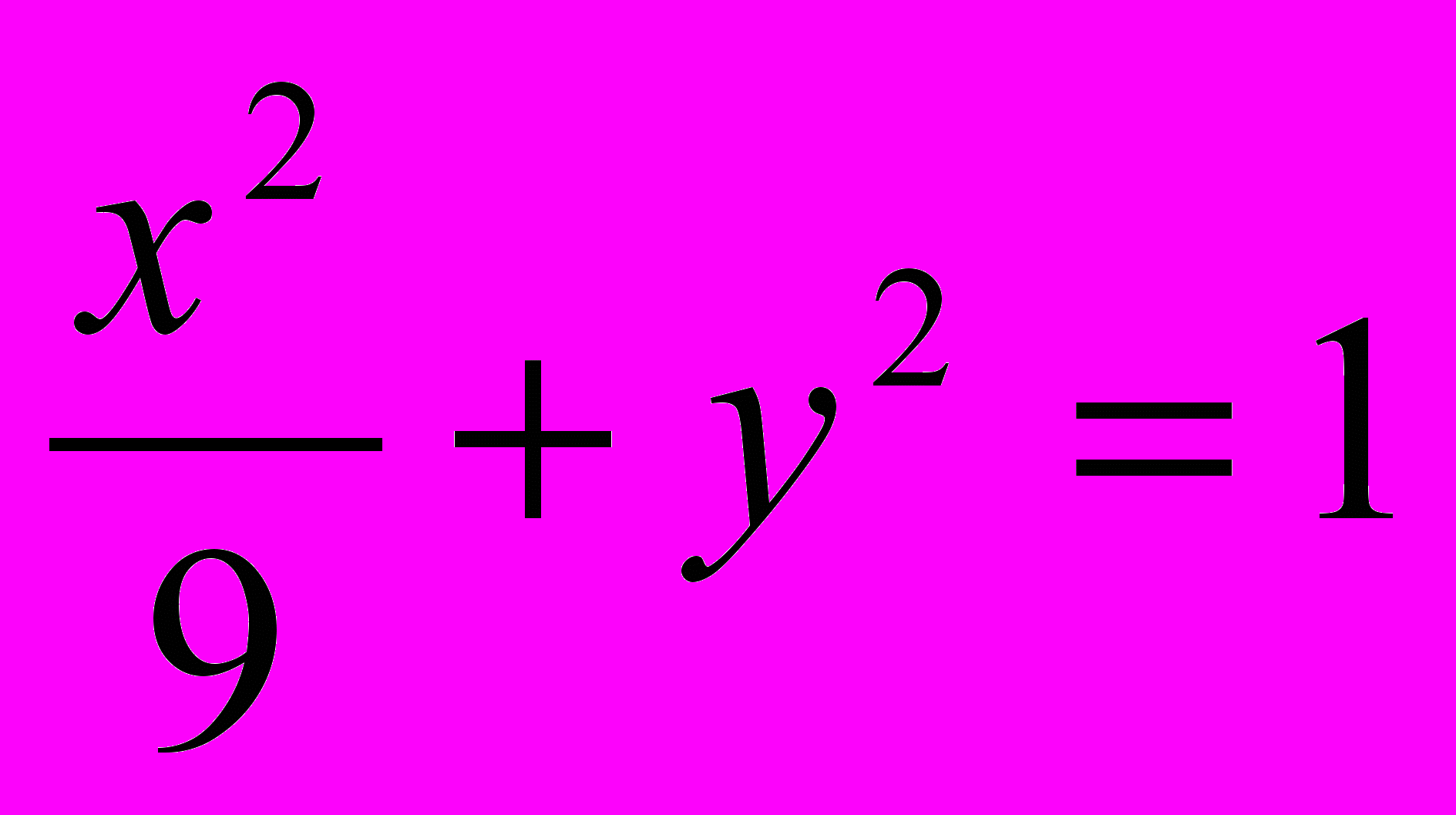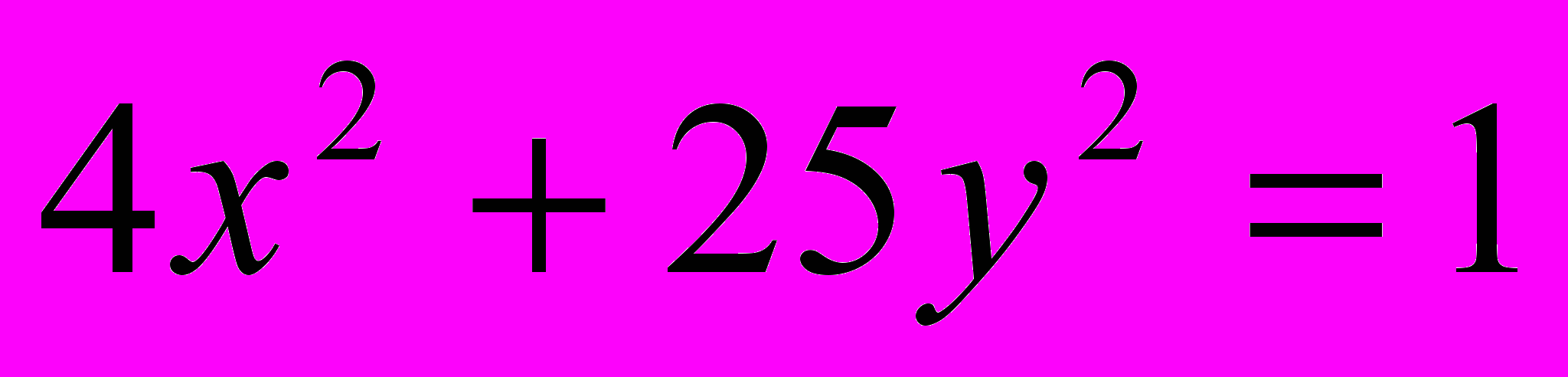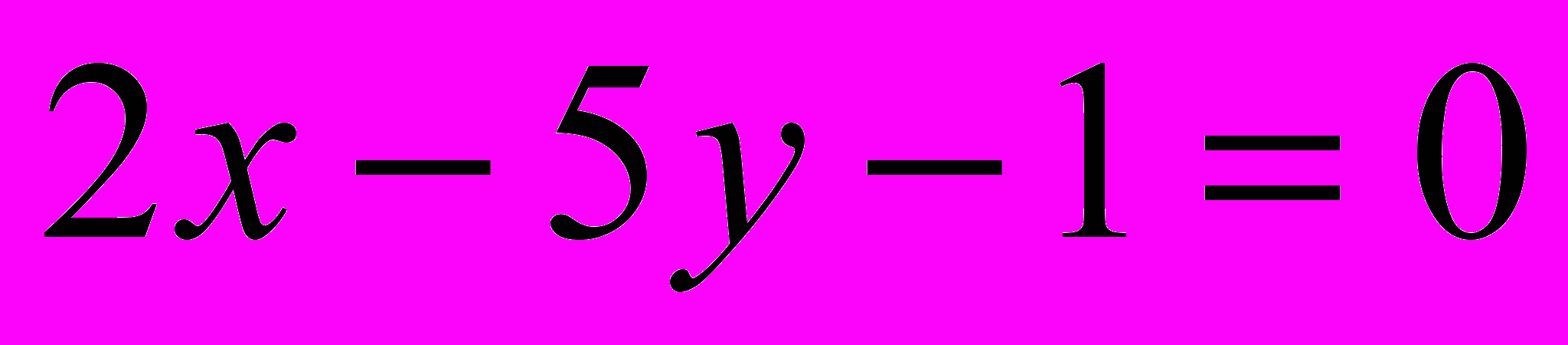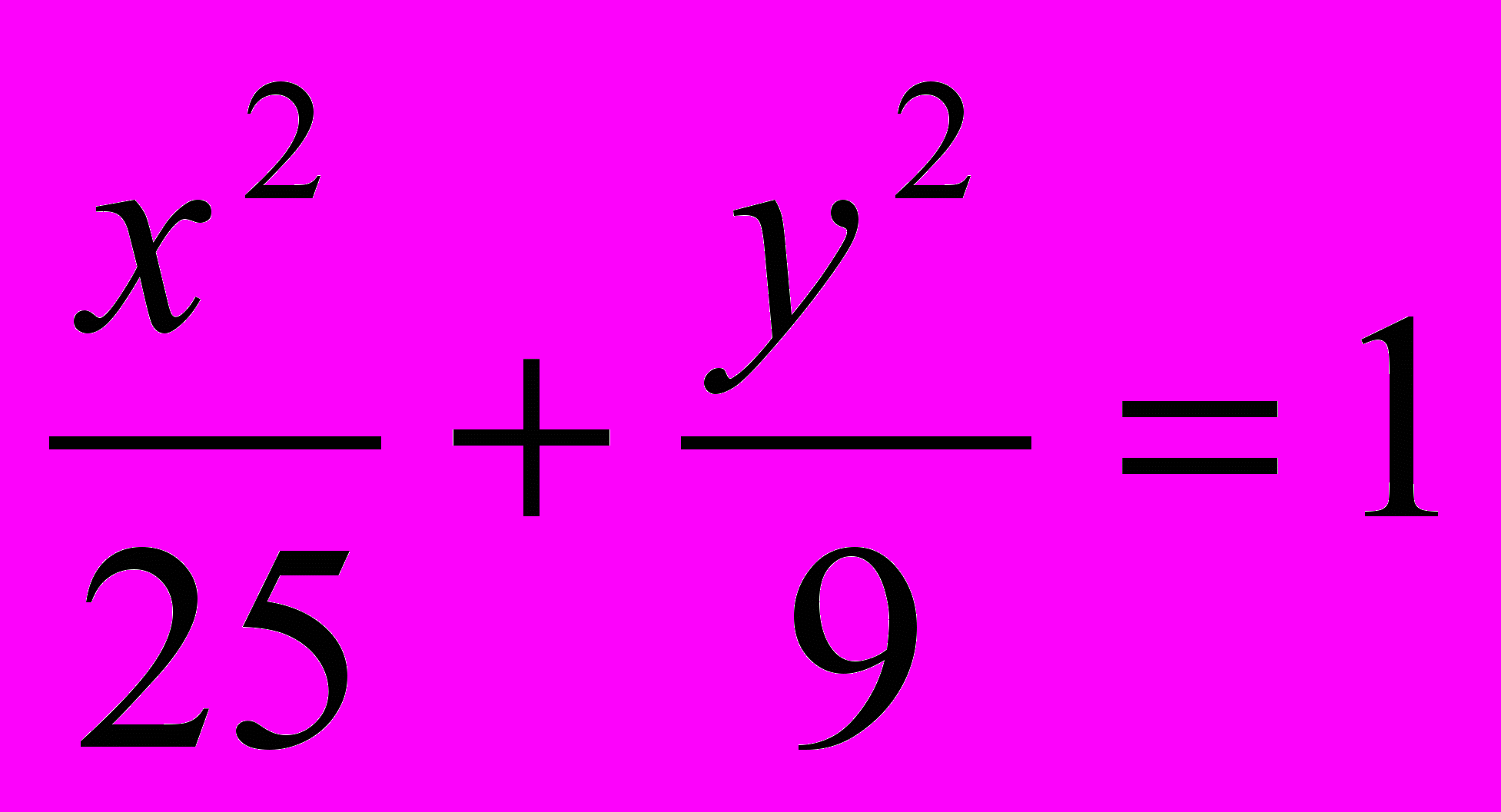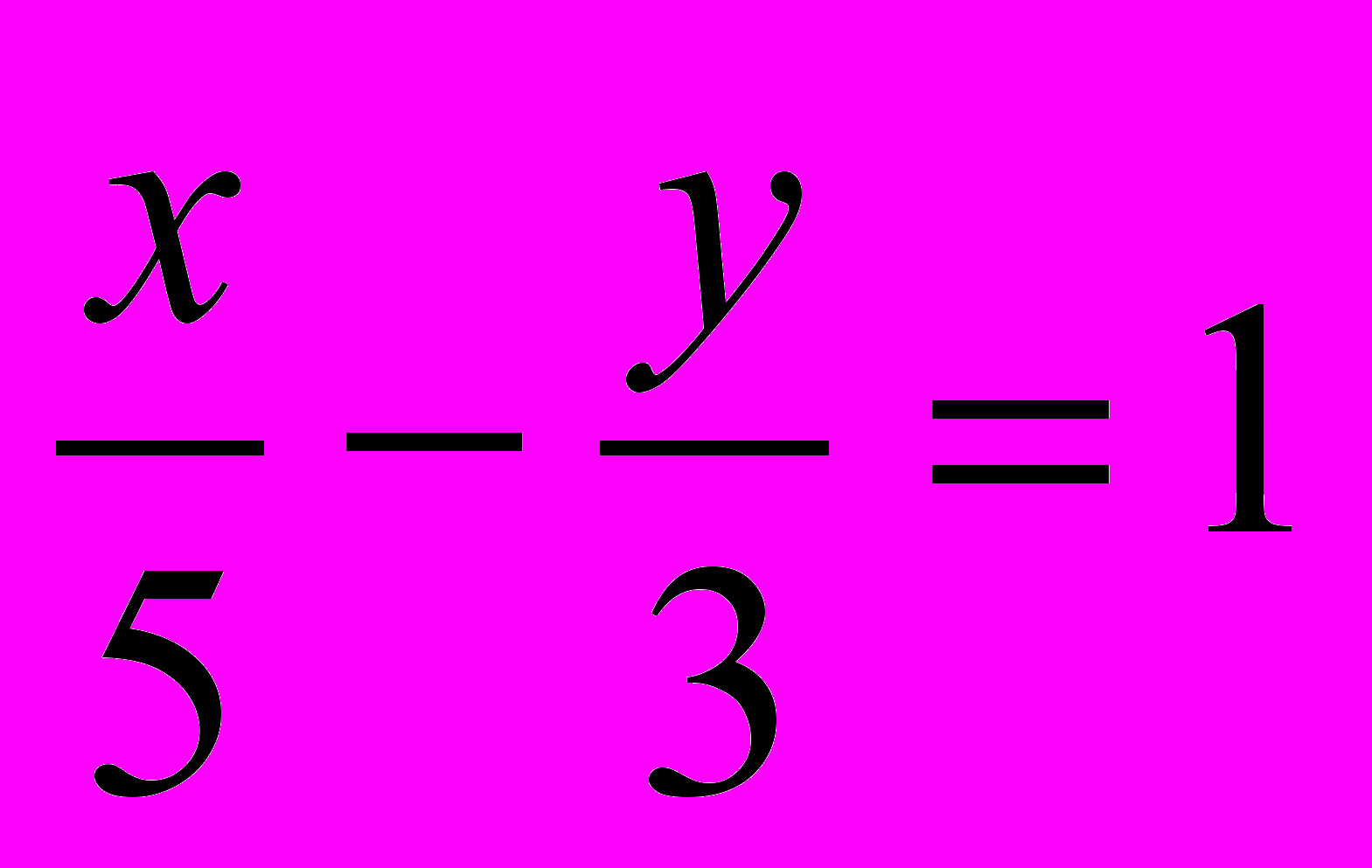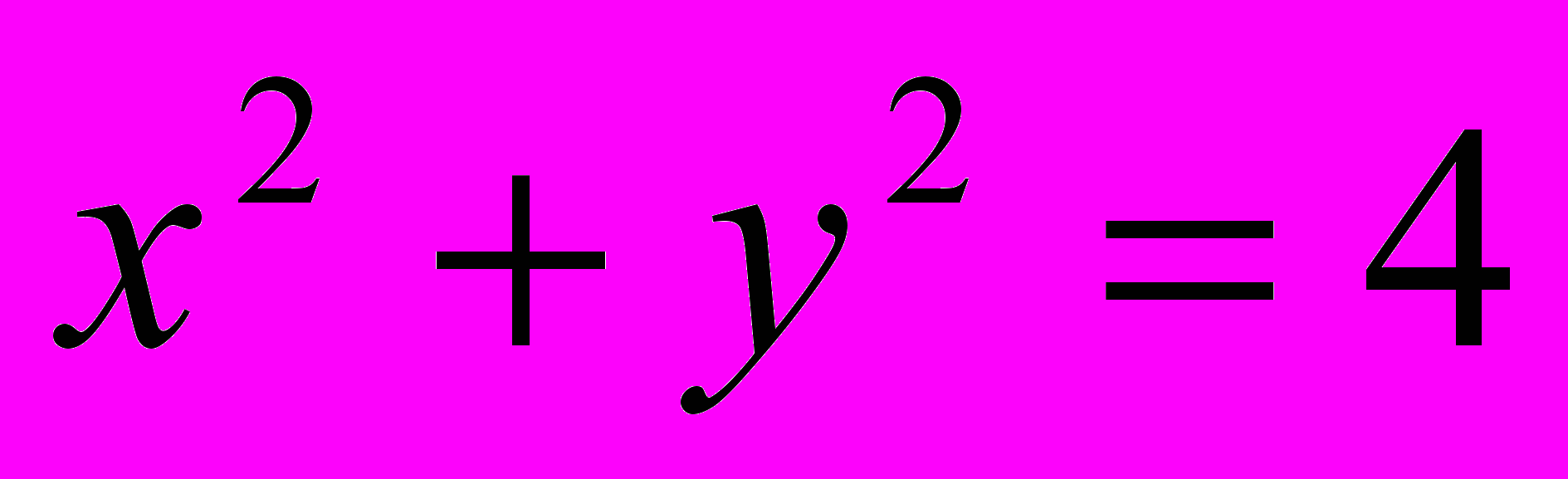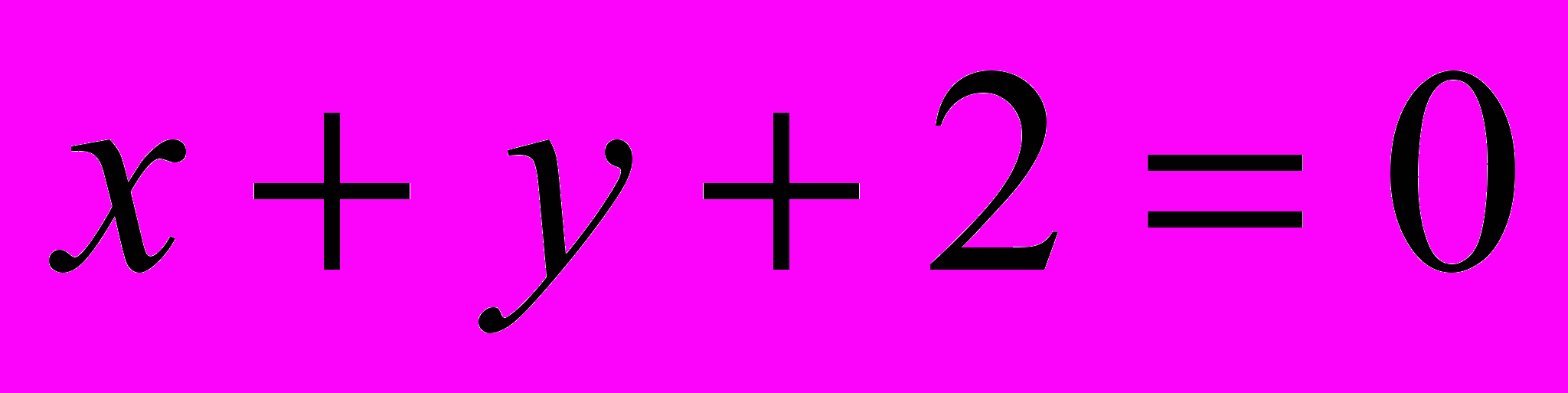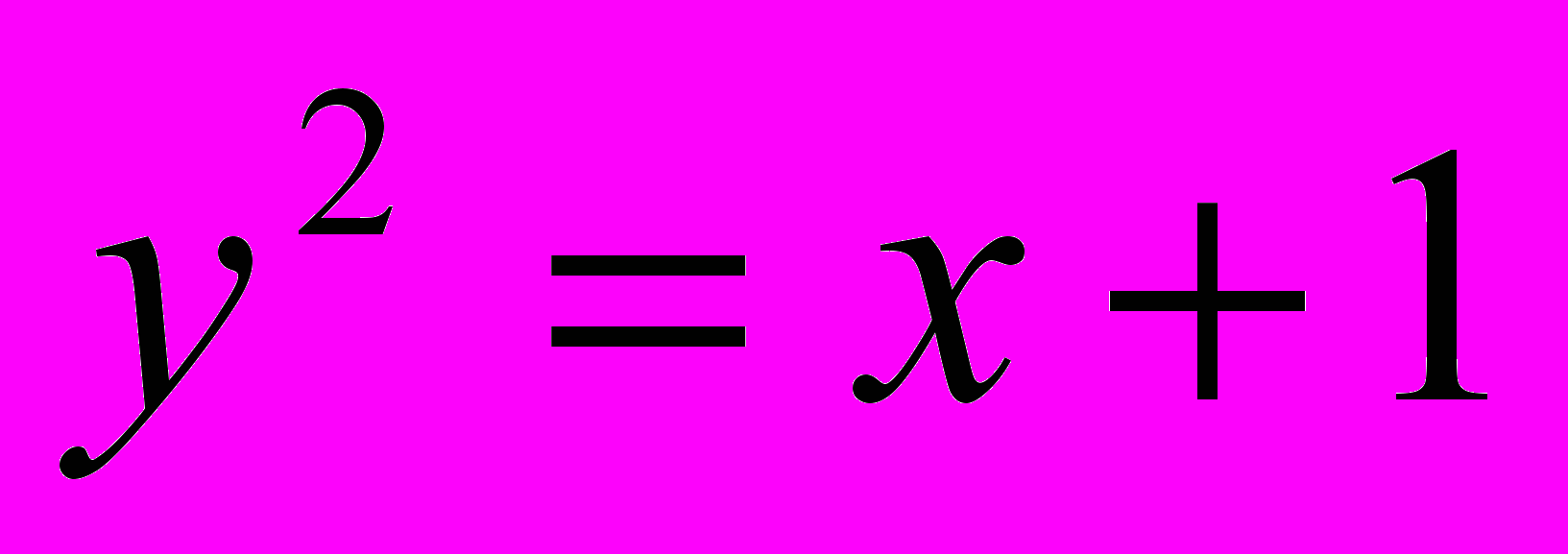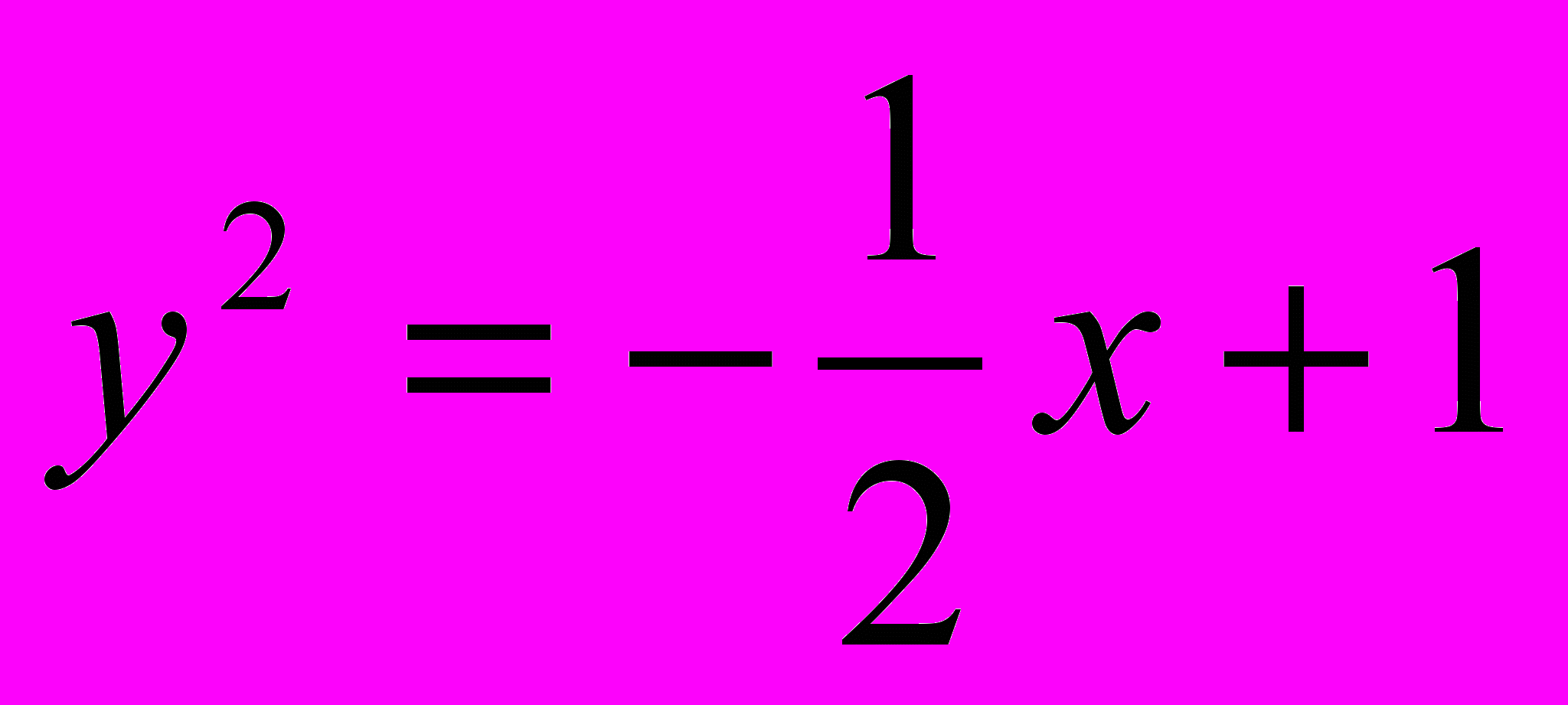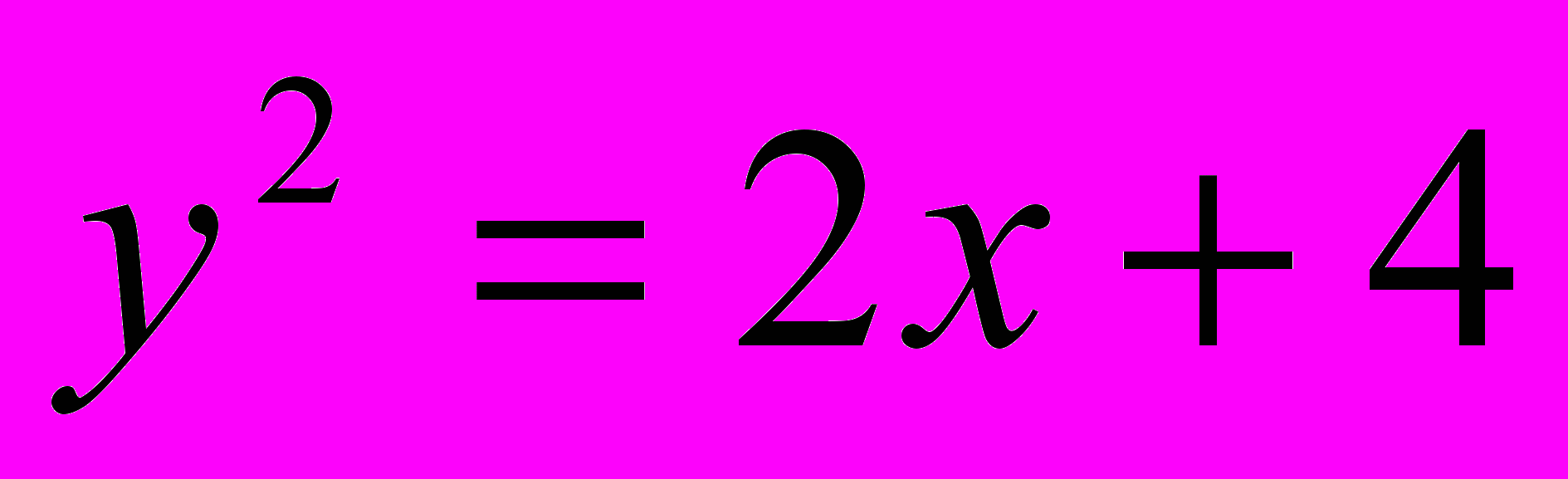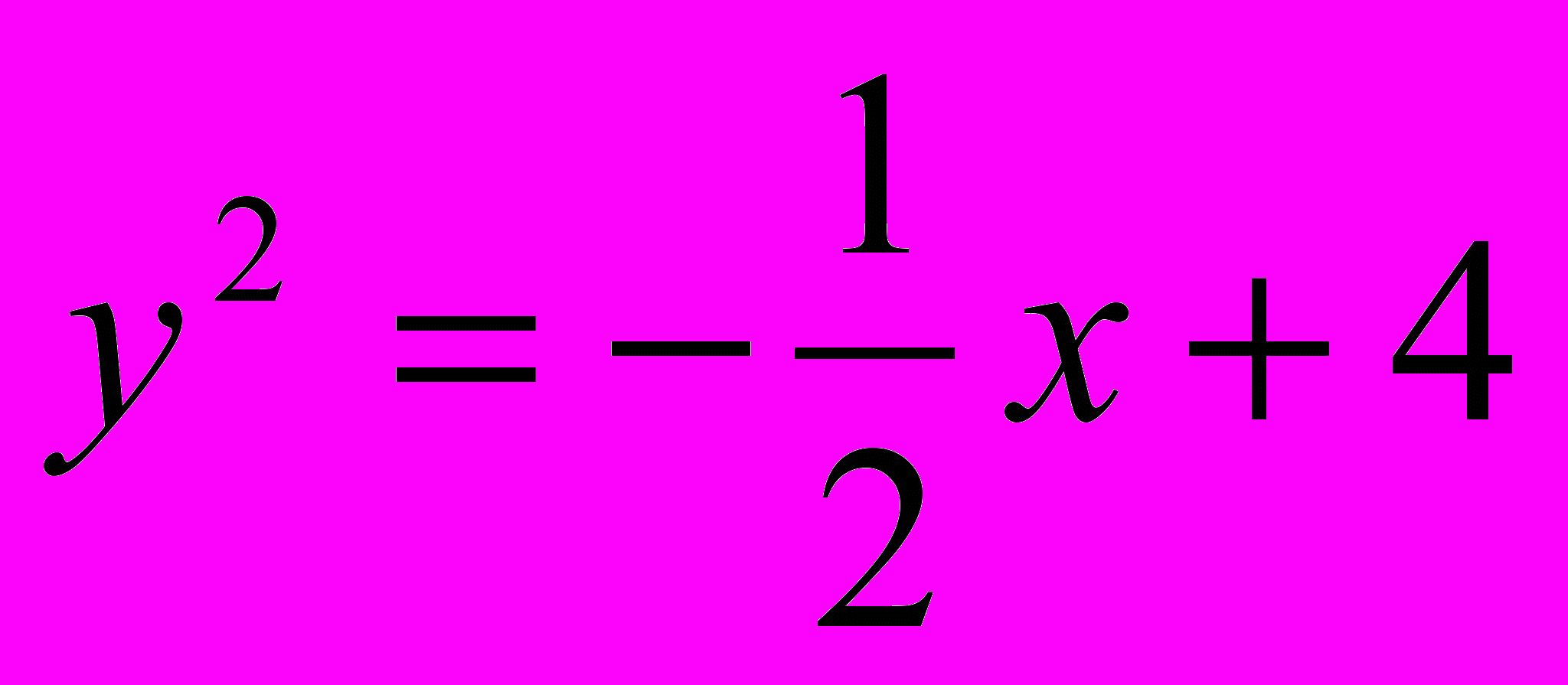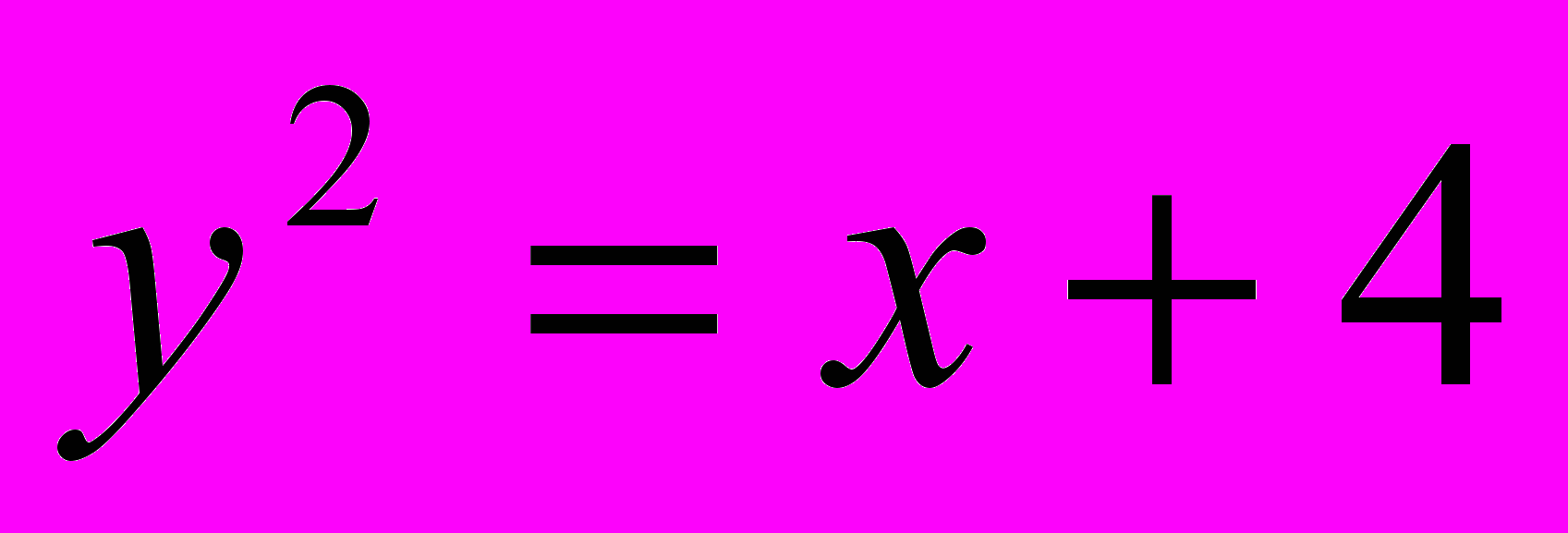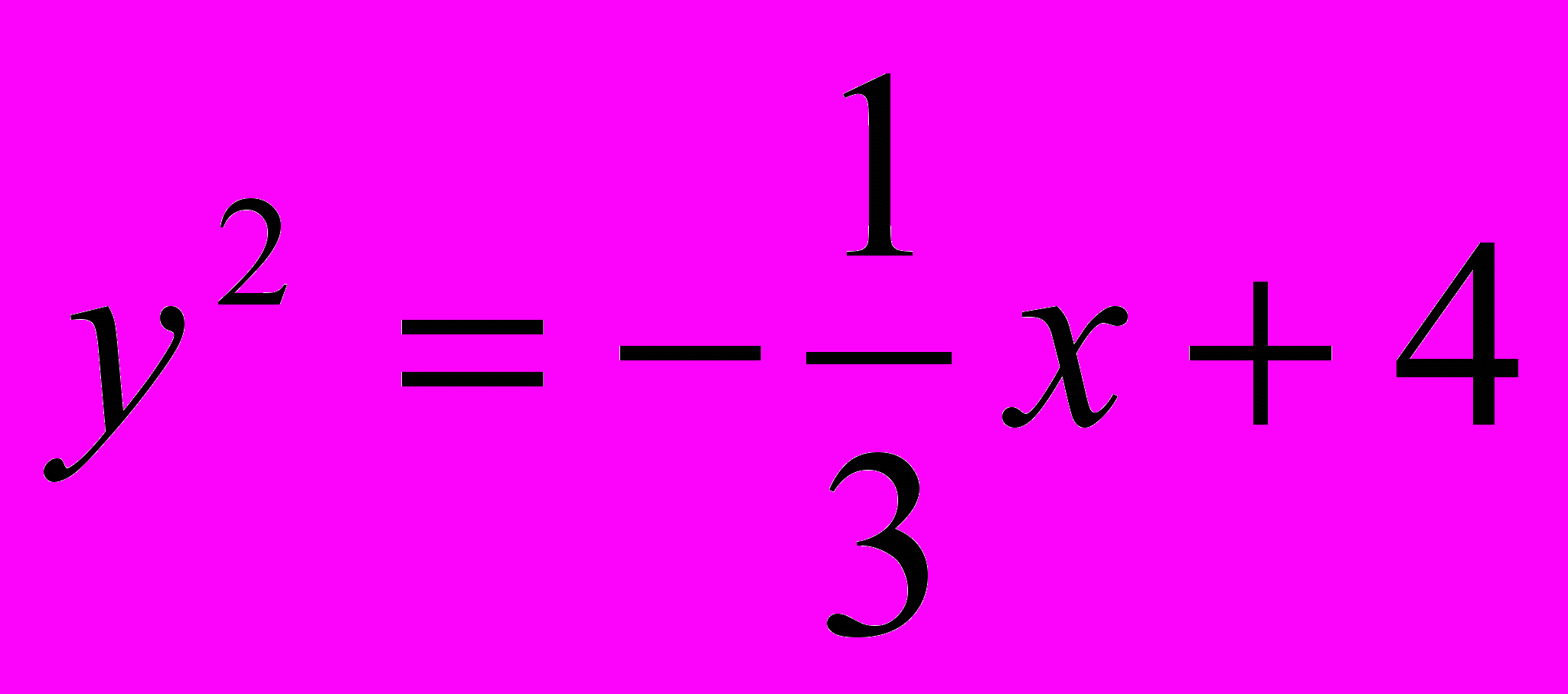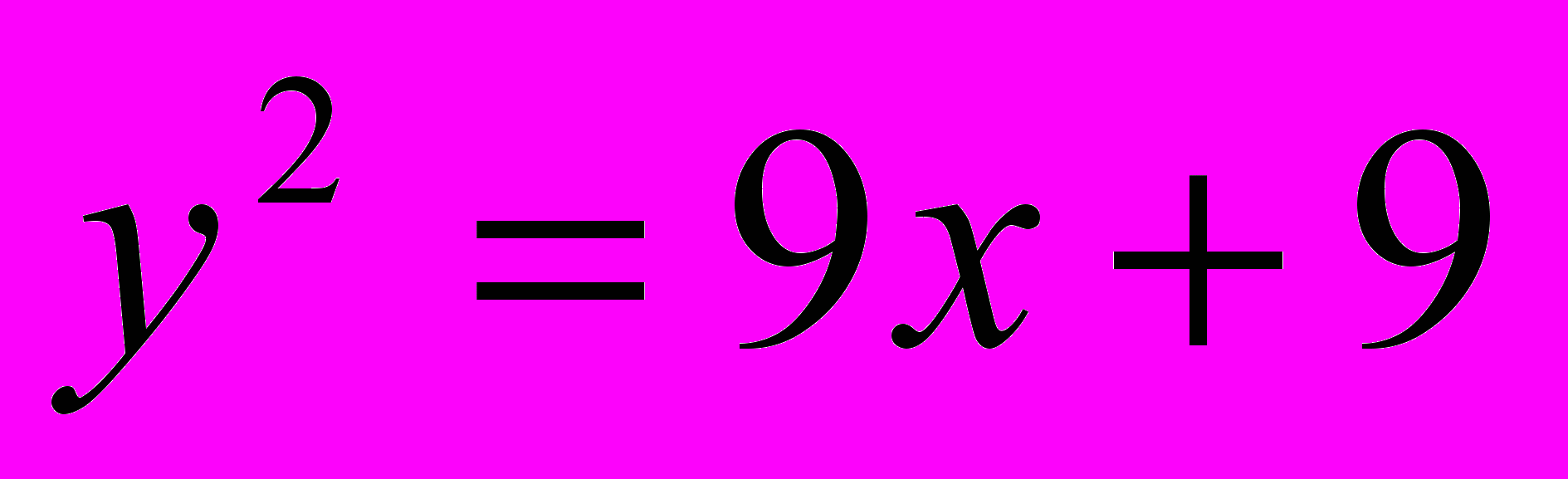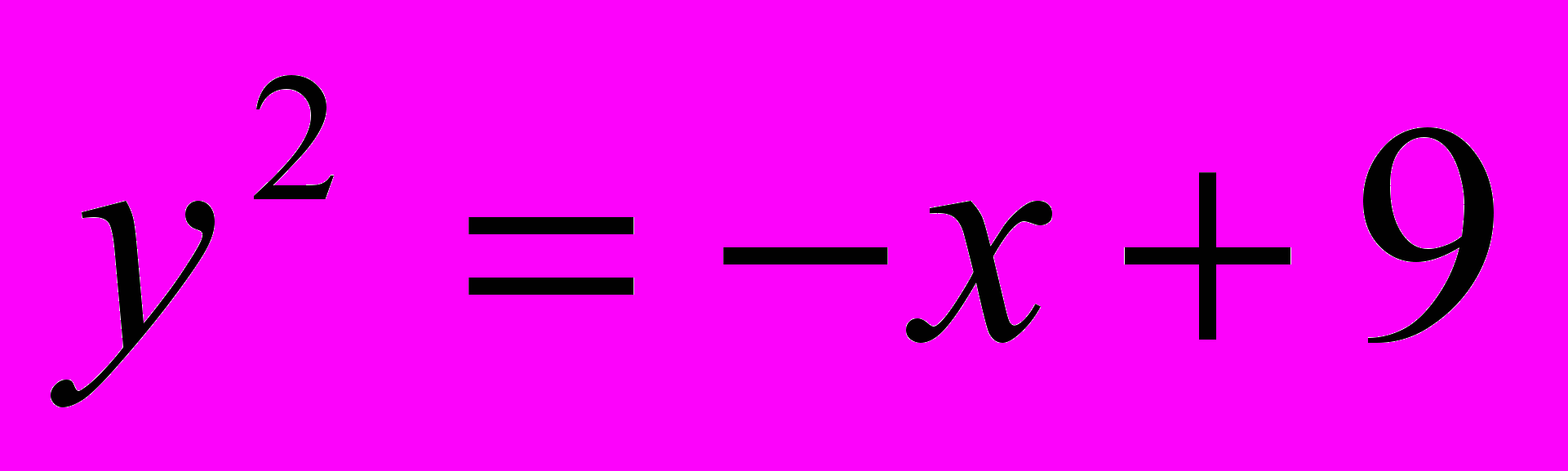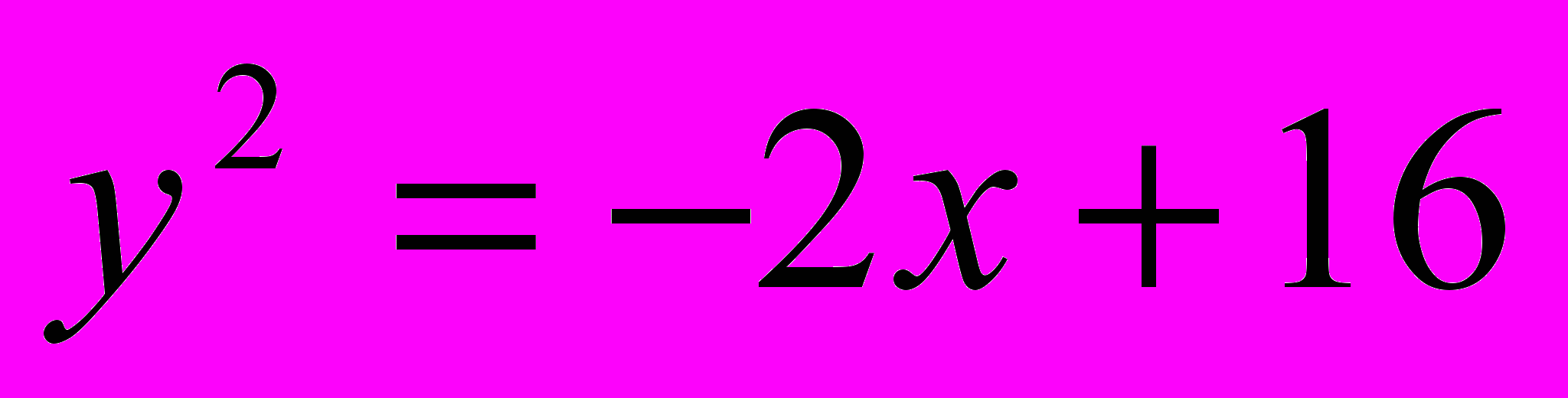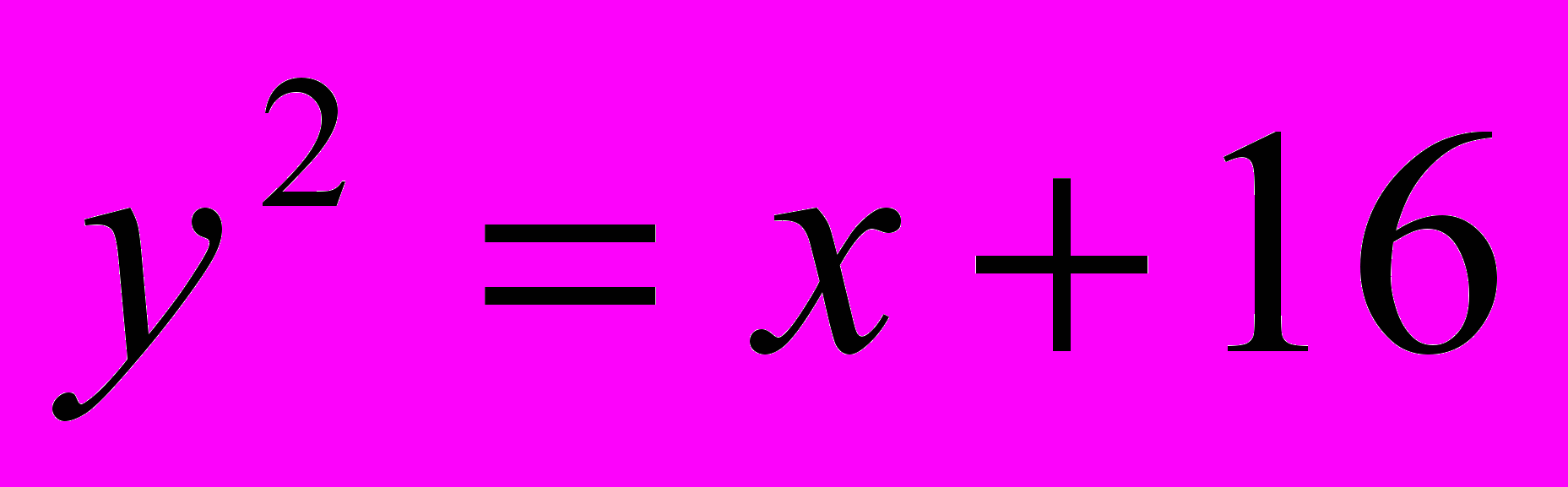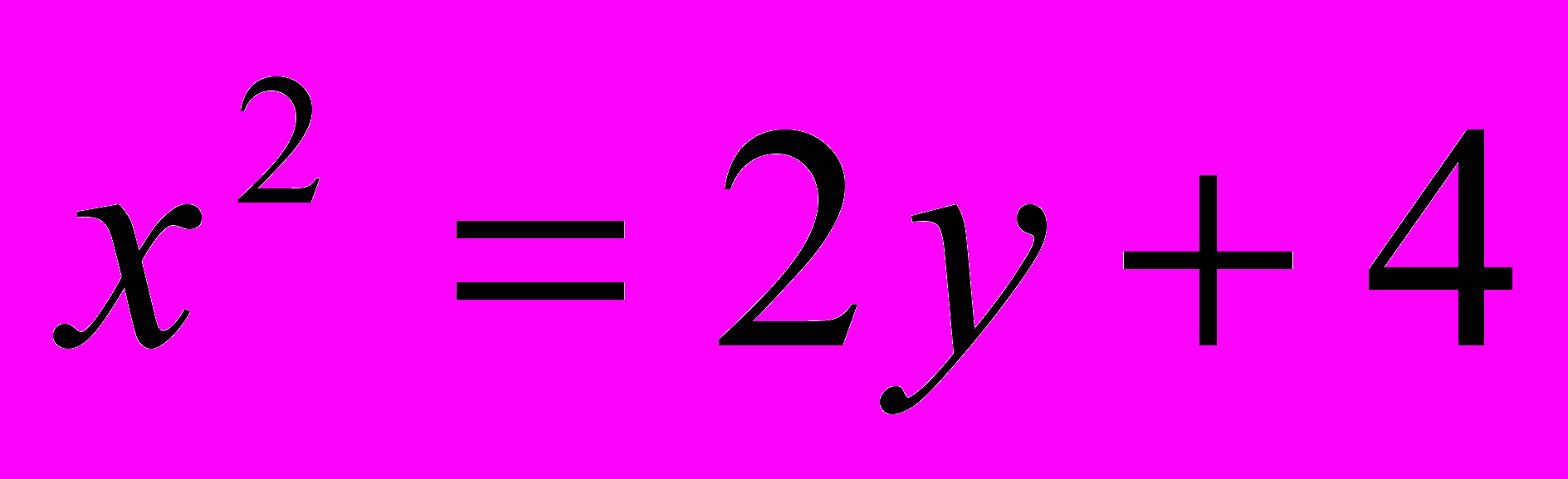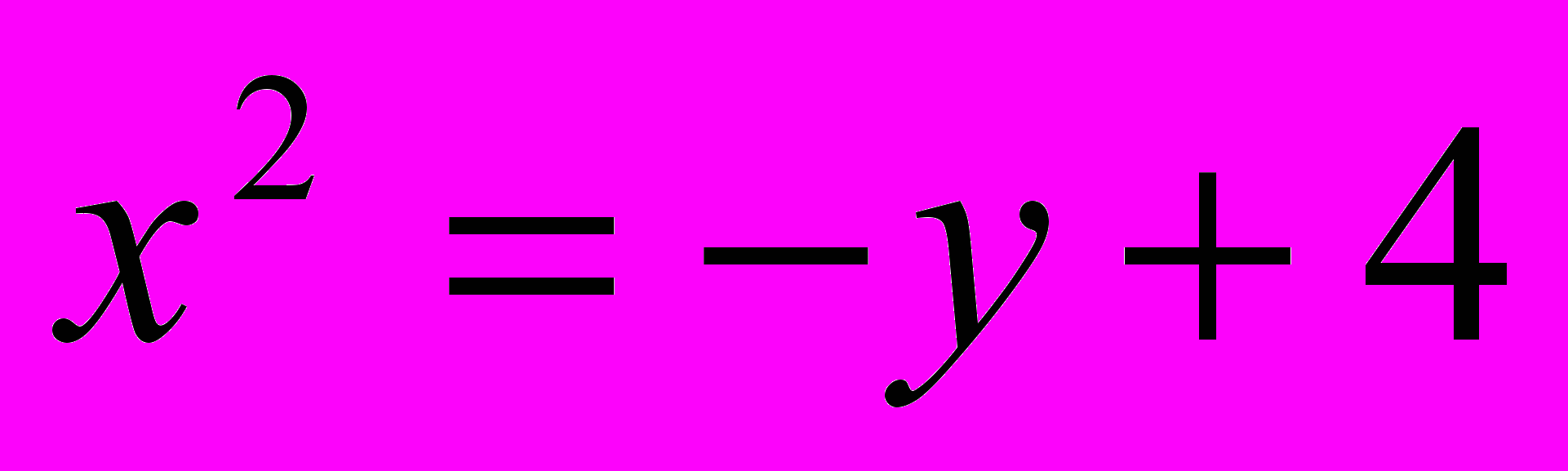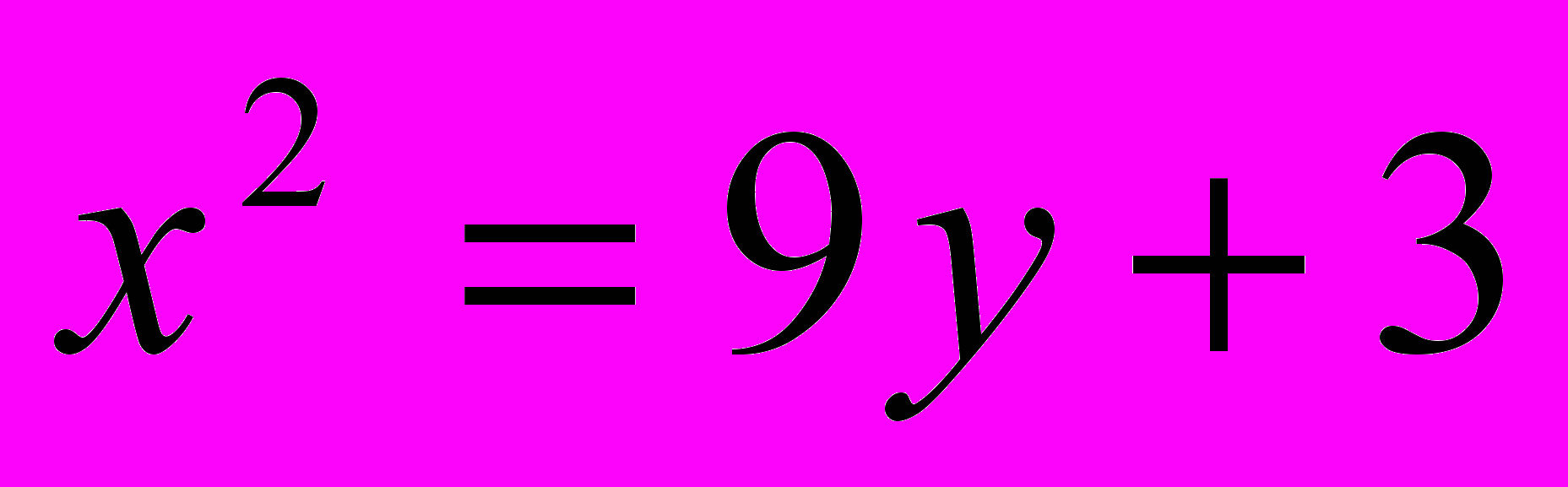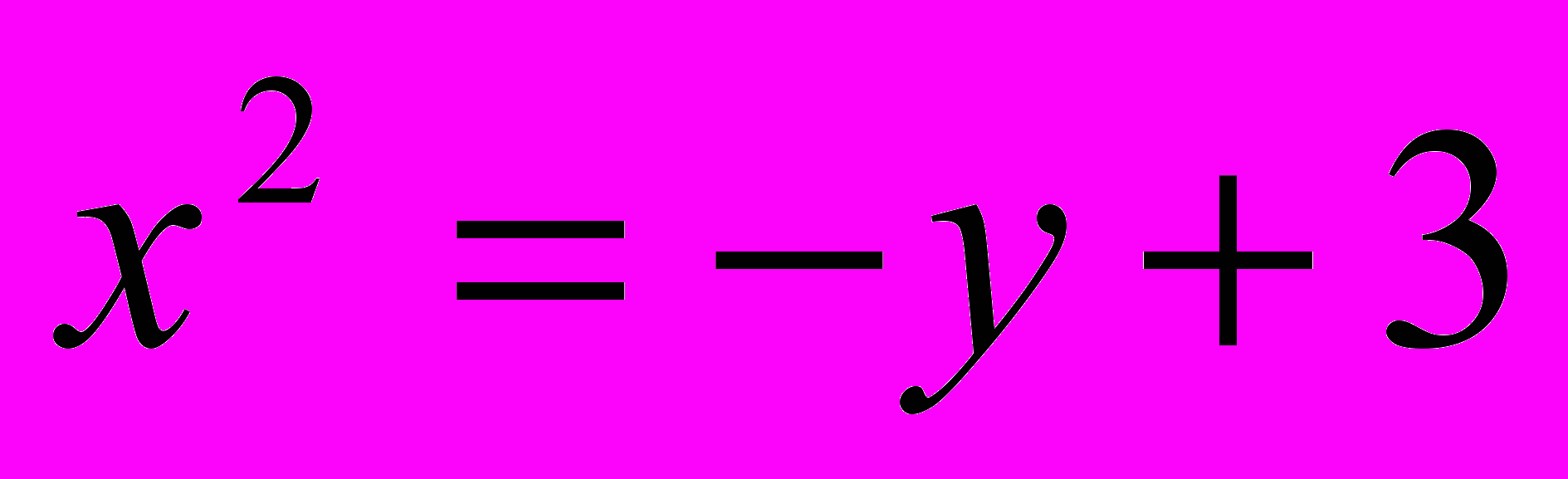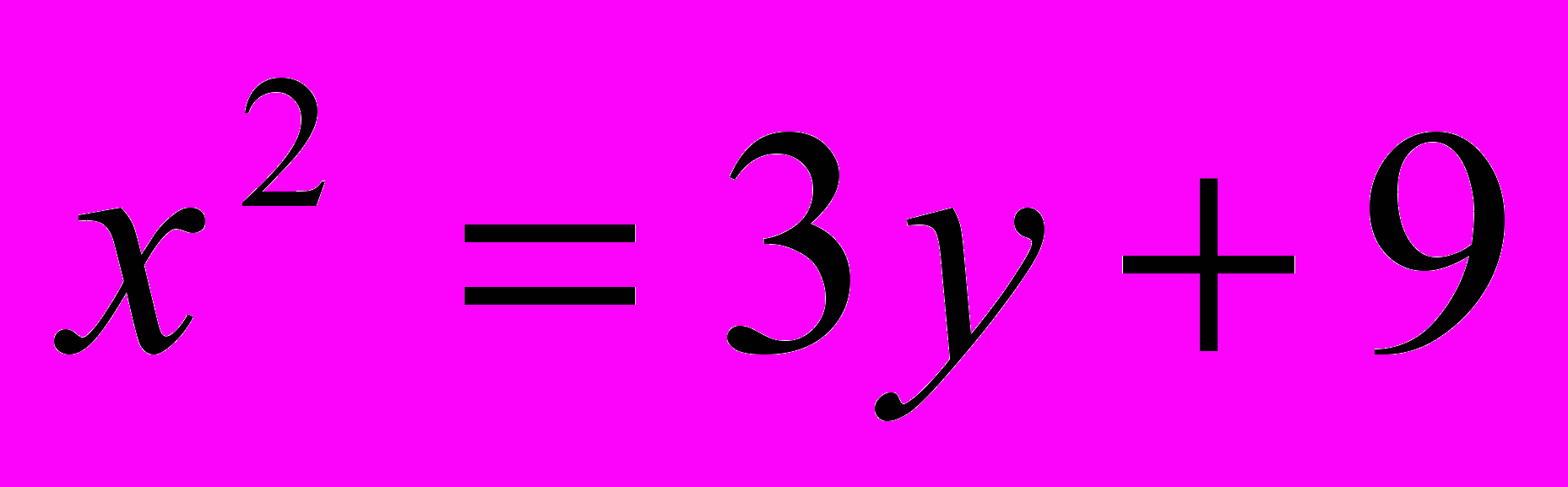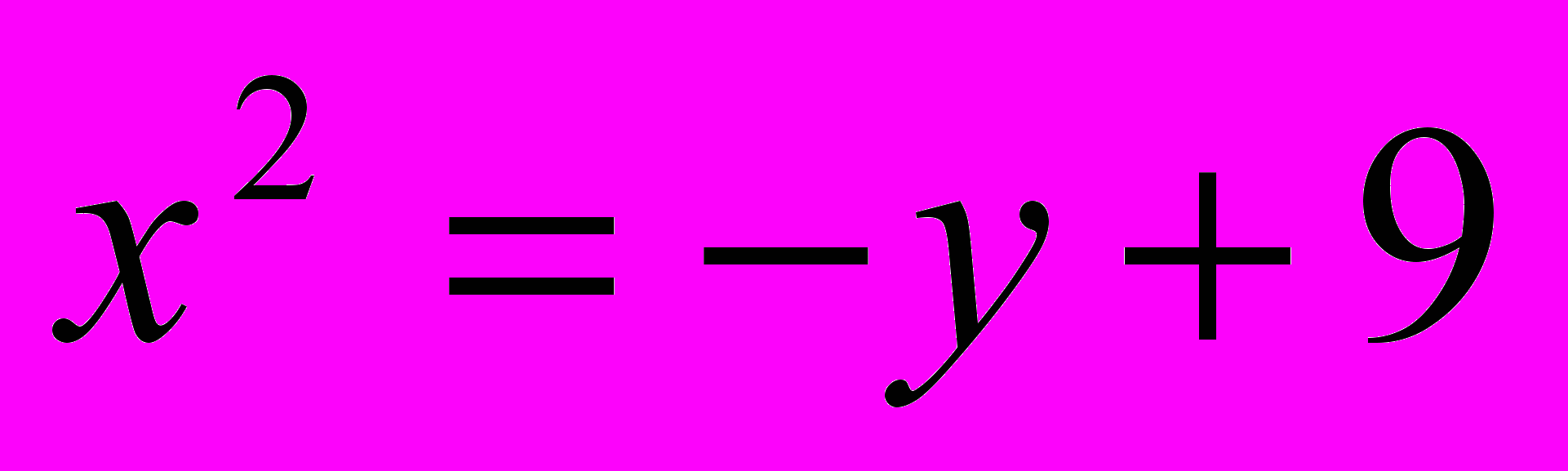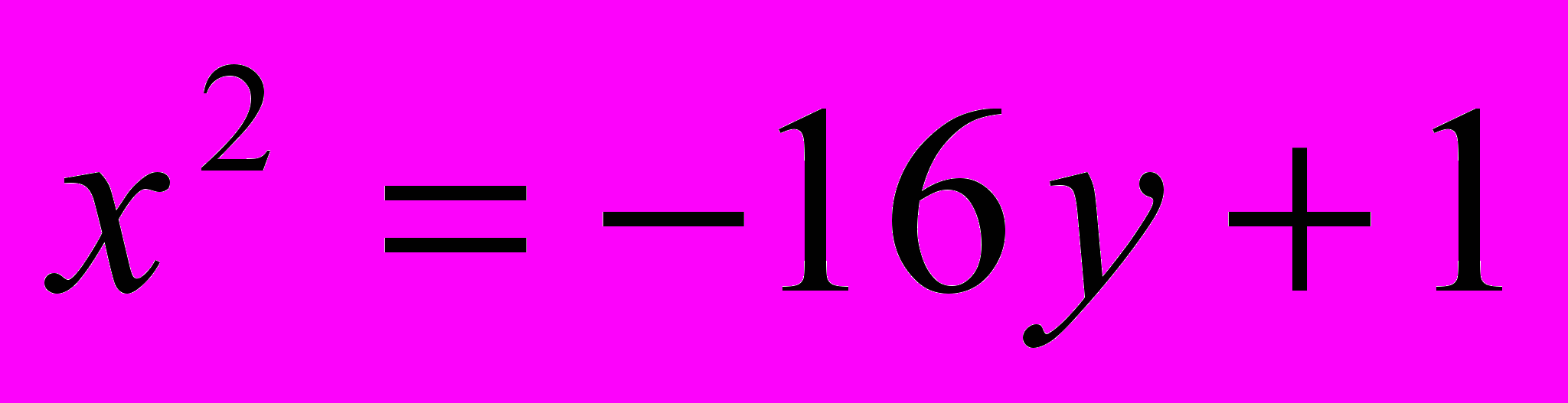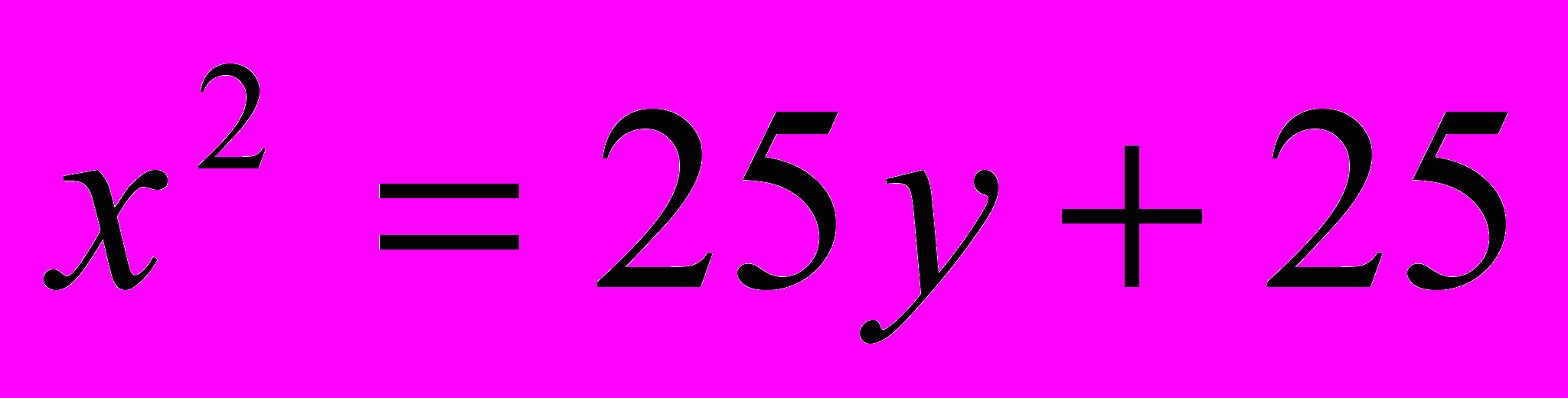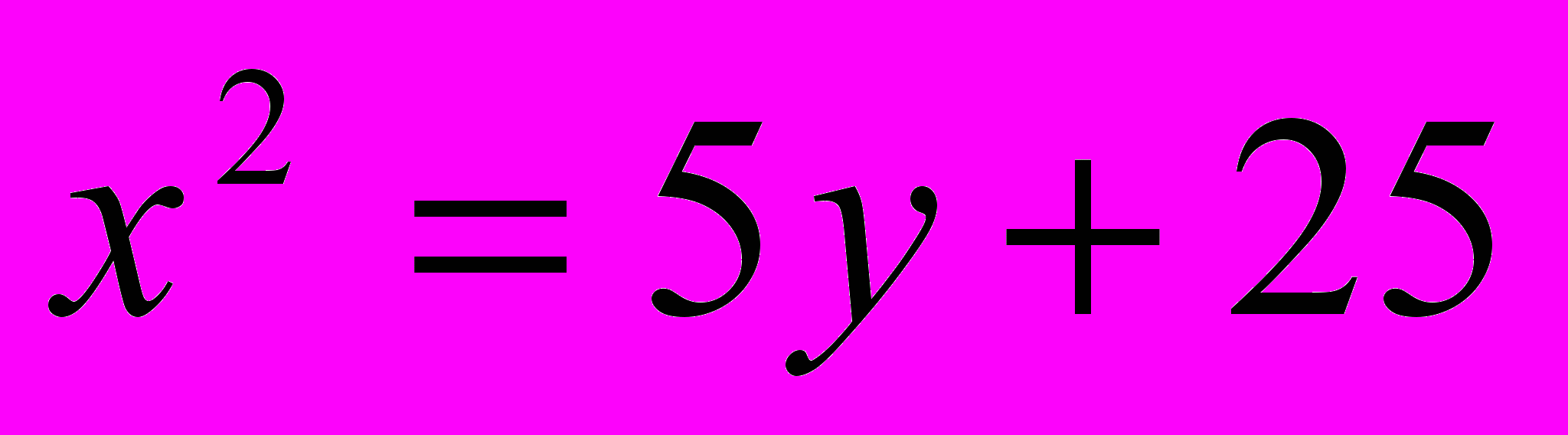Решение типовых примеров.