Калашникова Наталья Григорьевна, доктор педагогических наук, профессор Алтайского краевого института повышения квалификации работников образования. Аннотация программы программа курса

Вид материала

Программа курса

Содержание Пояснительная записка Основное содержание курса Общая схема организации работы на занятиях может быть описана следующими вопросами Задания к теме II.1 Задания к теме II.2 Задания к теме III.2 Задания к теме III.3 Задания к теме IV.1 Задания к теме IV.2 Задания для самостоятельной работы Вопросы, помогающие школьнику освоить рефлексивное оценивание V. Заключительное занятие.

Подобный материал:

• В. И. Дружинин ректор Института повышения квалификации и переподготовки работников, 2270.79kb.
• Н. А. Криволапова и о. ректора Института повышения квалификации и переподготовки работников, 3636.34kb.
• Программа повышения квалификации педагогических работников образовательных учреждений, 181.3kb.
• В. И. Дружинин ректор Института повышения квалификации и переподготовки работников, 4936.4kb.
• Разработчики программы повышения квалификации: Михеева Т. М. к п. н., доцент кафедры, 486.62kb.
• Программа повышения квалификации педагогических работников образовательных учреждений, 153.75kb.
• Программа повышения квалификации педагогических работников «Информатизация образования., 153.97kb.
• Их наук, профессор, проректор по научно-методической работе и международной деятельности, 344.47kb.
• Программа повышения квалификации педагогических работников образовательных учреждений, 133.85kb.
• Программа повышения квалификации научно-педагогических работников «Инновационная деятельность, 355.82kb.

Комитет Алтайского края по образованию


Программа курса по выбору


для предпрофильной подготовки

«Как решать уравнения, неравенства и системы уравнений с

параметрами»

(16 часов)


Составитель:

Гончарова Тамара Ивановна

МОУ «Гимназия №74»


Барнаул – 2004 г.


Рецензент:

Калашникова Наталья Григорьевна, доктор педагогических наук, профессор Алтайского краевого института повышения квалификации работников образования.


Аннотация программы

Программа курса предназначена для углубления знаний по математике, для поддержки основного базового курса, а также для ориентации учащихся в выборе профиля обучения и индивидуального образовательного пути.

Программа курса предполагает дальнейшее развитие у школьников навыков организации умственного труда и самообразования, распознание и раскрытие их способностей.

Выбрав данный курс, учащиеся за полгода пройдут путь от решения простейших уравнений и неравенств с параметрами до открытия алгоритмов и способов решения заданий с параметрами.

Курс рассчитан на 16 часов, однако программа может корректироваться, исходя из его сложности. Эта программа курса может служить и основой для элективного курса в 10-11 классах, кроме того, он поможет учителю подготовить учащихся к выполнению заданий экзаменов, в том числе и ЕГЭ. В программу могут быть включены и такие важные темы, как «рациональные задачи с параметрами», «критические значения параметра» и др. Программа может быть ориентирована на различные группы учащихся, с разным уровнем подготовки.

^ Пояснительная записка

Данная программа курса по выбору своим содержанием может привлечь учащихся 9 классов, которым интересна математика и которым хочется глубже и основательнее познакомиться с её методами и идеями.

Целью данного курса является развитие представлений об исследовательской деятельности в математике, через решение уравнений, неравенств, систем, расширение представлений школьников о математике и своих собственный возможностях.

Задачи курса:

• Формирование способов логических рассуждений;
  
• Формирование способов самостоятельного приобретения знаний;
  
• Помочь учащимся «открывать» способы решения.
  

Предлагаемый курс освещает слабо проработанные в общем курсе школьной математики вопросы, методы решения.

Уравнения, неравенства, системы с параметром относятся к иному типу задач – задач, для решения которых необходимо, прежде всего, умение проводить логические построения, кроме того, арсенал стандартных преобразований должен быть существенно пополнен некоторыми специфическими преобразованиями.

Доминантной формой обучения является поисково-исследовательская деятельность. Учащиеся в ходе освоения данного курса имеют возможность познакомиться с научно-популярной литературой по теме, провести самостоятельный поиск и изучение информации, провести необходимое самостоятельное исследование (индивидуально или в группе). Это даст возможность каждому школьнику соотнести свои потребности («хочу») со своими возможностями («могу»).

Средствами для осуществления этой работы являются задания, которые предлагаются учащимся, а также тематика исследовательских проектов на выбор учащихся


Предполагается использование и таких форм как лекции, лекции с элементами беседы, семинары. Занятия посвящены разрешению проблемных ситуаций, разработке мини-теорий в группах, обсуждению результатов индивидуальных и коллективных исследований.

Учебно-тематическое планирование

№		Количество часов	Учебное время
			лекции	Семинар
I	Введение	1
II II.1 II.2	Уравнения Линейные уравнения, уравнения с модулем Квадратные уравнения. Уравнения, приводимые к квадратным	5 2 3	1 1	1 2
III III.1 III.2 III.3	Неравенства Линейные неравенства, Модульные неравенства Квадратные неравенства Неравенства высших степеней	5 2 2 1	1 1 -	1 1 1
IV IV.1 IV.2	Системы уравнений Линейные системы Системы высших степеней	4 2 2	1 -	1 2
V	Заключительное занятие	1	-	1

^ Основное содержание курса

I. Организационное занятие. Знакомство учащихся с темами спецкурса, чем завершается спецкурс. О написании мини-докладов и рефератов по теме «Уравнения, неравенства, системы уравнений с параметром».

II. Уравнения с параметром.

Определение. Связь с базовым курсом.

1. Линейные уравнения.
   

Правила решения уравнений. Методы решения уравнений. Уравнение стандартного вида. Уравнение с модулем. Метод интервалов. «Собирание» ответа при решении уравнений с параметрами. Сущность проверки.

2. Квадратные уравнения.
   

Определение. Виды. Способы решения. Замена переменной. Решение относительно параметра. Метод разложения. Геометрический способ решения. Исследование квадратного трёхчлена. Необходимые и достаточные условия. Мини-теоремы.

III. Неравенства с параметром.

1. Определение линейного неравенства. Правила решения. Простейшие неравенства. Исследование решения. Способы решения. Следование и равносильность. Мини-теоремы.
   
2. Квадратные неравенства. Определение. Способы решения. Исследование квадратного трёхчлена для решения неравенств с параметром.
   
3. Неравенства высших степеней.
   

Дробно-рациональные неравенства. Метод интервалов. Аналитические способы решения неравенств. Системы неравенств.

IV. Системы уравнений с параметром.

1. Линейные системы.
   

Определение. Число решений. Виды систем. Способы решения. Исследование количества решений систем. Некоторые теоремы о решении систем. Определители графический способ решения.

2. Системы высших степеней.

Системы уравнений второй степени. Способ сложения. Подстановки. Замена переменной. Графический способ.


^ Общая схема организации работы на занятиях может быть описана следующими вопросами:

Что я об этом уже знаю?

Чего не знаю, не понимаю?

Какую проблему буду решать?

Как я должен действовать, чтобы получить результат?

Что я буду делать сначала, что потом?

Что мне мешает решить эту проблему?


^ Задания к теме II.1

Тема для обсуждения: Сколько решений может иметь уравнение? От чего зависит количество корней уравнения?

Задания для самостоятельной работы:

а) приведите примеры линейных уравнений с параметром;

б) приведите примеры модульного уравнения с параметром;

в) выясните, при каких значениях параметра имеет решение уравнение;

г) решите уравнения:

|x|+|x+3|+|x-4|=a

|ax|+|x-4|-|x-3|=5

|x-a|+|x+3|-|x-4|=2

|x+3|=a|x-2|

При каких а уравнение имеет единственное решение?





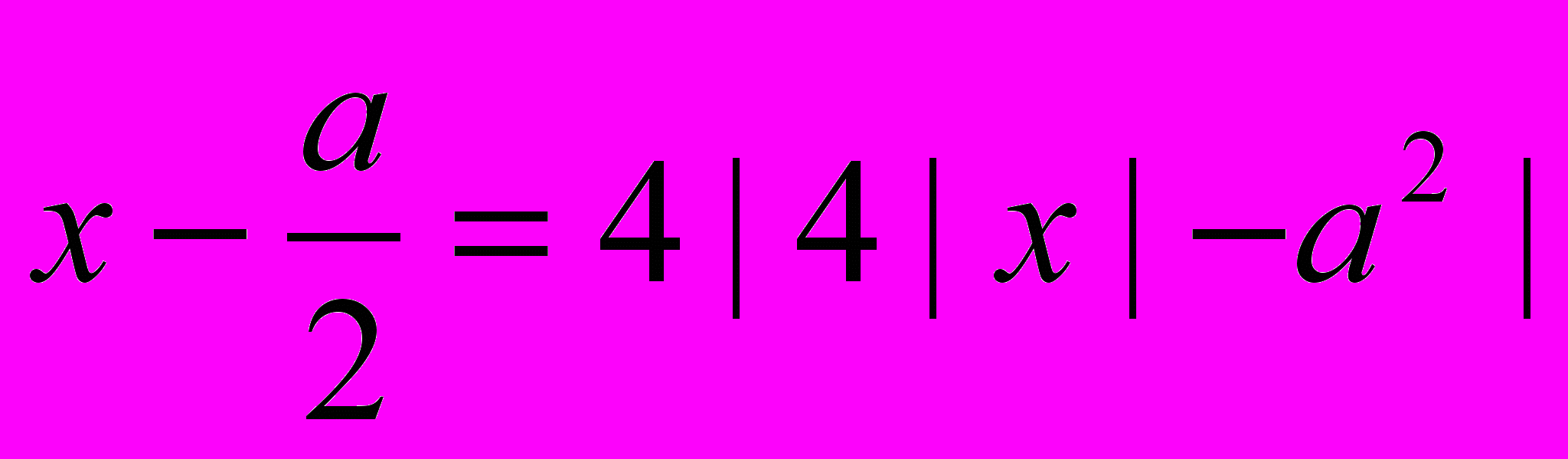
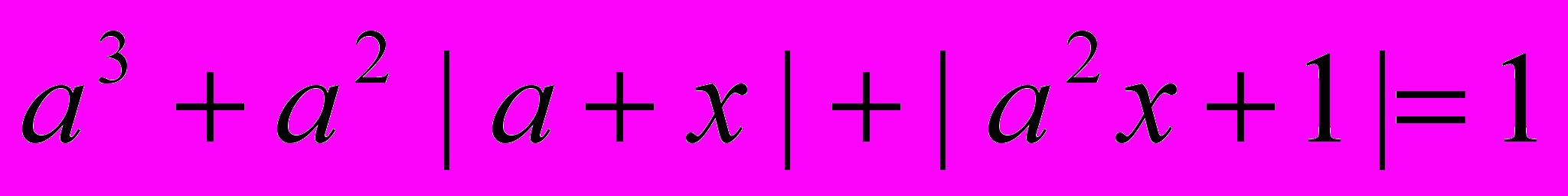
При каких значениях а уравнение имеет не мене четырёх различных решений, которые являются целыми числами?

д) составьте задания для зачёта, обоснуйте выбор;

е) подберите задания по теме, почему вы их выбрали;

ж) выделите наиболее интересные для себя здания»

з) выберите наиболее трудные для себя задания.


^ Задания к теме II.2

Тема для дискуссии: Какой способ решения лучший? За и против. Защита своего способа решения.

Задания для самостоятельной работы:

а) приведите примеры квадратного уравнения с параметром;

б) от чего зависит количество корней уравнения?;

в) решите уравнения:







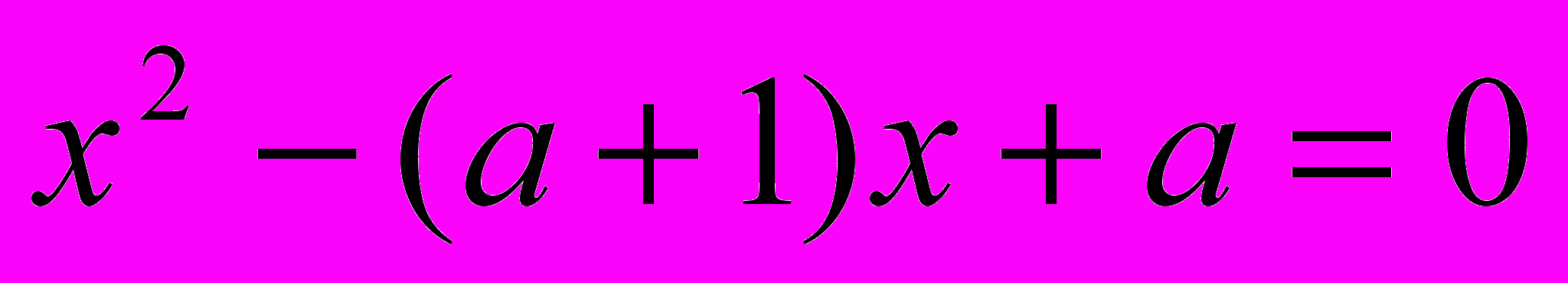
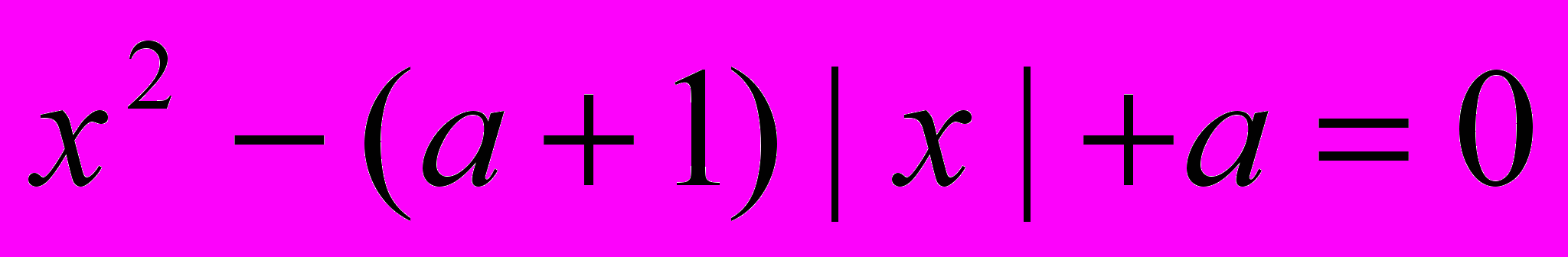
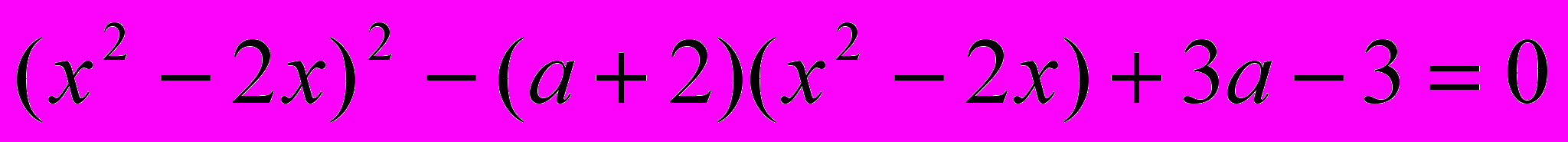
При каких а уравнение имеет 4 решения?



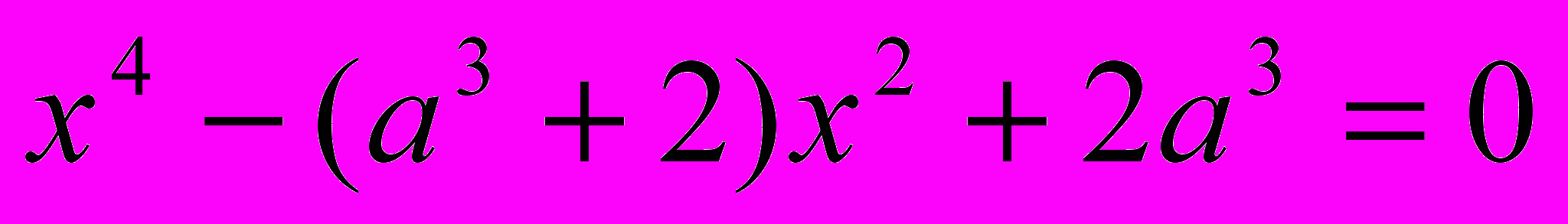
При каком значении параметра m сумма квадратов корней уравнения

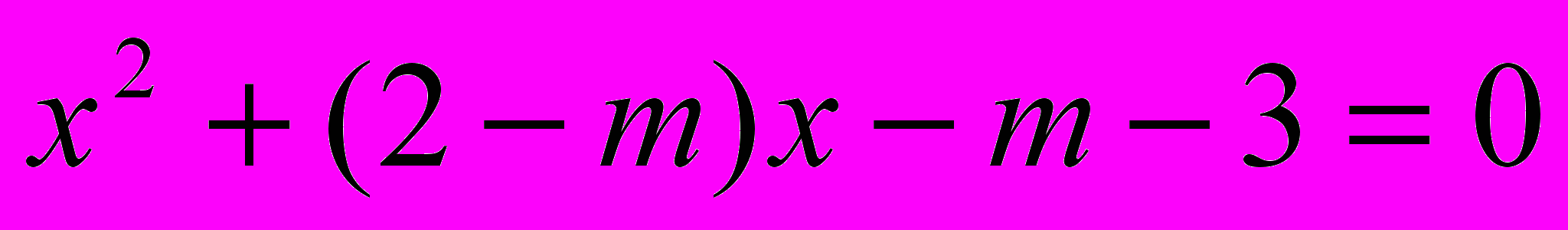наименьшая?

Сумма квадратов корней уравнения

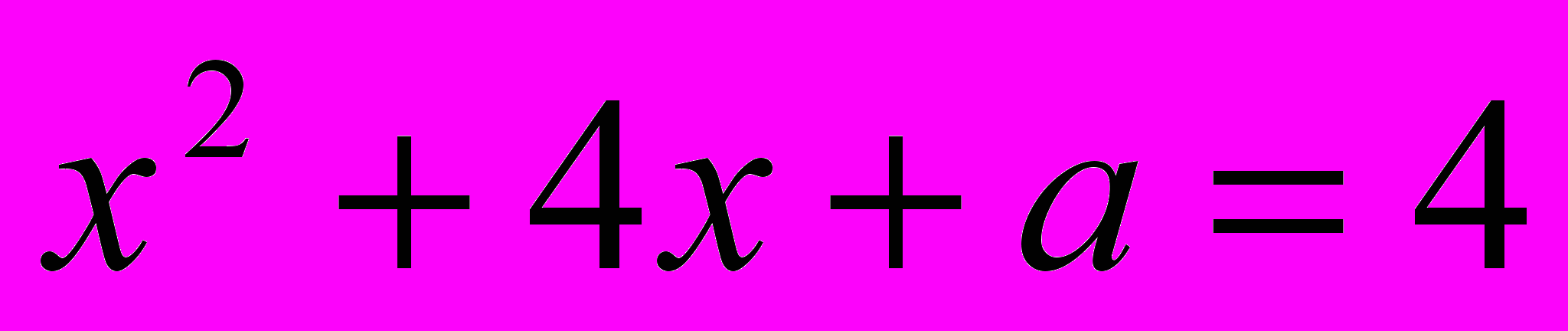равна 12.

Найдите а.

Можно предложить учащимся зачет:

1. Решите уравнение:

.

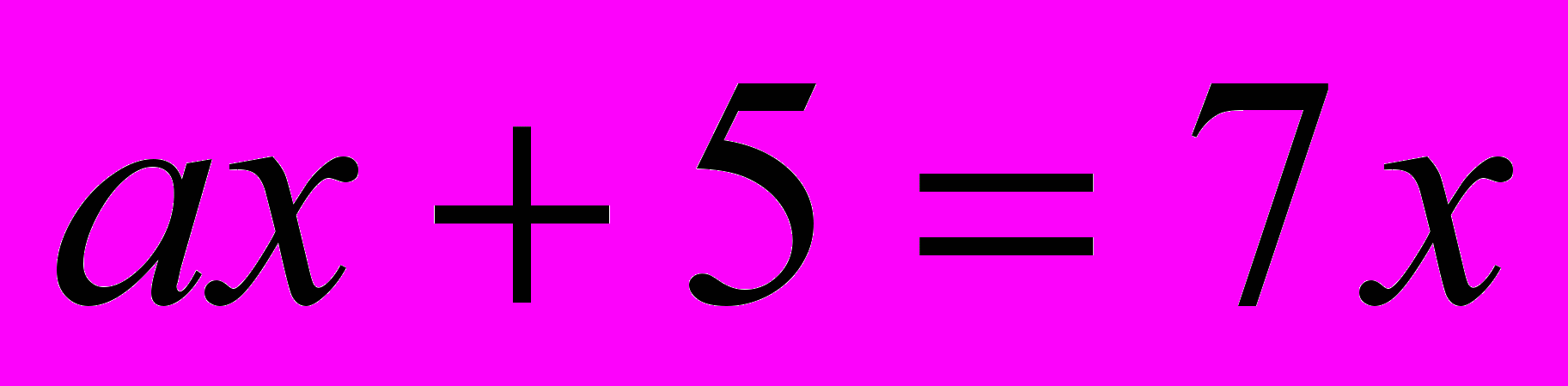2. При каких значениях а уравнение не имеет решения?
   
3. При каком значении а уравнение имеет единственный корень?
   
4. При каких значения а уравнение 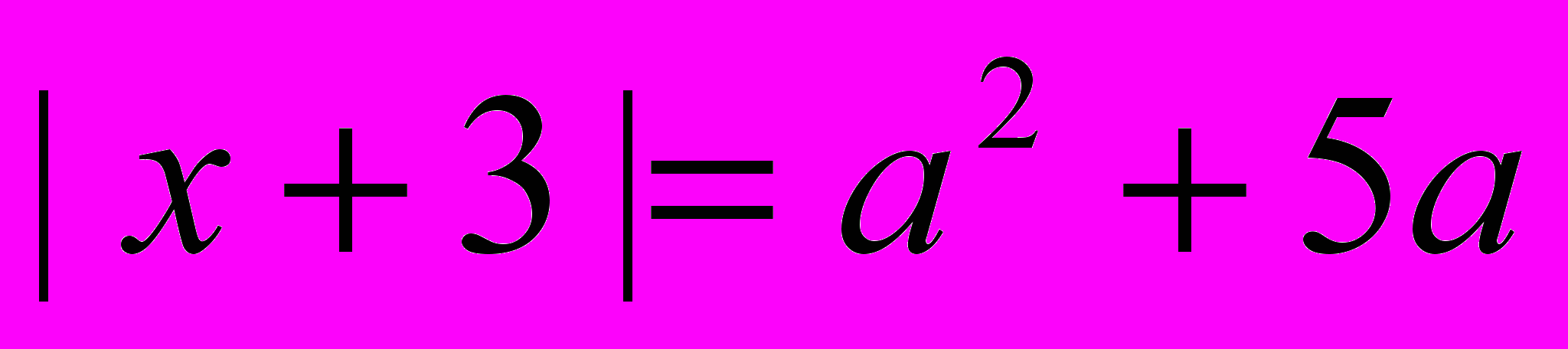имеет два решения?
   
5. Решите графически уравнение:
   

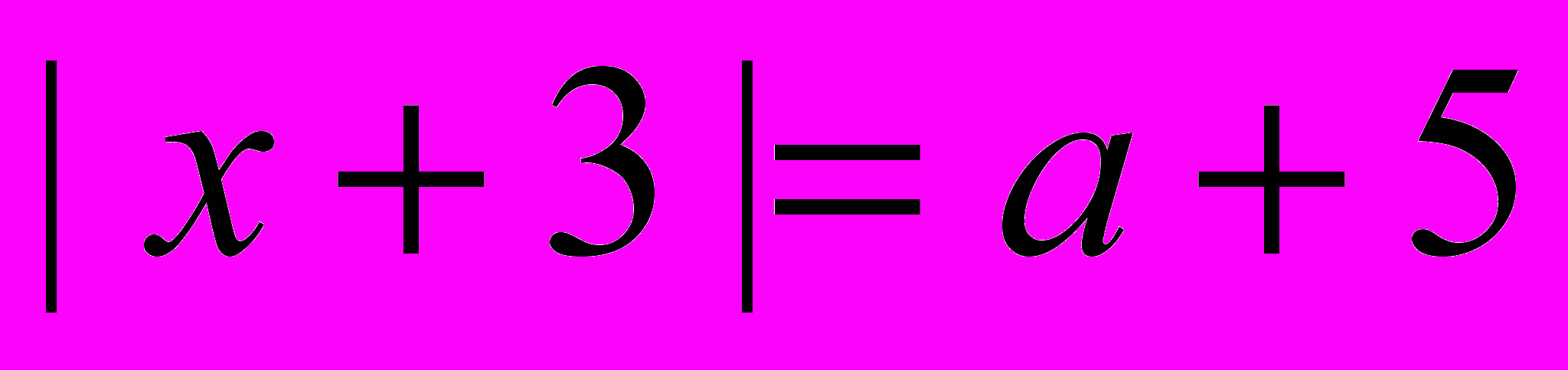
Можно провести зачёт одного уравнения:

|3x - a|=6 – x

1. Какие х не могут быть решениями уравнения?
   
2. При каких значениях а уравнение имеет один корень?
   
3. При каких значениях а уравнение не имеет корней?
   
4. При каких значениях а уравнение имеет два корня?
   
5. При каких значениях а уравнение имеет положительный корень?
   
6. Предложите разные способы решения уравнения.
   

Задания к теме III.1

Задания для самостоятельной работы:

а) найти линейные неравенства с параметром и подготовить выступление о решениях неравенств;

б) решите неравенства:



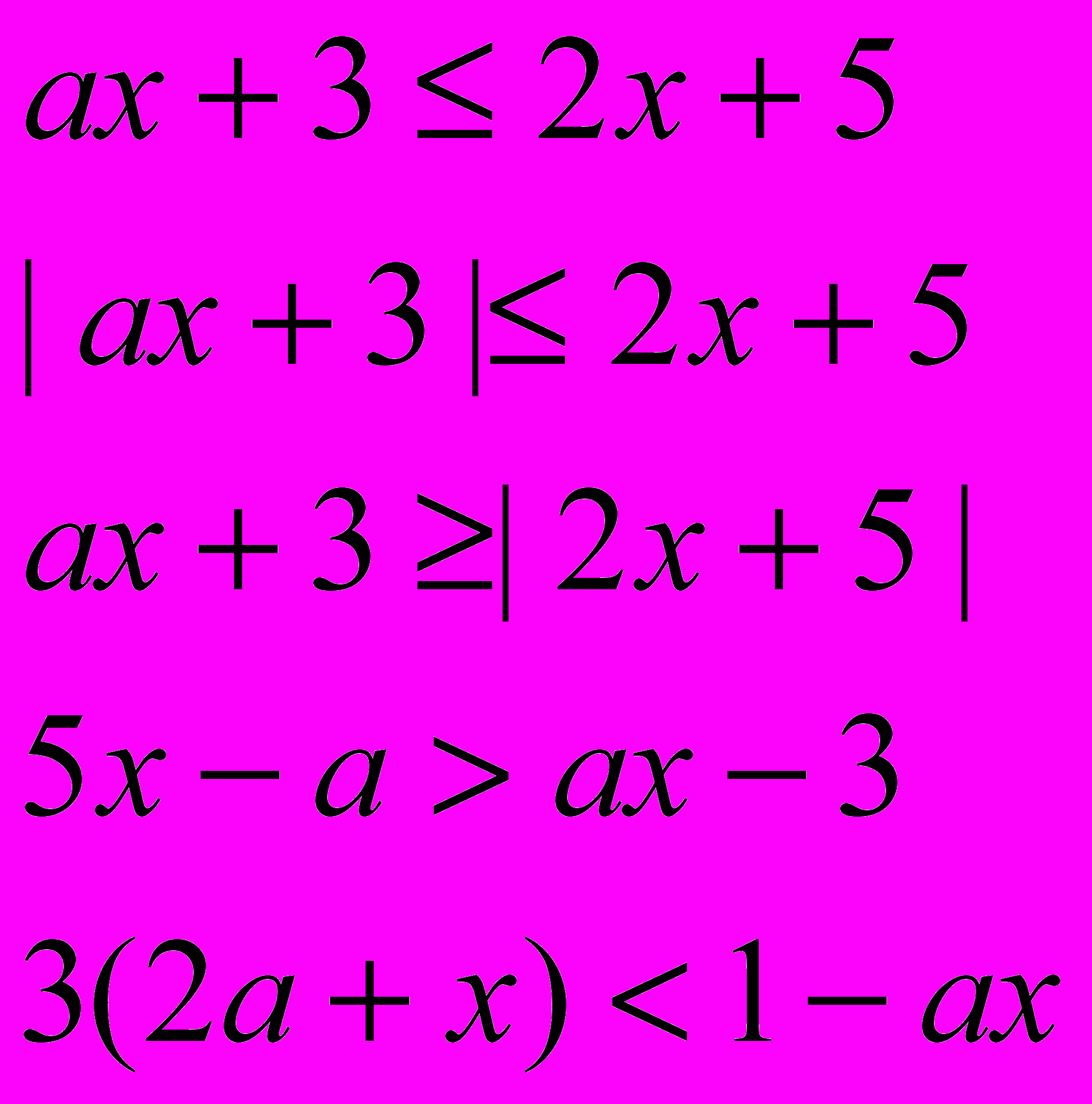
^ Задания к теме III.2

Тема для обсуждения: Какие условия необходимы для того, чтобы неравенство имело решения?

Задания для самостоятельной работы:

а) приведите примеры неравенств с параметром второй степени, не имеющих решения;

б) приведите примеры неравенств с параметром, имеющих одно решение;

в) найдите или составьте сами неравенства и подготовьте сообщение о решении неравенств с параметром;

г) решите неравенства:



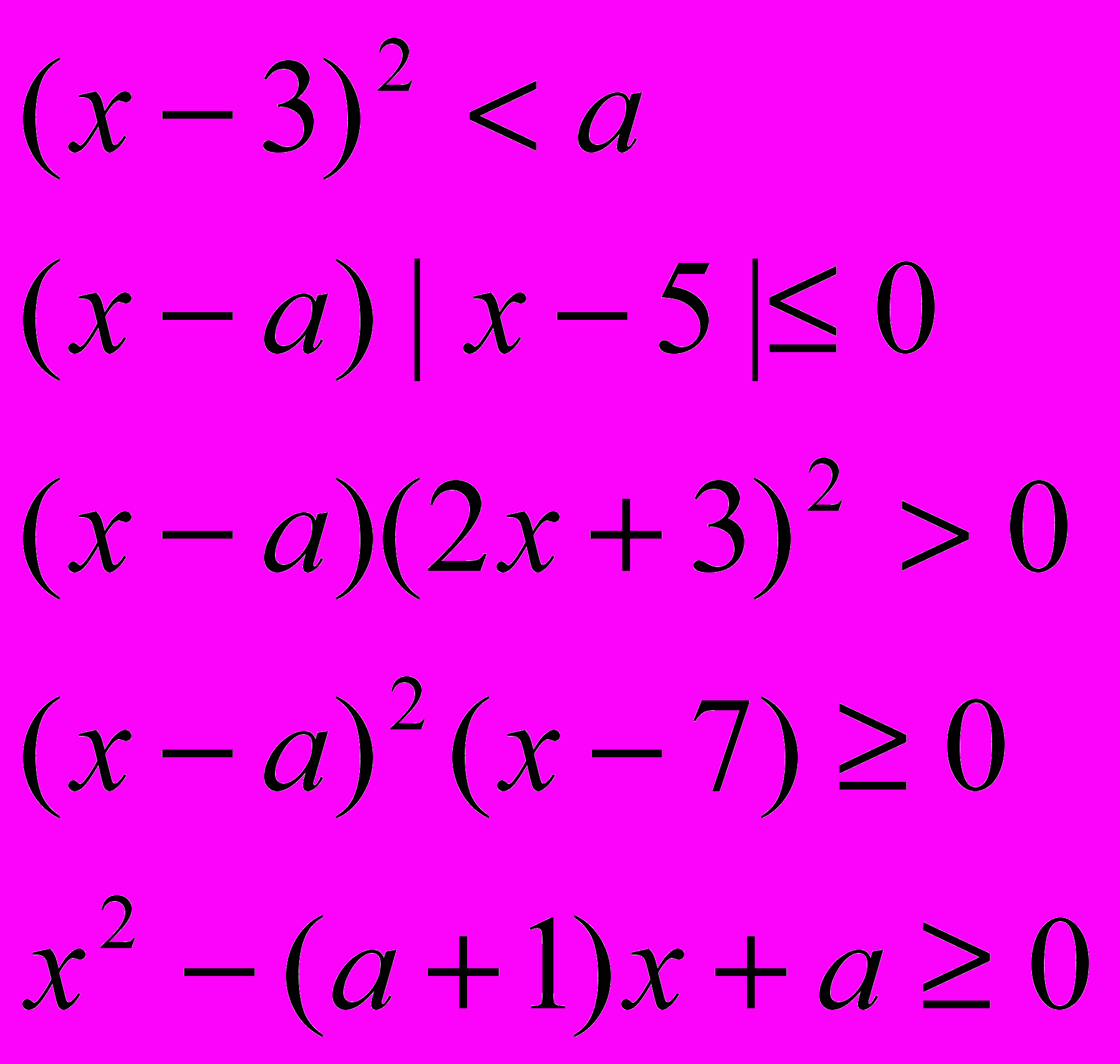
При каких а неравенство



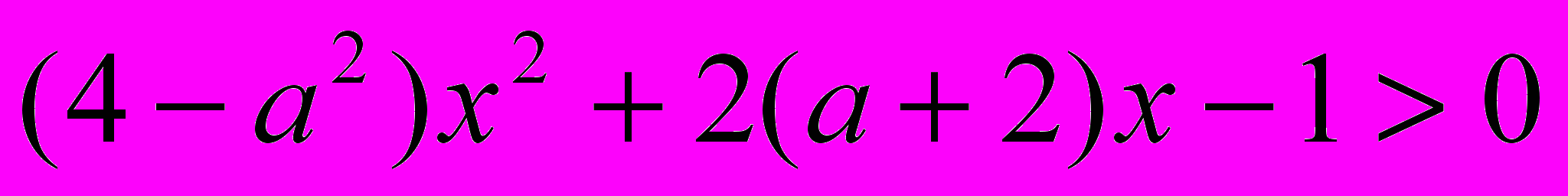
не имеет решений?


При каких а неравенство

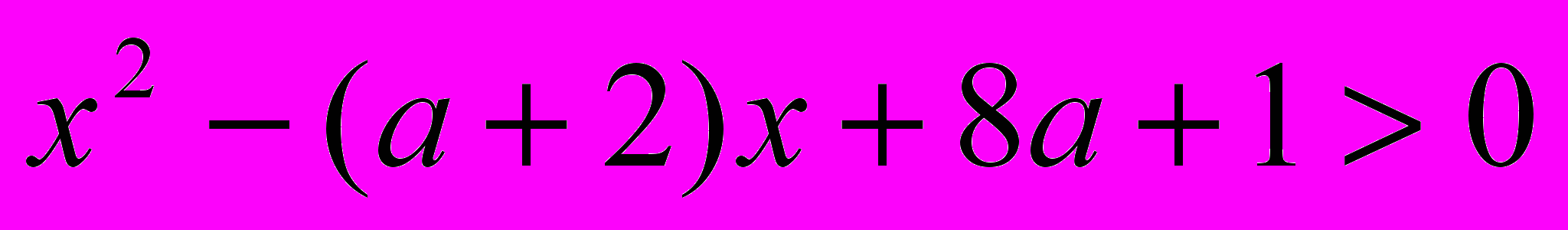верно при любых х?

^ Задания к теме III.3

Тема для обсуждения: Отчего зависит количество решений неравенства? Как найти целые решения неравенства?

Задания для самостоятельной работы:

а) подготовьте выступление на тему: «Решение одного неравенства несколькими способами»;

б) решите неравенства:



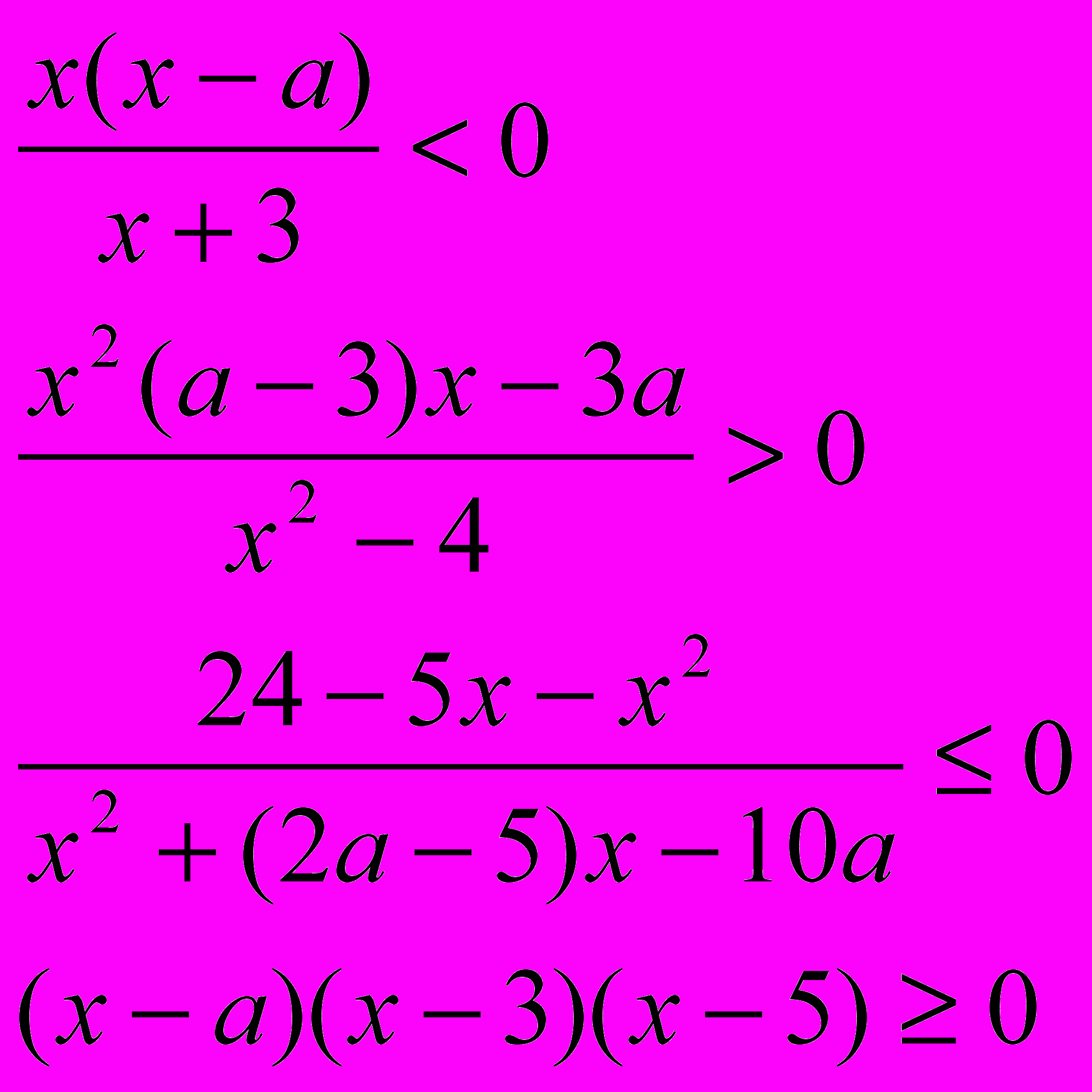
Зачёт по теме.

Решите неравенства:



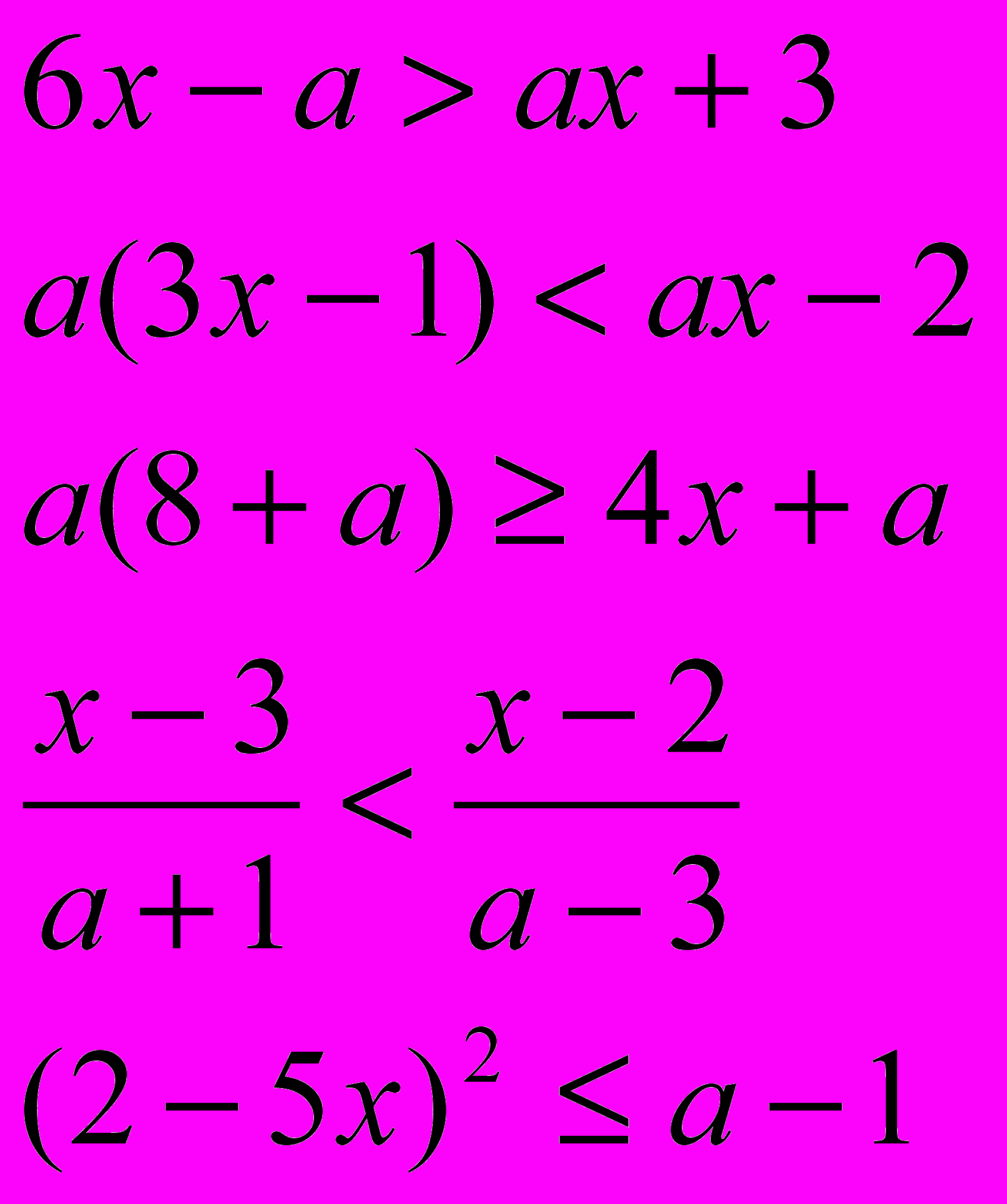
^ Задания к теме IV.1

Тема для дискуссии: «Графический способ решения. За или против?».

Задания для самостоятельной работы:

а) найти системы, подготовить сообщения о решении систем.


б) при каких значениях а прямые

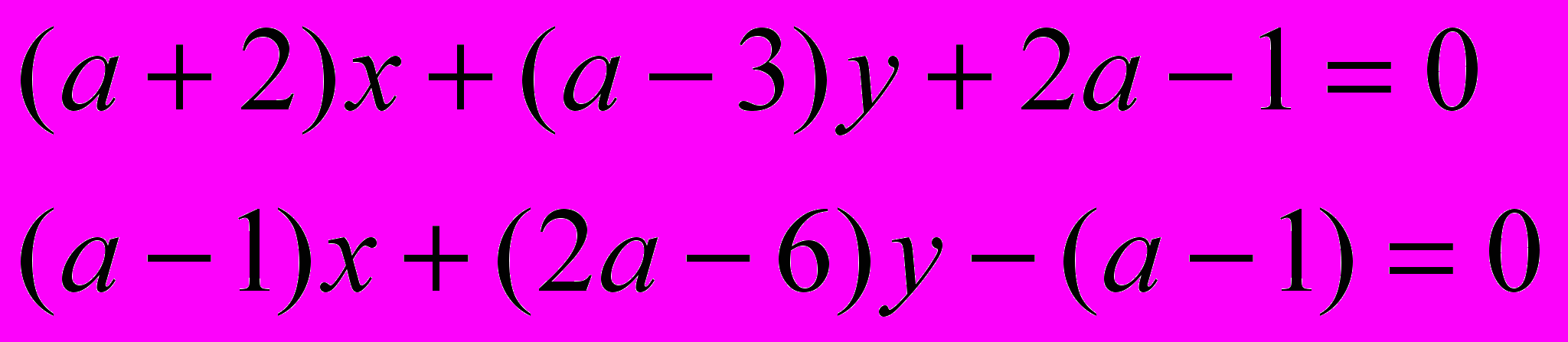и

1. пересекаются;
   
2. параллельны;
   
3. совпадают.
   

При каких m система

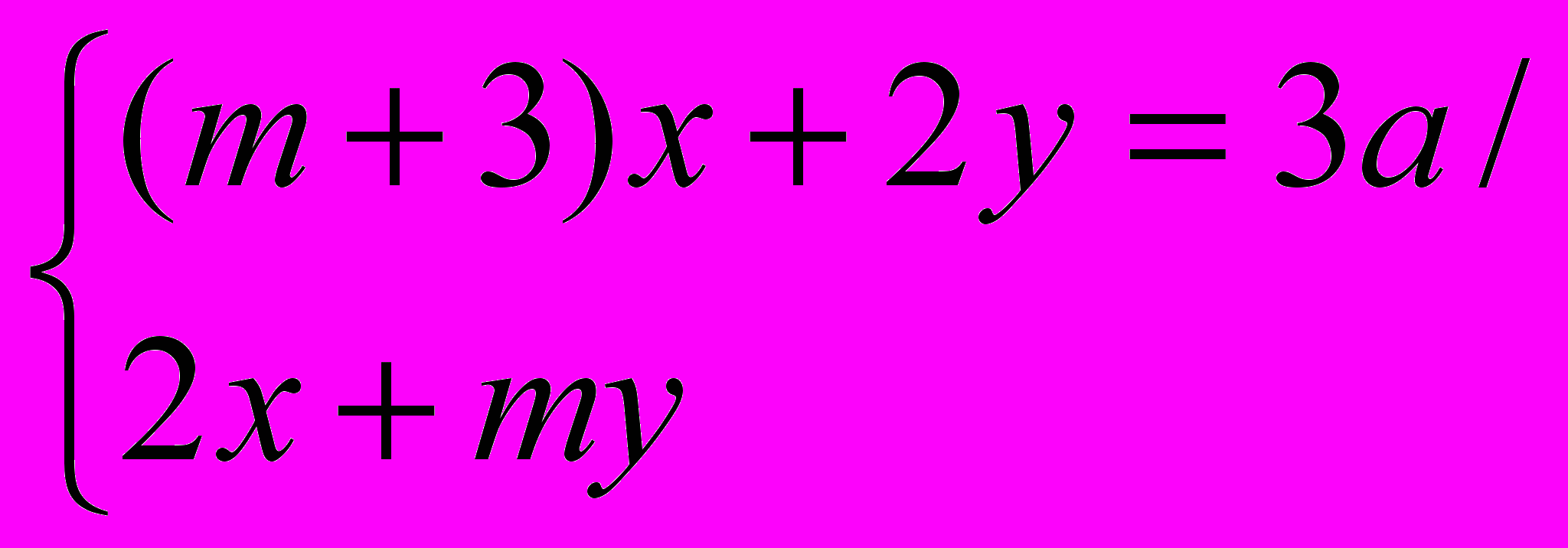имеет единственное решение?

Найти, при каких значениях параметра а решение системы уравнений



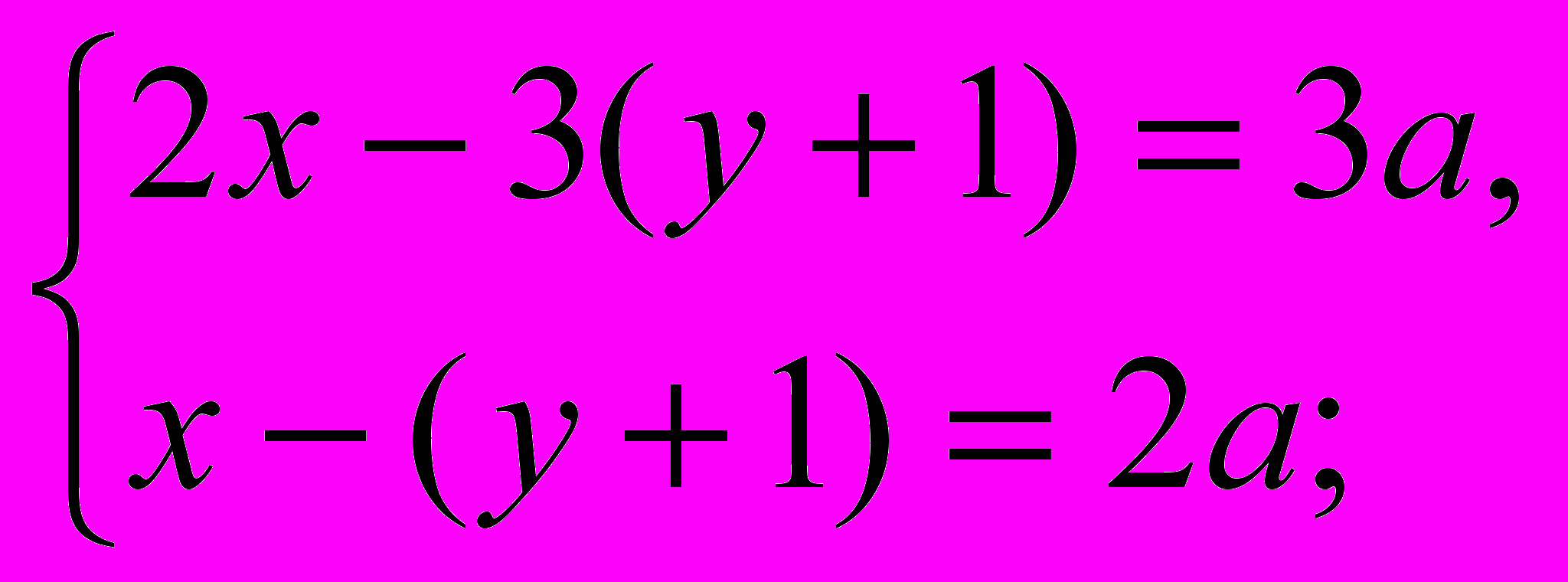
Удовлетворяет соотношению


^ Задания к теме IV.2

Вопросы для обсуждения: Легко ли определить число решений системы? Какое действие алгоритма вызывает у вас затруднение? Можно ли изменить порядок решения? Составьте схему решения. Что из этого вы можете решить сразу?

^ Задания для самостоятельной работы:

а) найти систему и исследовать её;

б) подготовить небольшой доклад в дополнение к лекции учителя;

в) решить системы:

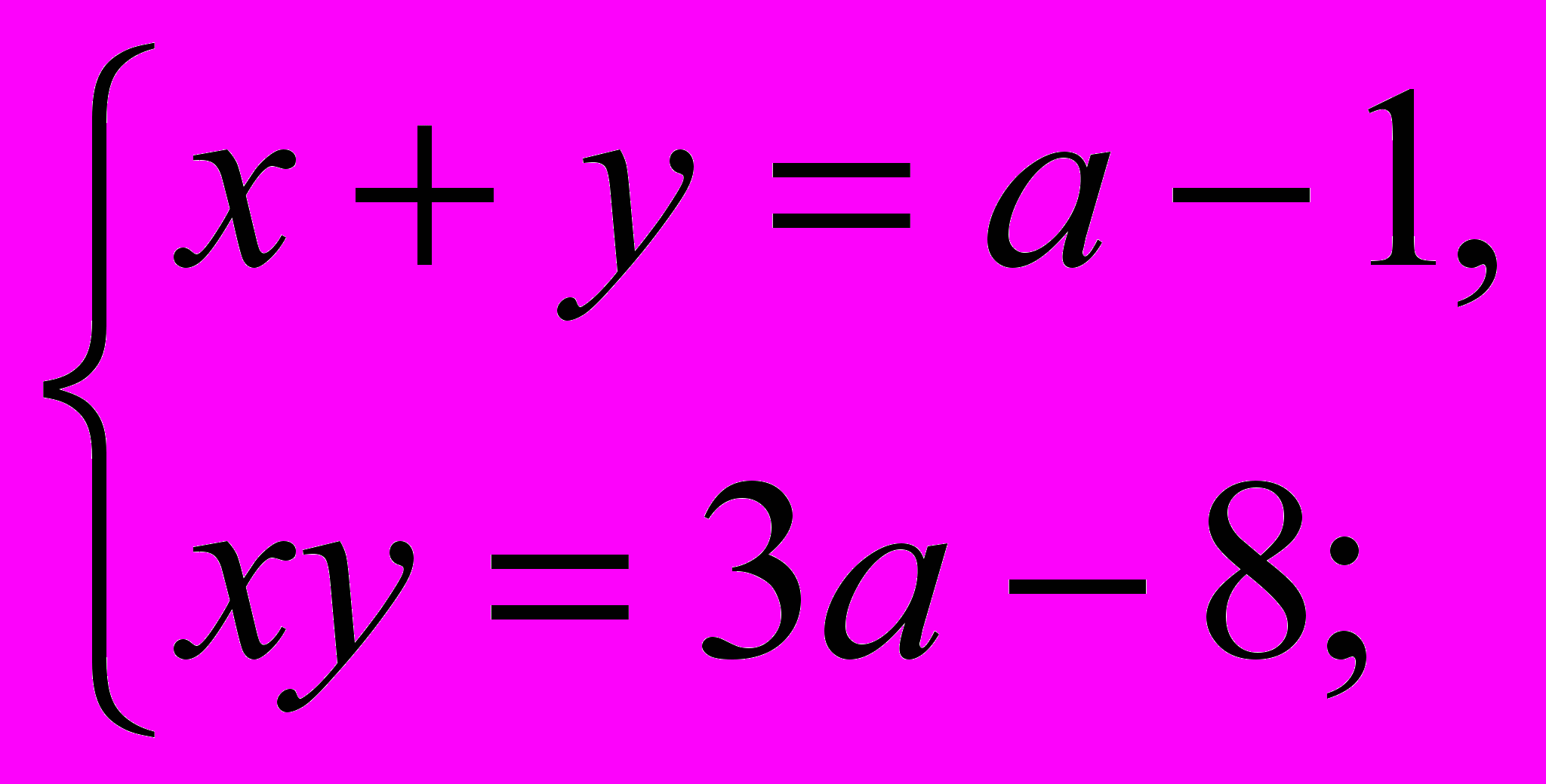при каких а система имеет единственное решение?

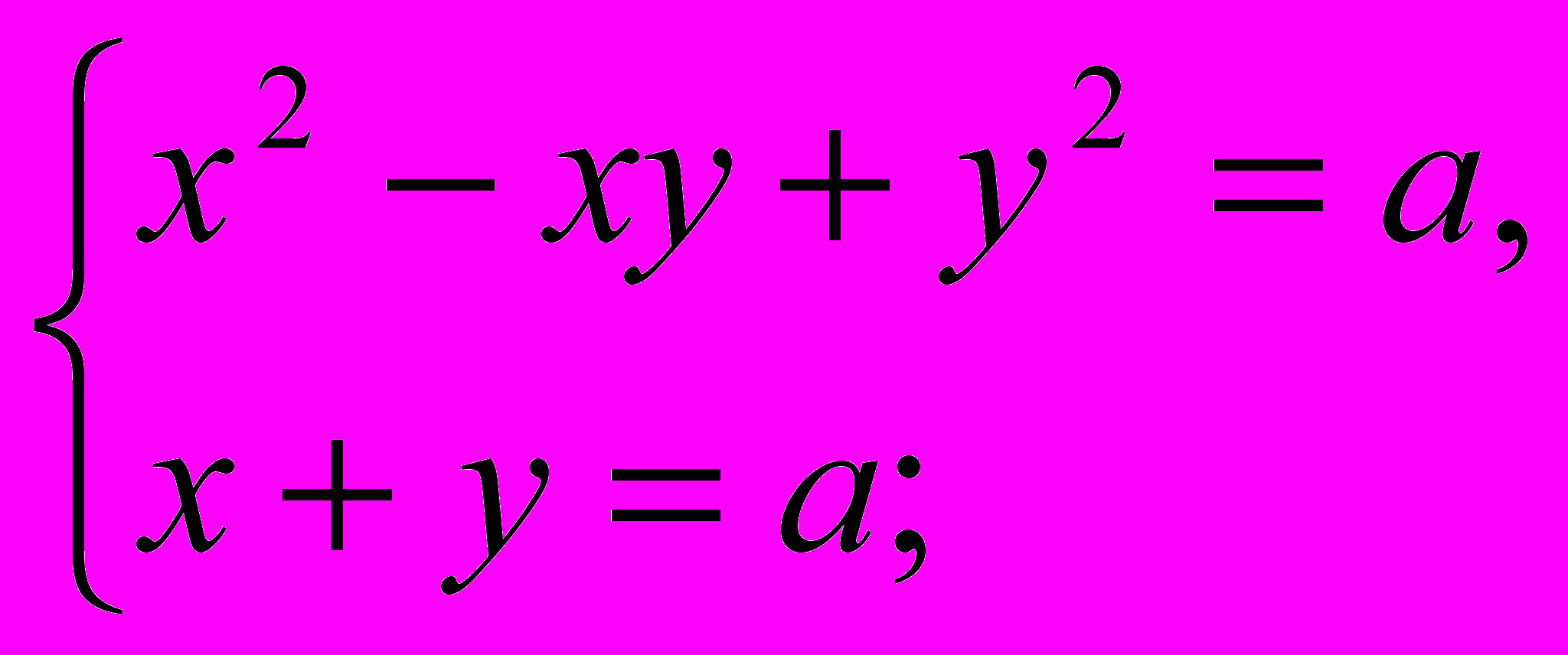сколько решений имеет система в зависимости от а?

г) составить систему, которая не имеет решения;

д) подготовить к заключительному занятию реферат, в котором отражается тема спецкурса.

^ Вопросы, помогающие школьнику освоить рефлексивное оценивание

Что я узнал о себе, изучая курс?

Что изменил бы в курсе?

Какие формы учебных занятий понравились больше всего?


^ V. Заключительное занятие.

Выступления учащихся с рефератами по теме курса.

Литература для учащихся:

1. Энтина С.Б., Юдовин М.Э. Сборник задач. Темы: Уравнения и неравенства. С- Пб., 1995г.
   
2. Шестаков С.А., Юрченко Е.В. Уравнение с параметром. М., 1993г.
   
3. Квантор: Абсолютная величина чисел. №8, 1991.
   
4. Фарков А.В. Математические олимпиады. М., 2004.
   
5. Сканави М.И. Сборник задач по математике.
   

Литература для учителя.

1. Абрамович М.И.: Алгебра. М., 1976.
   
2. Бартенев Ф.А. Нестандартные задачи по алгебре. М., 1976.
   
3. Горбачев В.И. Общие методы решения уравнений и неравенств с параметрами. – 1999. №6. С. 60-68.
   
4. Горбачёв В.И. Общие методы решения уравнений и неравенств с параметрами не выше второй степени. – 2000. №2. С. 61-68.
   
5. Дегтяренко В.А. Три решения одной задачи с параметром. – 2001. №5. С. 62-64.
   
6. Джиоев Н.Д. Нахождение графическим способом числа решений уравнений с параметром. – 1996. №2. С. 54-57.
   
7. Евсеева А.И. Уравнение с параметрами. – 2003. №7. С. 10-17.
   
8. Епифанова Т.Н. Графические методы решения задач с параметрами. – 2003. №7. С. 17-20.
   
9. Зубов А.Б. Использование симметрии при анализе систем с параметрами. – 2002. №5. С. 56-63.
   
10. Кожухов С.К. Об одном классе параметрических задач. – 1996. №3.С. 45-49.
    
11. Кожухов С.К. Различные способы решения задач с параметром. – 1998. №6. С. 9-12.
    
12. Кожухова С.А., Кожухов С.К. Свойства функций в задачах с параметрами. – 2003. №7. С. 14-17.
    
13. Кормихин А.А. Об уравнениях с параметром. – 1994. №1. С. 33-35.
    
14. Кочарова К.С. Об уравнениях с параметром и модулем (графический способ решения). – 1995. №2. С. 2-4.
    
15. Мещерякова Г.П. Задачи с параметром, сводящиеся к квадратным уравнениям. – 2001. №5. С. 60-62.
    
16. Мещерякова Г.П. Функционально-графический метод решения задач с параметрами. – 1999. №6. С. 69-71.
    
17. Ратников Н.П. От уравнения с параметром – к графику, задающему параметр. – 1990. №3. С. 80; 3-4 обл.
    
18. Хэкало С.П. Необходимые и достаточные условия в задачах с параметрами. – 2003. №7.С. 20-23.
    
19. Шабулин М.И. Уравнения, системы уравнений с параметрами. – 2003. №3. С. 22-28.