Преобразование Хевисайда. Преобразование Лапласа. Устойчивость системы. Условие усточивости. Критерий устойчивости Гурвица и Льенара-Шипара

Вид материала

Лекция

Содержание Диагональные миноры

Подобный материал:

• 5 семестр. Контрольные вопросы для подготовки к экзамену: Игры с природой. Принятие, 40.09kb.
• Спектры сигналов, 22.85kb.
• Распознавание и преобразование образов указатель документов описания первоисточников., 52.79kb.
• Курс «Теория массового обслуживания» Читается для студентов специальности «Прикладная, 12.97kb.
• Игра как математическая модель конфликтной ситуации. Антагонистические игры, 56.39kb.
• Kirgizistan-tüRKİye manas üNİversitesi ders biLGİ formu, 113.45kb.
• Программа курса «Математическая логика и теория алгоритмов», 37.76kb.
• 33. Денежная реформа, результаты ее проведения Денежная реформа это преобразование, 40.27kb.
• Я установка на преобразование системы высшего профессионального образования требует, 45.48kb.
• Материалы к экзамену, 51.46kb.

Лекция №3

Преобразование Хевисайда. Преобразование Лапласа. Устойчивость системы. Условие усточивости. Критерий устойчивости Гурвица и Льенара-Шипара. Общая постановка задачи устойчивости.


Как уже говорилось, линейные системы описываются с помощью дифференциальных уравнений. Ввиду их относительной сложности сведение их к уравнениям алгебраическим сильно упростит задачу их решения. Методика такого сведения была впервые предложена Хевисайдом . Суть её в том, чтобы заменять взятие производной умноженим на оператор p. Таким образом уравнение

а_n*dⁿx/dtⁿ+....a₁dx/dt+a_ox=b_md^mu/dt^m+b₁du/dt+b_ou (3.1)

примет вид

а_n*pⁿx+....a₁px+a_ox=b_mp^m*u+b₁*p*u+b_ou (3.2)

Метод широко применяется в электротехнике.

Его недостаток - то, что не учитываются начальные условия- значение x , u и их производных при t=0.


Этого недостатка лишено более строгое математическое преобразование - преобразование Лапласа. Суть этого преобразования заключается в записи вместо х(t) некоего x(s) причём

x(s)= 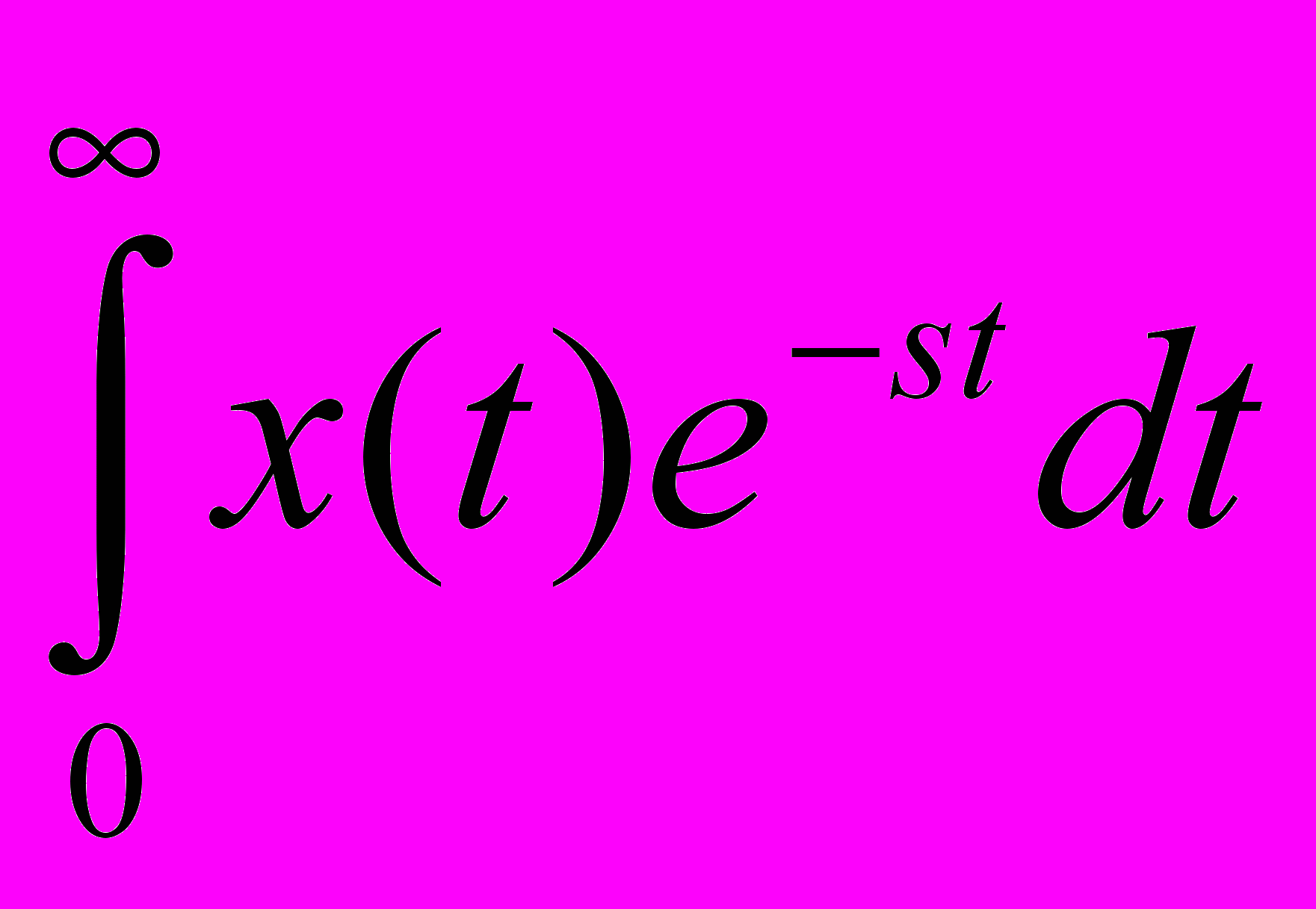(3.3)

На деле преобразование проводится по таблицам.

Производные и интегралы от функций берутся так:

После решения системы производится обратное преобразование. Уравнение в операторной форме имеет вид

а_n*sⁿx+....a₁sx+a_ox=b_ms^m*u+b₁*s*u+b_ou или (а_n*sⁿ+....a₁s+a_o)x=(b_ms^m*u+b₁*s*u+b_o)u или

A(s)*x(s)=B(s)*u(s) (3.4) где A(s), B(s) - полиномы из степеней s.

В такой форме записи существует такое понятие, как передаточная функция W(s).

W(s)=x(s)/u(s)=B(s)/A(s).

Очень часто W(s) можно разложить на несколько множителей, среди которых типовые множители ( звенья ) такие:

W_i(s)=const -усиливающее звено.

W_i(s)=1/(Ts+1)- апериодическое звено.

W_i(s)=1/(Ts²+2Ts+1)- колебательное звено.

W_i(s)=1/s- интегрирующее звено.

W_i(s)=Ts- дифференцирующее звено.

W_i(s)=Ts+1- дифференцирующее звено 1-го порядка.

W_i(s)=Ts²+2Ts+1- - дифференцирующее звено 2-го порядка.


Как уже упоминалось, решение дифференциального уравнения делится на общее однородное и частное неоднородное.

x(t)=x_оо(t)+x_чн(t) . (3.4)

Если система при устремление t к бесконечности решение будет приближаться к частному неоднородному, что система устойчива. Если разница при устремлении t к бесконечности

x_оо(t) не будет стремится к 0, а будет стремится к бесконечности, то система неустойчива. Если не будет стремления ни к 0 не к бесконечности, то перед нами пограничный случай.

Ясно, что неустойчивая система ведёт к непредсказуемым результатам, выходящим за рамки возможностей любой реальной системы, что приведёт или к её поломке и/или к неполучению нужного результата. Поэтому задача анализа системы на устойчивость является принципиальной при работе с системами.

Уже отмечалось, что решение дифференциального уранения первого порядка производится методом подстановки x₀₀=e^t . Для уравнения n-го порядка решение будет иметь вид:

x_оо=С₁e^1t+...+ С_ne^nt (3.5)

В общем случае коэффициенты ₁-_n комплексные и равны

_i=_i+i_i . Совершенно очевидно, что решения будет устойчиво только в том случае, если все _i<0 , иначе система будет неустойчива ( Эспонента с положительным показателем стемится к бесконечности).

Не всегда, однако система является линейной и её так просто решить и проверить на устойчивость. В этом случае на помощь приходят теоремы Ляпунова, которые позволяют определить устойчивость только лишь линеаризованной части системы и на этом основании сделать вывод о всей системе.

1-я теорема Ляпунова. Если все корни характерестического уравнения линеаризованной системы находятся в отрицательной действительной части комплексной плоскости (т.е. _i<0), то исходная нелинейная система устойчива.

2-я теорема Ляпунова. Если хотя бы один корень характеристического уравнения линеаризованной системы находятся в положительной действительной части комплексной плоскости (т.е. _i>0), то исходная нелинейная система неустойчива.

Если линейная система получилось нейтральной, то по ней нельзя судить об устойчивости и надо рассматривать нелинейную систему. Такой случай называется критическим.

Также для решения систем используют запись уравнений в отклонениях от положения равновесия. Поясним:

Пусть у нас есть уравнение dy_i/dt=Y_i(y₁,y₂, ...y_n) . Пусть у нас есть точка равновесия при t= 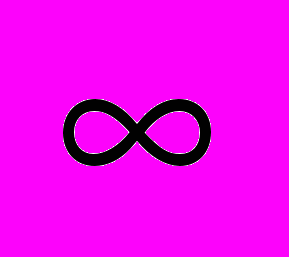со значениями y₁*...y_n^* . Тогда записав y_i=x_i+y_i* помещают точку равновесия в 0, решая уравнения dx_i/dt=X_i(x₁,x₂, ...x_n). Видно, что запись в такой форма не влияет на путь сходимости, а только её точку.


Одним из наиболее распространённым способом определения устойчивости системы является метод Гурвица. Пусть у нас есть уравнение, записанное в оператороной форме.

а₀*sⁿ+....a_n-1s+a_n=0 (3.6)

Тогда , если a₀>0 и матрица формы

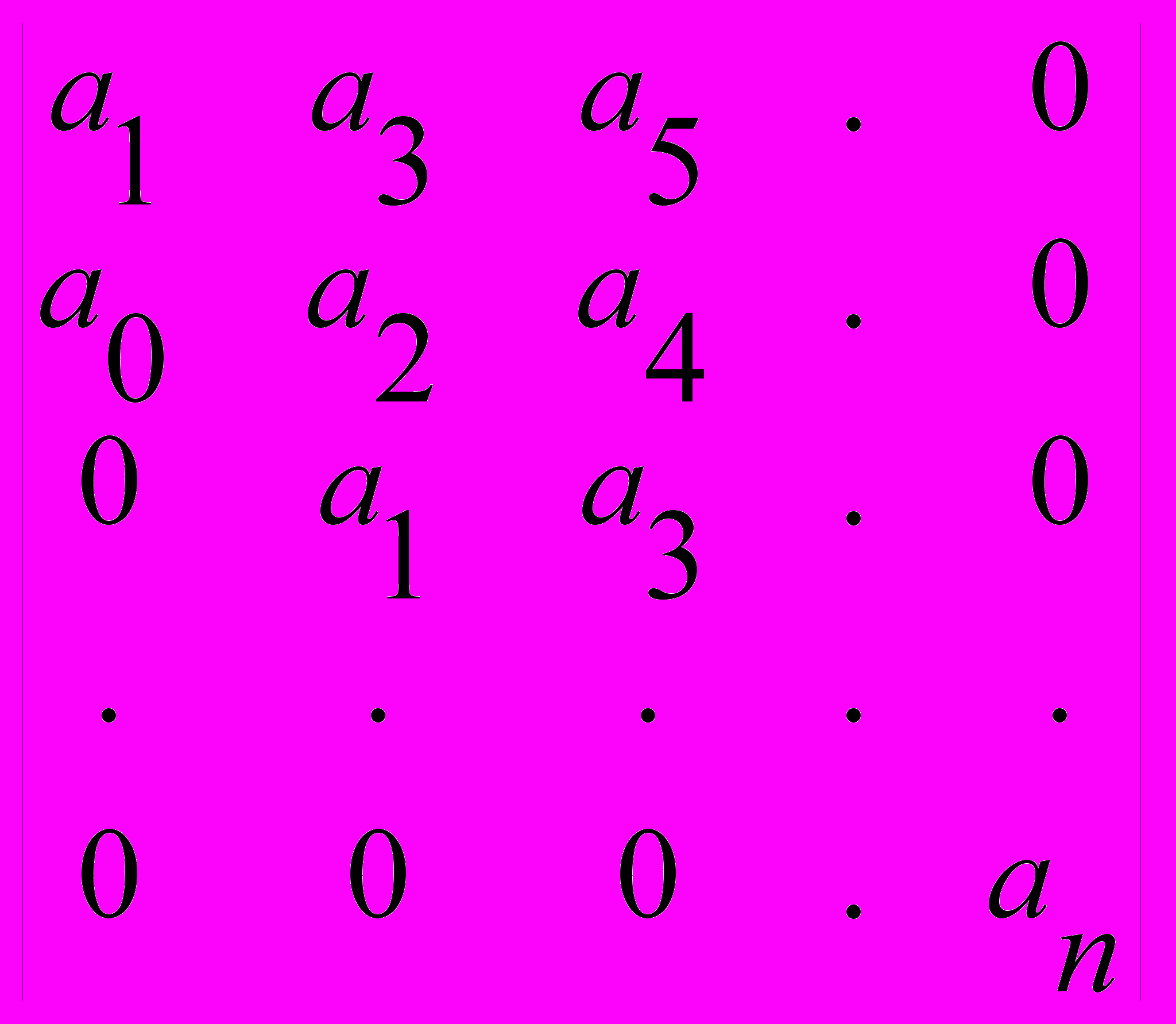-(3.7) - Матрица Гурвица


Если все диагональные миноры этой матрицы положительны, то система усточива.Это критерий устойчивости Гурвица. Напомним:

^ Диагональные миноры- это миноры, включающие в себя n первых диогональных элементов, если размерность минора n*n.

Минор - матрица, полученная путём "взятие" из основной матрицы n любых строк и столбцов. (Т.е. сначало выбираем из матрицы n строк, потом в этих строках n столбцов. Получится матрица размером n*n). Под положительностью минора понимают положительность его определителя.

Определитель - для матрицы 2*2 вида 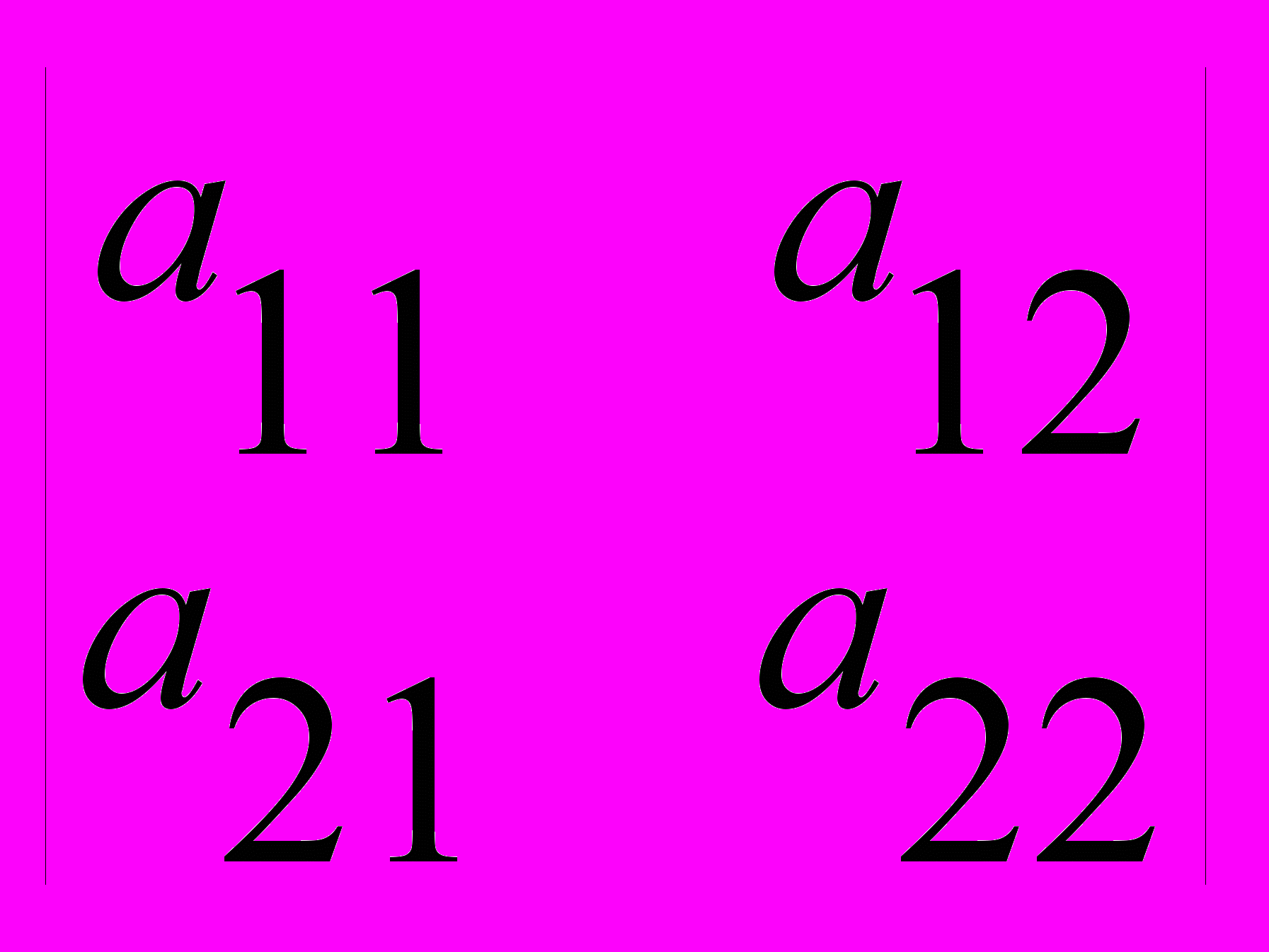=a₁₁*a₂₂-a₂₁*a₁₂ . Для матрицы 3х3 это сумма элементов 3-й стоки , умноженных на минор, не содержащий той же строки и того же столбца, что и этот элемент. Аналогично для матриц более высокого порядка.

Было доказано, что необязательно вычислять все диагональные миноры, а можно вычислить только чётные или нечётные и если они положительны, то система устойчива. Это- критерий устойчивости Льенара-Шипара.