Спектры сигналов
| Вид материала | Документы |
- Курс лекций «Основы радиоэлектроники» Часть Сигнал и его свойства. Линии передачи, 33.21kb.
- Программа вступительных испытаний для поступления в магистратуру по направлению 210400, 26.59kb.
- Программа вступительного испытания в магистратуру в форме экзамена по направлению 210400., 74.7kb.
- Тема пространство и метрология сигналов физическая величина более точно определяется, 595.48kb.
- Физические величины, измеряемые в аэрогидромеханике и теплофизическом эксперименте., 39.57kb.
- Программа курса лекций, 51.42kb.
- Гармонический анализ и спектры некоторых периодических сигналов. Преобразование Фурье, 127.46kb.
- Программа учебной дисциплины «Теория сигналов» Специальности 071500, 013900 (СД. 05), 82.24kb.
- Модуляция сигналов, 64.06kb.
- Н. Г. Чернышевского кафедра радиофизики и нелинейной динамики рабочая программа, 145.34kb.
Спектры сигналов
Спектр сигнала - в радиотехнике это результат разложения сигнала на более простые в базисе ортогональных функций. В качестве разложения обычно используются преобразование Фурье, разложение по функциям Уолша, вейвлет-преобразование и др.
Базисные функции
В радиотехнике в качестве базисных функций используют синусоидальные функции. Это объясняется рядом причин:
- функции cos(ωt), sin(ωt) являются простыми и определены при всех значениях t, являются ортогональными и составляют полный набор при кратном уменьшении периода;
- гармоническое колебание является единственной функцией времени, сохраняющей свою форму при прохождении колебания через линейную систему с постоянными параметрами, могут только изменяться амплитуда и фаза;
- для гармонических функций имеется математический аппарат комплексного анализа;
- гармоническое колебание легко реализуемо на практике.
Кроме гармонического ряда Фурье применяются и другие виды разложений: по функциям Уолша, Бесселя, Хаара, Лежандра, полиномам Чебышева и др.
В цифровой обработке сигналов для анализа применяются дискретные преобразования: Фурье, Хартли, вейвлетные и др.
Применение
Разложение сигнала в спектр применяется в анализе прохождения сигналов через электрические цепи (спектральный метод). Спектр периодического сигнала является дискретным и представляет набор гармонических колебаний, в сумме составляющий исходный сигнал. Одним из преимуществ разложения сигнала в спектр является следующее: сигнал, проходя по цепи, претерпевает изменения (усиление, задержка, модулирование, детектирование, изменение фазы, ограничение и т. д.). Токи и напряжения в цепи под действием сигнала описываются дифференциальными уравнениями, соответствующими элементам цепи и способу их соединения. Линейные цепи описываются линейными дифференциальными уравнениями, причём для линейных цепей верен принцип суперпозиции: действие на систему сложного сигнала, который состоит из суммы простых сигналов, равно сумме действий от каждого составляющего сигнала в отдельности. Это позволяет при известной реакции системы на какой-либо простой сигнал, например, на синусоидальное колебание с определённой частотой, определить реакцию системы на любой сложный сигнал, разложив его в ряд по синусоидальным колебаниям.
На практике спектр измеряют при помощи специальных приборов: анализаторов спектра.
Математическое представление
Если под сигналом s(t) понимать электрическое напряжение на резисторе сопротивлением 1 Ом, то спектр этого сигнала S(ω) можно записать следующим образом:
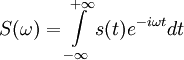, где ω - угловая частота равная 2πf.Спектр сигнала является величиной комплексной и представляется в виде: S(ω) = A(ω)e − iφ(ω), где A(ω) - амплитудно-частотная характеристика сигнала, φ(ω) - фаза-частотная характеристика сигнала.
Энергия сигнала, выделяемая на резисторе, будет равна
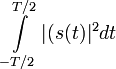, средняя мощность - 
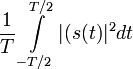.Литература
- Гоноровский И. С. Радиотехнические цепи и сигналы: Учебник для вузов, 1977.
- Баскаков С.И. Радиотехнические цепи и сигналы, 1987.
- Рабинер, Голд. Теория и практика цифровой обработки сигналов.
Вопрос:
В цифровой обработке сигналов для анализа не применяются дискретные преобразования:
1. Фурье
2. Хартли
3. Чебищева*
4. Вейвлетные