Домаевская Ольга Алексеевна, учитель математики му сош №7 г. Конаково г. Конаково 2009 Цель исследования Исследовать решение
| Вид материала | Решение |
- Организационно-педагогические условия функционирования педагогической технологии исследования, 304.79kb.
- «О порядке управления и распоряжения имуществом, находящимся в собственности муниципального, 320.45kb.
- Доклад о результатах оценки качества предоставления государственных услуг (исполнения, 213.18kb.
- Егорова Ольга Юрьевна учитель математики моу сош №6 п. Нежинский Алгебра и начала анализа,, 36.36kb.
- Тема: Чрезвычайные ситуации природного и техногенного характера потенциально угрожающие, 203.37kb.
- Яковлева Виктория Александровна, учитель информатики сош №37 г. Саранска республики, 3289.25kb.
- Публичный доклад, 347.18kb.
- В форме лекции, которую проводит учитель с использованием электронного пособия «Виртуальная, 157.07kb.
- Кашичкина Наталья Евгеньевна, сош №4; > решение, 27.52kb.
- Дундукова Татьяна Алексеевна Учитель математики Романчева Ирина Викторовна Учитель, 11.44kb.
Российская Федерация
Министерство образования
Тверская область
Муниципальное образование «Конаковский район»
Муниципальное учреждение
«Средняя общеобразовательная школа №7 г. Конаково»
__________________________________________________
Диофантовы уравнения
Автор:
Жуков Станислав Дмитриевич,
учащийся 9 «А» класса
МУ СОШ №7 г. Конаково
Научный руководитель:
Домаевская Ольга Алексеевна,
учитель математики
МУ СОШ №7 г. Конаково
г. Конаково - 2009
Цель исследования
- Исследовать решение диофантовых уравнений с одним неизвестным.
- Исследовать решение уравнений второй степени (пифагоровы тройки).
- Изучить один из способов решения диофантовых уравнений высших степеней – способ разложения на множители.
Задачи:
- Познакомиться с биографией Диофанта Александрийского.
- Познакомиться с трудами Диофанта.
- Вспомнить необходимый теоретический материал и систематизировать его.
- На конкретных примерах показать простоту решения диофантовых уравнений методом разложения на множители.
Гипотеза
Предположим, что:
1. Существуют способы нахождения пифагоровых троек
- подбором;
- с помощью формул.
^ 2. Метод разложения на множители применим при решении некоторых диофантовых уравнений высших степеней.
Методы и средства исследования.
- Изучение литературы.
- Проведение эксперимента.
- Наблюдение и анализ увиденного.
План исследования.
- Изучение биографии Диофанта и его трудов.
- Изучение теории, связанной с делимостью чисел.
- П
 овторить методы разложения на множители.
овторить методы разложения на множители.
- Исследование решения уравнений вида
- Исследовать применение метода разложения на множители при решении диофантовых уравнений.
СОДЕРЖАНИЕ
I. Введение ………………………………………………………………………….
II. Диофант и его труды ……………………………………………………………
III. Использование делимости чисел и метода разложения на множители при решении диофантовых уравнений.……………………………….
- Теоритические сведения
- Диофантовы уравнения с одним неизвестным ……………………………
- Уравнения с двумя неизвестными………………………………………….
- Уравнения с тремя неизвестными
IV. Заключение ………………………………………………………………………
VI. Список используемой литературы …………………………………………….
^ I. Введение.
Принимая участие в олимпиадах, которые проводились в 2008 году в г. Конаково и Конаковском районе, я впервые узнал о диофантовых уравнениях. Мне стала интересна эта тема, и я решил расширить свои знания в этой области. За помощью обратился к своему учителю по алгебре, Домаевской Ольге Алексеевне, которая помогла мне подобрать для изучения необходимую литературу.
В процессе изучения специальной литературы на тему «Диофантовы уравнения», а также их решения, мы с Ольгой Алексеевной приняли совместное решение об участии в Фестивале исследовательских и творческих работ учащихся «Портфолио» и в школьной научно-практической конференции учащихся.
^ II. Диофант и его труды.
О подробностях жизни Диофанта Александрийского практически ничего не известно. С одной стороны, Диофант цитирует Гипсикла (II век до нашей эры), с другой стороны, о Диофанте пишет Теон Александрийский (около 350 года нашей эры), следовательно, можно предположить, что его жизнь протекала в границах этого периода.
Возможное уточнение времени жизни Диофанта основано на том, что его «Арифметика» посвящена «достопочтеннейшему Дионисию». Полагают, что этот Дионисий - никто иной, как епископ Дионисий Александрийский, живший в середине III века нашей эры.
Зато место жительства Диофанта хорошо известно – это знаменитая Александрия. Центр научной мысли эллинистического мира.
В Палатинской антологии содержится эпиграмма–задача, из которой можно сделать вывод, что Диофант прожил 84 года:
^ Прах Диофанта гробница покоит; дивись ей - и камень
Мудрым искусством его скажет усопшего век.
Волей богов шестую часть жизни он прожил ребенком.
И половину шестой встретил с пушком на щеках.
^ Только минула седьмая. С подругой он обручился.
С нею, пять лет проведя, сына дождался мудрец;
Только полжизни отцовской возлюбленный сын его прожил.
Отнят он был у отца ранней могилой своей.
^ Дважды два года родитель оплакивал тяжкое горе,
Тут и увидел предел жизни печальной своей.
(Перевод Боброва С.Н.)


Используя современные методы решения уравнений можно сосчитать, сколько лет прожил Диофант.
Пусть Диофант прожил x лет. Составим и решим уравнение:
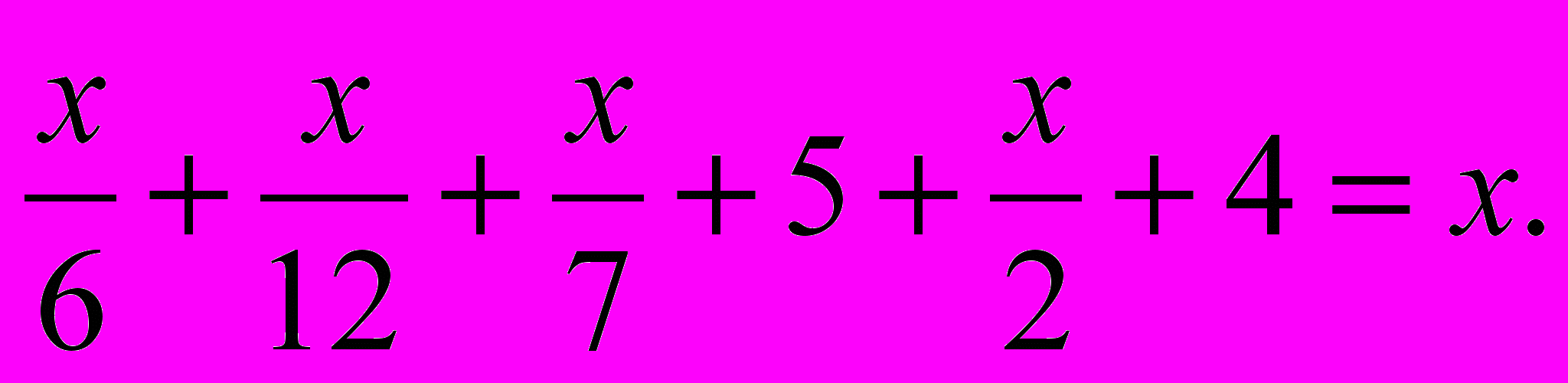
Умножим уравнение на 84, чтобы избавиться от дробей:
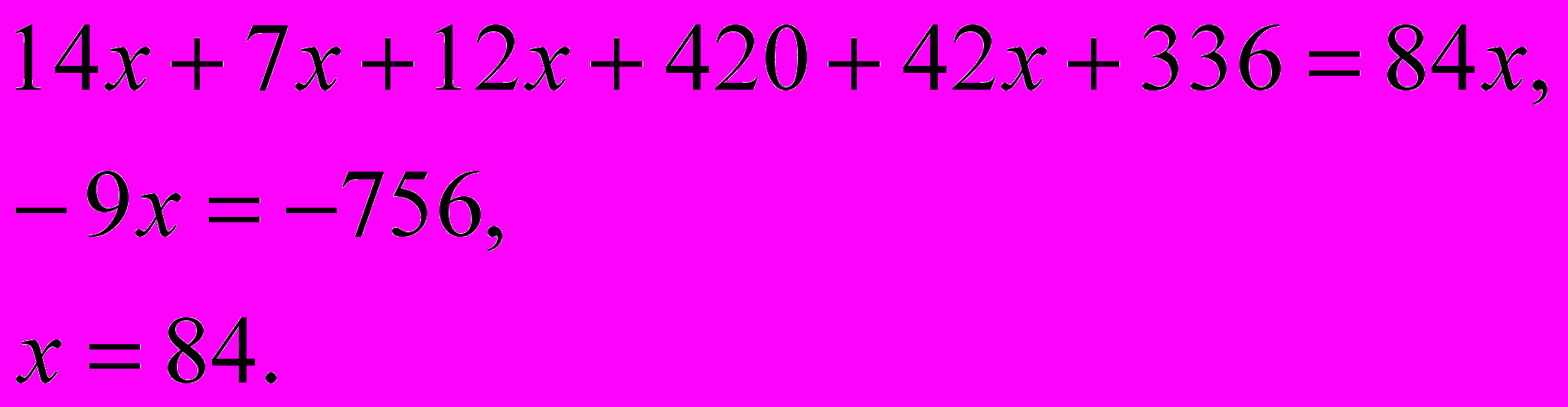
Таким образом, Диофант прожил 84 года.
Основное произведение Диофанта – «Арифметика» в тринадцати книгах. К сожалению, до наших дней сохранились только шесть первых книг из тринадцати.
«Арифметика» Диофанта – это сборник задач (их всего 189), каждая из которых снабжена решением (или несколькими способами решения) и необходимыми пояснениями. Поэтому, с первого взгляда, кажется, что она не является теоретическим произведением. Однако, при внимательном чтении видно, что задачи тщательно подобраны и служат для иллюстрации вполне определенных, строго продуманных методов. Как это было принято в древности, методы не формулируются в общем виде, а повторяются для решения однотипных задач.
Главная проблематика «Арифметики» – это нахождение положительных рациональных решений неопределенных уравнений. Рациональные числа трактуются Диофантом так же, как и натуральные, что не типично для античных математиков.
Сначала Диофант исследует системы уравнений второго порядка от двух неизвестных. Он указывает метод нахождения других решений, если одно уже известно. Затем аналогичные методы он применяет к уравнениям высших степеней.
В X веке «Арифметика» была переведена на арабский язык, после чего математики стран ислама (Абу Камил и другие) продолжили некоторые исследования Диофанта. В Европе интерес к «Арифметике» возрос после того, как Рафаэль Бомбелли обнаружил это сочинение в Ватиканской библиотеке и опубликовал 143 задачи из его в своей «Алгебре» (1572 года). В 1621 году появился классический, подробно прокомментированный латинский перевод «Арифметики», выполненный Баше де Мезириаком. Методы Диофанта оказали огромное влияние на Франсуа Виета и Пьера Ферма, впрочем, в Новое время неопределенные уравнения обычно решаются в целых числах, а не в рациональных, как это делал Диофант.
Известны и другие сочинения Диофанта. Трактат «О многоугольных числах» сохранился не полностью. В сохранившейся части методами геометрической алгебры выводится ряд вспомогательных теорем.
Из сочинений Диофанта «Об измерении поверхностей» и «Об умножении» также сохранились лишь отрывки.
Книга Диофанта «Поризмы» известна только по нескольким теоремам, используемым в Арифметике.
III. Использование делимости чисел и метода разложения на множители при решении диофантовых уравнений.
- Теоритические сведения
^ Некоторые определения и утверждения, необходимые для дальнейшего изложения материала.
Натуральные числа.
Числа 1,2,3,… называются натуральными.
^ Целые числа.
Множество чисел, состоящее из всех натуральных чисел, нуля и чисел, противоположных натуральным, называется множеством целых чисел.
Делитель.
Делителем натурального числа а называют натуральное число, на которое а делится без остатка.
Кратное.
Кратным натуральному числу а называют натуральное число, которое делится на а без остатка.
^ Простые числа
Натуральное положительное число, большее 1 и не имеющее натуральных положительных делителей, отличных от 1 и самого себя, называется постым. Остальные натуральные числа, большие 1, называются составными. Число 1 не является ни простым, ни составным.
^ Основная теорема арифметики.
Всякое натуральное число, большее 1, разлагается в произведение простых чисел (не обязательно различных), причем указанное разложение единственно с точностью до порядка следования множителей.
Формулы сокращённого умножения.
1.

2.

3.
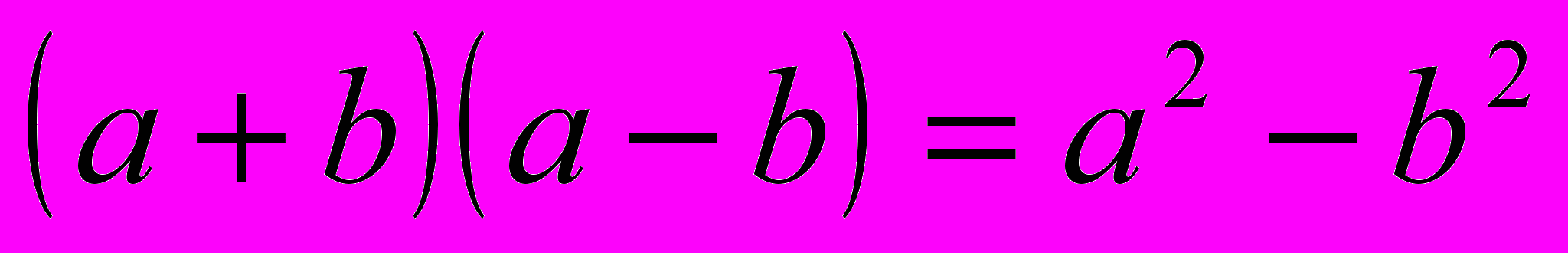
4.
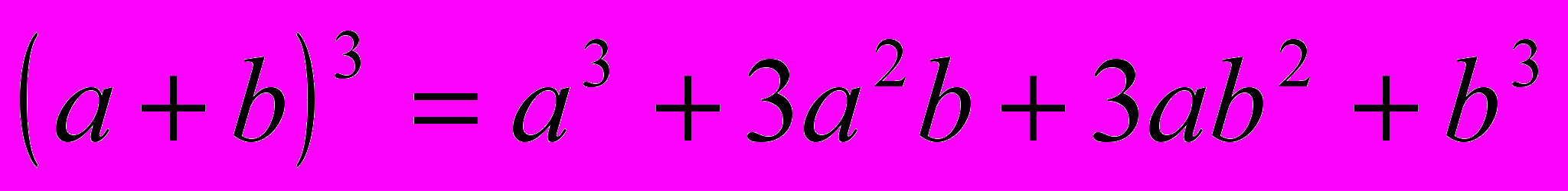
5.

6.

7.

Способы разложения многочленов на множители.
- Вынесение общего множителя за скобки.
- По формулам сокращённого умножения.
- Способ группировки.
При исследовании диофантовых уравнений обычно ставятся следующие вопросы:
- имеет ли уравнение целочисленные решения;
- конечно или бесконечно множество его целочисленных решений;
- решить уравнение на множестве целых чисел, т. е. найти все его целочисленные решения;
- решить уравнение на множестве целых положительных чисел;
- решить уравнение на множестве рациональных чисел.
Мы будем рассматривать первые четыре вопроса.
^ 2. Диофантовы уравнения с одним неизвестным.
Рассмотрим уравнение
 ,
,где
 - целые числа.
- целые числа.Теорема. Если уравнение
 с целыми коэффициентами имеет целый корень, то этот корень является делителем числа
с целыми коэффициентами имеет целый корень, то этот корень является делителем числа 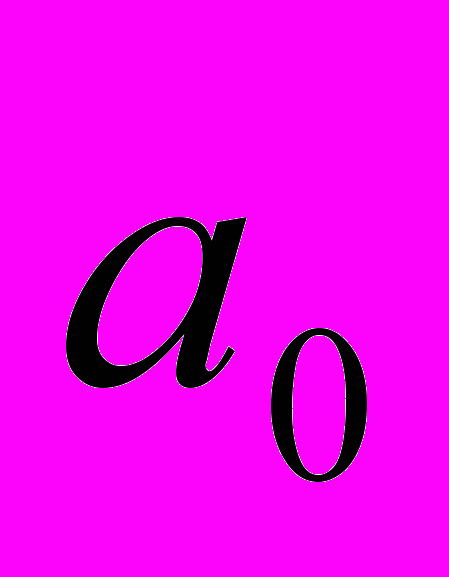 (свободного члена уравнения).
(свободного члена уравнения).Таким образом, при отыскании целых корней уравнения с целыми коэффициентами достаточно испытать лишь делители свободного члена.
Задача 1. Решить в целых числах уравнение
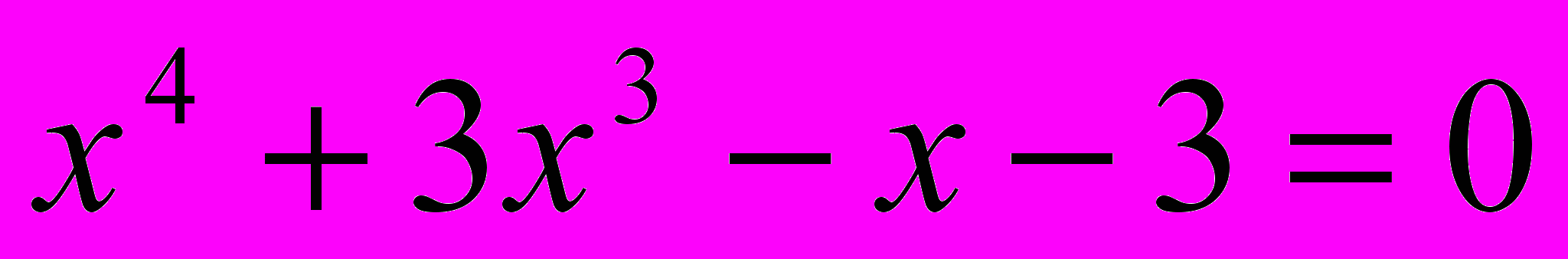 .
.Решение. Свободный член уравнения имеет следующие делители
 .
.Среди этих чисел и будем искать целые корни данного уравнения. Подстановкой убеждаемся, что корнями являются числа 1 и – 3.
Ответ:
 .
.Задача 2. Решить в целых числах уравнение
2x4 + 7x3 - 12x2 - 38x + 21 = 0.
Решение. Свободный член уравнения имеет следующие делители
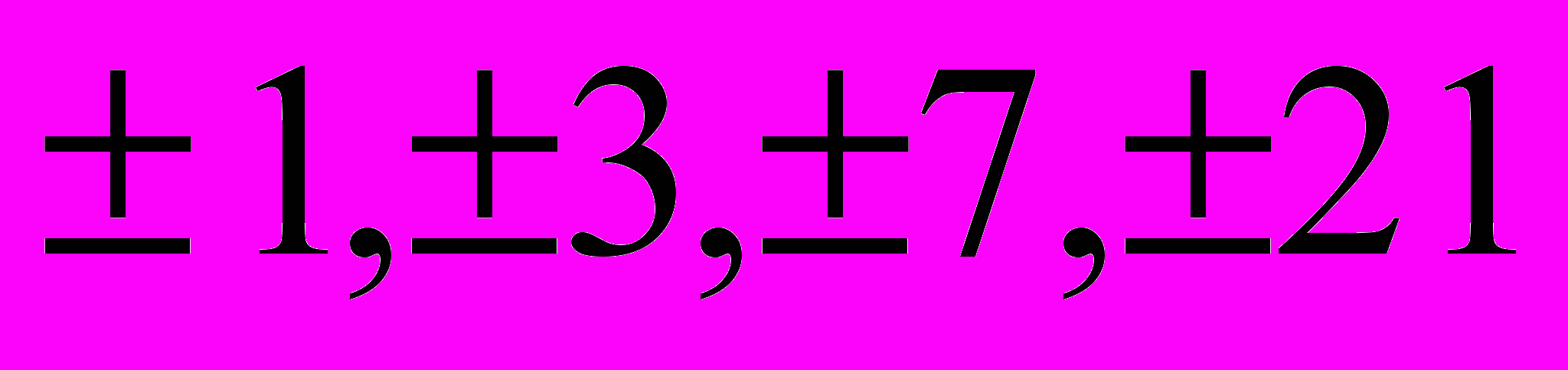 .
.Подстановкой в исходное уравнение убеждаемся, что из этого множества только число -3 является его целым корнем.
Ответ: х=-3.
3. Диофантовы уравнения с двумя неизвестными.
^ НЕОРЕДЕЛЕННЫЕ УРАВНЕНИЯ II-ОЙ СТЕПЕНИ ВИДА x2 + y2 = z2
Вот, например, еще одна частная задача на неопределенные уравнения – теперь уже второй степени, возникшая примерно за две тысячи лет до Диофанта в Древнем Египте.
Если стороны треугольника пропорциональны числам 3, 4 и 5, то этот треугольник – прямоугольный. Этот факт использовали для построения на местности прямых углов. Поступали довольно просто. На веревке на равном расстоянии друг от друга завязывали узлы (Рис. 1)
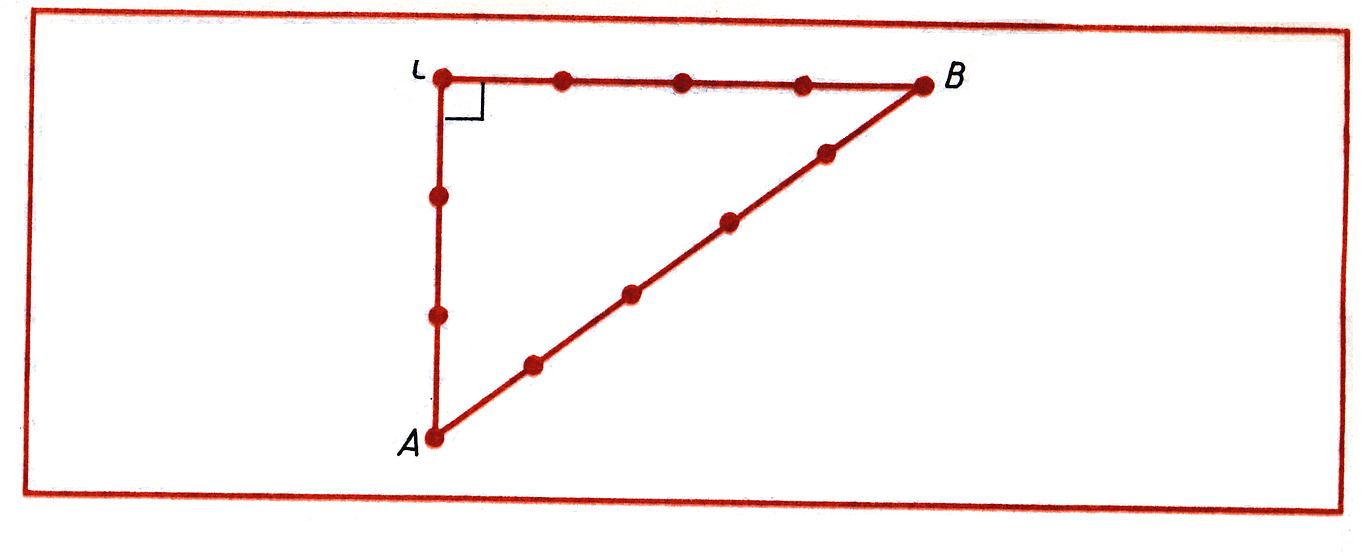
Рис. 1.
В точке С, где надо было построить прямой угол, забивали колышек, веревку натягивали в направлении, нужном строителям, забивали колышек в точке В (СВ = 4) и натягивали веревку так, чтобы АС = 3 и АВ = 5. Треугольник с такими длинами сторон называют египетским. Мы, конечно, понимаем, что безошибочность такого построения следует из теоремы, обратной теореме Пифагора. Действительно,
32 + 42 = 52. Говоря иначе, числа 3, 4, 5 – корни уравнения
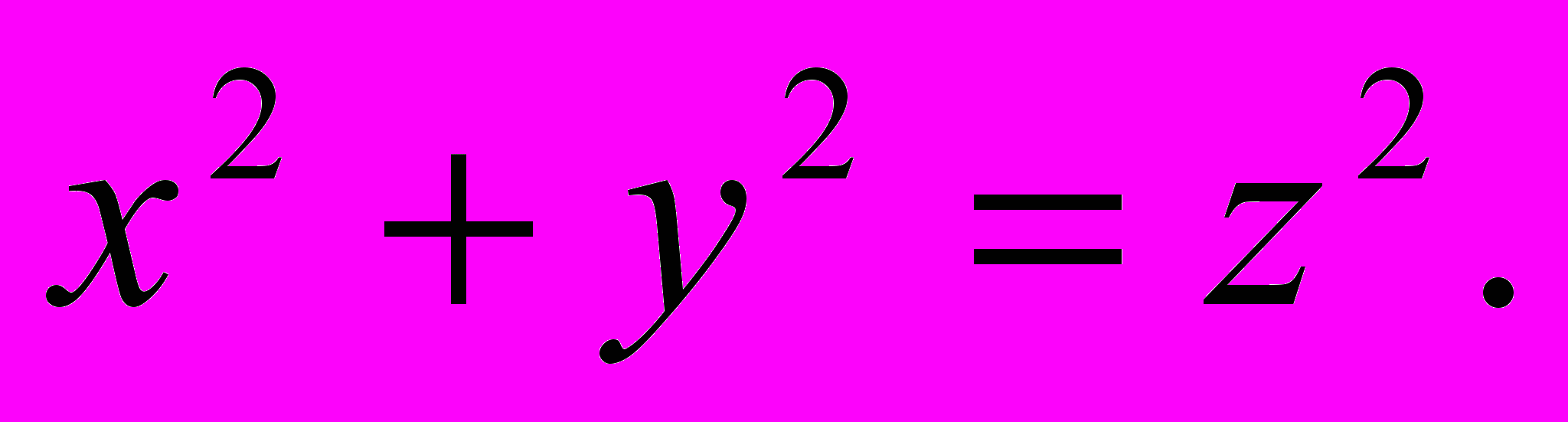
Сразу же возникает вопрос: нет ли у этого уравнения других целочисленных решений?
Один из путей решения уравнения
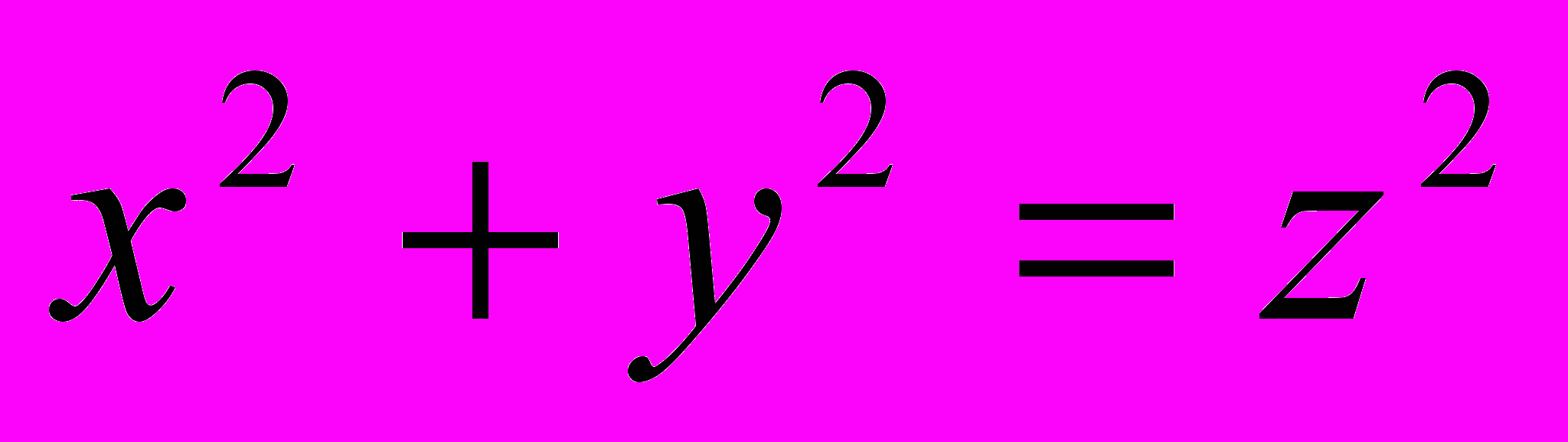 в целых числах оказался довольно простым. Запишем подряд квадраты натуральных чисел, отделив их друг от друга запятой. Под каждой запятой запишем разность между последовательными квадратами:
в целых числах оказался довольно простым. Запишем подряд квадраты натуральных чисел, отделив их друг от друга запятой. Под каждой запятой запишем разность между последовательными квадратами:1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196 … .
3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27 … .
А теперь внимание! Нет ли и в нижней строке квадратных чисел? Есть! Первое из них 9 = 32, над ним 16 = 42 и 25 = 52, знакомая нам тройка 3, 4, 5.
Следующее квадратное число в нижней строке 25, ему соответствует 144 и 169, отсюда находим вторую известную нам тройку 5, 12, 13 и т. д. Отсюда мы имеем право сформулировать такую теорему:
Каждое нечетное число есть разность двух последовательных квадратов.
Составлять такие строки – довольно скучное и трудоемкое занятие. По формулам находить такие тройки чисел и проще и быстрее.
Проверим что если
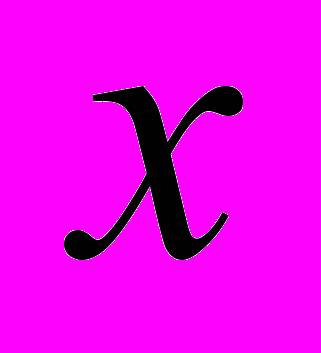 - нечетное число, то
- нечетное число, то 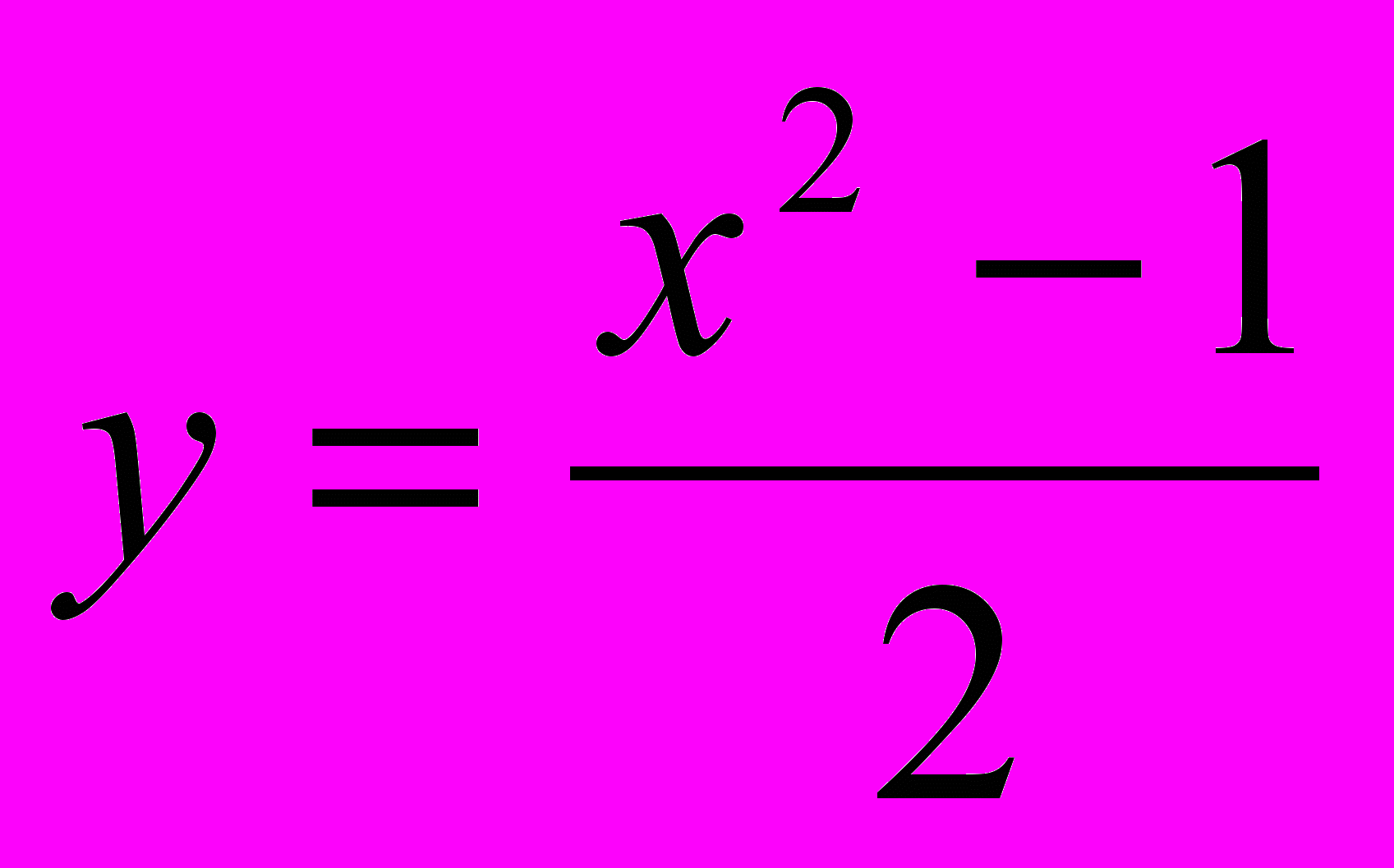 и
и 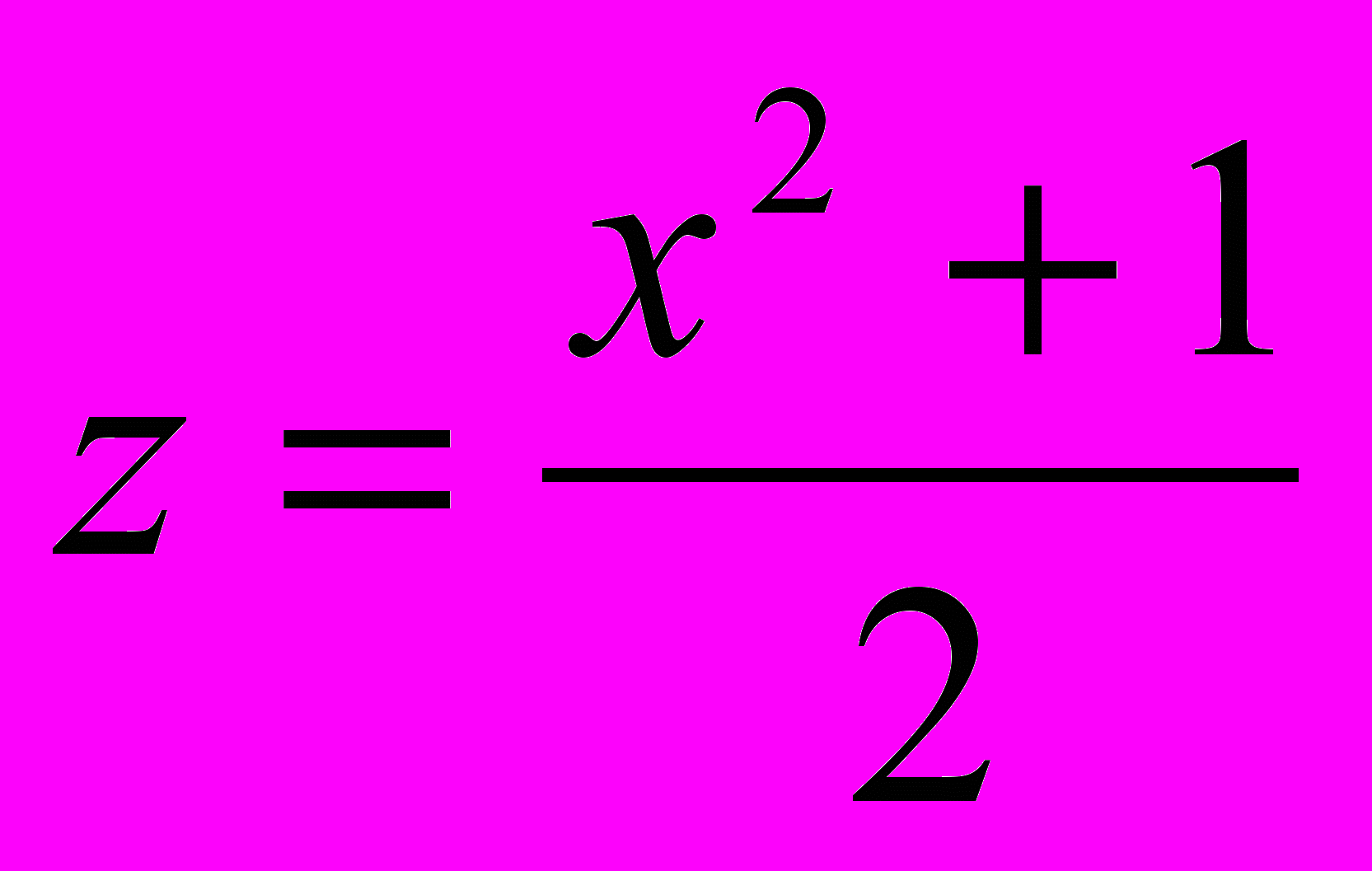 . Проверим также, что в этом случае равенство
. Проверим также, что в этом случае равенство 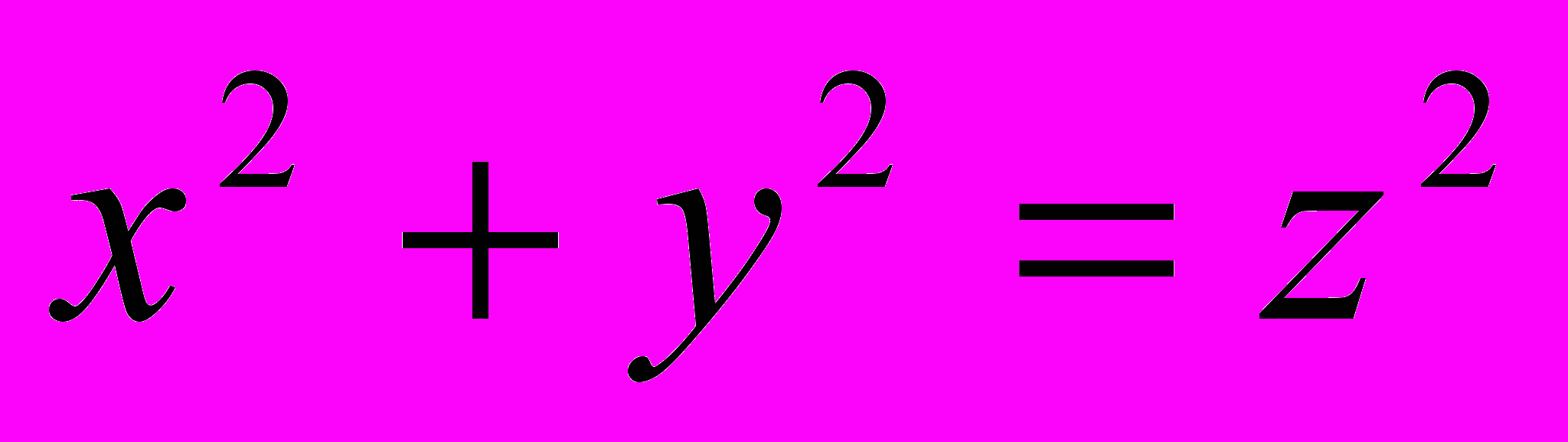 выполняется, т. е. числа, найденные по такому правилу, всегда будут составлять решение интересующего нас неопределенного уравнения. Это уравнение будем называть «уравнением Пифагора», а его решения – «пифагоровыми тройками». По этому правилу можно получить уже известные нам тройки:
выполняется, т. е. числа, найденные по такому правилу, всегда будут составлять решение интересующего нас неопределенного уравнения. Это уравнение будем называть «уравнением Пифагора», а его решения – «пифагоровыми тройками». По этому правилу можно получить уже известные нам тройки:если
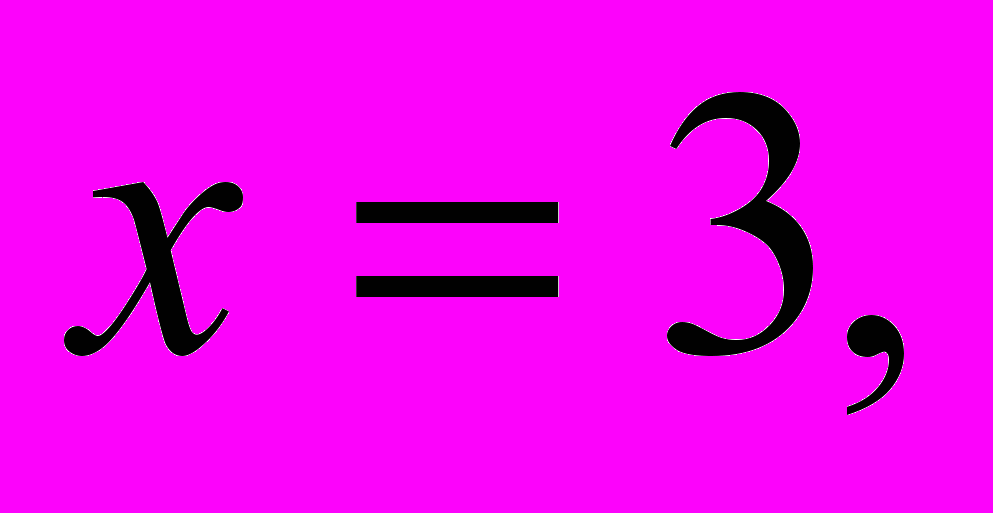 то
то 
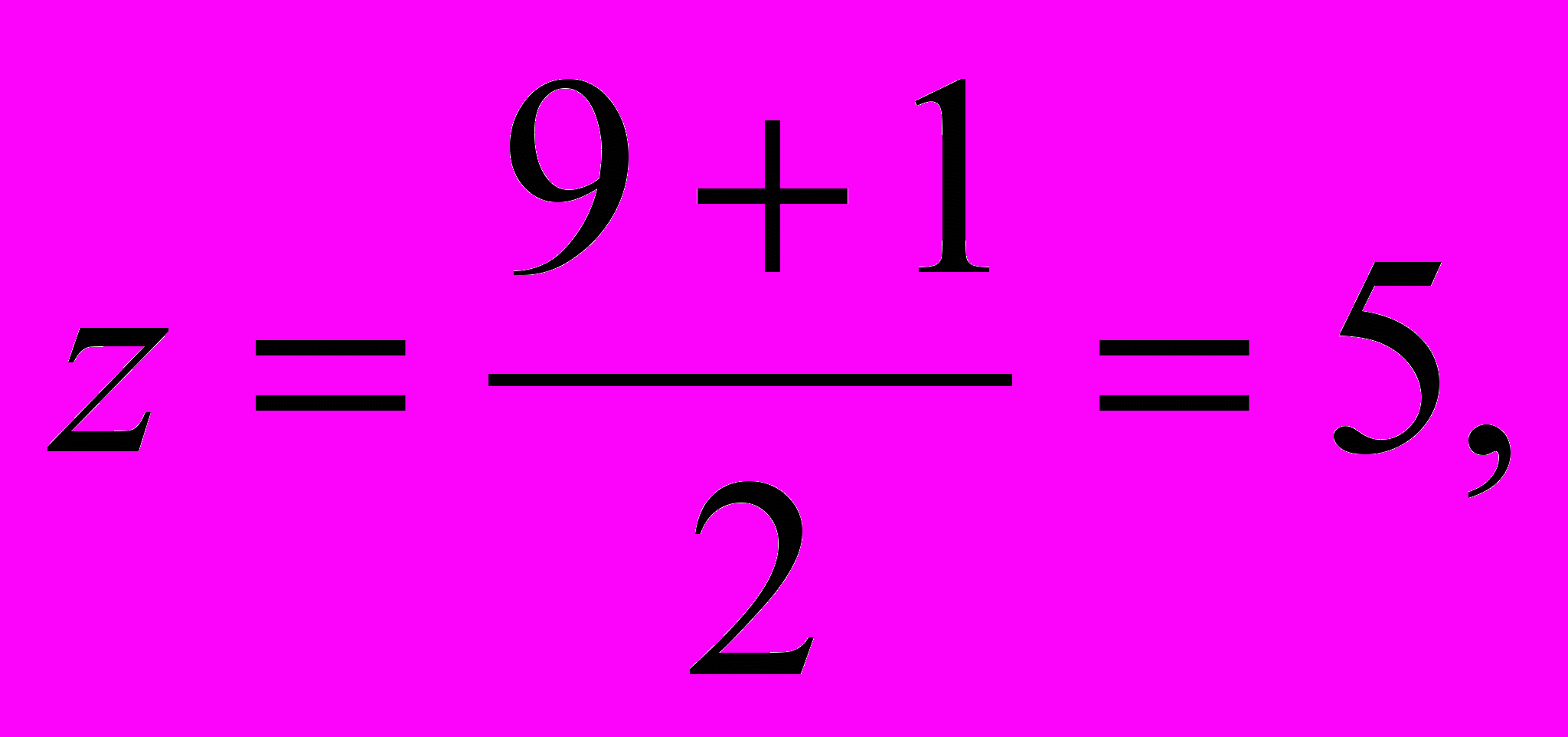 получилась первая пифагорова тройка;
получилась первая пифагорова тройка;если
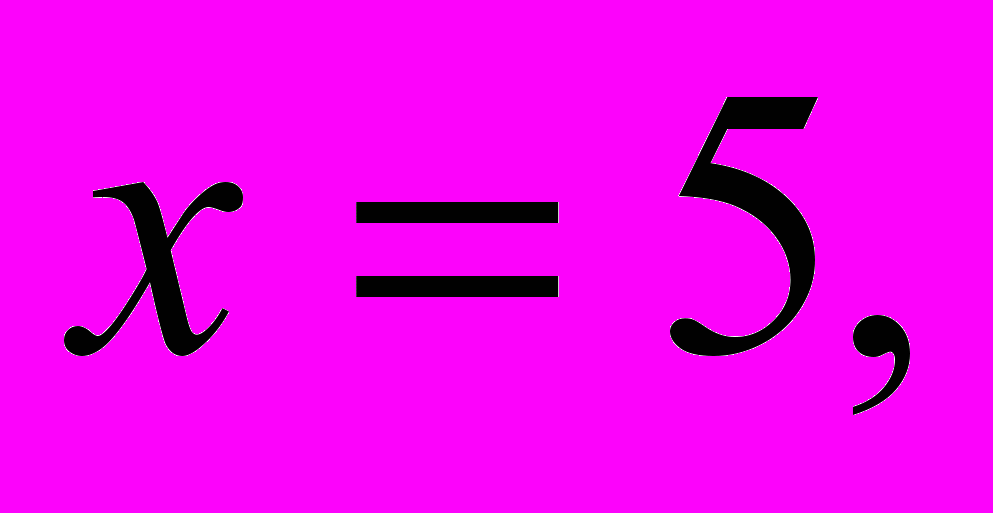 то
то  и
и 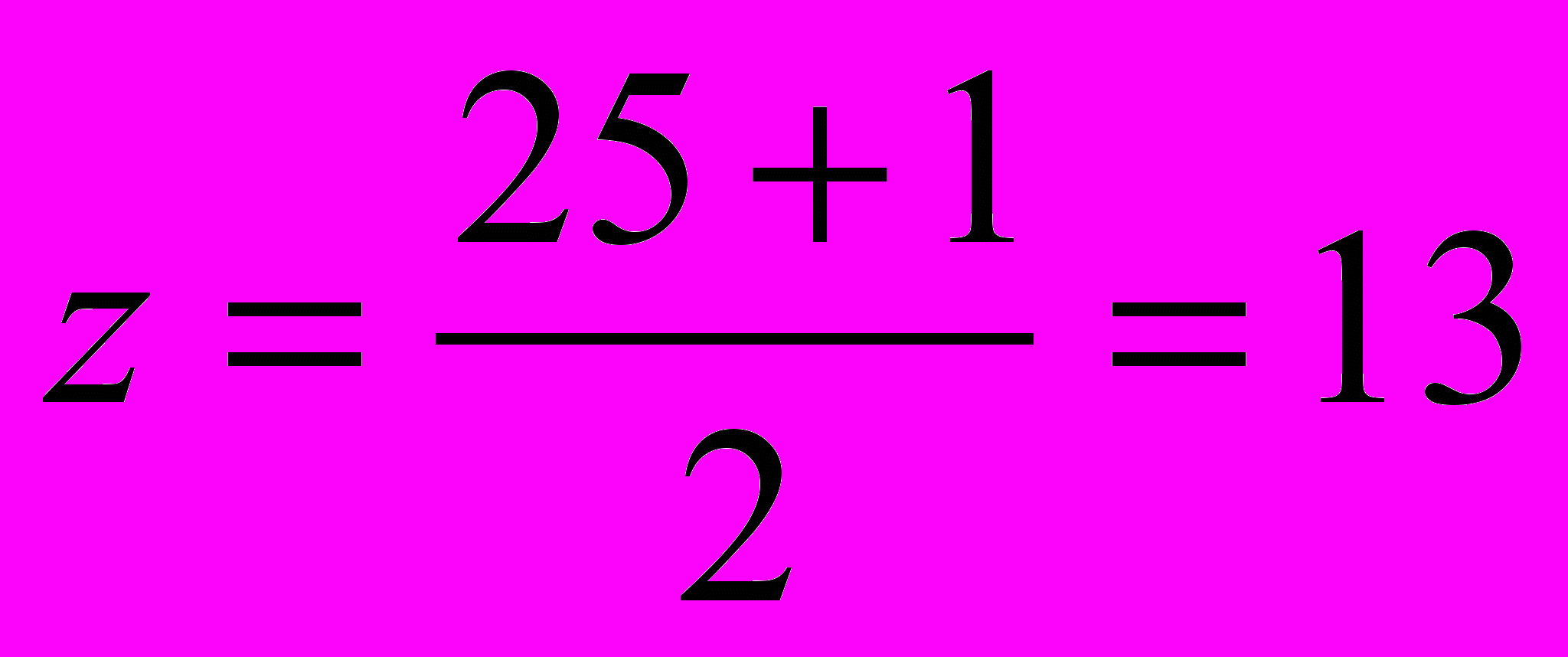 - вторая тройка и т. д.
- вторая тройка и т. д.Задача 3.Найти все пары натуральных чисел, удовлетворяющих уравнению
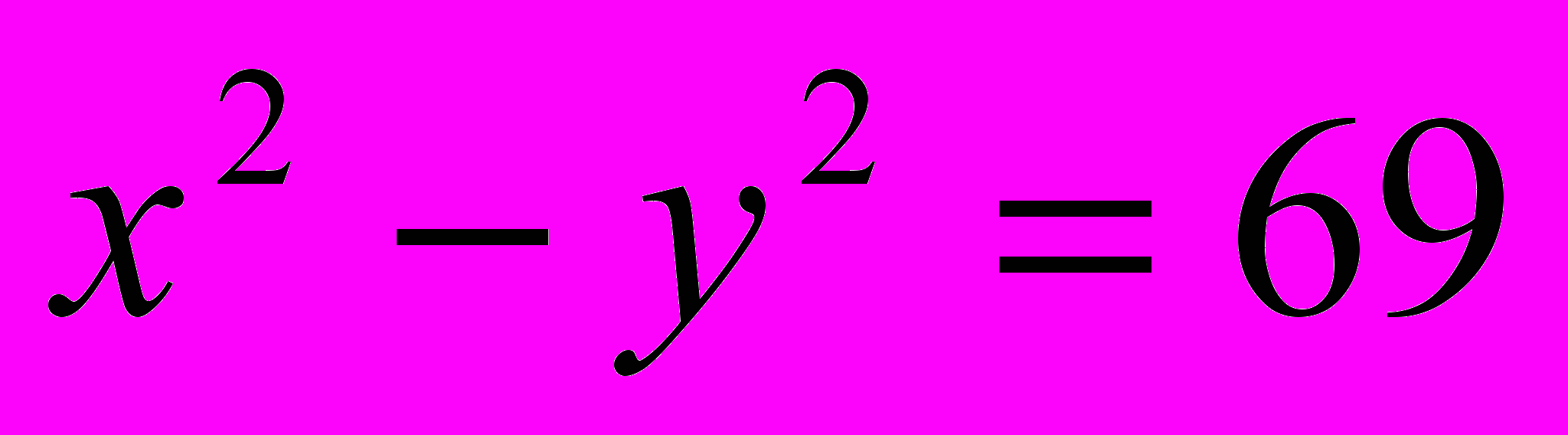 .
.Решение. Разложим левую часть уравнения на множители и запишем уравнение в виде
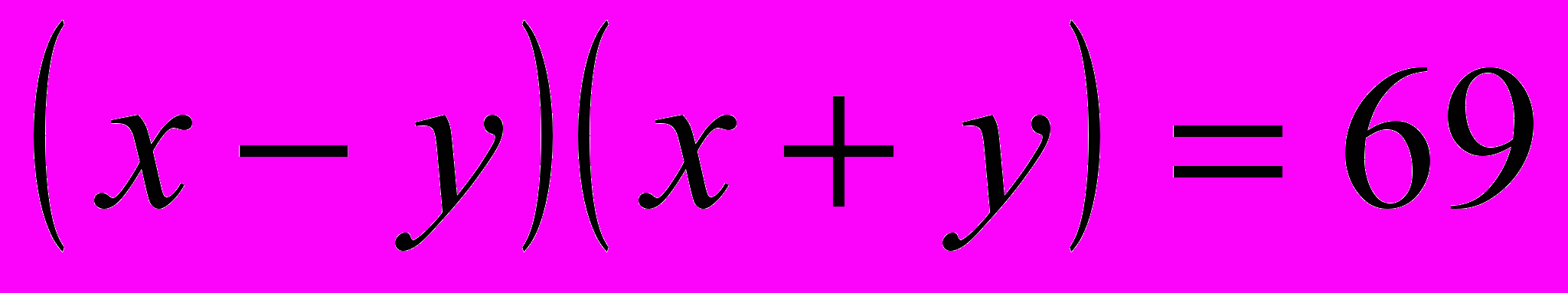 .
.Т.к. делителями числа 69 являются числа 1, 3, 23 и 69, то 69 можно получить двумя способами: 69=1·69 и 69=3·23. Учитывая, что
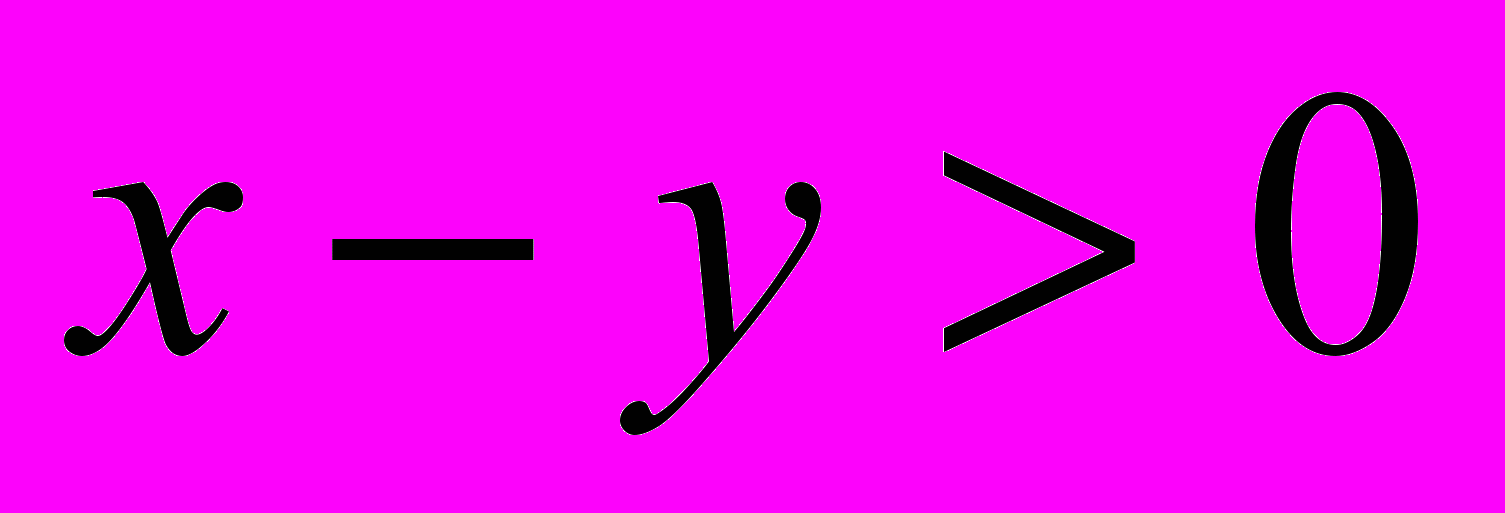 , получим две системы уравнений, решив которые мы сможем найти искомые числа:
, получим две системы уравнений, решив которые мы сможем найти искомые числа: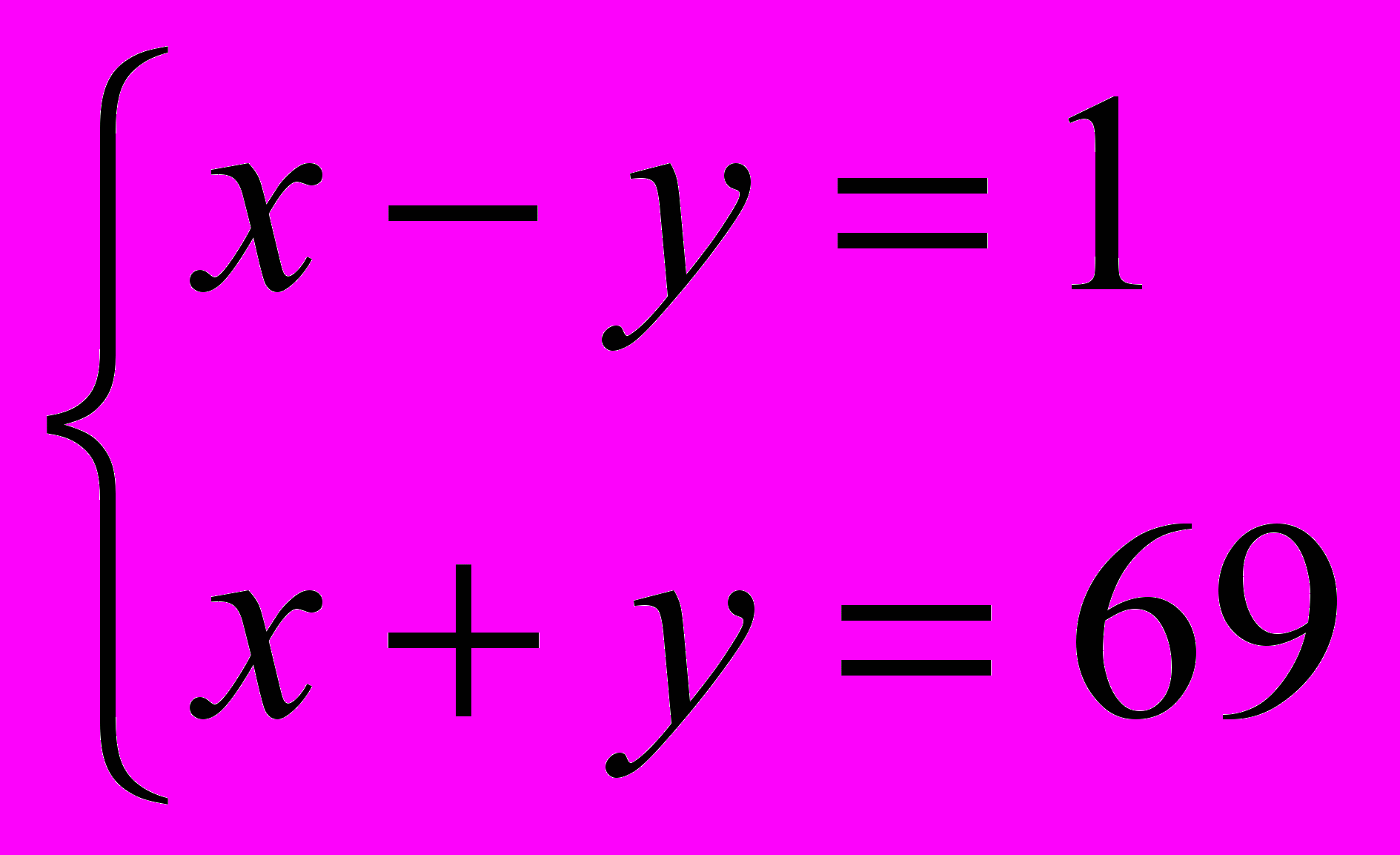 или
или 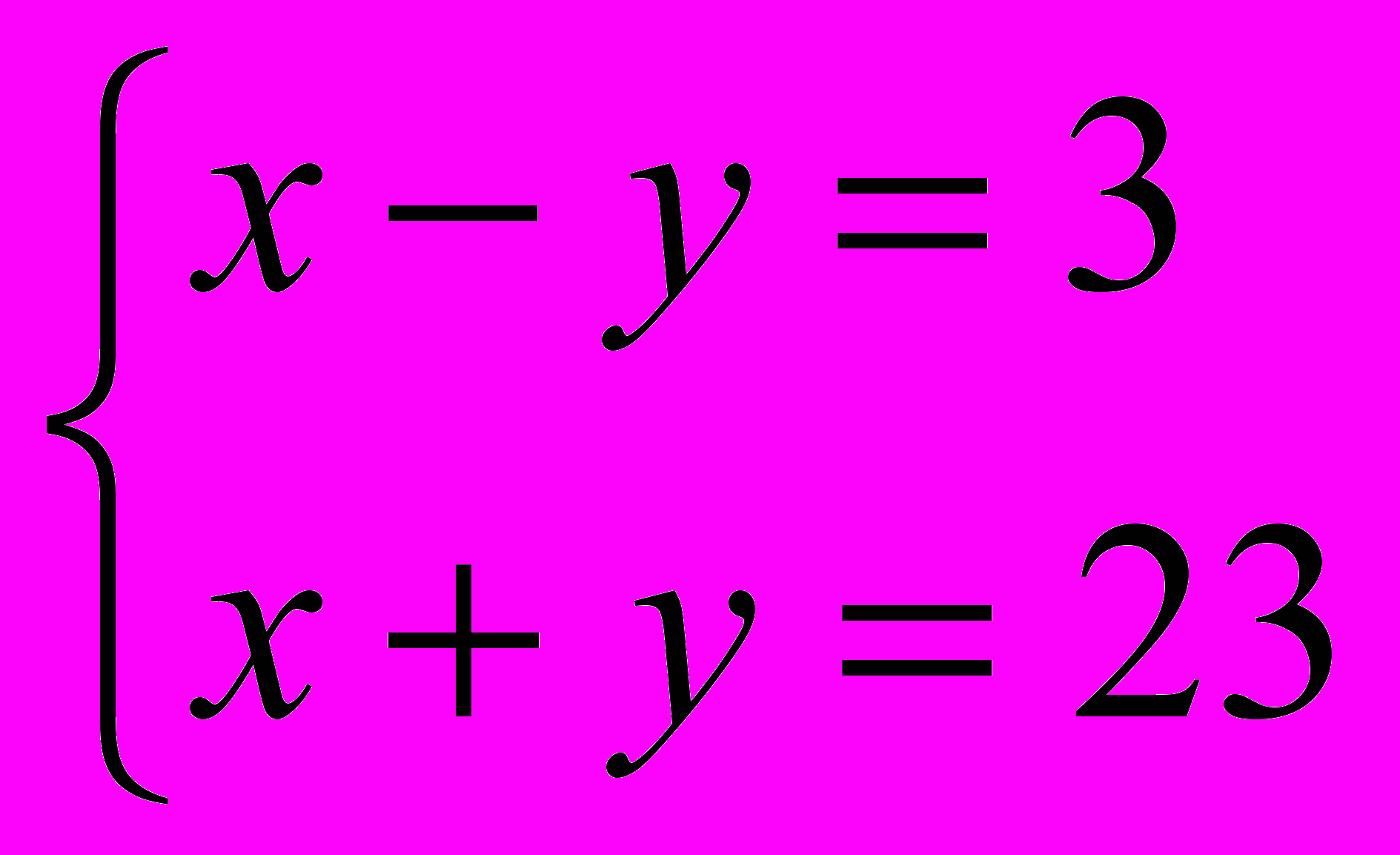 .
.Первая система имеет решение
 , а вторая система имеет решение
, а вторая система имеет решение 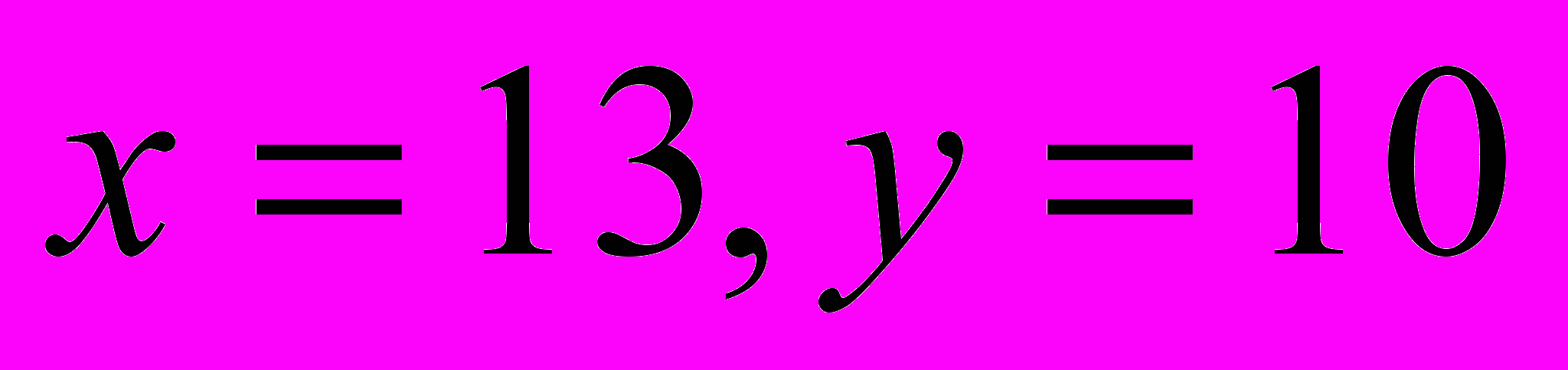 .
.Ответ:
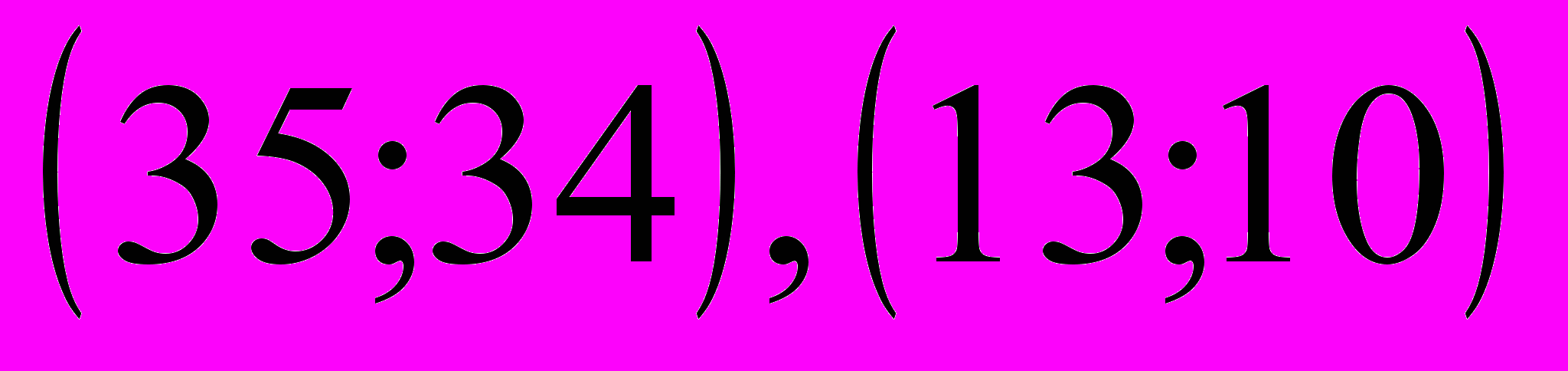 .
.Задача 4. Решить уравнение в целых числах:
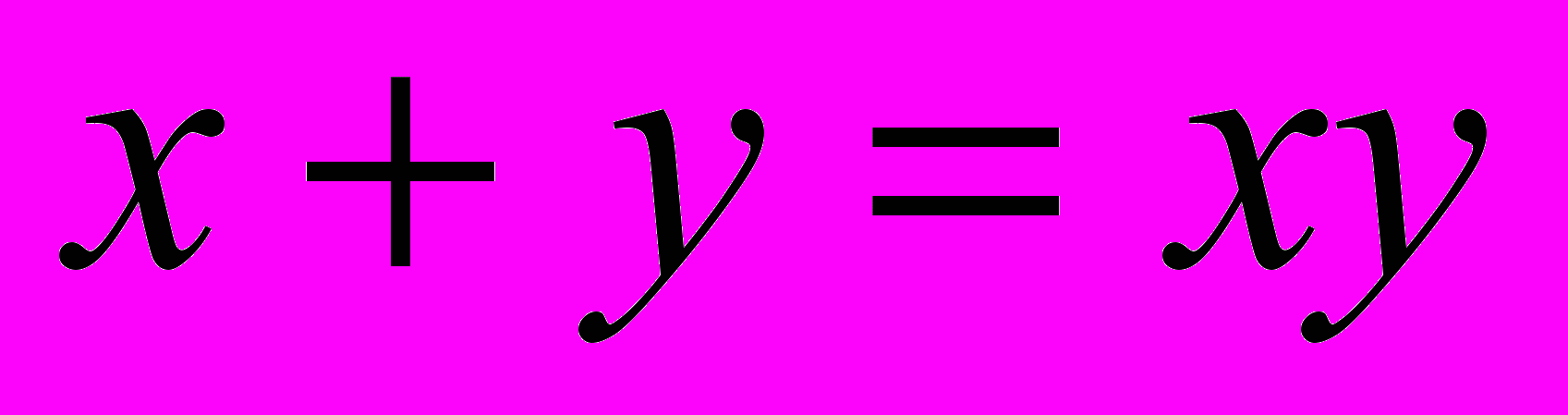 .
.Решение. Запишем уравнение в виде
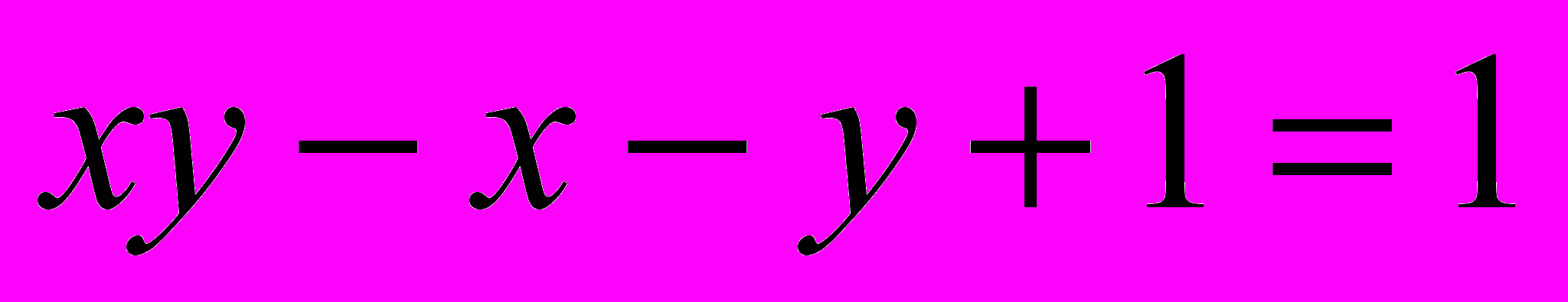 .
.Разложим левую часть уравнения на множители. Получим
 .
.Произведение двух целых чисел может равняться 1 только в двух случаях: если оба они равны 1 или -1. Получим две системы:
 или
или 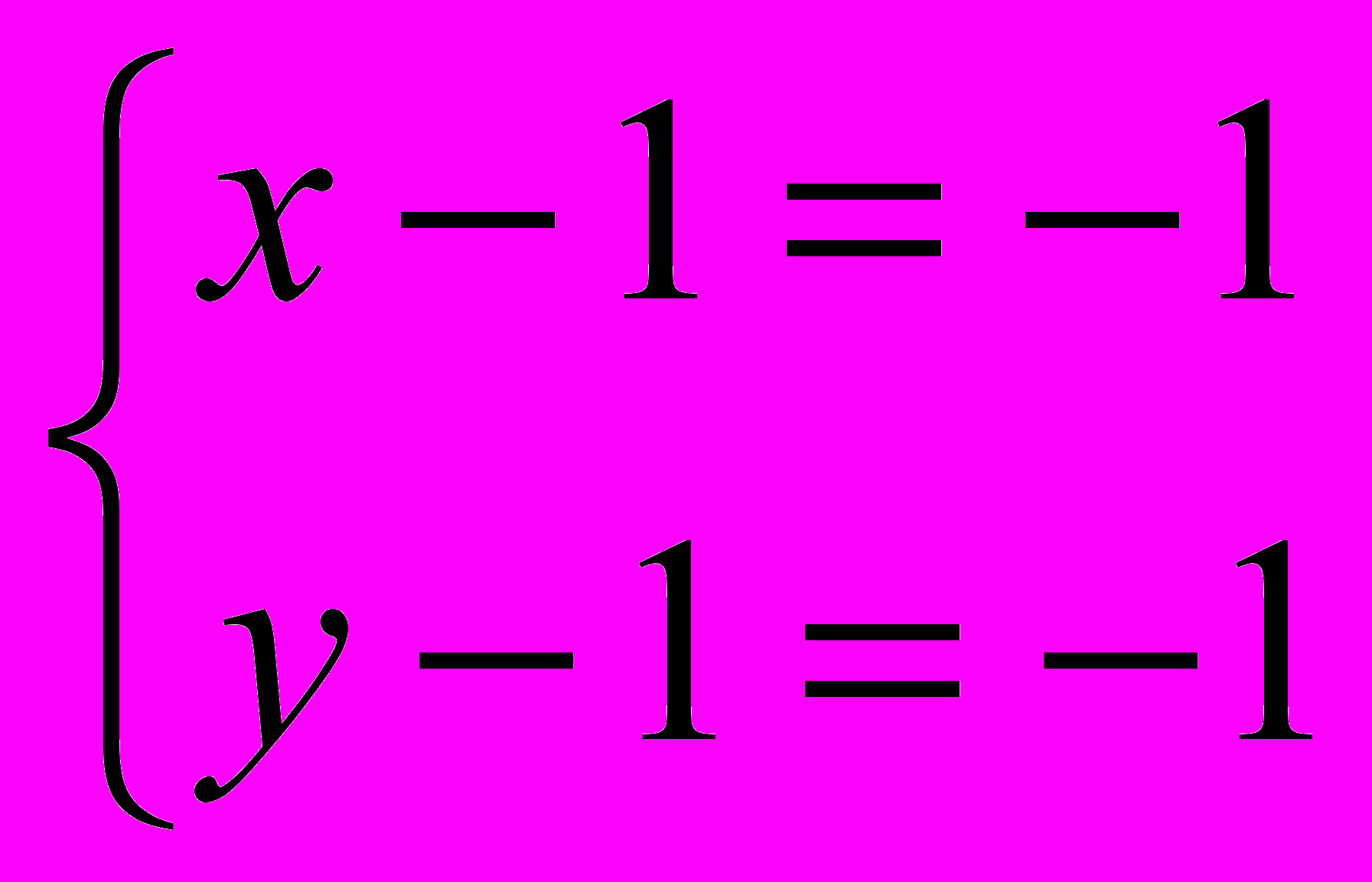 .
.Первая система имеет решение х=2, у=2, а вторая система имеет решение х=0, у=0.
Ответ:
 .
.Задача 5. Решить в целых числах уравнение
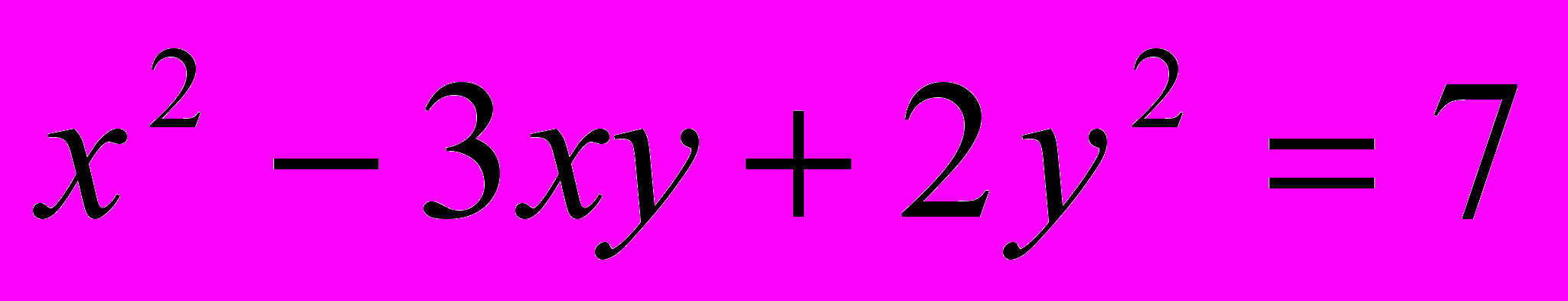 .
.Решение. Запишем данное уравнение в виде
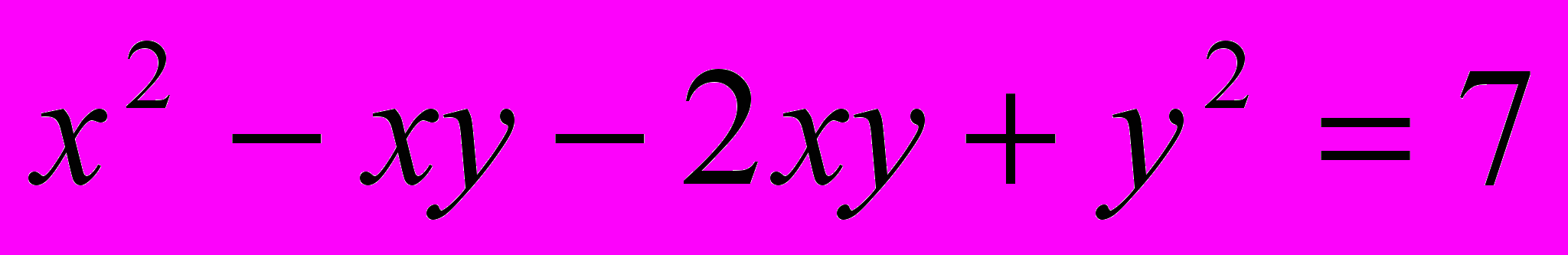 .
.Разложим левую часть уравнения на множители способом группировки, получим
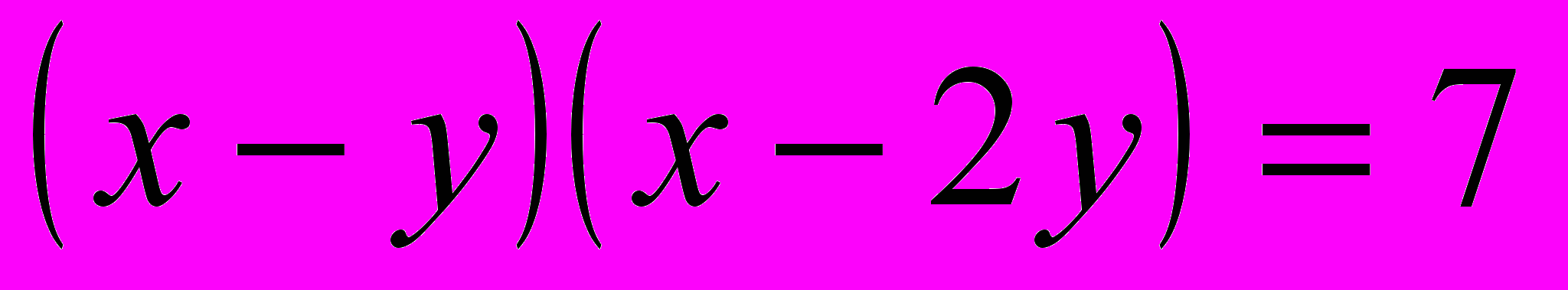 .
.Произведение двух целых чисел может равняться 7 в следующих случаях:
7=1· 7=7·1=-1·(-7)=-7·(-1).Таким образом, получим четыре системы:
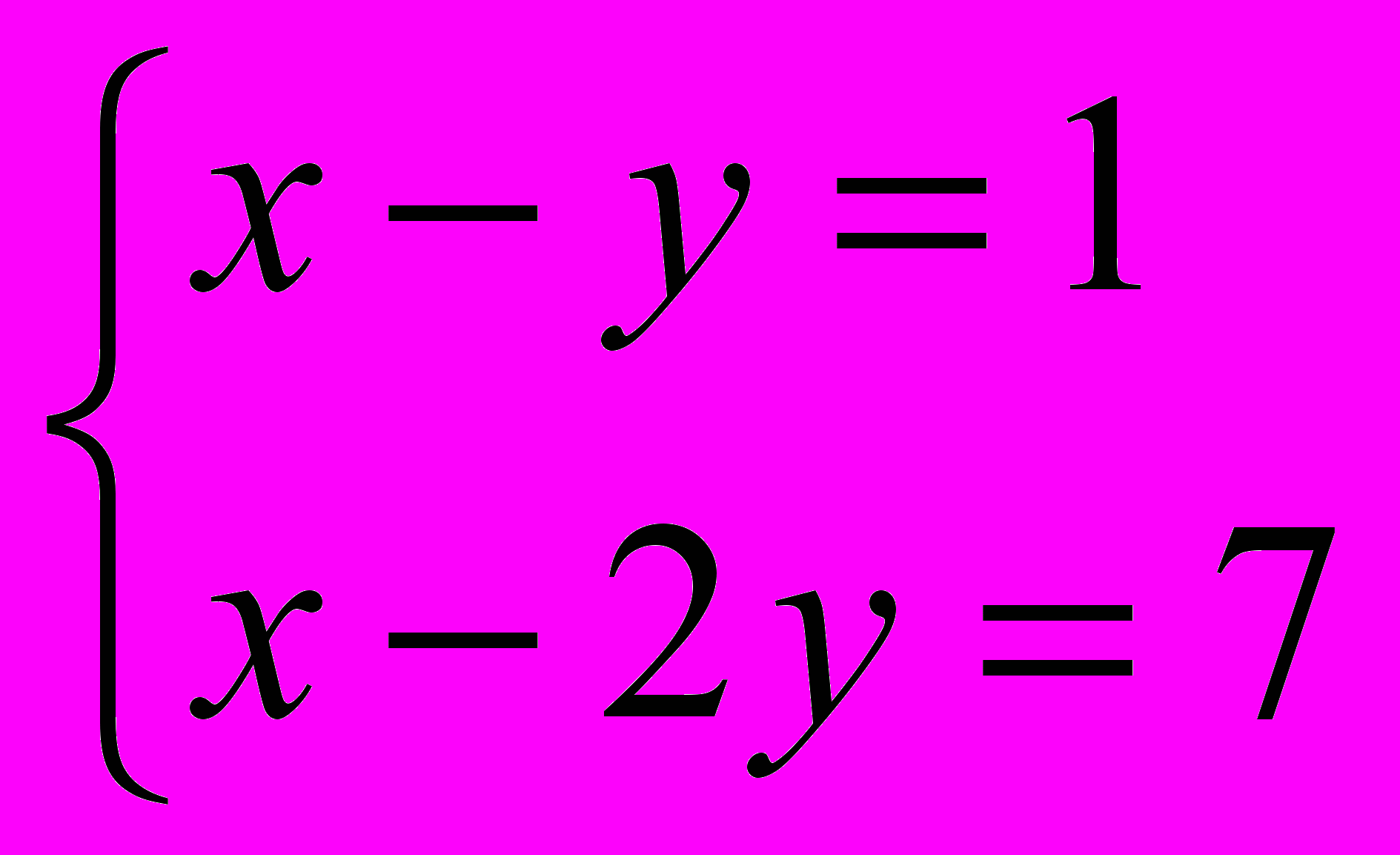 или
или 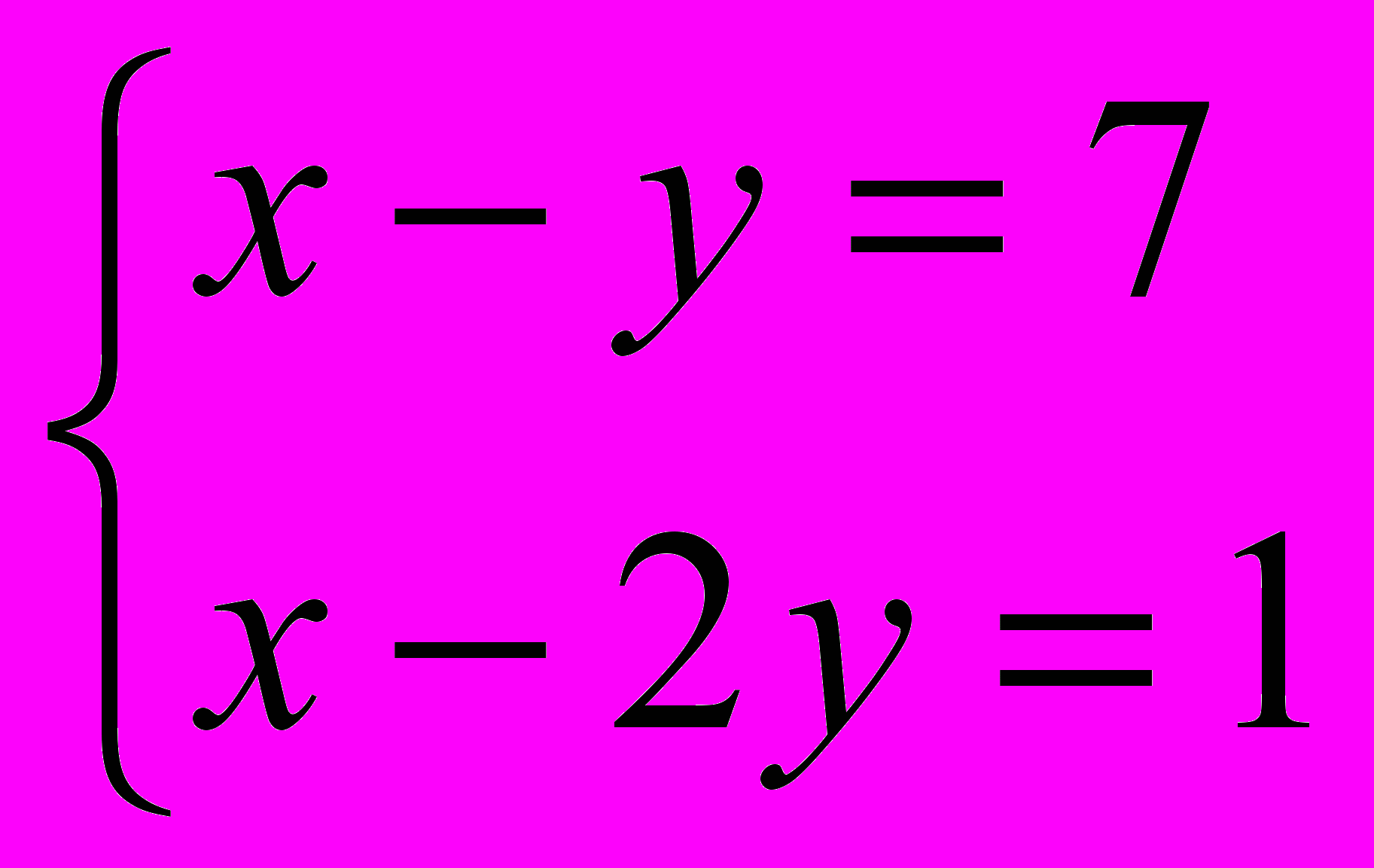 , или
, или 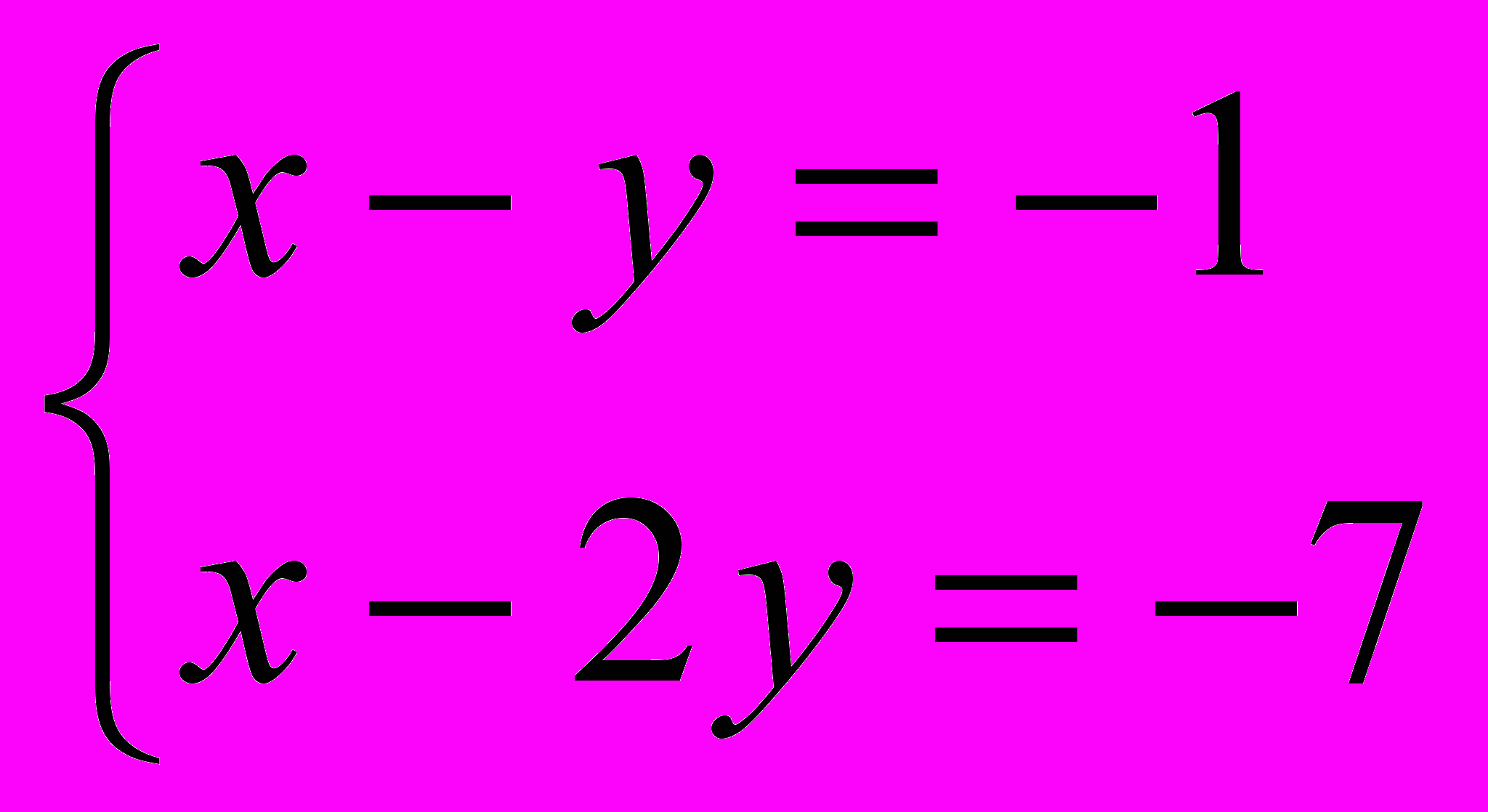 , или
, или  .
.Решением первой системы является пара чисел х = - 5, у = - 6. Решая вторую систему, получим х = 13, у = 6.Для третьей системы решением являются числа х = 5, у = 6. Четвёртая система имеет решение х = - 13, у = - 6.
Ответ:
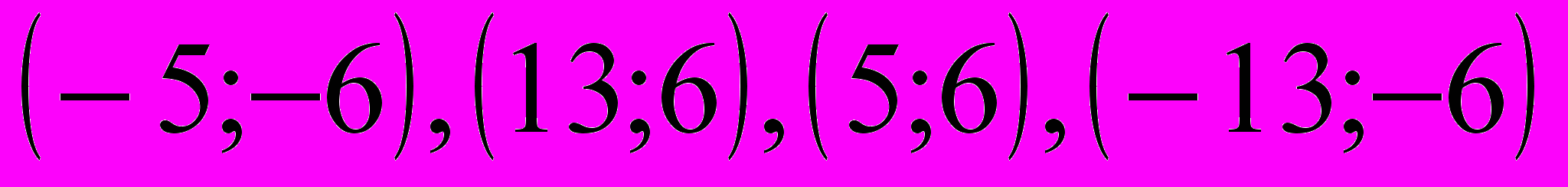 .
.Задача 6. Доказать, что уравнение

не имеет целых решений.
Решение. Разложим левую часть уравнения на множители и запишем данное уравнение в виде
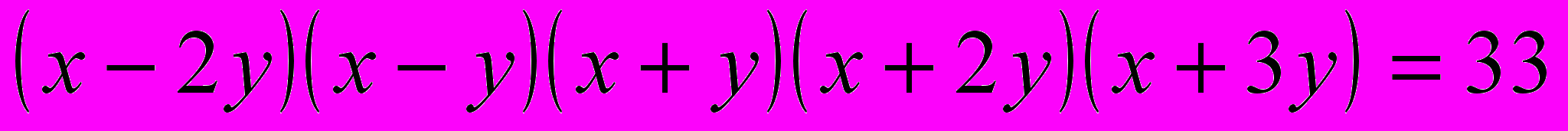 .
.1 случай. Пусть у=0, тогда исходное уравнение примет вид
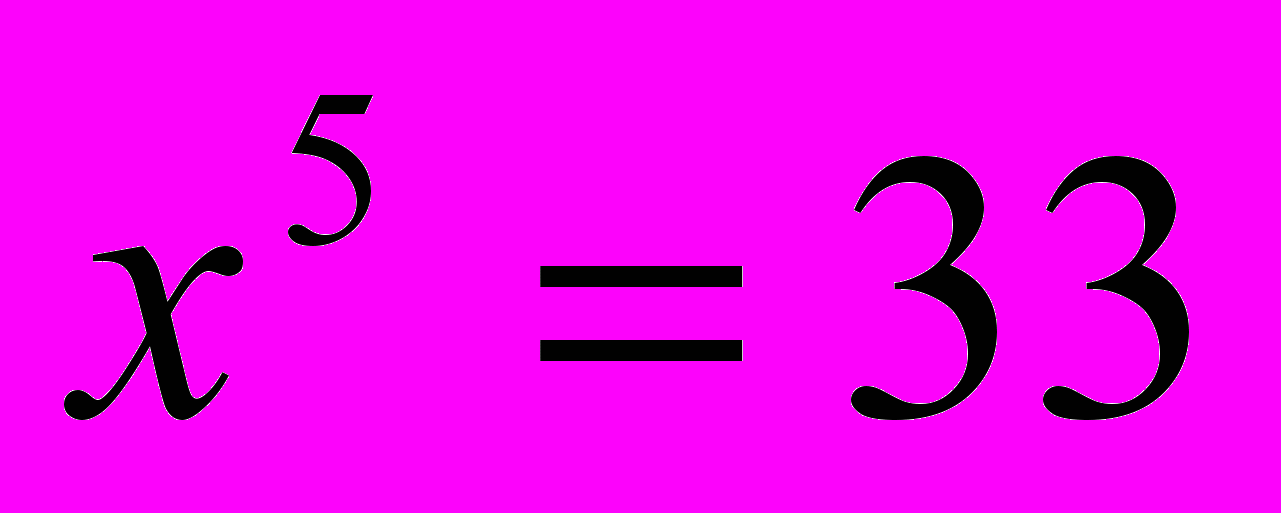 .
.Тогда
 , но это число не является целым. Значит, при у=0 данное уравнение не имеет целых решений..
, но это число не является целым. Значит, при у=0 данное уравнение не имеет целых решений..2 случай. Пусть
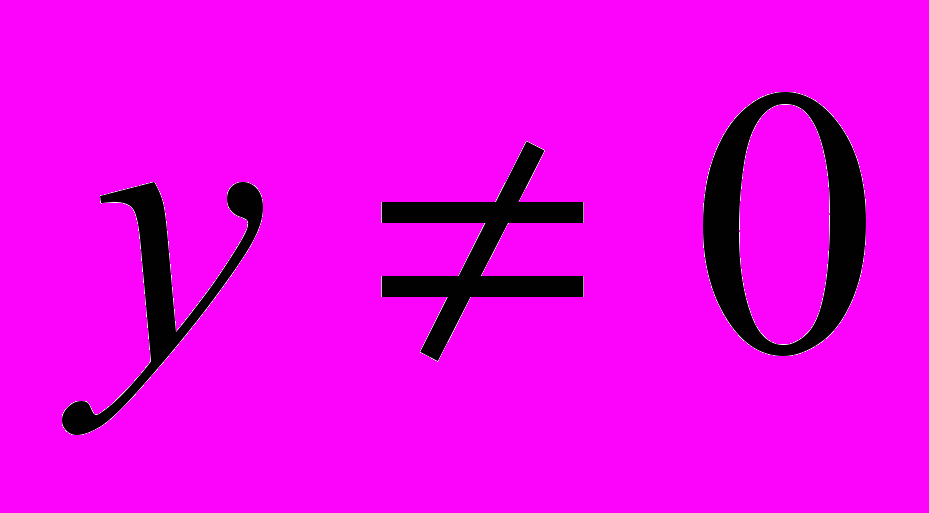 , тогда все пять множителей в левой части уравнения различны. С другой стороны число 33 можно представить в виде произведения максиму четырёх различных множителей ( 33=1·3·11 или 33=-1·3·(-11)·1 и т.д.). Следовательно, при
, тогда все пять множителей в левой части уравнения различны. С другой стороны число 33 можно представить в виде произведения максиму четырёх различных множителей ( 33=1·3·11 или 33=-1·3·(-11)·1 и т.д.). Следовательно, при 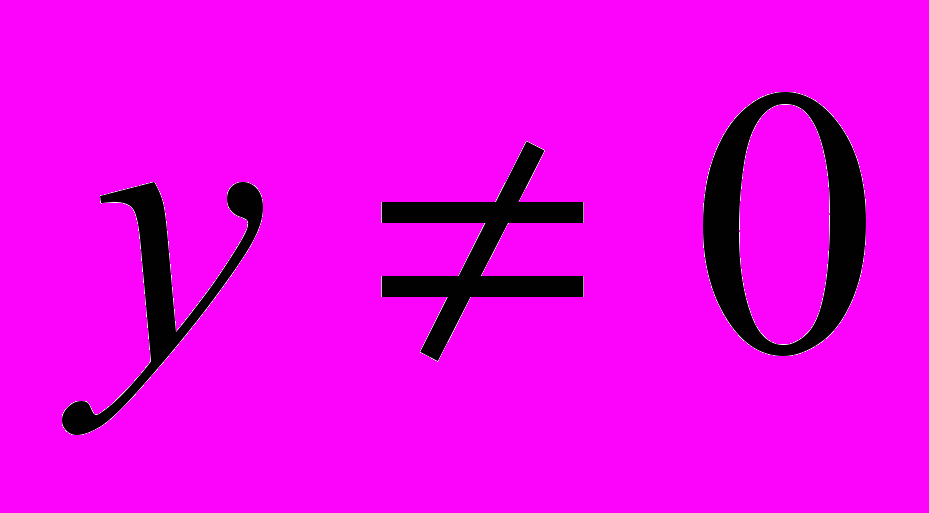 данное уравнение также не имеет целых решений.
данное уравнение также не имеет целых решений.^ 4. Диофантовы уравнения с тремя неизвестными.
Задача 7. Доказать, что уравнение

не имеет решений в целых числах.
Решение. Разложим левую часть уравнения на множители, приведём уравнение к виду
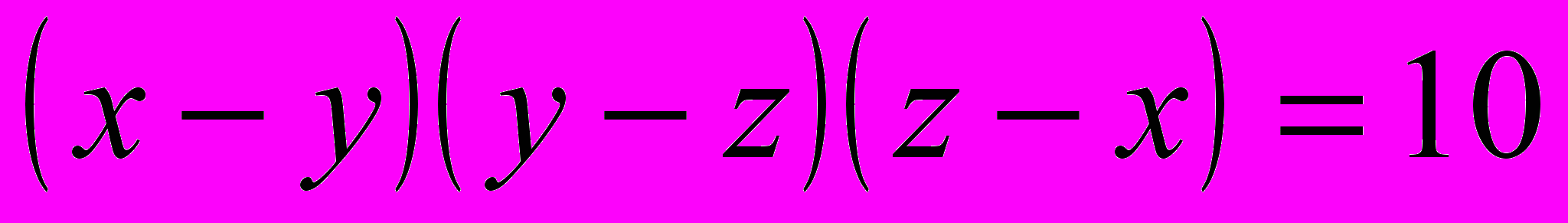 .
.С одной стороны, делителями числа 10 являются числа
 . С другой стороны,
. С другой стороны,  . Но сумма любых трёх делителей числа 10 не равна 0. Значит, данное уравнение не имеет целых решений.
. Но сумма любых трёх делителей числа 10 не равна 0. Значит, данное уравнение не имеет целых решений. IV. Заключение.
В заключительной части своей работы мне особенно хотелось подчеркнуть, что изучив специальную литературу, посвященную диафантовым уравнениям, я расширил свои математические навыки и получил дополнительные знания о самом Диофанте, его последователях, а также о влиянии его научных трудов на дальнейшее развитие научной математической мысли.
Именно благодаря методам Диофанта были разгаданы методы самого Архимеда. И если история интеграционных методов Архимеда в основном завершается созданием интегрального и дифференциального исчисления Ньютоном и Лейбницем, то история методов Диофанта растягивается еще на несколько сотен лет, переплетаясь с развитием теории алгебраических функций и алгебраической геометрии. Развитие идей Деофанта можно проследить вплоть до работ Анри Пуанкаре и Андре Вейля.
Именно Диофант открыл нам мир арифметики и алгебры. Поэтому история диафантова анализа показалась мне особенно интересной.
^ V. Список используемой литературы.
- Энциклопедический словарь юного математика. Составитель Савин А.П.– Москва: педагогика, 1989 г.
- Форков А.В. Математические олимпиады в школе. – Москва: Айрис-пресс, 2003 г.
- Задания городских и районных олимпиад.
- Перельман А.Я. Живая математика. – Москва, 1962 г.
- Новоселов С.И. Специальный курс элементарной алгебры. – М:Советская наука, 1956.
- Алимов Ш.А., Калягин Ю.М. и др. Алгебра 9 класс. – М.Просвещение, 2006.
- ВиленкинН.Я. Математика. Учебник для 6 класса. – М.Мнемозина. 2006.
- Черкасов О.Ю. Математика. Интенсивный курс подготовки к экзамену.- М.: Рольф. 2000.
- Арифметика и книга о многоугольных числах. Перевод с древнегреческого Ю.Н.Веселовского. Редакция и комментарии И.Г.Башмаковой.
