Geum.ru

Рабочая программа дисциплины «Математика» Направление подготовки

Вид материалаРабочая программа

Содержание


Схема междисциплинарных связей
2. Уровень усвоения умений (Б)
3. Степень научности (В)
Раздел 1. Введение в математический анализ
Раздел 2. Дифференциальное исчисление функции одной переменной
Раздел 3. Приложения дифференциального исчисления
Раздел 4. Неопределённый интеграл
Раздел 5. Определённый интеграл
Раздел 6. Несобственные интегралы
Раздел 8. Векторная алгебра
Раздел 9. Элементы аналитической геометрии
Раздел 10. Функции нескольких переменных
Раздел 11. Элементы высшей алгебры
Раздел 12. Числовые ряды
Раздел 13. Теория вероятностей
Раздел 14. Элементы математической статистики
Раздел 15. Модель спроса и предложения
Раздел 16. Линейное программирование
Раздел 17. Календарное планирование программ сетевыми методами
Раздел 18. Динамическое программирование
...
Полное содержание
Подобный материал:

Государственное образовательное учреждение высшего профессионального образования

Московский государственный университет геодезии и картографии (МИИГАиК)


«УТВЕРЖДАЮ»


Ректор МИИГАиК

проф. В.А.Малинников


______________________


«____»__________2010 г.


РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ


«Математика»


Направление подготовки

080500

Менеджмент


Квалификация (степень)

бакалавр


Форма обучения

очная


Москва 2010 г.


  1. Цели освоения дисциплины

Целями освоения дисциплины «Математика» являются формирование общекультурных и профессиональных компетенций, определяющих готовность и способность бакалавра к использованию знаний для решения практических задач в рамках производственно-технологической, проектно-изыскательской, организационно-управленческой и научно-исследовательской профессиональной деятельности, а именно:
  • Воспитание достаточно высокой математической культуры, привитие навыков современных видов математического мышления;
  • Способность к обобщению, анализу, восприятию информации, постановки цели и выбору путей её достижения, воспитание культуры мышления (ОК-1);
  • Способность логически верно, аргументировано и ясно строить устную и письменную речь (ОК-2);
  • Способность использовать основные законы естественнонаучных дисциплин в профессиональной деятельности, применять методы математического анализа и моделирования, теоретического и экспериментального исследования (ОПК-2);
  • Способность участвовать в работе над инновационными проектами, используя базовые методы исследовательской деятельности (ОПК-5);
  • Владеть базовыми знаниями фундаментальных разделов математики в объёме, необходимом для владения математическим аппаратом экономических наук, для обработки информации и анализа данных (ПК-1);
  • Готовность к сбору, систематизации и анализу научно-технической информации по заданию (теме) (ПК-13);



  1. Место дисциплины в структуре ООП ВПО

Данная учебная дисциплина входит в раздел «Б.2. Математический и естественнонаучный цикл. Базовая часть» ФГОС ВПО.

Для изучения дисциплины необходимы компетенции, сформированные в результате обучения в средней общеобразовательной школе.

Данная учебная дисциплина должна изучаться параллельно с дисциплинами «Информатика», «Экономическая теория», «Эконометрика», «Концепции современного естествознания», «Экономическая география», «Компьютерная графика», «Социология».

Дисциплина «Математика» формирует компетенции, необходимые для освоения модулей профессионального цикла.

^ Схема междисциплинарных связей



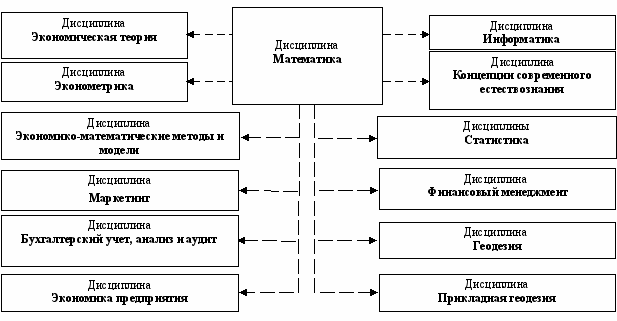
  1. Компетенции обучающегося, формируемые в результате освоения дисциплины

В результате освоения дисциплины «Математика» обучающийся должен:
  1. Знать: роль и место математики в современной цивилизации, базисные математические понятия и теоремы (ОК-1, ОК-2).
  2. Уметь: решать стандартные математические задачи, работать с математическими справочниками и ориентироваться в математическом аппарате, содержащемся в литературных источниках по специальности (ПК-1, ПК-13).
  3. Владеть: математической культурой рассуждений и доказательств, основными методами математического моделирования (ОПК-2, ОПК-5).



  1. Структура и содержание дисциплины

Общая трудоемкость дисциплины «Математика» составляет 12 зачетных единиц, 432 часа.

4.1. Структура преподавания дисциплины

№

п/п
Раздел
дисциплины
Семестр
Неделя семестра
Виды учебной работы, включая самостоятельную работу студентов
и трудоемкость

(в часах)
Формы текущего контроля успеваемости (по неделям семестра)

Форма промежуточной аттестации

(по семестрам)

лекции
лабораторные занятия
самостоятельная работа

1.
Введение в математический анализ
1
1-4
8
8
10
Проверка домашних заданий, приём контрольных заданий

2.
Дифференциальное исчисление функции одной переменной
1
5-8
8
6
10
Проверка домашних заданий, приём контрольных заданий

3.
Приложения дифференциального исчисления
1
9
2
4
10
Проверка домашних заданий, приём контрольных заданий

4.
Неопределенный интеграл
1
10-14
10
10
12
Проверка домашних заданий, приём контрольных заданий

5.
Определенный интеграл
1
15-17
6
6
12
Проверка домашних заданий, приём контрольных заданий

6.
Несобственные интегралы
1
18
2
2
10
Проверка домашних заданий, приём контрольных заданий




Аттестация
1












Экзамен

7.
Элементы линейной алгебры

2
1-5
10
10
6
Проверка домашних заданий, приём контрольных заданий

8.
Векторная алгебра
2
6-7
4
4
10
Проверка домашних заданий, приём контрольных заданий

9.
Элементы аналитической геометрии
2
8-10
6
6
10
Проверка домашних заданий, приём контрольных заданий

10.
Функции нескольких переменных
2
11-14
8
8
10
Проверка домашних заданий, приём контрольных заданий

11.
Элементы высшей алгебры
2
15-16
4
4
10
Проверка домашних заданий, приём контрольных заданий

12.
Числовые ряды
2
17-18
4
4
14
Проверка домашних заданий, приём контрольных заданий




Аттестация
2












Экзамен

13.
Теория вероятностей
3
1-12
12
12
20
Проверка домашних заданий, приём контрольных заданий

14.
Элементы математической статистики
3
13-18
6
6
20
Проверка домашних заданий, приём контрольных заданий




Аттестация
3












Экзамен

15.
Модель спроса и предложения
4
1-2
2
2
10
Проверка домашних заданий, приём контрольных заданий

16.
Линейное программирование
4
3-10
8
8
10
Проверка домашних заданий, приём контрольных заданий

17.
Календарное планирование программ сетевыми методами
4
11-12
2
2
12
Проверка домашних заданий, приём контрольных заданий

18.
Динамическое программирование
4
13-14
2
2
12
Проверка домашних заданий, приём контрольных заданий

19.
Нелинейное программирование
4
15-17
3
3
10
Проверка домашних заданий, приём контрольных заданий




Аттестация
4












Зачёт, экзамен


4.2. Содержание дисциплины и требования к уровню его освоения

Условные обозначения:

1. Качество усвоения знаний (А):

А1 -

знания, предусматривающие деятельность по воспроизведению;

А2 -
знания, предполагающие применение в ситуациях, аналогичных обучающим;

А3 -
знания, использующиеся в задачах, требующих установления новых связей между понятиями;

А4 -
знания, предполагающие способность достраивать систему связей новыми.

^ 2. Уровень усвоения умений (Б):

Б1 -

ученический – умение пользоваться системой понятий при алгоритмической деятельности с внешне заданным алгоритмическим описанием (подсказкой);

Б2 -
(типовой – алгоритмический – уровень) – умение пользоваться системой понятий в ситуации, аналогичной обучающей;

Б3 -
(продуктивный эвристического типа) – умение применять систему знаний в ситуациях, требующих перестройки связей между уже сформированными понятиями;

Б4 -
(продуктивный творческого типа) – умение достраивать сформированные системы понятий новыми, самостоятельно сформированными.

^ 3. Степень научности (В):

В1 -

(феноменологическая) – описательное изложение фактов и явлений; каталогизация объектов, констатация их свойств и качеств (известен определенный ряд однородных факторов), это использование преимущественно естественного языка и житейских понятий;

В2 -
(аналитико-синтетическая) – объяснение природы и свойств объектов и закономерностей явлений, часто качественное или полуколичественное (известны сущность первого порядка и свойства объектов и явлений, механизмов, управляющих функционированием анализируемых фактов и процессов);

В3 -
(прогностическая) – объяснение явлений данной области с созданием их количественной теории, моделирование основных процессов, аналитическим представлением законов и свойств (известны закономерности функционирования объектов конкретного вида);

В4 -
(аксиоматическая) – объяснение явлений с использованием высокой степени общности описания (большой объем материала и широкое использование научного языка, глубина проникновения в сущность явлений – известны общие законы функционирования объектов любой природы).



^ Раздел 1. Введение в математический анализ

Требуемая степень усвоения содержания раздела: А2Б2В1

Понятие множества. Операции над множествами. Множество вещественных чисел. Функция. Область ее определения. Способы задания. Основные элементарные функции, их свойства и графики. Числовые последовательности и их свойства, предел числовой последовательности. Предел функции. Непрерывность функции в точке и на отрезке. Бесконечно малые функции. Сравнение бесконечно малых. Вычисление пределов.

^ Раздел 2. Дифференциальное исчисление функции одной переменной

Требуемая степень усвоения содержания раздела: А2Б2В1

Производная функции, её смысл в различных задачах. Дифференциал функции. Правила нахождения производной и дифференциала. Таблица производных элементарных функций. Нахождение производной произведения функций, производной частного функций и производной сложной функции. Логарифмическая производная. Дифференцирование функций, заданных параметрически. Неявная функция и ее производная.

^ Раздел 3. Приложения дифференциального исчисления

Требуемая степень усвоения содержания раздела: А2Б2В1

Условия монотонности функции. Экстремумы и точки экстремума функции. Отыскание наибольшего и наименьшего значений функции, дифференцируемой на отрезке. Выпуклость и вогнутость функции. Точки перегиба. Асимптоты функции. Построение графика функции по результатам ее исследования.


^ Раздел 4. Неопределённый интеграл

Требуемая степень усвоения содержания раздела: А2Б2В1

Первообразная. Неопределённый интеграл и его свойства. Таблица интегралов от элементарных функций. Методы интегрирования. Теорема о замене переменной под знаком неопределенного интеграла. Занесение множителя под знак дифференциала. Интегрирование по частям. Интегрирование простейших рациональных функций. Разложение правильной рациональной дроби в сумму простых дробей. Интегрирование рациональных дробей. Интегрирование тригонометрических функций. Универсальная тригонометрическая замена.


^ Раздел 5. Определённый интеграл

Требуемая степень усвоения содержания раздела: А2Б2В1

Задачи, приводящие к понятию определённого интеграла. Определённый интеграл и его свойства. Формула Ньютона-Лейбница и ее применение для вычисления определенных интегралов. Замена переменной под знаком определенного интеграла. Интегрирование по частям в определенном интеграле. Геометрические приложения. Применение определенного интеграла для вычисления площади криволинейной трапеции.


^ Раздел 6. Несобственные интегралы

Требуемая степень усвоения содержания раздела: А2Б2В1

Несобственные интегралы и их сходимость.


Раздел 7. Элементы линейной алгебры

Требуемая степень усвоения содержания раздела: А2Б2В1

Матрицы, действия с ними. Системы линейных алгебраических уравнений. Матричная запись системы линейных уравнений. Метод Гаусса. Понятие n-мерного линейного (векторного) пространства. Вектор как элемент линейного пространства. Линейные операции над векторами. Базис. Ранг системы векторов. Отображения линейных пространств. Линейные отображения, их матрицы. Определители. Присоединенная и обратная матрица. Матричное решение системы линейных уравнений. Правило Крамера. Собственные векторы и собственные значения линейных операторов. Свойства собственных векторов и собственных значений сопряженных операторов. Билинейные и квадратичные формы. Евклидово n-мерное пространство. Неравенство Коши-Буняковского.

^ Раздел 8. Векторная алгебра

Требуемая степень усвоения содержания раздела: А2Б2В1

Скалярное произведение векторов и его свойства. Длина вектора и угол между двумя векторами в координатной форме. Векторное произведение двух векторов, его свойства и простейшие приложения. Смешанное произведение трех векторов, его свойства и геометрический смысл. Условия ортогональности, коллинеарности и компланарности векторов.


^ Раздел 9. Элементы аналитической геометрии

Требуемая степень усвоения содержания раздела: А2Б2В1

Уравнения прямой на плоскости. Угол между прямыми. Расстояние от точки до прямой. Уравнения плоскости и прямой в пространстве. Взаимное расположение. Угол между плоскостями. Угол между прямыми. Угол между прямой и плоскостью. Расстояние от точки до прямой в пространстве. Расстояние между скрещивающимися прямыми.


^ Раздел 10. Функции нескольких переменных

Требуемая степень усвоения содержания раздела: А2Б2В1

Функции нескольких переменных и их область определения. Предел функции нескольких переменных. Непрерывность. Частные производные. Полный дифференциал, его связь с частными производными. Дифференцирование сложных функций нескольких переменных. Касательная плоскость и нормаль к поверхности.


^ Раздел 11. Элементы высшей алгебры

Требуемая степень усвоения содержания раздела: А2Б2В1

Комплексные числа и действия с ними. Изображение комплексных чисел на плоскости. Модуль и аргумент комплексного числа. Алгебраическая и тригонометрическая формы комплексного числа. Формула Эйлера. Показательная форма комплексного числа. Корни из комплексных чисел.


^ Раздел 12. Числовые ряды

Требуемая степень усвоения содержания раздела: А2Б2В1

Числовые ряды. Сходимость и сумма ряда. Необходимое условие сходимости. Действия с рядами. Методы исследования сходимости рядов. Признаки сравнения. Признак Даламбера и радикальный признак Коши. Интегральный признак Коши.


^ Раздел 13. Теория вероятностей

Требуемая степень усвоения содержания раздела: А2Б2В1

Элементы комбинаторики. Основные понятия теории вероятностей. Пространство элементарных событий. Алгебра событий. Классическое и геометрическое определение вероятности. Теоремы сложения и умножения вероятностей. Полная вероятность. Формула Байеса. Формула Бернулли. Локальная и интегральная теоремы Муавра-Лапласа.

Дискретные случайные величины, их способы задания и числовые характеристики. Непрерывные случайные величины, их способы задания и числовые характеристики. Основные законы распределения. Многомерные случайные величины. Ковариация и коэффициент корреляции. Закон больших чисел. Теоремы Бернулли и Чебышева. Центральная предельная теорема Ляпунова. Цепи Маркова. Элементы теории случайных процессов и теории массового обслуживания.


^ Раздел 14. Элементы математической статистики

Требуемая степень усвоения содержания раздела: А2Б2В1

Вариационные ряды и их характеристики. Основы математической теории выборочного метода. Проверка статистических гипотез. Элементы корреляционного и регрессионного анализа.


^ Раздел 15. Модель спроса и предложения

Требуемая степень усвоения содержания раздела: А2Б2В1

Функции спроса и предложения. Функция полезности. Кривые безразличия.


^ Раздел 16. Линейное программирование

Требуемая степень усвоения содержания раздела: А2Б2В1

Постановка и различные формы записи задач линейного программирования. Стандартная и каноническая формы представления задач линейного программирования. Геометрическая интерпретация задач линейного программирования. Симплекс-метод. Симплексные таблицы. Экономическая интерпретация элементов симплексной таблицы. Двойственные задачи и методы. Экономическая интерпретация пары двойственных задач. Экономическая и математическая формулировки транспортной задачи. Потенциалы, их экономический смысл. Метод потенциалов. Основные способы построения начального опорного решения. Транспортные задачи с нарушенным балансом производства и потребления. Транспортные задачи с ограничениями на пропускную способность сети. Задача об оптимальных назначениях.


^ Раздел 17. Календарное планирование программ сетевыми методами

Требуемая степень усвоения содержания раздела: А2Б2В1

Сетевое представление программы. Критические и некритические пути. Раннее начало и позднее окончание операций. Полный и свободный резервы. Графическое и табличное решение задачи расчета сетевой модели. Определение ресурсов и последовательное улучшение сетевого плана. Построение календарного графика и распределение ресурсов.


^ Раздел 18. Динамическое программирование

Требуемая степень усвоения содержания раздела: А2Б2В1

Метод динамического программирования для решения задач оптимизации. Принцип оптимальности. Уравнение Беллмана. Простейшая задача управления запасами. Решение задачи методом динамического программирования. Построение оптимальной производственной программы выпуска продукции с постоянным, переменным и случайным спросом.


^ Раздел 19. Нелинейное программирование

Требуемая степень усвоения содержания раздела: А2Б2В1

Задачи нелинейного программирования. Гладкие конечномерные задачи оптимизации с ограничениями типа равенства и неравенства. Принцип Лагранжа снятия ограничений. Задачи квадратичного программирования. Примеры задач квадратичного программирования, допускающих экономическую интерпретацию.


4.3 Соотношение разделов учебной дисциплины и формируемых в них компетенций

^ Темы, разделы дисциплины
Коли-чество часов
Компетенции
Σ общее коли-

чество компе-тенций

ОК-1
ОК-2
ПК-1
ПК-13
ОПК-2
ОПК-5

Раздел 1
26
+
+
+
+
+



5

Раздел 2
24
+
+
+
+
+



5

Раздел 3
16
+
+
+
+
+



5

Раздел 4
32
+
+
+
+
+



5

Раздел 5
24
+
+
+
+
+



5

Раздел 6
14
+
+
+
+
+



5

Раздел 7
26
+
+
+
+
+



5

Раздел 8
18
+
+
+
+
+



5

Раздел 9
22
+
+
+
+
+



5

Раздел 10
26
+
+
+
+
+



5

Раздел 11
18
+
+
+
+
+



5

Раздел 12
22
+
+
+
+
+



5

Раздел 13
44
+
+
+
+
+
+
6

Раздел 14
32
+
+
+
+
+
+
6

Раздел 15
14
+
+
+
+
+
+
6

Раздел 16
26
+
+
+
+
+
+
6

Раздел 17
16
+
+
+
+
+
+
6

Раздел 18
16
+
+
+
+
+
+
6

Раздел 19
16
+
+
+
+
+
+
6

Итого
432























  1. Образовательные технологии

При реализации программы дисциплины «Математика» в часы, отведенные для аудиторных занятий (214 часа), занятия проводятся в виде лекций – 107 часов и по группам в виде практических занятий – 107 часа. Самостоятельная работа студентов подразумевает занятия в виде консультаций и индивидуальной работы студента.

  1. Оценочные средства для текущего контроля успеваемости, промежуточной аттестации по итогам освоения дисциплины и учебно-методическое обеспечение самостоятельной работы студентов




По каждому разделу студенту выдаются домашние задания и индивидуальные контрольные работы, которые оцениваются по пятибалльной системе.


Общие критерии оценки ответов студентов

Для отличной оценки
Для хорошей оценки
Для удовлетвори-

тельной оценки
Для неудовлетвори-

тельной оценки

Наличие глубоких, исчерпывающих знаний предмета в объеме освоенной программы; знание основной (обязательной) литературы; правильные и уверенные действия, свидетельствующие о наличии твердых знаний и навыков в использовании технических средств; полное, четкое, грамотное и логически стройное изложение материала; свободное применение теоретических знаний при анализе практических вопросов.
Те же требования, но в ответе студента по некоторым перечисленным показателям имеются недостатки принципиаль-ного характе-ра, что вызвало замечания или поправки преподавателя.
Те же требования, но в ответе имели место ошибки, что вызвало необходимость помощи в виде поправок и наводящих вопросов преподавателя.
Наличие ошибок при изложении ответа на основные вопросы программы, свидетельствующих о неправильном понимании предмета; при решении практических задач показано незнание способов их решения, материал изложен беспорядочно и неуверенно.



  1. Учебно-методическое и информационное обеспечение дисциплины

а) основная литература:

1. Письменный Д.Т. Конспект лекций по высшей математике (полный курс). Москва, Айрис пресс, 2006г.

2. Берман Г.Н. Сборник задач по курсу математического анализа. С.-Петербург, Профессия, 2004г.

3. Журбенко Л.Н. и др. Математика в примерах и задачах (учебное пособие). Москва, Инфа-М, 2009г.

4. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. Москва, Наука, 1989г.

5. Гмурман В.Е. Теория вероятностей и математическая статистика. Москва, Высшая школа, 2003г.

6. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. Москва, Высшая школа, 2002г.

7. Кремер Н.Ш. Теория вероятностей и математическая статистика. Москва, ЮНИТИ, 2002г.

8. Красс М.С., Чупырков Б.П. Основы математики и ее приложения в экономическом образовании. Москва, Дело, 2001г.

9. Исследование операций в экономике. /Под. Ред. Н.Ш. Кремера. Москва, ЮНИТИ, 1997г.

10. Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении. Москва, Дело, 2002г.

11. Мажукин В.И., Королева О.П. Математическое моделирование в экономике. В 2-х частях. Москва, Флипта-МосГУ, 2004г.

12. Шелобаев С.И. Экономико-математические методы и модели. Москва, ЮНИТИ-ДАМА, 2005г.


б) дополнительная литература:

1. Шипачев В.С. Курс высшей математики. Москва, Проспект, 2004г.

2. Пискунов Н.С. Дифференциальное и интегральное исчисления. Т.1,2. Москва, Интегралл-пресс, 2001г.

3. Данко Л.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Части 1 и 2. Москва, Оникс 21 век, Мир и Образование, 2003г.

4. Вентцель Е.С. Теория вероятностей. Москва, Наука, 1964г.

5. Письменный Д.Т. Конспект лекций по теории вероятностей и математической статистике. Москва, Айрис-Пресс, 2004г.;

6. Амосова Н.Н., Куклин Б.А. и др. Вероятностные разделы математики. Москва, 2001г.

7. Экономико-математические методы и прикладные модели под редакцией Федосеева В.В. Уч. Пособие для вузов. Москва, ЮНИТИ, 2001г.


в) программное обеспечение и Интернет-ресурсы:

1. программные пакеты: Matlab, Mathcad, Excel и другие;

2. информационно-справочные и поисковые системы: образовательный математический сайт «Exponenta» и другие учебные математические сайты и форумы интернета.

  1. Материально-техническое обеспечение дисциплины

Учебные аудитории факультета экономики и управления территориями МИИГАиК, оборудованные проекторами и электронными досками, компьютерные классы и доступ к сети Интернет.


Программа составлена в соответствии с требованиями ФГОС ВПО с учетом рекомендаций ПрООП ВПО по направлению подготовки 080500 «Менеджмент».


Авторы: Аристархова Анна Вячеславовна, доцент, к. ф-м. н., Московский государственный университет геодезии и картографии (МИИГАиК),

Программа одобрена на заседании Методической комиссии факультета экономики и управления территориями от _________ 2010 года, протокол № ___.