Рабочая программа дисциплины «Математика» Направление подготовки
| Вид материала | Рабочая программа |
- Рабочая программа учебной дисциплины «Математика» Направление подготовки, 206.48kb.
- Рабочая программа дисциплины «Дискретная математика» Направление подготовки, 125.26kb.
- Аннатационная программа дисциплины теория вероятностей, случайные процессы направление, 46.02kb.
- Рабочая программа учебной дисциплины «Дискретная математика» Направление подготовки, 139.29kb.
- Рабочая программа дисциплины «Математика» Направление подготовки, 174.11kb.
- Программа дисциплины математическая статистика, 31.07kb.
- Рабочая программа дисциплины «Математика» Направление подготовки, 351.74kb.
- Рабочая программа по дисциплине Численные методы для специальности 050202 Информатика,, 229.53kb.
- Рабочая программа дисциплины (модуля) асимптотические методы решения дифференциальных, 19.29kb.
- Рабочая программа дисциплины «теоретические основы теплотехники» Направление подготовки, 554.69kb.
Государственное образовательное учреждение высшего профессионального образования
Московский государственный университет геодезии и картографии (МИИГАиК)
«УТВЕРЖДАЮ»
Ректор МИИГАиК
проф. В.А.Малинников
______________________
«____»__________2010 г.
РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ
«Математика»
Направление подготовки
021300
Картография и геоинформатика
Квалификация (степень)
бакалавр
Форма обучения
очная
Москва 2010 г.
- Цели освоения дисциплины
Целью математического образования бакалавра является:
- Воспитание достаточно высокой математической культуры
- Привитие навыков современных видов математического мышления
- Способность к обобщению, анализу, восприятию информации, постановки цели и выбору путей её достижения (ОК-1)
- Владеть базовыми знаниями фундаментальных разделов математики в объёме, необходимом для владения математическим аппаратом географических наук и картографии, для обработки информации и анализа географических и картографических данных (ПК-1)
- Место дисциплины в структуре ООП ВПО
Данная учебная дисциплина входит в раздел «Б.2. Математический и естественнонаучный цикл. Базовая часть» ФГОС ВПО.
Для изучения дисциплины необходимы компетенции, сформированные в результате обучения в средней общеобразовательной школе.
Данная учебная дисциплина должна изучаться параллельно с дисциплинами «Информатика», «Физика», «Экология», «Биология», «География».
Дисциплина «Математика» формирует компетенции, необходимые для освоения модулей профессионального цикла.
3.Компетенции обучающегося, формируемые в результате освоения дисциплины
В результате освоения дисциплины «Математика» обучающийся должен:
- Владеть: культурой мышления, способностьюк анализу, базовыми знаниями фундаментальных разделов математики (ОК-1, ПК-1).
- Уметь: логически верно, аргументированно строить свою речь (ОК-2).
- Владеть: методами математико-статистического моделирования (ПК-21).
Схема междисциплинарных связей
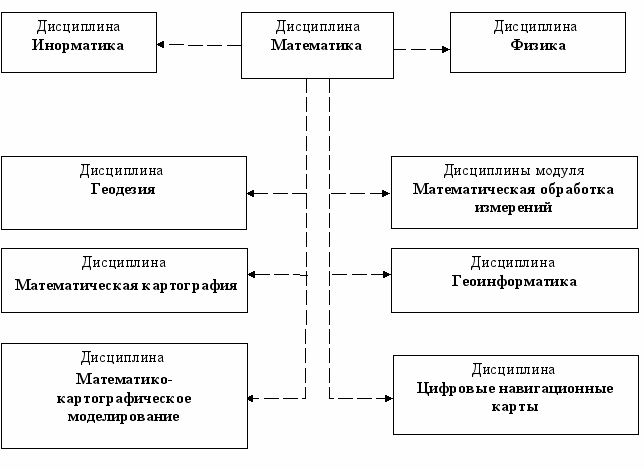
4. Структура и содержание дисциплины
Общая трудоемкость дисциплины «Математика» составляет 14 зачетных единиц, 504 часа.
4.1. Структура преподавания дисциплины
| № п/п | Раздел дисциплины | Семестр | Неделя семестра | Виды учебной работы, включая самостоятельную работу студентов и трудоемкость (в часах) | Формы текущего контроля успеваемости (по неделям семестра) Форма промежуточной аттестации (по семестрам) | ||
| лекции | лабораторные занятия | самостоятельная работа | |||||
| 1. | Введение в математический анализ | 1 | 1-4 | 8 | 12 | 13 | Проверка домашних заданий, приём контрольных заданий |
| 2. | Дифференциальное исчисление функции одной переменной | 1 | 5-8 | 8 | 12 | 13 | Проверка домашних заданий, приём контрольных заданий |
| 3. | Приложения дифференциального исчисления | 1 | 9-10 | 4 | 6 | 8 | Проверка домашних заданий, приём контрольных заданий |
| 4. | Неопределённый интеграл | 1 | 11-14 | 8 | 12 | 13 | Проверка домашних заданий, приём контрольных заданий |
| 5. | Определённый интеграл | 1 | 15-18 | 8 | 12 | 13 | Проверка домашних заданий, приём контрольных заданий |
| | Аттестация | 1 | | | | | Зачёт, экзамен |
| 6. | Векторная алгебра | 2 | 1-3 | 6 | 9 | 6 | Проверка домашних заданий, приём контрольных заданий |
| 7. | Плоскость и прямая | 2 | 4-7 | 8 | 12 | 8 | Проверка домашних заданий, приём контрольных заданий |
| 8. | Кривые второго порядка | 2 | 8-10 | 6 | 9 | 6 | Проверка домашних заданий, приём контрольных заданий |
| 9. | Поверхности второго порядка | 2 | 11-12 | 4 | 6 | 6 | Проверка домашних заданий, приём контрольных заданий |
| 10. | Матрицы. Системы линейных уравнений | 2 | 13-18 | 12 | 18 | 12 | Проверка домашних заданий, приём контрольных заданий |
| | Аттестация | 2 | | | | | Зачёт, экзамен |
| 11. | Функции многих переменных | 3 | 1-2 | 4 | 4 | 65 | Проверка домашних заданий, приём контрольных заданий |
| 12. | Числовые ряды | 3 | 3-4 | 4 | 4 | 6 | Проверка домашних заданий, приём контрольных заданий |
| 13. | Комплексные числа | 3 | 5-6 | 4 | 4 | 6 | Проверка домашних заданий, приём контрольных заданий |
| 14. | Типы дифференциальных уравнений | 3 | 7 | 2 | 2 | 2 | Проверка домашних заданий, приём контрольных заданий |
| 15. | Дифференциальные уравнения первого порядка | 3 | 8-11 | 8 | 8 | 10 | Проверка домашних заданий, приём контрольных заданий |
| 16. | Дифференциальные уравнения второго порядка | 3 | 12-14 | 6 | 6 | 10 | Проверка домашних заданий, приём контрольных заданий |
| 17. | Уравнения высших порядков | 3 | 15-18 | 8 | 8 | 10 | Проверка домашних заданий, приём контрольных заданий |
| | Аттестация | 3 | | | | | Зачёт, экзамен |
| 18. | Теория вероятностей | 4 | 1-6 | 12 | 12 | 8 | Проверка домашних заданий, приём контрольных заданий |
| 19. | Математическая статистика | 4 | 7-12 | 12 | 12 | 8 | Проверка домашних заданий, приём контрольных заданий |
| 20. | Дискретная математика | 4 | 13-17 | 10 | 10 | 8 | Проверка домашних заданий, приём контрольных заданий |
| | Аттестация | 4 | | | | | Зачёт, экзамен |
4.2. Содержание дисциплины и требования к уровню его освоения
Условные обозначения:
1. Качество усвоения знаний (А):
-
А1 -
знания, предусматривающие деятельность по воспроизведению;
А2 -
знания, предполагающие применение в ситуациях, аналогичных обучающим;
А3 -
знания, использующиеся в задачах, требующих установления новых связей между понятиями;
А4 -
знания, предполагающие способность достраивать систему связей новыми.
2. Уровень усвоения умений (Б):
-
Б1 -
ученический – умение пользоваться системой понятий при алгоритмической деятельности с внешне заданным алгоритмическим описанием (подсказкой);
Б2 -
(типовой – алгоритмический – уровень) – умение пользоваться системой понятий в ситуации, аналогичной обучающей;
Б3 -
(продуктивный эвристического типа) – умение применять систему знаний в ситуациях, требующих перестройки связей между уже сформированными понятиями;
Б4 -
(продуктивный творческого типа) – умение достраивать сформированные системы понятий новыми, самостоятельно сформированными.
3. Степень научности (В):
-
В1 -
(феноменологическая) – описательное изложение фактов и явлений; каталогизация объектов, констатация их свойств и качеств (известен определенный ряд однородных факторов), это использование преимущественно естественного языка и житейских понятий;
В2 -
(аналитико-синтетическая) – объяснение природы и свойств объектов и закономерностей явлений, часто качественное или полуколичественное (известны сущность первого порядка и свойства объектов и явлений, механизмов, управляющих функционированием анализируемых фактов и процессов);
В3 -
(прогностическая) – объяснение явлений данной области с созданием их количественной теории, моделирование основных процессов, аналитическим представлением законов и свойств (известны закономерности функционирования объектов конкретного вида);
В4 -
(аксиоматическая) – объяснение явлений с использованием высокой степени общности описания (большой объем материала и широкое использование научного языка, глубина проникновения в сущность явлений – известны общие законы функционирования объектов любой природы).
Раздел 1. Введение в математический анализ
Требуемая степень усвоения содержания раздела: А2Б2В1
Функция. Область определения. Способы задания. Основные элементарные функции, их свойства и графики. Числовые последовательности, их роль в вычислительных процессах. Предел числовой последовательности. Предел функции. Непрерывность функции в точке и на отрезке. Бесконечно малые функции. Сравнение бесконечно малых. Умение вычислять пределы.
Раздел 2. Дифференциальное исчисление функции одной переменной
Требуемая степень усвоения содержания раздела: А2Б2В1
Производная функции, её смысл в различных задачах. Дифференциал функции. Нахождение производной и дифференциала функции. Экстремум функции, её нахождение.
Раздел 3. Приложения дифференциального исчисления
Требуемая степень усвоения содержания раздела: А2Б2В1
Условия монотонности функции. Исследование на экстремум. Отыскание наибольшего и наименьшего значений функции. Точки перегиба. Асимптоты функций. Умение строить график функции по результатам исследования функции.
Раздел 4. Неопределённый интеграл
Требуемая степень усвоения содержания раздела: А2Б2В1
Первообразная. Неопределённый интеграл и его свойства. Методы интегрирования. Использование таблиц интегралов.
Раздел 5. Определённый интеграл
Требуемая степень усвоения содержания раздела: А2Б2В1
Задачи, приводящие к понятию определённого интеграла. Определённый интеграл и его свойства. Формула Ньютона-Лейбница. Геометрические приложения. Умение вычислять площадь криволинейной трапеции.
Раздел 6. Векторная алгебра
Требуемая степень усвоения содержания раздела: А2Б2В1
Линейные операции над векторами. Направляющие косинусы и длина вектора. Скалярное произведение векторов. Определители второго и третьего порядков, их свойства. Векторное произведение двух векторов. Смешанное произведение трёх векторов. Условия коллинеарности, ортогональности и компланарности векторов.
Раздел 7. Плоскость и прямая
Требуемая степень усвоения содержания раздела: А2Б2В1
Плоскость и прямая в пространстве. Взаимное положение. Прямая на плоскости. Угол между прямыми. Расстояние от точки до прямой.
Раздел 8. Кривые второго порядка
Требуемая степень усвоения содержания раздела: А2Б2В1
Кривые второго порядка: окружность, эллипс, гипербола, парабола; их геометрические свойства и уравнения. Технические приложения геометрических свойств кривых.
Раздел 9. Поверхности второго порядка
Требуемая степень усвоения содержания раздела: А2Б2В1
Цилиндрические поверхности. Сфера, конусы, эллипсоид, гиперболоиды, параболоиды. Геометрические свойства этих поверхностей. Технические приложения геометрических свойств поверхностей.
Раздел 10. Матрицы. Системы линейных уравнений
Требуемая степень усвоения содержания раздела: А2Б2В1
Матрицы, действия с ними. Обратная матрица. Системы линейных алгебраических уравнений. Правило Крамера. Метод Гаусса. Умение решать системы из трёх уравнений.
Раздел 11. Функции многих переменных
Требуемая степень усвоения содержания раздела: А2Б2В1
Функции нескольких переменных. Частные производные и дифференциал функции двух переменных. Умение дифференцировать функции двух переменных.
Раздел 12. Числовые ряды
Требуемая степень усвоения содержания раздела: А2Б2В1
Числовые ряды. Сходимость, Методы исследования сходимости.
Раздел 13. Комплексные числа
Требуемая степень усвоения содержания раздела: А2Б2В1
Комплексные числа, действия с ними. Геометрическое представление.
Раздел 14. Типы дифференциальных уравнений
Требуемая степень усвоения содержания раздела: А2Б2В1
Физические задачи, приводящие к дифференциальным уравнениям. Обыкновенные дифференциальные уравнения. Понятие о дифференциальных уравнениях в частных производных.
Раздел 15. Дифференциальные уравнения первого порядка
Требуемая степень усвоения содержания раздела: А2Б2В1
Обыкновенные дифференциальные уравнения первого порядка. Основные типы, их интегрирование.
Раздел 16. Дифференциальные уравнения второго порядка
Требуемая степень усвоения содержания раздела: А2Б2В1
Дифференциальные уравнения второго порядка. Линейные дифференциальные уравнения с постоянными коэффициентами. Уравнения с правой частью специального вида.
Раздел 17. Уравнения высших порядков
Требуемая степень усвоения содержания раздела: А2Б2В1
Простейшие дифференциальные уравнения высших порядков. Линейные дифференциальные уравнения n-ого порядка.
Раздел 18. Теория вероятностей
Требуемая степень усвоения содержания раздела: А2Б2В1
Основные понятия теории вероятностей. Теоремы сложения и умножения вероятностей. Полная вероятность. Формула Байеса. Непрерывная случайная величина.
Раздел 19. Математическая статистика
Требуемая степень усвоения содержания раздела: А2Б2В1
Статистическое распределение выборки. Характеристики вариационного ряда. Точечные оценки параметров распределения. Элементы корреляционного анализа.
Раздел 20. Дискретная математика
Требуемая степень усвоения содержания раздела: А2Б2В1
Элементы алгебры логики высказываний. Элементы теории множеств. Элементы комбинаторики. Основные понятия теории графов.
4.3. Соотношение разделов учебной дисциплины и формируемых в них компетенций
-
Темы,разделы дисциплины
Количество часов
Компетенции
Σ общее коли-
чество компетенций
ок-1
ок-2
Пк-1
Пк-21
Раздел 1
33
+
+
+
3
Раздел 2
33
+
+
+
3
Раздел 3
18
+
+
+
3
Раздел 4
33
+
+
+
3
Раздел 5
33
+
+
+
3
Раздел 6
21
+
+
+
3
Раздел 7
28
+
+
+
3
Раздел 8
21
+
+
+
3
Раздел 9
16
+
+
+
3
Раздел 10
42
+
+
+
3
Раздел 11
14
+
+
+
3
Раздел 12
14
+
+
+
3
Раздел 13
14
+
+
+
3
Раздел 14
6
+
+
+
3
Раздел 15
26
+
+
+
3
Раздел 16
22
+
+
+
3
Раздел 17
26
+
+
+
3
Раздел 18
32
+
1
Раздел 19
32
+
1
Раздел 20
28
+
1
Итого
504
5. Образовательные технологии
При реализации программы дисциплины «Математика» в часы, отведенные для аудиторных занятий (320 часов), занятия проводятся в виде лекций – 142 часа и по группам в виде практических занятий – 178 часа. Самостоятельная работа студентов подразумевает занятия в виде консультаций и индивидуальной работы студента (184 часа).
6. Оценочные средства для текущего контроля успеваемости, промежуточной аттестации по итогам освоения дисциплины и учебно-методическое обеспечение самостоятельной работы студентов
По каждому разделу студенту выдаются домашние задания и индивидуальные контрольные работы, которые оцениваются по пятибалльной системе.
Общие критерии оценки ответов студентов
| Для отличной оценки | Для хорошей оценки | Для удовлетвори- тельной оценки | Для неудовлетвори- тельной оценки |
| Наличие глубоких, исчерпывающих знаний предмета в объеме освоенной программы; знание основной (обязательной) литературы; правильные и уверенные действия, свидетельствующие о наличии твердых знаний и навыков в использовании технических средств; полное, четкое, грамотное и логически стройное изложение материала; свободное применение теоретических знаний при анализе практических вопросов. | Те же требования, но в ответе студента по некоторым перечисленным показателям имеются недостатки принципиаль-ного характе-ра, что вызвало замечания или поправки преподавателя. | Те же требования, но в ответе имели место ошибки, что вызвало необходимость помощи в виде поправок и наводящих вопросов преподавателя. | Наличие ошибок при изложении ответа на основные вопросы программы, свидетельствующих о неправильном понимании предмета; при решении практических задач показано незнание способов их решения, материал изложен беспорядочно и неуверенно. |
7. Учебно-методическое и информационное обеспечение дисциплины
а) основная литература:
1. Письменный Д.Т. Конспект лекций по высшей математике (полный курс). Москва, Айрис пресс, 2006г.
2. Берман Г.Н. Сборник задач по курсу математического анализа. С.-Петербург, Профессия, 2004г.
3. Журбенко Л.Н. и др. Математика в примерах и задачах (учебное пособие). Москва, Инфа-М, 2009г.
4. Гмурман В.Е. Теория вероятностей и математическая статистика. Москва, Высшая школа, 2003г.
5. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. Москва, Высшая школа, 2002г.
б) дополнительная литература:
1. Шипачев В.С. Курс высшей математики. Москва, Проспект, 2004г.
2. Пискунов Н.С. Дифференциальное и интегральное исчисления. Т.1,2. Москва, Интегралл-пресс, 2001г.
3. Данко Л.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Части 1 и 2. Москва, Оникс 21 век Мир и Образование, 2003г.
4. Вентцель Е.С. Теория вероятностей. Мрсква, Наука, 1964г.
5. Письменный Д.Т. Конспект лекций по теории вероятностей и математической статистике. Москва, Айрис-Пресс, 2004г.;
в) программное обеспечение и Интернет-ресурсы:
программные пакеты: Matlab, Mathcad, Excel и другие;
информационно-справочные и поисковые системы: образовательный математический сайт «Exponenta» и другие учебные математические сайты и форумы интернета.
- Материально-техническое обеспечение дисциплины
Учебные аудитории с доской для проведения занятий.
Программа составлена в соответствии с требованиями ФГОС ВПО с учетом рекомендаций ПрООП ВПО по направлению подготовки 021300 «Картография и геоинформатика».
Авторы: Бабаева Нахида Гасановна, доцент, к.ф-м.н., Московский государственный университет геодезии и картографии (МИИГАиК).
Программа одобрена на заседании Методической комиссии факультета картографии и геоинформатики от ___________ года, протокол № ________.
