Рабочая программа по дисциплине Численные методы для специальности 050202 Информатика, математика

Вид материала

Содержание

Подобный материал:

КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Математический факультет

Кафедра Информационных образовательных технологий

УТВЕРЖДЕНО

Научно-методическим Советом

математического ф-та КубГУ

протокол №____

"____"__________2005г.

РАБОЧАЯ ПРОГРАММА

по дисциплине

Численные методы

для специальности

050202 - Информатика, математика.

	Дневная форма обучения 5 семестр	Дневная форма обучения 6 семестр
Лекции, ч.	26	16
Практические занятия, ч.	26	18
Аудиторных часов	52	34
Всего часов	260
Экзамен		Экз.
Зачёт	Зач.
Самостоятельная работа, ч.	58	58

Рекомендовано кафедрой

Информационных образовательных технологий

« 01 » __ 09 ____ 2005г.

д.п.н., проф.

Грушевский С.П.

Краснодар, 2005

Рабочая программа составлена на основании ГОСУДАРСТВЕННОГО ОБРАЗОВАТЕЛЬНОГО СТАНДАРТА ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ, направление подготовки дипломированного специалиста - 050202 – Информатика, математика.

Составитель программы:

д.ф.-м.н., проф.

Усатиков С.В.

Программа одобрена на заседании НМС математического ф-та

«__»_________ 2005г., протокол №___

Председатель НМС

1. ЦЕЛИ И ЗАДАЧИ ДИСЦИПЛИНЫ, ЕЁ МЕСТО В УЧЕБНОМ ПРОЦЕССЕ. ТРЕБОВАНИЯ К УРОВНЮ ОСВОЕНИЯ СОДЕРЖАНИЯ ДИСЦИПЛИНЫ.

Цель курса – формирование у студента представлений о численных методах решения задач на ЭВМ.

Основная задача курса – углубление математического образования и развитие практических навыков в области прикладной математики. Студенты должны быть готовы использовать полученные в этой области знания как при изучении смежных дисциплин, так и в профессиональной деятельности, в частности при обучении информатике старшеклассников средней школы.

В результате изучения дисциплины студент должен знать:

основы теории погрешностей и теории приближений;
основные численные методы алгебры;
методы построения интерполяционных многочленов;
методы численного дифференцирования и интегрирования;
методы численного решения дифференциальных уравнений;

а также должен уметь:

численно решать уравнения, применяя для этого следствия из теоремы о сжимающих отображениях;
использовать основные понятия теории среднеквадратичных приближений для построения элемента наилучшего приближения (в интегральном и дискретном вариантах);
интерполировать и оценить возникающую погрешность;
применять формулы численного дифференцирования и интегрирования;
применять методы численного решения дифференциальных уравнений.

Перечень дисциплин, усвоение которых студентами необходимо для изучения данной дисциплины:

Наименование дисциплины	Наименование разделов (тем)
Школьный курс математики Математический анализ Алгебра и геометрия	Все темы Все темы Все темы

2. СОДЕРЖАНИЕ ДИСЦИПЛИНЫ.

2.1.Содержание лекций.

Тема 1. Приближение функций.

Предмет вычислительной математики. Специфика машинных вычислений. Элементарная теория погрешностей. Задача алгебраической интерполяции. Существование и единственность решения. Интерполяционный полином в форме Лагранжа и в форме Ньютона. Оценка погрешности интерполяционных формул, остаточный член интерполяции. Оценка погрешности интерполяции для функций, заданных с ошибками. Тригонометрическая интерполяция. Сглаживание функций. Сплайны. Интерполяция сплайнами, понятие о сглаживающих сплайнах.

Тема 2. Численное дифференцирование и интегрирование.

Численное дифференцирование. Простейшие формулы численного дифференцирования. Оценка погрешности. Оптимальный шаг численного дифференцирования. Численное интегрирование. Простейшие квадратурные формулы (прямоугольников, трапеций, Симпсона) и оценка их погрешности..

Тема 3. Решение уравнений и систем, методы линейной алгебры.

Методы приближенного решения нелинейных алгебраических уравнений. Принцип сжимающих отображений. Метод простой итерации. Метод Ньютона. Теорема о квадратичной сходимости метода Ньютона. Понятие о дискретных отображениях, их связь с итерационными методами. Решение систем линейных алгебраических уравнений. Прямые методы: Гаусса, Гаусса с выбором главного элемента. Обусловленность матрицы линейной системы. Оценка погрешности численных методов решения алгебраических систем. Итерационные методы решения линейных систем. Метод простых итераций, метод Зейделя, метод верхней релаксации. Проблема поиска собственных значений матрицы.

Тема 4. Обыкновенные дифференциальные уравнения и уравнения математической физики.

Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений (ОДУ). Простейшие численные методы. Аппроксимация, устойчивость, сходимость. Теорема о связи аппроксимации, устойчивости, сходимости. Методы Рунге-Кутты решения систем ОДУ. Устойчивость методов Рунге-Кутты. Экспоненциальная оценка устойчивости, устойчивость при различных типах поведения решения (на устойчивых и «не неустойчивых» траекториях). Линейные многошаговые методы (типа Адамса). Управление длиной шага при численном интегрировании систем ОДУ. Правило Рунге оценки погрешности. Численное решение краевых задач для ОДУ. Линейное уравнение второго порядка. Метод стрельбы. Метод прогонки для задачи Штурма-Лиувилля. Численные методы решения краевой задачи для дифференциальных уравнений в частных производных (уравнение теплопроводности, волновое уравнение, задача Дирихле для уравнения Пуассона). Явные и неявные разностные схемы, метод дробных шагов.

Раздел, подраздел, содержание	Продолжительность, час.	Литература для самостоятельной работы
1). Особенности математических вычислений, реализуемых на ЭВМ. Приближённые числа и действия с ними.	2	1-4
2) Приближение функций многочленами. Интерполяционный полином в форме Лагранжа.	2	1-4
3) Интерполяционный полином в форме Ньютона.	2	1-4
4) Кубические сплайны.	2	1-4
5) Метод наименьших квадратов, тригонометрический многочлен. Сглаживание наблюдений.	2	1-4
6) Численное дифференцирование. Простейшие формулы численного дифференцирования. Оценка погрешности. Оптимальный шаг численного дифференцирования.	2	1-4
7) Численное интегрирование. Квадратурные формулы: прямоугольников, трапеций, Симпсона. Правило Рунге и уточнение по Ричардсону.	2	1-4
8) Метод Монте-Карло.	2	1-4
9) Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений (ОДУ). Аппроксимация, устойчивость, сходимость. Сеточные функции. Метод Эйлера.	2	1-4
10) Методы Рунге-Кутты решения систем ОДУ. Применение правила Рунге практической оценки погрешности.	2	1-4
11) Метод Адамса. Проверка существования точного решения по найденному приближённому.	2	1-4
12)Обзор.	2	1-4
13) Резерв.	2
14) Решение систем линейных алгебраических уравнений. Прямые методы: Гаусса, Гаусса с выбором главного элемента. Вычисление определителей и обратной матрицы.	2	1-4
15) Обусловленность матрицы линейной системы. Оценка погрешности численных методов решения алгебраических систем.	2	1-4
16) Итерационные методы решения линейных систем. Метод простых итераций, метод Зейделя. Метод прогонки.	2	1-4
17) Частичные проблемы собственных значений матрицы.	2	1-4
18) Методы приближенного решения нелинейных алгебраических уравнений. Метод деления отрезка пополам. Метод простой итерации.	2	1-4
19) Метод Ньютона (метод касательных). Решение системы алгебраических уравнений.	2	1-4
20) Численные методы решения краевой задачи для дифференциальных уравнений в частных производных (уравнение теплопроводности, волновое уравнение, задача Дирихле для уравнения Пуассона). Явные и неявные разностные схемы. Метод сеток.	2	1-4
21) Резерв	2

2.2. Перечень практических занятий.

Тема занятия	Количество часов
Тема занятия	Количество часов
1) Численное и аналитическое решение алгебраических и дифференциальных уравнений в MathCAD и Maple.	2
2) Средства языка программирования MathCAD и Maple.	2
3) Алгоритмы интерполяции функций.	2
4) Численное дифференцирование.	2
5) Численное интегрирование.	2
6) Сглаживание функций.	2
7) Численные методы решения задачи Коши для обыкновенного дифференциального уравнения 1-го порядка.	2
8) Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений.	2
9) Выполнение ИЗ№1.	2
10) Выполнение ИЗ№1.	2
11) Защита ИЗ№1.	2
12) Резерв.	2
13) Ликвид. долгов.	2
14) Решение систем линейных алгебраических уравнений: прямые методы.	2
15) Решение систем линейных алгебраических уравнений: итерационные методы.	2
16) Методы приближенного решения нелинейных алгебраических уравнений.	2
17) Численные методы решения краевой задачи для дифференциальных уравнений в частных производных.	2
18) Выполнение ИЗ№2.	2
19) Выполнение ИЗ№2.	2
20) Защита ИЗ№2.	2
21) Резерв.	2
22) Ликвид. долгов.	2

2.5 Самостоятельная работа студентов.

Вид работы (индивидуальное задание)	Сроки выполнения (недели семестра)	Форма отчётности
ИЗ№1: Программная реализация алгоритмов численных методов (средствами языка Maple): интерполяция функций, численное дифференцирование и интегрирование, задача Коши и краевая задача.	15	Защита
ИЗ№2: Программная реализация алгоритмов численных методов (средствами языка Maple): системы линейных уравнений, нелинейные алгебраические уравнения, уравнения в частных производных.	15	Защита

3. УЧЕБНО-МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ ПО ДИСЦИПЛИНЕ.

3.1. Основная литература.

Рябенький В. С. Введение в вычислительную математику. 2-е изд. - М: Физматлит, 2000. – 296 с.
Бахвалов Н.С., Жидков Н.П., Кобельков Г.Г. Численные методы. 8-е изд. – М.: Лаборатория Базовых Знаний, 2000. – 624 с.
Лобанов А.И., Петров И.Б. Вычислительные методы для анализа моделей сложных динамических систем. Часть 1. – М.: МФТИ, 2000. – 168 с.
Косарев В.И. 12 лекций по вычислительной математике. 2 изд. – М.: Изд-во МФТИ, 2000. – 224 с.

Дополнительная литература

Федоренко Р.П. Введение в вычислительную физику. – М.: Изд. МФТИ, 1994.– 528 с.
Калиткин Н.Н. Численные методы. – М.: Наука, 1978. – 512с.
Хайрер Э., Нерсетт С., Боннер Г. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи. – М.: Мир, 1990. – 512с.
Хайрер Э., Боннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально алгебраические задачи. – М.: Мир, 1999. – 685 с.
Амосов А.А., Дубинский Ю.А., Копченова Н.П. Вычислительные методы для инженеров. – М.: Высшая школа, 1994.
Каханер Д., Моулер К., Нэш С. Численные методы и программное обеспечение. – М.: Мир, 1998. – 575 с.
Марчук Г.И. Методы вычислительной математики. – М.: Наука, 1989. – 608с.
Самарский А.А., Гулин А.В. Численные методы. – М.: Наука, 1989.
Прохоров Г.В., Леденёв М.А., Колбеев В.В. Пакет символьных вычислений Maple V - М.: Петит, 1997.
Прохоров Г.В.Пакет символьных вычислений Maple V - М.: Изд.МГТУ им.Н.Э.Баумана, 2001.
Дьяконов В.П. MathCAD 2000: Учебный курс. - СПб.: Питер, 2001.

3.2. Перечень пособий, методических указаний и материалов,

используемых в учебном процессе.

Усатиков С.В., Фёдоров А.А. Введение в MathCAD. Методич. указания для слушателей ФПКП и студ. всех форм обучения - Краснодар: Изд. КубГТУ, 1998. - 23с.

3.3.Перечень компьютерных программ, используемых в учебном процессе.

1.Mathematica Computer Aided Design (MathCAD) 2000 Professional, (MathSoft Inc., USA).

2.Maple V Power Edition ver. 4.0, (Maple Waterloo Inc., Canada).

3. Statistica ver.5.5, (StatSoft Inc., USA).

ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ВОПРОСОВ К ЭКЗАМЕНУ

Особенности математических вычислений, реализуемых на ЭВМ.
Приближённые числа и действия с ними.
Приближение функций многочленами. Интерполяционный полином в форме Лагранжа.
Интерполяционный полином в форме Ньютона.
Кубические сплайны.
Метод наименьших квадратов, тригонометрический многочлен.
Сглаживание наблюдений.
Численное дифференцирование. Простейшие формулы численного дифференцирования. Оценка погрешности. Оптимальный шаг численного дифференцирования.
Численное интегрирование. Квадратурные формулы: прямоугольников, трапеций, Симпсона. Правило Рунге и уточнение по Ричардсону.
Метод Монте-Карло.
Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений (ОДУ). Аппроксимация, устойчивость, сходимость. Сеточные функции. Метод Эйлера.
Методы Рунге-Кутты решения систем ОДУ. Применение правила Рунге практической оценки погрешности.
Метод Адамса. Проверка существования точного решения по найденному приближённому.
Решение систем линейных алгебраических уравнений. Прямые методы: Гаусса, Гаусса с выбором главного элемента. Вычисление определителей и обратной матрицы.
Обусловленность матрицы линейной системы. Оценка погрешности численных методов решения алгебраических систем.
Итерационные методы решения линейных систем. Метод простых итераций, метод Зейделя.
Метод прогонки.
Частичные проблемы собственных значений матрицы.
Методы приближенного решения нелинейных алгебраических уравнений. Метод деления отрезка пополам. Метод простой итерации.
Метод Ньютона (метод касательных). Решение системы алгебраических уравнений.
Численные методы решения краевой задачи для дифференциальных уравнений в частных производных (уравнение теплопроводности, волновое уравнение, задача Дирихле для уравнения Пуассона). Явные и неявные разностные схемы.
Метод сеток. Задача Дирихле. Уравнение Лапласа в конечных разностях.

ПРИМЕРНАЯ ТЕМАТИКА КУРСОВЫХ РАБОТ

Генерация вариантов заданий контрольных мероприятий дисциплины «Численные методы».

Является разработкой вспомогательного ПО для преподавателя дисциплины, с целью выдачи заданного количества вариантов определённых заданий, с ответами и основной промежуточной информацией для проверки хода выполнения этих заданий. Руководитель оговаривает тему и тип заданий, алгоритм их генерации, требования к интерфейсу с преподавателем. Цель работы- реализация указанных алгоритмов на языках программирования Delphi или C++.

ссылка скрыта

ссылка скрыта

Усатиков С.В., Грушевский С.П. Опыт разработки и применения в курсе высшей математики компьютерных автоматизированных систем генерации вариативных индивидуальных заданий // Современные технологии обучения и контроля. Юбилейный сб. научн. тр. КубГТУ, - Краснодар: Изд. КубГТУ, 1998.- с.38-47.

ссылка скрыта

ссылка скрыта

ссылка скрыта

Java и PHP – реализации генерации заданий для самопроверки по дисциплине «Дискретная математика».

Является разработкой части электронного учебного пособия, следующей после изучения теоретического материала и разбора решений практических задач. Руководитель оговаривает тему и тип заданий, алгоритм их генерации, требования к интерфейсу с обучаемым. Цель работы - реализация указанных алгоритмов на языках программирования Java или PHP.

Усатиков С.В., Грушевский С.П., Натальченко А.Р., Грушевский П.С. Об одном подходе к конструированию автоматизированных систем генерации индивидуальных заданий / Инновационные процессы в высшей школе. Материалы V Всероссийской научн.-практич. конф., часть II – Краснодар: Изд. КубГТУ, 1999 – с.95-97

ссылка скрыта

ссылка скрыта

Flash – анимация технологии решения практических заданий по дисциплине «Математическая логика и теория алгоритмов».

Является разработкой части электронного учебного пособия, следующей после изучения теоретического материала курса. Руководитель оговаривает тему и содержание заданий, методику изложения хода их решения и способы иллюстрации технологии их выполнения. Цель работы - реализация методики разбора решений практических задач в виде, максимально приближенном к устному объяснению с вычислительным и графическим сопровождением.

ссылка скрыта

ссылка скрыта

Flash – анимация логики вывода утверждений и теорем курса математического анализа.

Является разработкой первой части электронного учебного пособия, предназначенной для изучения теоретического материала курса. Руководитель оговаривает тему и содержание теоретического материала, методику изложения доказательств утверждений и теорем курса, способы иллюстрации логики их вывода. Цель работы - реализация методики логического построения курса, приближенной к устному объяснению с вычислительным и графическим сопровождением.

ссылка скрыта

ссылка скрыта

Олимпиады по математике для студентов нематематических специальностей.

Разработка учебно-методических материалов для подготовки к I (внутривузовскому) туру Всероссийской студенческой олимпиады по математике. Классификация задач по темам и хронологически, составление указаний, вариантов решений, ответов.

Беркович Ф.Д., Федий В.С., Шлыков В.И.Задачи студенческих математических олимпиад с указаниями и решениями: Учеб. пособие / Новочеркасск: ЮРГТУ (НПИ), 2001. -192с.

ИЗ№1. Программная реализация алгоритмов численных методов (средствами языка Maple):

интерполяция функций, численное дифференцирование и интегрирование, задача Коши и краевая задача.

Ниже перечислены варианты задач, которые необходимо выполнить в системе Maple (или в системе MathCAD) применительно к данным, записанным в виде текстовых файлов (имя файла означает номер варианта). Номер задачи совпадает с номером варианта данных (= номеру по списку группы).

Задача 1. Дан файл с n значениями некоторой функции f(x). Интерполировать f(x) с помощью многочлена Лагранжа в 10n точках, построить график и сравнить с линейной интерполяцией. Проверить результат с помощью модуля numapprox.

Задача 2. Дан файл с n значениями некоторой функции f(x). Интерполировать f(x) с помощью многочлена Ньютона в 10n точках, построить график и сравнить с линейной интерполяцией. Проверить результат с помощью модуля numapprox.

Задача 3. Дан файл с n значениями некоторой функции f(x). Интерполировать f(x) с помощью кубических сплайнов (со свободными концами) в 10n точках, построить график и сравнить с линейной интерполяцией. Проверить результат с помощью модуля numapprox.

Задача 4. Дан файл с n значениями некоторой функции f(x). Интерполировать f(x) с помощью кубических сплайнов (периодических) в 10n точках, построить график и сравнить с линейной интерполяцией. Проверить результат с помощью модуля numapprox.

Задача 5. Дан файл с n значениями некоторой функции f(x). Найти численную производную и построить её график. Проверить результат с помощью оператора diff.

Задача 6. Дан файл с n значениями некоторой функции f(x). Найти численную производную с помощью многочлена Лагранжа и построить её график. Проверить результат с помощью оператора diff.

Задача 7. Дан файл с n значениями некоторой функции f(x). Найти численную производную с помощью кубического сплайна и построить её график. Проверить результат с помощью оператора diff.

Задача 8. Дан файл с n значениями некоторой функции f(x) с шумом ε(x), 0≤x≤n-1, шаг по x равен 1. Сгладить значения функции и построить её график. Проверить результат с помощью модуля numapprox.

Задача 9. Дан файл с n значениями некоторой функции f(x) с шумом ε(x), 0≤x≤n-1, шаг по x равен 1. Найти производную от f(x) и построить её график. Проверить результат с помощью модуля numapprox.

Задача 10. Дан файл с n значениями некоторой функции f(x) на некотором отрезке. Найти определённый интеграл по формуле трапеций. Проверить результат с помощью оператора int.

Задача 11. Дан файл с n значениями некоторой функции f(x) на некотором отрезке. Найти определённый интеграл по формуле Симпсона. Проверить результат с помощью оператора int.

Задача 12. Дан файл с n значениями некоторой функции f(x) на некотором отрезке. Найти определённый интеграл методом Монте-Карло. Проверить результат с помощью оператора int.

Задача 13. Дан файл с таблично заданной функцией f(x,y). Найти решения задачи Коши

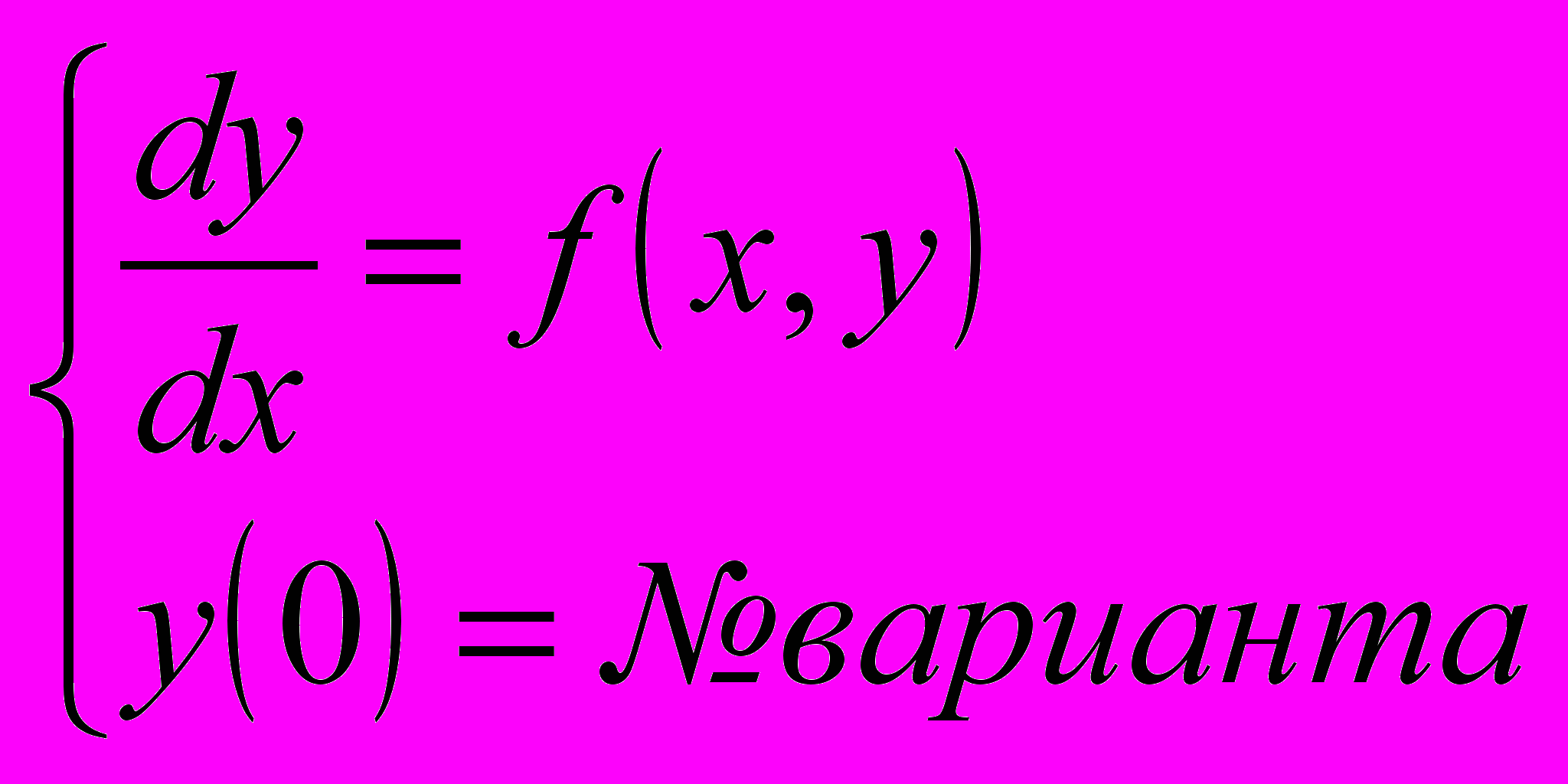методом Рунге-Кутта (предиктор-корректор). Проверить результат с помощью оператора dsolve или модуля DEtools.

Задача 14. Дан файл с таблично заданной функцией f(x,y). Найти решения задачи Коши

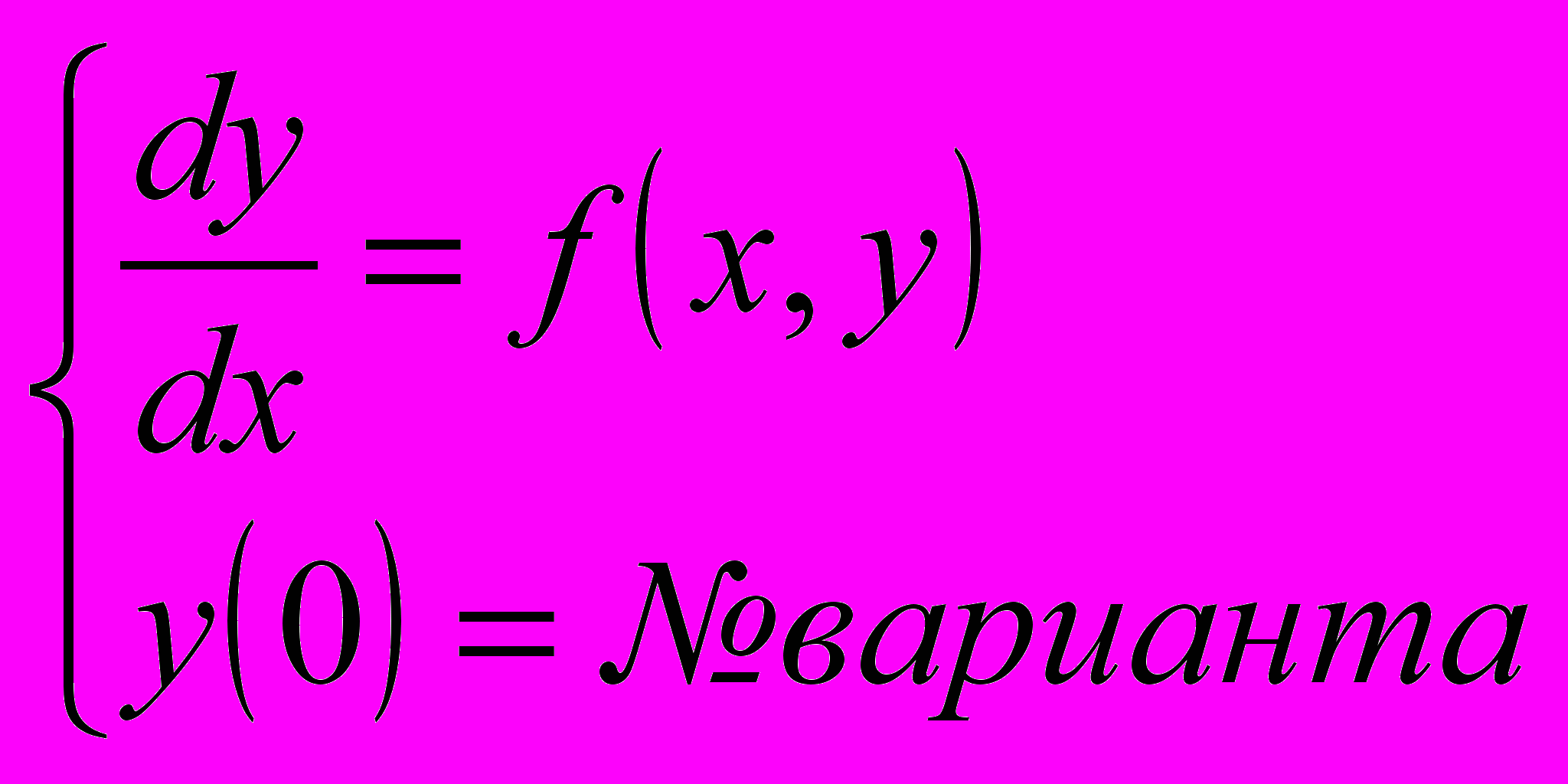усовершенствованным методом Эйлера. Проверить результат с помощью оператора dsolve или модуля DEtools.

Задача 15. Дан файл с таблично заданной функцией f(x,y). Найти решения задачи Коши

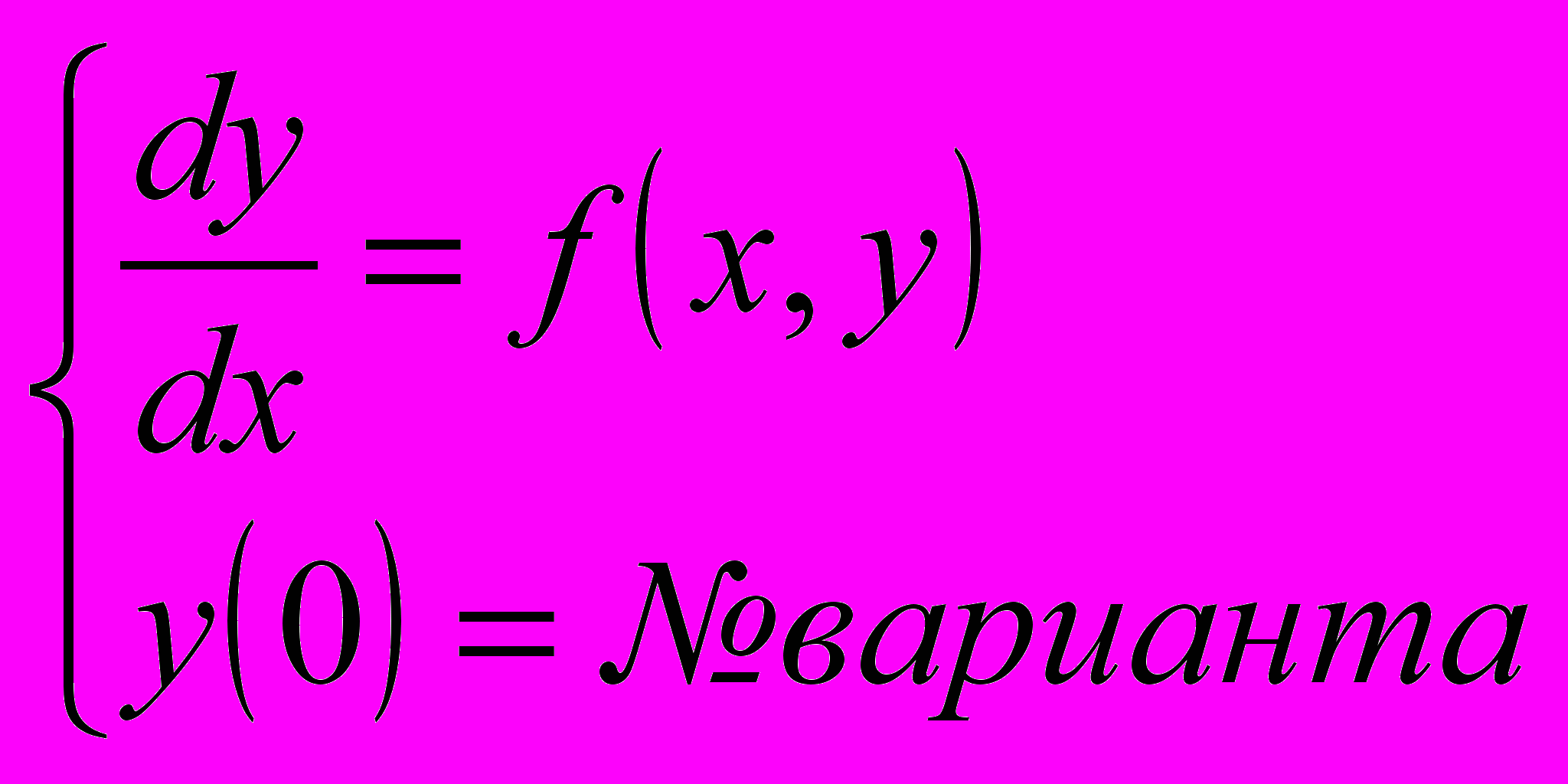методом Рунге-Кутта (4-го порядка точности). Проверить результат с помощью оператора dsolve или модуля DEtools.

Задача 16. Дан файл с таблично заданной функцией f(x,y). Найти решения задачи Коши

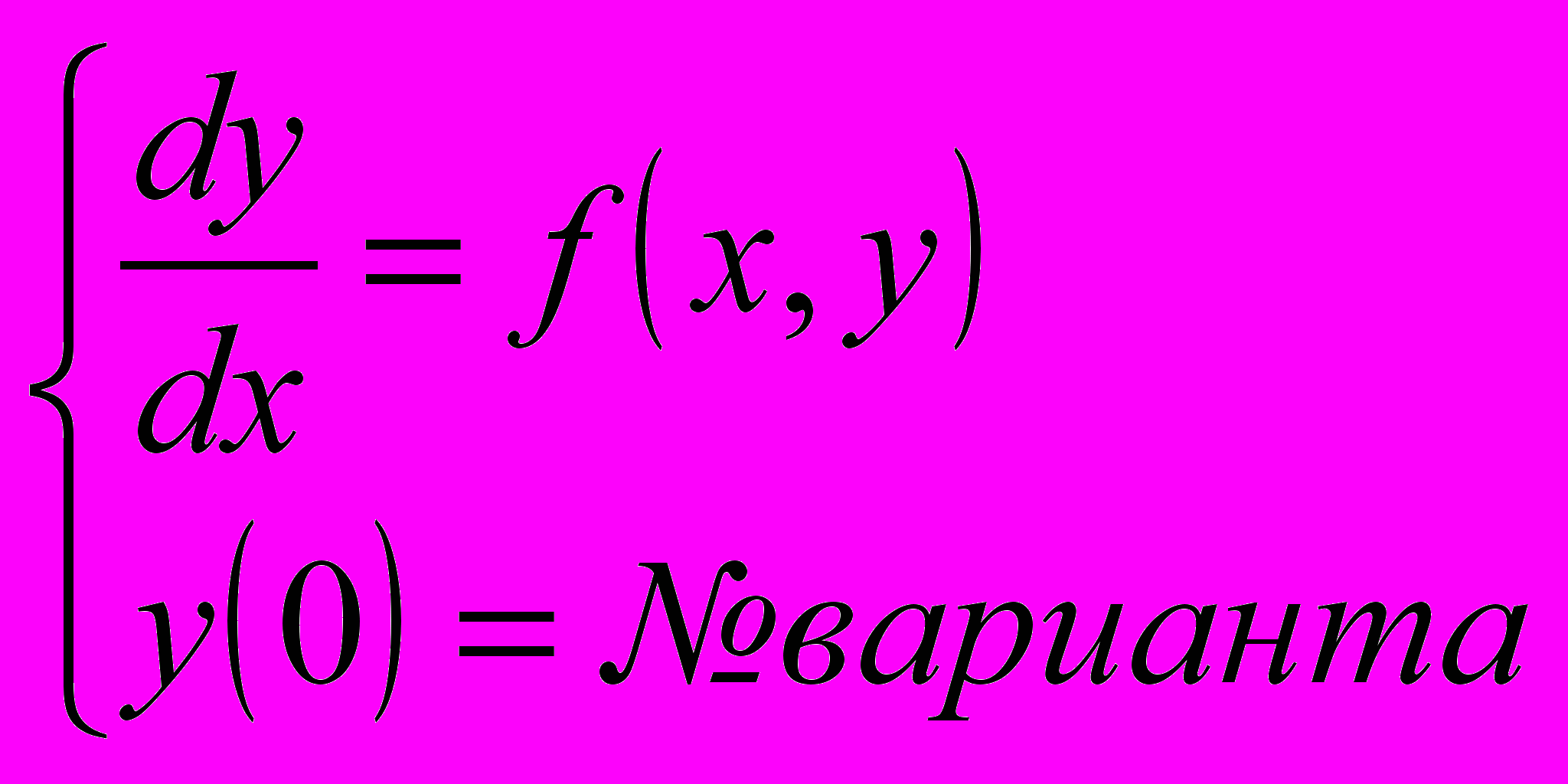методом Адамса. Проверить результат с помощью оператора dsolve или модуля DEtools.

Задача 17. Дан файл с таблично заданной функцией f(x), a≤x≤b. Найти решение краевой задачи

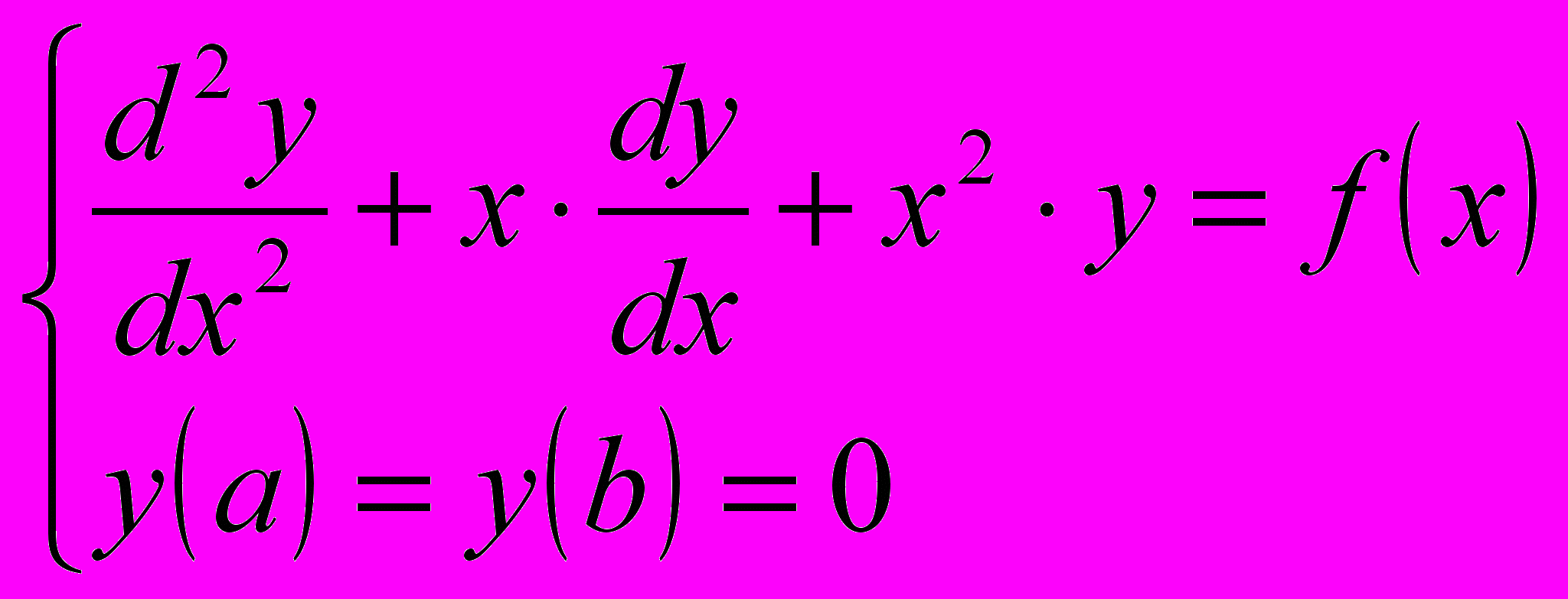разностным методом. Проверить результат с помощью оператора dsolve или модуля DEtools.

Задача 18. Дан файл с таблично заданной функцией f(x), a≤x≤b. Найти решение краевой задачи

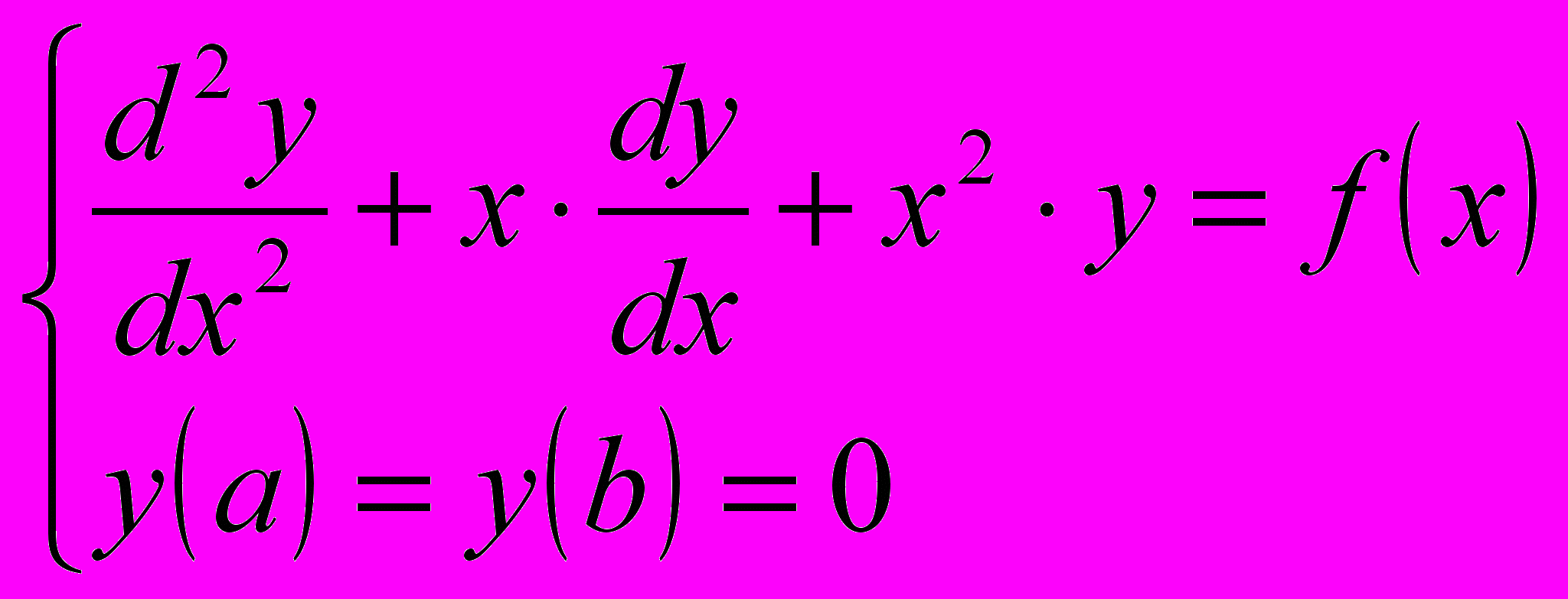методом минимизации невязки (коллокаций). Проверить результат с помощью оператора dsolve или модуля DEtools.

Задача 19. Дан файл с таблично заданной функцией f(x), a≤x≤b. Найти решение краевой задачи

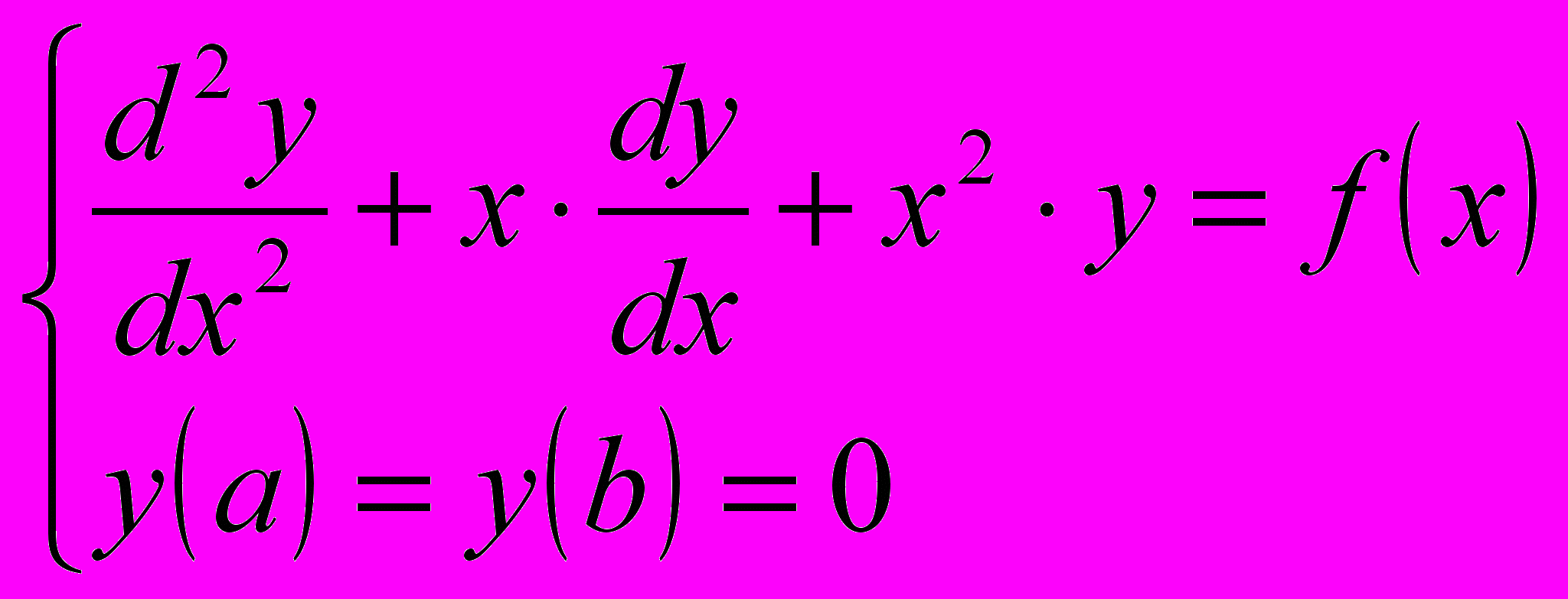методом минимизации невязки (интегральный МНК). Проверить результат с помощью оператора dsolve или модуля DEtools.

Задача 20. Дан файл с таблично заданной функцией f(x), a≤x≤b. Найти решение краевой задачи

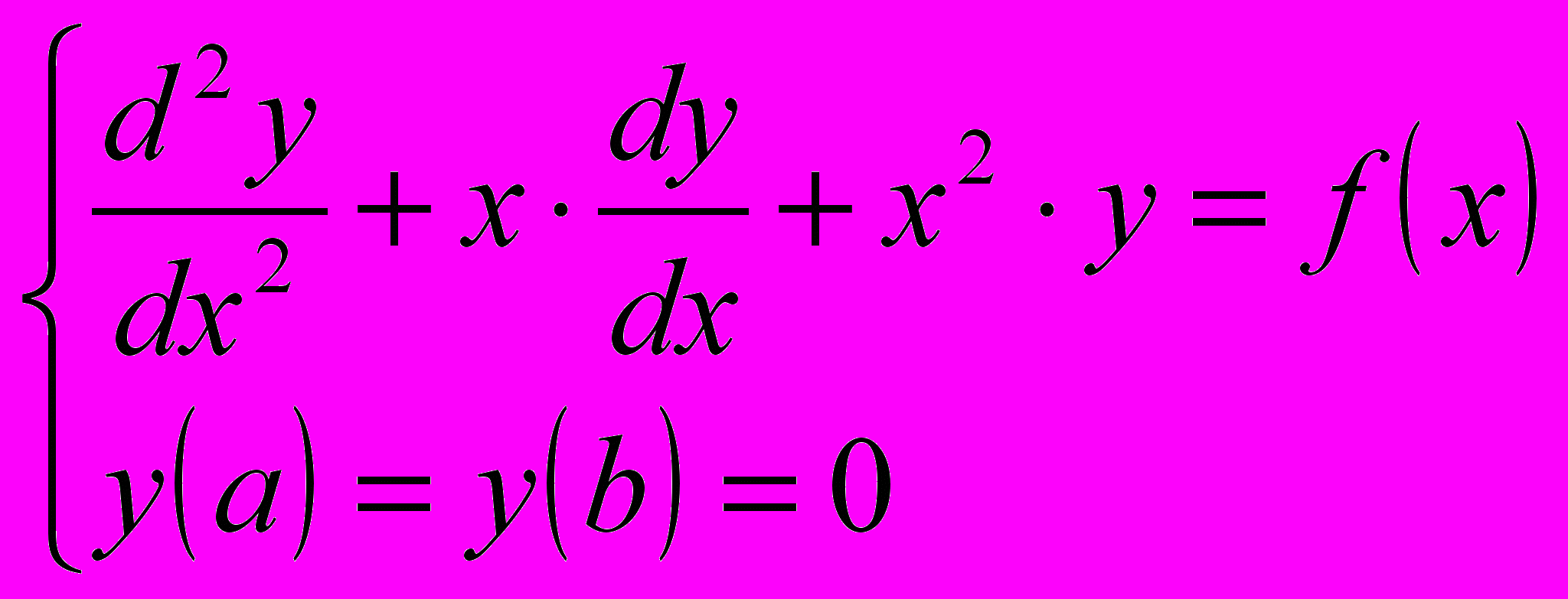методом минимизации невязки (дискретный МНК). Проверить результат с помощью оператора dsolve или модуля DEtools.

Задача 21. Дан файл с таблично заданной функцией f(x), a≤x≤b. Найти решение краевой задачи

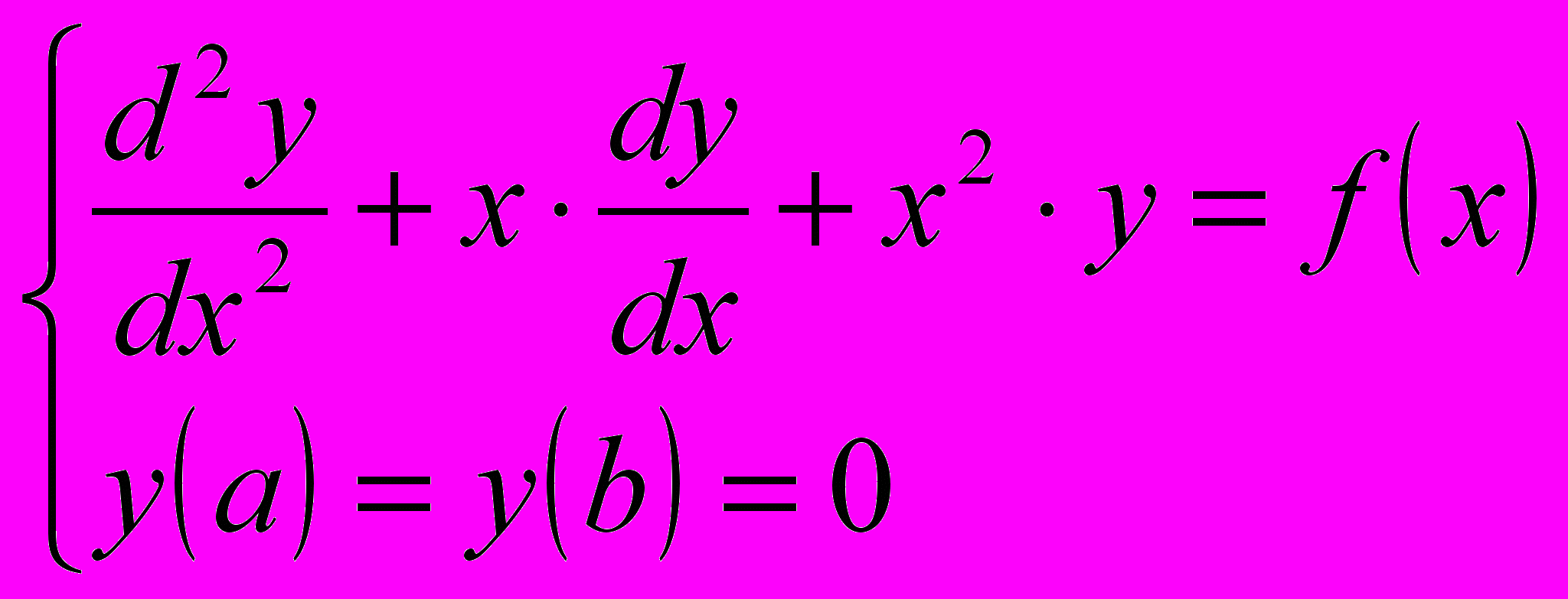методом минимизации невязки (подобластей). Проверить результат с помощью оператора dsolve или модуля DEtools.

Задача 22. Дан файл с таблично заданной функцией f(x), a≤x≤b. Найти решение краевой задачи

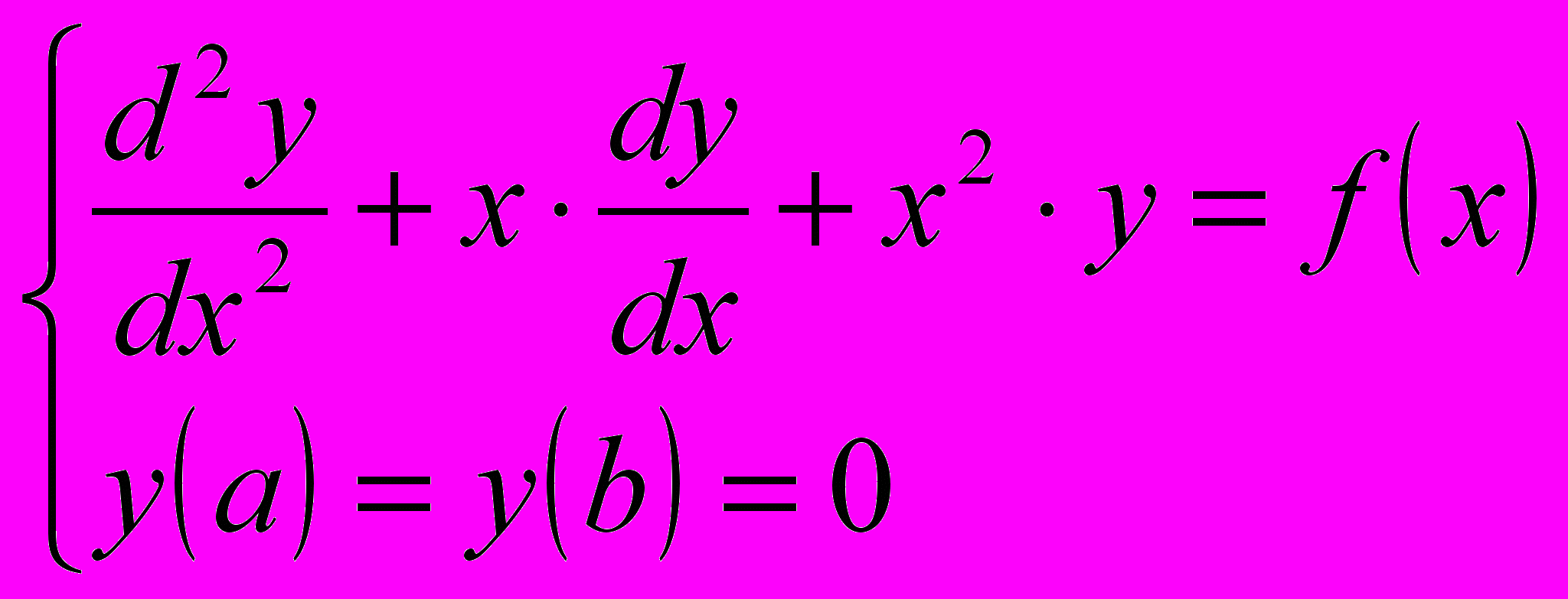методом Галёркина. Проверить результат с помощью оператора dsolve или модуля DEtools.

ИЗ№2. Программная реализация алгоритмов численных методов (средствами языка Maple):

системы линейных уравнений, нелинейные алгебраические уравнения, уравнения в частных производных.

Ниже перечислены варианты задач, которые необходимо выполнить в системе Maple (или в системе MathCAD) применительно к данным, записанным в виде текстовых файлов (имя файла означает номер варианта). Номер задачи указывается при выдаче задания и не обязательно совпадает с номером варианта данных (= номеру по списку группы).

Задача 1. Дан файл с матрицей A размером n∙n и вектором

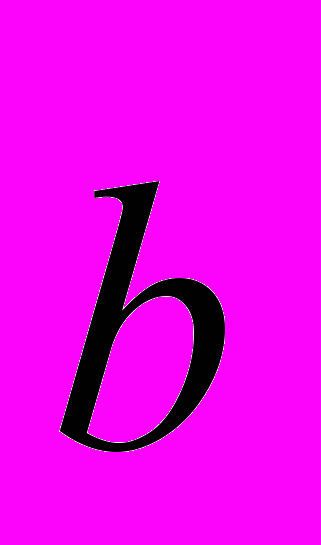размерности n. Решить систему линейных уравнений

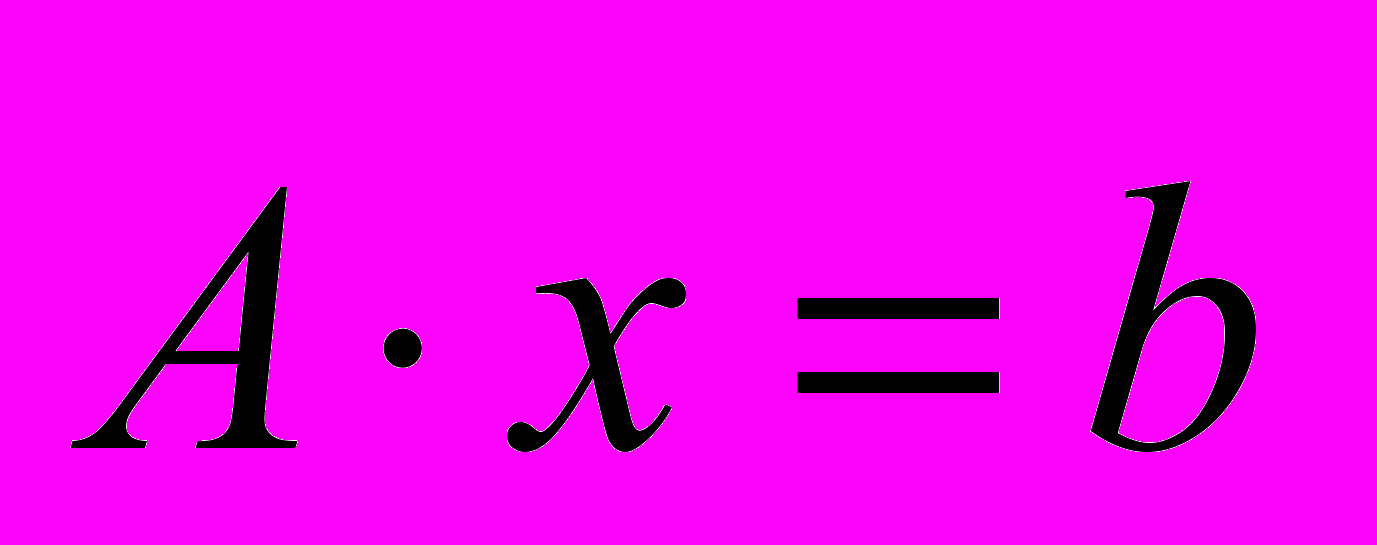методом Гаусса. Проверить результат с помощью модуля linalg.

Задача 2. Дан файл с матрицей A размером n∙n. Найти обратную матрицу к А методом Гаусса. Проверить результат с помощью модуля linalg.

Задача 3. Дан файл с матрицей A размером n∙n. Найти определитель матрицы А методом Гаусса. Проверить результат с помощью модуля linalg.

Задача 4. Дан файл с матрицей A размером n∙n и вектором

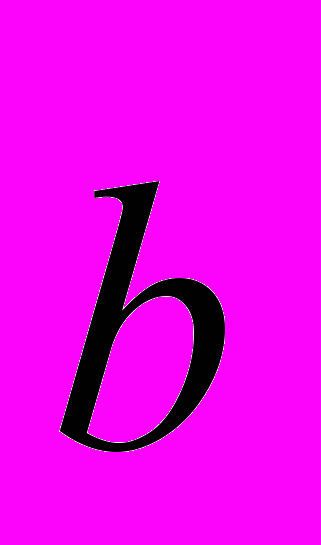размерности n. Решить систему линейных уравнений

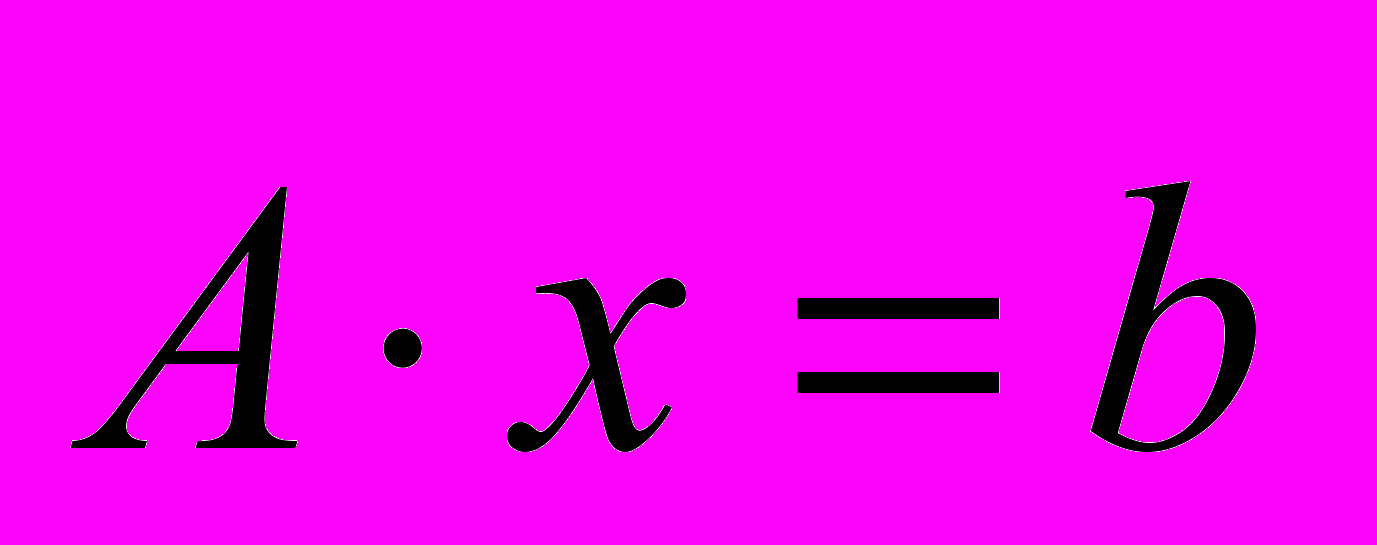методом Зейделя. Проверить результат с помощью модуля linalg.

Задача 5. Дан файл с матрицей A размером n∙n. Найти максимальное собственное значение матрицы А. Проверить результат с помощью модуля linalg.

Задача 6. Дан файл с n значениями некоторой функции f(x). Найти все решения уравнения f(x)=0 методом Ньютона. Проверить результат с помощью оператора fsolve.

Задача 7. Дан файл с n значениями некоторой функции f(x). Найти все решения уравнения f(x)=0 методом итераций. Проверить результат с помощью оператора fsolve.

Задача 8. Дан файл с n значениями некоторой функции f(x). Найти все решения уравнения f(x)=0 методом градиентного спуска. Проверить результат с помощью оператора fsolve.

Задача 9. Дан файл с таблично заданными функциями f₁(x,y) и f₂(x,y). Найти все решения системы уравнений f₁(x,y)=0 и f₂(x,y)=0 методом Ньютона. Проверить результат с помощью оператора fsolve.

Задача 10. Дан файл с таблично заданными функциями f₁(x,y) и f₂(x,y). Найти все решения системы уравнений f₁(x,y)=0 и f₂(x,y)=0 методом градиентного спуска. Проверить результат с помощью оператора fsolve.

Задача 11. Дан файл с таблично заданной функцией f(x), a≤x≤b. Найти решение краевой задачи 1-го порядка

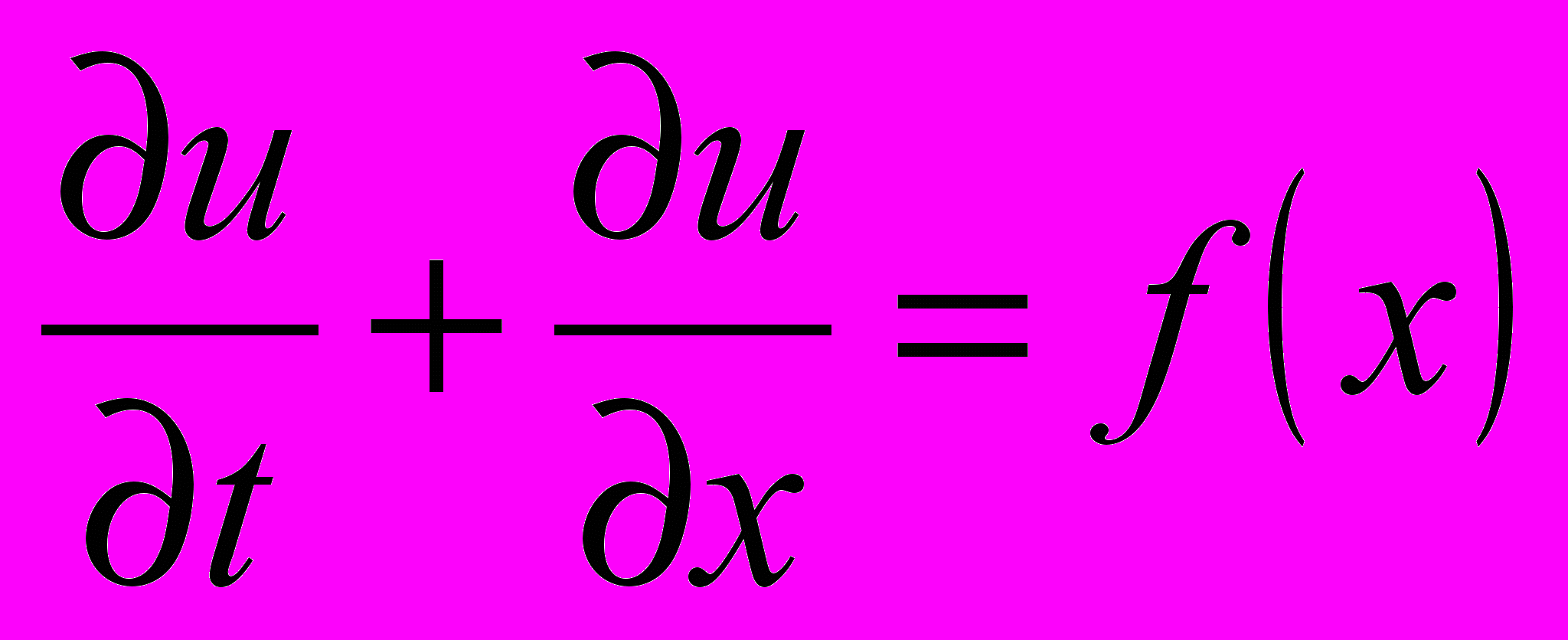с однородными граничными и начальными условиями с помощью явной разностной схемы. Проверить результат с помощью оператора PDEplot.

Задача 12. Дан файл с таблично заданной функцией f(x), a≤x≤b. Найти решение краевой задачи 1-го порядка

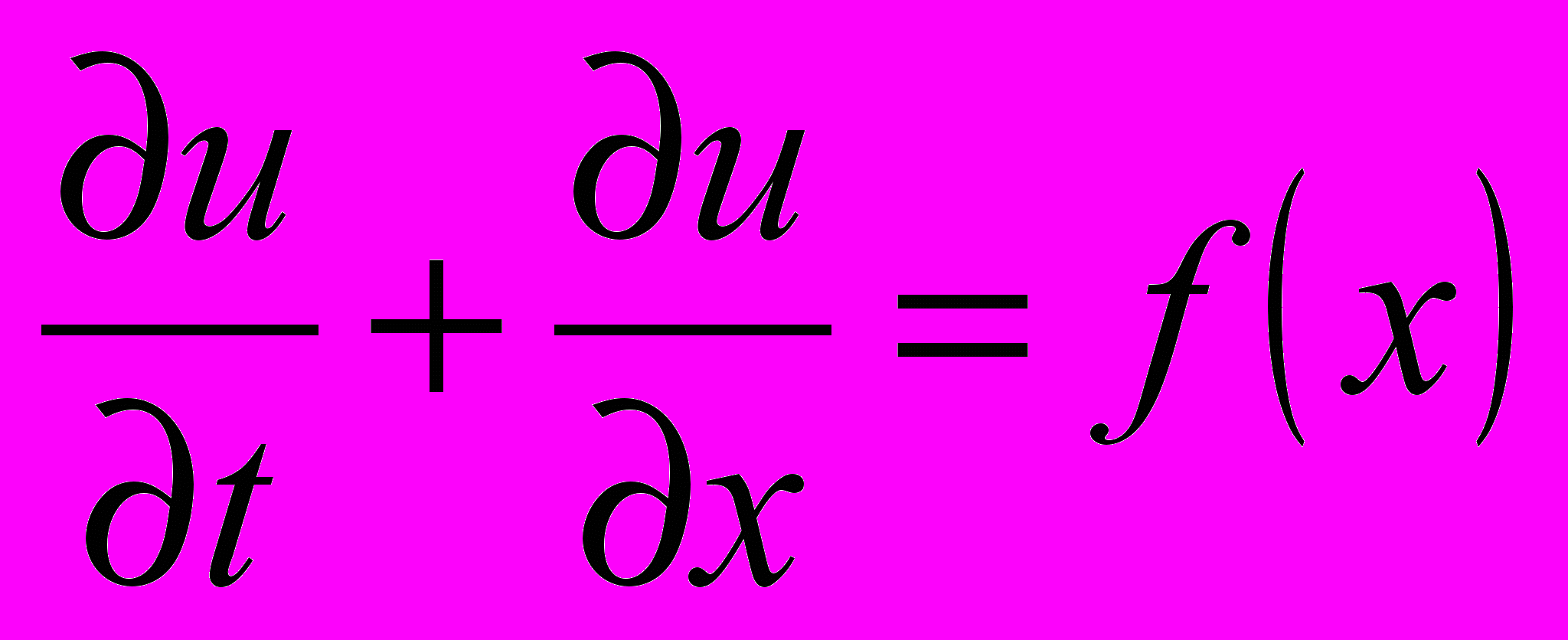с однородными граничными и начальными условиями с помощью неявной разностной схемы. Проверить результат с помощью оператора PDEplot.

Задача 13. Дан файл с таблично заданной функцией f(x), a≤x≤b. Найти решение краевой задачи 1-го порядка

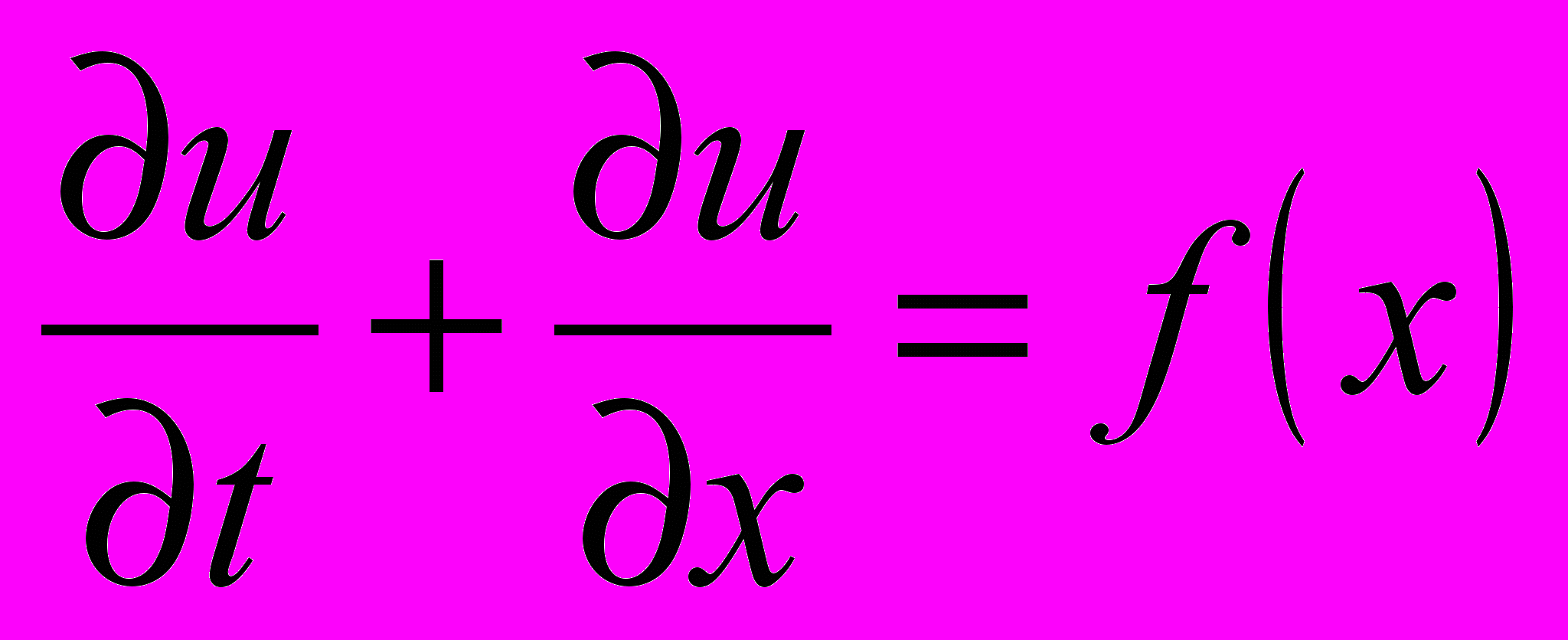с однородными граничными и начальными условиями методом дробных шагов. Проверить результат с помощью оператора PDEplot.

Задача 14. Дан файл с таблично заданной функцией f(x), a≤x≤b. Найти решение краевой задачи уравнения теплопроводности

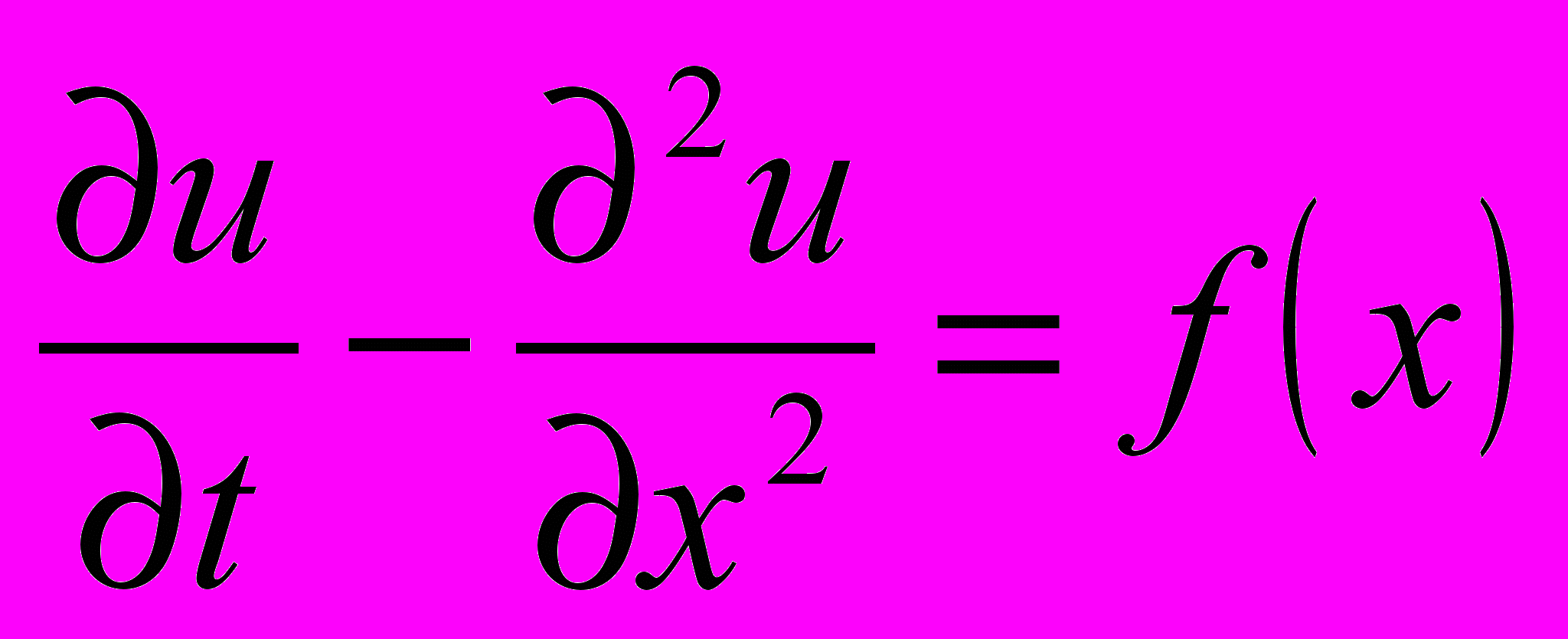с однородными граничными и начальными условиями с помощью явной разностной схемы. Проверить результат с помощью оператора PDEplot.

Задача 15. Дан файл с таблично заданной функцией f(x), a≤x≤b. Найти решение краевой задачи уравнения теплопроводности

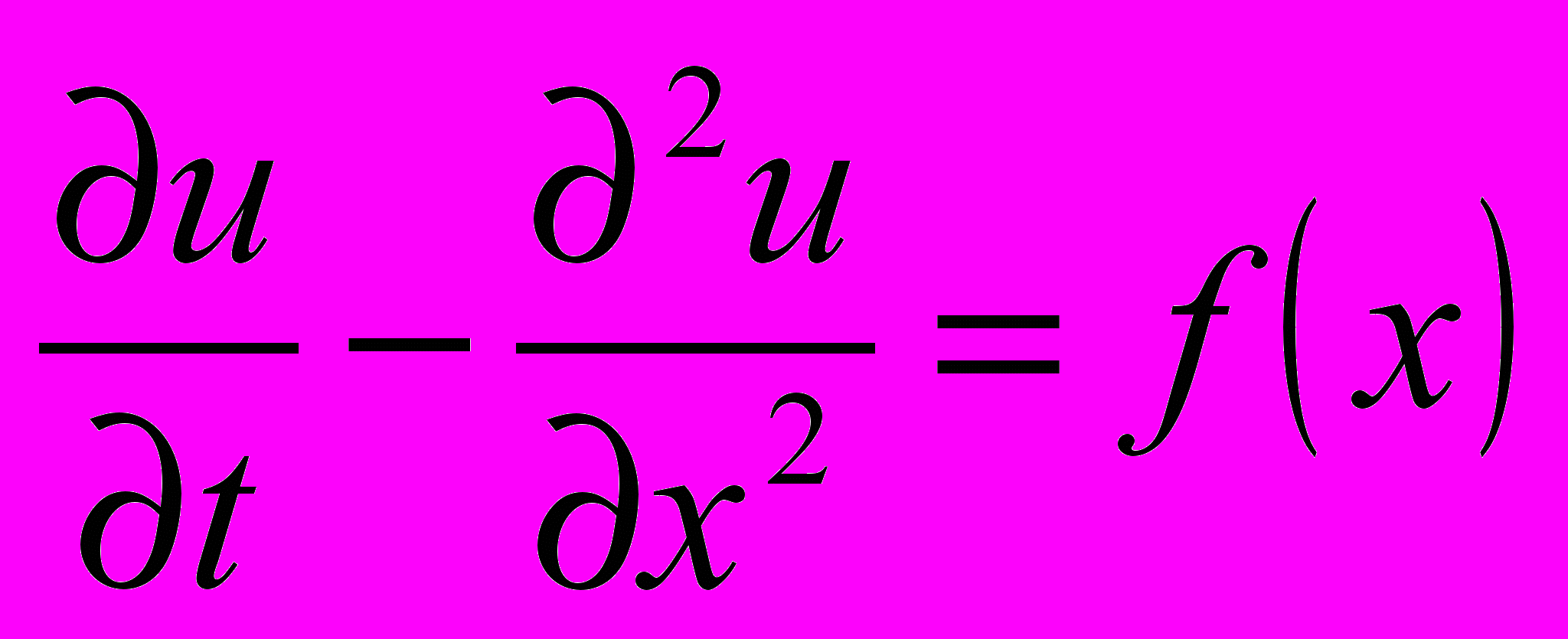с однородными граничными и начальными условиями с помощью неявной разностной схемы. Проверить результат с помощью оператора PDEplot.

Задача 16. Дан файл с таблично заданной функцией f(x), a≤x≤b. Найти решение краевой задачи уравнения теплопроводности

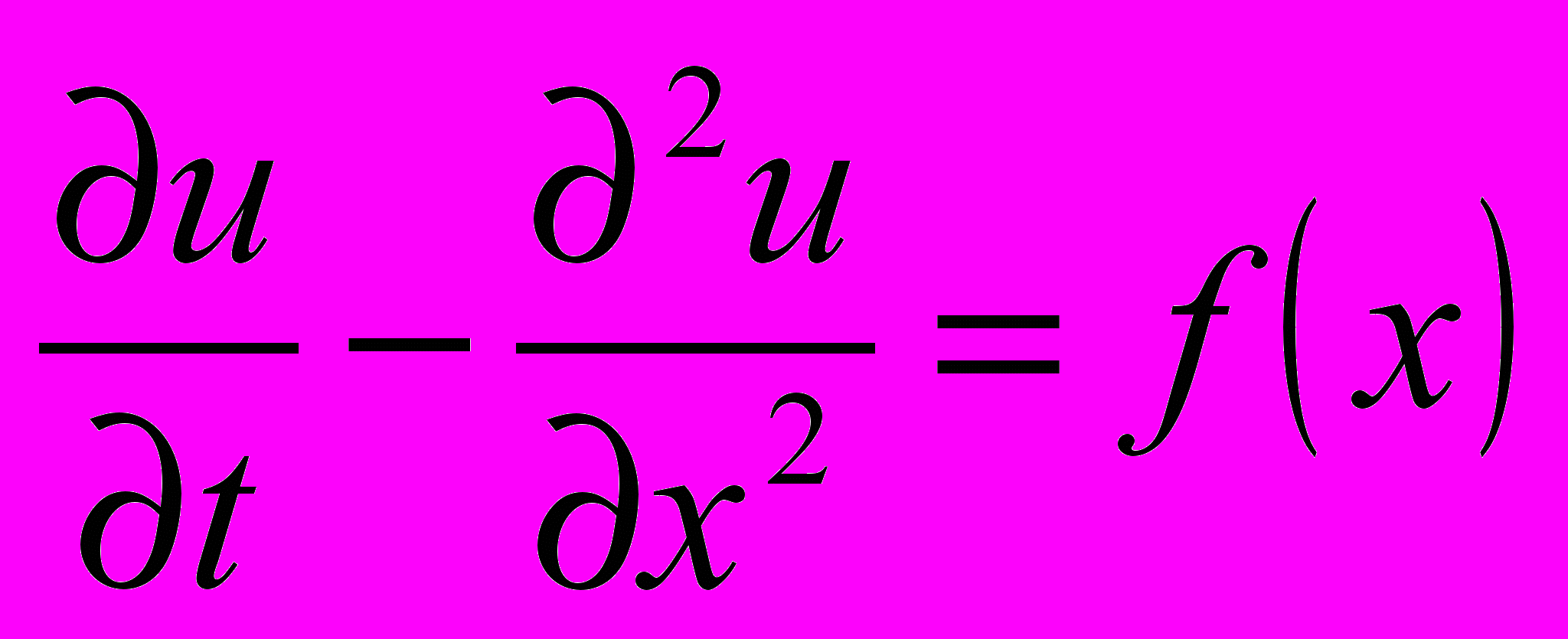с однородными граничными и начальными условиями методом дробных шагов. Проверить результат с помощью оператора PDEplot.

Задача 17. Дан файл с таблично заданной функцией f(x), a≤x≤b. Найти решение краевой задачи волнового уравнения

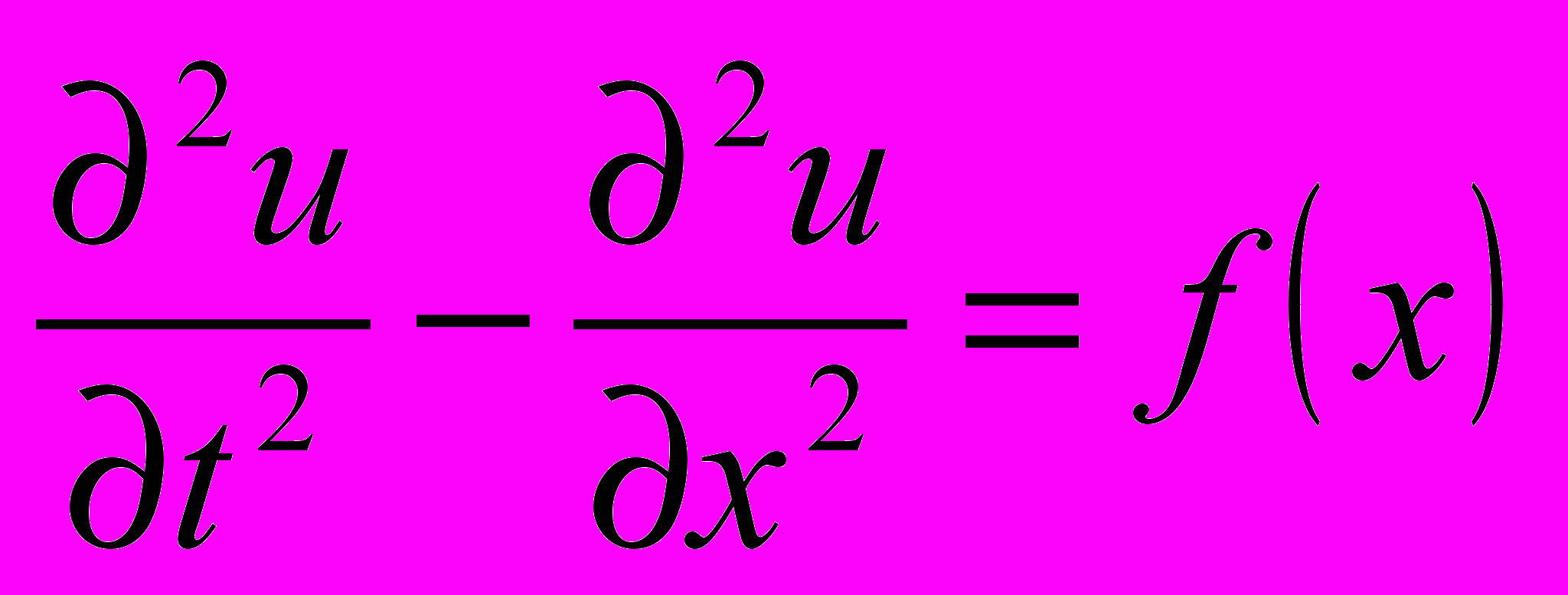с однородными граничными и начальными условиями с помощью явной разностной схемы. Проверить результат с помощью оператора PDEplot.

Задача 18. Дан файл с таблично заданной функцией f(x), a≤x≤b. Найти решение краевой задачи волнового уравнения

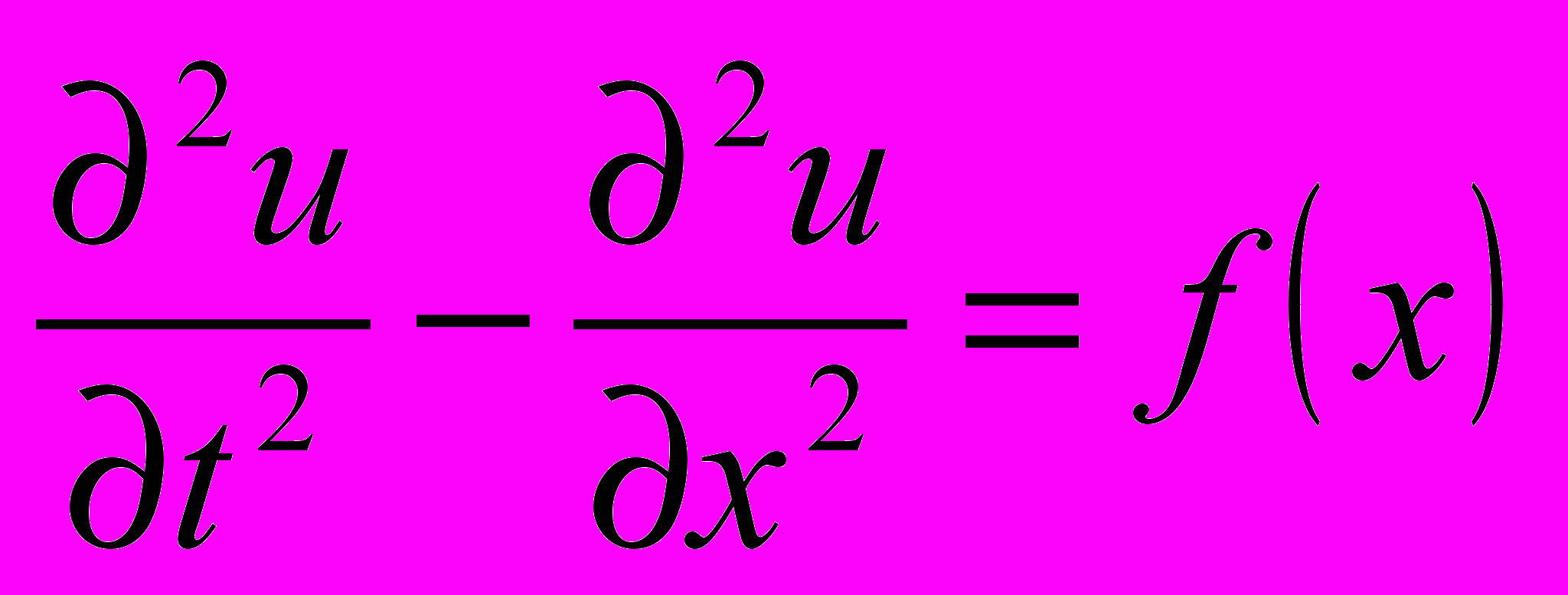с однородными граничными и начальными условиями с помощью неявной разностной схемы. Проверить результат с помощью оператора PDEplot.

Задача 19. Дан файл с таблично заданной функцией f(x), a≤x≤b. Найти решение краевой задачи волнового уравнения

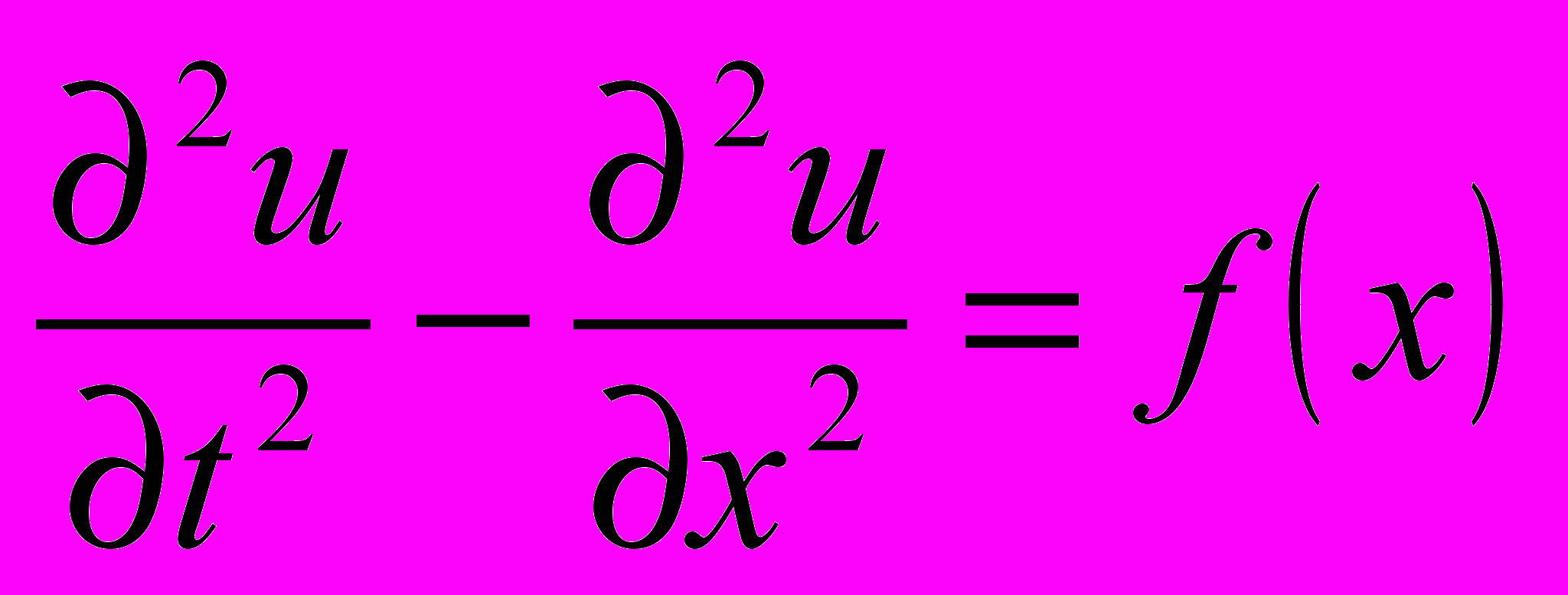с однородными граничными и начальными условиями методом дробных шагов. Проверить результат с помощью оператора PDEplot.

Задача 20. Дан файл с таблично заданной функцией f(x,y). Найти решение задачи Дирихле для уравнения Пуассона

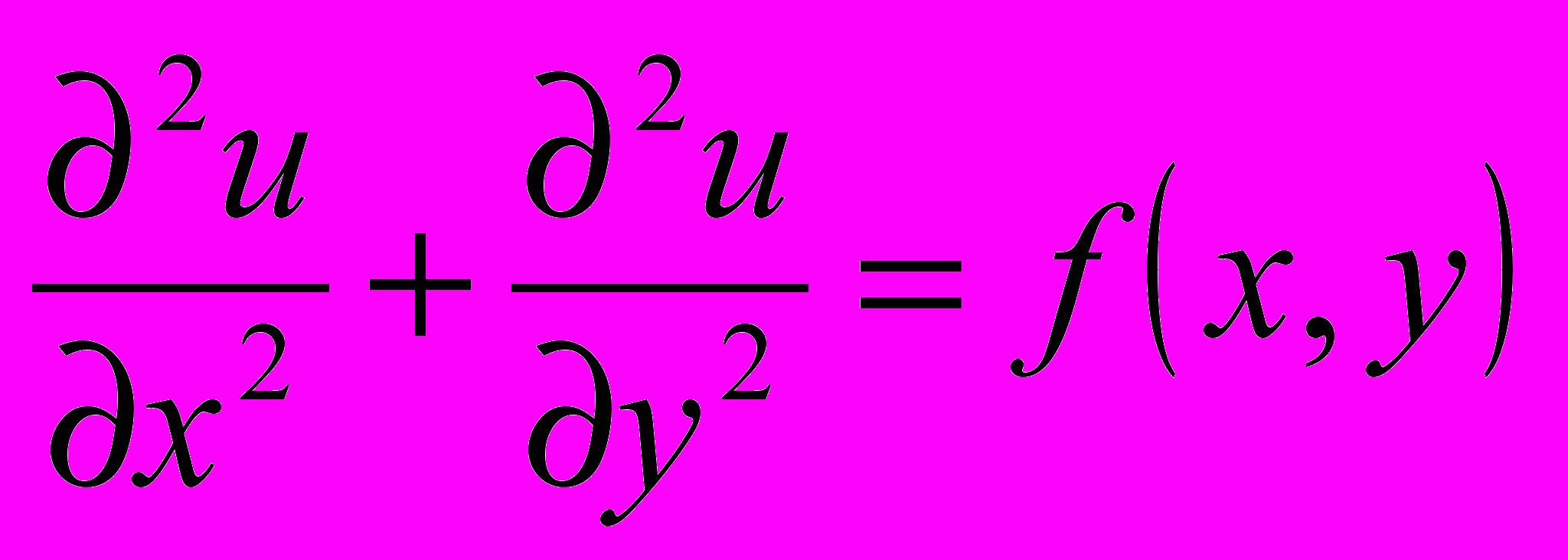с однородными граничными условиями с помощью явной разностной схемы. Проверить результат с помощью оператора PDEplot.

Задача 21. Дан файл с таблично заданной функцией f(x,y). Найти решение задачи Дирихле для уравнения Пуассона

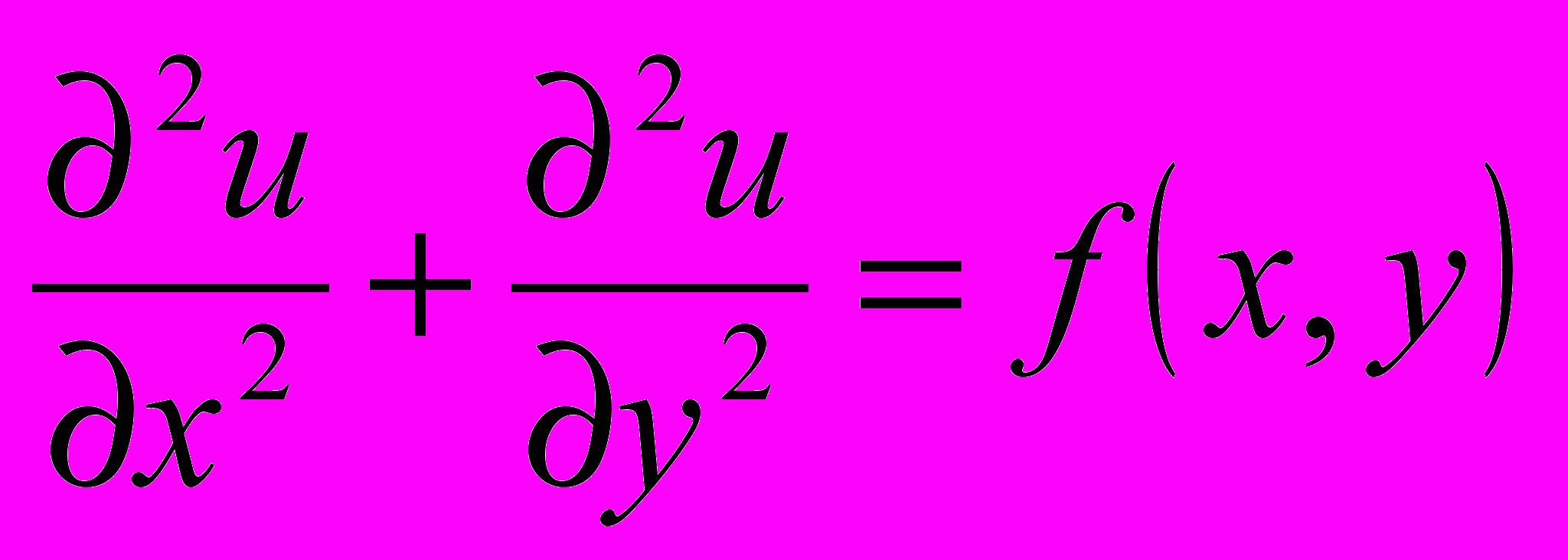с однородными граничными условиями с помощью неявной разностной схемы. Проверить результат с помощью оператора PDEplot.

Задача 22. Дан файл с таблично заданной функцией f(x,y). Найти решение задачи Дирихле для уравнения Пуассона

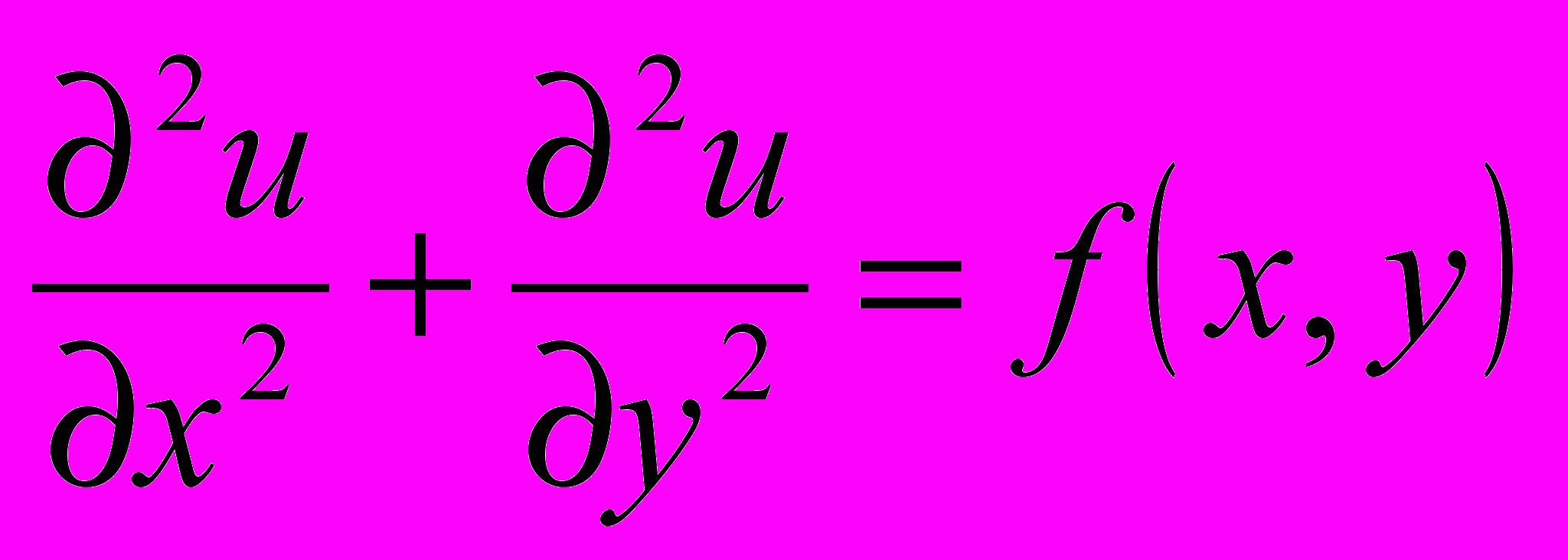с однородными граничными условиями методом дробных шагов. Проверить результат с помощью оператора PDEplot.

Blog

Рабочая программа по дисциплине Численные методы для специальности 050202 Информатика, математика

Содержание

Раздел, подраздел, содержание

Тема занятия

Количество часов