Курсовая работа по дисциплине «Математические методы» Тема: «Применение линейного программирования для оптимизации прибыли в издательском бизнесе»

Вид материала

Курсовая

Содержание Тема задания Хочу подчеркнуть, что выделяют особые случаи применения симплекс-метода. Теоретические основы Если задана общая задача ЛП Методы решения задач линейного программирования Направленный перебор Алгоритм симплекс-метода Конец работы алгоритма Практическая задача Решение практической задачи Разработка программного обеспечения Графическая часть Список использованной литературы

Подобный материал:

• План чтения лекции по учебной дисциплине «Математические методы» Раздел, 120.82kb.
• Темы курсовых работ «Методы оптимизации» Графический метод решения задачи линейного, 11.12kb.
• Рабочая программа по дисциплине Численные методы оптимизации для специальности 220400, 70kb.
• Кафедра «Прикладная математика» Экономические приложения линейного программирования, 27.15kb.
• Рабочая программа По дисциплине «Организация управления международной деятельностью, 223.24kb.
• Ф-рабочая программа по дисциплине утверждено ученый совет факультета математики и информационных, 193.23kb.
• Задачи математического и линейного программирования. Математическая модель задачи использования, 25.82kb.
• Задачи линейного программирования Геометрическая интерпретация задач линейного программирования, 132.4kb.
• Рабочая программа дисциплины математическое моделирование (Математические методы оптимизации), 521.88kb.
• Курс Методы визуального программирования при разработке системного программного обеспечения., 30.14kb.

ФГОУ СПО «Московский Технический Колледж»


Курсовая работа по дисциплине

«Математические методы»

Тема: «Применение линейного программирования для оптимизации прибыли в издательском бизнесе»


Выполнил студент группы П-427

Расторгуева Вера Юрьевна


Руководитель проекта

Преподаватель спец. дисциплин

Кулаков В.С.


Москва 2010 г.


Утверждено

На заседании цикловой комиссии «Программное обеспечение ВТ и АС»

«__»____ 201_г.

Представитель цикловой комиссии

______________________________


Задание

Для курсового проектирования по дисциплине «Математические методы»

студента 4-го курса группы П-427 Московского Технического Колледжа

Расторгуевой Веры Юрьевны.

^ ТЕМА ЗАДАНИЯ:

«Реализация Применение линейного программирования для оптимизации прибыли в издательском бизнесе»

Часть I. Пояснительная записка

• Титульный лист
  
• Задание курсового проектирования
  
• Оглавление
  
• Введение
  
• Основная часть
  

1. Теоретические основы. Решение задач линейного программирования Симплекс-методом.

2. Практическая задача

2.1 Постановка задачи

Компания производит большие и маленькие книги. Каждая книга должна быть напечатана и склеена. На печать маленькой книги уходит 1 час, а на склеивание 2 часа. На печать большой книги уходит 2 часа, на склеивание 2 часа. Печатный цех работает 90 часов в неделю, а склеивательный 80. Прибыль, получаемая с маленькой книги составляет 10$, а с большой 12$. Сколько книг каждого вида должна производить компания для максимизации прибыли?

X₁-количество больших книг;

X₂-количество маленьких книг;

Цех/Тип	Маленькие книги	Большие книги	Всего часов
Печатный	1	2	90
Склеивательный	2	2	80
Прибыль	10	12

Целевая

функция:

L=10*X₁+12*X₂ - > max


Система ограничений:

1*X₁+2*X₂<=90
2*X₁+2*X₂<=80

2.2 Решение задачи

3. Разработка программного обеспечения

3.1 Описание входных данных.

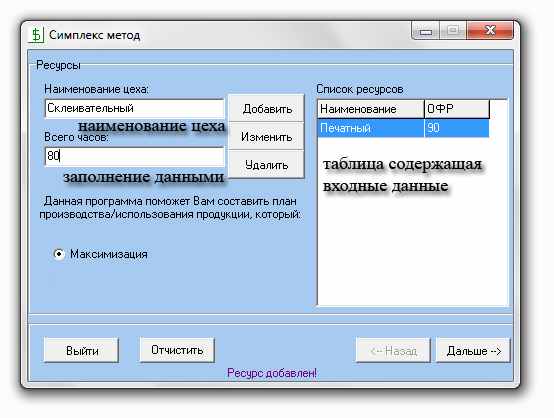
Edit1 – наименования цеха

Edit2 - заполнение данными этого цеха.

Stringgrid 1 –таблица содержащая входные данные .



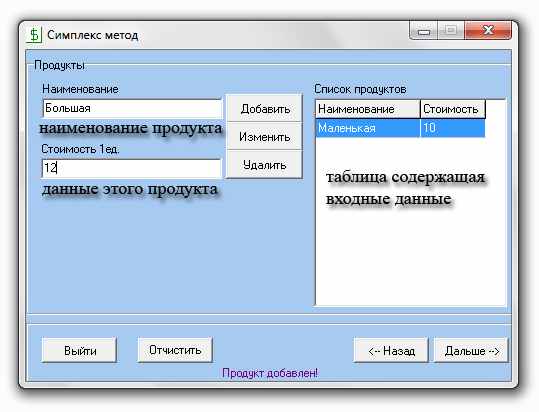
Edit3 –названия продукта.

Edit4 – заполнение данными этого продукта.

Stringgrid 2 –таблица содержащая входные данные.




3.2 Выходные данными.

Получение симплекс-таблицы для максимизации прибыли.

Stringgrid 2 – таблица содерщая конечный результат.

Memo1 – вывод результата.


3.3 Описание основных функций программного обеспечения.

1) Ввод входных данных;

2) Составление симплекс-таблицы.

3) Вывод выходных данных.

4) Вывод решения задачи.


4. Проведение исследования.

Вывод

Заключение

Список рекомендуемой литературы


Приложение

1. Распечатка вычислительной программы
   
2. Материалы решения задачи и проведения исследования
   

Часть II. Графическая часть

1. Блок-схема вычислительной программы

2. Графические материалы решения задач

3. Графические материалы проведения исследования


Часть III. Отзыв руководителя

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________


Дата выдачи «___» ____ 201_г.

Срок окончания «___» ____ 201_г.

Заведующий отделения «___» ____ 201_г.

Преподаватель «___» ____ 201_г

Оглавление:

Введение …………………………………………………………………….. ……………….3

1. Теоретические основы...……….………………….…………….…………… ……………….5
   

Решение задач линейного программирования Симплекс-методом.

2. Практическая задача …………………………………………………… …… ……………...12
   

2.2 Постановка задачи

2.3 Решение практической задачи

3. Разработка программного обеспечения ……………………………………………………..14
   
   1. Описание входных данных.
      
   2. Описание выходных данных.
      
   3. Описание основных функций программного обеспечения.
      
   4. Ход вычислений программы.
      
   5. Руководство пользователя по использованию ПО.
      

Приложения…..…………………………………………………………… ..…………………18

1. Распечатка вычислительной программы….……….………...………...…...……………...18

2. Материал решения задачи и проведения исследования …………………………............36

Графическая часть……………………………………………………………………………...38

1. Блок-схема вычислительной программы ………………………………………………… 38

2. Графические материалы решения практической задачи и проведения исследований... 36

Заключение …………………………………………………………………………………….39

Список использованной литературы ....……………………………………………………...40

ВВЕДЕНИЕ

Симплекс-метод – это один из первых специализированных методов оптимизации, нацеленный на решение задач линейного программирования, в то время как методы простого и направленного перебора могут быть применены для решения практически любой задачи оптимизации. Он был предложен американцем Г. Данцигом в 1951 г.

Симплекс-метод состоит в продвижении по выпуклому многограннику ограничений от вершины к вершине, при котором на каждом шаге значение целевой функции улучшается до тех пор, пока не будет достигнут оптимум.

Существует ручное (не апплетом) решение двух задач симплекс-методом (аналогичным решению апплетом) с подробными объяснениями для того, чтобы понять алгоритм решения задач симплекс-методом. В первом случае задача содержит знаки неравенства только " ≤ " (задача с начальным базисом), во втором случае задача может содержать знаки " ≥ ", " ≤ " или " = " (задача с искусственным базисом), они решаются по-разному.