Обязательный курс «Математика» для студентов направления «Архитектура», обучающихся на бакалавра Объем учебной нагрузки: 16 час лекции, 16 час семинары
| Вид материала | Лекции |
- Обязательный курс для направления 552700 Энергомашиностроение. Объем учебной нагрузки:, 41.74kb.
- Курс: Организация, нормирование и оплата труда на предприятии апк. Кафедра экономики,, 35.41kb.
- Обязательный курс (Магистратура, специальность «Архитектура») Объем учебной нагрузки:, 29.11kb.
- Спецкурс по выбору для студентов 4 курса направления «экономика» Объем учебной нагрузки:, 131.69kb.
- Обязательный курс объем учебной нагрузки: Лекции 72 часа Семинары 36 часов Внеделю, 24.67kb.
- Обязательный курс для направления 550100 Строительство на 5-м семестре обучения. Объем, 38.06kb.
- Курс по выбору. Объем учебной нагрузки: 18 час лекции, 18 час семинары, 101.87kb.
- Бакалаврская программа Обязательный курс Курс: гфб-1 Семестр: 2 Количество кредитов:, 356.08kb.
- Обязательный курс для специальности 550600 Горное дело, 4 семестр. Объем учебной нагрузки:, 19.78kb.
- Курс по выбору для студентов 5-го курса Объем учебной нагрузки: 60 час лекции, 22.28kb.
Кафедра высшей математики, Факультет физико-математических и естественных наук
Обязательный курс «Математика» для студентов направления «Архитектура», обучающихся на бакалавра
Объем учебной нагрузки: 16 час. – лекции, 16 час. – семинары
Цель курса
Основной целью курса является обучение студентов-архитекторов основам теории множеств, высшей алгебры и аналитической геометрии.
Для реализации поставленной цели в процессе преподавания курса решаются следующие задачи:
- выработка у обучающихся способности проводить вычисления с помощью основных формул,
- выработка у них навыка к построению математических суждений и выводов,
- обучение их теоретико-множественному, алгебраическому и геометрическому подходам к операциям со зданиями и сооружениями, нужным будущему архитектору.
^ Содержание курса
Тема 1. Пространства, множества, числа.
Евклидовы пространства
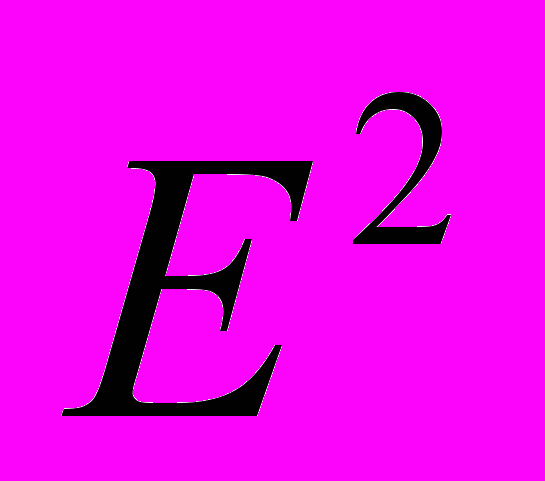и 
. Формула расстояния между точками в 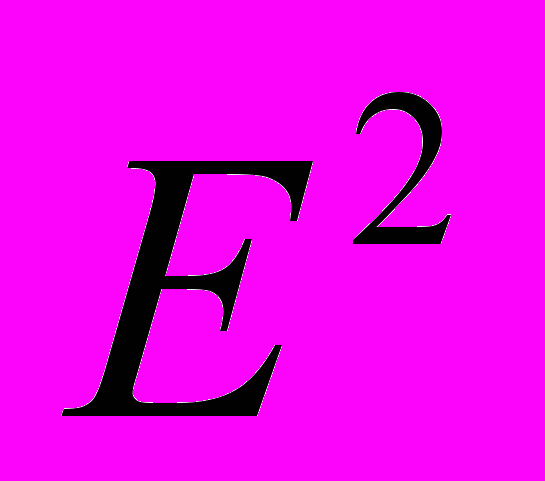и . Понятие о геометриях Н.И. Лобачевского и Б. Римана. Векторные пространства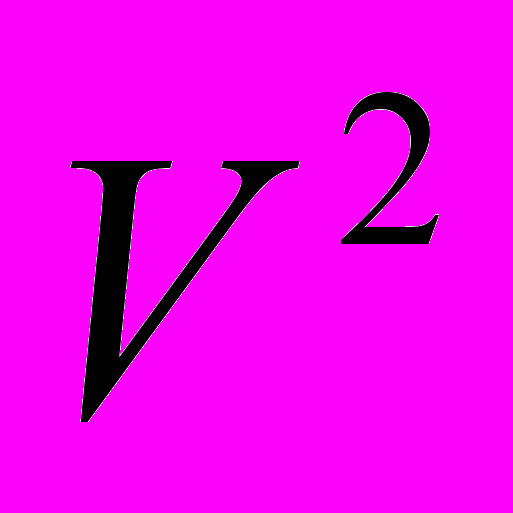 
и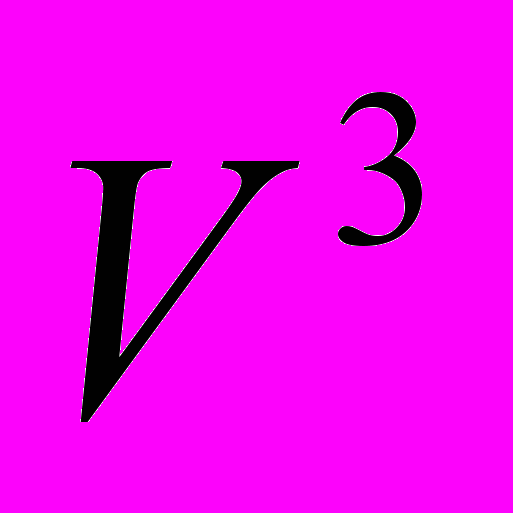 
. Скалярное произведение векторов в 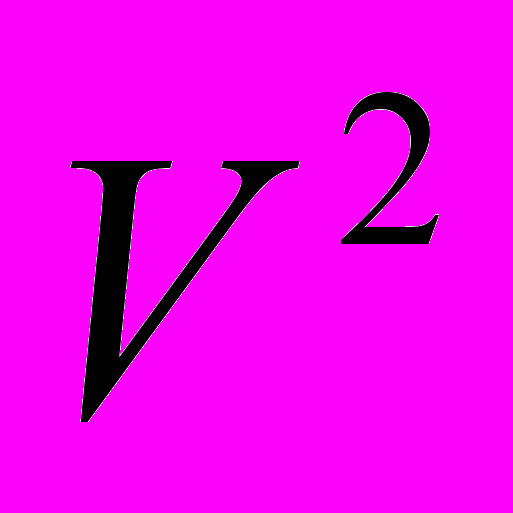и 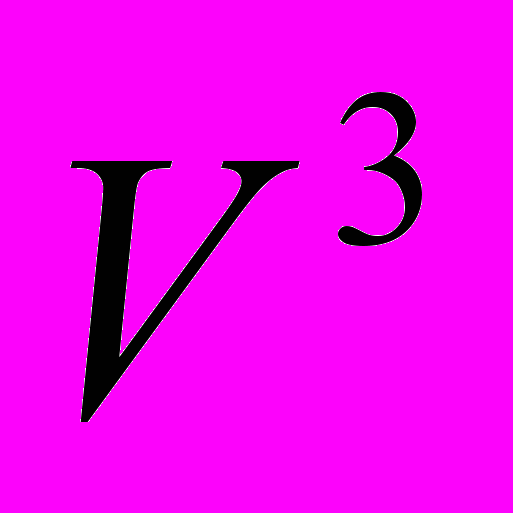. Векторное произведение векторов в 
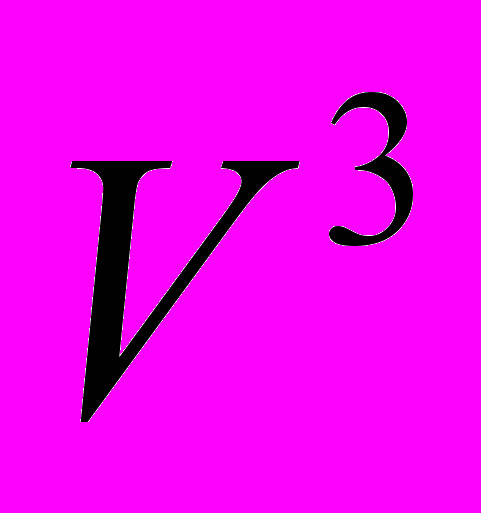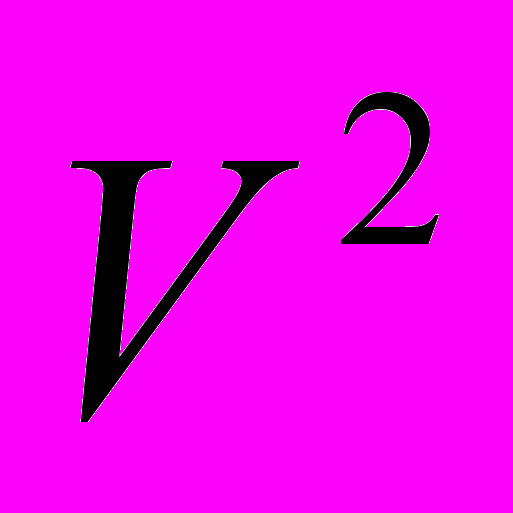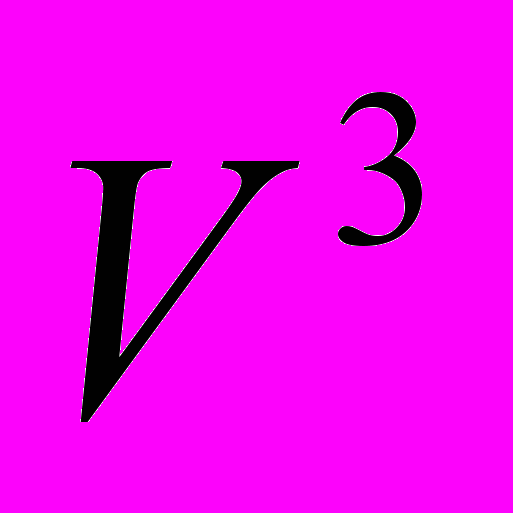. Операции сложения, вычитания и умножения на число в и . Определение множества по Г. Кантору. Конечные и бесконечные множества. Мощность множества. Операции объединения, пересечения и разности множеств. Кардинальные числа.^ Тема 2. Высшая алгебра.
Понятие матрицы. Матрицы размерности 2х2 и 3х3. Квадратная матрица. Единичная матрица. Операции над матрицами: сложение, вычитание, умножение на число, деление на число, умножение. Ранг матрицы. Минор матрицы. Обратная матрица. Нахождение обратной матрицы с помощью определителя. Нахождение обратной матрицы по методу Гаусса. Определители 2-го и 3-го порядка. Способы их вычисления. Свойства определителя. Теорема Кронекера-Капелли. Методы решения системы линейных алгебраических уравнений: графический метод, метод обратной матрицы, метод Крамера и метод Гаусса. Комплексное число, его модуль и аргумент. Алгебраическая и тригонометрическая формы записи комплексного числа. Формула Л. Эйлера. Операции над комплексными числами: сложение, вычитание, умножение, деление и извлечение квадратного корня.
^ Тема 3. Высшая геометрия.
Прямая линия в
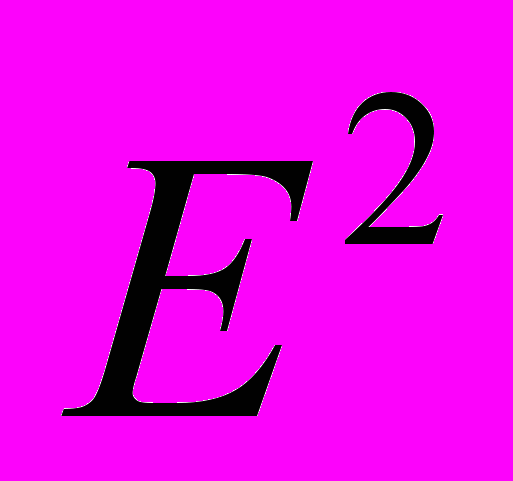. Уравнение прямой, проходящей через две точки. Уравнение прямой, записанное через точку и направляющий вектор. Угол между двумя прямыми в 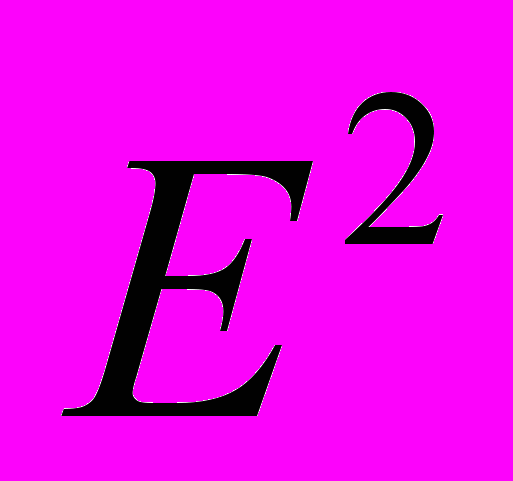. Расстояние от точки до прямой в 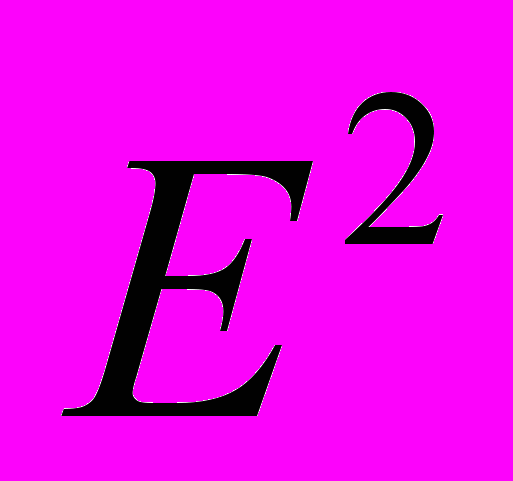. Уравнение эллипса в каноническом виде и его графическое представление в 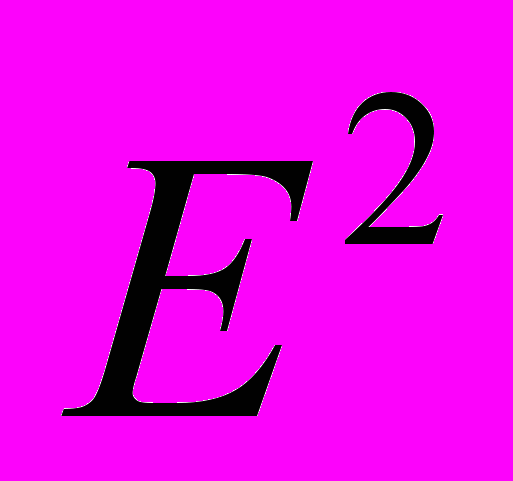. Уравнение гиперболы в каноническом виде и ее графическое представление в 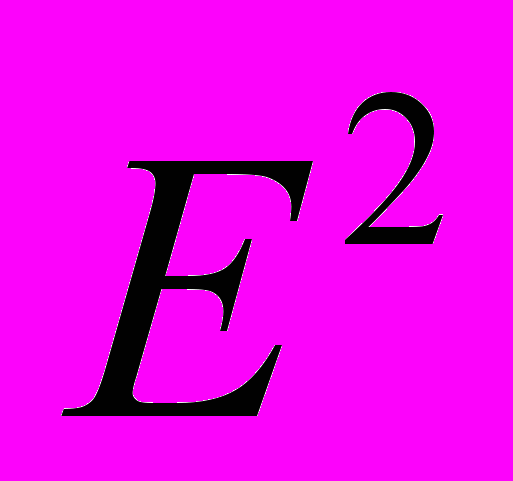. Уравнение параболы в каноническом виде и ее графическое представление в 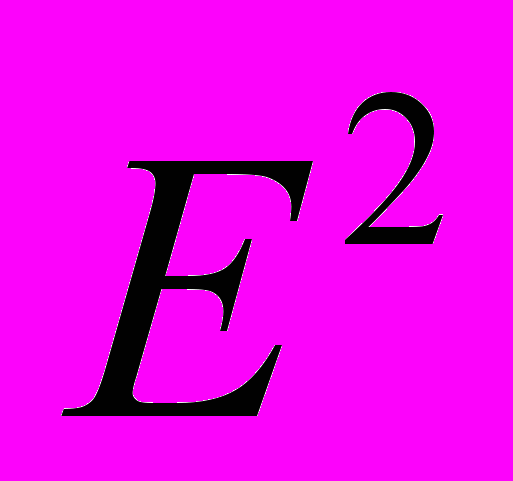. Прямоугольная Декартова система координат в 
. Метод координат. Направляющие косинусы вектора. Скалярное произведение векторов в 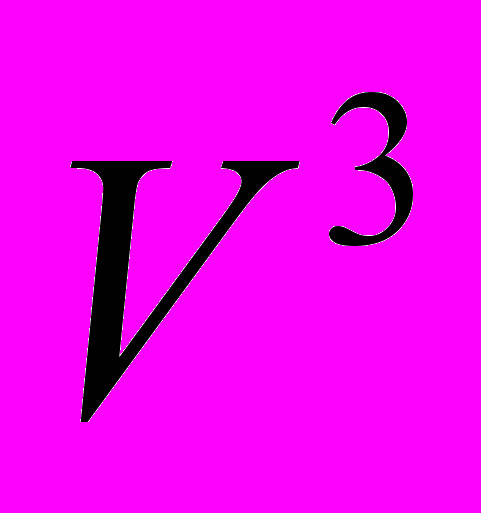. Свойства скалярного произведения. Длина и модуль вектора в . Угол между векторами в . Условие их ортогональности. Прямая линия в . Уравнение прямой, проходящей через две точки. Уравнение прямой, записанное через точку и направляющий вектор. Параметрическое уравнение прямой. Угол между прямыми в . Уравнение плоскости в . Угол между прямой и плоскостью. Угол между двумя плоскостями. Расстояние от точки до прямой в . Расстояние от точки до плоскости. Уравнение эллиптического цилиндра в каноническом виде и его графическое представление в . Уравнение параболического цилиндра в каноническом виде и его графическое представление в . Уравнение гиперболического цилиндра в каноническом виде и его графическое представление в . Уравнение конуса второй степени в каноническом виде и его графическое представление в . Уравнение однополостного гиперболоида в каноническом виде и его графическое представление в . Уравнение двуполостного гиперболоида в каноническом виде и его графическое представление в . Уравнение эллипсоида в каноническом виде и его графическое представление в . Уравнение эллиптического параболоида в каноническом виде и его графическое представление в . Уравнение гиперболического параболоида в каноническом виде и его графическое представление в .Литература
Обязательная
1. Примерная программа дисциплины “математика” для направления 521700 “Архитектура”. – Министерство образования Российской Федерации, 2000г.
2. Игнатьев Ю.А. Учебное пособие по высшей математике для студентов специальности «Архитектура». – Часть I. – Москва: Издательство РУДН, 2005.
Дополнительная
1. Магазинников Л.И. Высшая математика I. Линейная алгебра. Аналитическая геометрия. Дифференциальное исчисление. – Томск: ТМЦДО, 1999.
2. Мишина А., Проскуряков И. Высшая алгебра. Справочная математическая библиотека. – Москва: Физматгиз, 1962.
3. Виноградов И. М. Аналитическая геометрия. - Москва: Наука, 1986.
4. Ильин В., Позняк Э. Аналитическая геометрия. – Москва: Наука 1988.
Программа составлена
Игнатьевым Юрием Анатольевичем,
кандидатом физико-математических наук, доцентом
кафедры высшей математики, факультета физико-математических и естественных наук,
^ Ваганяном Виктором Оганесовичем,
кандидатом педагогических наук, доцентом
кафедры высшей математики, факультета физико-математических и естественных наук
^ Кафедра высшей математики, Факультет физико-математических и естественных наук
Обязательный курс «Математика» для студентов направления «Архитектура», обучающихся на бакалавра
^ Объем учебной нагрузки: 16 час. – лекции, 16 час. – семинары
Цель курса
Основной целью курса является обучение студентов-архитекторов дифференциальному и интегральному исчислениям, теориям рядов и дифференциальных уравнений.
Для реализации поставленной цели в процессе преподавания курса решаются следующие задачи:
- выработка у обучающихся способности проводить вычисления с помощью основных формул,
- выработка у них навыка к построению математических суждений и выводов,
- обучение их аналитическому подходу (с использованием дифференциального и интегрального исчислений, теорий рядов и дифференциальных уравнений) к операциям со зданиями и сооружениями, нужным будущему архитектору.
^ Содержание курса
Тема 1. Дифференциальное и интегральное исчисления.
Отображения и функции действительной переменной. Области определения и изменения функции. Способы ее задания. Числовые последовательности и их пределы. Пределы функции в точке и бесконечности. Теоремы о пределах. Правила вычисления пределов. Пять замечательных пределов. Понятие непрерывности функции. Точки разрыва первого и второго рода. Производная функции, ее смысл в прикладных задачах (скорость, плотность). Правила нахождения производной. Таблица производных. Производная неявной, сложной и обратной функций. Дифференцирование функций, заданных параметрически. Производные высших порядков. Уравнение касательной к кривой в данной точке. Правило Лопиталя. Дифференциал функции. Использование дифференциала в приближенных вычислениях. Архитектура плоскости. Полное исследование функции: монотонность функции, ее области определения и изменения, экстремумы, выпуклость и вогнутость, точки перегиба, асимптоты. Примеры функций, имеющих значение для архитектуры: спираль Ферми, спираль Архимеда, астроида, лемниската Бернулли, овал Кассини, спираль Галилея, гиперболическая спираль, гипотрохоида, гипоциклоида, лист Декарта, овал Декарта, жезл, кардиоида, трисектриса Каталана, спираль Корню, кохлноида, логарифмическая спираль, трисектриса Маклорена, конхоида Никомеда, серпантина Ньютона, офиурида, параболическая гипербола, спираль Ферма, улитка Паскаля, визиера Пеано, парабола Нейля, розы, конхоида Слюза, строфоида, трактриса, трохоида, узлы, циклоида, циссоида Диоклеса, эпитрохоида, эпициклоида. Первообразная. Неопределенный интеграл. Свойства неопределенных интегралов. Таблица интегралов. Методы интегрирования: непосредственное интегрирование, замена переменной, интегрирование по частям. Определенный интеграл. Формула Ньютона-Лейбница. Основные свойства определенного интеграла. Методы нахождения определенных интегралов: непосредственное интегрирование, замена переменной, интегрирование по частям. Численное интегрирование: методы Симпсона, Г. Конроя и «химический» метод. Двойной интеграл. Вычисление двойного интеграла через повторные в декартовых и полярных координатах. Вычисление площадей с помощью двойного интеграла. Объем цилиндроида как двойной интеграл. Площадь поверхности в декартовых и полярных координатах как двойной интеграл. Масса пластины как двойной интеграл. Центр тяжести пластины как двойной интеграл. Моменты инерции пластины относительно осей координат как двойной интеграл. Центробежный момент инерции пластины как двойной интеграл. Тройной интеграл. Вычисление тройного интеграла через повторные в декартовых, цилиндрических и сферических координатах. Объем трехмерного тела как тройной интеграл. Масса тела как тройной интеграл. Координаты центра тяжести тела как тройные интегралы. Моменты инерции тела относительно координатных плоскостей, координатных осей и начала координат.
^ Тема 2. Числовые и функциональные ряды.
Числовые ряды. Сходимость и расходимость рядов. Необходимое условие сходимости рядов с положительными членами. Признак сходимости Даламбера. Признак сходимости Коши. Интегральный признак сходимости. Знакопеременный числовой ряд. Абсолютная сходимость. Достаточный признак сходимости знакопеременного числового ряда. Условная сходимость по признаку Лейбница. Функциональные ряды: их область определения и область сходимости. Ряд Маклорена. Ряд Тейлора. Ряд Фурье.Тема 3. Дифференциальные уравнения.
Обыкновенные дифференциальные уравнения. Начальные условия. Порядок обыкновенного дифференциального уравнения. Обыкновенные дифференциальные уравнения первого порядка с разделяющимися переменными. Обыкновенные однородные дифференциальные уравнения первого порядка. Обыкновенные линейные дифференциальные уравнения первого порядка. Обыкновенные линейные дифференциальные уравнения в полных дифференциалах. Дифференциальные уравнения в частных производных второго порядка. Начальные и граничные условия. Волновое уравнение и его решение методом Фурье. Уравнение Лапласа и его фундаментальное решение. Уравнение теплопроводности и его решение методом Фурье.
Литература
Обязательная
1. Примерная программа дисциплины “математика” для направления 521700 “Архитектура”. – Министерство образования Российской Федерации, 2000г.
2. Игнатьев Ю.А. Учебное пособие по высшей математике для студентов специальности «Архитектура». – Часть I. – Москва: Издательство РУДН, 2005.
Дополнительная
1. Ильин В., Позняк Э. Основы математического анализа. – Т.1-2. – Москва: Физматлит, 1998.
2. Кудрявцев Л. Д. Краткий курс математического анализа. Учебное пособие для вузов. – Москва: Наука, 1989.
3. Берман Г. Н. Сборник задач по курсу математического анализа. Учебник для вузов. - Москва: Наука, 1975.
4. Шипачев В.С. Высшая математика. - 5-е изд. - Москва: Высшая школа, 2002.
5. Данко П., Попов А., Кожевникова Т. Высшая математика в упражнениях и задачах. – Т.1-2. – Москва: Высшая школа, 1986.
Программа составлена
Игнатьевым Юрием Анатольевичем,
кандидатом физико-математических наук, доцентом
кафедры высшей математики, факультета физико-математических и естественных наук.
Кафедра высшей математики, Факультет физико-математических и естественных наук
^ Обязательный курс «Математика» для студентов направления «Архитектура», обучающихся на бакалавра
Объем учебной нагрузки: 16 час. – лекции, 16 час. – семинары
^ Цель курса
Основной целью курса является обучение студентов-архитекторов основам теории групп, дифференциальной геометрии, топологии, комбинаторики, теории вероятностей и статистики.
Для реализации поставленной цели в процессе преподавания курса решаются следующие задачи:
- выработка у обучающихся способности проводить вычисления с помощью основных формул,
- выработка у них навыка к построению математических суждений и выводов,
- обучение их применению теории групп, дифференциальной геометрии, топологии, комбинаторики, теории вероятностей и статистики к операциям со зданиями и сооружениями, нужным будущему архитектору.
^ Содержание курса
Тема 1. Теория групп.
Определение группы и подгруппы. Группы в геометрии: группа вращений отрезка, группа вращений треугольника, группа вращений квадрата, группа вращение тетраэдра. Конечные группы. Групповая таблица. Образующие элементы группы. Группы подстановок. Использование теории групп в архитектуре.
^ Тема 2. Дифференциальная геометрия.
Понятие дифференциальной геометрии. Кривизна, радиус кривизны и эволюта плоской кривой. Нормальная плоскость и нормаль к поверхности. Кривые на поверхности. Первая основная квадратичная форма и ее приложения. Вторая основная квадратичная форма на поверхности. Кривизна кривой на поверхности. Главные направления в точке поверхности. Три типа точек на поверхности. Линии кривизны на поверхности.
^ Тема 3. Топология.
Понятие топологии. Гомеоморфизм пространственных фигур. Внутренние топологические свойства фигуры. Основная проблема топологии. Примеры из топологии: «лист Мëбиуса» и «бутылка Клейна». Связные и несвязные множества. Представление о связности
и . Значение топологии для архитектуры.Тема 4. Комбинаторика.
Понятие комбинаторики. Правило умножения. Размещения, перестановки и сочетания. Комбинаторные задачи. Применение комбинаторики в архитектуре.
^ Тема 5. Теория вероятностей.
Вероятности событий. Теорема сложения вероятностей. Условные вероятности. Теорема умножения вероятностей. Формула полной вероятности. Формула Байеса. Дискретные и непрерывные случайные величины. Законы распределения случайных величин. Математическое ожидание, дисперсия и среднее квадратическое отклонение случайной величины. Использование теории вероятностей в архитектуре.
^ Тема 6. Статистика.
Понятие статистики. Статистическое наблюдение. Сводка и группировка статистических данных. Абсолютные, относительные и средние обобщающие статистические показатели. Значение статистики для архитектуры. Понятие корреляционной зависимости. Корреляция двух количественных признаков. Линейный коэффициент корреляции. Коэффициенты корреляции Фехнера, Спирмэна и Кендэла.
Литература
Обязательная
1. Примерная программа дисциплины “математика” для направления 521700 “Архитектура”. – Министерство образования Российской Федерации, 2000г.
2. Игнатьев Ю.А. Учебное пособие по высшей математике для студентов специальности «Архитектура». – Часть I. – Москва: Издательство РУДН, 2005.
3. Волкотруб И.Т. Основы комбинаторики в художественном конструировании. – Киев: Вища школа, 1986.
4. Виленкин Н.Я. Популярная комбинаторика. – Москва: Наука, 1975.
5. Гихман И.И., Скороход А.В., Ядренко М.И. Теория вероятностей и математическая статистика. – Москва: Вища школа, 1979.
6. Сборник задач по теории вероятностей, математической статистике и теории случайных функций / Под ред. А.А. Свешникова. – Москва: Наука, 1965.
7. Мешалкин Л.Д. Сборник задач по теории вероятностей. – Москва: МГУ, 1963.
8. Александров П.С. Введение в теорию множеств и общую топологию. – Москва: Наука, 1977.
9. Рашевский П.К. Курс дифференциальной геометрии. – Москва: ГИТТЛ, 1950.
Курош А.Г. Теория групп. – Москва: ОГИЗ, 1944.
10. Теория статистики: Учебник / Под ред. Г.Л. Громыко. – Москва: ИНФРА-М, 2000.
Дополнительная
1. Гроссман И., Магнус В. Группы и их графы. – Москва: Мир, 1971.
2. Баумгартнер Л. Теория групп. – Москва: ГТТИ, 1934.
3. Зейферт Г., Трельфалль В. Топология. – Москва: ОНТИ, 1938.
4. Гиленко Н.Д. Задачник по теории вероятностей. – Москва: ГУПИ, 1942.
5. Мостеллер Ф., Рурке Р., Томас Дж. Вероятность. – Москва: Мир, 1969.
6. Лоэв М. Теория вероятностей. – Москва: ИЛ, 1962.
7. Гнеденко Б.В. Курс теории вероятностей. – Москва: ГИФМЛ, 1961.
8. Смирнов Н.В., Дунин-Барковский И.В. Краткий курс математической статистики для технических приложений. – Москва: Физматгиз, 1959.
9. Виленкин Н.Я. Индукция. Комбинаторика. – Москва: Просвещение, 1976.
10. Холл М. Комбинаторика. – Москва: Мир, 1970.
Программа составлена
Игнатьевым Юрием Анатольевичем,
кандидатом физико-математических наук, доцентом
кафедры высшей математики, факультета физико-математических и естественных наук,
Кафедра высшей математики, Факультет физико-математических и естественных наук
^ Обязательный курс «Математика» для студентов направления «Архитектура», обучающихся на магистра
Объем учебной нагрузки: 16 час. – лекции, 16 час. – семинары
^ Цель курса
Основной целью курса является обучение студентов-архитекторов основам теорий алгоритмов и графов, линейного и нелинейного программирования, теории игр и имитационного моделирования.
Для реализации поставленной цели в процессе преподавания курса решаются следующие задачи:
- выработка у обучающихся способности проводить вычисления с помощью основных формул,
- выработка у них навыка к построению математических суждений и выводов,
- обучение их использованию аппарата теорий алгоритмов и графов, линейного и нелинейного программирования, теории игр и имитационного моделирования для решения практических задач, встречающихся в архитектурной практике.
^ Содержание курса
Тема 1. Теория алгоритмов.
Понятие алгоритма. Алгоритмические системы. Рекурсивные функции. Тезис Чëрча. Тезис Тьюринга. Машины Поста. Машины Тьюринга. Алгоритмическая система Маркова. Алгоритмические проблемы в архитектуре.
^ Тема 2. Теория графов.
Графы и их разновидности. Операции над графами. Свойства графов. Конечные и бесконечные графы. Деревья. Ориентированные графы и деревья. Использование графов в архитектуре.
^ Тема 3. Линейное программирование.
Задача линейного программирования. Решение методами линейной алгебры. Симплекс-метод. Метод Гомори. Двойственная задача линейного программирования. Задача о назначении персонала. Задача о кормлении персонала. Задача об использовании и хранении сырья. Задача о планировании работы персонала и оборудования. Задача о заключении контрактов. Задача об адаптации работы к требованиям рынка. Задача о доставке. Линейное программирование в архитектуре.
^ Тема 4. Нелинейное программирование.
Задача нелинейного программирования. Условия Куна-Такера первого и второго порядка. Двойственная задача нелинейного программирования. Алгоритмы золотого сечения и Фибоначчи в одномерном случае. Нелинейное программирование в архитектуре.
^ Тема 5. Теория игр.
Понятие игры. Игры двух лиц с нулевой суммой. Стратегии игры. Теорема фон Неймана. Примеры. О связи теории игр и линейного программирования. Использование теории игр в архитектуре.
^ Тема 6. Имитационное моделирование.
Имитационный эксперимент и его этапы. Формирование имитационной модели. Генерация случайных чисел. Методы уменьшения дисперсии. Статистический анализ данных. Имитационное моделирование в архитектуре.
Литература
Обязательная
1. Примерная программа дисциплины “математика” для направления 521700 “Архитектура”. – Министерство образования Российской Федерации, 2000г.
2. Игнатьев Ю.А. Учебное пособие по высшей математике для студентов специальности «Архитектура». – Часть I. – Москва: Издательство РУДН, 2005.
3. Капитонова Ю.В. и др. Лекции по дискретной математике. – СПб.: БХВ-Петербург, 2004.
4. Кофман А. Методы и модели исследования операций. – Москва: Мир, 1966.
5. Исследование операций. / Под ред. Дж. Моудера, С. Элмаграби. – Т.1-2. – Москва: Мир, 1981.
6. Нейман Дж. фон, Моргенштерн О. Теория игр и экономическое поведение. – Москва: Наука, 1970.
Дополнительная
1. Матричные игры. / Под ред. Н.Н. Воробьева. – Москва: ГИФМЛ, 1961.
2. Морз Ф.М., Кимбелл Д.Е. Методы исследования операций. – Москва: Советское радио, 1956.
3. Муртаф Б. Современное линейное программирование: Теория и практика. – Москва: Мир, 1984.
4. Карпелевич Ф.И., Садовский Л.Е. Элементы линейной алгебры и линейного программирования. – Москва: Физматгиз, 1963.
5. Кофман А., Анри-Лабордер А. Методы и модели исследования операций: Целочисленное программирование. – Москва: Мир, 1977.
Программа составлена
Игнатьевым Юрием Анатольевичем,
кандидатом физико-математических наук, доцентом
кафедры высшей математики, факультета физико-математических и естественных наук.
Российский Университет Дружбы Народов
Кафедра высшей математики факультета физико-математических и естественных наук (ул. Орджоникидзе, д.3, ауд. 424).
Курс (по выбору В. 06, 2 кредита) «Математика: наука, культура, искусство » для студентов по специальности «Искусство и гуманитарные науки», «История» (520800), «Философия» (520400) , «Политология» (520900) (бакалавриат).
III и IV семестр: Аудиторных – 2часа, самостоятельных – 2 часа. Лекций- 36 часов, самостоятельная работа – 36 часов («Искусства и гуманитарные науки»), лекций- 36 часов, самостоятельная работа – 36 часов («История»), лекций- 36 часов, самостоятельная работа – 36 часов («Социология»), лекций- 36 часов, самостоятельная работа – 36 часов («Философия»), лекций- 36 часов, самостоятельная работа – 36 часов («Политология»).
Преподаватель: доктор педагогических наук,
профессор Михеев В. И.
Часы консультаций (индивидуальной работы со студентами):
По договоренности.
Цель курса
– формирование у будущих бакалавров широкого взгляда на фундаментальные идеи и концепции методологии и методики решения широкого круга научно-теоретических и практических задач, а также формирования целостного диалектического представления об основных этапах становления и исторического развития данной научной области знаний;
– воспитание у бакалавров определённой культуры мышления путём формирования целого ряда обобщённых мыслительных действий, таких как умение аргументировать свою позицию, анализировать, сравнивать, классифицировать и, в конечном счете, активно и успешно участвовать в профессиональной дискуссии;
– формирование у бакалавров определённых знаний, умений и навыков для грамотной постановки профессиональных задач, возникающих при исследовании различных по своей природе объектов и явлений, с последующим «переводом» проблемы их описания на уровень построения различных моделей, в том числе и математических, когда речь идет об использовании различных математических методов классификации и шкалирования объектов.
Идейное содержание курса
Программа направлена на формирование передового современного мировоззрения и построена с учётом того, что в связи с непрерывно возрастающим влиянием математики на современную общественную жизнь математическое образование становится одной из важнейших составляющих фундаментальной базовой подготовки бакалавра-гуманитария. Значимость прикладных разделов математики обусловлена тем, что как наука и учебный предмет она оперирует универсальным языком, что и позволяет ей не только стать мощным средством решения специальных прикладных задач путём моделирования сложных явлений и процессов, но и играть значительную роль в формировании логического мышления и других ценных качеств личности обучаемого, способствуя, таким образом, его культурному и интеллектуальному развитию и доводя до требуемого высокого уровня его общеобразовательную и профессиональную подготовку.
Организационно-методическое построение курса
Курс состоит из 36 часов лекционных и 36 часов самостоятельных занятий. В начале каждого лекционного занятия излагается теоретическая часть, вводятся основные для каждого подраздела необходимые понятия (в том числе и математические), формулируются утверждения, лежащие в основе развития предмета обсуждения, и анализируются пути их дальнейшего применения в решении различных по своей направленности задач и области приложения полученных результатов (к примеру, при изучении исторических явлений, языков наук и искусства, роли точности наблюдений в искусстве и т.д.). Каждый теоретический пассаж сопровождается примерами, поясняющими различные стороны рассматриваемой проблемы. На каждом лекционном занятии выдается домашнее задание и обсуждаются вопросы, возникшие в предшествующей домашней работе учащихся, сравниваются разные подходы к решению одной и той же задачи с целью выработки умения находить разные решения и их сравнивать с позиции точности и интерпретации при формировании определенных суждений и выводов.
В процессе чтения курса предусмотрены консультации, призванные облегчить студентам понимание многих ключевых вопросов по темам лекций и тех трудностей, которые могут иметь место при самостоятельном выполнении домашних заданий. Последнее особенно важно для работы учащихся в плане подготовки курсовой работы (или контрольной зачетной работы), которая выступает в качестве итоговой аттестации уровня подготовки и усвоения курса. Таким образом, в рамках курса проводится основательная работа на то, чтобы каждый студент, выполняющий домашние задания, посещающий все занятия и проявляющий активность, т. е. настроенный учиться, успешно справился со всеми формами контроля.
Содержание курса
Курс включает темы, касающиеся вопросов моделирования и теоретических основ решения различных по своей направленности научно-практических задач. На отдельных задачах, почерпнутых из конкретных областей знаний поведенческих и точных наук, дается описание специальных методов и процедур для изучения различных по своей природе явлений, процессов и систем. В этом плане обсуждаются вопросы анализа качественных признаков и структур, рассматриваемых в рамках исследований в области культуры, науки и искусства.
Тема 1
Цикл первый «Математика и наука». Ознакомление студентов с организацией учебной работы по разделу. Введение в предмет курса: цели, методы и задачи, составляющие основу содержания курса. Значение методологии и научных методов исследований. Диалектическая связь между ними и математикой в историческом ракурсе.
Тема 2
Историк и математика. Методология качественных описаний объекта: исходные положения, основные понятия и определения; этапы изучения его свойств, выступающих как объекты измерения.
Тема 3
Измерить – значит объяснить. Количество, величина, число. История вопроса. Объект измерения и единицы измерения (именование и размерность). Классификация величин. Понятие «эмпирический объект».