Л. В. Логика Предмет и цель логики Предметом формальной (традиционной) логики являются закон
| Вид материала | Закон |
- Методические материалы для студентов 1 курса Юридического факультета, 874.23kb.
- Диалектическая логика логика движения, развития, изменения, 503.9kb.
- Предмет и 3начение логики, 9309.47kb.
- Всей системы риторического образования: создание смыслового каркаса речевого произведения, 78.92kb.
- В. Г. Уткин Кандидат философских наук, доцент логика (краткие тексты лекций) Москва, 459.83kb.
- Логика темы рефератов, 43.71kb.
- Вопросы по курсу: Математическая логика и теория алгоритмов (2 курс), 30.21kb.
- Настоящий курс «Логика» читается как курс общей формальной логики гуманитарных специальностей., 571.6kb.
- Математическая логика, 1012.22kb.
- Попов Владлен Александрович литература, 7.67kb.
^ Фигуры категорического силлогизма и правила.
В категорическом силлогизме средний термин может занимать различные места в посылках. В зависимости от этого различают 4 фигуры.
1. В первой фигуре средний термин является субъектом в большей и предикатом в меньшей посылке.
^ Всякий учебник должен быть написан понятным языком.
Логика Гетмановой – учебник.___________________________
Логика Гетмановой доложна быть написана понятным языком
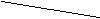
M P M - PS
M S - M S - P S - P
Правила первой фигуры:
А) Большая посылка всегда общее суждение
Б) Меньшая посылка всегда утвердительное суждение
2. Вторая фигура. Средний термин занимает место предиката в обеих посылках.
P
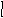M P - M S
M S - M S - P S - P
Правила первой фигуры:
А) Большая посылка всегда общее суждение
Б) Одна из посылок должна быть отрицательной
Все науки изучают законы действительности.
Ни одна религия не изучает законов действительности.
Ни одна религия не является наукой.
3. Третья фигура. Средний термин занимает место субъекта в двух посылках.
M
P M - PМ
S M - S_ S - P S - P
Ртуть - не тверда.
Ртуть металл.______________
Некоторые металлы не тверды.
Правила третьей фигуры:
А) Меньшая посылка всегда утвердительное суждение
Б) Заключение должно быть частным.
4. Четвёртая фигура. Средний термин является предикатом в большей и субъектом в меньшей посылке.
P
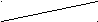
M P - MM
S M - SS - P S - P
Все киты являются млекопитающими.
Ни одно млекопитающее не является рыбой.
Ни одна рыба ни кит.
Правила четвёртой фигуры:
А) Когда большая посылка утвердительна, то меньшая должна быть общей.
Б) Если одна из посылок утвердительна, то большая должна быть общей.
^ Сокращенные силлогизмы
Наряду с простым категорическим силлогизмом существуют различные виды сложных силлогизмов. Существуют также сокращенные силлогизмы – результаты сокращения простого категорического силлогизма – энтимемы. В переводе с греческого это слово означает "в уме", "в мыслях".
^ Сокращенный силлогизм (энтимема) – это умозаключение с какой-либо пропущенной частью силлогизма (посылкой или заключением). Так как в энтимемах воспроизводится лишь часть силлогизма, то поэтому в них только два суждения, одно из понятий повторяется в обоих, так что терминов все равно три, как это и должно быть в силлогизме.
Например: "Собака не может лазать по портьерам, Ватсон, следовательно, это не собака" (Ш. Холмс).
Весь силлогизм запишется в следующем виде:
(1) Собака (P) не может лазать по портьерам (M).
(2) Данное животное (S) может лазать по портьерам (M).
(3) Данное животное (S) - не собака (P).
Возможны вида три энтимемы, в зависимости от того, какая часть силлогизма пропущена.
Возьмем для примера умозаключение:
Все химически простые вещества состоят из однородных атомов
Ни один сплав не есть химически простое вещество
Ни один сплав не есть вещество, состоящее из однородных атомов
Это умозаключение можно представить в виде одной из следующих энтимем:
1. «Ни один сплав не есть вещество, состоящее __________из однородных атомов, так как ни один сплав не есть химически простое вещество» – в данной энтимеме не сформулирована большая посылка.
2. «Все химически простые вещества состоят из однородных атомов, следовательно, ни один сплав не есть вещество, состоящее из однородных атомов» – в этой энтимеме выпущена меньшая посылка.
3. «Все химически простые вещества состоят из однородных атомов, а ни один сплав не есть химически простое вещество» – в этом случае не сформулировано заключение.
Основная задача, которую ставит перед собой логика при изучении энтимемы, состоит в том, чтобы указать приемы и правила, которые давали бы возможность точно восстанавливать недостающую часть силлогизма.
В общем виде можно выделить три этапа в операции восстановления недостающих частей силлогизма:
• Определение пропущенного элемента. Если в энтимеме встречаются выражения: «так как», «потому что», «следовательно», «значит» и им подобные, то в ней присутствует заключение. Если указанных выражений или их эквивалентов нет, то в энтимеме опущено заключение.
^ При наличии энтимемы с пропущенным заключением восстановление силлогизма сводится к тому, чтобы вывести это заключение – это не представляет особых трудностей, однако при этом следует помнить, что если даны две посылки, из которых не следует никакого заключения по правилам категорического силлогизма, то это не энтимема.
Следует отметить, что умозаключение, где пропущена одна из посылок, восстановить сложнее, чем энтимему с пропущенным заключением. В этом случае основным принципом восстановления недостающих частей силлогизма является следующий: «Если дана какая-либо из посылок и заключение, то недостающая посылка должна быть таким суждением, из которого при сочетании с данной посылкой с логической необходимостью вытекает данное заключение». Таким образом, операция восстановления недостающей посылки сводится к отысканию указанного суждения и эта операция должна выполняться на основе знания правил и форм правильных умозаключений.
• Определение ткрминов: большего, меньшего и среднего
• При наличии заключения становятся известными термины, по которым определяется присутствие одной из посылок.
• Определяется фигура силлогизма, модус и порядок посылок.
• Формулировка силлогизма в полной форме.
^ Правдоподобные умозаключения.
В правдоподобных умозаключениях вывод не обязательно будет совершенно истинным, даже при наличии истинных посылок. В таких умозаключениях вывод следует из посылок не обязательно с полной необходимостью, он в той или иной мере предположительный. К этому разряду умозаключений относятся индуктивные умозаключения (точнее бы сказать, неполная индукция) и аналогия.
Аналогия. Слово «аналогия» у греков означало пропорцию и первоначально употреблялось для обозначения совпадений отношений между числами. Так, 6 и 9 были аналогией 8 и 12.
^ Умозаключения по аналогии - это вывод о принадлежности единичному предмету определенного признака, основанный на сходстве этого предмета в существенных признаках с другим единичным предметом.
А имеет признаки ^ Авсd...
В имеет признаки АВс...
Вероятно, что В имеет признаки d.
Умозаключение по аналогии не обращается к какому-нибудь определённому общему закону. В умозаключении по аналогии мы умозаключаем не от ряда случаев, но от известного числа пунктов сходства. Заключение по аналогии не может дать ничего, кроме вероятности.
^ Степень вероятности умозаключения по аналогии зависит от трёх обстоятельств:
1) количества усматриваемых нами сходств,
2) количества известных несходств между ними
3) объёма нашего знания сравниваемых вещей.
Именно вероятность заключения по аналогии может считаться очень высокой, если число пунктов сходства между рассматриваемыми вещами очень велико и если в то же время число пунктов несходства незначительно, но при этом мы знаем, что число известных нам свойств изучаемой вещи достаточно велико. Чем больше число неизвестных свойств, тем меньше достоверность нашего вывода.
Умозаключению по аналогии всегда предшествует операция сравнения двух объектов, которая позволяет установить сходства и различия между ними. При этом для аналогии требуются не любые совпадения, а сходства в существенных признаках при несущественности различий.
Логический переход от известного к новому знанию регулируется в выводах по аналогии следующим правилом: если два единичных предмета сходны в определенных признаках, то они могут быть сходны и в других, обнаруженных в одном из сравниваемых предметов, признаках.
В умозаключениях по аналогии используются следующие понятия:
- образец аналогии - объект, признак которого переносится на другой объект;
- субъект аналогии - объект, на который переносится признак;
- термины аналогии - это образец и субъект аналогии;
- переносимый признак - признак, который переносится с образца на субъект;
- основание аналогии - признак, одновременно присущий обоим терминам аналогии и служащий основанием для переноса интересующего нас признака.
Переносимый признак, обычно, является простым, а основание аналогии - сложным признаком.
В структуру аналогии входят следующие суждения:
1) суждение о наличии основания аналогии у образца;
2) суждение о наличии, основания аналогии у субъекта;
3) суждение о наличии переносимого признака у образца;
4)суждение о наличии переносимого признака у субъекта.
Первые три суждения являются посылками умозаключения по аналогии, а четвертое - его заключением.
В зависимости от характера признака, пере носимого с одного предмета на; другой различают аналогию свойств и аналогию отношений.
^ Аналогия свойств (предметов) - умозаключение, в котором объектом уподобления выступают два единичных предмета, события или явления, а переносимым признаком - свойства этих предметов.
Схематично аналогию свойств можно изобразить следующим образом:
^ Предмет А имеет признаки а, b, с.
Предмет В имеет признаки а, b, с.
Предмет А имеет Признак d
Вероятно, предмет В имеет признак d
Например:
Высокая, стройная, красивая, брюнетка средних лет - известная актриса.
^ Данная (встречная) высокая, стройная, красивая, брюнетка средних лет.
Наверное, она тоже актриса.
Аналогия отношений - умозаключение, в котором объектом уподобления выступают отношения между двумя парами предметов, а переносимым признаком - свойства этих отношений.
Аналогия отношений имеет место тогда, когда мы сопоставляем несколько отношений, чем-то сходных друг с другом.
Схема аналогии отношений:
^ Предмет а подобен предмету с.
Предмет b подобен предмету d.
Между предметами с и d имеется отношение R.
Вероятно, между предметами а и b имеется отношение R.
Например: Арифметика так же относится к высшей математике, как формальная логика к диалектической.
В аналогии отношений выделяют фигуральную и буквальную аналогию. ^ Фигуральная аналогия - это умозаключение, основывающееся на сходстве отношений между предметами из качественно отличных областей действительности, связь которых имеет только символическое значение.
Пример. «Трудно определить, что такое демократия. Она подобна жирафу. Раз посмотришь - и уж больше ни с чем не перепутаешь».
По другому критерию аналогию можно разделить на следующие три вида: строгая, нестрогая и ложная.
Строгая аналогия (сильная)
Это умозаключение, в котором переносимый признак необходимым образом связан с другими, сходными признаками (будучи, например, их следствием или, наоборот, причиной). В этом случае вывод может стать достоверным.
Например, студент А часто строит выводы на основе поспешных обобщений и потому рассуждения его часто бывают ошибочными.
Зная, что студент Б также часто делает поспешные обобщения, можно заключить, что его рассуждения часто бывают ошибочными.
Нестрогая аналогия (слабая)
Это умозаключение, в котором переносимый признак непосредственно не связан со сходным, но может иметь место. Такая аналогия даёт вероятный вывод.
Например, железо обладает специфическим блеском, ковкостью теплопроводимостью, электропроводимостью. Неизвестное тело серо-стального цвета обладает теплопроводимостью. Это неизвестное тело принадлежит к группе металлов и значит, обладает ковкостью и электропроводимостью. Строгая аналогия применяется в научных исследованиях, в математических доказательствах. Она достаточно близка по своим признакам к дедуктивным умозаключениям.
^ Причины ошибок выводов по аналогии:
1) несущественность признаков, служащих основанием аналогии;
2) отсутствие связи между признаками, служащими основанием
аналогии, и переносимым признаком.
Для повышения степени вероятности заключений по аналогии следует придерживаться следующих правил:
1) число общих признаков должно быть возможно большим и разнородным;
2) общие признаки должны быть существенными;
3) количество и значительность пунктов различия должны быть небольшими;
4) зависимость между сходными и переносимыми признаками.
При нарушении указанных выше правил аналогия становится ложной. Иногда их нарушают сознательно с целью выдать ложное заключение за истинное.
Таким способом создается софизм, например:
Чем больше делаешь добра, тем лучше.
Принимать лекарство от болезни - добро.
Чем больше принимаешь лекарств, тем лучше.
^ Индуктивное умозаключение
В индуктивном умозаключении мысль идёт от частного к общему.
Например, к выводу, что все тела при нагревании расширяются люди пришли в результате обобщения личного опыта и единичных данных.
Индуктивным умозаключением называется умозаключение от меньшей степени общности к заключению большей степени общности, от частных положений к общим, от фактов к их обобщению, и построению на их основе теории.
Вывод, полученный на основе индуктивных умозаключений может быть достоверен при соблюдении 2 условий:
1. если исследовали все предметы данного класса и обобщили их на основании знаний данного признака, выделенного у данных предметов. Такая индукция называется полной.
2. если знаем причину, свойства входящих в этот класс предметов.
Индуктивные умозаключения.
1. Полное – такое умозаключение, в котором общий вывод о некотором классе предметов делается на основании изучения всех предметов данного класса. Число предметов должно быть ограничено.
Например:
Земля светится отражённым светом Солнца.
Марс светится отражённым светом Солнца.
Венера светится отражённым светом Солнца.
и т.д. светятся отражённым светом Солнца.
^ Земля, Марс, Венера – планеты солнечной системы.
Все планеты солнечной системы светятся отражённым светом.
Формула:
S1 есть Р. (S обладает признаком Р)
S2 есть Р.
S3 есть Р.
…
Sn есть Р.
S1, S2, S3, Sn - составляют весь класс S
Все S есть Р.
Индукция полная если рассмотрены все предметы анного класса, если признак принадлежит всем предметам.
Неполное индуктивное умозаключение – общий вывод о классе предметов делается на основании изучения только части однородных предметов данного класса. Такое заключение не достоверно на все 100%.
Ворона – летает.
Синица – летает
Утка – летает.
^ Ворона, синица, утка – птицы.
Вероятно, все птицы летают.
Формула:
S1 есть Р.
S2 есть Р.
S3 есть Р.
…
Sn есть Р.
S1, S2, S3, Sn - некоторые представители класса S
Все S есть Р.
Виды неполной индукции:
1. Популярная – вывод обо всём классе предметов делается на основании изучения некоторых предметов данного класса при отсутствии противоречащих случаев.
2. Научная - такое умозаключение, в котором общий вывод обо всех предметах данного класса делается на основании знания необходимих признаков части предметов данного класса, если знают их причину.
Железо – электропроводно.
Медь – электропроводна.
Натрий – электропроводен.
Железо, Медь, Натрий – металлы.
Все металлы – электропроводны.