Курс лекций дисциплины «Компьютерные технологии и сапр» для студентов специальностей 120500, 120507, 120700 очной, очно-заочной и заочной форм обучения

Вид материала

Курс лекций

Содержание 4.2. Библиотека конечных элементов 4.3. Препроцессорная подготовка Типы моделей. Построение сеточной модели. Контроль качества сеточной модели и ее модификация. Определение данных и ограничений. Управление работой решателя. 4.4. Постпроцессорная обработка результатов 4.5. Анализ динамических процессов систем управления Библиотеки типовых блоков. Основные этапы работы с программой. 5. Автоматизация технологической подготовки производства

Подобный материал:

• Курс лекций дисциплины «Компьютерные технологии и сапр» для студентов специальностей, 559.5kb.
• Методические указания по написанию курсовой работы для студентов очной, заочной и очно-заочной, 318.34kb.
• Учебное пособие для студентов очной, очно-заочной и заочной форм обучения (дистанционное, 929.04kb.
• Реферат как форма самостоятельной работы студента: методическое пособие по выполнению, 325.87kb.
• Курс лекций для студентов заочного факультета самара, 1339.16kb.
• Методические рекомендации по выполнению практических работ по курсу «Экология» для, 474.71kb.
• Методические указания к курсовой работе по дисциплине «Стратегический менеджмент» для, 76.01kb.
• Методические рекомендации для студентов очно-заочной и заочной форм обучения Тематика, 268.03kb.
• Методические указания к курсовой работе по дисциплине «Экономика отрасли» для студентов, 197.88kb.
• Методические указания по выполнению рефератов и контрольных работ по курсу «экология», 187.76kb.

4.1. Постановка задачи конечно-элементного анализа

Различные виды анализа, выполняемые в программных систе­мах первой, второй и третьей групп, основаны на классических инженерных подходах к разработке математических моделей по­ведения изделия при различных воздействиях. В конечно-элемент­ной постановке задачи моделирования исследуемая область пред­варительно разбивается на ограниченное множество конечных эле­ментов, связанных между собой конечным числом узлов. Искомы­ми переменными уравнений математических моделей являются перемещения, повороты, температура, давление, скорость, потен­циалы электрических или магнитных полей. Эти переменные оп­ределяют степени свободы узлов. Их конкретное содержание за­висит от типа (физической природы) элемента, который связан с данным узлом. Например в задачах прочностного анализа для каж­дого элемента с учетом степеней свободы его узлов могут быть сформированы матрицы масс, жесткости (или теплопроводности) и сопротивления (или удельной теплоемкости). Множество степе­ней свободы, определяющих состояние всей системы в данный момент, называют волновым фронтом, который может расширяться или сужаться по мере того, как неизвестные переменные вводятся в рассматриваемую совокупность или исключаются из нее. После прохождения волнового фронта через все элементы и вычисления всех искомых переменных можно анализировать полученные ре­зультаты и строить гипотезы о поведении исследуемого изделия.

В постановке задачи прочностного динамического анализа учи­тывается возмущающее воздействие, которое является функцией времени. Можно принимать во внимание рассеяние энергии, инер­ционные эффекты и переменные во времени нагрузки. Примерами таких нагрузок являются:

• циклические нагрузки (например, вращение коленчатого вала двигателя);

• внезапно прикладываемые нагрузки (удар или взрыв);

• случайные нагрузки и любые другие переменные нагрузки. Общее уравнение движения в конечно-элементной форме запи­сывается в виде

MU"+CU'+KU=F(t),

где М, С, К - матрицы соответственно масс, сопротивлений, жесткостей; U", U', U - векторы соответственно узловых ускорений, узловых скоростей, узловых перемещений; F - вектор нагрузок; t - время.

Искомые переменные системы уравнений - это элементы век­тора узловых перемещений U, которые в любой момент времени должны удовлетворять условиям равновесия системы при нали­чии сил инерции и рассеяния энергии. Решение этой системы урав­нений выполняется либо прямым методом Ньюмарка, либо мето­дом суперпозиции форм колебаний. К такому типу анализа отно­сятся: динамика переходных процессов, модальный анализ, отклик на гармоническое воздействие, спектральный анализ и отклик на случайную вибрацию.

Если действие сил инерции или процессы рассеяния энергии пренебрежимо малы и не оказывают существенного влияния на поведение изделия, то задача может быть сформулирована в виде статического прочностного анализа. Такой тип анализа наиболее часто используется, например, для определения концентрации на­пряжений в галтелях конструктивных элементов или для расчета температурных напряжений, для определения перемещений, на­пряжений, деформаций и усилий, которые возникают в изделии в результате приложения механических сил.

Уравнение статического анализа записывается в виде

KU=F,

где К- матрица жесткостей; U - вектор перемещений; F - вектор сил.

Компоненты вектора сил: сосредоточенные силы, тепловые на­грузки, давления и силы инерции. В процессе анализа можно учи­тывать такие нелинейные свойства, как пластичность и ползучесть материала, большие прогибы, большие деформации и контактное взаимодействие при условии, что нагрузки возрастают постепен­но.

^ 4.2. Библиотека конечных элементов

В каждой программе, реализующей конечно-элементный ана­лиз, описывается совокупность используемых элементов. Чем шире набор и функциональные свойства элементов, тем большими воз­можностями обладает тот или иной программный комплекс. При­меры некоторых конечных элементов, их графическое представле­ние и краткое описание приведены в табл. 1.1. При этом не ставилась задача сравнить возможности библиотек тех или иных пакетов, равно как и не преследовалась цель описать все особенности, ко­торыми отличаются элементы этих библиотек. Эти и многие дру­гие сведения могут быть найдены в специальной литературе.

Конечные элементы обычно группируются по их назначению, например:

• элементы стационарного и нестационарного теплообмена;

• элементы для моделирования вязкоупругих и вязкопластичных материалов;

• элементы сплошной среды для анализа движения потоков жидкости и газа, решения задач гидроаэромеханики, акустики и течения сред в каналах;

• элементы для расчета статических и динамических напряже­ний;

• элементы для анализов, включающих как тепловые, так и элек­трические эффекты;

• элементы для анализа произвольно меняющихся во времени магнитных полей;

• элементы связанной задачи для расчетов, в которых учитыва­ется взаимовлияние результатов двух или более видов анализа (прочностного, теплового, магнитного, сплошной среды, электрического);

• элементы для моделирования нелинейного контакта;

• элементы комбинированные, матричные, поверхностные и др.

Таблица 1.1

Название элемента	Графическое представление	Коли­чество узлов	Размерность пространства	Степени свободы
Стержень		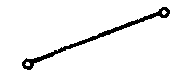2	2D	Перемещения (X, Y)
Упругая балка		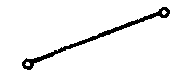2	2D	Перемещения (X, Y), вращение (Z )
Гибкая нить		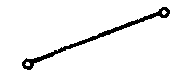2	3D	Перемещения (X, Y ), вращение (Z )
Упругая балка		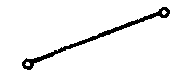2	3D	Перемещения (X.Y, Z), вращение (X, Y, Z)
Треугольный твердотельный элемент		6	2D	Перемещения (X, Y )
Осесимметричный твердотельный элемент для гармонического анализа		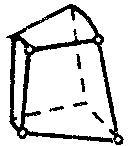4	2D	Перемещения (X, Y, Z]
Прочностной твердотельный элемент		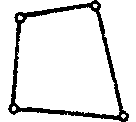4	2D	Перемещения (X, Y )
Прочностной твердотельный элемент		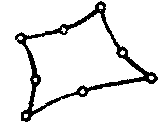8	3D	Перемещения (X, Y)
Прочностной оболочечный элемент		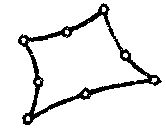8	3D	Перемещения (x,y, Z), вращение (X, Y, Z)
Оболочечный элемент с конечными деформациями		4	3D	Перемещения (X,Y, Z) вращение (X, Y, Z)
Прочностной твердотельный элемент		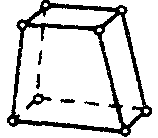8	3D	Перемещения (X, Y, Z)
Твердотельный элемент со степенями поворота		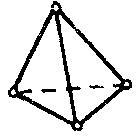4	3D	Перемещения (X, Y, Z) вращение (X, Y, Z)
Прочностной твердотельный элемент		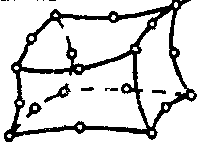20	3D	Перемещения (X, Y, Z)
Название элемента	Графическое представление	Коли­чество узлов	Размерность пространства	Степени свободы
Вязкоупругий твердотельный элемент		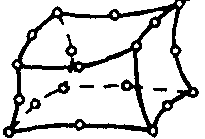20	3D	Перемещения (X, Y, Z)
Твердотельный элемент с конечными деформациями		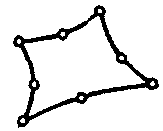8	2D	Перемещения (X, Y, Z)
Прочностной твердотельный элемент		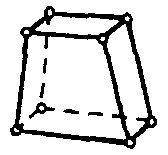8	3D	Перемещения (X,Y, Z) скорости (X, Y, Z), вектор магнитных потенциалов (X, Y, Z)
Гиперупругий смешанный U-P твердотель­ный элемент		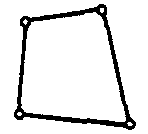4	3D	Перемещения (X, Y, Z)
Гиперупругий твердотельный элемент		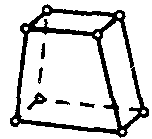8	3D	Перемещения (X,Y, Z)
Теплопроводящий стержень		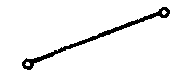2	3D	Температура
Осесимметричный тепловой твердо­тельный элемент для гармоничес­кого анализа		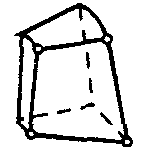4	2D	Температура
Тепловой твердотельный элемент		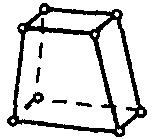8	3D	Температура
Прочностной твердотельный элемент		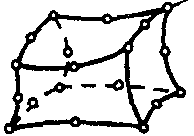20	3D	Температура
Акустический элемент сплошной среды		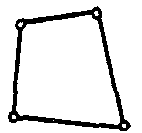4	3D	Перемещения (X, Y), давление
Трубчатый элемент тепло-массообмена		2	3D	Температура, давление
Элемент контакта		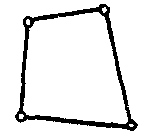4	3D	Перемещения (X, Y, Z)
Электро­статический твердотельный элемент		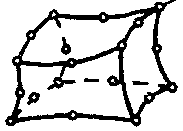20	3D	Напряжение
Название элемента	Графическое представление	Коли­чество узлов	Размерность пространства	Степени свободы
Твердотельный элемент связанной задачи (тепло+ электричество)		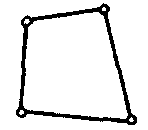4	2D	Температура, напряжение
Источник тока		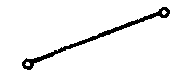2	2D	Скалярный магнитный потенциал
Твердотельный элемент связанной задачи		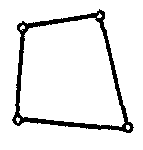4	2D	Перемещения (X, Y), температура, напряжение, вектор магнитных потенциалов (Z)
Твердотельный элемент связанной задачи		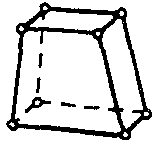8	3D	Перемещения (X, Y,Z), температура, напряжение, скалярный магнитный потенциал
Осесимметричный гармонический элемент ддя анализа течения среды в каналах		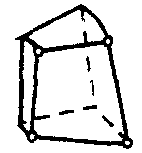4	2D	Перемещения (X, Y, Z)
Элемент тепломассообмена модуля FLOTRAN		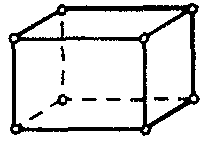8	3D	Перемещения (X,Y, Z), давление, температура, кинетическая энергия турбулентного потока, параметр рассеяния турбулентной энергии
Амортизатор		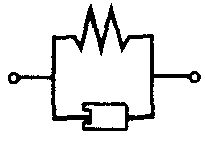2	3D	Перемещения (X,Y, Z), вращение (X, Y, Z) давление, температура
Элемент пограничного эффекта		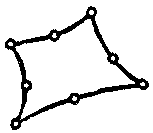8	3D	Перемещения (X,Y,Z), температура
Матричный элемент жесткости, массы или сопротивления		2	3D	Перемещения (X.Y,Z), вращение (X, Y, Z )
Элемент условий на бесконечность		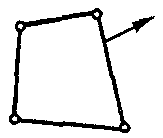4	3D	Вектор магнитных потенциалов (Z), напряжение, температура

Конечные элементы предназначены для формализации задач в двумерной (2D) или трехмерной (3D) постановке. Графическими примитивами элементов являются «узел», «связь», «грань».

Элементы могут быть линейными или нелинейными (с проме­жуточными узлами в середине связи). Нелинейные элементы по­зволяют получать более достоверные результаты.

^ 4.3. Препроцессорная подготовка

Конечно-элементный анализ состоит из трех основных этапов:

начальной подготовки (препроцессорной подготовки), получения решений и обработки результатов моделирования (постпроцессор­ной обработки).

Среди задач, которые инженер решает на первом этапе, можно выделить создание модели изделия, создание неточной модели, контроль качества сеточной модели и ее модификацию, определе­ние данных и ограничений и др.

^ Типы моделей. В инженерном анализе различают три типа моделей: геометрическую, расчетную и сеточную. Геометрическая модель обычно представляет собой модель машиностроительного изделия в целом или его детали. Расчетная модель - это упрощен­ная геометрическая модель, которая используется для анализа. Нередко эта модель является составной частью самого анализа. Уп­рощение или идеализация геометрической модели достигается пу­тем удаления тех ее элементов, которые несущественно влияют на результаты анализа. Сеточная модель представляет собой совокуп­ность узлов и элементов, которая натягивается на расчетную мо­дель (рис. 1.38). Как уже отмечалось, геометрическая и расчетная модели обычно создаются на этапе конструирования средствами твердотельного и поверхностного моделирования.

^ Построение сеточной модели. В универсальных программах существуют несколько способов генерации сетки. Например, в программе ANSYS используются методы экструзии, создания упо­рядоченной сетки, создания произвольной сетки и адаптивного построения. В программе SAMCEF кроме перечисленных мето­дов применяются методы балок, Delaunay-Voronoi, Pavior и др.

Экструзия (выдавливание) - способ построения трехмерной модели сетки путем перемещения и сдвига основания в опреде­ленном направлении или путем вращения поперечного сечения вокруг заданной оси (рис. 1.39). Этот способ позволяет создать се­точную модель, не используя ассоциированную расчетную модель изделия.





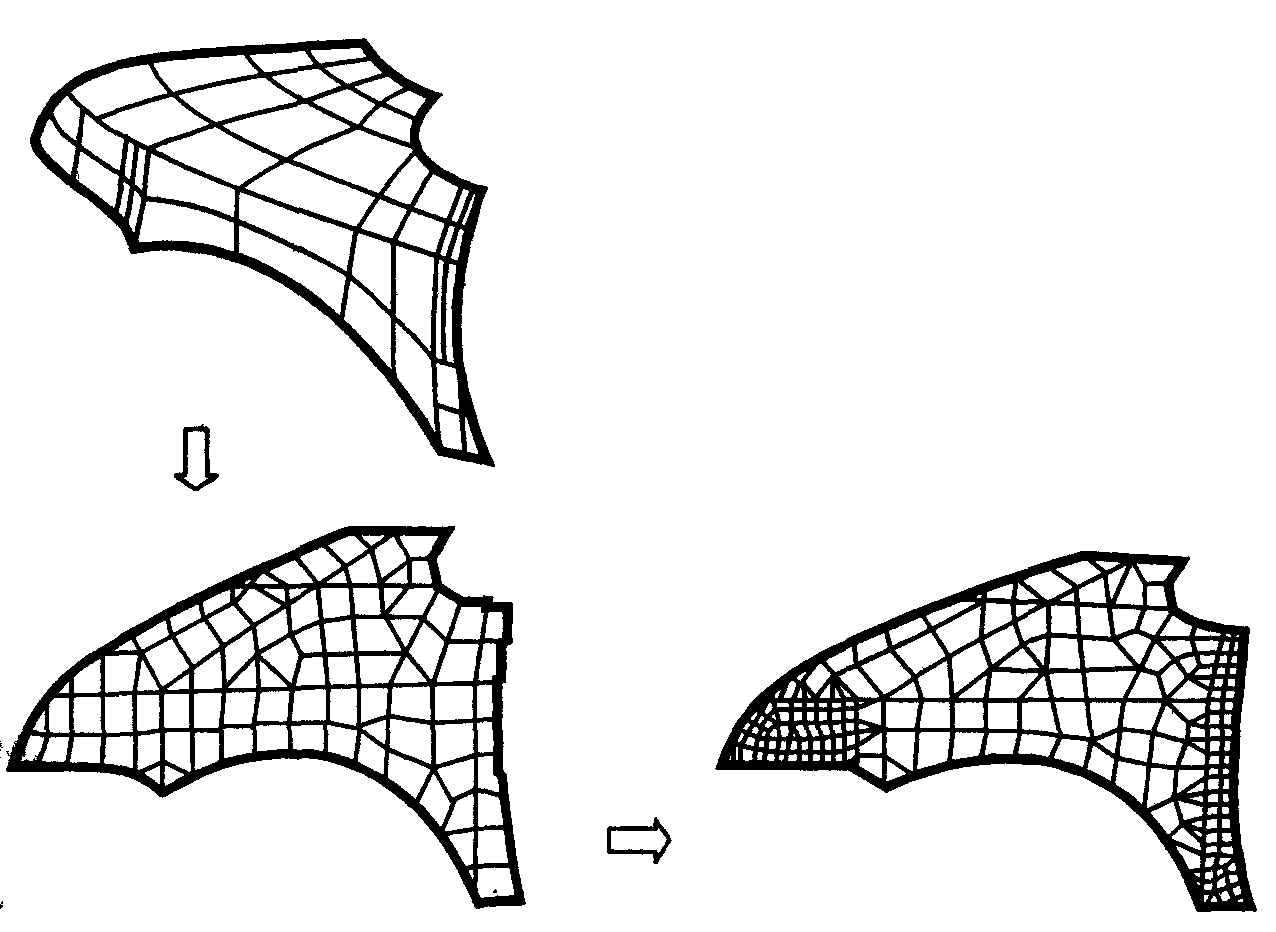
Рис. 1.38. Переход от геометрической модели к сеточным моделям



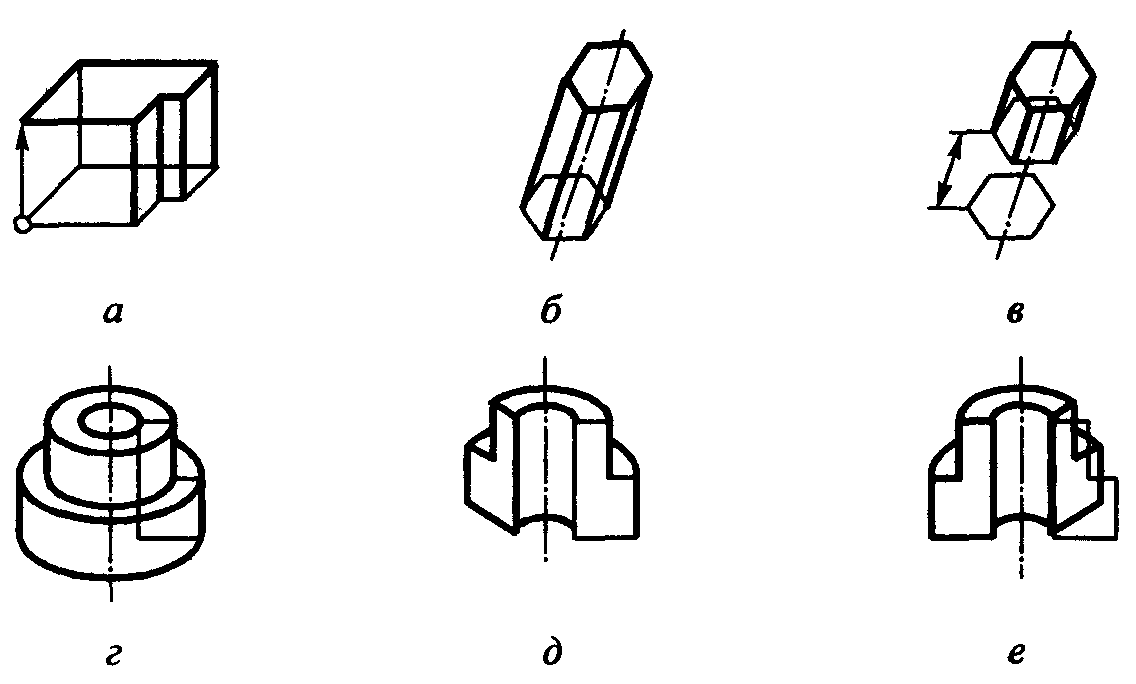
Рис. 1.39. Генерация элементов сетки методом экструзии:

а, б - перемещенное основания вдоль заданного направления;

в - перемещением со сдвигом основания; г - полный поворот сечения на 360°, вокруг заданной оси; д - неполный поворот вокруг заданной оси;

е - неполный поворот со сдвигом

Методом экструзии можно генерировать одномерные элемен­ты, двумерные элементы (обычно четырехугольники) и трехмерные элементы (пяти- и шестигранники). Так, треугольник генери­рует пятигранник, а четырехугольник - шестигранник.

Основание, на котором строится экструзия, может быть ском­поновано из узлов или одно- и двумерных элементов. В качестве основания также может использоваться ранее созданная вся сеточ­ная модель. Можно использовать результат экструзии в качестве основания следующей экструзии. Например, при помощи экстру­зии одномерного элемента будет получен двумерный элемент, ко­торый может быть использован как основание для экструзии трех­мерного элемента.

При построении упорядоченной сетки необходимо предвари­тельно разбить расчетную модель на участки с простой геометри­ей, ввести ограничения и критерии качества сеточной модели, а затем запустить программу генерации сетки. Сетка может состо­ять из шести-, четырех- и треугольных элементов. Например, ме­тод Pavior предназначен для генерации сетки преимущественно в виде четырехугольников. Им можно воспользоваться для предва­рительных расчетов, так как часто сетка получается невысокого качества. Чтобы получить треугольную сетку, программа выделя­ет области расчетной модели, предназначенные для нанесения упо­рядоченной сетки, используя ранее заданные ограничения и кри­терии качества сеточной модели. Затем полученная методом Pavior или любым другим методом четырехугольная сетка перестраива­ется в сетку из треугольных элементов (рис. 1.40). В этом случае для построения треугольной сетки высокого качества можно вос­пользоваться методом Delaunay-Voronoi. На завершающем этапе отдельные участки сетки собираются в единую сеточную модель. Метод построения упорядоченной сетки является одним из наибо­лее распространенных и базируется на использовании расчетной модели.



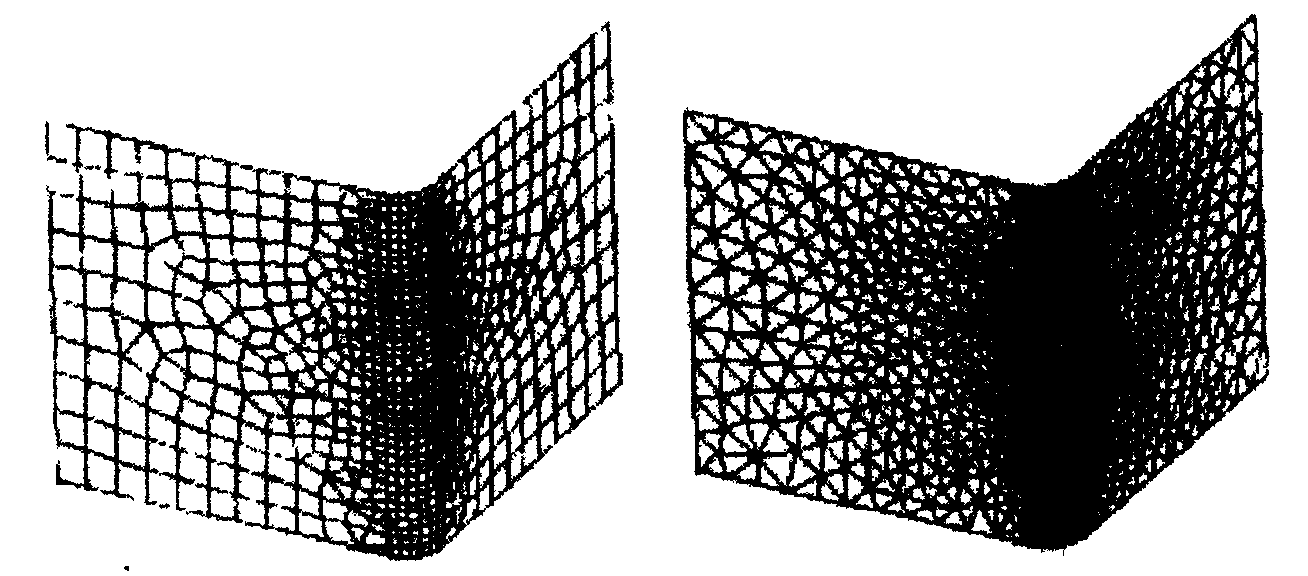
Рис. 1.40. Результаты построения сетки различными методами

В различных программах анализа имеются специальные сред­ства генерации произвольной сетки, с помощью которых она мо­жет наноситься непосредственно на модель достаточно сложной геометрии. Произвольную сетку можно строить из треугольных, четырехугольных и четырехгранных элементов. Генераторы про­извольной сетки обладают широким набором функций управления качеством сетки. Например, в программе ANSYS реализован алго­ритм выбора размеров конечного элемента, позволяющий строить сетку элементов с учетом кривизны поверхности модели и наилуч­шего отображения ее реальной геометрии.

Метод построения тетраэдной сетки полезен для создания трех­мерных элементов, в основе которых лежат треугольники. Исполь­зуемая базовая геометрия двумерной сетки не должна иметь свободных незамкнутых граней. На предварительном этапе прове­ряется качество сетки, а именно выявляются и предъявляются пользователю незамкнутые элементы и элементы с несогласован­ной ориентацией.

Адаптивное построение сетки состоит в том, что после созда­ния расчетной модели и задания граничных условий генерируется конечно-элементная сетка, затем выполняется анализ, оценивает­ся ошибка дискретизации сетки, после чего меняется размер сет­ки. Процесс протекает до тех пор, пока значение погрешности не станет меньше заданного, или число итераций не достигнет допу­стимого значения.

Универсальные программы анализа (ANSYS, SAMTECH и др.) располагают дополнительными возможностями формирования се­точных моделей, к которым относятся метод суперэлеменгов и метод подмоделей.

В методе суперэлементов некоторая часть смежных элементов сводится к одному эквивалентному элементу. Суперэлемент может формироваться из конечных элементов любого типа, однако нуж­но учитывать, что в этом случае поведение суперэлемента предпо­лагается линейным даже в том случае, когда в его состав введен нелинейный элемент. Аналогичные упрощения можно выполнить и с расчетной моделью - простые участки расчетной модели изде­лия рассматриваются как домен, на котором создается один конеч­ный суперэлемент. В основе такого подхода лежит матричное уп­лотнение, с помощью которого такие параметры, как жесткость (проводимость), масса (удельная теплоемкость) и сопротивление приводятся к системе ведущих степеней свободы. Метод супермо­делей позволяет сократить время решения.

На подготовительном этапе важно так сформулировать задачу анализа, чтобы, с одной стороны, получить правильное решение, а с другой - не потерять много ресурсов и времени. Поэтому инже­нер может вначале попытаться создать крупную сетку, так как в этом случае преимущество заключается в том, что потребуется от­носительно меньше времени для решения задачи. Однако работа с крупной сеткой может привести к потере значимых физических явлений.

Для того чтобы повысить эффективность моделирования, мож­но воспользоваться методом подмоделей. Сущность этого метода сводится к следующему.

По опыту своей работы инженер знает, на каких участках гео­метрической модели могут возникнуть повышенные напряжения, изменения плотности потока, скачки температур и т.п. В сеточной модели можно выделить эти участки и для них построить сетку с параметрами, отличными от параметров сетки остальных участ­ков. Теперь методом подмоделей можно провести анализ как для всей сетки, так и получить более подробный анализ только для выделенной области.

Важной особенностью этого метода является возможность за­дания граничных условий для подмодели на основе отклика на­чальной сеточной модели. В программе ANSYS, например, исполь­зуя результаты решения для грубой модели, можно определить соответствующие ограничения степеней свободы на границах под­модели (перемещения, температуры, напряжения или потенциалы) и использовать их при проведении анализа подмодели. Повторять анализ всей модели нет необходимости.

Использование метода подмоделей дает следующие преимуще­ства [5]:

• исключается необходимость осуществления трудновыполни­мого перехода между областями модели с крупной и мелкой сет­кой;

• исследование влияния вносимых в проект локальных измене­ний геометрии проводится без повторного анализа целиком всей модели;

• уточнение подробностей в зонах особого внимания (напри­мер, в областях высоких напряжений) можно выполнить, не рас­полагая до начала анализа информацией о местоположении этих зон;

• исключается необходимость описывать мелкие подробности геометрии (отверстия, галтели и др.), которые можно рассмотреть с помощью подмоделей;

• пользователь может создавать твердотельные подмодели из оболочечных элементов грубой модели.

^ Контроль качества сеточной модели и ее модификация.

В универсальных программах анализа заложены широкие возмож­ности оценки качества сеточных моделей и широкий спектр мето­дов их модификаций. Качество сетки можно оценить как визуаль­но в интерактивном, так и в пакетном режиме. В процессе визуаль­ного контроля есть возможность отображать на экране монитора

• любой тип модели (геометрическую, расчетную или сеточную);

• нумерацию узлов и элементов;

• пограничные узлы или связи;

• ориентацию 2D-элементов или наружных ребер 3D-элементов;

• целиком сеточную модель, ее элементы, связи и узлы.

Графические элементы могут быть представлены в виде карка­са, однотонной заливки граней, путем отображения только границ участков.

Для управления работой программы в пакетном режиме необ­ходимо сформировать файл, содержащий критерии качества сетки и ограничения на ее геометрию. Совокупность критериев и огра­ничений позволяет контролировать размеры всей сеточной модели или ее отдельных элементов, их форму, границы и связность групп элементов, относительное удлинение 2D- или ЗВ-элементов, угол наклона, конусность, величину угла между геометрическими объек­тами, деформированность элемента, наличие одинаковых номеров узлов, смыкание группы узлов и ориентацию элементов.

Приведем несколько примеров вычисления критериев и огра­ничений.

Так, относительное удлинение 2D- и ЗВ-элементов находится путем деления длин наибольшей и наименьшей связей элемента. Элементы с меньшим значением этой величины предпочтитель­нее. Отношение, равное единице, описывает равносторонние эле­менты и является идеальным.

Угол наклона четырехугольных элементов проверяется следу­ющим образом. Середины противоположных сторон четырехуголь­ника соединяются отрезками и находится наименьший угол между этими отрезками. Идеальный угол наклона равен 90°, что характе­ризует прямоугольный четырехугольник.

Ориентация 20-элемента по умолчанию принимается такой же, что и у исходного геометрического элемента, если он имеет место и т.д.

Средства управления качеством сетки также позволяют контро­лировать такие параметры, как размер элемента, деление гранич­ной линии, размеры в окрестности заданных геометрических то­чек, коэффициенты растяжения или сжатия вдали от границ, ограничения на кривизну и возможность задания «жестких» точек (т.е. задание точного положения узла вместе с размерами сетки в такой точке).

Модификация конечно-элементной сетки может вестись как в интерактивном, так и в пакетном режиме. Широкие возможности визуализации различных графических примитивов и имеющиеся средства редактирования позволяют пользователю выполнять мо­дификацию, при необходимости, вручную, хотя эффективность этого режима низкая.

Основным режимом модификации сетки является пакетный ре­жим. В этом случае используются различные алгоритмы сглажива­ния сетки, изменения атрибутов узлов и элементов, измельчения и улучшения формы элементов и др. Например, процедура слияния узлов позволяет модифицировать сеточную модель путем объеди­нения в один узел тех из ее узлов, расстояние между которыми меньше заданного значения. Так формируется новая сеточная мо­дель с меньшим количеством неоднородностей и более согласо­ванной длиной связей (рис. 1.41).

Программы могут выполнять контроль соответствия элементов расчетной и сеточной моделей, вводить, удалять и изменять поло­жение конечных элементов, обеспечивая тем самым формирова­ние сетки высокого качества.



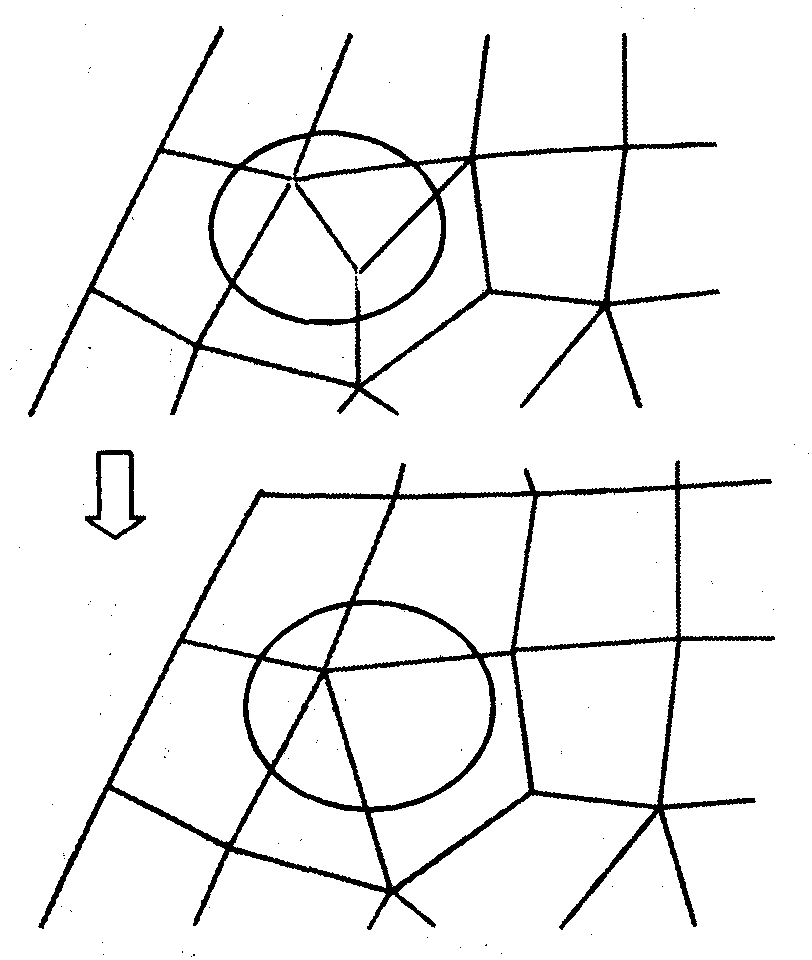
Рис. 1.41. Редактирование элементов сетки

^ Определение данных и ограничений. Исходные данные ана­лиза, введенные на этапе предварительной подготовки, становятся частью базы данных пакета. Содержанием базы данных являются множества типов элементов, свойств материала, параметров узлов, нагрузок и др., которые соответствующим образом группируются и этим группам присваиваются идентификаторы (число или имя). Выбор необходимых данных осуществляется либо путем указания графических примитивов расчетной модели на экране монитора, либо используя идентификаторы групп конечных элементов, видов материалов, узлов и элементов и др. Например, граничные ус­ловия можно вызвать из базы данных и отредактировать, исполь­зуя геометрию модели, а не номера отдельных узлов или элементов.

Для описания свойств материала изделия используются параметры, необходимые для выполнения требуемого вида анализа. Так, в прочностном анализе учитываются модуль упругости (модуль Юнга), коэффициент теплового расширения при заданной темперaтype, коэффициент Пуассона, плотность, коэффициент трения, модуль сдвига, коэффициент внутреннего трения. Для проведения теплового анализа следует задать удельную теплоемкость, энталь- пию, коэффициент теплопроводности, коэффициент конвективной теплоотдачи поверхности, степень черноты и т.д. Необходимые параметры материалов содержатся в соответствующих библиотеках. Свойства могут быть постоянными, нелинейными или зави­сеть от температуры. Списки существующих материалов в базе данных могут быть дополнены новыми материалами.

^ Управление работой решателя. Прежде чем конкретный ва­риант задачи будет передан на расчет, выполняются проверка и Подтверждение входных данных анализа на соответствие их выбранному методу решения задачи и настройкам опций решателя. Для этих целей используются, как правило, многочисленные контекст­но-зависимые меню. Например, меню среды анализа отражает об­щую информацию о решаемой задаче и содержит описание вида анализа, типа выбранного решателя, размерности модели, метода решения и др.

Группы назначаемых нагрузок формируются на этапе подготов­ки данных. Каждая группа имеет свое имя. В процессе проверки можно дополнить необходимые нагрузки в группу, используя со­ответствующее меню.

Затем можно перейти к следующим действиям:

• выбор рабочей директории, т.е. директории, в которой реша­тель будет формировать файл результатов и временные файлы;

• выбор имени задачи. Это имя будет использоваться как пре­фикс всех имен файлов, создаваемых в процессе решения;

• выбор шага анализа. Шаг всегда может быть модифицирован;

• выбор группы нагрузок.

В следующем окне диалога можно модифицировать значения переменных параметров, используемых при вычислениях:

• память - выделяемый для решателя объем памяти (Мб);

• удаленный узел - имя компьютера, используемого для вычис­лений. Если этот параметр не указан, то используется локальная вычислительная машина;

• удаленная память - место для запоминания файлов;

• исполняемая директория - путь к выбранному решателю. Можно изменить условия вычислений, если предположения не оправдываются. Эти опции включают:

• переназначение имени ведущего вычисления компьютера;

• назначение диска или директории, где решатель будет сохра­нять свои результаты, так как вычисления требуют значительного дискового пространства;

• назначение объема памяти на диске: минимальный объем па­мяти определяется размером сетки, большой объем памяти значи­тельно ускоряет вычисления.

После завершения проверки данных анализа запускается про­цесс вычисления, который требует больших затрат компьютерного времени. В значительной степени потери времени зависят от выб­ранного решателя. Многочисленные решатели разных фирм-раз­работчиков используют различные алгоритмы решения систем уравнений.

Решатели явного типа, к которым относится фронтальный ре­шатель, определяют точное решение для совместной системы ли­нейных уравнений. Например, фронтальный решатель программы ANSYS использует так называемый Rank-n алгоритм, обеспечива­ющий параллельную обработку системы уравнений. Решатель яв­ного типа ANSYS/LS-DYNA фирмы Livermore Software Technology (США) дает возможность эффективно проводить анализ динами­ческих процессов.

Кроме фронтальных решателей разработаны итеративные ре­шатели, которые сокращают время решения и ресурсы компьюте­ра при анализе больших моделей. При расчетах систем совмест­ных линейных уравнений итеративные решатели дают сходящее­ся, от итерации к итерации приближенное решение. Например, в программе ANSYS используются три итеративных алгоритма: ал­горитм PowerSolver на основе метода обусловленных сопряжен­ных градиентов (PCG), алгоритм на основе метода сопряженных градиентов Якоби и алгоритм метода частично сопряженных гра­диентов Чолески и др.

Протекание процесса в реальном режиме времени отражается в окне текущего контроля решателя. В этом окне указывается общее время, необходимое для решения задачи, а также некоторая допол­нительная информация: свободное пространство на диске, требуе­мое пространство на диске, площадь поверхности модели, ее объем, масса, предупреждающие сообщения или сообщения об ошибках и др.

Пользователь имеет возможность выполнить решение задачи в интерактивном или групповом режиме. Когда назначен интерак­тивный режим, обновление данных осуществляется решателем автоматически. В случае группового режима пользователь может произвольно запрашивать информацию о протекании процесса.

По завершении вычислений:

• полученные результаты будут визуализированы в окне дан­ных;

• предельные значения результата будут показаны в области выходных данных протокола анализа;

• решатель сформирует текстовый файл выходных данных, ко­торый может открываться любым текстовым редактором.

^ 4.4. Постпроцессорная обработка результатов

Результаты решателя в виде нескольких таблиц могут быть за­писаны в текстовый или бинарный файлы, не пригодные для чте­ния. Поэтому существуют следующие возможности представления результатов.

• Области напряжений, деформаций, температур и т.д. отобра­жаются функциями визуализации в виде геометрии или сетки (см. рис. 8 на вклейке).

• Функции выделения, рекомбинации и сортировки параметров позволяют найти предельные значения полей напряжений, дефор­маций или температур.

• Иногда инженера могут заинтересовать те значения, которые не вошли как результаты решателя в файл отчета и которые могут быть выведены из него в результате математических манипуляций. Им могут быть назначены дополнительные расчеты.

Приведем некоторые параметры настройки постпроцессора.

• Визуализация деформированного состояния на исходном объе­ме.

• Режим отображения результата (способ представления):

- градуированное цветоделение до 10 цветов;

- тонирование - спектр от синего до красного (см. рис. 9 (справа) на вклейке);

- символьный - стрелки вектора в узлах или многогранни­ки, размер и цвет которых отражают величину соответствующего значения (см. рис. 9 (слева) на вклейке);

- цифровой - значения параметра располагаются в центре элемента или в узле (см. рис. 10 на вклейке).

• Графическое представление значений результата в виде:

объемной оболочки - показывает значения на внешней оболочке объема, например, для визуализации деформаций пока­зывает изменение результата, уменьшая и увеличивая его значения от нулевого до максимального;

- плоского сечения - показывает значения внутри объема, разрезая геометрию плоскостью и двигая это сечение в любом на­правлении внутри объема от места максимального значения до места минимального значения;

- патча поверхности - показывает результаты внутри объе­ма в виде изоповерхности, она искажается, изображая значения от нижней границы до верхней границы результата.

• Анимация любого из графических режимов.

• Листинг результатов - интерактивное окно с числовыми ре­зультатами, в динамическом режиме позволяет вести обработку полученных значений, например, сортировать полученные значе­ния по порядковому номеру и величине или в каких-либо границах значений (ограниченном поле значений).

• Оценка погрешности результатов в линейном статическом ана­лизе для объемных элементов. Ошибки представляются в виде:

- абсолютной ошибки (в единицах параметра, например давления);

о относительной ошибки напряжения (в %);

- количества элементов, имеющих совокупную ошибку, бо­лее 10%.

Эти данные могут быть получены с помощью специальной на­стройки контроля решателя на этапе задания условий анализа.

^ 4.5. Анализ динамических процессов систем управления

В отдельную группу задач анализа можно выделить исследова­ния динамических процессов, протекающих в системах автомати­ческого регулирования и управления наукоемких машиностроительных изделий. К таким изделиям можно отнести тепловые энер­гетические установки, ядерные установки различного назначения, системы автоматического управления следящих приводов и робо­тов, двигателей, а также других технических систем, описание ди­намики которых может быть выполнено методами структурного моделирования. Для решения задач этого класса широкое приме­нение находят специальные программные комплексы MATRIX, Simulink, VisSim, МВТУи др.

Рассмотрим некоторые особенности работы с такими комплек­сами на примере программы МВТУ, разработанной в МГТУ им. Н. Э. Баумана.

Здесь возможно решение целого ряда задач:

- моделирование;

- оптимизация;

- анализ;

- контроль и управление (программа позволяет создавать вир­туальные аналоги измерительных приборов и управляющих уст­ройств контроля и управления переходными процессами).

^ Библиотеки типовых блоков. Вся совокупность типовых бло­ков программного комплекса условно может быть разделена на две группы: общетехническая библиотека и специализированные биб­лиотеки. Общетехническая библиотека типовых блоков содержит следующие каталоги (см. рис. 11 на вклейке):

- субструктуры;

- динамические звенья;

- нелинейные звенья;

-ключи;

- логические звенья;

- функции математические;

- дискретные звенья;

- источники входных воздействий;

- операции математические;

- векторные операции;

- данные и т.д.

В каждом из перечисленных каталогов содержатся типовые или специально разработанные модели элементов динамических сис­тем.

Например, из каталога «Динамические звенья» можно выбрать:

динамическое звено общего вида, идеальное интегрирующее звено, интегратор с насыщением, интегратор с изменяемыми начальны­ми условиями, апериодическое звено первого порядка, колеба­тельное звено, инерционно-интегрирующее звено, инерцион­но-дифференцирующее звено, инерционно-форсирующее звено, переменные состояния, идеальное запаздывающее звено.

­ В каталоге «Нелинейные звенья» хранятся следующие звенья:

квадратичный функционал качества, линейное с насыщением, ли­нейное с зоной нечувствительности, линейное с насыщением и зоной нечувствительности, релейное неоднозначное, релейное нео­днозначное с зоной нечувствительности, зазор, люфт, излом, произвольная однозначная нелинейность, запоминание минимума, за­поминание максимума, запоминание макс./мин. из двух скалярных сигналов, запоминание макс./мин. из п векторных сигналов, пере­менное транспортное запаздывание, дифференцирование, ограни­чение скорости изменения, дельта-функция и др.

Специализированные библиотеки содержат каталоги различных приложений: «Реакторные блоки», «Логика АСУТП ВВЭР», «Ро­боты», «Элементы подземных хранилищ газа». Ряд фрагментов структурных схем, сформированных в процессе выполнения при­кладных НИР и ОКР, хранится в виде субмоделей в отдельных ка­талогах. Фактически эти каталоги представляют собой дополни­тельные специализированные библиотеки, из элементов которых могут быть скомпонованы значительные фрагменты новых струк­турных схем.

^ Основные этапы работы с программой. Формирование и ре­дактирование структурной схемы проекта, ввод параметров звень­ев, начальных условий, выбор метода и параметров интегрирова­ния осуществляется как с помощью специальных графических процедур, так и посредством команд. Структурную схему исследу­емой задачи рекомендуется Предварительно выполнить на черно­вике примерно в том же виде, в каком она должна быть представ­лена на экране монитора.

Формирование структурной схемы и параметров ее элементов, выбор метода, параметров интегрирования и т.п. целесообразно проводить в следующей последовательности.

• В окне монитора, предназначенного для формирования схемы моделирования, необходимые элементы размещают примерно так, как они должны быть расположены в структурной схеме.

• Предварительно подобранные элементы схемы можно пере­компоновать, используя процедуры их перемещения, изменения ориентации элементов, изменения их размеров и др.

• Информационные связи между элементами указывают на эк­ране монитора, манипулируя «мышью».

• Параметры элементов (коэффициенты усиления, постоянные времени, начальные условия и т.д.) задают на структурной схеме.

• Для расчета процессов указывают конечное время интегриро­вания, метод интегрирования и другие параметры.

• Подготовленную схему (проект) необходимо сохранить, запу­стить задачу на расчет, наблюдая и анализируя результаты проте­кания процессов.

В качестве примера, демонстрирующего особенности исполь­зования программного комплекса, остановимся на задаче модели­рования динамики системы автоматического регулирования ядер­ной паропроизводящей установки (ЯППУ) малой мощности с реактором интегрального типа. В процессе проектирования систе­мы автоматического регулирования исследовались проблемы рас­четного обоснования ядерной безопасности ЯППУ в переходных режимах и в проектных аварийных ситуациях (обесточивание, «стоп-вода», «стоп-пар», отключение главного циркуляционного насоса и секций парогенератора и др.). Структурная схема моде­лируемой системы (см. рис. 11 на вклейке) скомпонована с помо­щью элементов каталога «Реакторные блоки», а субмодели «Кине­тика нейтронов», «Система управления», «Теплофизические параметры A3» и т.д., представляющие собой сложные многоуров­невые структуры, набраны из каталогов общетехнической библио­теки типовых блоков. Общее число элементов в схеме - более 370, функциональных переменных - около 3000. На этом же рисунке размещены окна визуализации поведения физических параметров системы автоматического регулирования в процессе моделирова­ния.

^ 5. АВТОМАТИЗАЦИЯ ТЕХНОЛОГИЧЕСКОЙ ПОДГОТОВКИ ПРОИЗВОДСТВА

5.1. Прототипирование

В процессе разработки технических изделий широкое приме­нение находят их физические прототипы. Быстрое прототипиро­вание является актуальным как на этапе конструирования, так и в производственном цикле. Наличие прототипа позволяет наглядно оценить результаты геометрического моделирования, проанализи­ровать параметры изделия, провести рекламную кампанию и ис­следовать рынок, использовать прототип на отдельных этапах из­готовления изделия, например при литье по выплавляемым моделям. Для реализации быстрого прототипирования в настоя­щее время созданы специальные установки с ЧПУ, разработано со­ответствующее программное обеспечение, подготовлены форма­ты обмена информацией с сопутствующими автоматизированными системами проектирования и производства.

Прототип можно изготавлятъ различными способами, например такими, как стереолитография, LOM-технология, с помощью тер­мопринтера, ускоренного фрезерования и др. Технологии всех ме­тодов прототипирования строятся на непосредственном использо­вании геометрической модели изделия. Так, для стереолитографии и LOM-технологии с помощью специального интерфейса, который полностью интегрирован с системами сквозного проектирования, предварительно создается промежуточный файл в формате STL, что позволяет получать доступ ко всем популярным платформам стереолитографических систем (например, фирм 3D Systems или Stratasys). При этом сохраняется полная целостность данных. Дан­ные STL-файла также могут быть использованы для механической обработки по LOM-технологии фирмы HELISYS.

При создании прототипов способом ускоренного фрезерования (гравирования) используется геометрическая модель изделия. Структурная схема процессов прототипирования приведена на рис. 1.42.



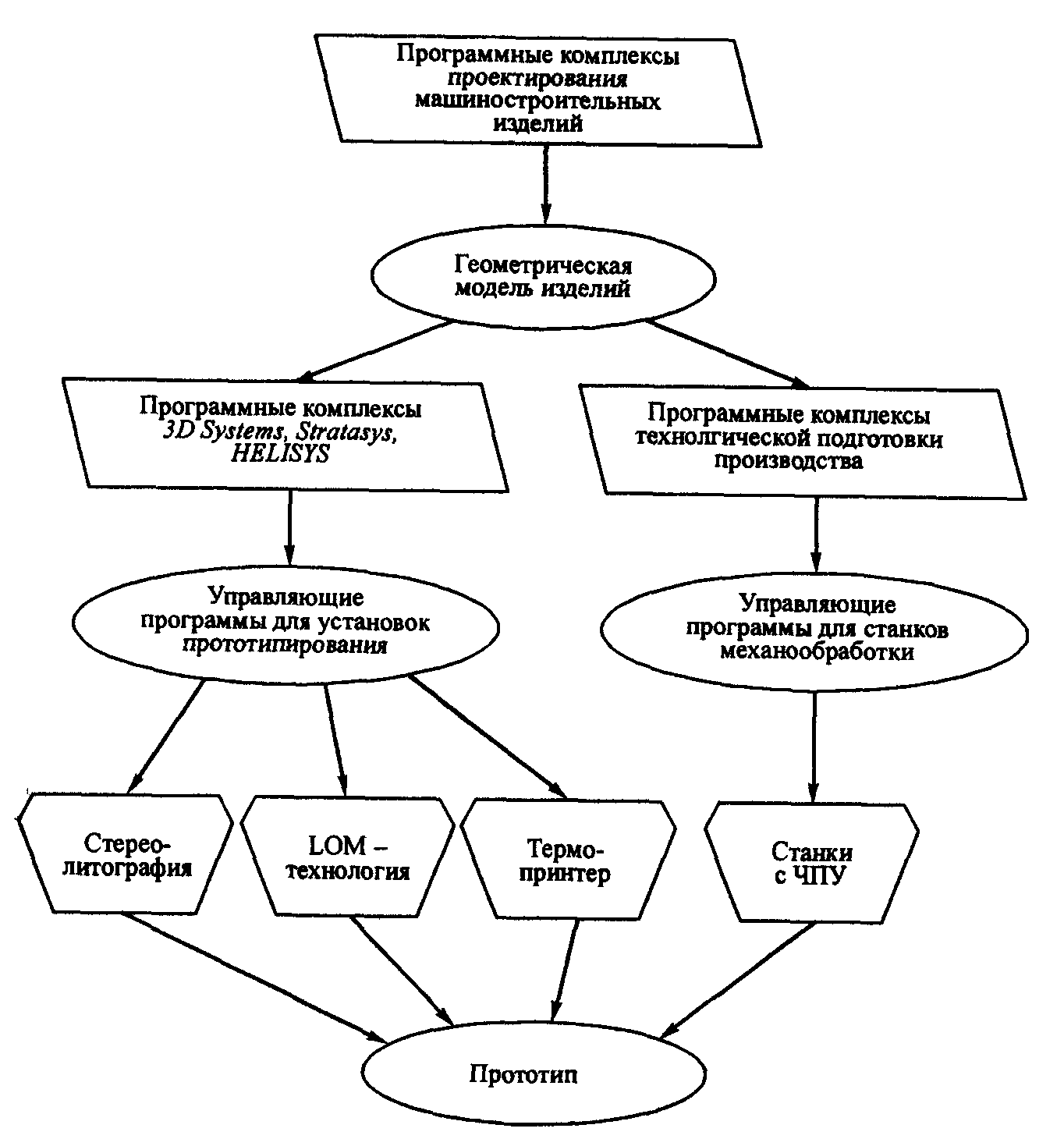
Рис. 1.42. Обобщенная структурная схема прототипирования