1. Предмет, метод, задачи курса

Вид материала

Закон

Содержание 2. Статистические показатели: сущность, значение, формы изложения. 3. Формы, виды, способы проведения статистических наблюдений. 4. Программно методологические и организационные вопросы проведения статистических наблюдений. Единица наблюдения и единица учета 5. Сводка и группировка статистических данных. Виды группировок 6. Контроль статистических данных. Логический контроль 7. Статистические таблицы. 8. Вариационные ряды и их графическое изображение. 9. Виды средних величин. 10. Средняя арифметическая: свойства, способы вычисления. 11. Мода и медиана. Мода — наиболее распространенное значение или признак статистической величины в совокупности, а медиана 12. Показатели вариации. Среднее линейное отклонение 13. Дисперсия и её свойства. 14. Абсолютные и относительные величины. Относительные величины 15. Виды динамических рядов. ... Полное содержание

Подобный материал:

• 1. Предмет, метод и задачи курса Предмет и метод науки организации производства. Организация, 852.65kb.
• 1. Культурология как наука и учебная дисциплина. Предмет, метод и задачи курса культурологии, 2457.22kb.
• Программа курса «уголовное право» общая часть тема Понятие, предмет, метод, задачи, 667.72kb.
• Тема: Введение. Предмет, цель, задачи курса "Общее языкознание", 74.47kb.
• В. П. Лега программа курса наука и религия (научная апологетика) Москва 2012 Тема Введение., 391.46kb.
• Тема определение недвижимости > Объект, предмет, задачи и логика курса, 1180.66kb.
• Задачи: Изучить предмет метод и структуру изучения курса Ознакомиться с состояние агропромышленного, 4441.19kb.
• Решение задачи одним из математических методов, 440.71kb.
• Предмет и метод курса ипиПУ, 3008.42kb.
• Тематико-календарный план лекций по эпидемиологии для студентов 5 курса «Общественное, 400.05kb.

1. Предмет, метод, задачи курса.

Предметом изучение является изучение количественных параметров массовых общественных явлений и процессов, взаимосвязей, взаимозависимостей, закономерностей функционирования и развития.

Метод статистики базируется на законах, согласно которым общественные явления и процессы рассматриваются в развитии, взаимной связи и причинной обусловленности. Специфика статистических методов заключается в комплексности, соответствии принципу системного научного исследования, имеющего 3 стадии: 1) статистическое наблюдение, включающее сбор и оценку качества первичных статистических данных; 2) сводку первичного статистического материала; 3) обобщение и анализ сведенного материала.

Статистические показатели (фигурируют в виде абсолютных, относительных и средних величин) – это количественные параметры массовых общественных явлений и процессов места и времени. Статистические совокупности имеют 2 признака: 1) однородны по какому-либо свойству; 2) изучаемый статистический признак варьируется при переходе от одной единицы совокупности к другой. Цель исследования – выявление статистических закономерностей. Закон больших чисел – чем больше единиц совокупности, тем в большей степени отклонение от истинной меры процесса взаимноисключаются.

Задачи определяются через функции статистических показателей: 1) познавательная, 2) управленческая (чем выше уровень управления, тем выше значение статистических показателей), 3) идеологическая. Виды учета (регистрация количественных фактов): 1) первичный учет, 2) бухгалтерский учет (на основе данных кругооборота материальных ресурсов и денежных средств), 3) статистический учет (на основе 2-х первых).

Структура статистики: 1) общая теория статистики (методы работы с большими совокупностями), 2) социально-экономическая статистика, 3) отраслевая статистика, 4) подотраслевая статистика.

^ 2. Статистические показатели: сущность, значение, формы изложения.

Статистические показатели (фигурируют в виде абсолютных, относительных и средних величин) – это количественные параметры массовых общественных явлений и процессов места и времени. Статистические совокупности имеют 2 признака: 1) однородны по какому-либо свойству; 2) изучаемый статистический признак варьируется при переходе от одной единицы совокупности к другой.

Каждый показатель имеет 2 стороны: количественную и качественную. Качественная сторона показывает модель расчета показателя, его общее содержание безотносительно к конкретному размеру, а количественная характеризует конкретный размер показателя, его величину. Статистические показатели строятся как обобщение значений признака. Он может определяться путем вычисления средних значений признака, суммированием абсолютных значений признака и относительных величин. Статистический показатель указывает на территориальные границы объекта и границы времени. Он является инструментом познания, изучаемых явлений и процессов, но не отражает с абсолютной точностью все свойства и особенности изучаемого объекта.

^ 3. Формы, виды, способы проведения статистических наблюдений.

Статистическое наблюдение – это массовое планомерное, научно организованное наблюдение за явлениями социальной и экономической жизни, к-рое заключается в регистрации отображенных признаков у каждой единицы совокупности.

Статистическое наблюдение может проводиться органами го­сударственной статистики, научно-исследовательскими институ­тами, экономическими службами банков, бирж, фирм. Оно обя­зательно должно быть массовым, систематическим, проводиться на научной основе по заранее разработанным плану и программе.

Формами статистического наблюдения являются отчет­ность и специально организованные наблюдения.

Статистическая отчетность – это основная форма статис. наблюдения, с помощью которой статис. органы в определенные сроки получают от предприятий, учреждений, организаций необходимые данные в виде установленных в законном порядке отчетных документов, скрепленных подписями лиц, ответственных за их предоставление и достоверность собираемых сведений.

Специально организованное статистическое наблюдение пред­ставляет собой сбор сведений посредством переписей, едино­временных учетов и обследований. С целью получе­ния сведений об уровне потребительских расходов и доходов населения организована отчетная сеть статистики семейных бюджетов рабочих, служащих и крестьян.

Регистрационная форма наблюдения. Регистровое наблюдения – это форма непрерывного статист. наблюдения за долговременными процессами, имеющими фиксированное начало, стадию развития и фиксированный конец. Оно основано на введении статис-ого регистра. Регистр представляет собой систему, постоянно следящую за состояние единицы наблюдения и оценивавшую силу воздействия различных факторов на изучаемые показатели.

Виды статистического наблюдения. Статистические наблюдении можно разбить на группы: 1) по охвату единиц совокупности; 2) по времени регистрации фатов. По степени охвата исследуемой совокупности статис­тическое наблюдение подразделяется на два вида: сплошное и несплошное. При сплошном (полном) наблюдении ох­ватываются все единицы изучаемой совокупности. Сплош­ное наблюдение обеспечивает полноту информации об изучаемых явлениях и процессах. При несплошном наблюдении охватывается только опре­деленная часть изучаемой совокупности, при этом важно заранее определить, какая именно часть изучаемой сово­купности будет подвергнута наблюдению, и какой критерий будет положен в основу выборки. Существует несколько видов несплошного наблюдения: выборочное, наблюдение основ­ного массива, монографическое.

Выборочным называют наблюдение части единиц иссле­дуемой совокупности, выделенной методом случайного от­бора. При правильной организации выборочное наблюде­ние дает достаточно точные результаты, которые можно применить с определенной вероятностью на всю совокуп­ность. Наблюдение основного массива охватывает собой обсле­дование определенных, наиболее существенных по значи­мости изучаемых признаков единиц совокупности. Для монографического наблюдения характерно всесто­роннее и глубокое изучение лишь отдельных единиц со­вокупности, обладающих какими-либо особенными ха­рактеристиками или представляющими какое-либо новое явление. Цель такого наблюдения — выявление имеющих­ся или только зарождающихся тенденций в развитии дан­ного процесса или явления.

По времени регистрации фактов наблюдение может быть непрерывным и прерывным. Прерывное в свою оче­редь включает периодическое и единовременное. Непре­рывное (текущее) наблюдение осуществляется путем не­прерывной регистрации фактов по мере их возникновения. Непрерывно ведется, например, регистра­ция органами записи актов гражданского состояния (ЗАГСа) смертей, рождений, браков.

Прерывное наблюдение проводится либо регулярно, че­рез определенные промежутки времени (периодическое наблюдение), либо нерегулярно, однократно, по мере необ­ходимости (единовременное наблюдение). Примером периодического наблюдения может являться перепись насе­ления, которая проводится через достаточно длительные промежутки времени, и все формы статистических наблю­дений, которые носят ежемесячный, квартальный, полуго­довой, годовой и т.д. характер. Единовременное наблюдение характерно тем, что факты регистрируются не в связи с их возникновением, а по состоянию или наличию их на опре­деленный момент или за период времени.

Наряду с видами статистического наблюдения в общей теории статистики рассматриваются способы получения статистической информации, важнейшими из которых яв­ляются документальный способ наблюдения, способ не­посредственного наблюдения, опрос.

Документальное наблюдение основано на использовании в качестве источника информации данных различных докумен­тов, например регистров бухгалтерского учета.

Непосредственное наблюдение осуществляется путем регистрации фактов, лично установленных регистраторами в результате осмотра, измерения, подсчета признаков изу­чаемого явления. Таким способом регистрируются цены на товары и услуги, производятся замеры рабочего времени, инвентаризация остатков на складе и т.д.

Опрос базируется на получении данных от респонден­тов (участников опроса). Опрос применяют в тех случаях, когда наблюдение другими способами не может быть осу­ществлено. Статистическая информация может быть получена разными видами опросов: экспедиционным, корреспондентским, анкетным, явочным.

^ 4. Программно методологические и организационные вопросы проведения статистических наблюдений.

Программно методологические вопросы: 1) Постановка задач, цели 2) Выбор объекта наблюдения 3) Составление программы наблюдения (содержит перечень признаков подлежащих регистрации) 4) Разработка методики наблюдения.

Организационные вопросы: 1) Определение места наблюдения 2) времени (объективное – тот период за который собрали данные, субъективное – в течение которого вы провели работу) 3) круг лиц занимающихся этой работой.

^ Единица наблюдения и единица учета. Перепись скота: Единица наблюдения – скот единица учета – ферма. Статистические показатели могут быть интервальными (подлежат суммированию) и моментными (не подлежат)

^ 5. Сводка и группировка статистических данных.

Сводка - это вторая стадия С исслед-я, научно обработаный материал СН в целях получения обобщенной хар-ки изуч-го явл-я. В широком смысле это научная обработка первичных С сведений, которые включают: груп-ку исследуемых явл-й; подсчет групповых и общих итогов; составление таблиц и графи­ков. В узком смысле это комплекс опред-х операций по подсчету итоговых данных. Организ-я работа, связ-я с проведением С сводки включает этапы: опред-е задач сводки на основе целей С иссле­д-я; формир-е групп и подгрупп, опред-е группировочных при­знаков, числа групп и величины интервала; выбор груп-ки и ее постр-е; проверка полноты и кач-ва собранного материала и исчисление С показателей. Сводка – перечень значений, статистических материалов.

Группировка – распределение единиц совокупности в однородные группы на основании одного или нескольких взятых в комбинацию друг с другом признаков. Классификация – группировка устойчивая во времени и пространстве. Группировки различ. в зависимости от вида решаемых с их помощью задач: 1) типологическая – выделение типов социально-экономических процессов и явлений 2) структурная – изучение структуры, явлений и процессов 3) аналитическая – анализ взаимосвязей изучаемых процессов и явлений.

^ Виды группировок: аналитические (исследует взаимосвязи варьирующих признаков в пределах одно­р-й совок-ти, с измен-м значения факторного признака системат-ки возраст-т или убы­вает знач-е признака результат-го); типологические (Г, кот-е выясняют соц-экон типы явл-й); структурные (Г, кот-е исп-т для исслед-я однор-й совокупности). Определение группировочного признака. Признаки бывают количественные и качественные. Определение количества групп. Определение ширины интервалов. i=(X_max-X_min)/n. Интервалы бывают открытые и закрытые. Интервалом наз-ся разница между макс и мин значением признака в каждой группе.

^ 6. Контроль статистических данных.

На качество материалов статистического наблюдения влияет характер контроля формуляров и другой учетной документации, осуществляемого в процессе их приемки. Контроль осуществляет­ся в двух формах: счетный и логический. Счетный контроль за­ключается в проверке итогов подсчета данных формуляров. Там, где имеет место расчет взаимосвязанных показателей, контроль возможен в результате установления некоторой их количествен­ной связи, а также балансовым методом.

^ Логический контроль осуществляют путем проверки содержа­тельной связи между значениями признаков по каждой единице наблюдения. В тех случаях, когда нарушается логическая связь признаков, необходимо установить, содержит ли формуляр действительно допущенную ошибку регистрации либо данное со­четание признаков предопределено неординарностью ситуации. Следовательно, логический контроль, в отличие от счетного, не­посредственно не устанавливает ошибку наблюдения, а лишь сигнализирует о ее возможности и требует дополнительной связи с единицей наблюдения.

^ 7. Статистические таблицы.

Статистические таблицы служат средством отображения результатов исследования, позволяют отдельные статистические данные рассматривать совместно, охватывая достаточно полно и точно сложную природу изучаемых явлений и процессов. Любая статистическая таблица представляет собой форму наглядного и компактного изложения статистических данных.

Статистическая таблица имеет объект наблюде­ния, характеризующийся перечнем единиц или групп совокупности и числовые данные по каждой единице или группе. Сущность объект наблюде­ния раскрывается в заголовках строк, а числовых данных — в заголовках граф (колонок, столбцов).

По построению объекта наблюдения таблицы могут быть простыми, груп­повыми и комбинированными. В простых таблицах нет групп, поэтому они бывают перечневыми (просто перечень единиц совокупности), территориальными (дается наименование стран, регионов, городов и т.д.) и хронологическими, где системно приводятся даты или периоды времени.

Групповыми называются таблицы, в объекте исследования которых изучае­мая статистическая совокупность разделена на группы по какому-либо одному признаку.

Комбинированными называются таблицы, в объекте исследования которых произведена группировка единиц совокупности по двум и более при­знакам.

По разработке числовых данных таблица может простой и сложной. Про­стая таблица содержит набор самостоятельных граф (колонок, столб­цов), а в сложной - некоторые из них могут содержать зависимые под­графы, обозначаемые «в т.ч.», «из них» и т.п.

Статистическая таблица должна быть по возможности краткой, без излишних подробностей. Если в ней приведены величины одной раз­мерности, то она указывается в заголовке таблицы, если разной — то в заголовках строк или граф (колонок, столбцов).

Обычный принцип размещения данных в таблице — от частного к общему, т.е. сначала показывают слагаемые, а в конце подводят итоги. Когда приводятся не все, а лишь наиболее важные слагаемые, применя­ется противоположный принцип — от общего к частному. В строке «Ито­го» суммируется часть совокупности, а в строке «Всего» — она полностью. Округление чисел ведется с одинаковой степенью точности по всей таблице.

^ 8. Вариационные ряды и их графическое изображение.

Вариационным рядом распределения называется упорядоченная статистическая совокупность, где значения вариант (отдельные значения группировочного признака упорядоченной совокупности) расположены в порядке возрастания или убывания и указаны их частоты. Иногда в виде вариационного ряда распределения может быть представлена совокупность, сгруппированная по качественному признаку. Вариационный ряд распределения состоит из 2-х элементов: вариант и частот.

Анализ рядов распределения сопровождается их графическим изображением. Именно с помощью графиков можно судить о форме распределения. Для отображения вариационных рядов распределения используют следующие графики: полигон, гистограмма, кумулята, огива.

В виде полигона распределения обычно изображаются дискретные вариационные ряды распределения, и этот график является разновидностью статистических лома­ных. В прямоугольной системе координат по оси абсцисс откладываются отдельные значения вариант, а по оси ор­динат — частости каждого варианта. На пересечении абс­циссы и ординаты фиксируются точки, которые соответст­вуют данному ряду распределения. Соединив эти точки прямыми, получаем ломаную, которая и является полиго­ном. У полигона площадь над каждым интервалом значений признака не всегда точно соответствует численности наблюдений в этом интервале.

Гистограмма. При графическом изображении интер­вальных вариационных рядов распределения частоты выражают в виде прямоугольников соответствующей дли­ны. При этом на оси абсцисс откладывают интервалы зна­чения признака. На этих отрезках строят прямоугольники, которые сомкнуты друг с другом, с равными основаниями и ординатами. Полученный ступенчатый многоугольник, состоящий из определенного числа следующих друг за другом прямоугольников различной высоты, и называется гистограммой. Следует также отметить, что гистограмма строится исходя из предположения, что внутри интервала плотность распределения остается постоянной независи­мо от изменения признака. Высота отдельного прямо­угольника гистограммы соответствует средней плотности распределения в данном интервале. В случае неравенст­ва интервалов график строится не по частотам, а по плот­ности распределения, и тогда высоты прямоугольников будут соответствовать величинам этой плотности.

Кумулята представляет собой ряды распределения, где по оси абсцисс откладываются варианты признака, а по оси ординат — накопленные частоты. Полученные точки соединяют прямыми, которые образуют кумуляту. При ее построении на оси абсцисс откладываются значе­ния признака, а на оси ординат — накопленные частоты, при этом нижней границе первого интервала соответству­ет частота, равная нулю, а верхней границе — вся частота данного интервала. Вариационный ряд с накопленными частотами на графике изображается в виде кривой, получившей название кумуляты распределения.

Огива является статистической совокупностью, изобра­женной графически и представленной в виде ранжирован­ного ряда распределения. Она наглядно показывает ин­тенсивность изменения изучаемого признака. Огива стро­ится следующим образом: на ось абсцисс наносятся но­мера элементов совокупности по ранжиру, а на ось ординат откладывают значения признака.

^ 9. Виды средних величин.

Общественные явления в статистике изучаются с помощью обобщающих показателей, таких, как средние величины. Под средней величиной понимается обобщенная количественная харак­теристика признака в статистической совокупности.

Средняя выражает величину признака, отнесенную к единице совокупности и абстрагированную от индивидуальных особеннос­тей отдельных единиц.

Существуют различные виды средних величин, но наи­более часто применяются четыре: средняя арифметиче­ская, средняя гармоническая, средняя квадратическая и средняя геометрическая. Выбор вида средней опреде­ляется экономическим содержанием определенного пока­зателя и исходных данных, а также путем конкретного анализа изучаемой совокупности, материальным содер­жанием изучаемого явления и принципами суммирования и взвешивания.

Перечисленные виды средних величин можно объеди­нить общей формулой:

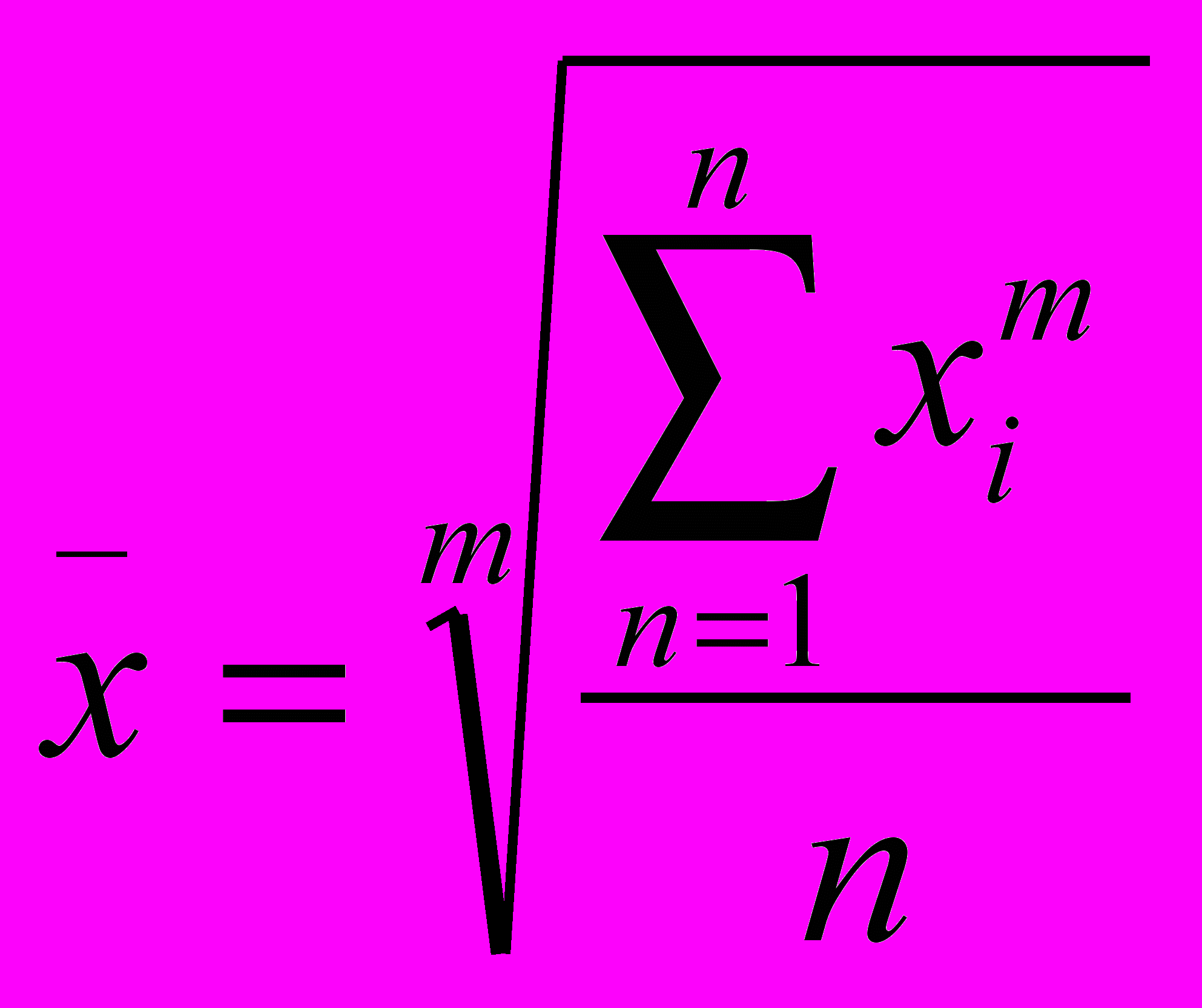где х — среднее значение исследуемого явления; m — показатель степени средней; х — текущее значение усредняемого признака; n — число признаков.

В зависимости от значения показателя степени m разли­чают следующие виды степенных средних, если: m = -1 — средняя гармоническая; m=0 — средняя геометрическая; m = 1 — средняя арифметическая; m = 2 — средняя квадратическая.

^ 10. Средняя арифметическая: свойства, способы вычисления.

Средняя арифметическая величина представляет со­бой такое среднее значение признака, при вычислении ко­торого общий объем признака в совокупности сохраняет­ся неизменным. Для того чтобы исчислить среднюю ариф­метическую, необходимо сумму всех значений признаков разделить на их число.

Она применяется в тех случаях, когда объем варьирую­щего признака для всей совокупности является суммой значений признаков отдельных ее единиц. Примеров средней арифметической может служить общий фонд за­работной платы — это сумма заработных плат всех работников.

Используются следующие свойства средней арифметической:

1. Ā=А

2.

3.

4.

5. Если каждую статистическую величину изменить на одно число (прибавить или отнять), то средняя арифметическая изменится на это число.

6. Если каждую статистическую величину изменить в одинаковое число раз (умножить или разделить), то средняя арифметическая изме­нится во столько же раз.

Расчет средней арифметической простой:

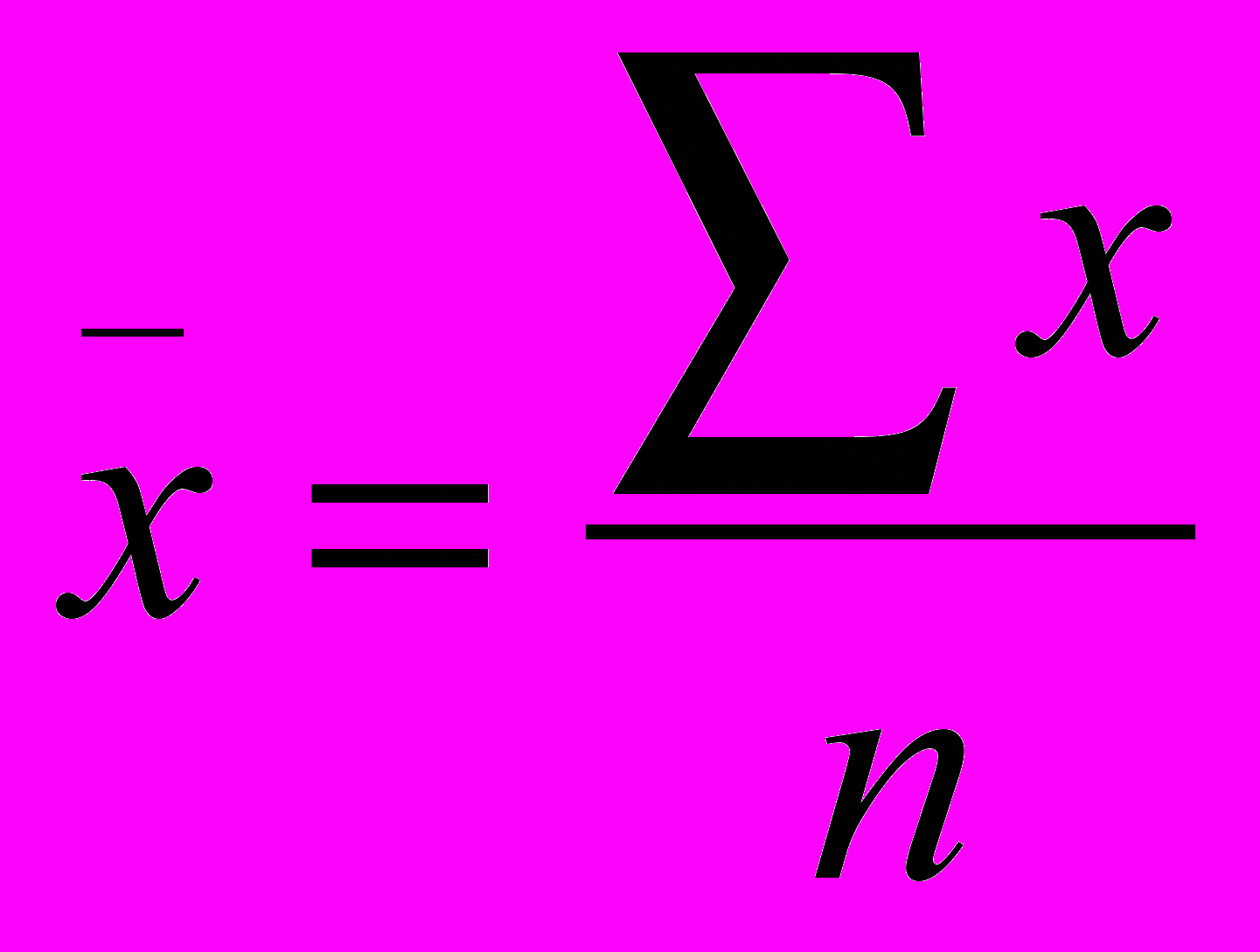
Расчет средней арифметической взвешенной:

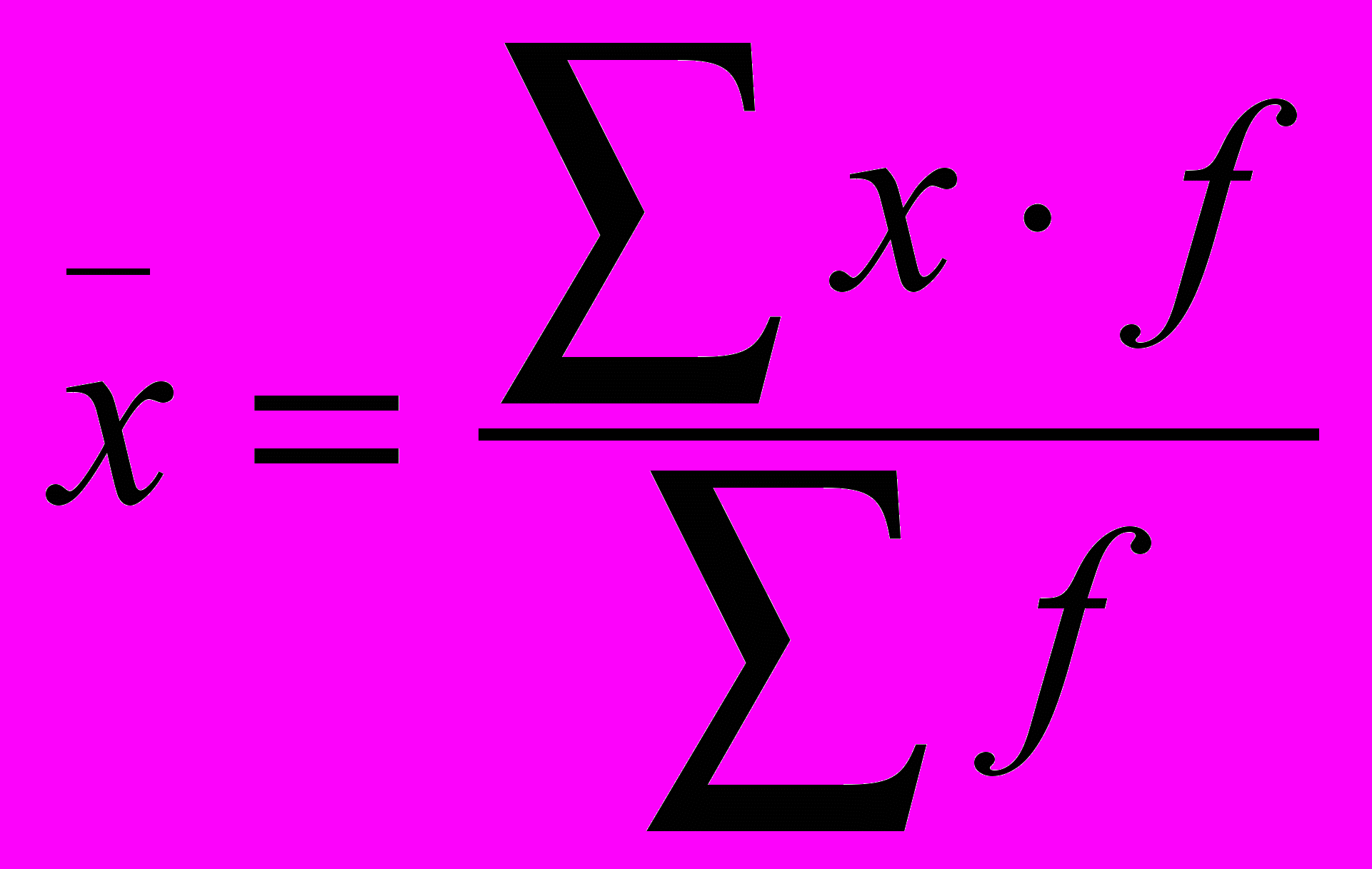, f – частота или вес варианта.

Расчет средней арифметической взвешенной по способу момента:

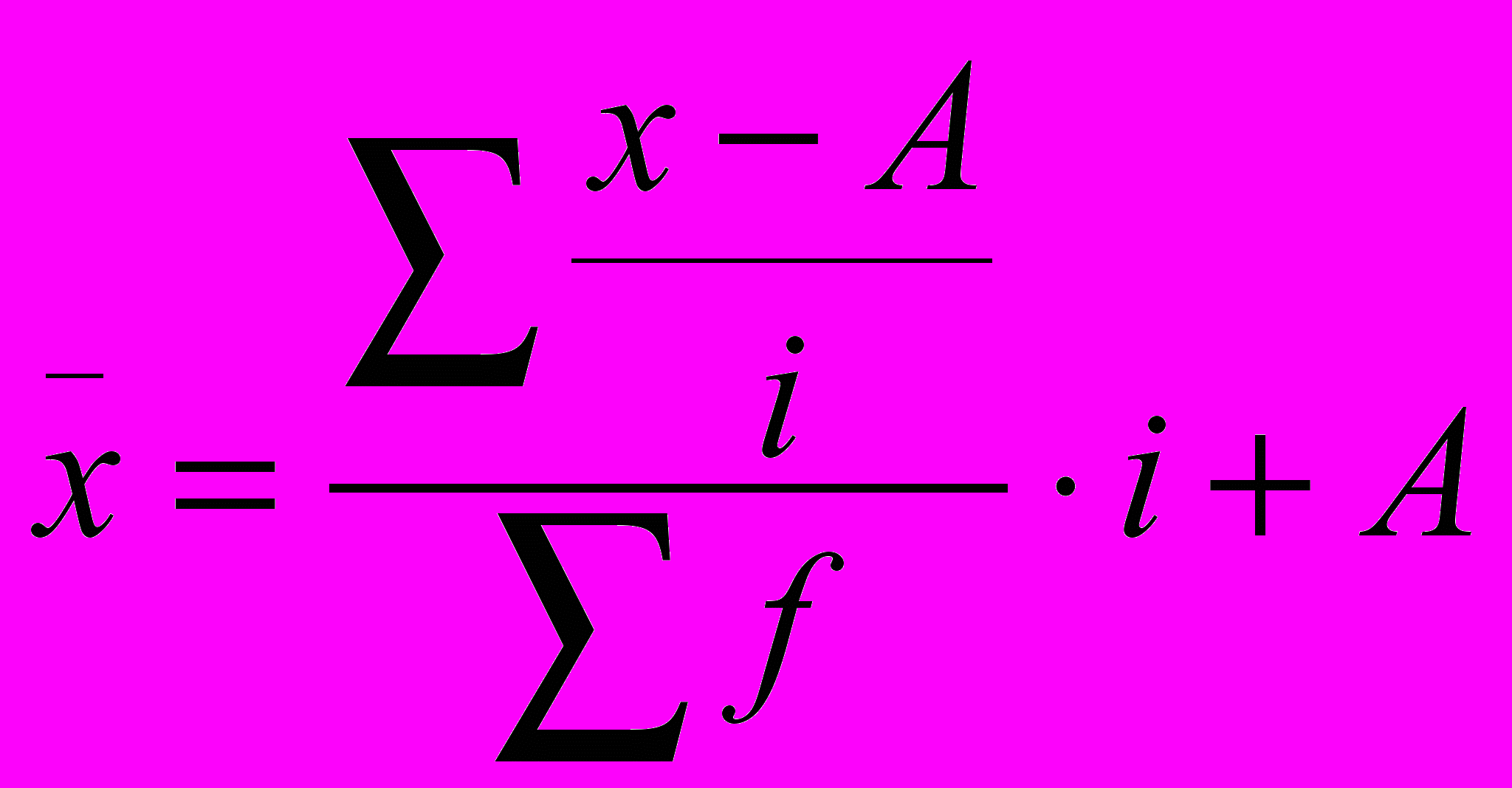, где А – значение варианта обладающего наибольшей частотой (тот x, у которого самое большое f), i – величина интервала.

^ 11. Мода и медиана.

Очень часто статистические величины бывают представлены в сгруппированном виде, когда для каждой группы приводится частота ее повторения.

В такой ситуации применяются структурные средние величины, из которых чаще всего используются мода и медиана. ^ Мода — наиболее распространенное значение или признак статистической величины в совокупности, а медиана — такое значение, которое делит совокуп­ность на две половины, в одной из которых значения меньше медиан­ного, а в другой больше.

Мода: M₀=x_m0+i_m0*f_m0-f_m0-1/(f_m0-f_m0-1)+(f_m0-f_m0+1), где Х_М0 – начальное значение интервала, f_M0 – частота модального интервала, i_M0 – величина модального интервала, f_M0-1 – частота предыдущего интервала, f_M0+1 – частота интервала следующего за модальным.

Медиана: M_e=x_Me+i_Me*(1/2∑f-S_Me-1)/f_Me, где Х_Ме – начальное значение медианного интервала, i_Mе - величина медианного интервала, f_Mе – частота медианного интервала, S_Mе-1 – частота, накопленная до медианного интервала.

^ 12. Показатели вариации.

1) Размах вариации – между max и min значением признака. R=X_max - X_min. Размах вариации показывает лишь крайнее отклонение от признака и не отражает отдельных отклонений всех вариантов в ряду. Он характеризует пределы изменения варьирующего признака и зависит от колебаний 2-х крайних вариантов. Он совершенно не связан с частотами в вариационном ряду, т.е. с характером распределения, что придает ему неустойчивость, случайный характер.

2) . ^ Среднее линейное отклонение (d_cp) представляет собой среднюю величину отклонений значений признака от их средней величины. При его расче­те все отклонения берутся со знаком плюс. Бывает простое: d_cp =  (x – x_cp) / n и взвешенное: d_cp =  (x – x_cp)f / f. В отличие от размаха вариации среднее линейное отклонение учитывает все возможные отклонения.

Дисперсия, или средний квадрат отклонений вариантов признака от их средней величины (G²), вычисляется по формулам: простая G² =  (x – x_cp)² / n; взвешенная G² = ( (x – x_cp)² * f ) / f. Затем возвращаясь к линейному измерению, надо из величины дис­персии извлечь квадратный корень и мы получим наиболее точный пока­затель - среднее квадратическое отклонение: простое G² =  (x – x_cp)² / n и взвешенное G² = ( (x – x_cp)² * f ) / f.

^ 13. Дисперсия и её свойства.

Дисперсия – это средняя арифметическая квадратов отклонений каждого значения признака от его средней. Cвойства дис­персии: 1)если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А, то дисперсия от этого не изменится; 2)если все значения признака уменьшить или увеличить в одно и то же число раз (i раз), то дисперсия соответст­венно уменьшится или увеличится в i² раз. 3) Дисперсия признака относительно произвольной величины всегда больше дисперсии относительно средней арифметической на квадрат разности между средней и и произвольной величины 4) увеличение или уменьшение весов варьирующегося признака в определённое число раз дисперсии не изменит.



1. δ²(А)=0.

2. δ²(Ах)=А²δ²(х)

3. Min дисперсии ( (x – A)² * f ) / f.=δ²(x)+(x_ср-A)²

1.

2.

3.

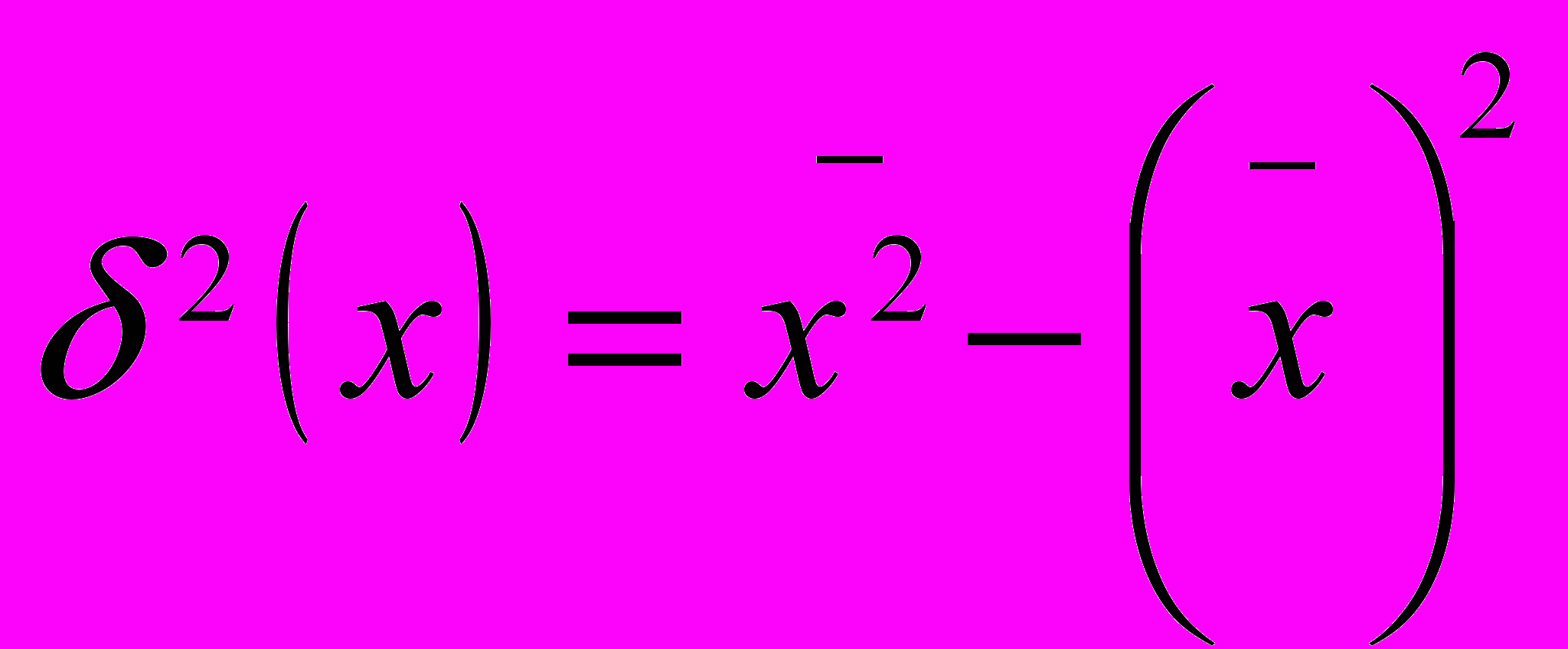
Правила сложения дисперсий

- общая дисперсия (колеблимость всех вариантов относительно их общей средних)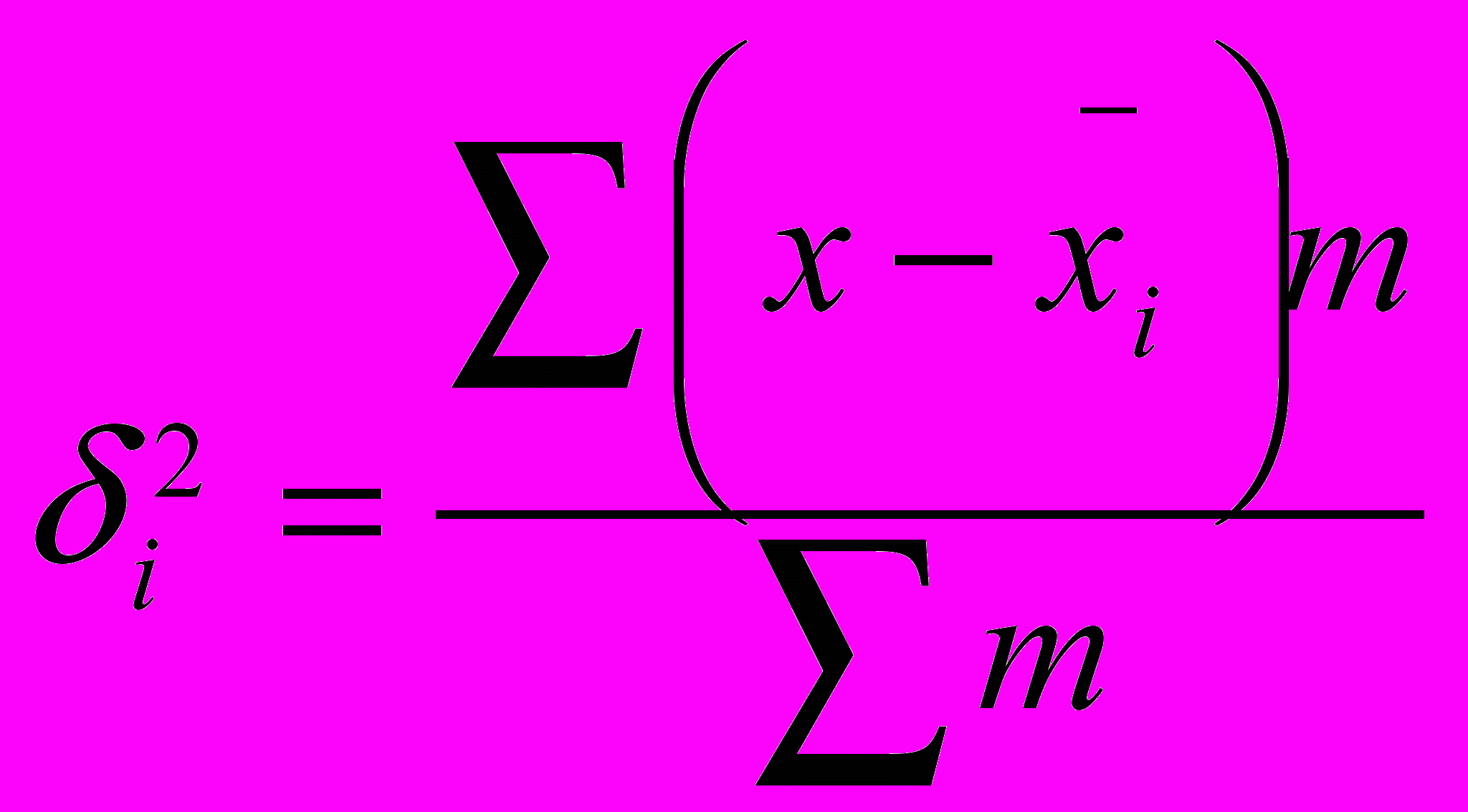

i=1, 2, …, - внутригрупповая (колеблимость вариантов в группе)

- межгрупповая (групповые средние относительно общей средней)

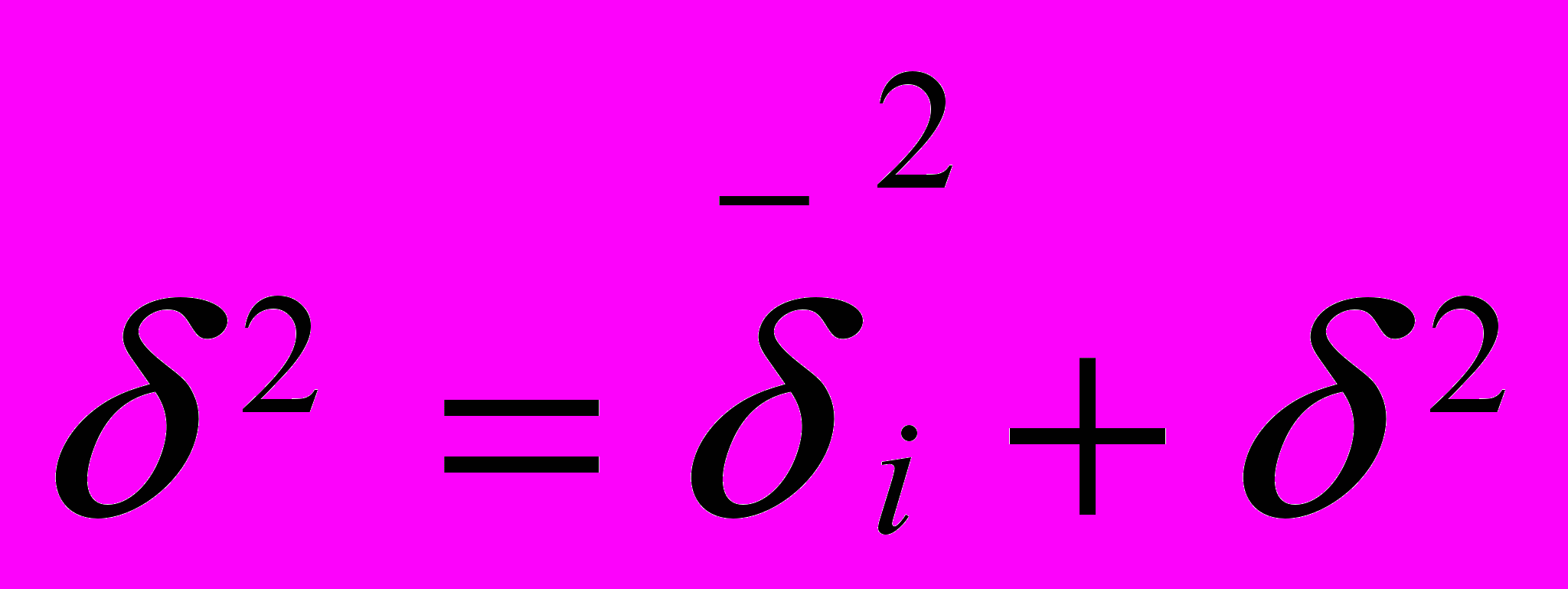, где 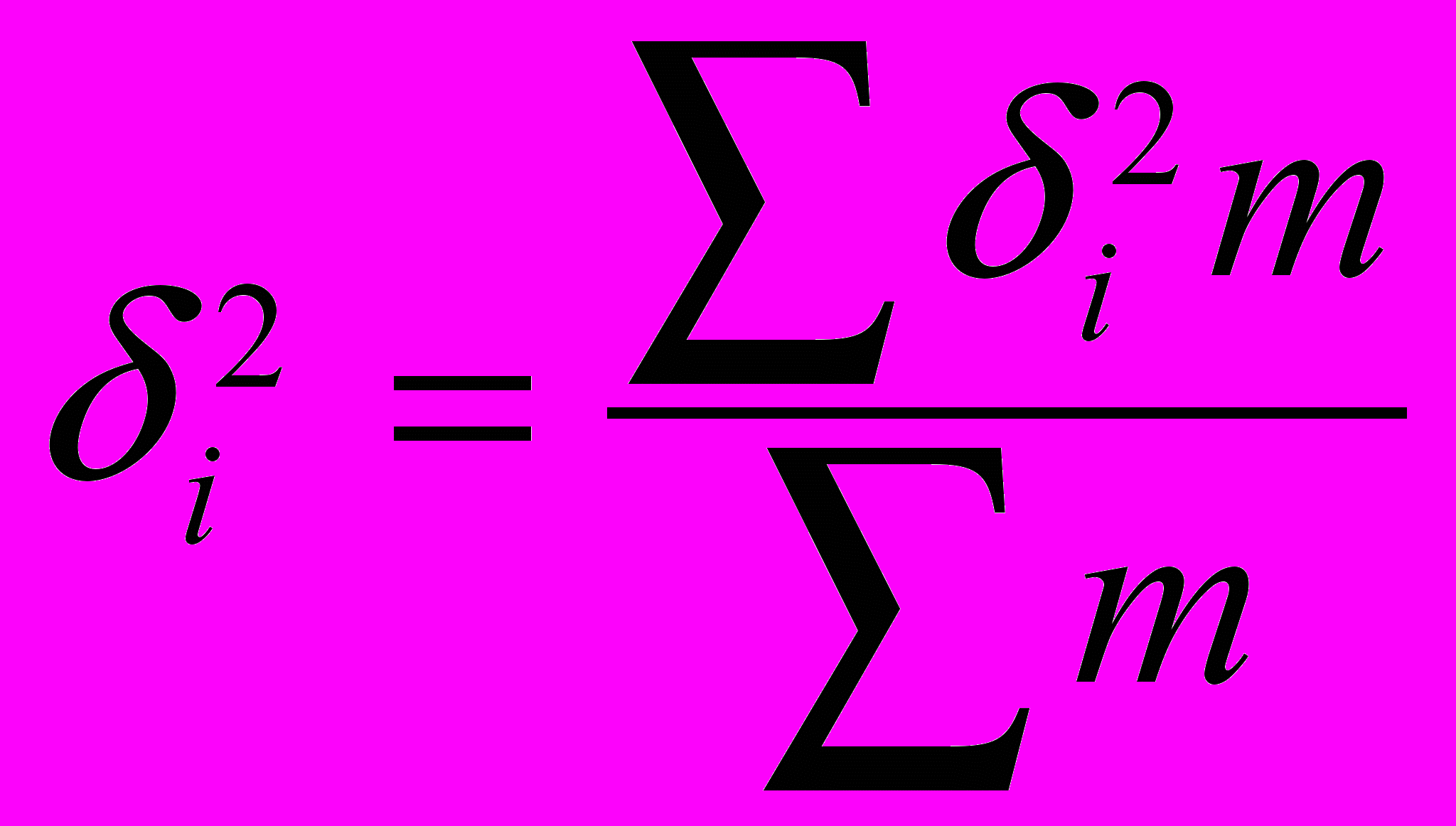- правило сложения дисперсий

^ 14. Абсолютные и относительные величины.

Под абсолютными статистическими величинами в статистике подразумеваются суммарные обобщающие показатели, характеризующие размеры общественных явлений в конкретных условиях места и времени. Они вы­ражают социальную, экономическую и естественную основу явления, его свойство, а также характеризуют эко­номическую мощь страны и социальную жизнь населения (ВВП, реальные располагаемые денежные до­ходы населения, объемы промышленного производства и т.д.). Это всегда именованное число с опре­деленной размерностью и единицей измерения. Они могут быть как положительными, например доход, так и отрицательными, например потери либо убытки.

^ Относительные величины - показатели, выр-е кол-е соотн-я числен-й или величин признаков изучаемых явлений. ОВ получают в рез-те сравнения двух по­казателей. Тот показатель, который сравнивается, называют отчетной ве­личиной (числитель дроби). Знаменатель отношения, т. е. та величина с которой сравнивают, называют основанием или базой ср-я. Если основание принять за единицу, то ОВ выра­зится в форме коэф-та и покажет, во сколько раз сравнимая величи­на больше или меньше отчетной. ОВ может быть выражена в процентах, в промилле, в продецимилле и т. д.Относительные величины – отношение абсолютных величин (сравнимая величина на базу сравнения). Могут быть представлены в форме: 1) коэффициент (база сравнения 1), 2) процентов (100%), 3) промилле (1000).

Виды относительных величин: 1) относительная величина планового задания характеризует уровень планового задания по сравнению с базисным годом (У_{плановое}/У_{базисное}) – коэффициент планового роста, 2) относительная величина степени выполнения плана характеризуют, дают количественную оценку выполнения планового задания (У1/У плановое), 3)относительная величина структуры (удельный вес) деление размера показателя на общий итог, 4) относительная величина динамики характеризует изменение какого-либо показателя во времени (текущий год на базисный), 5) относительная величина координации характеризует отношение отдельных частей совокупности друг с другом.

^ 15. Виды динамических рядов.

Различные явления, изучаемые С, претерпевают непрерывные изменения во времени - изменяется их объем, состав, структура. Исходной базой для выявл-я и изменения этих процессов служат ряды динамики (ряд С чисел, которые хар-т изменения величины общественного явления во времени. В каждом ряду динамики имеются два основных элемента: показатель времени «t»; уровни развития изучаемого явления «у». В кач-ве показ-й времени в РД выступают либо определенные даты (моменты) времени, либо отдельные периоды (сутки, месяцы, кварталы и т. д.). Уровни РД отобр-т количественную оценку развития во времени изуч-го явления. Они могут выражаться абсолютными, от­носительными и средними величинами. РД имеют свои уровни: начальные, конечные, средние. В зав-ти от хар-ра изуч-го явл-я уровни РД могут относиться или к опред-м датам (моментам) времени, или к отд-м периодам времени. В соотв-и с этим РД подр-ся на два вида: моментный и интервальный. Моментный ряд- это РД, уровни кот-го хар-т размеры общ-экон явл-й по сост-ю на опред-й момент. Особенностью моментального РД явл-ся то, что в его уров­ни могут входить одни и те же единицы измеренийй совокупности. Посредством моментных РД в пром-ти изучают объем ВП, расход сырья и материалов, состояние кадров и других показателей, отображающих состоя­ние изучаемых явлоний на определенные даты (моменты) времени. В моментнх РД средние уровни вычисляются: если моментный РД имеет равные промежутки времени между днумя составными датами, то средний уровень вычисляется по формуле средней арифметической простой. Если моментный РД имеет неодин-е промежутки м/у двумя составными датами, то ср-й уровень вычисл-ся по формуле средней взвешенной по времени уср = yt / t, где t – веса, длительность интервалов времени (дней, ме­сяцев) между смежными датами. Периодический {иитеовальньный)_ряд_ - это РД, уровни ко­торого хар-т размеры общ-экон явлений за опр-е периоды времени (недели, месяц, полугодие и т. д.). Особенностью периодического РД является то, что каж­дый его уровень складывается из данных за более короткие интервалы времени. Например, суммируя товарооборот за первые три месяца года, получают его объем за квартал, а сумма товарооборота четырех кварта­лов дает объем товарооборота за год и т. д. Свойство суммирования уровней за последовательные интервалы времени позволяет получить ряды динамики более укрупненных перио­дов. Средние уровни в периодических рядах исчисляются как простая средняя арифм-я, то есть путем деления суммы всех уровней на их количество: ycp = y / n. С отображение развития изучаемого явления во време­ни может быть представлено РД с нарастающими итогами. Их применение обусловлено потребностями отображения результатов раз­вития изучаемых показателей не только за данный отчетный период, но и с учетом предшествующих периодов. При составлении таких рядов произ­водится последовательное суммирование смежных уровней. Этим дости­гается суммарное обобщение результата развития изучаемого показатели с начала отчетного периода (месяц, квартал, полугодие и т. д.).

^ 16. Показатели динамики.

В С для того, чтобы выявить ос-ти развития изучае­мых явлений и процессов за отдельные периоды времени, исчисляются абсолютные и относительные показатели изменения ряда динамики: абсолютные приросты; средний абсолютный прирост; абсолютное значение одного процента прироста; темп роста; темп прироста; средний темп роста; средний темп прироста. В основе расчета показателей РД лежит сравнение его уровней. В зав-ти от применяемого способа сопоставления показа­тели Д могут вычисляться на постоянной и переменной базах срав­нения. Для расчета показателей динамики на постоянной базе каждый уро­вень ряда сравнивается с одним и тем же базисным уровнем. Исчислен­ные при этом показатели называются базисными. Для расчета показате­лей динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели динамики называются цепными. Абсолютный прирост (^у) - это разность между уровнями данно­го периода и периода, принятого за базу сравнения (предыдущего перио­да). Он вычисляется по формулам: базисный ^yб = yn – y0, цепной ^yц = yn – yn-1, где ^yб – абсол-й прирост базисный, ^yц – абсол-й прирост цепной, yn – уровень сравниваемый, у0 – уровень периода, принятого за базу сравнения, yn-1 – уровень, предш-й сравниваемому периоду. Средний абсолютный прирост предст-т собой обобщенную хар-ку индивид-х абсол-х приростов РД. Он определяется по формулам: ^ycp = å^y / n; ^y = (yn – y0) / (n-1), где n – число показателей в периоде. Абсолютное значение одного процента прироста (А) хар-т абсол-й эквивалент одного % прироста: A = ^y / ^T, где ^T – темп прироста. Темп роста хар-т средний отн-й рост явления за рассм-й период: К_б = уn / у0; К_ц = уn / уn-1. Темп прироста (^К) хар-т относ-й прирост явле­ния в отч-м периоде по ср-ю с тем уровнем, с которым ос-ся сравнение: ^К_б = ^yn / y0; ^К_б = К_б – 1 (или 100%); ^К_ц = ^yn / yn-1 или ^К_ц = К_ц – 1 (или 100%).

^ 18. Механическое выравнивание динамических рядов.

*Одним из наиболее простых методов изучения основной тенденции в рядах динамики является укрупнение интервалов. Он основан на укрупнении периодов времени, к которым отно­сятся уровни ряда динамики (одновременно уменьшается коли­чество интервалов). Например, ряд ежесуточного выпуска про­дукции заменяется рядом месячного выпуска продукции и т.д. Средняя, исчисленная по укрупненным интервалам, позволяет выявлять направление и характер (ускорение или замедление роста) основной тенденции развития. Метод скользящей средней, как и предыдущий предполагает преобразование исходного ряда динамики. Для выявления тенденции формируются интервал, состоящий из одинакового числа уровней. При этом каждый последующий интервал получается путем смещения на 1 уровень от начального. По образованным таким образом интервалам определяются в начале сумма, а затем средние. Технически удобнее определять скользящие средние для нечетного интервала. В этом случае рассчитанная средняя величина будет относиться к конкретному уровню ряда динамики, т.е. к середине интервала скольжения. При определении скользящей средней по четному интервалу, расчетное значение средней величины относится к промежутку между двумя уровнями, и таким образом теряют экономический смысл. Это делает необходимыми дополнительные расчеты связанные с центрированием по формуле арифметической простой из двух соседних не центрированных средних.

^ 19. Аналитическое выравнивание.

Основным содержанием метода аналитического выравнива­ния в рядах динамики является то, что общая тенденция разви­тия рассчитывается как функция времени. Определение теоретических уровней y_t произ­водится на основе так называемой адекватной математической модели, которая наилучшим образом отображает основную тенденцию ряда динамики. Выбор типа модели зависит от цели исследования и должен быть основан на теоретическом анализе, выявляющем характер развития явления, а также на графическом изображении ряда динамики (линейной диаграмме).

Например, простейшими моделями (формулами), выражаю­щими тенденцию развития, являются: линейная функция — прямая yt = a0 + a1t, где a0,a1 — параметры уравнения; t — время; показательная функция yt = A0A_1t

Способ наименьших квадратов даёт сумму двух нормальных уравнений для нахождения параметров a0,a: a₀n+a₁∑t=∑y; a₀∑t+a₁∑t²=∑yt, где у – исходные уровни ряда динамики, n - число членов ряда, t – время. • Выравнивание по прямой используется, как правило, в тех случаях, когда абсолютные приросты практически постоянны, т. е. когда уровни изменяются в арифметической прогрессии (или близко к ней).

• ^ Выравнивание по показательной функции используется в тех случаях, когда ряд отражает развитие в геометриче­ской прогрессии, т. е. когда цепные коэффициенты рос­та практически постоянны.

^ 20. Измерение сезонных колебаний.

Многие процессы хозяйственной деятельности, торговли, сельского хозяйства и других сфер человеческой деятельности подвержены сезонным изменениям, например, продажа мороженого, потребление электроэнергии, производство молока, сахара, продажа сельхозпродукции и др.

Для анализа рядов динамики, подверженных сезонным изменениям, используются специальные методы, позволяющие установить и описать особенности изменения уровней ряда. Прежде, чем использовать методы изучения сезонности, необходимо подготовить данные, приведённые в сопоставимый вид, за несколько лет наблюдения по месяцам или кварталам. Изменения сезонных колебаний производится с помощью индексов сезонности. В зависимости от существующих в ряду динамики тенденций используются различные правила построения индексов.

1. Ряд динамики не имеет общей тенденции развития, либо она не велика.

Индекс сезонности: I_s=y_срi/y_ср где y_срi— средний уровень ряда, полученный в результате осреднения уровней ряда за одноимённые периоды времени (например, средний уровень января за все годы наблюдения); y_ср — общий средний уровень ряда за всё время наблюдения.

2. С общей тенденцией роста. I_{ср s i}=[∑(y_i/y_ti)]/n, где y_i – исходные уровни ряда, y_t - выравненные уровни ряда, n – число годовых периодов. y_t=a₀+a₁t; a₀=∑y_i/n; a₁=∑ty_i/∑t². Выберем начало отсчёта t таким образом, чтобы было выполнено условие ∑t=0.

^ 22. Понятие об индексах. Виды индексов.

В статистике под индексом понимается относительная величина (показатель), выражающая изменение сложного экономического явления во времени, в пространстве или по сравнению с планом. В качестве меры соизмерения разнородных продуктов можно использовать цену, себестоимость или трудоемкость единицы продукции. В развитии индексной теории сложились два направления: синтетическое и аналитическое. Различие между этими направлениями обусловлено двумя возможностями интерпретации индексов в их приложении.

Синтетическое направление трактует индекс как показатель среднего изменения уровня изучаемого явления. В аналитической теории индексы воспринимаются как показатели изменения уровня результативной величины под влиянием изменения индексируемой величины.

Развитие второго направления было обусловлено применением индексного метода в экономическом анализе. Способы построения индексов зависят от содержания изучаемых явлений, методологии расчета исходных статистических показателей и целей исследования. Индивидуальными называются индексы, характеризующие изменение только одного элемента совокупности. Например, изменение выпуска легковых автомобилей определенной марки. Индивидуальный индекс обозначается i. Сводный индекс отражает изменение по всей совокупности элементов сложного явления. Если индексы охватывают не все элементы сложного явления, а лишь часть, то их называют групповыми, или субиндексами. Например, индексы продукции по отдельным отраслям промышленности. В зависимости от содержания и характера индексируемой величины различают индексы количественных (объемных) показателей (например, индекс физического объема продукции) и индексы качественных показателей (например, индексы цен, себестоимости). При вычислении индексов различают сравниваемый уровень и уровень, с которым производится сравнение, называемый базисным. При этом возможны два способа расчета индексов - цепной и базисный. Цепные индексы получают сопоставлением текущих уровней с предшествующим. Базисные индексы получают сопоставлением с уровнем какого-то одного определенного периода, принятого за базу сравнения. В зависимости от методологии расчета различают агрегатные индексы и средние из индивидуальных индексов. Индивидуальные индексы делятся на средние арифметические и средние гармонические индексы. Агрегатные индексы качественных показателей могут быть рассчитаны как индексы переменного состава и индексы фиксированного (постоянного) состава. В индексах переменного состава сопоставляются показатели, рассчитанные на базе изменяющихся структур явлений, а в индексах фиксированного состава - на базе неизменной структуры явлений.