Специальная математика

Вид материала

Конспект

Содержание 5.1. Понятие группы 5.2. Морфизмы групп 5.3. Инвариантные (нормальные) подгруппы

Подобный материал:

• Направления работы семинара, 152.43kb.
• «Математика. Прикладная математика», 366.03kb.
• Программа подраздела «Философские проблемы математики», 94.9kb.
• Рабочая программа по курсу «Специальная педагогика и специальная психология» на 5 курсе, 94.48kb.
• Специальная обработка, 1624.5kb.
• Расшифровка : Математика, 146.94kb.
• Abramson Family Cancer Research Institute University of Pennsylvania (usa) Роль апоптоза, 15.2kb.
• Программа дисциплины "Математика и информатика" (раздел «Математика») (специальность:, 399.2kb.
• Пангеометризм и математическая мифология, 956.71kb.
• Строительство. Система производственного контроля. Часть, 84.92kb.

5.1. Понятие группы

Группу можно задать как алгебру с одной операцией , удовлетворяющей следующим законам:


1. Существование операции.

xyz(x  y = z)

2. Ассоциативность
   

xyz(x  (y  z)) = ((x  y)  z)

3. Существование единицы (е)
   

еy(е  y = y)

4. Существование обратного элемента.

x!y(x  y = е)

5. Коммутативность

xy (x  y = y  x)


Выполнение лишь первого закона дает группоид. Если дополнительно выполняется второй – полугруппа (популярна при исследовании свойств формальных грамматик).

Выполнение первого, второго и третьего законов дает моноид.

Выполнение аксиом с первой по четвертую дает группу.

Если для группы выполняется также коммутативный закон, то группа называется абелевой.

5.2. Морфизмы групп

Рассмотрим вращения квадрата вокруг центра до совмещения вершин.

4 3

a₁ = 0⁰ В качестве элементов – углы поворота.

a₂ = 90⁰ В качестве операции - доворачивание.

a₃ = 180⁰ Выполняются все законы для группы.

a₄ = 270⁰

1 2

Например, а₁  а₂ = а₂; а₂  а₂ = а₃; а₃  а₃ = а₁

Популярны со времен Галуа и так называемые подстановки. Можно записать подстановки, соответствующие каждому из четырех вращений предыдущего примера:


1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4

       

1 2 3 4 4 1 2 3 3 4 1 2 2 3 4 1

А в качестве операции взять композицию подстановок. Например,



=
1 2 3 4 1 2 3 4 1 2 3 4

     

2 3 4 1 2 3 4 1 3 4 1 2


В результате также получится группа.


Возьмем корни уравнения x⁴ – 1 = 0

{1, i, -1, -i} - группа по операции умножения.


Таким образом, мы рассмотрели несколько конечных групп, содержащих по четыре элемента. Эти группы изоморфны между собой.

Например, можно отобразить друг в друга «единичные» элементы:

1 2 3 4

а₁  0⁰     1

1 2 3 4


Так что речь может идти об абстрактных группах, то есть о таких группах, для которых конкретное множество и конкретная операция несущественны.


Пусть f - некоторое отображение элементов одной группы в другую или в ту же самую и

f (a  b) = f(a)  f(b) a,b  G; f(a), f(b)  b₂.

то говорят, что f - гомоморфизм.

Если f(a)=F(b), тогда и только тогда, когда a = b, то имеем изоморфизм (однозначный гомоморфизм).

Гомоморфизм группы в себя называется эндоморфизмом.

Инъективный гомоморфизм называется мономорфизмом.

Сюръективный гомоморфизм называется эпиморфизмом.

Изоморфизм в себя называется автоморфизмом.

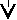
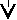
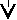
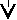
Пример : { . . .-3, -2, -1, 0, 1, 2, 3, . . . }


{ . . .-6, -4, -2, 0, 2, 4, 6, . . . } - эндоморфизм, эпиморфизм, мономорфизм, изоморфизм, автоморфизм.

5.3. Инвариантные (нормальные) подгруппы

Группа H называется подгруппой группы G, если она состоит из элементов группы G и сама является группой.

Элемент c=b^-1ab называется трансформацией элемента а с помощью элемента b. При этом элементы с и а называются сопряженными.

b^-1 - обратный элемент для b.

Здесь а и b - элементы группы, а обычное (необозначаемое) умножение, фактически, групповая операция.

Если b^-1 a b = а, то ab = ba (т.к. данная группа абелева, следовательно, коммутативна).

Доказательство: умножим b^-1ab = a слева и справа от знака равенства на b:

bb^-1ab = ba

Теорема: Трансформация разбивает группу на классы сопряженных элементов.

Доказательство:

1. Рефлексивность : a = 1^-1a1

2. Симметричность : c = b^-1ab 

bcb^-1 = bb^-1abb^-1

bcb^-1 = a

(b^-1)^-1cb^-1 = a ,пусть B = b^-1

B^-1cB = a, т.е. если а - трансформация с, то с - трансформация а

3. Транзитивность: c = b^-1ab, c=d^-1cd

e = d^-1b^-1abd

e = (bd)^-1abd

e = D^-1aD bdd^-1b^-1 =1, (bd)^-1 (bd)= 1  d^-1b^-1 = (bd)^-1

Теорема: Трансформация подгруппы H элементом bG есть подгруппа группы G, изоморфная Н.

Доказательство:

1. C₁= b^-1x₁b

C₂= b^-1x₂b , x₁ , x₁ H

C₁C₂= b^-1x₁bb^-1x₂b

2. b^-11b = 1 (т.е. 1 исходной группы остается 1 полученной группы )

3. a = b^-1xb

a^-1 = (b^-1xb)^-1 = b^-1x^-1(b^-1)^-1 = b^-1x^-1b

Т.е. в результате ( 1- 3) мы получаем группу, причем эта процедура сохраняет функциональность, сюръективность, всюду определенность, инъективность, т.е. полученная группа изоморфна исходной.


a²

ab = a²b



b ba²= ab




I a


Подгруппа К группы G называется инвариантной (нормальной), если трансформация любого элемента подгруппы К с помощью любого элемента этой группы дает снова элемент подгруппы К.

K = { I, a, a² } - подгруппа некоторой группы G

ab = ba² = ba^-1 ( или a²  a = I / *a^-1 , a²aa^-1 = Ia^-1 , a² = a^-1 )

b^-1ab = b^-1ba^-1

b^-1ab = a^-1 ( = a²) - трансформация элемента а с помощью элемента b и она есть элемент группы.