Тема III. Системы рациональных уравнений

Вид материала

Документы

Содержание Система, имеющая решение, называется совместной. Система называется линейной, если она содержит только линейные алгебраические уравнения.

Подобный материал:

• Конспект урока по теме «Методы решения систем рациональных уравнений», 20.25kb.
• Тема: «Рациональные и иррациональные уравнения, неравенства и системы», 199.57kb.
• Лекция № Тема 1: Системы линейных алгебраических уравнений. Метод Гаусса решения систем, 50.61kb.
• Тема: Исследование проблемы решения , 104.57kb.
• Методика изучения уравнений в курсе алгебры 7-9 классов Примерное содержание, 12.53kb.
• Тематическийпла н, 46.68kb.
• Лекция №1. Тема 1: Системы линейных алгебраических уравнений. Метод Гаусса решения, 47.04kb.
• Урок математики в 6 классе. Тема: Сложение и вычитание рациональных чисел, 159.97kb.
• Урок по теме «Системы линейных уравнений», 8.64kb.
• Исследование решений системы уравнений, 47.95kb.

Тема III. СИСТЕМЫ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ

Системой называется совокупность условий, которые должны удовлетворяться одновременно. Эти условия могут быть выражены в форме уравнений и неравенств.

Условия, входящие в систему, принято записывать в столбик и компоновать с левой стороны круглой скобкой.

Система, состоящая из уравнений, называется системой уравнений.

Система, состоящая из уравнений и неравенств, называется смешанной системой.

Решить систему, значит найти такую совокупность значений для неизвестных, которая удовлетворяет всем ее условиям.

Область определения системы – это общая часть области определения входящих в нее условий. Решение системы, если оно существует, всегда принадлежит области ее определения.

Система, имеющая решение, называется совместной.

Система, не имеющая решений, называется несовместной или противоречивой.


Глава I. РЕШЕНИЕ ЛИНЕЙНЫХ СИСТЕМ МЕТОДОМ ПОСЛЕДОВАТЕЛЬНОГО ИСКЛЮЧЕНИЯ НЕИЗВЕСТНЫХ (МЕТОДОМ ГАУССА)


§ I. Определение систем линейных алгебраических уравнений

Целое рациональное уравнение называется линейным алгебраическим, если обе его части состоят из слагаемых, степень которых не выше первой относительно определяемых неизвестных.

Система называется линейной, если она содержит только линейные алгебраические уравнения.

(Далее, следует программируемая часть пособия, в которой при ответе на вопросы или задания следует закрывать правую часть страницы. На этой части страницы проверяется правильность выполненного Вами задания или ответа. Последовательность работы с программируемым пособием опреде-ляется данными примерами, поставленными вопросами или заданиями Вашей реакцияей на них. Эта последовательность не должна нарушаться.)

Установите, являются ли системы, данные в примерах №1 и №2, линейными относительно х и у.

Пример №1 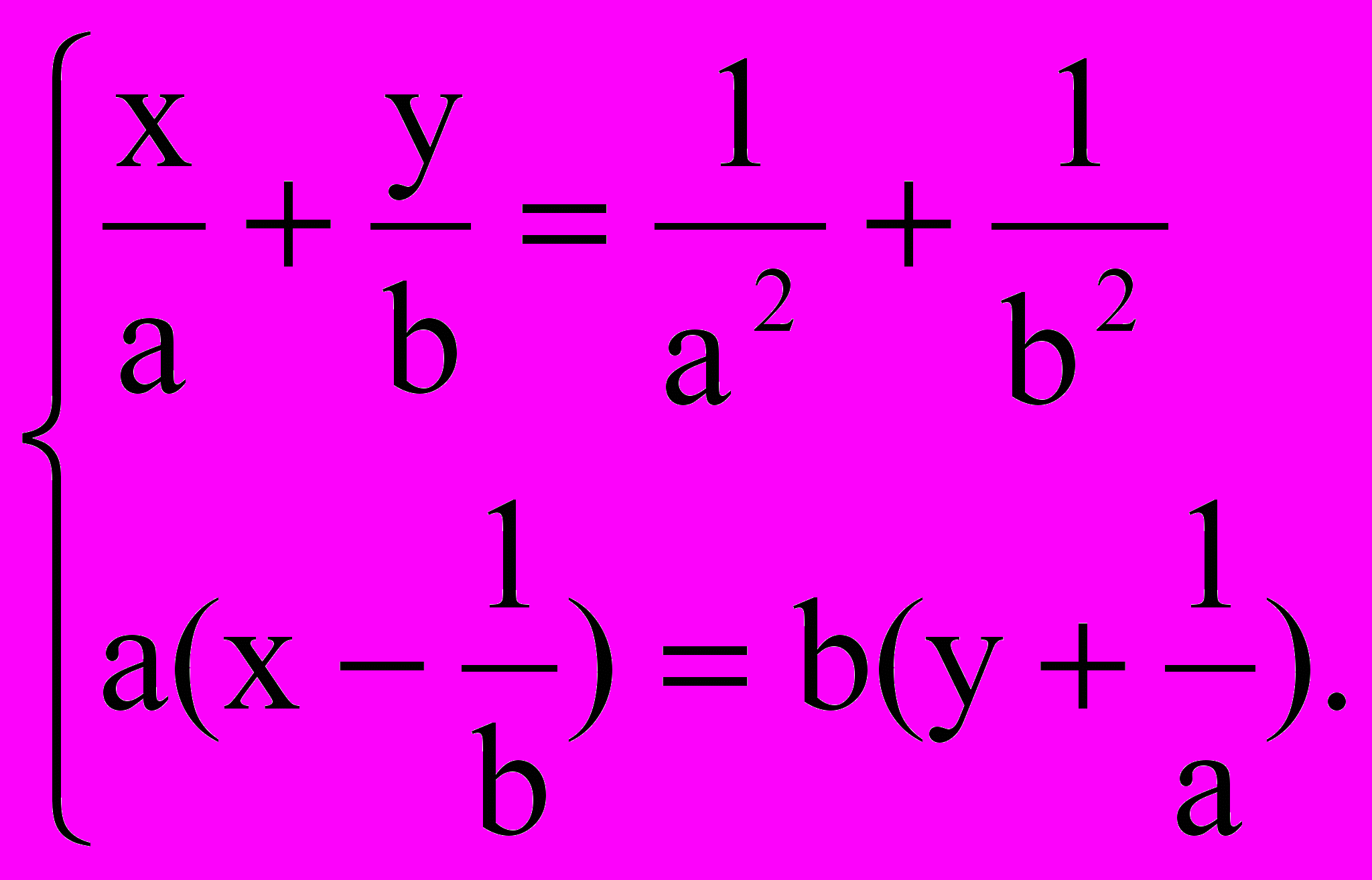Пример №2 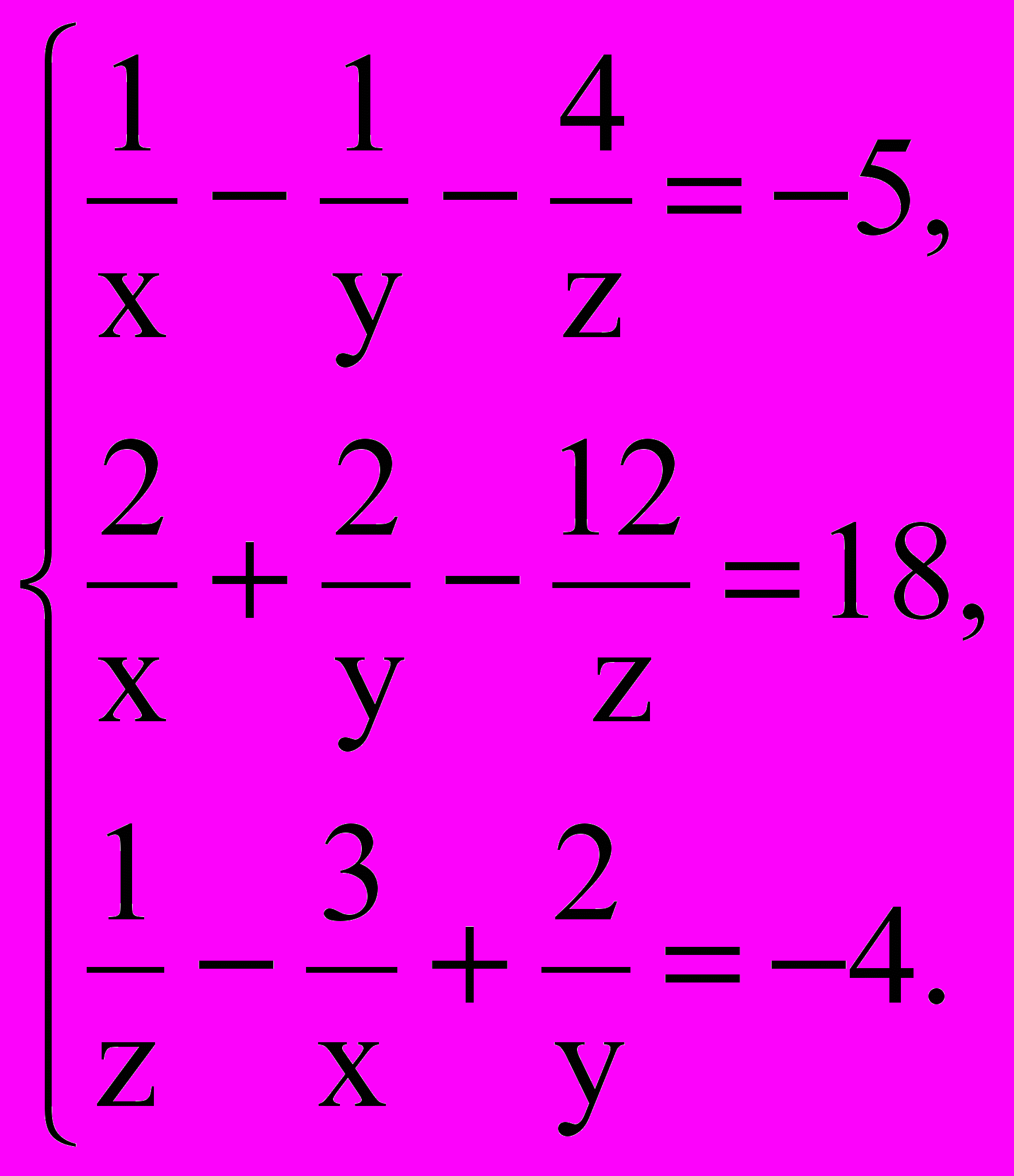В примере №3 выполните под-становку, приводящую данную систему к линейной. Пример №3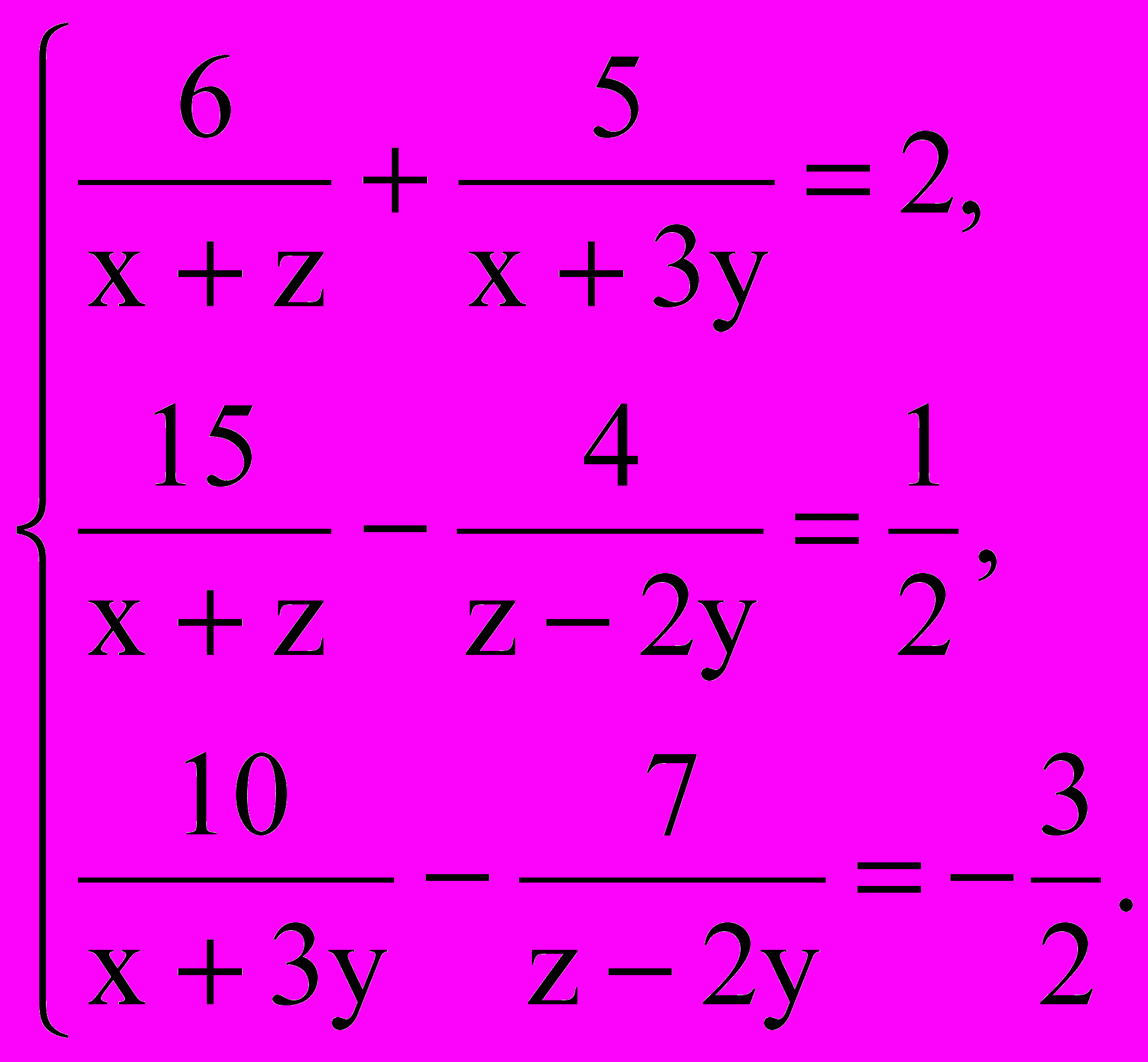

Ответы: Система линейная. См. «А». Система не линейная. См. «Б». А) Правильно. Переходите к примеру №2. Б) Не правильно. Данная система явля-ется линейной, так как, состоит из ли-нейных уравнений относительно х и у. Убедимся в том, что все слагаемые первого и второго уравнения имеют степень не выше 1-й относительно х и у. Действительно, левая часть первого уравнения содержит слагаемые 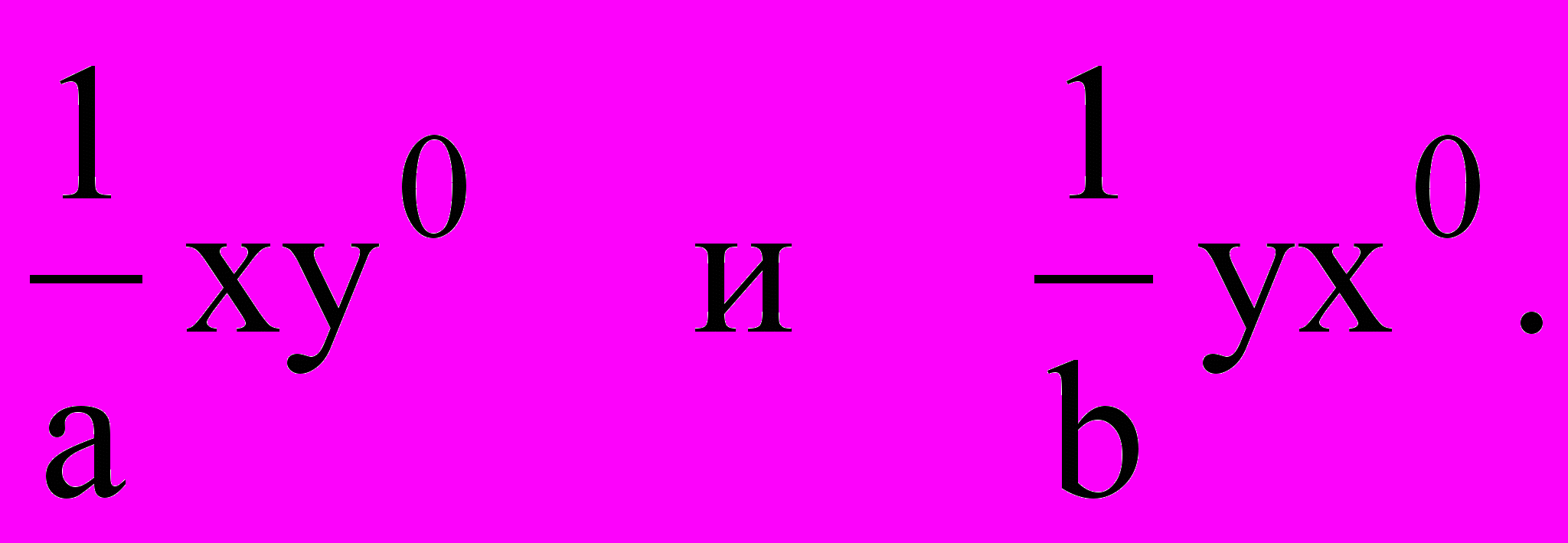Это слагаемые 1-й степени относительно х и у (сумма показателей при х и у в каждом из них равна единице). Слагаемые в правой части первого уравнения имеют относительно х и у нулевую степень. Так (сумма показателей при х и у в каждом из них равна нулю).Здесь мы воспользовались определением х0 ≡ 1 при х ≠0, y0 ≡ 1 при у ≠0. Второе уравнение системы, так же как и первое, можно представить в виде 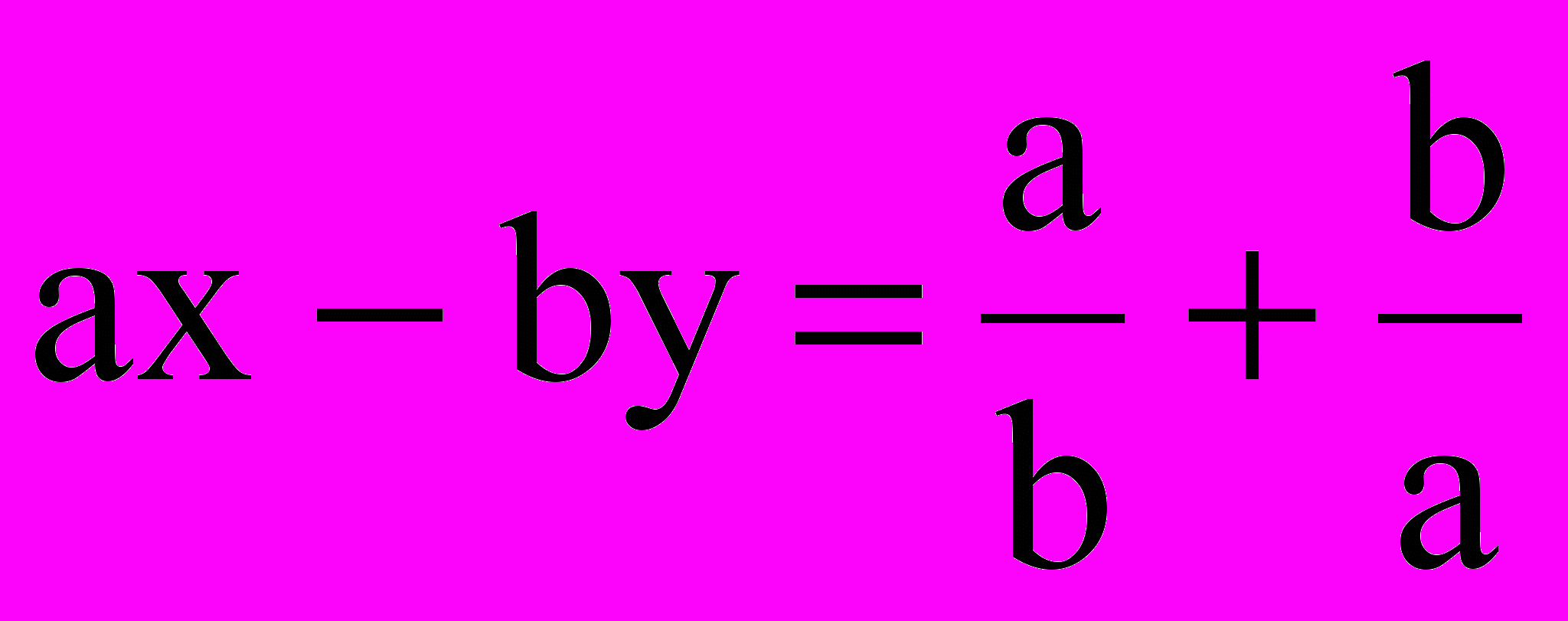. Теперь левая часть второго уравнения содержит слагаемые первой степени относительно х и у, а правая нулевой. Итак, данная система является линейной, т.к. состоит из линейных уравнений. Переходите к примеру № 2. Ответы: Система нелинейная. См. “А”. 2. Система линейная. См. “Б”. А) Правильно. Но подстановкой 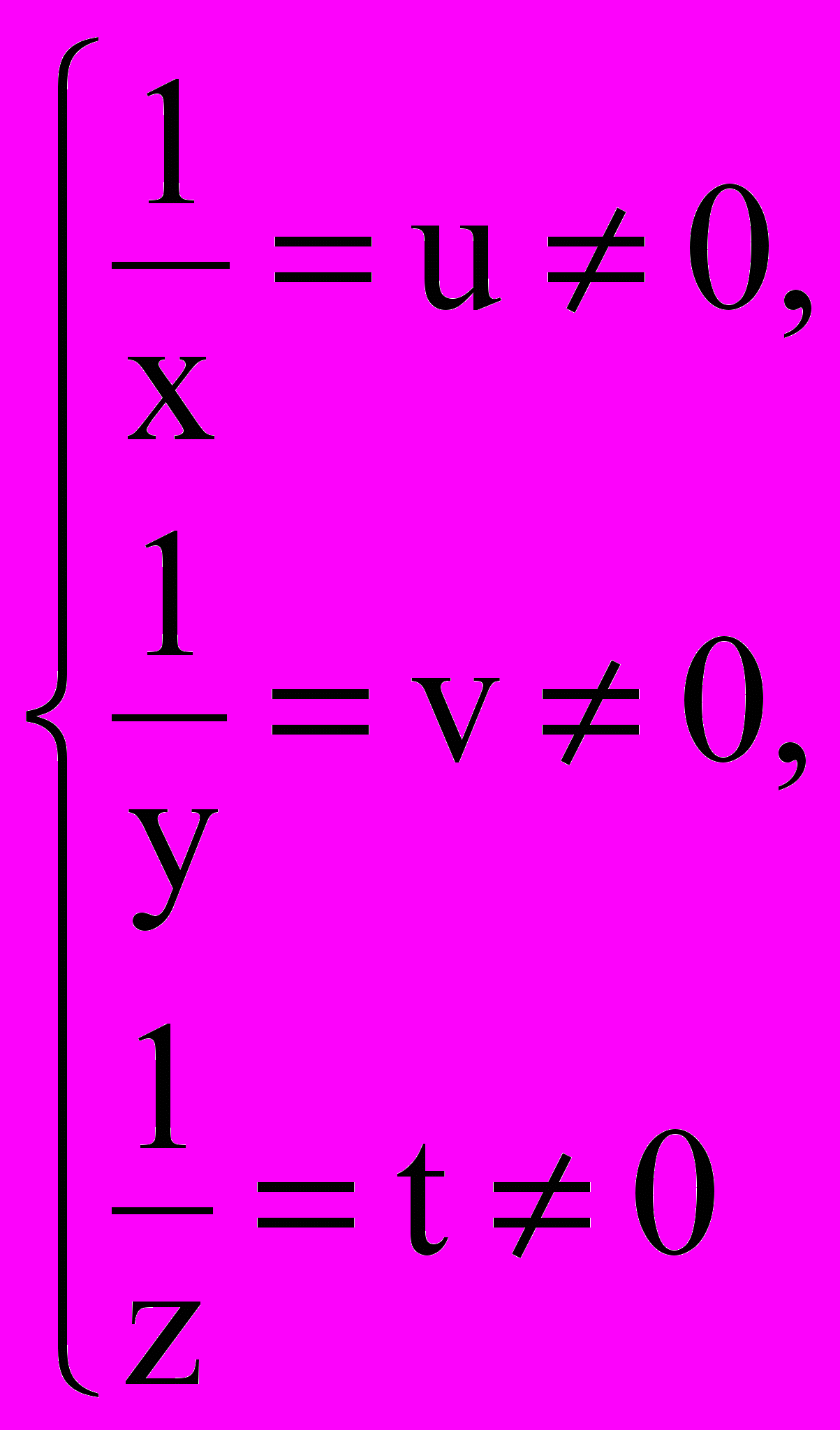данная система сводится к линейной относительно новых неизвестных u, v, t. Переходите к примеру №3. Б) Не правильно. Уравнения системы нельзя назвать линейными, т.к. левые части уравнения содержат сумму дробей, степени которых не определяются. (Определять можно только степень многочлена, т.е. такого аналитического выражения, в котором над буквами и числами производится не более двух действий: алгебраи-ческое сложение и умножение). Переходите к ответу 1 в примере № 2. Ответ: Подстановкой 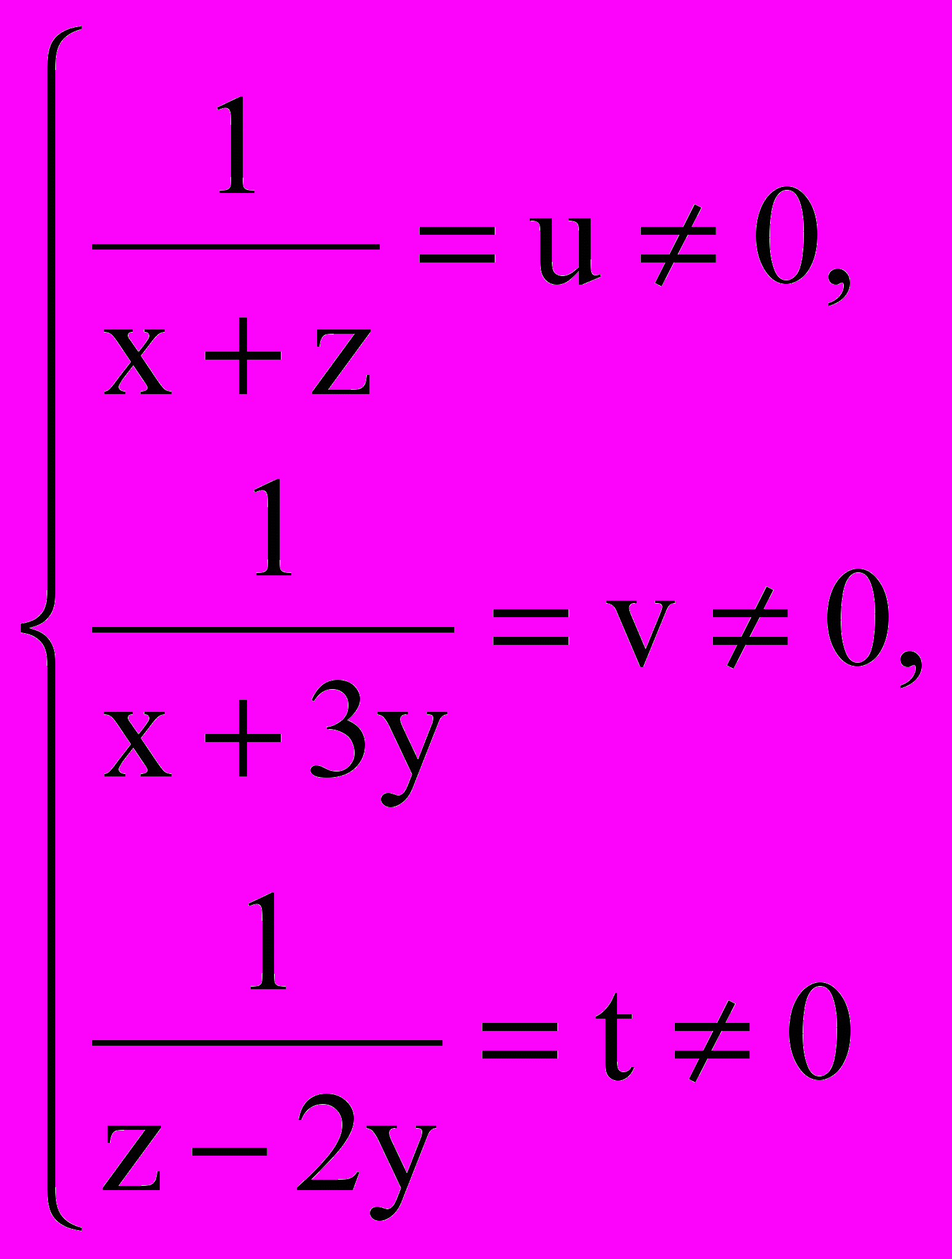решение данной системы сводится к последовательному решению двух линейных систем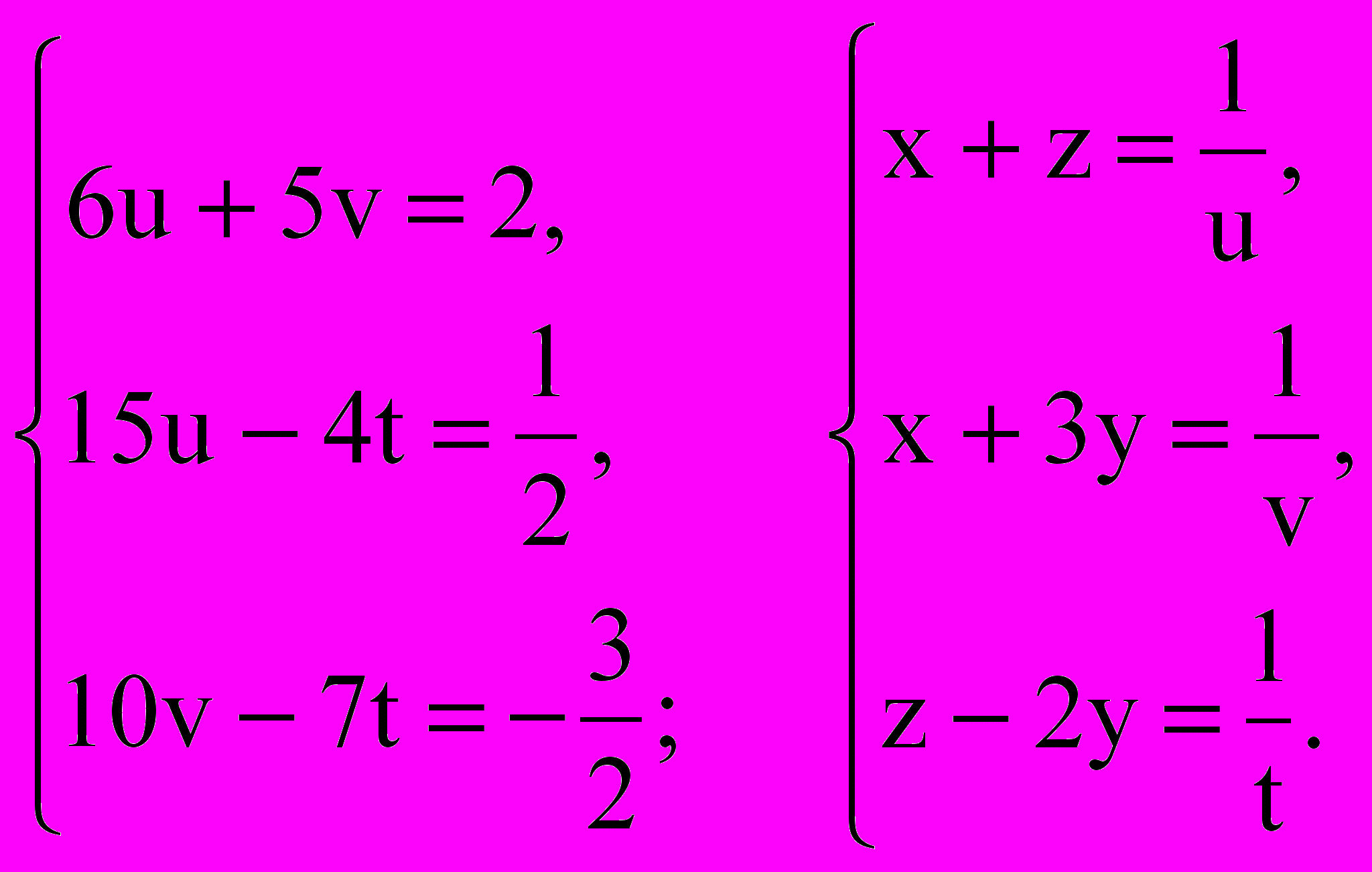 Переходите к § 2.