Молекулярная физика и термодинамика. Лекция №1 Молекулярно-кинетическая теория Основные положения мкт

Вид материала

Лекция

Содержание Последовательное и параллельное соединение проводников Правила Кирхгофа для разветвленных цепей Работа и мощность электрического тока .Закон Ома для полной цепи. Лекция №11

Подобный материал:

• Занятие №16 Основные положения мкт. Масса и размеры молекул. Мкт- молекулярно- кинетическая, 138.45kb.
• Молекулярная физика и термодинамика статистический и термодинамический методы Молекулярная, 12.67kb.
• Тема: Молекулярно-кинетическая теория, 131.48kb.
• Молекулярная структура вещества. Скорости газовых молекул, 140.08kb.
• Эртильская средняя общеобразовательная школа №1 «Молекулярно – кинетическая теория, 233.1kb.
• Контрольная работа "Молекулярно-кинетическая теория идеального газа. Газовые законы., 9.92kb.
• Молекулярно-кинетическая теория. Термодинамика. Задания с выбором ответа, 110.39kb.
• Лекция № Дата: Раздел: «Молекулярная физика. Термодинамика», 218.29kb.
• Программа по физике для 10-11 классов общеобразовательных, 75.87kb.
• Аннотация программы учебной дисциплины «Молекулярная физика» 2-й семестр, 42.3kb.

Последовательное и параллельное соединение проводников

Проводники в электрических цепях могут соединяться последовательно и параллельно.

При последовательном соединении проводников (рис. 4.9.1) сила тока во всех проводниках одинакова:

I1 = I2 = I.

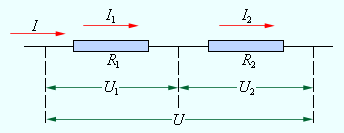Рисунок 4.9.1. Последовательное соединение проводников.

По закону Ома, напряжения U₁ и U₂ на проводниках равны

U1 = IR1,   U2 = IR2.

Общее напряжение U на обоих проводниках равно сумме напряжений U₁ и U₂:

U = U1 + U2 = I(R1 + R2) = IR,

где R – электрическое сопротивление всей цепи. Отсюда следует:

R = R1 + R2.

При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.

Этот результат справедлив для любого числа последовательно соединенных проводников.

При параллельном соединении (рис. 4.9.2) напряжения U₁ и U₂ на обоих проводниках одинаковы:

U1 = U2 = U.

Сумма токов I₁ + I₂, протекающих по обоим проводникам, равна току в неразветвленной цепи:

I = I1 + I2.

Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I₁Δt + I₂Δt. Следовательно, I = I₁ + I₂.

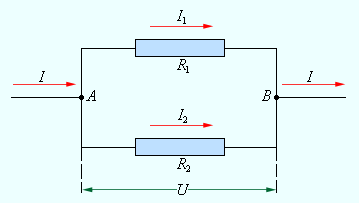Рисунок 4.9.2. Параллельное соединение проводников.

Записывая на основании закона Ома

где R – электрическое сопротивление всей цепи, получим

При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Этот результат справедлив для любого числа параллельно включенных проводников.

Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 4.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.

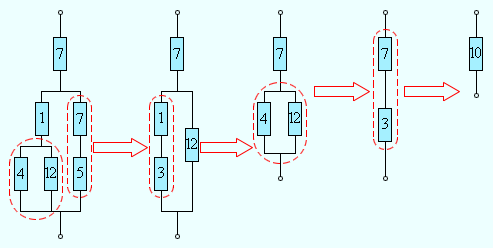Рисунок 4.9.3. Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны в омах (Ом).

Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 4.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.

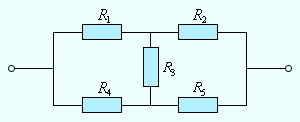Рисунок 4.9.4. Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников.

Цепи, подобные изображенной на рис. 4.9.4, а также цепи с разветвлениями, содержащие несколько источников, рассчитываются с помощью правил Кирхгофа.


Правила Кирхгофа для разветвленных цепей

Для упрощения расчетов сложных электрических цепей, содержащих неоднородные участки, используются правила Кирхгофа, которые являются обобщением закона Ома на случай разветвленных цепей.

В разветвленных цепях можно выделить узловые точки (узлы), в которых сходятся не менее трех проводников (рис. 4.10.1). Токи, втекающие в узел, принято считать положительными; токи, вытекающие из узла – отрицательными.

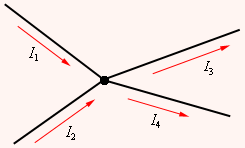Рисунок 4.10.1. Узел электрической цепи. I1, I2 > 0; I3, I4 < 0

В узлах цепи постоянного тока не может происходить накопление зарядов. Отсюда следует первое правило Кирхгофа:

Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю:

I1 + I2 + I3 + ... + In = 0.

Первое правило Кирхгофа является следствием закона сохранения электрического заряда.

В разветвленной цепи всегда можно выделить некоторое количество замкнутых путей, состоящих из однородных и неоднородных участков. Такие замкнутые пути называются контурами. На разных участках выделенного контура могут протекать различные токи. На рис. 4.10.2 представлен простой пример разветвленной цепи. Цепь содержит два узла a и d, в которых сходятся одинаковые токи; поэтому только один из узлов является независимым (a или d).

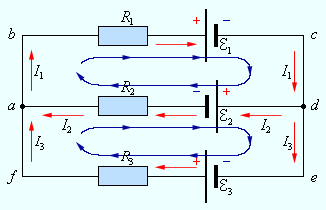Рисунок 4.10.2. Пример разветвленной электрической цепи. Цепь содержит один независимый узел (a или d) и два независимых контура (например, abcd и adef).

В цепи можно выделить три контура abcd, adef и abcdef. Из них только два являются независимыми (например, abcd и adef), так как третий не содержит никаких новых участков.

Второе правило Кирхгофа является следствием обобщенного закона Ома.

Запишем обобщенный закон Ома для участков, составляющих один из контуров цепи, изображенной на рис. 4.10.2, например, abcd. Для этого на каждом участке нужно задать положительное направление тока и положительное направление обхода контура. При записи обобщенного закона Ома для каждого из участков необходимо соблюдать определенные «правила знаков», которые поясняются на рис. 4.10.3.

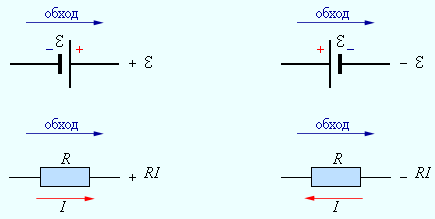Рисунок 4.10.3. «Правила знаков».

Для участков контура abcd обобщенный закон Ома записывается в виде:

Для участка bc: I₁R₁ = Δφ_bc – ₁.

Для участка da: I₂R₂ = Δφ_da – ₂.

Складывая левые и правые части этих равенств и принимая во внимание, что Δφ_bc = – Δφ_da , получим:

I1R1 + I2R2 = Δφbc + Δφda – 1 + 2 = –1 – 2.

Аналогично, для контура adef можно записать:

– I2R2 + I3R3 = 2 + 3.

Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура.

Первое и второе правила Кирхгофа, записанные для всех независимых узлов и контуров разветвленной цепи, дают в совокупности необходимое и достаточное число алгебраических уравнений для расчета электрической цепи. Для цепи, изображенной на рис. 4.10.2, система уравнений для определения трех неизвестных токов I₁, I₂ и I₃ имеет вид:

I1R1 + I2R2 = – 1 – 2,

– I2R2 + I3R3 = 2 + 3,

– I1 + I2 + I3 = 0.

Таким образом, правила Кирхгофа сводят расчет разветвленной электрической цепи к решению системы линейных алгебраических уравнений. Это решение не вызывает принципиальных затруднений, однако, бывает весьма громоздким даже в случае достаточно простых цепей. Если в результате решения сила тока на каком-то участке оказывается отрицательной, то это означает, что ток на этом участке идет в направлении, противоположном выбранному положительному направлению


Работа и мощность электрического тока .Закон Ома для полной цепи. Лекция №11

При протекании тока по однородному участку цепи электрическое поле совершает работу. За время Δt по цепи протекает заряд Δq = IΔt. Электрическое поле на выделенном учестке совершает работу

ΔA = (φ1 – φ2)Δq = Δφ12IΔt = UIΔt,

где U = Δφ₁₂ – напряжение. Эту работу называют работой электрического тока.

Если обе части формулы

RI = U,

выражающей закон Ома для однородного участка цепи с сопротивлением R, умножить на IΔt, то получится соотношение

RI2Δt = UIΔt = ΔA.

Это соотношение выражает закон сохранения энергии для однородного участка цепи.

Работа ΔA электрического тока I, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в тепло ΔQ, выделяющееся на проводнике.

ΔQ = ΔA = RI2Δt.

Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж. Джоулем и Э. Ленцем и носит название закона Джоуля–Ленца.

Мощность электрического тока равна отношению работы тока ΔA к интервалу времени Δt, за которое эта работа была совершена:

Работа электрического тока в СИ выражается в джоулях (Дж), мощность – в ваттах (Вт).

Рассмотрим теперь полную цепь постоянного тока, состоящую из источника с электродвижущей силой и внутренним сопротивлением r и внешнего однородного участка с сопротивлением R. Закон Ома для полной цепи записывается в виде

(R + r)I = .

Умножив обе части этой формулы на Δq = IΔt, мы получим соотношение, выражающее закон сохранения энергии для полной цепи постоянного тока:

RI2Δt + rI2Δt = IΔt = ΔAст.

Первый член в левой части ΔQ = RI²Δt – тепло, выделяющееся на внешнем участке цепи за время Δt, второй член ΔQ_ист = rI²Δt – тепло, выделяющееся внутри источника за то же время.

Выражение IΔt равно работе сторонних сил ΔA_ст, действующих внутри источника.

При протекании электрического тока по замкнутой цепи работа сторонних сил ΔA_ст преобразуется в тепло, выделяющееся во внешней цепи (ΔQ) и внутри источника (ΔQ_ист).

ΔQ + ΔQист = ΔAст = IΔt .

Следует обратить внимание, что в это соотношение не входит работа электрического поля. При протекании тока по замкнутой цепи электрическое поле работы не совершает; поэтому тепло производится одними только сторонними силами, действующими внутри источника. Роль электрического поля сводится к перераспределению тепла между различными участками цепи.

Внешняя цепь может представлять собой не только проводник с сопротивлением R, но и какое-либо устройство, потребляющее мощность, например, электродвигатель постоянного тока. В этом случае под R нужно понимать эквивалентное сопротивление нагрузки. Энергия, выделяемая во внешней цепи, может частично или полностью преобразовываться не только в тепло, на и в другие виды энергии, например, в механическую работу, совершаемую электродвигателем. Поэтому вопрос об использовании энергии источника тока имеет большое практическое значение.

Полная мощность источника, то есть работа, совершаемая сторонними силами за единицу времени, равна

Во внешней цепи выделяется мощность

Отношение равное

называется коэффициентом полезного действия источника.

На рис. 4.11.1 графически представлены зависимости мощности источника P_ист , полезной мощности P, выделяемой во внешней цепи, и коэффициента полезного действия η от тока в цепи I для источника с ЭДС, равной , и внутренним сопротивлением r. Ток в цепи может изменяться в пределах от I = 0 (при ) до (при R = 0).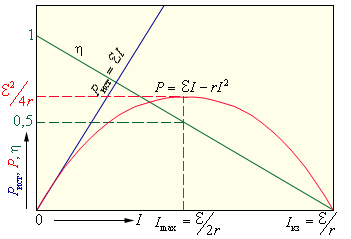

Рисунок 4.11.1. Зависимость мощности источника Pист, мощности во внешней цепи P и КПД источника η от силы тока.

Из приведенных графиков видно, что максимальная мощность во внешней цепи P_max , равная

достигается при R = r. При этом ток в цепи

а КПД источника равен 50 %. Максимальное значение КПД источника достигается при I → 0, т. е. при R → ∞. В случае короткого замыкания полезная мощность P = 0 и вся мощность выделяется внутри источника, что может привести к его перегреву и разрушению. КПД источника при этом обращается в нуль