Geum.ru

Молекулярная физика и термодинамика. Лекция №1 Молекулярно-кинетическая теория Основные положения мкт

Вид материалаЛекция

Содержание


Работа в электрическом поле. Потенциал
Подобный материал:
1   2   3   4   5   6   7   8   9   ...   21

Теорема Гаусса *)

Экспериментально установленные закон Кулона и принцип суперпозиции позволяют полностью описать электростатическое поле заданной системы зарядов в вакууме. Однако, свойства электростатического поля можно выразить в другой, более общей форме, не прибегая к представлению о кулоновском поле точечного заряда.

Введем новую физическую величину, характеризующую электрическое поле – поток Φ вектора напряженности электрического поля. Понятие потока вектора аналогично понятию потока вектора скорости при течении несжимаемой жидкости. Пусть в пространстве, где создано электрическое поле, расположена некоторая достаточно малая площадка ΔS. Произведение модуля вектора на площадь ΔS и на косинус угла α между вектором и нормалью к площадке называется элементарным потоком вектора напряженности через площадку ΔS (рис. 4.3.1):




ΔΦ = EΔS cos α = EnΔS,




где En – модуль нормальной составляющей поля



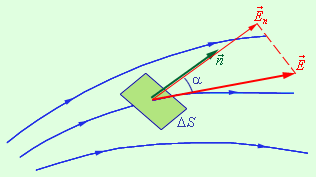Рисунок 4.3.1.

К определению элементарного потока ΔΦ.

Рассмотрим теперь некоторую произвольную замкнутую поверхность S. Если разбить эту поверхность на малые площадки ΔSi, определить элементарные потоки ΔΦi поля через эти малые площадки, а затем их просуммировать, то в результате мы получим поток Φ вектора через замкнутую поверхность S (рис. 4.3.2):









В случае замкнутой поверхности всегда выбирается внешняя нормаль.

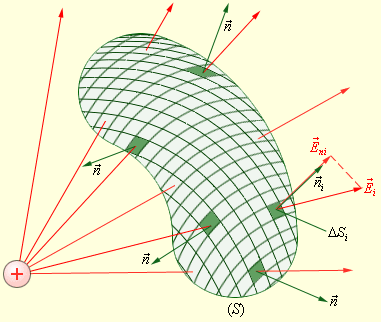Рисунок 4.3.2.

Вычисление потока Ф через произвольную замкнутую поверхность S.

Теорема Гаусса утверждает:

Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0.









Для доказательства рассмотрим сначала сферическую поверхность S, в центре которой находится точечный заряд q. Электрическое поле в любой точке сферы перпендикулярно к ее поверхности и равно по модулю









где R – радиус сферы. Поток Φ через сферическую поверхность будет равен произведению E на площадь сферы 4πR2. Следовательно,

Окружим теперь точечный заряд произвольной замкнутой поверхностью S и рассмотрим вспомогательную сферу радиуса R0 (рис. 4.3.3).

Рисунок 4.3.3.

Поток электрического поля точечного заряда через произвольную поверхность S, окружающую заряд.

Рассмотрим конус с малым телесным углом ΔΩ при вершине. Этот конус выделит на сфере малую площадку ΔS0, а на поверхности S – площадку ΔS. Элементарные потоки ΔΦ0 и ΔΦ через эти площадки одинаковы. Действительно,




ΔΦ0 = E0ΔS0,   ΔΦ = EΔS cos α = EΔS '.




Здесь ΔS ' = ΔS cos α – площадка, выделяемая конусом с телесным углом ΔΩ на поверхности сферы радиуса r.

Так как а следовательно ΔΦ0 = ΔΦ. Отсюда следует, что полный поток электрического поля точечного заряда через произвольную поверхность, охватывающую заряд, равен потоку Φ0 через поверхность вспомогательной сферы:









Аналогичным образом можно показать, что, если замкнутая поверхность S не охватывает точечного заряда q, то поток Φ = 0. Такой случай изображен на рис. 4.3.2. Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность S насквозь. Внутри поверхности S зарядов нет, поэтому в этой области силовые линии не обрываются и не зарождаются.

Обобщение теоремы Гаусса на случай произвольного распределения зарядов вытекает из принципа суперпозиции. Поле любого распределения зарядов можно представить как векторную сумму электрических полей точечных зарядов. Поток Φ системы зарядов через произвольную замкнутую поверхность S будет складываться из потоков Φi электрических полей отдельных зарядов. Если заряд qi оказался внутри поверхности S, то он дает вклад в поток, равный если же этот заряд оказался снаружи поверхности, то вклад его электрического поля в поток будет равен нулю.

Таким образом, теорема Гаусса доказана.

Теорема Гаусса является следствием закона Кулона и принципа суперпозиции. Но если принять утверждение, содержащееся в этой теореме, за первоначальную аксиому, то ее следствием окажется закон Кулона. Поэтому теорему Гаусса иногда называют альтернативной формулировкой закона Кулона.

Используя теорему Гаусса, можно в ряде случаев легко вычислить напряженность электрического поля вокруг заряженного тела, если заданное распределение зарядов обладает какой-либо симметрией и общую структуру поля можно заранее угадать.

Примером может служить задача о вычислении поля тонкостенного полого однородно заряженного длинного цилиндра радиуса R. Эта задача имеет осевую симметрию. Из соображений симметрии, электрическое поле должно быть направлено по радиусу. Поэтому для применения теоремы Гаусса целесообразно выбрать замкнутую поверхность S в виде соосного цилиндра некоторого радиуса r и длины l, закрытого с обоих торцов (рис. 4.3.4).

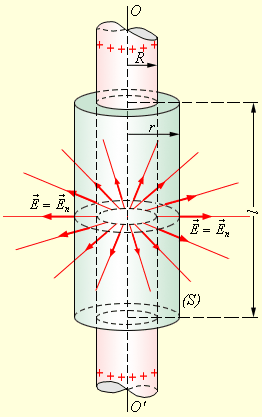Рисунок 4.3.4.

Вычисление поля однородно заряженного цилиндра. OO' – ось симметрии.

При r ≥ R весь поток вектора напряженности будет проходить через боковую поверхность цилиндра, площадь которой равна 2πrl, так как поток через оба основания равен нулю. Применение теоремы Гаусса дает:









где τ – заряд единицы длины цилиндра. Отсюда












Этот результат не зависит от радиуса R заряженного цилиндра, поэтому он применим и к полю длинной однородно заряженной нити.

Для определения напряженности поля внутри заряженного цилиндра нужно построить замкнутую поверхность для случая r < R. В силу симметрии задачи поток вектора напряженности через боковую поверхность гауссова цилиндра должен быть и в этом случае равен Φ = E2πrl. Согласно теореме Гаусса, этот поток пропорционален заряду, оказавшемуся внутри замкнутой поверхности. Этот заряд равен нулю. Отсюда следует, что электрическое поле внутри однородно заряженного длинного полого цилиндра равно нулю.

Аналогичным образом можно применить теорему Гаусса для определения электрического поля в ряде других случаев, когда распределение зарядов обладает какой-либо симметрией, например, симметрией относительно центра, плоскости или оси. В каждом из таких случаев нужно выбирать замкнутую гауссову поверхность целесообразной формы. Например, в случае центральной симметрии гауссову поверхность удобно выбирать в виде сферы с центром в точке симметрии. При осевой симметрии замкнутую поверхность нужно выбирать в виде соосного цилиндра, замкнутого с обоих торцов (как в рассмотренном выше примере). Если распределение зарядов не обладает какой-либо симметрией и общую структуру электрического поля угадать невозможно, применение теоремы Гаусса не может упростить задачу определения напряженности поля.

Рассмотрим еще один пример симметричного распределения зарядов – определение поля равномерно заряженной плоскости (рис. 4.3.5).

Рисунок 4.3.5.

Поле равномерно заряженной плоскости. σ – поверхностная плотность заряда. S – замкнутая гауссова поверхность.

В этом случае гауссову поверхность S целесообразно выбрать в виде цилиндра некоторой длины, закрытого с обоих торцов. Ось цилиндра направлена перпендикулярно заряженной плоскости, а его торцы расположены на одинаковом расстоянии от нее. В силу симметрии поле равномерно заряженной плоскости должно быть везде направлено по нормали. Применение теоремы Гаусса дает:












где σ – поверхностная плотность заряда, т. е. заряд, приходящийся на единицу площади.

Полученное выражение для электрического поля однородно заряженной плоскости применимо и в случае плоских заряженных площадок конечного размера. В этом случае расстояние от точки, в которой определяется напряженность поля, до заряженной площадки должно быть значительно меньше размеров площадки

Работа в электрическом поле. Потенциал

При перемещении пробного заряда q в электрическом поле электрические силы совершают работу. Эта работа при малом перемещении равна (рис. 4.4.1):














Рисунок 4.4.1.

Работа электрических сил при малом перемещении заряда q.

Электростатическое поле обладает важным свойством:

Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Аналогичным свойством обладает и гравитационное поле, и в этом нет ничего удивительного, так как гравитационные и кулоновские силы описываются одинаковыми соотношениями.

Следствием независимости работы от формы траектории является следующее утверждение:

Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

Силовые поля, обладающие этим свойством, называют потенциальными или консервативными.

На рис. 4.4.2 изображены силовые линии кулоновского поля точечного заряда Q и две различные траектории перемещения пробного заряда q из начальной точки (1) в конечную точку (2). На одной из траекторий выделено малое перемещение Работа ΔA кулоновских сил на этом перемещении равна









Таким образом, работа на малом перемещении зависит только от расстояния r между зарядами и его изменения Δr. Если это выражение проинтегрировать на интервале от r = r1 до r = r2, то можно получить














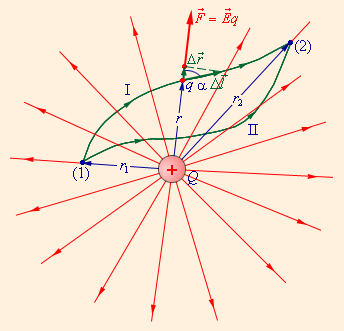Рисунок 4.4.2.

Работа кулоновских сил при перемещении заряда q зависит только от расстояний r1 и r2 начальной и конечной точек траектории.

Полученный результат не зависит от формы траектории. На траекториях I и II, изображенных на рис. 4.4.2, работы кулоновских сил одинаковы. Если на одной из траекторий изменить направление перемещения заряда q на противоположное, то работа изменит знак. Отсюда следует, что на замкнутой траектории работа кулоновских сил равна нулю.

Если электростатическое поле создается совокупностью точечных зарядов Qi, то при перемещении пробного заряда q работа A результирующего поля в соответствии с принципом суперпозиции будет складываться из работ Ai кулоновских полей точечных зарядов: Так как каждый член суммы Ai не зависит от формы траектории, то и полная работа A результирующего поля не зависит от пути и определяется только положением начальной и конечной точек.

Свойство потенциальности электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. Для этого в пространстве выбирается некоторая точка (0), и потенциальная энергия заряда q, помещенного в эту точку, принимается равной нулю.

Потенциальная энергия заряда q, помещенного в любую точку (1) пространства, относительно фиксированной точки (0) равна работе A10, которую совершит электрическое поле при перемещении заряда q из точки (1) в точку (0):

Wp1 = A10.







(В электростатике энергию принято обозначать буквой W, так как буквой E обозначают напряженность поля.)

Так же, как и в механике, потенциальная энергия определена с точностью до постоянной величины, зависящей от выбора опорной точки (0). Такая неоднозначность в определении потенциальной энергии не приводит к каким-либо недоразумениям, так как физический смысл имеет не сама потенциальная энергия, а разность ее значений в двух точках пространства.

Работа, совершаемая электрическим полем при перемещении точечного заряда q из точки (1) в точку (2), равна разности значений потенциальной энергии в этих точках и не зависит от пути перемещения заряда и от выбора точки (0).

A12 = A10 + A02 = A10 – A20 = Wp1 – Wp2.







Потенциальная энергия заряда q, помещенного в электрическое поле, пропорциональна величине этого заряда.

Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:









Потенциал φ является энергетической характеристикой электростатического поля.

Работа A12 по перемещению электрического заряда q из начальной точки (1) в конечную точку (2) равна произведению заряда на разность потенциалов (φ1 – φ2) начальной и конечной точек:




A12 = Wp1 – Wp2 = qφ1 – qφ2 = q(φ1 – φ2).




В Международной системе единиц (СИ) единицей потенциала является вольт (В).




1 В = 1 Дж / 1 Кл.



Во многих задачах электростатики при вычислении потенциалов за опорную точку (0) удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом:

Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.









Потенциал φ∞ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:









Как следует из теоремы Гаусса, эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R, где R – радиус шара.

Для наглядного представления электрического поля наряду с силовыми линиями используют эквипотенциальные поверхности.

Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала.

Силовые линии электрического поля всегда перпендикулярны эквипотенциальным поверхностям.

Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы. На рис. 4.4.3 представлены картины силовых линий и эквипотенциальных поверхностей некоторых простых электростатических полей.

Рисунок 4.4.3.

Эквипотенциальные поверхности (синие линии) и силовые линии (красные линии) простых электрических полей: a – точечный заряд; b – электрический диполь; c – два равных положительных заряда.

В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей.

Если пробный заряд q совершил малое перемещение вдоль силовой линии из точки (1) в точку (2), то можно записать:




ΔA12 = qEΔl = q(φ1 – φ2) = – qΔφ,




где Δφ = φ1 – φ2 – изменение потенциала. Отсюда следует









Это соотношение в скалярной форме выражает связь между напряженностью поля и потенциалом. Здесь l – координата вдоль силовой линии.

Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов:




φ = φ1 + φ2 + φ3 + ...