Молекулярная физика и термодинамика. Лекция №1 Молекулярно-кинетическая теория Основные положения мкт

Вид материала

Содержание

Изобретение радио А.С.Поповым
Приемник А.С. Попова
Основные законы геометрической оптики
Развитие представлений о природе света Лекция №21

Подобный материал:

1 ... 13 14 15 16 17 18 19 20 21

Следует обратить внимание на то, что максимальный поток электромагнитной энергии излучается в плоскости, перпендикулярной оси диполя. Вдоль своей оси диполь не излучает энергии. Герц использовал элементарный диполь в качестве излучающей и приемной антенн при экспериментальном доказательстве существования электромагнитных волн.

Работы Герца в области электромагнитных волн имели основополагающее значение для дальнейшего развития в этой области физики. Его опыты были многократно повторены, усовершенствованы и в конечном итоге привели к изобретению радио и телевидения.

Изобретение радио А.С.Поповым

Изучение свойств электромагнитных волн, теоретически предсказанных М. Фарадеем и Д. Максвеллом и практически доказанных Г. Герцем, приводило к мысли о возможности их использования для организации беспроволочной связи. Несколько исследователей попытались решить эту задачу. Добились успеха наш соотечественник А.С. Попов итальянец Г. Маркони.

7 мая 1895г. А. С. Попов впервые продемонстрировал работу своего "прибора для обнаружения и регистрирования электрических колебаний" на заседании Русского физико-химического общества в ходе обстоятельного доклада. Прибор откликался на посылки волн от "герцевского вибратора", возбуждаемого катушкой Румкорфа, на расстоянии 25 метров. Это была демонстрация первого в мире радиоприёмника, открывшего эру радио.

Приемник А.С. Попова

А.С. Попов использовал удачный индикатор электромагнитных волн, основанный на использовании металлических опилок. Свойство металлических порошков менять свои электрические свойства под действием электромагнитных волн было использовано в приборе, который назывался когерер: в стеклянную трубочку насыпаны мелкие опилки и сделаны металлические выводы из нее.

когерер

Приемник А.С. Попова выглядел так:

внешний вид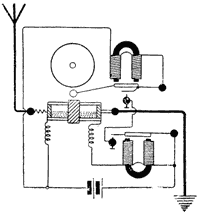

схема приемника А.С. Попова

Первая в мире смысловая радиограмма, осуществленная 7 марта 1895 года А.С. Поповым, содержала всего два слова: "Генрих Герц" как дань уважения памяти великого ученого, открывшего дверь в мир радио.

Оптика

Оптика – раздел физики, изучающий свойства и физическую природу света, а также его взаимодействие с веществом. Учение о свете принято делить на три части:

геометрическая или лучевая оптика, в основе которой лежит представление о световых лучах;
волновая оптика, изучающая явления, в которых проявляются волновые свойства света;
квантовая оптика, изучающая взаимодействие света с веществом, при котором проявляются корпускулярные свойства света.

Основные законы геометрической оптики

Основные законы геометрической оптики были известны задолго до установления физической природы света.

Закон прямолинейного распространения света: в оптически однородной среде свет распространяется прямолинейно. Опытным доказательством этого закона могут служить резкие тени, отбрасываемые непрозрачными телами при освещении светом источника достаточно малых размеров («точечный источник»). Другим доказательством может служить известный опыт по прохождению света далекого источника сквозь небольшое отверстие, в результате чего образуется узкий световой пучок. Этот опыт приводит к представлению о световом луче как о геометрической линии, вдоль которой распространяется свет. Следует отметить, что закон прямолинейного распространения света нарушается и понятие светового луча утрачивает смысл, если свет проходит через малые отверстия, размеры которых сравнимы с длиной волны. Таким образом, геометрическая оптика, опирающаяся на представление о световых лучах, есть предельный случай волновой оптики при λ → 0. Границы применимости геометрической оптики будут рассмотрены в разделе о дифракции света.

На границе раздела двух прозрачных сред свет может частично отразиться так, что часть световой энергии будет распространяться после отражения по новому направлению, а частично пройти через границу и распространяться во второй среде.

Закон отражения света: падающий и отраженный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости (плоскость падения). Угол отражения γ равен углу падения α.

Закон преломления света: падающий и преломленный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. Отношение синуса угла падения α к синусу угла преломления β есть величина, постоянная для двух данных сред:

Закон преломления был экспериментально установлен голландским ученым В. Снеллиусом (1621 г.).

Постоянную величину n называют относительным показателем преломления второй среды относительно первой. Показатель преломления среды относительно вакуума называют абсолютным показателем преломления.

Относительный показатель преломления двух сред равен отношению их абсолютных показателей преломления:

n = n₂ / n₁.

Законы отражения и преломления находят объяснение в волновой физике. Согласно волновым представлениям, преломление является следствием изменения скорости распространения волн при переходе из одной среды в другую. Физический смысл показателя преломления – это отношение скорости распространения волн в первой среде υ₁ к скорости их распространения во второй среде υ₂:

Абсолютный показатель преломления равен отношению скорости света c в вакууме к скорости света υ в среде:

Рис 6.1.1 иллюстрирует законы отражения и преломления света.

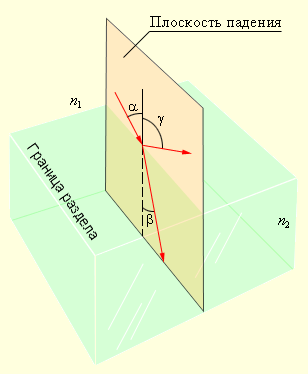Рисунок 6.1.1.

Законы отражения и преломления: γ = α; n₁ sin α = n₂ sin β.

Среду с меньшим абсолютным показателем преломления называют оптически менее плотной.

При переходе света из оптически более плотной среды в оптически менее плотную n₂ < n₁ (например, из стекла в воздух) можно наблюдать явление полного отражения, то есть исчезновение преломленного луча. Это явление наблюдается при углах падения, превышающих некоторый критический угол α_пр, который называется предельным углом полного внутреннего отражения (см. рис. 6.1.2).

Для угла падения α = α_пр sin β = 1 значение sin α_пр = n₂ / n₁ < 1.

Если второй средой является воздух (n₂ ≈ 1), то формулу удобно переписать в виде

sin α_пр = 1 / n,

где n = n₁ > 1 – абсолютный показатель преломления первой среды.

Для границы раздела стекло–воздух (n = 1,5) критический угол равен α_пр = 42°, для границы вода–воздух (n = 1,33) – α_пр = 48,7°.

Рисунок 6.1.2.

Полное внутреннее отражение света на границе вода–воздух; S – точечный источник света.

Явление полного внутреннего отражения находит применение во многих оптических устройствах. Наиболее интересным и практически важным применением является создание волоконных световодов, которые представляют собой тонкие (от нескольких микрометров до миллиметров) произвольно изогнутые нити из оптически прозрачного материала (стекло, кварц). Свет, попадающий на торец световода, может распространяться по нему на большие расстояния за счет полного внутреннего отражения от боковых поверхностей (рис 6.1.3). Научно-техническое направление, занимающееся разработкой и применением оптических световодов, называется волоконной оптикой.

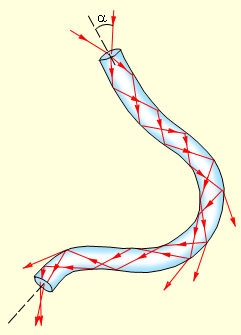Рисунок 6.1.3.

Распространение света в волоконном световоде. При сильном изгибе волокна закон полного внутреннего отражения нарушается, и свет частично выходит из волокна через боковую поверхность.

Зеркала

Простейшим оптическим устройством, способным создавать изображение предмета, является плоское зеркало. Изображение предмета, даваемое плоским зеркалом, формируется за счет лучей, отраженных от зеркальной поверхности. Это изображение является мнимым, так как оно образуется пересечением не самих отраженных лучей, а их продолжений в «зазеркалье» (рис 6.2.1).

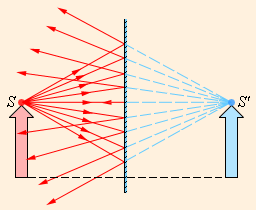Рисунок 6.2.1.

Ход лучей при отражении от плоского зеркала. Точка S' является мнимым изображением точки S.

Вследствие закона отражения света мнимое изображение предмета располагается симметрично относительно зеркальной поверхности. Размер изображения равен размеру самого предмета.

Сферическим зеркалом называют зеркально отражающую поверхность, имеющую форму сферического сегмента. Центр сферы, из которой вырезан сегмент, называют оптическим центром зеркала. Вершину сферического сегмента называют полюсом. Прямая, проходящая через оптический центр и полюс зеркала, называется главной оптической осью сферического зеркала. Главная оптическая ось выделена из всех других прямых, проходящих через оптический центр, только тем, что она является осью симметрии зеркала.

Сферические зеркала бывают вогнутыми и выпуклыми. Если на вогнутое сферическое зеркало падает пучок лучей, параллельный главной оптической оси, то после отражения от зеркала лучи пересекутся в точке, которая называется главным фокусом зеркала F. Расстояние от фокуса до полюса зеркала называют фокусным расстоянием и обозначают той же буквой F. У вогнутого сферического зеркала главный фокус действительный. Он расположен посередине между центром и полюсом зеркала (рис 6.2.2).

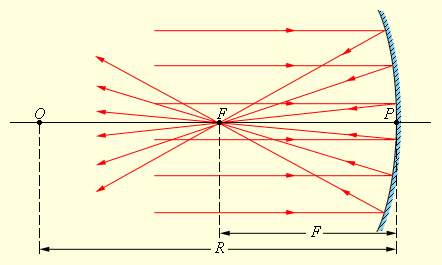Рисунок 6.2.2.

Отражение параллельного пучка лучей от вогнутого сферического зеркала. Точки O – оптический центр, P – полюс, F – главный фокус зеркала; OP – главная оптическая ось, R – радиус кривизны зеркала.

Следует иметь в виду, что отраженные лучи пересекаются приблизительно в одной точке только в том случае, если падающий параллельный пучок был достаточно узким (так называемый параксиальный пучок).

Главный фокус выпуклого зеркала является мнимым. Если на выпуклое зеркало падает пучок лучей, параллельных главной оптической оси, то после отражения в фокусе пересекутся не сами лучи, а их продолжения (рис 6.2.3).

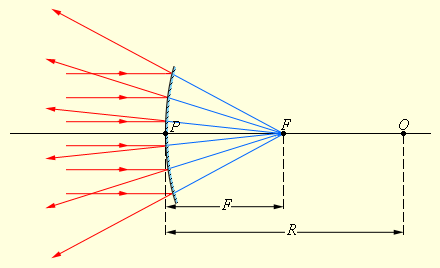Рисунок 6.2.3.

Отражение параллельного пучка лучей от выпуклого зеркала. F – мнимый фокус зеркала, O – оптический центр; OP – главная оптическая ось.

Фокусным расстояниям сферических зеркал приписывается определенный знак: для вогнутого зеркала

для выпуклого

где R – радиус кривизны зеркала.

Изображение какой-либо точки A предмета в сферическом зеркале можно построить с помощью любой пары стандартных лучей:

луч AOC, проходящий через оптический центр зеркала; отраженный луч COA идет по той же прямой;
луч AFD, идущий через фокус зеркала; отраженный луч идет параллельно главной оптической оси;
луч AP, падающий на зеркало в его полюсе; отраженный луч симметричен с падающим относительно главной оптической оси.
луч AE, параллельный главной оптической оси; отраженный луч EFA₁ проходит через фокус зеркала.

На рис 6.2.4 перечисленные выше стандартные лучи изображены для случая вогнутого зеркала. Все эти лучи проходят через точку A', которая является изображением точки A. Все остальные отраженные лучи также проходят через точку A'. Ход лучей, при котором все лучи, вышедшие из одной точки, собираются в другой точке, называется стигматическим. Отрезок A'B' является изображением предмета AB. Аналогичны построения для случая выпуклого зеркала.

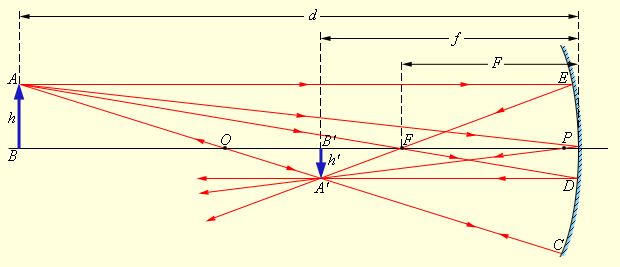Рисунок 6.2.4.

Построение изображения в вогнутом сферическом зеркале.

Положение изображения и его размер можно также определить с помощью формулы сферического зеркала:

Здесь d – расстояние от предмета до зеркала, f – расстояние от зеркала до изображения. Величины d и f подчиняются определенному правилу знаков:
d > 0 и f > 0 – для действительных предметов и изображений;
d < 0 и f < 0 – для мнимых предметов и изображений.

Для случая, изображенного на рис 6.2.4, имеем:

F > 0 (зеркало вогнутое); d = 3F > 0 (действительный предмет).

По формуле сферического зеркала получаем:

следовательно, изображение действительное.

Если бы на месте вогнутого зеркала стояло выпуклое зеркало с тем же по модулю фокусным расстоянием, мы получили бы следующий результат:

F < 0, d = –3F > 0,

– изображение мнимое.

Линейное увеличение сферического зеркала Γ определяется как отношение линейных размеров изображения h' и предмета h.

Величине h' удобно приписывать определенный знак в зависимости от того, является изображение прямым (h' > 0) или перевернутым (h' < 0). Величина h всегда считается положительной. При таком определении линейное увеличение сферического зеркала выражается формулой, которую можно легко получить из рис 6.2.4:

В первом из рассмотренных выше примеров

– следовательно, изображение перевернутое, уменьшенное в 2 раза. Во втором примере

– изображение прямое, уменьшенное в 4 раза.

Развитие представлений о природе света Лекция №21

Первые представления о природе света возникли у древних греков и египтян. По мере изобретения и совершенствования различных оптических приборов (параболических зеркал, микроскопа, зрительной трубы) эти представления развивались и трансформировались. В конце XVII века возникли две теории света: корпускулярная (И. Ньютон) и волновая (Р. Гук и Х. Гюйгенс).

Согласно корпускулярной теории, свет представляет собой поток частиц (корпускул), испускаемых светящимися телами. Ньютон считал, что движение световых корпускул подчиняется законам механики. Так, отражение света понималось аналогично отражению упругого шарика от плоскости. Преломление света объяснялось изменением скорости корпускул при переходе из одной среды в другую. Для случая преломления света на границе вакуум–среда корпускулярная теория приводила к следующему виду закона преломления:

где c – скорость света в вакууме, υ – скорость распространения света в среде. Так как n > 1, из корпускулярной теории следовало, что скорость света в средах должна быть больше скорости света в вакууме. Ньютон пытался также объяснить появление интерференционных полос, допуская определенную периодичность световых процессов. Таким образом, корпускулярная теория Ньютона содержала в себе элементы волновых представлений.

Волновая теория, в отличие от корпускулярной, рассматривала свет как волновой процесс, подобный механическим волнам. В основу волновой теории был положен принцип Гюйгенса, согласно которому каждая точка, до которой доходит волна, становится центром вторичных волн, а огибающая этих волн дает положение волнового фронта в следующий момент времени. С помощью принципа Гюйгенса были объяснены законы отражения и преломления. Рис. 6.6.1 дает представление о построениях Гюйгенса для определения направления распространения волны, преломленной на границе двух прозрачных сред.

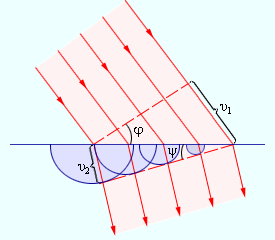Рисунок 6.6.1.

Построения Гюйгенса для определения направления преломленной волны.

Для случая преломления света на границе вакуум–среда волновая теория приводит к следующему выводу:

Закон преломления, полученный из волновой теории, оказался в противоречии с формулой Ньютона. Волновая теория приводит к выводу: υ < c, тогда как согласно корпускулярной теории υ > c.

Таким образом, к началу XVIII века существовало два противоположных подхода к объяснению природы света: корпускулярная теория Ньютона и волновая теория Гюйгенса. Обе теории объясняли прямолинейное распространение света, законы отражения и преломления. Весь XVIII век стал веком борьбы этих теорий. Однако в начале XIX столетия ситуация коренным образом изменилась. Корпускулярная теория была отвергнута и восторжествовала волновая теория. Большая заслуга в этом принадлежит английскому физику Т. Юнгу и французскому физику О. Френелю, исследовавшим явления интерференции и дифракции. Исчерпывающее объяснение этих явлений могло быть дано только на основе волновой теории. Важное экспериментальное подтверждение справедливости волновой теории было получено в 1851 году, когда Ж. Фуко (и независимо от него А. Физо) измерил скорость распространения света в воде и получил значение υ < c.

Хотя к середине XIX века волновая теория была общепризнана, вопрос о природе световых волн оставался нерешенным.

В 60-е годы XIX века Максвеллом были установлены общие законы электромагнитного поля, которые привели его к заключению, что свет – это электромагнитные волны. Важным подтверждением такой точки зрения послужило совпадение скорости света в вакууме с электродинамической постоянной

Электромагнитная природа света получила признание после опытов Г. Герца (1887–1888 гг.) по исследованию электромагнитных волн. В начале XX века после опытов П. Н. Лебедева по измерению светового давления (1901 г.) электромагнитная теория света превратилась в твердо установленный факт.

Важнейшую роль в выяснении природы света сыграло опытное определение его скорости. Начиная с конца XVII века предпринимались неоднократные попытки измерения скорости света различными методами (астрономический метод А. Физо, метод А. Майкельсона). Современная лазерная техника позволяет измерять скорость света с очень высокой точностью на основе независимых измерений длины волны λ и частоты света ν (c = λ · ν). Таким путем было найдено значение

превосходящее по точности все ранее полученные значения более чем на два порядка.

Свет играет чрезвычайно важную роль в нашей жизни. Подавляющее количество информации об окружающем мире человек получает с помощью света. Однако, в оптике как разделе физике под светом понимают не только видимый свет, но и примыкающие к нему широкие диапазоны спектра электромагнитного излучения – инфракрасный ИК и ультрафиолетовый УФ. По своим физическим свойством свет принципиально неотличим от электромагнитного излучения других диапазонов – различные участки спектра отличаются друг от друга только длиной волны λ и частотой ν. Рис. 6.6.2. дает представление о шкале электромагнитных волн.

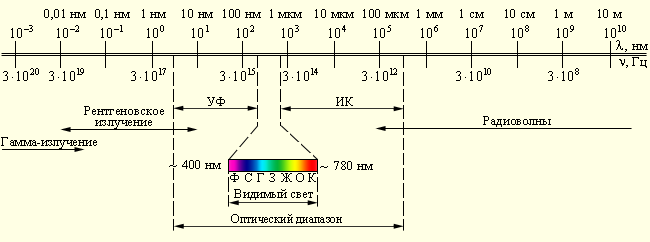Рисунок 6.6.2.

Шкала электромагнитных волн. Границы между различными диапазонами условны.

Для измерения длин волн в оптическом диапазоне используются единицы длины 1 нанометр (нм) и 1 микрометр (мкм):

1 нм = 10^–⁹ м = 10^–⁷ см = 10^–³ мкм.

Видимый свет занимает диапазон приблизительно от 400 нм до 780 нм или от 0,40 мкм до 0,78 мкм.

Электромагнитная теория света позволила объяснить многие оптические явления, такие как интерференция, дифракция, поляризация и т. д. Однако, эта теория не завершила понимание природы света. Уже в начале XX века выяснилось, что эта теория недостаточна для истолкования явлений атомного масштаба, возникающих при взаимодействии света с веществом. Для объяснения таких явлений, как излучение черного тела, фотоэффект, эффект Комптона и др. потребовалось введение квантовых представлений (см. гл. VIII). Наука вновь вернулась к идее корпускул – световых квантов. Тот факт, что свет в одних опытах обнаруживает волновые свойства, а в других – корпускулярные, означает, что свет имеет сложную двойственную природу, которую принято характеризовать термином корпускулярно

Blog

Молекулярная физика и термодинамика. Лекция №1 Молекулярно-кинетическая теория Основные положения мкт

Содержание