Социально-экономических и политических процессов
| Вид материала | Документы |
- Программа и организация исследований в исследовании социально-экономических и политических, 124.03kb.
- «Исследование социально-экономических и политических процессов», 46.76kb.
- Программа дисциплины «Исследование социально-экономических и политических процессов», 221.09kb.
- Рабочая программа дисциплины (модуля) «исследование социально-экономических и политических, 448.53kb.
- Экзаменационные вопросы по курсу «Исследование социально-экономических и политических, 21.31kb.
- Программа учебной дисциплины «Исследование социально-экономических и политических процессов», 280.21kb.
- Учебно методический комплекс по дисциплине «Исследование социально-экономических, 600.67kb.
- Понятие социально-экономических и политических процессов, их виды и типы. (Анисимова), 2489.59kb.
- Кафедра государственного и муниципального управления, 138.72kb.
- «Исследование социально-экономических и политических институтов и процессов», 52.77kb.
Подставляя полученные значения в формулу коэффициента корреляции, получаем:
Л = -1 = и, О.
1,3
,(193 )х(179,7-0,144)
V 10
Проиллюстрировать полученный результат можно по шкале Чед-дока (табл. 2.14).
Таблица 2.14 Шкала Чеддока
| Показатели тесноты связи | Характеристика силы связи |
| 0,1-0,3 | слабая |
| 0,3-0,5 | умеренная |
| 0,5-0,7 | заметная |
| 0,7-0,9 | высокая |
| 0,9-0,99 | весьма высокая |
По мере приближения значения коэффициента к единице корреляционная связь практически трансформируется в причинную.
Полученный выше результат свидетельствует в пользу достаточно высокого значения коэффициента корреляции между показателями, что подчеркивает высокую степень их внутренней взаимозависимости.
Корреляционный анализ может использоваться для измерения связи между различными показателями исследуемых процессов, что обеспечивает возможность контролировать и направлять эти процессы. Наличие корреляционной связи между показателями позволяет через воздействие на один показатель оказывать влияние на другой показатель, выстраивая порядок управления процессом.
Широкую популярность в процессе использования корреляционного анализа получила формула коэффициента ассоциации известного британского ученого Дж. Юла (1871-1951).
Проиллюстрировать применение коэффициента ассоциации для решения конкретной проблемы позволит формулировка следующей задачи.
Для оценки влияния факторов на производительность труда в организации было проведено исследование, в ходе которого рассматривалась связь между фактором удовлетворенности трудом, изученного в результате социологических исследований и производительностью труда, дифференцированной исследователями на два уровня. В ходе опроса 100 человек были получены следующие результаты (табл. 2.15).
Таблица 2.15
Связь между производительностью труда и удовлетворенностью трудом в организации (вариант)
| Производительность труда | Удовлетворенность (Y1) либо | N(Xi) | |
| (X) | неудовлетворенность | | |
| | профессией (Y2) | | |
| Высокая | 20 | 0 | 20 |
| | (N11) | (N12) | |
| Низкая | 30 | 50 | 80 |
| | (N21) | (N22) | |
| N(Yi) | 50 | 50 | 100 |
Числа, приведенные в таблице, выражают количество человек, относящихся к одной из четырех групп образованной матрицы.
Корреляционную зависимость между полученными в результате исследования показателями, выраженную в значении коэффициента ассоциации, можно вычислить по формуле:
(ΝηχΝ22+ΝηχΝ2ΙΥ
Подставляем числовые значения в формулу:
(20x50-0x30)
2 = 7 ( = 1-
(20x50 + 0x30)
Значение коэффициента указывает на глубокую корреляционную связь между производительностью труда и удовлетворенностью профессией, однако зависимость здесь является односторонней (производительность влияет на удовлетворенность, но влияет ли удовлетворенность на производительность?).
Из табл. 2.14. хорошо видно, что если один из показателей таблице отсутствует, то величина коэффициента ассоциации всегда будет равна единице, что дает преувеличенную оценку степени связи между исследуемыми показателями. Поэтому, чтобы сделать анализ более точным и учесть двухстороннюю связь между показателями используется коэффициент контингенции К. Пирсона:
Φ = (л/м хЛ/22 -Νη χ Ν η}/ (х\)х N (xl)x N (у\)х N (yl).
Коэффициент контингенции измеряется в диапазоне от +1 до -1, но всегда меньше коэффициента ассоциации.
Φ = (20x50-θ)/V20x80x50x50 = 1000/2000 = 1/2.
Если Φ меньше или равно 0,5, то существует двухсторонняя связь. В данном случае удовлетворенность труда также оказывает влияние на производительность труда.
Для оценки значимости коэффициента корреляции применяется (ί) критерий Стьюдента, вычисляемый по формуле:
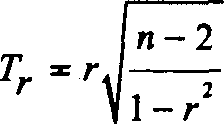
Полученная в процессе этих расчетов величина сравнивается с критическим (tt), которая берется из специальной таблицы значений с учетом заданного уровня значимости и числа степеней свободы.
Другим критерием, подтверждающим гипотезу о случайном или неслучайном распределении частот исследуемого признака, является, X2 — хи-квадрат. Для проверки такой гипотезы сравниваются эмпирические (наблюдаемые) и теоретические частоты. Численное значение X2 определяется по формуле:
χ2 _ Σ (/-/')
/'
где / — эмпирические частоты, a f — теоретические частоты.
Теоретическое значение определяется с учетом числа степеней свободы, определяемого по формуле: К = η - г - 1, где η - число групп, г — число параметров и степени вероятности. В случае фактического значения X2 ниже табличного (в соответствии с таблицей критических значений критерия К. Пирсона) в основе распределения частоты исследуемого признака лежит закон нормального распределения.
Таким образом, с помощью данного критерия можно установить статистически значимую взаимосвязь между переменными, составляющими параметры исследуемого объекта.
Использование корреляционного анализа будет неполным, если в расчет не берется значение среднего арифметического распределения, позволяющего сглаживать случайные и неслучайные колебания в динамике исследуемых рядов данных.
Среднее арифметическое распределение
Среднее арифметическое распределение, обозначаемое X, вычисляется по следующей формуле:
N
- Άχί
Ν
где Χ. — значение каждого отдельного случая; N — количество случаев;
N
- ·? Xi
χ = ί=ί — знак суммы значений всех отдельных случаев от 1 до N.
N
Среднее арифметическое исчисляется в тех случаях, когда необходимо определить объем усредняемого признака, выявленный путем обобщения суммы значений всех единиц исследуемой совокупности. К примеру, вычисленная таким образом средняя заработная плата в регионе позволяет сравнивать с этой величиной заработную плату различных социальных и профессиональных групп, определять оптимальную величину бюджетных дотаций и надбавок для выравнивания уровня жизни населения региона.
Так, распределяя в ходе вычисления среднего арифметического между отдельными элементами общую величину признака, исследователь выстраивает медиану. Медианой называется значение признака у той единицы совокупности, которая расположена в середине ряда частотного распределения. Для вычисления медианы необходимо в первую очередь проранжировать индивидуальные значения признаков, расположить соответствующие этому ряду частоты и найти их срединный интервал. Так, к примеру, вычисляется средняя численность населения ведущих городов региона (табл. 2.16).
Таблица 2.16
Разделение городов по численности населения
| № п/п | Город | Численность |
| 1 | А | 1 ООО ООО |
| 2 | Б | 400 ООО |
| 3 | В | 250 000 |
| 4 | Г | 120 000 |
| 5 | Д | 50 000 |
| 6 | Ε | 30 000 |
Срединные ранги в ряду представленных данных составляют 3-4 строку, и поэтому медиана равна
250 000 + 120 000
= 185 000.
2
Таким образом, медиана для данной выборки свидетельствует о том, что три города в регионе располагают численностью выше данного значения, а три города не дотягивают до этого значения. Если объем значений делит исследуемую совокупность на четыре,части, то величина каждой из них именуется квартилями, на десять — децилями, на сто — процентилями.
Однако использование среднеарифметического при определении характера рядов распределений может быть некорректным, если разброс значений в исследуемой совокупности является очень большим. Зафиксировать такой разброс помогут два важнейших статистических показателя: показатель дисперсии и коэффициент вариации.
Показатель дисперсии
Дисперсию можно вычислить по формуле:
σ = .
η
Корень квадратный из дисперсии σ2 представляет собой среднее квадратическое отклонение.
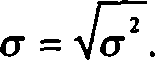
Показатель дисперсии, иногда называемый средним квадратом отклонений, призван определить степень размытости распределенного признака относительно среднего арифметического. Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает собой всю исследуемую совокупность. Если величина квад-ратического отклонения высока, то использование среднеарифметического значения показателя переменной для характеристики всей совокупности недопустимо.
Коэффициент вариации
Коэффициент вариации отображает отношение среднего квадрати-ческого отклонения к среднему арифметическому и вычисляется по формуле:
2
υ = — χ 100%. X
Коэффициент вариации (X) является наиболее распространенным показателем колеблемости, вариативности признаков, используемым для оценки типичности средних величин. Статистиками доказано, что если коэффициент вариации больше 40 %, то это говорит о значительной степени вариативности признака в исследуемой совокупности, свидетельствующей о широком разбросе признака.
Значение коэффициента вариации особенно наглядно выявляется при характеристике региональной асимметрии. К примеру, по объемам ВРП размах вариации из 88 регионов (кроме Чечни) в 1999 г. составил 29,4 раза (на краях ряда Ханты-Мансийский автономный округ и Республика Дагестан), коэффициент вариации — 91,3%. В Европе аналогичное соотношение между регионами Европейского союза составляет 4,6 раза, а между всеми европейскими странами — около 13 раз.
Разновидностью корреляционного анализа является корреляционно-регрессионный метод. Одной из распространенных аналитических задач, решаемых с применением корреляционно-регрессивного метода, является задача на запуск-выпуск.
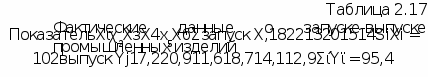
Допустим, что имеются фактические данные о запуске и выпуске промышленных изделий (тыс. шт) (табл. 2.17).
Требуется определить зависимость выпуска изделий (в среднем) от их запуска, составив соответствующее уравнение регрессии. Значения X и У определяются по формулам:
X - SX - η; Υ = S.Y, - η; η - 6,1 = 1.....6;
Χ - 102 - 6 - 17; Υ - 95,4 - 6 - 15,9.
Дальнейшим вычислениям придается табличная форма, что повышает их наглядность (табл. 2.18).
Таблица 2.18
Представление вычислений в табличной форме
| (Х,-Х) | (Xi-X)2 | (Υ.-Υ) | (Υ.-Υ)2 | (Χ,-Χ) (Υ.-Υ) |
| 1 | 1 | 1,3 | 1,69 | 1,3 |
| 5 | 25 | 5 | 25 | 25 |
| -4 | 16 | -4,3 | 18,49 | 17,2 |
| 3 | 9 | 2,8 | 7,84 | 8,4 |
| -2 | 4 | -1,8 | 3,24 | 3,6 |
| -3 | 9 | -3 | 9 | 9 |
SX, - Χ)2 - 64 SYj - Υ)2 = 65,26 S.{X.- X)(Y.t - Υ) = 64,5.
Теснота связи между показателями запуска и выпуска измеряется коэффициентом корреляции, который исчисляется по формуле:
η = d2xy + dxdy. Подставляя соответствующие значения, получим:
δχ = /liix" - Хер)2 + η = V64 + 6 = 3,27;
dy - VSY, - Υ)2 + η - V65.26 + 6 ■= 3,30; d2xv = S(X - X)(Yi - Y) - 64,5 + 6 - 10,75; η - 10,75 + (3,27 χ 3,30) - 10,75 + 10,79 « 0,996.
Считая формулу линейной (Υ - а0 + а,Х), определим зависимость выпуска промышленных изделий от их запуска. Для этого решается система нормальных уравнений:
na0 + ajSjXj - S,Y.;
a + a.S-SXY,
Величины SXj2 и SXjYj представлены в табл. 2.20.

Подставляя найденное выражение а0 во второе уравнение, находим значение а,:
102(15,9 - 17а,) + 1798а, - 1686,3; 1621,8- 1734а, + 1798а, - 1686,3; 64а,- 1686,3- 1621,8; 64а,-64,5; а,-1,01; а0- 15,9-(17 χ 1,01); а0- 15,9-17,17; а,--1,27.
Итак, уравнение регрессии в окончательном виде имеет следующий вид:
Υ - - 1,27 + 1.01Х.
Проверка:
Υ - - 1,27+1,01 χ 17 - - 1,27 + 17,17; Υ - 15,9.
Ранговая корреляция
Ранговая корреляция вычисляется на основе формулы, созданной Ч. Спирменом для определения тесноты связи как между количественными, так и между качественными признаками исследуемого процесса при условии, что значения этих признаков будут проранжи-рованы или упорядочены по степени убывания или возрастания признака. Коэффициент ранговой корреляции вычисляется по формуле:
6Σά2
k-ι ,
(п3-п)
где d — разность рангов; η — общее число рангов; Σά2 — сумма квадратов в разности рангов.
Главной задачей ранговой корреляции является определение того, насколько исследуемые объекты, сравниваемые процессы идентичны по их признакам, и насколько эта идентичность (или неидентичность) является значимой, чтобы принимать ее во внимание при их оценке.
Примером, подтверждающим применение ранговой корреляции, может служить сравнение приоритетов потребительского выбора между различными категориями потребителей, заключающееся в совпадении их потребительских ориентации в отношении того или иного товара или внедренной новации.
С помощью вычисления коэффициента ранговой корреляции возможно решение таких задач, как:
- выявление факторов производства и их влияния на производственные показатели;
- определение приоритетов разработке стратегии предприятий;
- разработка эффективной торговой политики предприятий;
- измерение общественного мнения на основе общности ориентации различных социальных групп и пр.
Механизм реализации метода ранговой корреляции предполагает ряд этапов.
- Выделение не менее двух рядов последовательностей, характеризующих динамические характеристики объекта исследования.
- Определение места каждому показателю в структуре динамического ряда и распределение полученных результатов по рангам. Полное совпадение мест показателей в динамических рядах означает положительную корреляцию, тогда как обратный порядок, соответственно, свидетельствует об отрицательной корреляции.
- Вычисление фактического коэффициента ранговой корреляции, располагающегося в диапазоне от -1 до +1.
Проиллюстрировать процедуру исчисления ранговой корреляции можно на конкретном примере.
Опрашиваются две группы экспертов, потребителей в разных частях города с целью получения информации об источниках сведений о потребительских качествах товара. Ответы распределяются следующим образом (табл. 2.21).

Данные обследования заносятся в формулу: К=1- (6 χ (1 + 1+ 0+1+9+1 + 1)/(343-7)=- 1 -84/336-0,75.
Полученный результат свидетельствует о достаточно высокой степени корреляции между приведенными в таблице рядами данных. Это подтверждает версию, что между двумя торговыми точками значительной разницы в оценке потребителями приоритетов в получении информации не наблюдается. И поэтому предприятие в своей маркетинговой политике может и не принимать во внимание факт пространственной отдаленности между своими торговыми представительствами.
Использование метода ранговой корреляции также эффективно при наличии нормативной структуры показателей, отображающей условия потенциального экономического роста фирмы в сложившихся условиях.
К примеру, если в основу развития предприятия положен принцип экономического роста, в соответствии с которым снижение затрат живого труда должно осуществляться более опережающими темпами по сравнению с темпами затрат труда овеществленного, то нормативный ряд показателей развития предприятия будет выглядеть следующим образом:
Тзп < Тсс < Тмз < Ттп < Тнчп < Тр < Тп, где Τ — показатель темпов роста, π — прибыль, нчп — нормативно-чистая продукция, тп — стоимость товарной продукции, мз —материальные затраты, ρ — расчетный показатель, измеряемый как π + мз, сс — полная себестоимость товарной продукции, зп — трудовые затраты, выраженные в показателе заработной платы.
В нормативном ряду должны быть как ограничивающие показатели, имеющие в данном случае минимальные темпы роста, так и результативные, закладывающие приоритетные цели развития предприятия. Оценивая соответствие между нормативной и фактической структурами показателей, можно сделать вывод о результативности стратегической политики предприятия и о необходимости проведения корректирующих мер.
Алгоритм использования метода ранговой корреляции для оценки стратегической политики предприятия относительно темпов его развития будет включать в себя следующие этапы.
- Выявление динамики ключевых показателей роста, определяющих стратегическую политику предприятия за определенный период и выстроенных в направлении от ограничивающих показателей к результативным.
- Представленная таблица преобразуется в таблицу темпов выделенных показателей, измеренных в процентах на стадиях ежегодного изменения. На основании данных составленной таблицы формируются динамические ряды фактических показателей.
- На основании соответствия фактического динамического ряда нормативному производим расчет коэффициента ранговой корреляции по каждому фактическому динамическому ряду.
- По имеющимся данным коэффициента ранговой корреляции выявляем зависимости изменения данного коэффициента во времени, объясняя волнообразный характер этих изменений.
Индексный метод
Целью индексного метода является определение сущностных показателей, необходимых для характеристики процессов, развертываемых в пространстве и времени. С помощью индексов выявляются индикаторы оценки происходящих в управляемых системах изменений, концентрируется информация о наиболее существенных процессах.
Основой индексного метода является перевод натурально-вещественной формы выражения процесса в форму индикатора.
Статистическим индексом является относительная величина сравнения сложных совокупностей и отдельных их единиц. При этом сложной понимается такая статистическая совокупность, отдельные элементы которой непосредственно не подлежат суммированию.
Индексный метод выполняет как аналитическую, так и синтетическую функцию. Аналитическая функция индексного метода заключается в способности определять влияние факторов на изменение изучаемого показателя, синтетическая — в объединении (агрегировании) разнородных единиц статистической совокупности. Например, индекс цитируемости, используемый для оценки квалификации ученого-исследователя, выполняет скорее синтетическую функцию, определяя совокупность множества признаков (количество научных трудов, ученая степень, занимаемая должность и пр.) при помощи отдельного показателя, тогда как индекс цен имеет скорее аналитическую природу, будучи ориентирован на оценку экономических изменений в обществе, их вектора.
В зависимости от степени охвата подвергнутых обобщению единиц изучаемой совокупности выделяются индивидуальные и общие индексы.
Индивидуальные индексы характеризуют изменения отдельных единиц статистической совокупности, а общие — сводных.
К примеру, показатель изменения объема реализации товарной массы продуктов питания за определенный период является общим индексом физического объема товарооборота. Тогда как изменения в продаже-отдельных групп товаров фиксируются индивидуальным индексом.
Индивидуальные индексы определяются по формуле:
