Geum.ru

К. А. Свасьян становление европейской науки

Вид материалаДокументы

Содержание


B. Russell
Лейбниц и Гёте
Подобный материал:
1   ...   40   41   42   43   44   45   46   47   ...   54
джиннами» и совершенно беспомощен вновь закупоривать их 402. Между тем дело принимало уже необратимый характер; странно наблюдать этот двоящийся образ математики на самом пороге Нового времени, где, скажем, испытанный платоник Кеплер способен уже, с другой стороны, и на такое признание: подобно тому как уши созданы для звуков, а глаза для цвета, так и ум создан для «количеств», без которых участь его блуждать во мраке;403 потрясающая



401 Henri Corneille-Agrippa, La Philosophie occulte ou la Magie, t. 1, Paris, 1910, p. 213.

402 Это еще раз ex post facto откупоренных уже бутылок подчеркнет Новалис: «Подлинная математика – непосредственная стихия мага». Novalis, Fragmente, op. cit., S. 146.

403 См. H. Butterfield, The Origins of Modern Science. 1300-1800, op. cit., p. 78.

371

математическая «Джоконда», в ускользающей улыбке которой «жизнь Богов» транспарирует уже оскалом сатанических наваждений; когда улыбка полностью сойдет с лица, начнется история второй математики в образе и подобии «математического аппарата», отшелушится Кеплер и явится Декарт.

Декарт – первый грандиозный обморок математики и ее начисто отшибленная память; математика в нем уже с такой силой врастает в физику, что о различении обеих не может быть и речи. Галилеевский афоризм о книге природы подтвержден здесь окончательно, но окончательность эта ограничена только кантовской экспликацией; в лозунге Декарта: «apud me omnia fiunt mathematice in natura» нет и следа намека на «авторство», которое зарезервировано отныне на «трудные случаи». Самый решительный шаг: если понимать математику как учение о числах (а так именно и понималась она в первой своей истории), то платоновский запрет на природу останется в силе; небывалость математического гения Декарта сказалась прежде всего в методическом третировании чисел; ни у одного математика неприязнь к числу как таковому не проявлялась столь явным образом, как у создателя аналитической геометрии. Заниматься числовой символикой для него равносильно бестолочи («s’occuper de bagatelles»); Мерсенну от открыто признается в полном невежестве во всем, что касается чисел,404 ибо, как ему кажется, нет ничего более пустого (rien de plus vide). Еще раз возвращаясь к афоризму Галилея: в картезианской редакции он выглядел уже совершенно иначе; опустошение числа равнялось здесь отчуждению числа от собственной сущности и извечной содержательности; что мешало Декарту, а вместе с ним и всему будущему естествознанию, так это именно содержание числа, стало быть, качество его и полнота, в



404 «Pour ce qui est de nombres, je n’ai jamais prétendu d’y rien savoir». Oeuvres complètes, t. 7, p. 50.

372

итоге: онтология и космогенез. Число в платоновско-пифагорейском опыте оттого и было «всем», что шифровало, или цифровало, в себе сокровенный смысл «всего»; у Декарта оно уже не есть «всё», а может стать «всем», ибо, очищенное до пустоты, теперь оно оказывается голым инструментом, приложимым к чему угодно волею «правил для эксплуатации». Иначе: лишь теряя самособственную содержательность, математика лишилась онтологического первородства и отождествлялась с навыками выхолощенной технологии; формализация математики, всегда равной форме, но никогда прежде не мыслящей эту форму формально, выступала прямым следствием дезонтологизации; содержание и смысл книги природы, теперь она становилась лишь ее грамматикой, или системой формальных принципов, пустых в себе, но всецело уже зависящих от только чувственных содержаний. Характерна сама эта рокировка векторов направленности: математика вверх, оттого и «падающая вверх», что полная сверхчувственных энергий, и математика вниз, пустая ладонь, нищенски протянутая к ощущениям. Чтобы понять, что же все-таки случилось, достаточно провести простейший мысленный эксперимент; возьмите какое-нибудь число, скажем, «5» и спросите себя, что вы под ним понимаете? Ответ придет моментально: пять единиц, т. е. 1 + 1 + 1 + 1 + 1; говоря психологически, число «5» как результат пяти актов внимания 405. Уже обходя молчанием то, какая комедия ожидала бы нас в случае чисел побольше, скажем, «единицы» с тремя, а то и шестью «нулями», заметим: эта операция не выдерживает и малейшего логического нажима; ведь прибавляя друг к другу именно пять единиц, мы заведомо предпосылаем сложению число «5» как таковое, которое в качестве «целого» предшествует своему



405 Эта убийственная характеристика принадлежит Расселу. См. B. Russell, The Principles of Mathematics, 1, Cambridge, 1903, p. 114.

373

суммативному эрзатцу 406. Тщетно; автоматизм привычки беспардонно пренебрегает любой логикой, и среди четырех правил арифметики первое место всё еще остается за сложением; говоря по существу, число как бы отдано на откуп сложению, которое не только открывает его, но и определяет прочие процедуры счета: вычитание как голая инверсия сложения, умножение как последовательное сложение равных слагаемых и деление как инверсия умножения, т. е. как последовательное вычитание равных вычитаемых 407. Этой математике чистых «количеств», пережившей невиданный триумф с наступлением Нового времени, противопоставлена иная математика, ставшая духовным изгоем в условиях торжествующего механицизма: математика «качеств», отталкивающаяся не от сложения, а от деления, где «два» предстает не как внешнее повторение «одного», но как внутренний результат его саморасщепления. Рудольф Штейнер, характеризуя этот процесс как органическое расчленение единства, подчеркивает тем самым изначальную «актуальную бесконечность» числа, так что канторовская революция в математике, вспыхнувшая в самом конце XIX века, была на деле лишь реставрацией ее первородства; мы воспользуемся прекрасной схемой Эрнста Бинделя, наглядно демонстрирующей противоположность обоих подходов к числу 408.



406 С неопровержимой ясностью подчеркнуто это у Кантора: «Сложение единиц никогда не может служить для определения числа, так как здесь указание главного факта, а именно как часто должны складываться единицы, не может быть получено без самого определяемого числа. Это доказывает, что число, получаемое единым актом абстракции, должно задаваться как органическое единство единиц». Г. Кантор, К учению о трансфинитном. «Труды по теории множеств», М., 1985, с. 271.

407 E. Bindel, Die geistigen Grundlagen der Zahlen, Frankfurt/Main, 1983, S. 23.

408 E. Bindel, op. cit., S. 24.

374



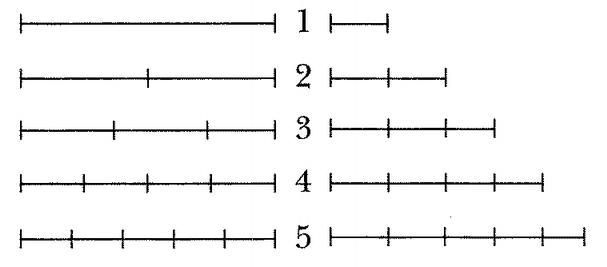
Первофеномен правого столбца – машина, левого – организм; живое вынуждает нас к надлежащему пользованию числами; мы переходим от одной клетки к двум и больше, не прибавляя к ней новые, а деля ее до бесконечности, которая выражается не символом бреда n+1, а самым определенным образом: 1:n. Необыкновенно важно отметить при этом, что если правая – механическая – модель числа отрицает левую (органическую), то левая включает ее в себя как относительно правомерное и вспомогательное средство анализа; с отчуждением числа от человека, выпадением его из круга живых представлений и сплошной инструментализацией, не могло уже быть и речи об органической качественной математике;409 Рудольф Штейнер в острейших формулировках диагностирует провал: «Бесполезно размышлять о понятиях, которые требуют, чтобы их переживали… Математическое жонглерство начинается у Ньютона с того момента, когда он пользуется этими понятиями для объяснения мира; он буквально жонглирует ими… В ньютоновской физике мы впервые соприкасаемся с представлениями о природе, полностью оторванными от человека… Современная



409 А вместе с нею и биологии sensu stricte. Кантор: «Ведь наряду или вместо механического объяснения природы... не появилось – даже в начатках – органическое объяснение природы, выходящее из рамок механицизма и вооруженное такой же математической строгостью». Г. Кантор, Основы общего учения о многообразиях. Математически-философский опыт учения о бесконечном. «Труды по теории множеств», ук. соч., с. 75.

375

наука, стремясь подчинить себе природные явления с помощью математики, изолированной от человека и внутренне уже не переживаемой, способна в своем обособленном математическом созерцании и со своими оторванными от человека понятиями рассматривать только мертвое; с отторжением математики от живого ее можно применять лишь к мертвому» 410. Отныне история математики ближайших трех столетий, а вместе с нею и история естествознания, обретшего, наконец, в ней единственного поводыря, помечена тональностью и темповыми отметками «восходящего нигилизма»; этот жуткий призрак, провиденный Ницше в конце прошлого века и на два века вперед,411 начинал свой ход двумя веками раньше; когда о нем вскричат дозорные европейской культуры – Шуман в жалящих диссонансах «Крейслерианы» и уже во всю грудь ужаленный ими Ницше, – опухоль уже разойдется гигантскими метастазами, выедая всё вокруг, так что очаг будет и вовсе не заметен; современники и потомки будут уже фиксировать чудовищные аберрации духовности, всё еще поклоняясь идолу математизированной научности, на прогрессивном челе которой не окажется и малейшего следа самоответственности за происходящее. Как будто прокладкой железных дорог или изобретением беспроволочного телеграфа можно будет смыть с себя вину за Бодлера и «юношей» с горящими глазами, которым за невозможностью стать «Вертерами» и «Муциями Сцеволами» в мире, отнятом у духа и отданном круговороту мертвых частиц, останется изживать свою «невыразимость» в метании бомб и «шигалевщине»! Как будто в хозяйственных успехах нумерически-количественного мышления (валовой продукт)



410 R. Steiner, Der Entstehungsmoment der Naturwissenschaft in der Weltgeschichte und ihre seitherige Entwickelung, Dornach, 1977, S. 61, 66.

411 «То, что я рассказываю, есть история ближайших двух столетий». F. Nietzsche, Der Wille zur Macht, Stuttgart, 1952, S. 3.

376

удастся скрыть проекцию этого мышления на мир людей, преобразованных в занумерованное поголовье «человеческого фактора»! Начиналось, конечно, не так, не с таким «расчетом»; в повестке дня стояло, конечно же, «познание» и «в интересах познания»; будущие хозяева планеты, доведенной до грани самоубийства, были еще полны взрывного восторга поиска и готовности душу положить за «вертится или не вертится»; нарождался тип «мученика науки»,412 но более реальным представал уже «комплекс полноценности и превосходства»: apud me omnia fiunt mathematice in natura. Коронация новой математики – факт первых десятилетий XVII века; поразительнее всего то, что лозунги продолжали оставаться традиционными – «математика может всё», – менялось лишь внутреннее их содержание. Группа одиноких «гениев», рассеянных по европейским городам, но уже и сводимых жанром «научной корреспонденции» (патент Мерсенна!) или явками «салонов», навязывала миру новый стиль; история европейской науки с момента рождения и до наших дней есть история собственно науки и плетущейся за нею, а позднее чаще всего и обгоняющей ее гигантской тени; таков генезис «личности» самого ученого и клубящихся вокруг нее миазмов «научного мнения»; наука в ритмах индивидуальной мысли и наука как «мода» и «непогрешимость»: «Декарт доказал», «Галилей доказал», «Ньютон доказал», а потом и вовсе: «наука доказала» – какая? та, что всё еще как биография, или та, что уже как сеанс массового гипноза! Математика может всё; посмотрите, какой плоской самопародией оборачивается эта мистериальная истина в потугах рефлексии Гоббса («Левиафан», ч. 1, гл. V): правильно мыслить значит считать понятия путем их



412 Бонавентура высмеял его до его появления, в XIII веке, Макс Шелер после его появления, в ХХ веке. См. Bonaventura, Itinerarium mentis in Deum, III, 2; см. также: E. Gilson, La philosophie de St. Bonaventure, Paris, 1924, p. 91-93. M. Scheler, Wesen und Formen der Sympathie. Gesammelte Werke, Bd. 7, Bern, 1973, S. 115.

377

сложения и вычитания, ergo, математика – основа всех наук. В самом скором времени математизируют уже все; быть ученым, быть умным человеком, быть просто gentleman, значит заложить ум, честь и совесть математическому счетчику: физика, биология, философия, музыка, театр, этика, политика, досуг, «хорошие книги» и «хороший тон» уже перестраиваются à l’esprit géométrique. Спиноза исчисляет аффекты more geometrico; Роберт Уолпол утверждает, что в Британской Палате Общин можно большего добиться с помощью арифметики, нежели риторики; Уильям Петти создает «политическую арифметику», перенося метод сложения единиц на «душу населения» и провоцируя демографическим взрывом чисел в дурной математической бесконечности будущие прогрессии «рождаемости» и «голодных ртов» мальтузианства; Гаррингтон переносит в экономику механическое понятие «баланса», преображающееся здесь в «баланс собственности»; вообще «балансом» бредят все: от Томаса Овербери, строящего на нем идею европейского «целого», до Кромвеля, отталкивающегося от него в проектах создания конституции. Это математическое crescendo нарастает в разгоне одного-полутора веков до уже невыносимого fortissimo: математикой закупорены все поры жизни – в ее ведомстве давно уже: кровь, уши, глаза; «выходя из академий, – жалуется Вико, – молодые люди обнаруживают мир полностью геометрическим и полностью алгебраическим»;413 одному голландскому математику вздумалось даже физиогномически вычислить черты какого-то лица с помощью алгебраических формул. Наконец вмешались «дамы»: теперь их благосклонность переключалась с «поэтов» на «математиков»; этикет княжеских дворов предусматривал даже штат «придворного математика» 414. Менялся – в мозгах и составах – самый



413 Vico, Textes choisis, op. cit., p. 170.

414 Сюда: G. N. Clark, The Seventeenth Century, op. cit., p. 212-13. R. Friedental, Goethe. Sein Leben und seine Zeit, Bd. 2, München, 1968, S. 538.

378

генотип человека; паскалевский бред преследования – «меня, того гляди, примут самого за теорему» – неожиданно становился нормой совершенства; характерно, что Вольтер, желая воздать хвалу ньютонианцу Кларку (оппоненту Лейбница), не находит иного комплимента, как «настоящая рассуждающая машина» (une vraie machine à raisonnement). Вообще феномен «машины» приобретал нуминозно-архетипическое значение; эпоха, услаждающая свои досужие вкусы безделушками античной мифологии, в каком-то исступленном напряжении творила новую секретную мифологию, больше, религию «машины», и сенсационное сочинение Ламетри оказывалось не только «мифом XVIII столетия», но и порождающей моделью новой человеческой породы: «человекомашин»; несравненную комфортабельность этой антропологии засвидетельствует не кто иной, как Наполеон 415. Характерно: мы ничего не поймем в Ньютоне, если не перестанем «понимать» его только «в научном смысле»; современники Ньютона проявили в этом отношении гораздо бо́льшую смекалку; для них он был новым Моисеем и Воплощением самой Истины, отнюдь не только «научной», но как раз «самой». Говорить о Ньютоне в свете симптоматологии, значит исходить именно из этой «доксы»; Ньютон-творец математической физики оказывается частным случаем Ньютона-жизнетворца; речь идет о едином стиле жизни,



415 В передаче Лас-Каза: «Les divers objets et les diverses affaires se trouvaient casés dans sa tête comme ils eussent pu l’être dans un armoire. „Quand je veux interrompre une affaire, disait-il, je ferme son tiroir, et j’ouvre celui d’un autre... Veux-je dormir, je ferme tous les tiroirs et me voilà au sommeil“...» («Различные предметы и дела размещены в его голове, как они могли бы быть расположены в шкапе: „Когда я хочу покончить с каким-то делом, – говорил он, – я закрываю его ящик и открываю другой... Если я хочу заснуть, я закрываю все ящики и моментально засыпаю“…»). Las Cases, Le Mémorial de Sainte Hélène, Paris, 1935, t. 2, p. 329. В будущем бреде Дали оригинальности хватало лишь на то, чтобы заменить Наполеона Венерой.

379

метастаз которой не избежал в той или иной мере ни один жизненный срез; историк мысли не ошибется, фиксируя здесь некое гравитационное поле социокультурных и психологических характеристик эпохи. Остановить эту «махину», перемалывающую всё встречное, было уже невозможно; нужно было бежать от нее в отбрасываемые ею тени «природы» à la Руссо, мутной мистики ощущений, слащавых приторностей «иррационализма»; иррационализм – повторим это – был не противостоянием рационализму, а желаемым эффектом чисто рационалистического оболванивания, рационализмом наизнанку, неким вывернутым нутром картезианского функционера, дополняющего «Рассуждение о методе» приступами сартровской «Тошноты», – именно: блевотиной рационализма, которой усилиями философских компиляторов довелось прослыть «оппозицией». Мошенничество набирало темп; тщась во что бы то ни стало переиграть «понимание», рационализм провоцировал фокус самоотвращения, играя на пару с иррационализмом и дурача сознание: здесь – идеей «прогресса», там – мистическими «невыразимостями», здесь – «кнутом» познания, там – «пряником» морали. Все они как-то и по-своему компенсировали нанесенный ими ущерб; обворованный в познании «чистый разум» одерживал моральные победы в «разуме практическом»; звучало возвышенно: «верь в то, чего не можешь познать» – Абеляр из XII века задохнулся бы в такой атмосфере.

Он и в самом деле задыхался; этого не следует упускать из виду, если мы хотим понять земную миссию таких людей, как Лейбниц и Гёте. Лейбниц – величайший «энигм» мысли Нового времени – младший современник и поклонник Паскаля: поклонник во всем, кроме безумия и надрыва; поразительна в нем эта мимикрия, обеспечившая ему, до мозга костей «не-нашему», столь знатное место на почетной доске передовиков рационализма. Представьте себе здорового душой и телом Паскаля, Паскаля, изобретающего-таки счисление бесконечно-малых, но отнюдь не в ущерб «вечному молчанию»,

380

Паскаля, наконец, соответствующего собственному идеалу: «его невозможно угадать». Угадать Паскаля не представляло сложности; позднее дитя иррелигиозной эпохи, изживающее богобоязненные реминисценции прошлой жизни, он искал мученичества; его отказ от математики не в последнюю очередь вызревал из рокота обманутых надежд: хотел быть мучеником, стал математиком; математика сулила что угодно, кроме мученичества. Есть что-то романтически-галльское, в глубоком срезе обиженно-детское в этом честнейшем из людей, поломавшем в себе «Божьей милостью» математика и отдавшем себя на милость… «психиатров»; случай Лейбница диаметрально иной, но что роднит его с Паскалем – при всей угаданности того и неразгаданности этого, – так это (я заранее предупреждаю внезапность парадокса) отказ от математики, причем в масштабах, по сравнению с которыми паскалевский отказ выглядит всё еще просто личной драмой. Он преодолевал ее активнейшим приятьем; ничто не характеризует гений Лейбница лучше, чем эта открытость всему, в первую очередь, рационалистической эпистеме, но нет и более ложного способа, чем толковать ее в примиренческой тональности; формула Лейбница исчерпана изумительной строкой гётевского «Эпименида»: «Nachgiebigkeit bei grossem Willen», да, «податливость при большой воле»; в этой формуле – прямой намек на тайну его духовной сословности: он – манихей математики в точке, где она обернулась злом, и значит, не отказник во внешнем смысле слова, не романтический драчун с перчаткой вызова, ни тем более староколенный «ностальгик» по утраченному времени, а квалифицированный адепт зла, борющийся с ним путем вбирания его в себя и трансформации его в добро силами индивидуального гнозиса. Рационалистическая математика, обреченная на жесточайший саботаж в Паскале, празднует в Лейбнице неслыханный триумф; он не просто вбирал ее в себя, а сотворял ее в размерах, рассчитанных на грузоподъемность более чем

381

двухсотлетнего будущего, – неисправимейший платоник, рыцарь до гроба прежней, той, исчезающей математики, он спасает ее не там, где спасти ее уже невозможно, а в акте добровольного распятия ее в себе; формалист до формализма, логицист до логицизма и вместе с тем сама мистерия математики, катализатор ее потенций, ее прогрессирующей «болезни-к-смерти», творец первой математической антиутопии, доводящий ее в себе до кошмарного совершенства логической безжизненности и актом магической воли оживляющий ее в саму жизнь, в новую реинкарнацию ее платонической энтелехии: «