Geum.ru

К. А. Свасьян становление европейской науки

Вид материалаДокументы

Содержание


B. Russell
Подобный материал:
1   ...   37   38   39   40   41   42   43   44   ...   54


397 «Будь книгопечатание изобретено двумя веками раньше, – замечает Баттерфилд, – доктрина „импетуса“ намного ускорила бы общее развитие истории науки, и ей не пришлось бы столь долго ждать, чтобы перейти от Жана Буридана к Галилею». H. Butterfield, The Origins of Modern Science. 1300-1800., op. cit., p. 9.

367

системе координат. Такова она в изумительных интуициях Николая Кузанского, вполне готовая уже к революционным преобразованиям в естественнонаучном мышлении,398 и таков ее ренессансный актив, пышно замирающий в фигурах Бруно и Кеплера; рационализм еще раз перекроет пути пониманию, спешно подгоняя этот отрезок под рубрику «математической мистики» с успешным преодолением ее в «строго научных» фильтрациях ближайшего будущего; это будет очередной победой номенклатуры над живым восприятием в рамках шаблонного сценария «прогресса мысли», где математический гений Кузанца, экзаменуемый математическим гением Ньютона (или некой causa finalis истории математики), еще раз расколется надвое, демонстрируя всё то же полезное «ядро» и всё ту же беспрокую «шелуху». «Шелуха» окажется всего лишь… «качеством»; в сущности, путь к синтезу математики и физики раздавался в самой математике напряженнейшим единоборством двух ракурсов: «квантитас» и «квалитас»; двойственность ренессансной математики, еще верной «качеству» и уже влекомой к «количеству», была отчаянной попыткой приобретения без утрат; полагать, что мысль сдерживалась здесь наростом «шелухи» значит перевернуть эту мысль на голову, так как верным оказывается как раз противоположное: «шелуха» не сдерживала, а импульсировала, и учение Николая о бесконечности, ставшее едва ли не краеугольным камнем будущего математического анализа, было, по сути дела, не «ядром» его системы, а своеобразным математическим тропом его метафизического мировоззрения. Путь через Кеплера вел к Ньютону;399 в



398 Ср. E. J. Dijksterhuis, Die Mechanisierung des Weltbildes, Berlin, 1956, S. 258.

399 См. D. Mahnke, Unendliche Sphäre und Allmittelpunkt, op. cit., S. 142. По Манке, «едва ли можно было бы поверить, не будь это столь определенным образом доказано, что даже кеплеровское предварительное открытие точно-математической формулы ньютоновского закона тяготения обязано, в сущности, мистико-теологическому символу сферы Кузанца».

368

Ньютоне, казалось бы, уже отшелушилась «шелуха», обнаружив голое «ядро» математической техники; на деле произошло другое: «шелуха» здесь попросту менялась местами с «ядром», и если в космографиях Николая и даже Кеплера «чуть-чуть» божественности (или всё еще извечной «качественности») органически створялось с процедурами калькуляции, преображая их в «произведения искусства» sui generis (будущий лирико-эстетический балласт, или уже «шелуху» собственно), то именно механическое вытеснение этого «чуть-чуть» с переднего плана в калькуляциях Ньютона и обеспечивало им репутацию математической точности в современном расхожем смысле слова. Психоаналитические выходки уже не шли в счет; вытесненное «чуть-чуть» могло временами вскрикивать в Ньютоне алхимическими эмоциями и контактами памяти с идеей Творца мира; еще величайший математик мог искуплять отредактированный им мир Божий соломинкой «дитяти» в «Океане Истины» – всё равно: серьезно считаться с этим в рамках научного мышления было уже нельзя: математика, отчужденная от «шелухи», оборачивалась уже сплошной теоретической техникой и автоматикой мышления, некой умственной способностью «в-себе», функционирующей независимо от биографии и личных драм самого математика – вполне «объективно» и «общезначимо». Нужно представить себе некое «государство в государстве», совершенную машину в человеке, неподотчетную его переживаниям и его «Я», машину, к тому же заведенную и работающую без перебоев, – и параллельно жизнь ее знаменитого владельца ли, сожителя ли, идущую своим чередом: набожную или безбожную, с толкованиями пророка Даниила или рыбной ловлей в выходные дни – патологический казус будущего «отца атомной бомбы», смогшего бы вскрикнуть в отчаянии: «Это не я, а она»: математически точный вскрик, ибо «Я» и в самом деле не при чем, ибо в самом деле «она». Просто «Я» оказалось «шелухой», досадным «субъективным» фактором в научной одержимости бесом «объективности»…

369

Экстаз калькулирования вскруживал головы; даже «математическая мистика» Ренессанса не избежала ледяных восторгов этого головокружения; в каком-то срезе даже мысль Николая (не говоря уже о Леонардо, Кардане, Кеплере) транспарирует безжизненными перспективами чисто компьютерной техники, но Николай, автор «Опыта с весами», всё еще балансирует в себе эту тяжесть мистериальным образом «простеца» – будущий «Клингзор-Винер» столкнут в нем с рыцарем Грааля, лик которого за опущенным забралом остается пока неузнанным: «Парсифаль» или «Амфортас»; в столкновении этом вызвучена лейттема судьбы новой математики, а вместе с ней и новой науки вообще. Колоссальный подъем пифагореизма в ренессансной математике, подчеркнутость маго-мифической значимости числовой символики напоминают последнюю вспышку пламени перед затуханием; дело было не в «суевериях», как постарается представить это суд будущего, а в героическом сопротивлении механизму отчуждения, отрывающему число от материнской пуповины «качественности» и набивающему его голой суммативностью следующих друг за другом «единиц»; потомки оценят это сопротивление как ребячество, и Лагранж в «Аналитической механике» начнет родословную новой науки прямо с Галилея, обходя молчанием славную когорту визионеров, о многих из которых 400самому Галилею пришлось обронить любовное слово: «mathematice mei». Впечатление таково, что уже вдосталь вкусившие запретный плод «только счисления», они как бы заговаривают неотвратимость будущего яростным энтузиазмом мистических контемпляций; во всяком случае, бесспорным предстает одно: все они слишком знали еще, с чем собственно имеют дело. Связь математики и магии – тривиальность высшего порядка



400 Маурлико, Бенедетти, Бальди, Гвидобальдо дель Монте. Сюда: Л. Ольшки. История научной литературы на новых языках. Т.2. С.30.

370

в измерении недавнего прошлого – подчеркивается с особой силой, звуча уже не откровением, а предостережением; «математические науки, – говорит Корнелий Агриппа, – столь необходимы для магии и настолько связаны с ней, что те, кто занимаются одним, не используя другого, обрекают его на никчемность, тратят впустую свое время и никогда не достигают своих намерений» 401. Сказано очень сильно, если учесть, что в ближайшем будущем тратить впустую свое время будет не кто иной, как Декарт; понятно, что возмездная реакция картезианства должна была принять условия альтернативы и доказывать обратное; если, однако, отвлечься от тщетностей перебранки и вглядеться в суть, то радикальный выпад Агриппы окажется не палкой, просунутой в колесо «чистой» математики, а всего лишь попыткой удержать ее в зоне личных переживаний; «магия» сигнализирует здесь, во-первых, об опасностях, связанных с утратой контроля над миром чисел, во-вторых, о реальной действенности самих чисел, и, в-третьих, о необходимости математику быть магом, чтобы избежать участи того разгильдяя, который горазд откупоривать бутылки с «джиннами» и совершенно беспомощен вновь закупоривать их 402. Между тем дело принимало уже необратимый характер; странно наблюдать этот двоящийся образ математики на самом пороге Нового времени, где, скажем, испытанный платоник Кеплер способен уже, с другой стороны, и на такое признание: подобно тому как уши созданы для звуков, а глаза для цвета, так и ум создан для «количеств», без которых участь его блуждать во мраке;403 потрясающая



401 Henri Corneille-Agrippa, La Philosophie occulte ou la Magie, t. 1, Paris, 1910, p. 213.

402 Это еще раз ex post facto откупоренных уже бутылок подчеркнет Новалис: «Подлинная математика – непосредственная стихия мага». Novalis, Fragmente, op. cit., S. 146.

403 См. H. Butterfield, The Origins of Modern Science. 1300-1800, op. cit., p. 78.

371

математическая «Джоконда», в ускользающей улыбке которой «жизнь Богов» транспарирует уже оскалом сатанических наваждений; когда улыбка полностью сойдет с лица, начнется история второй математики в образе и подобии «математического аппарата», отшелушится Кеплер и явится Декарт.

Декарт – первый грандиозный обморок математики и ее начисто отшибленная память; математика в нем уже с такой силой врастает в физику, что о различении обеих не может быть и речи. Галилеевский афоризм о книге природы подтвержден здесь окончательно, но окончательность эта ограничена только кантовской экспликацией; в лозунге Декарта: «apud me omnia fiunt mathematice in natura» нет и следа намека на «авторство», которое зарезервировано отныне на «трудные случаи». Самый решительный шаг: если понимать математику как учение о числах (а так именно и понималась она в первой своей истории), то платоновский запрет на природу останется в силе; небывалость математического гения Декарта сказалась прежде всего в методическом третировании чисел; ни у одного математика неприязнь к числу как таковому не проявлялась столь явным образом, как у создателя аналитической геометрии. Заниматься числовой символикой для него равносильно бестолочи («s’occuper de bagatelles»); Мерсенну от открыто признается в полном невежестве во всем, что касается чисел,404 ибо, как ему кажется, нет ничего более пустого (rien de plus vide). Еще раз возвращаясь к афоризму Галилея: в картезианской редакции он выглядел уже совершенно иначе; опустошение числа равнялось здесь отчуждению числа от собственной сущности и извечной содержательности; что мешало Декарту, а вместе с ним и всему будущему естествознанию, так это именно содержание числа, стало быть, качество его и полнота, в



404 «Pour ce qui est de nombres, je n’ai jamais prétendu d’y rien savoir». Oeuvres complètes, t. 7, p. 50.

372

итоге: онтология и космогенез. Число в платоновско-пифагорейском опыте оттого и было «всем», что шифровало, или цифровало, в себе сокровенный смысл «всего»; у Декарта оно уже не есть «всё», а может стать «всем», ибо, очищенное до пустоты, теперь оно оказывается голым инструментом, приложимым к чему угодно волею «правил для эксплуатации». Иначе: лишь теряя самособственную содержательность, математика лишилась онтологического первородства и отождествлялась с навыками выхолощенной технологии; формализация математики, всегда равной форме, но никогда прежде не мыслящей эту форму формально, выступала прямым следствием дезонтологизации; содержание и смысл книги природы, теперь она становилась лишь ее грамматикой, или системой формальных принципов, пустых в себе, но всецело уже зависящих от только чувственных содержаний. Характерна сама эта рокировка векторов направленности: математика вверх, оттого и «падающая вверх», что полная сверхчувственных энергий, и математика вниз, пустая ладонь, нищенски протянутая к ощущениям. Чтобы понять, что же все-таки случилось, достаточно провести простейший мысленный эксперимент; возьмите какое-нибудь число, скажем, «5» и спросите себя, что вы под ним понимаете? Ответ придет моментально: пять единиц, т. е. 1 + 1 + 1 + 1 + 1; говоря психологически, число «5» как результат пяти актов внимания 405. Уже обходя молчанием то, какая комедия ожидала бы нас в случае чисел побольше, скажем, «единицы» с тремя, а то и шестью «нулями», заметим: эта операция не выдерживает и малейшего логического нажима; ведь прибавляя друг к другу именно пять единиц, мы заведомо предпосылаем сложению число «5» как таковое, которое в качестве «целого» предшествует своему



405 Эта убийственная характеристика принадлежит Расселу. См. B. Russell, The Principles of Mathematics, 1, Cambridge, 1903, p. 114.

373

суммативному эрзатцу 406. Тщетно; автоматизм привычки беспардонно пренебрегает любой логикой, и среди четырех правил арифметики первое место всё еще остается за сложением; говоря по существу, число как бы отдано на откуп сложению, которое не только открывает его, но и определяет прочие процедуры счета: вычитание как голая инверсия сложения, умножение как последовательное сложение равных слагаемых и деление как инверсия умножения, т. е. как последовательное вычитание равных вычитаемых 407. Этой математике чистых «количеств», пережившей невиданный триумф с наступлением Нового времени, противопоставлена иная математика, ставшая духовным изгоем в условиях торжествующего механицизма: математика «качеств», отталкивающаяся не от сложения, а от деления, где «два» предстает не как внешнее повторение «одного», но как внутренний результат его саморасщепления. Рудольф Штейнер, характеризуя этот процесс как органическое расчленение единства, подчеркивает тем самым изначальную «актуальную бесконечность» числа, так что канторовская революция в математике, вспыхнувшая в самом конце XIX века, была на деле лишь реставрацией ее первородства; мы воспользуемся прекрасной схемой Эрнста Бинделя, наглядно демонстрирующей противоположность обоих подходов к числу 408.



406 С неопровержимой ясностью подчеркнуто это у Кантора: «Сложение единиц никогда не может служить для определения числа, так как здесь указание главного факта, а именно как часто должны складываться единицы, не может быть получено без самого определяемого числа. Это доказывает, что число, получаемое единым актом абстракции, должно задаваться как органическое единство единиц». Г. Кантор, К учению о трансфинитном. «Труды по теории множеств», М., 1985, с. 271.

407 E. Bindel, Die geistigen Grundlagen der Zahlen, Frankfurt/Main, 1983, S. 23.

408 E. Bindel, op. cit., S. 24.

374



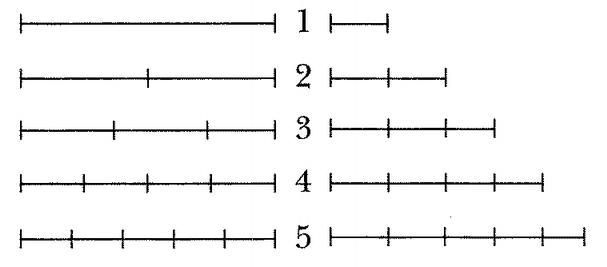
Первофеномен правого столбца – машина, левого – организм; живое вынуждает нас к надлежащему пользованию числами; мы переходим от одной клетки к двум и больше, не прибавляя к ней новые, а деля ее до бесконечности, которая выражается не символом бреда n+1, а самым определенным образом: 1:n. Необыкновенно важно отметить при этом, что если правая – механическая – модель числа отрицает левую (органическую), то левая включает ее в себя как относительно правомерное и вспомогательное средство анализа; с отчуждением числа от человека, выпадением его из круга живых представлений и сплошной инструментализацией, не могло уже быть и речи об органической качественной математике;409 Рудольф Штейнер в острейших формулировках диагностирует провал: «Бесполезно размышлять о понятиях, которые требуют, чтобы их переживали… Математическое жонглерство начинается у Ньютона с того момента, когда он пользуется этими понятиями для объяснения мира; он буквально жонглирует ими… В ньютоновской физике мы впервые соприкасаемся с представлениями о природе, полностью оторванными от человека… Современная



409 А вместе с нею и биологии sensu stricte. Кантор: «Ведь наряду или вместо механического объяснения природы... не появилось – даже в начатках – органическое объяснение природы, выходящее из рамок механицизма и вооруженное такой же математической строгостью». Г. Кантор, Основы общего учения о многообразиях. Математически-философский опыт учения о бесконечном. «Труды по теории множеств», ук. соч., с. 75.

375

наука, стремясь подчинить себе природные явления с помощью математики, изолированной от человека и внутренне уже не переживаемой, способна в своем обособленном математическом созерцании и со своими оторванными от человека понятиями рассматривать только мертвое; с отторжением математики от живого ее можно применять лишь к мертвому» 410. Отныне история математики ближайших трех столетий, а вместе с нею и история естествознания, обретшего, наконец, в ней единственного поводыря, помечена тональностью и темповыми отметками «восходящего нигилизма»; этот жуткий призрак, провиденный Ницше в конце прошлого века и на два века вперед,411 начинал свой ход двумя веками раньше; когда о нем вскричат дозорные европейской культуры – Шуман в жалящих диссонансах «Крейслерианы» и уже во всю грудь ужаленный ими Ницше, – опухоль уже разойдется гигантскими метастазами, выедая всё вокруг, так что очаг будет и вовсе не заметен; современники и потомки будут уже фиксировать чудовищные аберрации духовности, всё еще поклоняясь идолу математизированной научности, на прогрессивном челе которой не окажется и малейшего следа самоответственности за происходящее. Как будто прокладкой железных дорог или изобретением беспроволочного телеграфа можно будет смыть с себя вину за Бодлера и «юношей» с горящими глазами, которым за невозможностью стать «Вертерами» и «Муциями Сцеволами» в мире, отнятом у духа и отданном круговороту мертвых частиц, останется изживать свою «невыразимость» в метании бомб и «шигалевщине»! Как будто в хозяйственных успехах нумерически-количественного мышления (валовой продукт)



410 R. Steiner, Der Entstehungsmoment der Naturwissenschaft in der Weltgeschichte und ihre seitherige Entwickelung, Dornach, 1977, S. 61, 66.

411 «То, что я рассказываю, есть история ближайших двух столетий». F. Nietzsche, Der Wille zur Macht, Stuttgart, 1952, S. 3.

376

удастся скрыть проекцию этого мышления на мир людей, преобразованных в занумерованное поголовье «человеческого фактора»! Начиналось, конечно, не так, не с таким «расчетом»; в повестке дня стояло, конечно же, «познание» и «в интересах познания»; будущие хозяева планеты, доведенной до грани самоубийства, были еще полны взрывного восторга поиска и готовности душу положить за «вертится или не вертится»; нарождался тип «мученика науки»,412 но более реальным представал уже «комплекс полноценности и превосходства»: apud me omnia fiunt mathematice in natura. Коронация новой математики – факт первых десятилетий XVII века; поразительнее всего то, что лозунги продолжали оставаться традиционными – «математика может всё», – менялось лишь внутреннее их содержание. Группа одиноких «гениев», рассеянных по европейским городам, но уже и сводимых жанром «научной корреспонденции» (патент Мерсенна!) или явками «салонов», навязывала миру новый стиль; история европейской науки с момента рождения и до наших дней есть история собственно науки и плетущейся за нею, а позднее чаще всего и обгоняющей ее гигантской тени; таков генезис «личности» самого ученого и клубящихся вокруг нее миазмов «научного мнения»; наука в ритмах индивидуальной мысли и наука как «мода» и «непогрешимость»: «Декарт доказал», «Галилей доказал», «Ньютон доказал», а потом и вовсе: «наука доказала» – какая? та, что всё еще как биография, или та, что уже как сеанс массового гипноза! Математика может всё; посмотрите, какой плоской самопародией оборачивается эта мистериальная истина в потугах рефлексии Гоббса («Левиафан», ч. 1, гл. V): правильно мыслить значит считать понятия путем их



412 Бонавентура высмеял его до его появления, в XIII веке, Макс Шелер после его появления, в ХХ веке. См. Bonaventura, Itinerarium mentis in Deum, III, 2; см. также: E. Gilson, La philosophie de St. Bonaventure, Paris, 1924, p. 91-93. M. Scheler, Wesen und Formen der Sympathie. Gesammelte Werke, Bd. 7, Bern, 1973, S. 115.

377

сложения и вычитания, ergo, математика – основа всех наук. В самом скором времени математизируют уже все; быть ученым, быть умным человеком, быть просто gentleman, значит заложить ум, честь и совесть математическому счетчику: физика, биология, философия, музыка, театр, этика, политика, досуг, «