Готфрид вильгельм лейбниц сочинения в четырех томах том 3

Вид материала

Документы

Содержание А @ D (по построению). Далее, A@D Предложение 23. Для двух данных раздельных {терминов} А и В найти третий, отличный от них, С К оглавлению Схолия. Достаточно взять [термины], которые последовательно содержатся один в другом, такие, как М, N, и Примечания указатели Предисловие к изданию сочинения мария низолия «об истинных принципах и истинном методе философствования против псевдофилософов» Rothwelschen Sprache —

Подобный материал:

• Готфрид вильгельм лейбниц сочинения в четырех томах том , 8259.23kb.
• Монадология, 209.43kb.
• Готфрид вильгельм лейбниц сочинения в четырех томах том, 9222.8kb.
• Лейбниц Г. В. Сочинения в четырех томах:, 241.84kb.
• Готфрид Вильгельм Лейбниц, 94.22kb.
• Лейбниц Готфрид Вильгельм (Leibniz Gottfried Wilhelm) немецкий ученый (философ, математик,, 271.47kb.
• Лейбниц (Leibniz) Готфрид Вильгельм (1646-1716), немецкий философ, математик, физик,, 201.35kb.
• Установочная лекция вткс, 212.41kb.
• Георг Фридрих Риман Готфрид Вильгельм Лейбниц литература, 208.32kb.
• Источник: Чехов А. П. Полное собрание сочинений и писем в тридцати томах. Сочинения, 565.43kb.

/ В /

@ D (в силу акс. 2). Подобным образом В @ С оо В @ //qg \ \ © А @ D (по построению). Далее, A@D есть в В СЭ к|-————i———————/X Q-} А © D (в силу опр. 3). Следовательно, А (Т) С есть в В @ С. Что требовалось получить.

SY и УХ — раздельны. Пусть RS @ SY оо YR, SY © ff) YR пусть будет в XY @ YR. Пусть А — равносторонний, В — параллелограмм, D — равноугольный, С — равносторонний равноугольный, или правильный. Отсюда ясно, что, хотя «равносторонний» и «параллелограмм» будут раздельны (так что одно в другом не содержится), ]все же «правильный равносторонний» содержится в «правильном параллелограмме», т. е. в «квадрате». Но вы скажете, что подобная конструкция не во всех случаях достижима. Если, например, А будет трехсторонний, а В — четырехсторонний, то нельзя будет найти такое понятие, в которое одновременно входили бы и Л, и В, а поэтому нельзя получить такое В @ С, в которое входило бы А @ С, ибо А и В несовместимы. На это я отвечу, что наша общая конструкция покоится на постулате 2, в силу которого любой [термин] может быть скомпонован с лю-

 

==649



бым [термином]. Так, Бог, душа, тело, точка, теплота составляют агрегат из этих пяти вещей. И таким же путем могут быть скомпонованы трехстороннее и четырехстороннее. Тем самым проблема разрешается. В таком случае берется некоторое D, такое, чтобы оно не содержалось в «трехстороннем», например «круг». А @ D будет «трехсторонним и круглым», что обозначается через С. Далее, С © А будет не чем иным, как опять-таки «трехсторонним и круглым». Тем более оно будет содержаться в С © В, т. е. в «трехстороннем, круглом и четырехстороннем». Но если бы кто-нибудь захотел применить указанное общее исчисление произвольных композиций к специальному виду составления [композиции], например если бы кто-то пожелал, чтобы трехсторонник, круг и четырёхсторонник не только составили один агрегат, но чтобы в то же самое время каждое из этих понятий было в одном и том же субъекте, тогда он должен был бы установить, совместимы ли они. Так, неподвижные расходящиеся прямые могут одновременно браться именно для составления одного агрегата, но не для составления одного континуума.

Предложение 23. Для двух данных раздельных {терминов} А и В найти третий, отличный от них, С⁶.

Решение. Берется (в силу постулата 2), что С оо А © © В, и получается искомое решение. Ибо, поскольку А и В раздельны (по условию), т. е. (по опр. 6) одно в другом не содержится, постольку (в силу предл. 13) не может быть С оо А пли С оо В. Поэтому все эти три [термина] являются различными, как того и требует задача. Далее,, А@СооА©А@В (по построению), т. е. (в силу акс. 2) оо А © В. Следовательно, А © С оо А @ В. Что и требовалось получить.

Предложение 24. Найти множество различных {терминов}, таких, что каждый отличен от всех других, сколько бы их ни было взято, и таких, чтобы из них нельзя было составить нового {термина}, т. е. {термина}, отличного от любого {из них}.

Решение. Берется сколь угодно много любых [терминов], отличных друг от друга: А, В, С, D (в силу постулата 1), и из них (в силу постулата 2) образуются А © @BooM,M@C<3oN,N@DooP.fl утверждаю, что А, В, М, N, Р и будут искомыми. Ибо (по построению) из Л и В получим М, и, далее, А или В есть в М, и М — в Ni и N — в Р. Следовательно (в силу предл. 16), любой

 

К оглавлению

==650

из предшествующих будет в любом из последующих далее, если два каких-либо термина [из них] скомпоновать друг с другом, то ничего нового не получится. Ибо если скомпоновать одно и то же с самим собой, ниче]⁰ нового не образуется: L © L оо L (в силу акс. 2). Если же скомпоновать разные [термины], то — предшествующий с последующим, а следовательно, содержимый с содержащим, как L © N, но L © N оо N (в силу предл i4.) Если же скомпоновать три [термина], так что L @ N © /* то скомпонуется пара L @ N с одним [термином] Р. то пара [терминов] L @ N сама по себе не составляет ничего нового, ведь один из них, как уже показано, есть последующий N. Поэтому компоновать пару [терминов] L © с одним [термином] Р — это то же самое, что компоновать V с Р, что, как мы показали, ничего нового не составляем Следовательно, пара вместе с одним, т. е. тройка [терминов], ничего нового не составляет. И так далее для всего множества. Что и требовалось доказать.

Схолия. Достаточно взять [термины], которые последовательно содержатся один в другом, такие, как М, N, и т. д., и действительно будем иметь в результате, ее положить в нашем построении А оо «ничто», что В оо ] Однако данное решение представляется более общим, хоть такого рода проблемы могут решаться еще и другими способами. Но чтобы выявить все их возможные решения* т. е. доказать, что нет никаких иных возможных способов, понадобилось бы много других предположений нуждающихся в предварительном доказательстве. Так например, чтобы пять вещей А, В, С, D, Е не могли составить ничего нового, они должны удовлетворять только следующим способам организации. Во-первых, если есть vB,BvC,CvDsDBE; во-вторых, если А © В оо ^с и С есть в D, а D в Е; в-третьих, если А ф В оо С, А ес в D и В © D оо Е. К этому третьему способу относятся указанные выше пять понятий: «равноугольное» А, «равностороннее» В, «правильное» С, «прямоугольное» D ^и «квадратное» Е. Из них нельзя составить ничего нового» такого, что уже не совпадало бы с каким-либо из них. Ибо «равноугольное равностороннее» совпадает с «правильным» и «равноугольное» содержится в «прямоугольном» а «равностороннее прямоугольное» совпадает с «квадратным». Отсюда «правильное равноугольное» есть то я самое, что «правильное», а также «правильное равностороннее», а «равноугольное прямоугольное» есть «прямо-

 

==651

угольное», «правильное же прямоугольное» есть «квадратное».

Схолия к определениям 3, 4, 5, 6. Мы говорим, что понятие рода содержится в понятии вида, индивиды вида — среди индивидов рода, часть — в целом и даже что неделимое содержится в континууме, как точка в линии, хотя точка и не будет частью линии. Таким образом, понятие состояния, т. е. предиката, содержится в понятии субъекта. И это положение распространяется на весь универсум. Мы говорим также, что содержащиеся содержатся в том, в чем они находятся. И в данном случае при таком общем представлении неважно, каким образом те, что содержатся, относятся друг к другу или к содержащему их. Поэтому наши доказательства относятся и к тем [терминам],, которые составляют нечто распределенное, как все виды вместе составляют род. Далее, все содержащиеся, которых достаточно для составления содержащего, т. е. такие, в число которых входят все, входящие в содержащее, называются составляющими данное содержащее. Например, говорят, что А © В составляет L, если А, и, L обозначают прямые RS, YX в RX, так как RS © YX оо оо RX. Таким же образом RS ф SX со RX. А такие части, которые комплектуют целое, я обычно называю «коинтегрантными», особенно если они не имеют никаких общих частей, так что могут быть названы «сочленами», как RS и RX, Отсюда ясно, что одно и то же может быть составлено многими способами, если те [термины], из которых оно составляется, будут сами составными. И далее, если они могут разлагаться до бесконечности, то и вариантов композиции будет бесконечно много. Поэтому синтез и анализ целиком зависят от указанных здесь оснований. Далее, если те [термины], которые содержатся в чем-то, будут однородны с тем, в чем они содержатся, они будут называться «частями», а содержащее их будет называться «целым». Если же имеются две какие-либо части, такие, что может найтись нечто третье, имеющее общую часть с одной из них и общую часть с другой, тогда то, что из них составляется, есть континуум. Отсюда ясно, как одно рассуждение постепенно возникает из другого. Далее, я называю «субальтернантами» те [термины], один из которых содержится в другом, как, например, вид в роде, прямая RS в прямой RX. «Раздельными» я называю те, которые не таковы, как, например, прямые RS и УХ два вида одного и того же рода, металл благо-

 

==652

водный и неблагородный. К раздельным относятся также и члены различных делений одного и того же целого, которые имеют нечто общее; например, если делить «металл» на «благородный» и «неблагородный» и, кроме того, на «растворимый» и «нерастворимый» в крепкой водке, будет ясно, что «металл, нерастворимый в крепкой водке» и «металл благородный» суть два раздельных [термина]. Имеем же мы металл благородный, т. е. сохраняющий свой блеск в тигле и все же растворимый в крепкой водке — такой, как серебро; и наоборот, имеем металл неблагородный и нерастворимый в крепкой водке, такой,, как олово.

Схолия к аксиомам 1 и 2. Поскольку общее знаковое искусство (speciosa generalis) есть не что иное, как репрезентация и истолкование комбинаций с помощью знаков и оперирование с ними, и поскольку изобретаемые законы комбинирования бывают разными, постольку возникают и различные способы вычисления. В данном же случае нет никакого смысла принимать во внимание различие, которое состоит единственно в изменении порядка, и для нас АВ есть то же самое, что и В А. Далее, в данном случае не имеет никакого смысла повторение, т. е. для нас АА есть то же самое, что и А, Поэтому настоящее исчисление может быть приложено всюду, где выполняются указанные законы. Но очевидно, что они выполняются в случае составления абсолютных понятий, где не имеет смысла ни порядок, ни повторение. Так, сказать: «теплое и светлое» — то же самое, что сказать: «светлое и теплое», а говорить вместе с поэтами: «жаркий огонь» или «белое молоко» — это значит говорить плеоназмы. И «белое молоко» есть не что иное, как «молоко», а «разумный человек» или «разумное животное, которое разумно» есть не что иное, как «разумное животное». То же самое происходит, когда некоторые определенные вещи полагаются содержащимися среди [тех же] вещей. Ибо реальное прибавление того же самого является бесполезным повторением. Когда говорят, что двойка и двойка дают четверку, последняя двойка должна отличаться от первой. Если бы она была той же самой, ничего нового не получилось бы и случилось бы так, как если бы, шутки ради, я пожелал из трех яиц сделать шесть, пересчитав сначала три яйца, затем, съев одно из них, — оставшиеся два и, наконец, съев еще одно, — оставшееся одно. Однако в исчислении чисел и Д величин А, В или иные знаки не обозначают определен-

 

==653

ную вещь, а [обозначают] любую вещь с одним и тем же числом конгруэнтных частей. Ведь любые два фута обозначаются через 2 (если единицей, или мерой, будет фут), откуда 2+2 дает нечто новое — 4, и 3, взятое 3 раза, дает нечто новое — 9. Ибо предполагается, что всегда оперируют различным (хотя и той же самой величины). Иное дело, когда вещь присутствует в других вещах, например когда речь идет о линиях. Пусть движущийся предмет описывает прямую RY @ YX oo RYX или же Р © В оо L движением от R к X. Положим, далее, что тот же [предмет] возвращается от Х обратно к У и там останавливается. Хотя он непременно дважды опишет [прямую] УХ, или В, не произойдет ничего другого в сравнении с тем, если бы он описал УХ однажды. Так что L © В будет тем же, что и L, т. е. Р © В © В; или же RY © УХ © ХУ будет тем же самым, что и RY © УХ. Очень важно быть осторожным при оценке величины и движения тех [вещей], которые порождаются из величины и движения порождающих или описывающих [вещей], ибо следует остерегаться,, как бы при описании одна вещь не выбрала своей траекторией след другой и часть описывающего не заступила место другой [части]; или же следует отделить его, чтобы не полагалось еще раз то же самое. Отсюда также ясно, что компоненты, согласно понятию, которое мы здесь используем, могут из своих величин составить величину,; большую, чем величина той вещи, которую они составляют. Поэтому есть большая разница в составлении вещей и величин. Например, если бы у целой прямой L, или ДХ, имелись части А, или RS, и В, или УХ, каждая из которых была бы больше половины данной RX (как если бы RX была величиной 5 футов, RS —4 фута, а УХ —3 фута), то было бы очевидно, что величины частей составили бы величину? футов, большую, чем величина целой [прямой]; и все же данные прямые RS и УХ не составляют ничего другого, кроме RX, т. е. RS © УХ оо RX. Вот почему это реальное прибавление я обозначаю через ©, тогда как прибавление величин обозначается через -+-. Наконец, если реальное прибавление касается многого, то, раз речь идет о вещах, действительно порождаемых, имеется какой-то порядок [порождения], ибо прежде закладывается фундамент, а потом строится здание. В мысленном же образовании вещей получается одно и то же, какой бы из ингредиентов мы ни рассматривали прежде других, хотя бы один способ рассмотрения и был полезнее другого. Значит,

 

==654

в данном случае порядок не изменяет порождаемой вещи. В свое время потребуется обратиться к порядку. В данном же случае RY @ YS @ SX есть то же самое, что YS © RY @ SX.

в©о

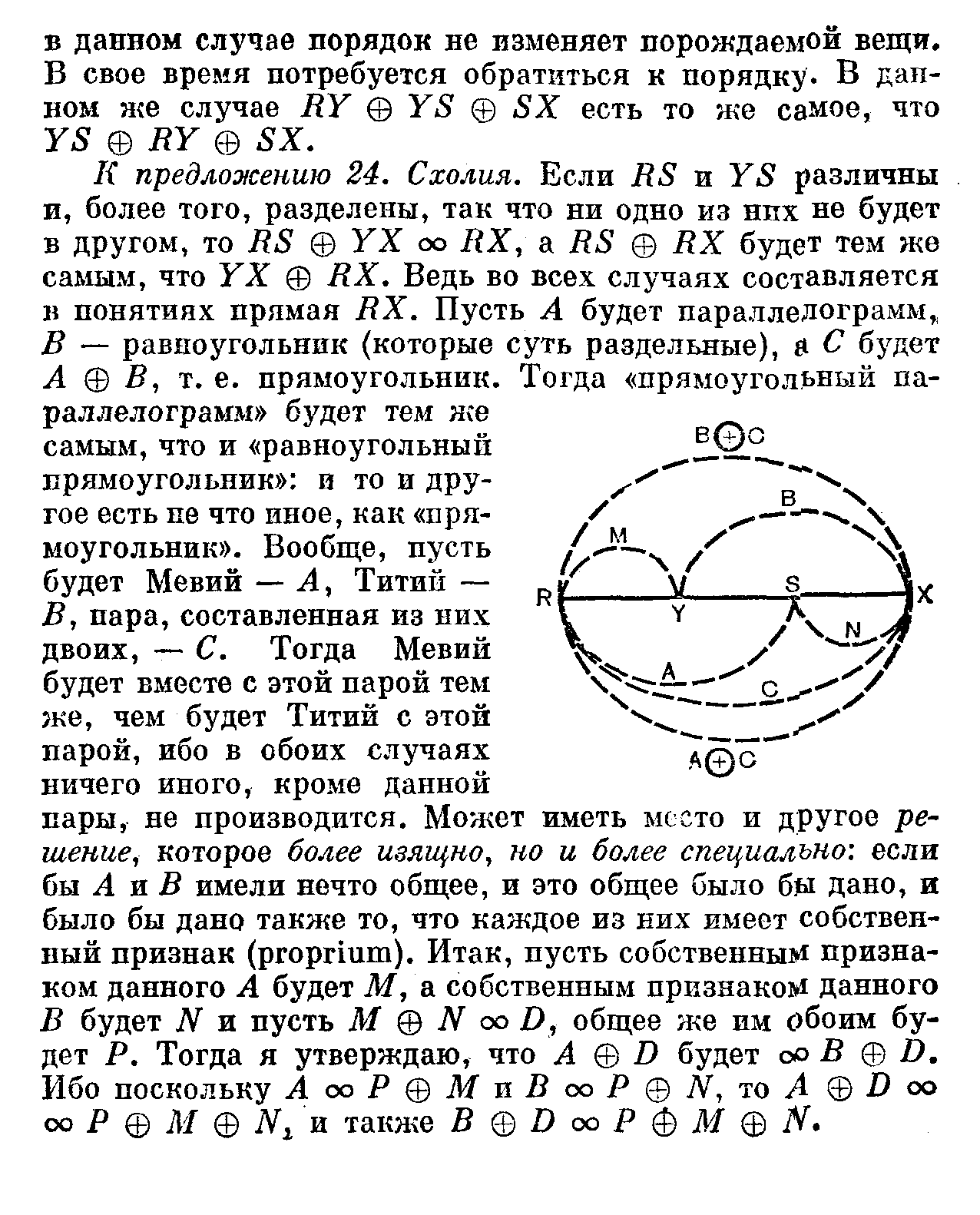К предложению 24. Схолия. Если RS и YS различны и, более того, разделены, так что ни одно из них не будет в другом, то RS © УХ оо RX, a RS © RX будет тем же самым, что УХ © RX. Ведь во всех случаях составляется в понятиях прямая RX. Пусть А будет параллелограмм, В — равноугольник (которые суть раздельные), а С будет А © В, т. е. прямоугольник. Тогда «прямоугольный параллелограмм» будет тем же самым, что и «равноугольный прямоугольник»: и то и другое есть не что иное, как «прямоугольник». Вообще, пусть будет Мевий — А, Титий — В, пара, составленная из них двоих, — С. Тогда Мевий будет вместе с этой парой тем же, чем будет Титий с этой парой, ибо в обоих случаях ничего иного, кроме данной пары, не производится. Может иметь место и другое решение, которое более изящно, но и более специально: если бы А и В имели нечто общее, и это общее было бы дано, и было бы дано также то, что каждое из них имеет собственный признак (proprium). Итак, пусть собственным признаком данного А будет М, а собственным признаке данного В будет N и пусть М @ N оо D, общее же им обоим будет Р. Тогда я утверждаю, что А © D будет оо В © D. Ибо поскольку AooP@MTiBooPQN,wA@D> оо Р © М © Л и также B@DooPiM.

 


 ПРИМЕЧАНИЯ УКАЗАТЕЛИ

ПРИМЕЧАНИЯ

Помещенные в настоящем толю гносеологические, теоретиконаучные, методологические и логические произведения Лейбница за немногими исключениями не были опубликованы при его жизни. В большинстве своем это наброски, небольшие статьи и трактаты, извлеченные на свет позднейшими издателями из рукописного архива Лейбница, хранящегося в Ганноверской библиотеке. В том вошла также избранная переписка мыслителя. Все публикуемые произведения написаны на латинском и французском языках с вкраплением отдельных слов и фраз на немецком и древнегреческом.

Если не говорить о прижизненных публикациях и отдельных работах, изданных Р. Э. Распе, издание этих произведений на языках оригинала началось лишь во второй половине XVIII в. Мы имеем в виду издание Л. Дютана: «G. G. Leibnitii opera omnia, nunc primam collecta in classes distributa prae fatigonibus et indicibus exornata, studio Ludovici Dutens». V. I—VI. Genovae, 1768 (в дальнейших ссылках — Дютан, первая (римская) цифра указывает том, последующие (арабские) — страницы тома). Из публикуемых нами работ в издание Дютана вошли только часть переписки и прижизненные публикации. Основная масса предлагаемых вниманию читателя произведений Лейбница впервые была опубликована только в XIX и начале XX в. Часть из них издана И. Эрдманом: «Godofredi Guilielmi opera philosophica quae extant latina gallica germanica omnia». Berolini, 1840 (в дальнейших ссылках — Эрдман, цифры указывают страницы издания). Другая часть опубликована К. Герхардтом: «Die philosophischen Schriften von Gottfried Wilhelm Leibniz». Bd. I—VII. Berlin, 1875—1890 (в дальнейших ссылках — Герхардт, первая (римская) цифра указывает том, последующие (арабские) — страницы). В издание Эрдмана вошли и сочинения, опубликованные Дютаном, а в издание Герхардта — произведения, опубликованные как Дютаном, так'и Эрдманом. Наконец, в начале нашего столетия Л. Кутюра выпустил солидный том ранее не издававшихся логических работ Лейбница: «Opuscules et fragments inedits de Leibniz. Extraits des manuscrits de la Bibhotheque royale de Hanovre par Louis Couturat». Paris, 1903 (в дальнейших ссылках — Кутюра, цифры указывают страницы тома).

Что касается переводов сочинений Лейбница на другие языки, то опыт таких изданий невелик. Существует издание переводов на немецкий язык под редакцией Э. Касспрера: «G. W. Leibniz. Hauptschriften zur Grondlegung der Philosophie ubersetzt von Dr. A. Buchenau. Durchgesehn und mit Einleitungen und Eriauterungen hrsg. von Ernst Cassirer». Bd. I—II. Leipzig, 1904—1906. В это издание вошла только небольшая часть работ, публикуемых в настоящем томе. Были изданы избранные логические сочинения Лейбница на немецком языке в переводе Ф. Шмидта: «Gottfried

==659

Wilhehn Leibniz. Fragmente zur Logik. Ausgewahit, iibersetzt und eriautert von Dr. phil. habil. Franz Schmidt». Berlin, AkademieVerlag, 1960, а также на английском языке в переводе Г. X. Р. Паркинсона: «Leibniz. Logical papers. A selection, translated and edited with introduction by G. H. R. Parkinson». Oxford, 1966. С этими изданиями мы сверялись, делая подборку логических произведений Лейбница для настоящего издания. Ряд сочинений Лейбница, публикуемых нами, никогда не переводился на другие языки.

Переводы выполнены с языков оригинала (латинского и французского) по изданиям Герхардта (т. I, III, IV, VI, VII) и Кутюра. Учтены также издания Дютана, Эрдмана п переводные издания Кассирера, Шмидта п Паркинсона. Две работы, уже публиковавшиеся в русском переводе, взяты из издания В. П. Преображенского: «Г. В. Лейбниц. Избранные философские сочинения». Москва, 1908. Перевод их сверен с оригиналом, существенно уточнен и исправлен.

В основной текст настоящего тома входит только то, что написало самим Лейбницем, без разъяснений, добавлений и подстрочных примечаний, принадлежащих издателям. Написанное Лейбницем на полях рукописей либо вносится в основной текст (когда это не нарушает последовательности изложения), либо выносится в текст примечаний. Так же мы поступали и с теми добавлениями и уточнениями, принадлежащими перу самого Лейбница, которые содержатся в подстрочных примечаниях его издателей. Кавычкам в тексте перевода соответствует прописная буква в оригинале. Курсивом выделены места, напечатанные в издании Герхардта в разрядку, полужирным илп жирным шрифтом или (в некоторых случаях) сплошь прописными буквами, а в издании Кутюра выделенные курсивом. Мелкие ошибки и описки Лейбница, а также опечатки в предшествующих изданиях, уже отмеченные и исправленные другими издателями, мы в большинстве случаев не оговариваем.

Публикуемые работы Лейбница в оригинале часто не имеют названия. Тогда название либо заимствуется у предшествующих издателей (чаще всего у Эрдмана, впервые давшего названия многим работам Лейбница), либо дается авторами настоящих примечаний. Эти случаи оговариваются. Многие работы Лейбница, по сведениям издателей, в рукописи не датированы. Даты их написания, когда это возможно, устанавливаются по косвенным данным.

Порядок размещения работ в томе тематический, а в отдельных тематических разделах, насколько это возможно, хронологический. Все работы группируются по шести разделам. В I разделе помещено «Предисловие к изданию сочинения Мария Низолия...». II раздел охватывает небольшие гносеологические сочинения. III раздел включает работы, содержащие критику учения Декарта и картезианцев. В IV раздел входит избранная переписка Лейбница, тематически связанная с работами предыдущих разделов. V раздел составляют работы, посвященные вопросам «универсальной науки» и «всеобщей характеристики». VI раздел состоит из логических произведений Лейбница.

При составлении настоящих примечаний частично использованы примечания, содержащиеся в изданиях Герхардта, Кутюра, Шмидта, Паркинсона и Академии наук ГДР. Примечания к сочинениям I—V разделов составлены Г. Г. Майоровым, к сочинениям VI раздела — А. Л. Субботиным. Примечания, сделанные другими авторами, оговариваются специально.

==660

ПРЕДИСЛОВИЕ К ИЗДАНИЮ СОЧИНЕНИЯ МАРИЯ НИЗОЛИЯ «ОБ ИСТИННЫХ ПРИНЦИПАХ И ИСТИННОМ МЕТОДЕ ФИЛОСОФСТВОВАНИЯ ПРОТИВ ПСЕВДОФИЛОСОФОВ»

На титуле изданного Лейбницем труда Низолия имеется название: «Мария Низолия об истинных принципах и истинном методе философствования против псевдофилософов четыре книги, посвященные сиятельнейшему барону Бойнебургскому издателем Г. В. Л. Л., присоединившим к тексту для лучшего его понимания предварительное рассуждение о цели издания, о том, как должно писать философу, а также письмо о том, как примирить Аристотеля с новейшими философами, и, кроме того, заметки и примечания на полях» (Франкфурт, 1670). На шмуцтитуле: «Превосходнейшему и сиятельнейшему господину Иоганну Христиану барону Бойнебургскому, рыцарю и проч., моему дражайшему повелителю издатель Г. В. Л. Л.». Аббревиатура Г. В. Л. Л. означает: Готфрид Вильгельм Людвиг Лейбниц. Работа была подготовлена Лейбницем к изданию в период его пребывания во Франкфурте, где он пользовался опекой и дружбой немецкого барона Бойнебурга. Барон высоко ценил молодого Лейбница и пророчил ему великое будущее. По просьбе Бойнебурга, проявлявшего интерес к гуманистическому движению, и было предпринято издание труда Низолия. Издание, по-видимому, имело успех, так как уже через четыре года Лейбниц выпустил второе издание этой работы с несколько измененным названием: «Мария Низолия философский Антибарбарус, или Поверженная схоластическая философия...» (Франкфурт, 1674). Уже из этого названия видно, что Лейбниц, в недавнем прошлом приверженец университетской схоластики, в духе которой написана его первая диссертация («О принципе индивиду ации», 1663), в данной работе выступает как критик схоластического метода философствования. 'Упомянутое на титуле первого издания письмо (к Якову Томазию) опубликовано в т. 1 наст. изд. Сочинение итальянского гуманиста, крупного филолога XVI в. Мария Низолия было впервые издано в Парме в 1553 г. и в дальнейшем неоднократно переиздавалось. Предисловие Лейбница как отдельное произведение было впервые издано Дютаном (IV, ч. I, 36—63). У Эрдмана (55—71) оно помещено под названием «Предварительное рассуждение о философском стиле Низолия». На русском языке публикуется впервые. Перевод с латинского выполнен H. А. Федоровым по изданию Герхардта (IV 131— 162).

¹ Годом раньше (в 1669) Лейбниц посвятил барону Бойнебургу Свою работу «Защита Троицы...» (Герхардт IV 111—125). — 54.

'¹ Т. е. плющом, растущим по стенам. — 55.

³ Эти издания был» позднее положены в основу «Патрологии» Ж. П. Миня — 387 томов патриотических и раннесредневековых христианских текстов, относящихся к философии и теологии («Patrologiae cursus completus, ed. J. P. Migne». Parisiis). — 56.

⁴ Крупнейший во времена Лейбница свод юридических сочинений, анонимно изданный в Лионе в 1549 г. под названием «Тгасtatus tractatuum ex van is interpretibus collectorum» (в 18-ти томах). — 5в.

° Репетентами или «комментаторами» называли юристов (X111-—XIV вв.), которые занимались толкованием глоссариев

6Й1

к римскому праву, составленных в предшествующий период главным образом школой болонских юристов. Свое имя репетеиты получили от обычного названия их трудов: «Repetitiones». Среди известны» юристов к репетентам относятся Чино (1270—1335), Бартоло (1314— 1357), Бальд (1327—1400). В данном случае речь пдет об издании «Kepetitiones seu commentarii in varia juris-consultorum responsa», т. I—VIII. Lyon, 1553. — 56.

⁶ «Георгики» IV 6 (пер. С. Шервинского). — 59.

⁷ Составленные Низолем «Цйцероновые конкордансы» (Сопcordantiae ciceronianae) лежат в основе позднейших, наиболее авторитетных индексов к Цицерону, издававшихся в XVII—XVIII вв. С филологической точки зрения они не потеряли своего значения и сегодня. — 60.

* В русском языке, как и в латинском, слово «рок» происходит от «рек», т. е. от глагола «речь» («говорить»). — 66.

^» Катекзоха (греч.) — в поэтике и риторике название тропа.—66.

¹⁰ Синекдоха и метонимия (греч.) — названия тропов. — 66.

¹¹ Сорит — непрерывный силлогизм. — 66.

¹² Речь идет о крупнейшем филологе п критике эпохи позднего Возрождения Иосифе Скалпгере (1540—1609), сыне выдающегося гуманиста и полнгистора Юлия Цезаря Скалигера (1484—1558). Среди других трудов Иосифа Скалигера, которые хорошо знал и высоко ценил Лейбниц, выделялись исследования по хронологии и истории, а также комментарии на античных авторов, в частности на Варрона. Эти комментарии были известны Лейбницу по изданию трудов Скалигера, предпринятому Исааком Казобоном: «Opuscula varia», 1610. — 66.

¹³ Rothwelschen Sprache — воровской жаргон (нем.). Конрад Геснер — выдающийся филолог XVI в. «Митридат» — по-видимому, лексикографический компендиум, созданный Геснером или при его участии. Назван так по имени понтийского царя Митридата VI Евпатора, который, согласно античному преданию, знал много языков. — 68.

¹⁴ Лейбниц намеренно берет здесь примеры из лексикона схоластики, в котором изобиловали искусственные, «технические» термины, часто образованные с нарушением правил латинской грамматики. Приблизительный перевод этих терминов на русский язык: haecceitas — «этовосты» (от haec — эти); quidditas или quaedeitas — «чтойность» (от quae — что). Латинское «-itas» соответствует русскому «-ость». Правильной модификацией от местоимения «это» было бы «этость», неправильной — «этовость», что соответствует правильной латинской форме hoccitas (от корня hoc — это) и неправильной haecceitas (от корня haec — эти). — 68.

¹⁵ Слово «квадрат» (quadratum) в буквальном переводе с латинского означает «учетверенное» и не содержит в этом значении идеи прямоугольное™ или равенства сторон. — 69.

^и Имеется в виду работа «De arte combinatorial», 1666 (Герхардт IV 27—102). Здесь Лейбниц помимо других вопросов затрагивал и вопросы оптимизации научного языка. — 70.

¹⁷ Лейбниц повсюду называет варварской философией схоластику, имея в виду, однако, не средневековую схоластику, а современную ему «школьную», университетскую философию. — 73.

¹⁸ Так Лейбниц называет здесь фламандский язык. — 73.

¹⁹ Имеется в виду комментарий Прокла Диадоха (412—485) к I книге »Элементов геометрии» Евклида, представляющий собой

==662

уникальный источник по истории античной математики. Лейбниц знал этот комментарий или по его первому латинскому переводу, сделанному Бароцием (1560), или по переводу Клавия (1654). —

75.

²⁰ Указанные греческие термины имеют следующие приблизительные русские эквиваленты: лоэоч — насколько; тсыом — каково, какого качества; •са тсрбзта — со стороны чего, в отношении чего; тсозотт)!: — количество, количественная определенность; Euto-si):: — качество, качественная определенность; оеоч; — отношение; г.рйс-т1'<6т:Т|': — непереводимое искусственное слово, близкое по смыслу к слову «отношение». — 7в.

²¹ Речь идет о схоластиках (средневековых п новых). Склонность к изобретению абстрактных философских и богословских терминов проявилась уже у Северина Боэция (4£0—524) — одного из «отцов» схоластики. Наиболее известным изобретателем схоластических терминов был Иоанн Дунс Скот (1266—1308). —•

76.

22 эту группу терминов Лейбниц выбирает преднамеренно, для большей иронии. — 76.

^м См. Гоббс. О теле II. — 76.

²⁴ Имеются в виду тропологическпе (переносные) значения, приданные этим латинским словам в средние века и позднее. Первоначальные значения этих слов таковы: dependere — свисать, отвисать, ниспадать; inhaerere — цепляться, липнуть, приставать; emanare — вытекать, струиться, проистекать; influere — втекать, вливаться, впадать, а также влиять в смысле «вливать». Во времена Лейбница узусы этпх слов стали иными: зависеть; корениться, быть прирожденным; эманировать, сущностно изливаться; влиять в смысле «оказывать воздействие». — 77.

²⁵ Первоначальное значение этого латпнского слова — «вливание». — 78.

²⁶ В смысле «вливает». — 78.

²⁷ Т. е. стиля тех средневековых поэтов, которые слагали стихи в форме загадок. — 79.

²⁸ Имеются в виду алхимики. — 79.

²⁹ См. Тацит. История V 9. — 79. ⁸⁰ Т. е. последователи французского философа и логика Петра Рамуса (Пьера де ла Раме, 1515—1572). — 80.

³¹ Известный итальянский гуманист Доренцо Балла (1407— 1457) был обвинен инквизицией в ереси за вольную трактовку «апостольского символа». Избежал расправы благодаря вмешательству неаполитанского короля Альфонса Арагонского. — 82.

³² Вероятно, то же, что и «полурамисты» (И. Г. Альштод, Б. Кеккерман, К. Дитерих, К. Бартолин). — 84.

³³ Схоластики больше всего эксплуатировали логическую часть учения Аристотеля, нередко в ущерб другим частям. Поэтому гуманисты, отвергая схоластическую умозрительную логику, часто осуждали и логику самого Аристотеля, как якобы непригодную для новой науки. Особенно критически относились к ней рамисты. — 86.

•" Схоластики-реалпсты считали реально, а не только идеально существующими все формально, т. е. логически корректно, полученные абстракции (formalitates). — 87.

³⁰ Речь пдет о письме к Якову Томазию (см, т. 1 наст. изд.), — W.

==663

³⁸ Т. е. родоначальник средневекового номинализма Иоанн Росцелин из Компьена (ок. 1050 — ок. 1122). — 89.

³⁷ Эта средневековая эпиграмма принадлежит, по-видимому, схоластику-реалисту. Реалисты считали, что диалектика имеет дело с общими понятиями, которые не сводятся только к словам (общим терминам), а представляют нечто реальное, некие вещи (res), сами по себе общие. Эти общие, «универсальные» объекты существуют независимо от единичных вещей и nci..'е до них. Аристопть полагал, что, хотя в чувственном мире суг \"твуют только единичные вещи, в области умопостигаемого имеют г ''то таюье п чистые формы, соответствующие общим умозрительным понятгям. Порфирий только поставил проблему универсалий, но не дал определенного решения. Будучи платоником, он больше склонялся к той трактовке, которая потом будет принята у реалистов. Как и у Порфирия, у Боэция нет однозначного, категорического решения проблемы универсалии. Вместе с тем он предложил в качестве одной из гипотез решение, близкое будущему номинализму. Согласно этой гипотезе, универсальное не имеет самостоятельного прсдмечнореального существования и является только абстракцией с\одного в вещах. Поэтому в эпиграмме п говорится, что Боэций 1ледает вещи, т. е. уничтожает универсалии как предмечтые реальности. Росцелин же признал универсалии простыми словами, «звуками речи»; поэтому он выгрызает вещи, оставляя от универсалии только внешнюю словесную оболочку. — &9.

³⁸ Т. е. крупнейшего средневекового метафизика Иоанна Дугса Скота. — 90.

³⁹ Это правило получило название «бритвы Оккача». — 90.

⁴⁰ Здесь Лейбниц намекает на преимущества астрономической гипотезы Коперника — Кеплера по сравнению с гипотезой Птолеыея — Тихо Браге. — 90.

⁴¹ У Гоббса встречается трактовка истинности как только логической правильности, а в ряде случаев он склоняется к конвенциональной ее трактовке. См. «О теле» III. — 91.

⁴² Как видно ил последующего расселения, Лейбниц вслед за Аристотелем объединяет здесь метафизику п теологию в одну наук). — 91.

⁴³ Разделение всей философии на логику, физику и ятику было весьма распространенным в античном мире, начиная с Древней Академии. Впервые его ввел, по-видимому, ученик Платона Ксеноьрот (393—314 до н. э.). — 91.

⁴⁴ Впоследствии Лейбниц предпринял ряд попыток сформулировать общую теорию доказательства (см. разд. V наст. тома). — 92.

⁴⁵ См. Цицерон. О природе богов I 13 (32). — 92.

⁴⁶ Моральная достоверность (certitude moralis) — от латинского слова mos (обычай, обыкновение, правило) — достоверность, основанная на предположении о ненарушаемости мировых законов, привычного хода вещей. В противоположность «метафизической достоверности»