Готфрид вильгельм лейбниц сочинения в четырех томах том 3
| Вид материала | Документы |
- Готфрид вильгельм лейбниц сочинения в четырех томах том , 8259.23kb.
- Монадология, 209.43kb.
- Готфрид вильгельм лейбниц сочинения в четырех томах том, 9222.8kb.
- Лейбниц Г. В. Сочинения в четырех томах:, 241.84kb.
- Готфрид Вильгельм Лейбниц, 94.22kb.
- Лейбниц Готфрид Вильгельм (Leibniz Gottfried Wilhelm) немецкий ученый (философ, математик,, 271.47kb.
- Лейбниц (Leibniz) Готфрид Вильгельм (1646-1716), немецкий философ, математик, физик,, 201.35kb.
- Установочная лекция вткс, 212.41kb.
- Георг Фридрих Риман Готфрид Вильгельм Лейбниц литература, 208.32kb.
- Источник: Чехов А. П. Полное собрание сочинений и писем в тридцати томах. Сочинения, 565.43kb.
опыт АБСТРАКТНЫХ ДОКАЗАТЕЛЬСТВ
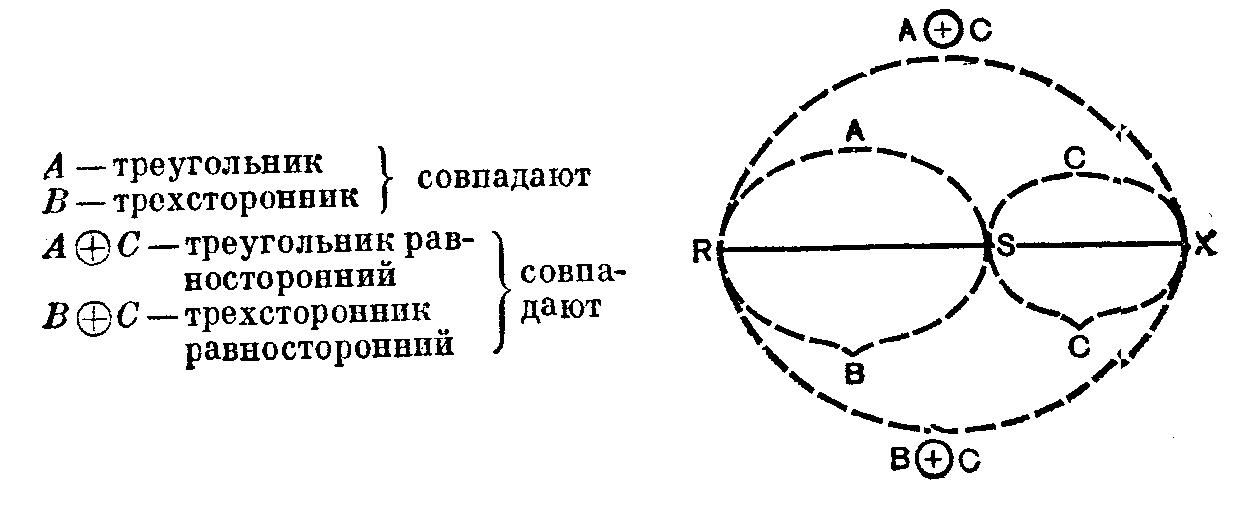
Определение 1. Тождественные, или совпадающие, [термины Г суть те, каждый из которых можно всюду подставить вместо другого с сохранением истинности. Например треугольник» и «трехсторонник», ибо во всех предложениях доказываемых Евклидом относительно треугольна можно с сохранением истинности вместо термина «треугольник» подставлять «трехсторонник», и обратно.
Х<- А оо В означает, что А и В тождественны. Так мы сказали бы о прямой XY и прямой УХ : YX оо XY, т. е. сказали бы, что кратчайшие пути движения от Х к Y и от Y к
Опрнеделение 2. Различные термины суть те, которые не тождественны или в которых подстановка иногда неосуществима. Таковы «круг» и «треугольник» или же квадрат с виду правильный, ибо так его всегда представляют геометры и «разносторонний четырехугольник», так как не все то, что можно сказать о ромбе, можно сказать о квадрате.
Х
А не оо В означает, что А и tf д__у____х
являются различными, как, например прямые XY и RS то и В оо А. Если что-
..Яг; — г г06 г"
тождественно. Ибо так как А оо В (по условию), то сГонр 1 " утверждении А оо В (истинном по условию подставлять В вместо А и А вместо В. Следовательно, будем иметь в, то и В не оо А. Если ПZoA то " - будет
"Тнче0'иметь: В оо Л. Следовательно (в силу докогое),-
roSU=\. тождеств

==641
Определение 1. Тождественные, или совпадающие, [термины Г суть те, каждый из которых можно всюду подставить вместо другого с сохранением истинности. Например треугольник» и «трехсторонник», ибо во всех предложениях доказываемых Евклидом относительно треугольна можно с сохранением истинности вместо термина «треугольник» подставлять «трехсторонник», и обратно.
Х<- А оо В означает, что А и В тождественны. Так мы сказали бы о прямой XY и прямой УХ : YX оо XY, т. е. сказали бы, что кратчайшие пути движения от Х к Y и от Y к
Опрнеделение 2. Различные термины суть те, которые не тождественны или в которых подстановка иногда неосуществима. Таковы «круг» и «треугольник» или же квадрат с виду правильный, ибо так его всегда представляют геометры и «разносторонний четырехугольник», так как не все то, что можно сказать о ромбе, можно сказать о квадрате.
Х
А не оо В означает, что А и tf д__у____х
являются различными, как, например прямые XY и RS то и В оо А. Если что-
..Яг; — г г06 г"
тождественно. Ибо так как А оо В (по условию), то сГонр 1 " утверждении А оо В (истинном по условию подставлять В вместо А и А вместо В. Следовательно, будем иметь в, то и В не оо А. Если ПZoA то " - будет
"Тнче0'иметь: В оо Л. Следовательно (в силу докогое),-
roSU=\. тождеств

==641
другу. Ибо если в утверждении А оо В (истинном, по условию) С будет подставлено вместо В (в силу опр. 1, так как В оо С}, то получится истинное предложение.
Королларий. Если А оо В, и В оо С, и С оо D, то А оо D, и так далее. Ибо А оо В оо С, следовательно, А оо С (согласно доказанному предложению). И опять же А оо С оо D, а значит (согласно доказанному), А оо D.
Отсюда, если равными считать тождественные по величине, следует, что [ величины ], равные одной и той же третьей, равны между собой. Евклид при построении равностороннего треугольника берет каждую из сторон равной основанию, откуда следует, что они равны между собой. Если что-либо движется по кругу, достаточно показать, что пути, [проходимые какой-либо точкой] за два ближайших периода, или оборота, всегда совпадают, чтобы заключить о том, что совпадают пути для любых периодов.
Предложение 4. Если А оо В и В не оо С, то и А не оо С. Если из двух {терминов}, которые тождественны друг другу, один отличен от третьего, то и другой будет. отличен от него же. Ибо если в предложении В не оо С (истинном, по условию) подставить А вместо В, то будет истинным (в силу опр. 1, так как А оо В) и предложение А не оо С.
Определение 3. «А находится в L» или «Z- содержит А» есть то же самое, что «Множество вместе взятых [терминов],; среди которых есть 4, полагается совпадающим с L».
Определение 4. Все термины, в которых содержится все содержащееся в L, вместе называются компонентами данного скомпонованного, или составленного, L.
В © N оо L означает, что В есть в L, или что L содержит В, и что В и N вместе составляют, или скомпоновывают, L. Аналогично в случае многих [терминов].
Определение 5. Субальтернантами я называю те [термины], один из которых содержится в другом, такие, как А и В, если либо В содержится в А, либо А содержится в В.
Определение 6. Раздельные [термины] — те, ни один из которых не содержится в другом.
Аксиома l.B QN oo N Q B , т..e. данная транспозиция ничего не меняет.
Постулат 1. Для любого данного [термина] можно найти от него отличный и, если угодно, раздельный, т. е. такой, что один в другом не содержится.
==642
Постулат 2. Любое множество [терминов], таких, жак А, В, могут быть взяты вместе для составления одного [термина] А @ В, или L.
Аксиома 2. А © А оо А. Если ничего нового не добавляется, то ничего нового и не получается; т. е. подобнее совторение ничего не меняет. (Ибо хотя 4 монеты и другие 4 монеты дадут 8 монет, но совсем другое дело — 4 монеты и те же самые 4 монеты, пересчитанные еще раз.)
Предложение 5. Если А есть в В и А оо С, то и С есть в В. Совпадающее с содержащимся. есть содержащееся. Ибо из предложения «Л есть в В» (истинного, по условию) подстановкой С вместо А (в силу опр. 1 совпадающих, так как А оо С, по условию) получим: С есть в В.
Предложение 6. Если С есть в В и А оо В, то и С бу/дет. в А. Что содержится в одном из совпадающих, то содержится и в другом. Ибо из предложения «С есть в В» подстановкой А вместо С (так как А оо С} получим: А есть» в В (обращение предыдущего предложения) 1.
Предложение 7, А есть в А. Одно и то же содержится в себе самом. Ибо А есть в А @ А (в силу определения «содержащегося», т. е. опр. 3) и А @ А оо А (в силу акс. 2). Следовательно (в силу предл. 6), А есть в А.
Предложение 8. А есть в В, если А оо В. Одно из совпадающих содержится в другом. Это явствует из предыдущего. Ибо А есть в А (в силу доказанного выше), т. е.. (по условию) в В.
Предложение 9. Если А оо В, то А @ С оо В Q) С. Если к тождественным [терминам] добавляются совпадающие, получаются совпадающие. Ибо, если в предложении А (+) С оо А @ С (истинном само собой) вместо А в одном случае подставить В (по опр. 1), получатся; А @ С оо В <Э С.
А©С
А—треугольник 1 .В—трехсторонний f А @С —треугольник равносторонний В @С — трехсторонник
равносторонний
совпадают
совпадают
/
• — \ \ . "
\
-————)-
У-У
==643

Схолия. Данное предложение не допускает обращения, и тем более — два нижеследующих; ниже (в проблеме, которая излагается в предл. 23) будет указан способ подтверждения этого.
Предложение 10. Если А оо L и ВссМ, то А @ В оо оо L @ М. Если к совпадающим добавляются совпадающие, получаются совпадающие. Ибо так как В оо М, то (в силу предшеств. предл.) А @ В оо А @ М, и подстановкой L вместо последнего А (поскольку А оо L, по
__ условию) получим: А@Воо Г©ЕГ""\ ooL@M.
\
\ /Л
——- Л——7/
У м/
/
А — треугольник и L — трехсторонник совпадают; L©M
В — правильный и М — наиболее емкий из изопериметрических, имеющих равное число сторон многосторонннков„ совпадают. Правильный треугольник и наиболее емкий из изопериметрических трехсторонников совпадают.
Схолия. Это предложение не допускает обращения. Ведь если было 6ыА@ВооЬ@МиАооЬ, отсюда еще не следовало бы, что и В оо М. Тем более не допускает обращения следующее предложение.
Предложение 11. Если А оо L, В оо М и С оо N, то А © В @ С оо L @ М @ N. И так далее. Если предполагается сколь угодно много {терминов} и столько же других [терминов}, соответственно совпадающих с ними один к одному, то составленное из первых совпадает с составленным из последних. Ибо (в силу предшеств., так как А оо L и В оо М) имеем: А @ В оо L @ М. Откуда, поскольку С оо N, получим (также в силу предшеств.): A Q) В @ С оо оо L © М @ N.
Предложение 12. Если В есть в L, то А @ В будет в А @ L. Если одно и то же добавляется к содержимому и содержащему, полученное из первого содержится в полученном из второго. Ибо пусть L оо В @ N (по определению'. «содержащегося»); тогда А @ В есть в В @ N @ А (в силу того же), т. е. в L @ А.
В — равносторонний, L — правильный, А — четырехсторонник. «Равносторонний» содержится в «правильном»,; т. е. свойствен «правильному». Следовательно, «равносторонний четырехсторонник» содержится в «правильном
==644

А©1_ А©В
\
\
\
четырехстороннике», т. е. в «совершенном квадрате». YS есть в RX. Следовательно, RT © YS, т. е. RS, есть в RT @ RX, или в RX.
Х2, "А \. В
/
Схолия. Это предложение не допускает обращения, R— ибо, если даже А @ В есть \ в А @ L, отсюда не следует, что В есть в L.
Предложение 13. Если L @ В оо L, то В будет в L.
Если что-либо с добавлением другого не становится другим, то добавленное в нем содержится. Ибо В есть в L @ В (по определению «содержащегося») и L @ В оо L (по условию); следовательно (в силу предл. 6), В есть в L. RY@RXooRX, следовательно, RY входит в RX. . -— •~'-~ - RY входит в RX, следова- . ~\ тельно ,RY @RX оо RX. / \ Пусть L — параллело- ______у______\
•7 в'
/
грамм (любая сторона которого параллельна некоторой другой стороне), B©L
В — четырехсторонний. «Четырехсторонний параллелограмм» есть то же самое, что и «параллелограмм». Следовательно, «быть четырехсторонним» содержится в [понятии] «параллелограмм».
И обратно: «быть четырехсторонним» содержится в [понятии] «параллелограмм». Следовательно, «четырехсторонний параллелограмм» есть то же самое, что и «параллелограмм».
Предложение 14. Если В есть в L, то L @ В оо L. Субалътернанты ничего нового не компонуют, т. е. если что-либо содержится в другом, то, добавленное к этому другому, оно не дает ничего от него отличного. Обращение предыдущего предложения. Если В есть в L, то (по определению «содержащегося») L оо В @ Р. Следовательно (в силу предл. 9), L @ В оо В @ Р @ В, т. е. (в силу акс. 2) оо В Qj Р, что (по условию) оо L.
Предложение 15. Если А есть в В и В есть в С, то и А есть в С. Содержимое содержимого есть содержимое содержащего. Ибо А есть в В (по условию), следовательно,
==645

А © L оо В (по определению «содержащегося»). Подобным образом так как В есть в С, то В @ М оо С. Подстановкой в данном утверждении А @ L вместо В (они, как мы показали, совпадают) получим: А @ L @ М оо С. Следовательно (по определению «содержащегося»), А есть в С.
RT есть в RS, и RS - в RX, У____т————s————х следовательно, -ЙГ есть в RX. V/д / * Л—четырехсторонник, В— • -/ / параллелограмм, С—прямоугольник.
«Быть четырехсторонником» содержится в понятии параллелограмма, и «быть параллелограммом» содержится в понятии прямоугольника (т. е. фигуры, все углы которой прямые). Следовательно, «быть четырехсторонником» содержится в [понятии] «прямоугольник». Если же вместо понятий, которые рассматриваются сами по себе, мы берем индивидуумы, охватываемые данным понятием, то указанные выше [понятия] допускают инверсию, и можно считать А прямоугольником, В — параллелограммом, С — четырехсторонником 2. Ибо все прямоугольники находятся в числе параллелограммов, а все параллелограммы — в числе четырехсторонников. Следовательно, и все прямоугольники содержатся среди четырехсторонников. Таким же образом все люди содержатся в [числе] всех животных и все животные — в числе всех телесных субстанций; следовательно, и все люди содержатся в [числе] телесных субстанций. С другой стороны, наоборот, понятие телесной субстанции содержится в понятии животного и понятие животного — в понятии человека. Ведь «быть человеком» содержит в себе «быть животным».
Схолия. Указанное предложение не допускает обращения, и тем более — следующее.
Королларий. Если А @ N есть в В, то и N есть в В. Ибо N есть в А @ N (по определению «содержащегося»).
Предложение 16. Если А есть в В, и В есть в С, и С есть в D, то и А есть в D. И так далее. Содержимое содержащего, взятого из содержимого, есть содержимое содержащего. Ибо если А есть в В и В есть в С, то и А есть в С (в силу предшеств.). Откуда если С есть в D, то (опять же в силу предшеств.) и А будет в D.
Предложение 17. Если А есть в В и В есть в А, то А оо В. Те [термины] которые взаимно содержатся один
==646
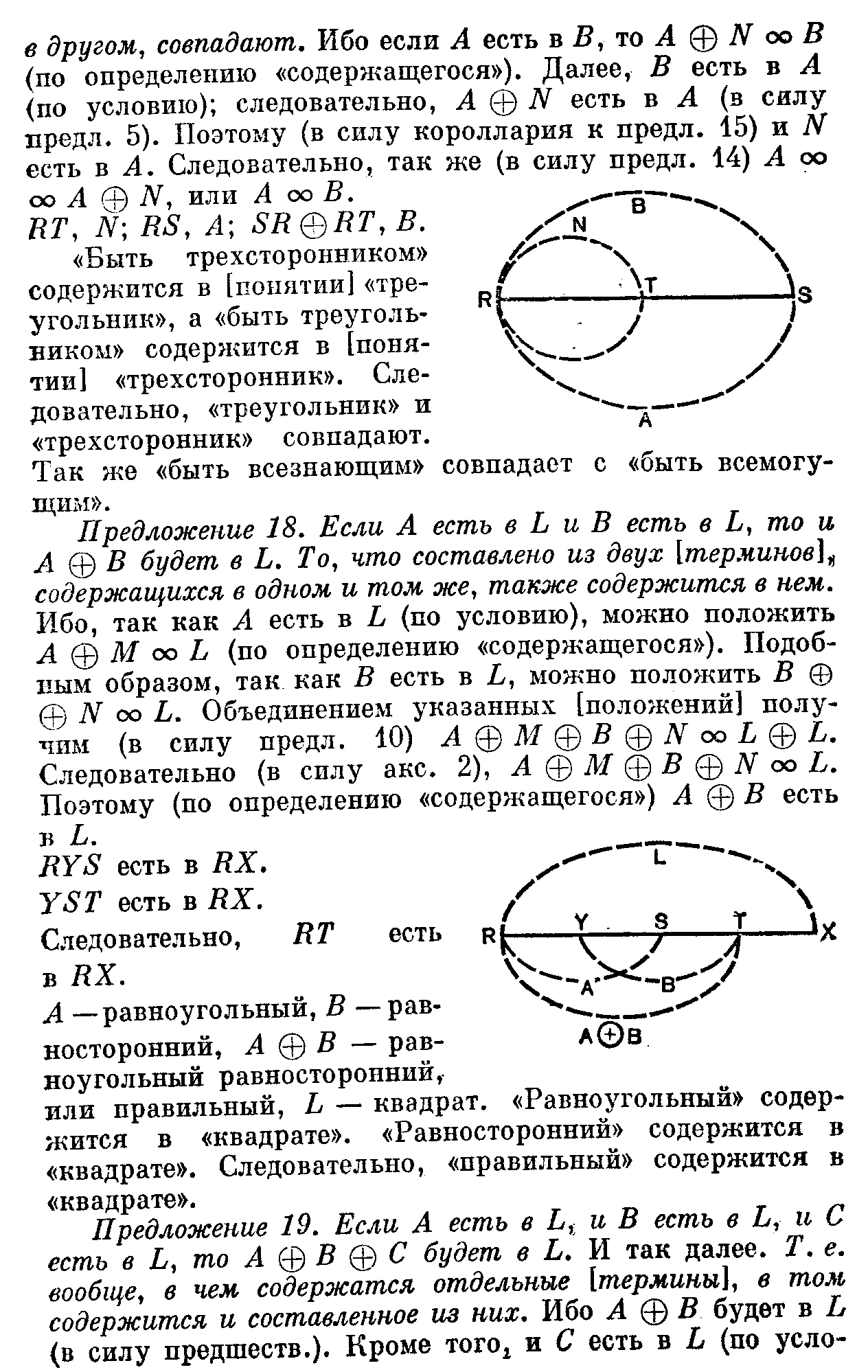 в другом, совпадают. Ибо если А есть BB,voA@NooB (по определению «содержащегося»). Далее, В есть в А <по условию); следовательно, А @ N есть в Л (в силу предл. 5). Поэтому (в силу короллария к предл. 15) и N есть в А. Следовательно, так же (в силу предл. 14) А оо оо А а) N, или А оо В. RT, N; RS, A; SR©RT,B.
в другом, совпадают. Ибо если А есть BB,voA@NooB (по определению «содержащегося»). Далее, В есть в А <по условию); следовательно, А @ N есть в Л (в силу предл. 5). Поэтому (в силу короллария к предл. 15) и N есть в А. Следовательно, так же (в силу предл. 14) А оо оо А а) N, или А оо В. RT, N; RS, A; SR©RT,B.«Быть трехсторонником» содержится в [понятии] «треугольник», а «быть треугольником» содержится в [понятии] «трехсторонник». Следовательно, «треугольник» и «трехсторонник» совпадают.
Так же «быть всезнающим» совпадает с «быть всемогущим».
| / - „; Y 8 Т \ |
| v |
Предложение 18. Если А есть в L и В есть в L, то и А @ В будет в L. То, что составлено из двух [терминов] содержащихся в одном и том же, также содержится в нем. Ибо, так как А есть в L (по условию), можно положить А @ М оо L (по определению «содержащегося»). Подобным образом, так как В есть в L, можно положить В © @ N оо L. Объединением указанных [положений] получим (в силу предл. 10) А ф М @ В @ N оо L @ L. Следовательно (в силу акс. 2), А @ М @ В © N оо L. Поэтому (по определению «содержащегося») А @ В есть в L. RYS есть в RX. ——-—.
YST есть в RX.
Следовательно, RT есть в RX.
А©В
А —равноугольный, В — равносторонний, А @ В — равноугольный равносторонний, или правильный, L — квадрат. «Равноугольный» содержится в «квадрате». «Равносторонний» содержится в «квадрате». Следовательно, «правильный» содержится в «квадрате».
Предложение 19. Если А есть в L, и В есть в L, и С есть в L, то А @ В @ С будет в L. И так далее. Г. е. вообще, в чем содержатся отдельные [термины], в том содержится и составленное из них. Ибо А ф В будет в L (в силу предшеств.). Кроме того, и С есть в L (по усло-
==647
вию). Следовательно (опять же в силу предшеств.), А @ © В ф С есть в L.
Схолия. Очевидно, что указанные два предложения и им подобные допускают обращение. Ибо если А @ В оо со L3, то ясно, что, по определению «содержащихся», А есть в L и В есть в L. Так же, если А @ В р С оо L, ясно, что А есть в L, В есть в L и С есть в L. Равным образом, что А @ В есть в L, А @ С есть в L и В Q С есть в L. II так далее.
Предложение 20. Если А есть в М и В есть в N, то Л @ В будет в М @ N. Если предшествующий [термин] содержится в последующем и другой предшествующий — а другом последующем., то составленное из двух предшествующих содержится в составленном из двух последующих. Ибо А есть в М (по условию) и М есть в М @ N (по определению «содержащегося»). Следовательно (в силу предл. 15), А есть в М @ N. Подобным образом поскольку В есть в N, а N есть в М @ N, то 5 будет в М @ N. Дачее, если А есть в М Q N и В есть в М © TV, то (в силу дредл. 18) и А Q) В будет в М (-> N.
RT есть в RY, и ST есть
m©n в SX. Следовательно, RT (j @ st,t. e. HY, есть в RY © © SY, т. e. есть в RY 4.
--".
Пусть А будет четырехсторонний, В—равноугольный,, А @ В — прямоугольный. Пусть М будет параллелограммом, N — правильным, а М @ N — квадратом. Тогда «четырехсторонний» содержится в «параллелограмме», а «равноугольный» содержится в «правильном». Следовательно, «прямоугольный» (т. e. «четырехсторонний равноугольный») содержится в «правильном параллелограмме», или «квадрате».
Схолия. Это предложение не допускает обращения. II пусть даже А будет в М, а также А @ В в М © N, отсюда вовсе не следует, что В есть в N, ибо может случиться, что как А, так и В будут в М или же что нечто такое, что будет в В, будет в М, а остальное — в N. По той же причине тем более не допускает обращения следующее и подобные ему предложения.
Предложение 21. Если А есть в М и В есть в N, и С
==648

есть в Р, то А © В ® С будет в М © N @ Р. И так далее. Составленное из содержимых содержится в составленном из содержащих. Ибо так как А есть в М и В есть в N, то (в силу предшоств.) А © В будет в М @ N. II далее, С есть в Р, следовательно (также в силу предшеств.), А @ В © С есть в М @ N @ Р.
Предложение 22. К двум данным раздельным [терминам} А и В найти третий, отличный от них, — С, такой, чтобы он вместе с ними составил субальтернанты А ( С и В О С. Т. e. такой, что, пусть даже А и В один в другом 1 е содержатся, все же один из А ® С и В @ С будет содержаться в другом.
Решение. Если мы хотим, чтобы А @ С содержалось в данном В @ С, и при этом допускаем, что А не будет в В, тогда это можно представить следующим образом. Берем (в силу постулата 1) некоторое D, любое, но такое, чтобы оно не содержалось в данном А, и (в силу постулата 2) получаем A @D оо С. Полученное будет искомым.
Ибо Asj)CooAQyA@ .--—- Q D" (по построению) оо А © '"'ь©с
„•v
А
