Готфрид вильгельм лейбниц сочинения в четырех томах том 3
| Вид материала | Документы |
СодержаниеBf + вр,:, gb-bp FC луч срС, который, будучи продолжен по прямой, пойдет по С ((G)) Об основных аксиомах познания К оглавлению Среднее знание Письмо к моланусу К оглавлению 00.php - glava14 |
- Готфрид вильгельм лейбниц сочинения в четырех томах том , 8259.23kb.
- Монадология, 209.43kb.
- Готфрид вильгельм лейбниц сочинения в четырех томах том, 9222.8kb.
- Лейбниц Г. В. Сочинения в четырех томах:, 241.84kb.
- Готфрид Вильгельм Лейбниц, 94.22kb.
- Лейбниц Готфрид Вильгельм (Leibniz Gottfried Wilhelm) немецкий ученый (философ, математик,, 271.47kb.
- Лейбниц (Leibniz) Готфрид Вильгельм (1646-1716), немецкий философ, математик, физик,, 201.35kb.
- Установочная лекция вткс, 212.41kb.
- Георг Фридрих Риман Готфрид Вильгельм Лейбниц литература, 208.32kb.
- Источник: Чехов А. П. Полное собрание сочинений и писем в тридцати томах. Сочинения, 565.43kb.
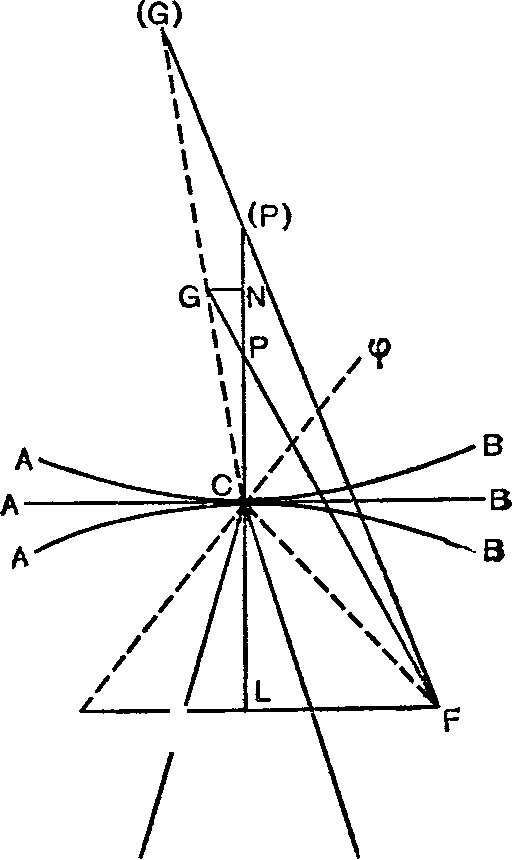
V(yy + хх + 2ах + аа); положим CF + CG = т, тогда,; исчисляя разности, получим16 d. CF + d. CG =0, т. е. (ydy + xdx — adx, : CF) + (ydy + xdx + adx, : CG) = 0„ или же CF : CG = a — x — ydy : dx, :, a + x + ydy : dx; и так как а — х есть BF и а + х есть GB, то CF : CG = = BF + ВР,:, GB-BP, или же CF : CG = PF : PG, а это и показывает, что угол FCG разбивается на две равные части посредством СР, перпендикулярной к кривой, т. е. что угол падения равен углу отражения, какова бы ни была отражающая поверхность.
То же справедливо и в отношении преломления, т. е., какова бы ни была поверхность раздела, плоская или кривая, лишь бы она была всюду единообразно регулярной, преломленный луч, исходящий из точки, находящейся в одной среде, достигает точки, находящейся в другой среде, наиболее определенным, единственным путем, не имеющим, так сказать, пути-близнеца, и происходит это в течение всего времени распространения луча, — не
==133
припоминаю, чтобы это было замечено ранее. Легко доказать это анализом, подобным предыдущему. Итак, пусть все будет задано так же, как и ранее, только вместо зеркала пусть имеется (рис. 2) поверхность АСВ — плоская, выпуклая либо вогнутая, разделяющая две среды, через которые распространяется луч, меняющий на поверхности свое направление. Пусть отношение сопротивления среды ACBF к сопротивлению среды ACBG будет как
f«.g, тогда /. CF + g.CG и, исчисляя разности, получим: (/, ydy + xdx — adx, : » CF) + (g, ydy + xdx + adx, B ((G))/ «Р» з
(М) М Рис. 3
т
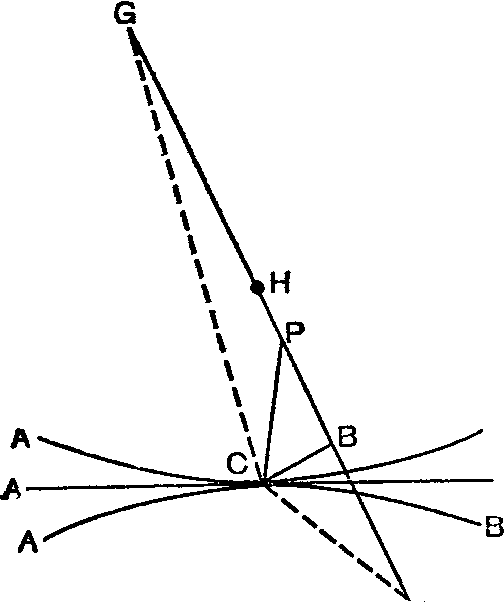
Рис. 2
t CG) = 0, а следовательно (вычисляя, как ранее), CF : : CG = i. PF : g. PG. Отсюда легко вывести теорему о пропорциональности синусов. Пусть (рис. 3) луч FC достигает в точке С поверхности АСВ, на которой он испытывает преломление, и пусть данный луч преломления CG равен лучу падения FC; соединим F и G отрезком, который пересечет в Р прямую СР, перпендикулярную к этой поверхности, и из точек F и G опустим на СР нормали FL и GN. Теперь, поскольку CG и CF приняты равными,; согласно полученному ранее уравнению имеем: PF относится к PG как g к /; тогда в силу подобия треугольников PLF и PNG синус FL будет относиться к синусу GN как g к , т. е. это отношение будет взаимообратным отношению
==134
сопротивлений сред. И синусы углов преломления будут пропорциональны синусам углов падения 1в.
Отсюда видно, что правило, задающее в любой момент племени единственный, или наиболее определенный, путь, верно как для прямого луча, так и для преломленного (т. е. полученного в результате отражения или преломления), причем и для плоских, и для кривых (вогнутых или выпуклых) поверхностей; при этом не требуется определять, будет ли время прохождения пути наиболее долгим или наиболее кратким. Хотя в действительности оно является наиболее кратким, в отношении чего должно служить так называемое правило тангенциальной плоскости, а именно: природа, управляемая высшей мудростью, которая повсюду проявляет свой общий замысел, должна подчинять кривые линии правилам, применяемым для прямых или плоскостей, которые касаются этих кривых, как если бы эти кривые были из них составлены, что, однако, если говорить строго, совсем не так.
Таким путем можно получить и некоторые другие общие теоремы, справедливые для катоптрики и для диоптрики, пбо площади прямоугольников, построенных на лучах одного направления и на противолежащем им отрезке основания (а именно прямоугольники CF. PG), всегда пропорциональны площадям противоположных прямоугольников, построенных на лучах другого направления (т. е. прямоугольников CG. PF), или же: прямоугольник, построенный на отрезке преломленного луча и на противолежащем ему отрезке основания, всегда находится в одном и том же отношении к прямоугольнику, ему противоположенному, и это отношение то же, что и отношение сопротивлений сред, где проходят эти отрезки. Следовательно» в случае простого отражения, когда среды той же самой природы, оно превращается в отношение равенства, и тогда общая теорема дает: CF : ({Р)) ((G)) = С {(G)) : ((Р)) F = 1, "ли CF. ((Р)) ((G)) = С ((G)). ((Р)) F, или, как и ранее, CF : С ((G)) = ((Р)) F : ((Р)) {(G)), т. е. равенство углов падения и отражения.
Но на практике может встретиться случай отражения,. смешанного с преломлением, ибо то, что предполагал уже Декарт, кажется неприменимым к свету, т. е. что, если луч FC в точке С встречает одновременно и зеркало АСВ, и новую среду МСА или (М)СА, в этом случае он отражается назад, однако угол отражения при этом не будет равен углу падения, и этот угол отражения не трудно
==135
определить, представив лишь для этого вместо луча FC луч срС, который, будучи продолжен по прямой, пойдет по С ((G)), и тогда окажется, что луч FC, падающий одновременно и на зеркало СВ, и на новую среду СМ, под воздействием и отражения, и преломления изменит свое направление и пойдет так, как это сделал бы луч ц>С под воздействием одного только преломления в среде СМ, которую он встретит. Однако следовало бы изучить этот случай и на опыте — не для того, чтобы определить количество, но чтобы разобраться, не будет ли здесь каких-либо особенностей в отношении цвета; кроме того, мне хотелось бы, чтобы на опыте был исследован еще и другой переход преломления в отражение, который имеет место тогда, когда падающий на среду луч идет слишком наклонно для того, чтобы проникнуть в эту среду, и был получен ответ, что в этом случае произойдет с цветом. Кроме того, для опытов по изучению цветов, порождаемых преломлением, стоило бы использовать также кристаллы с двойным отражением. Но об этом я говорю только мимоходом.
Этот принцип, согласно которому природа идет наиболее определенными путями и который мы только что использовали, является в действительности лишь архитектоническим, но тем не менее его всегда следует соблюдать. Предположим, например, что природа должна была бы построить некий треугольник, не имея для этого ничего, кроме заданного периметра, или суммы сторон, — она построила бы равносторонний треугольник. На этом примере видно различие между детерминацией архитектонической и геометрической. Детерминация геометрическая влечет за собой абсолютную необходимость, и противное ей порождает противоречие, а детерминация архитектоническая влечет за собой только необходимость выбора, и противное ей порождает несовершенство. Почти так же говорят в юриспруденции: quae contra bonos mores sunt, ea nec facere nos posse credendum est17. Так, даже в алгебраическом исчислении обнаруживается то, что я называю законом справедливости, который весьма помогает найти верные пути. Если бы природа была, если можно так выразиться, грубой, т. е. была бы чисто материальной, или геометрической, вышеупомянутый случай был бы невозможен и, не имея ничего более определенного, кроме одного только периметра, она не создала бы треугольника; однако, поскольку природа управляется архитектонически, геометрических полуопределенностей ей вполне достаточно, для
==136
того чтобы свершить свое творение, иначе она слишком часто задерживалась бы. И это и есть то, что составляет подлинную суть законов природы. Возможно, кое-кто будет отрицать, что я в данной работе выдвинул этот принцип и по отношению к законам, которые управляют движением, и подумает, что приведенное доказательство является чисто геометрическим, но я ограничусь указанием на обоснование мною противоположного мнения в другом рассуждении, где показывается, что они проистекают из того, что предполагает архитектонические обоснования. Наиболее значительным из того, что, как я считаю, было мною первым введено в физику, является закон непрерывности, о котором я сообщил несколько лет тому назад в «Новостях литературной республики» 18, где я показал на примерах, как этот закон служит краеугольным камнем всех физических учений. Более того, он не только служит для проверки, но и является весьма плодотворным принципом открытий, что я намереваюсь когда-нибудь показать. Но я нашел и другие прекрасные и весьма общие законы природы 19, сильно отличающиеся, однако, от тех, которые привыкли использовать; они полностью зависят от архитектонических принципов. И ничто не кажется более действенным для того, чтобы показать в самих началах всех вещей суверенную мудрость их творца и восхититься ею.
==137
00.php - glava11
ОБ ОСНОВНЫХ АКСИОМАХ ПОЗНАНИЯ
Поскольку я заметил, что почти все размышляющие о началах следуют скорее примеру других, нежели природе вещей, и не вполне избегают предрассудков, даже когда провозглашают, что отказались от них, я подумал, что мне следует попытаться начать с чего-либо более основательного.
А так как в доказательствах невозможно идти до бесконечности, то кое-что следует принять без доказательства, не умолчав при этом, как то обычно делают философы, о некоторой уловке, прикрывающей недостаточность [наших знаний], но точно указав, какими как бы главными утверждениями мы пользуемся, по примеру геометров, которые, чтобы засвидетельствовать свою добросовестность, с самого начала открыто заявляют, какими принятыми аксиомами они будут пользоваться, чтобы все знали, что выводы, по крайней мере сделанные на основе этих положений, гипотетичны.
Прежде всего я принимаю, что всякое высказывание (т. е. утверждение или отрицание) бывает либо истинным, либо ложным; при этом если истинным будет утверждение, то ложным будет отрицание; если истинным будет отрицание, то ложным будет утверждение. Если что-то отрицается как истинное, то (очевидно) оно является ложным; а если что-то отрицается как ложное, то оно является истинным. Если что-то отрицается как утверждение или утверждается как отрицание, то оно отрицается; если что-то утверждается как утверждение и отрицается как отрицание, то оно утверждается. Подобным же образом если истинно то, что нечто ложно, или ложно то, что нечто истинно, то утверждение является ложным; а если истинно то, что нечто истинно, и ложно то, что нечто ложно, то оно является истинным. Все это обычно выражается одним названием: принцип противоречия (principium contradiclionis).
Далее нужно посмотреть, каково же то, что может утверждаться и отрицаться, а следовательно, противоречащее ему — восприниматься как ложное. С другой стороны,
==138
среди истинных предложений первыми являются те, которые обычно называют тождественными, как «Л есть 4», где А есть не А», «Если истинно предложение L, то, следовательно, истинно предложение L». И хотя кажется, что в этих высказываниях имеется бесполезное повторение, однако из них при незначительном изменении получаются полезные аксиомы. Так, нз того, что А есть А или что трехфутовое есть трехфутовое, очевидно, что всякая вещь в данный момент такова по величине, какова она есть, т. е. равна себе самой. Отсюда (чтобы показать на примере использование тождеств) философы уже давно доказали, что часть меньше целого, использовав следующее определение: меньшее есть то, что равно части другого (большего). Доказательство делается так: часть равна части целого (ибо, согласно аксиоме, она тождественна себе); что равно части целого, то меньше целого (по определению меньшего); следовательно, часть меньше целого. Что и требовалось доказать. Подобным же образом с помощью тождественного предложения доказывается подчинение, или частный вывод из общего: «Всякое А есть В, следовательно, некоторое А есть В», подстановкой в силлогизм первой фигуры. Вывод таков: «Всякое А есть В (по предположению), некоторое А есть А (согласно тождеству), следовательно, некоторое А есть Z?». Хотя это и не относится к нашей теме, однако я привел это ради примера,, чтобы стало ясно, что тождества также находят свое применение и никакая истина, какой бы незначительной она ни казалась, не является совершенно бесплодной; напротив, вскоре станет ясно, что в них содержатся основания всего остального.
Бесспорно, что тождественные предложения являются первыми из всех и не допускают никакого доказательства, будучи тем самым истинными сами по себе, ибо, во всяком случае, нельзя найти ничего такого, что наподобие среднего термина связывало бы что-либо с самим собой; поэтому, как следствие, истинными являются виртуально тождественные, которые нетрудно свести через анализ терминов (если вместо первого термина подставляется понятие или эквивалентное, или включенное) к формальным, т. е. явно выраженным, тождествам. И очевидно, что все необходимые, иди вечно истинные, предложения являются виртуально тождественными — те, конечно, которые могут быть доказаны из одних только идей, или определений (т. е. разложением терминов), т. е. могут быть сведены к первым
==139
истинам, так что окажется, что противоположное содержит в себе противоречие и приходит в столкновение с каким-либо тождеством, или первой истиной. Исходя из этою и схоластики заметили, что истины, которые являются абсолютно, т. е. метафизически, необходимыми, можно доказать из терминов, так как противоположное содержит в себе противоречие.
В общем, всякое истинное предложение (которое не является тождественным, т. е. истинным самим по себе) может быть доказано априори с помощью аксиом, или предложений, истинных самих по себе, и с помощью определений, или идей. Ибо всякий раз, когда предикат истинно утверждается о субъекте, непременно считается, что между предикатом и субъектом имеется некая реальная связь, так что в любом предложении «А есть В» (т. е. «В истинно предицируется относительно А») В обязательно содержится в самом А, т. е. его понятие некоторым образом содержится в понятии самого А, и это происходит или благодаря абсолютной необходимости, содержащейся в вечно истинных: предложениях, или благодаря некоей достоверности, исходящей из предполагаемого решения свободной субстанции, касающегося случайностей (contingentes), а это решение никоим образом никогда не бывает произвольным и лишенным основания, но всегда может быть найдено некоторое его основание (однако склоняющее, а не необходимое), которое само могло бы быть выведено из анализа понятий (если бы это всегда было в человеческой власти) и которое не ускользает от субстанции, воистину всезнающей и все обнаруживающей априори из самих идей и своих решений. Следовательно, не подлежит сомнению, что все истины, даже совершенно случайные, доказываются априори, т. е. имеют некое разумное основание, почему они скорее существуют, чем не существуют. А это то же самое, что говорят обычно, а именно: ничто не случается без причины, т. е. ничего не бывает без основания. Однако это основание, каким бы оно ни было твердым (пусть оно и было бы достаточным для склонения в какую-либо сторону), даже если бы оно и создало уверенность в предвидящем (praesciens), все же не полагает в вещи необходимости и не уничтожает случайности, так как противоположное все же остается возможным само по себе и не содержит в себе никакого противоречия; иначе то, что мы взяли как случайное, будет скорее необходимым, т. е. вечно истинным.
К оглавлению
==140
А эта аксиома, что ничего не бывает без основания, должна считаться одной из самых важных и плодотворных аксиом во всем человеческом познании; на ней основывается большая часть метафизики, физики и нравственного учения, и без нее нельзя ни доказать существование Бога из творений, ни построить доказательство от причин к следствиям или от следствий к причинам, ни сделать какие-либо выводы в делах гражданских. Так что все, что не относится к математической необходимости (к формам логики и истинам чисел), должно вообще проистекать из нее. Например, Архимед или кто-то другой, кто является автором книги о равновесии тел 1, принял, что две равные тяжести, помещенные на весы, равноотстоящие от центра, или оси, находятся в равновесии. Этот вывод весьма близок к нашей аксиоме, так как если все располагается по обеим сторонам совершенно одинаково, то нельзя придумать никакого основания, по которому весы склонились бы в какую-либо одну сторону. Приняв же это, Архимед все остальное доказал, уже исходя из математической необходимости.
==141
00.php - glava12
СРЕДНЕЕ ЗНАНИЕ
Тот высший принцип, что ничего не бывает без основания, кладет конец большей части споров в метафизике. Ибо схоластики, кажется, не могут отрицать, что ничего не происходит без того, чтобы Бог был способен, если бы пожелал, дать основание тому, почему нечто скорее существует, чем не существует. И то же самое можно сказать об обусловленном будущем, в связи с чем Фонсека и Молина ввели понятие среднего знания (scientia media) 1. Бог заранее знает, чем станет младенец, когда вырастет,. но он, если захочет, может и дать основание этому своему знанию, и убедить сомневающегося; впрочем, какой-нибудь человек тоже мог бы сделать это, хотя и несовершенно. Следовательно, знание Бога состоит не в некоем видении, которое несовершенно и апостериорно, но в познании причины и оно априорно. Предположим, Петр оказался в некоторых обстоятельствах осененным благодатью и мне было бы позволено спросить у Бога, что будет делать Петр в этом положении. Я не сомневаюсь, что Бог смог бы ответить нечто определенное и безошибочное, хотя, к моему удивлению, некоторые схоластики осмелились сомневаться в этом. Итак, предположим, Бог отвечает, что Петр отвергнет благодать 2. Я спрашиваю далее, может ли Бог дать основание этому своему предсказанию, так чтобы он и мне смог передать знание об этом исходе. Если мы скажем, что Бог этого не может, то его знание будет несовершенным, а если скажем, что Бог это может, то очевидно оказывается низверженным «среднее знание» 3. Согласно истинным философам и св. Августину, основание, почему Бог знает действия вещей (прошлые или будущие), необходимые или свободные, абсолютные или обусловленные, есть совершенное познание их природы, подобно тому как геометр знает, что может быть построено в каждом конкретном случае с помощью циркуля и линейки или каков будет результат действия некоторого механизма, если он будет приложен к определенным вещам и силам. Предположим, что Павел * оказался в таких же обстоятельствах и с той же благо-,
==142
датью, что и Петр, и Бог говорит мне, что Петр отвергнет благодать, а Павел примет; необходимо непременно дать основание этому различию, а оно может быть получено не иначе как из «петровости» и «павловости» (Petrinitate et Pauliuitate), т. е. из природы воли Павла и природы воли Петра, каковое различие двух свобод воли и определяет, что один избирает одно, а другой — другое. Но необходимо, чтобы это различие было известно Богу также и в том, что касается выбора, и я понял бы это различие, если бы он удостоил меня объяснения, и таким образом достиг бы априори полного знания о будущем обусловленном исходе. Согласно сторонникам среднего знания. Бог не смог бы дать основания своему предсказанию и не смог бы объяснить его мне. Он смог бы, пожалуй, ответить вопрошающему его о том, почему так будет, только одно; сказав,. что так он видит это деяние в том великом зеркале, которое находится в нем и в котором представляется все настоящее, будущее, абсолютное или обусловленное. Это знание чисто эмпирическое и не удовлетворило бы самого Бога, так как он не понимает основания, почему в зеркале представляется именно то, а не это, подобно тому, кто находит в таблицах числа, но сам сосчитать их не может. Бог же знает абсолютное будущее, ибо знает, что он решил, и обусловленное будущее, ибо знает, что он решит. А он знает, что решит, поскольку знает, что будет в этом случае наилучшим, ибо он намерен избрать наилучшее, иначе из этого будет следовать, что Бог не может знать с уверенностью, что он сам будет делать в этом случае. Прекрасна мысль Скота 6 о том, что божественный разум не познает (из фактических вещей) ничего, чего бы он не предопределил, в противном случае он обесценился бы. Замечательно высказывание Васкеса в, что воля может выбрать из двух объектов тот, достоинство которого представлено сильнее.
==143
111
00.php - glava13
ПИСЬМО К МОЛАНУСУ
Мне доставило огромное удовольствие все, что Ты сообщил мне о господине Эккарде, профессоре из Ринтельиа. Я рад, что рядом с нами живет человек, у которого есть достаточно досуга, желания и таланта для истинной философии. А посему я полагаю, что хотя он и сам стремится к тому же, однако Твой авторитет и наше одобрение должны воодушевить его на продолжение усилий в столь славном начинании. Ведь, обладая, насколько мне известно, весьма основательными познаниями в математике, и прежде всего великолепно проявив себя в той общей части, которую некоторые называют анализом, он дает нам надежду, что, следуя этому примеру, и в других разделах философии он также сможет открыть или обосновать нечто достойное познания. И меня но обескураживает то, что он выше всех ставит Декарта: ведь невозможно отрицать, что, за исключением в древности Архимеда, а в Новое время Галилея, не существует другого автора, который бы путем размышления нашел столько прекрасных истин.
Я должен, однако, признать, что в трудах Декарта многое представляется мне недостаточным, даже несмотря на сложные и точные обоснования, и я не могу согласиться с ним, как бы мне этого ни хотелось, в вопросе о мироздании. Ибо я не допускаю, что природа тела состоит в одной только протяженности, и не принимаю его весьма опасного положения о том, что материя последовательно принимает все формы, на которые она способна. Особенно же несообразным представляется мне утверждение, что равенство трех углов треугольника двум прямым или то, что круг есть самая емкая из всех изопериметрических фигур, являются результатом божественной воли. Как будто бы Бог дал кругу как некую привилегию то, что он мог бы передать и квадрату. Все это достаточно ясно показывает,; что наш автор не проник в глубинные основания истины.
==144
Мне кажется, что я понимаю, какие доводы привели его к этому утверждению. Он установил критерий истины — наше ясное и отчетливое восприятие. Поэтому истинность утверждения, что круг — самая емкая из всех фигур одного и того же периметра, может быть познана только из того, что мы ясно и отчетливо воспринимаем, что это — его свойство. Значит, если бы Бог создал нашу природу таким образом, что мы ясно и отчетливо воспринимали бы противоположное, то истинным было бы противоположное. Я совершенно не согласен с этим его тезисом. Но и его метафизический принцип в целом неверен, — принцип, утверждающий, что в нас обязательно заложена идея всего того, о чем мы мыслим и рассуждаем, например тысячеугольника или абсолютно совершенного существа; вооружившись этим принципом, как Ахиллесовым щитом, он с высокомерным презрением взирает на всех, кто сомневается в его доказательствах существования Бога. Но с помощью этого же аргумента он, конечно, легко бы мог утверждать, что в нас существует также и идея невозможного, например наибыстрейшего движения, на что те, кто пожелает оспорить его доказательства, скажут, что именно такого рода идеей и является абсолютно совершенное существо. Я, правда, знаю, что смысл понятия абсолютно совершенного существа совсем иной, чем понятия наибыстрейшего движения, но все же я полагаю, что аргументация Декарта несовершенна, и тот, кто захочет довести ее до совершенства, должен внести многое еще и от себя.
Я считаю весьма замечательными его труды по этике, где он использовал и развил взгляды Эпиктета и других древних. Все это учение зиждется на различении того, что присуще нам, и того, что не находится в нашей власти: ведь если мы станем желать только того, что нам доступно, мы никогда не испытаем боли неудачи. А размышления, с одной стороны, опыт — с другой, убеждают нас в легкомысленное™ стремления к другому. Однако в этом есть трудность, ибо здесь принимается за несомненное, что по крайней мере деятельность разума в нашей власти» что, однако, далеко не всегда очевидно, ибо яд, укус бешеной собаки, тяжелое несчастье или болезнь могут до такой степени изменить все душевное состояние, что человек из сильного и мудрого превращается в пугливого и жалкого, более того — в безумца и, одним словом, из счастливого становится несчастным. Поэтому, хотя я и допускаю, что
==145
постоянным упражнением можно добиться, чтобы человек был доволен в настоящем, все же эта философия не в состоянии сделать нас уверенными в будущем. Но того, в чем я отказываю картезианской или, если угодно, стоической философии (потому что в области этики они совпадают), я не отнимаю вообще у всей философии, ибо существуют я полагаю, и более возвышенные доводы (что не делает их менее верными), с помощью которых, если не ошибаюсь, только н можно достичь того, чтобы наше спокойствие не нарушалось никаким страхом в будущем.
В натуральной философии Декарт с полным правом торжествует победу, и после Галилея нелегко найти еще кого-то, кто смог бы не говорю уже превзойти, но хотя бы сравниться с ним. Ведь далеко не одно и то же открывать что-то опытным путем, что зависит чаще от случая, а не от рассуждения, и извлекать глубоко скрытые причины вещей. Впрочем, я не стану отрицать, что Декарт в физике получил весьма мало несомненно убедительных результатов, но я, однако, утверждаю, что многое у него здесь поражает своей гениальностью. Среди этого выделяются теории радуги и магнита. Мне бы хотелось, чтобы мы располагали всеми медицинскими и анатомическими его наблюдениями, публикации которых помешала горестная для науки смерть ученого. Я сам видел и читал в Париже написанную рукой Декарта черновую тетрадь, в которую он занес некоторые свои анатомические наблюдения; часть из них я выписал и могу сообщить друзьям. Я видел также его незаконченную работу «Об исследовании истины», в которой он намеревался, если верить началу, изложить все, чем он занимался. Много замечательного было в нем, но все это, однако, укрепило меня во мнении, к которому я уже пришел раньше: Декарт был весьма далек от истинного метода и совершенного анализа. Я не могу принять в целом всю его физическую гипотезу. Ведь его утверждение, что вся материя разделена на равные части, каждая из которых вращается вокруг своего центра, совершенно не имеет никаких оснований. В этом со мной согласен Гюйгенс, единственный из всех, имеющий правильное суждение об этих предметах, кого я не перестаю побуждать, чтобы он написал свои замечания на Декарта, а он может сделать это великолепно.
Совершенно несомненно также и то, что Декарт заблуждался относительно законов движения, и притом во многом и самым невероятным образом, что, однако, совсем не уди-
==146
вительно, тем более что никто еще до сих пор не дал вполне удовлетворительного их описания, хотя это, по-моему, вполне возможно сделать. Выше я сказал, что Декарту недоставало совершенного метода и истинного анализа, а сейчас я хочу прибавить, что он обладал умом творческим, но склонным скорее к открытию общих теоретических принципов, а не к изобретению приборов и орудий утилитарного характера. Поистине существуют какие-то своеобразные пределы у любого таланта, и Бог никогда не дает всего одному человеку. Ведь если бы, например, Декарт обладал многосторонностью Кардана или Кардан — глубиной Декарта, то, конечно, мы обладали бы тем, чего только можно желать от человека, занимающегося наукой. Построенный Декартом прибор для полировки гиперболических линз не самый лучший, да и в целом, по мнению Гудде, наиболее глубоко изучившего этот вопрос, все, чего на практике можно ожидать от гиперболических линз, способны дать сферические, и это, как он сказал мне, доказано им. И все же Гудде принадлежит к самым пылким почитателям Декарта. Впрочем, чтобы не создалось впечатления, что я безосновательно не признаю у Декарта истинного и совершенного анализа, я приведу в пример его геометрию, которой он заслуженно гордится. Он даже заявил где-то, что превосходство его метода в физике и метафизике вполне возможно, в геометрии же оно вообще несомненно. Мы же сегодня благодаря нашей эпохе превзошли Декарта, во всяком случае настолько, насколько он сам — Аполлония; и мы располагаем не только тем, что дает нам наследие Декарта, но и совершенно другими вещами, к которым его открытия не указывали никакого пути.
По моему убеждению, Декарт разработал только часть геометрии, и к тому же очень узкую, а именно рассматривающую те задачи, в которых даются или отыскиваются только длины прямых. Эту геометрию я называю Аполлопиевой. Ведь Декарт только поднял на более высокую ступень то, что на более низких ступенях дал Аполлоний, показывая, каким образом описанием соответствующих кривых или мест можно решить эти задачи. Но геометрия, в которой рассматриваются величины криволинейных фигур,— наука уже совершенно иного рода, я называю ее обычно Архимедовой. Ведь из древних только один Архимед понял ее, а все остальные — Аполлоний, Папп, Феодосии и другие — не дали нам сколько-нибудь значитель-
==147
ного образца ее разработки. Только одну небольшую часть Архимедовой науки начал вновь разрабатывать Кавальери, другую часть — Гульдин, третью — Григорий из Сен-Винцента. Ибо до сих пор никто не смог охватить целиком всей ее мощи. Теперь же, если говорить о положении дела, мы достигли того, о чем сам Архимед не осмеливался и мечтать. Декарт же, насколько можно судить по его сочинениям, почти не касался этой темы. Более того, он осмелился утверждать, что кривая линия не может геометрически перейти в прямую, что, к счастью, впоследствии отвергла наша эпоха.
Поистине замечательны результаты, которые уже после смерти Декарта получили совершенно иными, чем он предполагал, путями Валлис, Хейрат, Гюйгенс, Меркатор и др. Среди всего остального выделяется, на мой взгляд, открытие бесконечных рядов, которые Гудде и Меркатор применили к гиперболе, а я с большим успехом — к кругу. Ведь этот метод бесконечных рядов является столь общим;
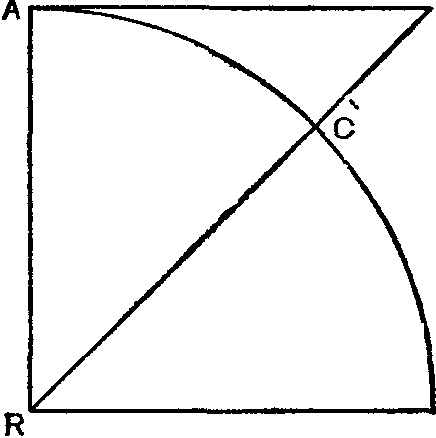
что с его помощью может быть аналитически, чисто, рационально выражено значение любой неизвестной величины, правда через бесконечную формулу, а между тем мало кому, по-видимому, известен всеобщий характер этого метода. Поясню на примере. Пусть из центра R будет описан круг, радиус которого AR будет 1, тангенс AT данной дуги круга АС будет t; он, однако, не должен быть больше радиуса; я утверждаю, что аналитическое, чистое, рациональное, но бесконечное значение данной дуги А С следующее: дуга равна
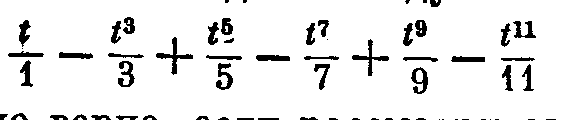
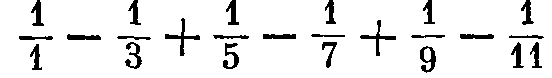
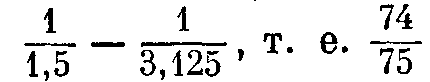
Это значение абсолютно верно, если рассматривать целиком весь бесконечный ряд, и в этих пределах оно указывает путь уму; если же взять лишь часть его, то этот же ряд оказывается удивительно полезным для практики. Например, если считать AT пятой частью радиуса АН, или единицы, т. е. считать данный t равным 1 то уравнением дуги будет - + и т. ц.\ и поэтому
==148
если в данном случае использовать только два первых члена ряда, то получим практически удовлетворительное значение такой дуги, а именно: если предположить, что
эта дуга — g-, т. е. -, то, хотя значение и будет
меньшим, ошибка не составит
уравнение дуги будет у—-з-+-5-—у+-—и т.д.
Отсюда следует тот удивительный факт, что круг относится
1 1 , 1 1 , к описанному квадрату как этот ряд: -т—-q-+-c-~-•7'+
1 1 4- — — .. и т.д. — к единице, хотя, впрочем, этот ряд, как
он здесь представлен, не годится для быстрого приближения (ибо в других случаях мы имеем ряды, значительно быстрее сходящиеся и так же продолжающиеся в бесконечность); но я не знаю, можно ли представить что-нибудь более удобное и более простое для теоретического выражения истинного отношения круга к квадрату или квадрата к диаметру. Эти выражения через бесконечные ряды имеют огромное значение, ибо они отличаются от приближений тем, что ряды дают нам некую теорему определенного значения и в то же время дают бесконечные приближения без новых расчетов, тогда как другие приближения, например Людольфовы 2, не могут быть продолжены без новых расчетов. Таким способом те величины, которые Декарт исключил из своей геометрии, могут трактоваться аналитически, и мы получаем возможность достичь чего, чего никто не мог раньше, а именно того, что любой человек без инструментов и таблиц синусов в любой момент может решать тригонометрические задачи с помощью не очень сложных расчетов, тогда как раньше для решения какого-нибудь единственного тригонометрического примера было необходимо пересчитывать от начала до конца целые таблицы. Теперь же с помощью вышеупомянутого бесконечного или, если угодно, конечного уравнения, выражающего значение данной дуги, мы легко можем, зная стороны треугольника, найти его углы, и наоборот, и это без всяких таблиц. Все это будет весьма полезным для путешественников, которые могут потерять книги и инструменты, но не так-то легко забудут столь простое

==149

правило. А это правило дает возможность в самой беспросветной глуши без какой бы то ни было помощи книг производить наблюдения и тригонометрические операции. Этим же методом можно измерять все кривые линии, производить расчеты всех пространств, всех плотных тел и поверхностей, находить центры тяжестей и возбуждений и бесчисленное множество других вещей, что в другом случае, по-видимому, едва ли было бы возможным для нас. Я, однако, признаю, что это не самое главное, чего мы хотим от анализа, ибо совершенные значения неизвестных величин состоят в некоем конечном выражении, если его можно получить, или, если его получить невозможно,: в доказательстве невозможности. Впрочем, его всегда можно получить, когда задачи сводятся к уравнению, выраженному обычным способом, хотя и любой степени.
Некий араб, по имени Мухаммед, первым открыл, что корень общего уравнения второй степени х2 + рх + qTIO (которое я для простоты выражаю по способу Виета и Декарта)3 имеет значение ± Т/ -t- r — q — t- - (Обычно я выражаю его в таком виде, не обращая внимания га знаки, которые не должны нам мешать, как я заметил в другом месте.)
Сципион Ферро первым нашел, что корень х общего уравнения третьей степени (второй член которого отсутствует), а именно r3 + рх + qQO имеет значение
V-+Vi+py--V+p3-
Лудовико Феррари, современник Кардана, первым нашел решение квадратно-квадратичного уравнения введением кубического уравнения, откуда с помощью такого рода общей формулы можно выразить и его корень.
К этим, с моей точки зрения истинно аналитическим, открытиям (поскольку они чисто и абсолютно выражают значение неизвестной величины) ни Виет, ни Декарт не прибавили ничего, что по крайней мере имело бы отношение к этому вопросу; более того, потеряв надежду продвинуться дальше в этом деле и найти способ аналитического извлечения корней из уравнений, они вообще изменили направление своих исследований. Виет нашел поистине прекрасный способ извлечения корней, сколь угодно приближенных к истинным в числах, а Декарт построил их в линиях и, таким образом, хотя один дал арифмети-
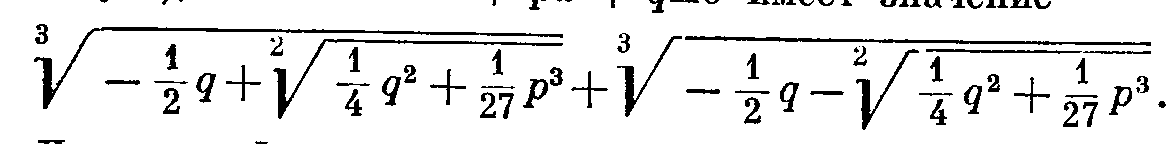
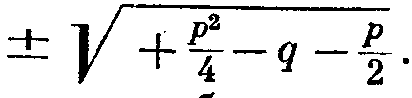
К оглавлению
==150
ческое, а другой — геометрическое решение, они оба отказались от истинно аналитического решения, включающего все прочие. В наше время вместо Виетова извлечения в числах мы имеем значительно более удобный способ — через бесконечные ряды, а вместо Декартовых построений из различных кривых линий я создал уникальный инструмент, который дает возможность, умножив в зависимости от обстоятельств число частей, строить любые уравнения. Таким образом, и в этих двух вопросах мы сегодня далеко превзошли и Виета, и Декарта. Мне кажется, что сравнительно недавно я пришел все же к удачному аналитическому решению всех уравнений, которое не только Декарту, но и многим выдающимся ученым нашего времени представлялось почти безнадежным, т. е. к методу, с помощью которого общей формулой (в соответствующей степени) может быть выражено значение неизвестного корня любого уравнения, подобно тому как это сделал Сципион Ферро в кубическом уравнении, хотя в более высоких степенях (например, в пятой степени) мы до сих пор так далеки от общей формулы, что не дали даже ни одной частной: у меня есть доказательство метода, а пример его применения в пятой степени (чего до сих пор никому не удавалось сделать) я дам, когда у меня будет время. Во всяком случае несомненно: во всем анализе едва ли можно найти что-нибудь более трудное и мой метод опирается на такую длинную цепь, что достаточно ясно, что я натолкнулся на него не случайно. В нем заключен прогресс и совершенствование всей алгебры (а я называю собственно алгеброй решение уравнений само по себе, безотносительно к числам и линиям); ведь когда мы однажды получим корни всех уравнений, мы будем иметь решения всех задач, сводимых к уравнениям. Однако слишком малая часть листа, оставшаяся незаполненной, напоминает мне о чрезмерном и неожиданном многословии. А посему я закончу просьбой передать привет от меня ученейшему мужу Экарду и, если сочтешь нужным, рассказать ему об этих моих мыслях. Впрочем, и беседа с этим человеком, и переписка с ним будут для меня весьма приятны. Прощай и будь счастлив.
00.php - glava14
