Готфрид вильгельм лейбниц сочинения в четырех томах том 3

Вид материала

Документы

Содержание Абсолютно первые истины Первыми же для нас истинами Благо есть то, что содействует совершенству. Совершенство То же самое Tentamen anagogicum К оглавлению

Подобный материал:

• Готфрид вильгельм лейбниц сочинения в четырех томах том , 8259.23kb.
• Монадология, 209.43kb.
• Готфрид вильгельм лейбниц сочинения в четырех томах том, 9222.8kb.
• Лейбниц Г. В. Сочинения в четырех томах:, 241.84kb.
• Готфрид Вильгельм Лейбниц, 94.22kb.
• Лейбниц Готфрид Вильгельм (Leibniz Gottfried Wilhelm) немецкий ученый (философ, математик,, 271.47kb.
• Лейбниц (Leibniz) Готфрид Вильгельм (1646-1716), немецкий философ, математик, физик,, 201.35kb.
• Установочная лекция вткс, 212.41kb.
• Георг Фридрих Риман Готфрид Вильгельм Лейбниц литература, 208.32kb.
• Источник: Чехов А. П. Полное собрание сочинений и писем в тридцати томах. Сочинения, 565.43kb.

АБСОЛЮТНО ПЕРВЫЕ ИСТИНЫ

Среди истин разума абсолютно первыми ¹ являются тождественные истины, а среди истин факта — те, из которых априори могли бы быть доказаны все опыты. Ведь все возможное требует существования, а потому [любое возможное] и существовало бы, если бы не препятствовало другое [возможное], которое также требует существования и несовместимо с первым. Отсюда следует, что в любом случае осуществляется такая комбинация вещей, в которой существует наибольшее их число. Так, если мы предположим, что А, В, С, D равносильны по своей сущности, равно совершенны или равно требуют существования, и предположим, что D несовместимо с А и В, тогда как А совместимо со всеми другими, кроме Р, и подобным же образом рассмотрим В и С, то получится,, что в этом случае будет существовать комбинация АВС с исключением D; ибо если бы мы допустили существование D, которое ни с чем, кроме С, не могло бы сосуществовать, то существовала бы комбинация CD, которая во всяком случае менее совершенна, чем комбинация АВС. Отсюда ясно, что вещи существуют наиболее совершенным способом.

Этот тезис: «Все возможное требует существования» — может быть доказан апостериори при допущении, что нечто существует. Ведь или все существует, и тогда все возможное так же требовало бы существования, как и существовало бы, или что-то [из возможного] не существует, и тогда должно быть представлено основание, почему нечто существует предпочтительно перед другим. А это может быть установлено не иначе как из общего основания сущности, или возможности, через допущение, что возможное по самой своей природе требует существования, именно — сообразно основанию возможности, или степени сущности. Если бы в самой природе сущности не было никакой наклонности к существованию, то ничего и не существовало бы; ибо сказать, что у некоторых сущностей есть такая наклонность, а у некоторых нет, — значит сказать нечто бессмысленное , так как существование, по-видимому,

 

==123

вообще относится ко всякой сущности одним и тем же образом. Однако людям до сих пор неизвестно, откуда берется несовместимость противоположностей, или как могло случиться, что различные сущности противоречат друг другу, в то время как чисто положительные термины, казалось бы, совместимы один с другим.

Первыми же для нас истинами являются опытные.

Всякая истина, которая не является абсолютно первой, может быть доказана из абсолютно первых.

Всякая истина или может быть доказана из абсолютно первых (можно доказать, что те сами не доказуемы), или же сама есть абсолютно первая. И, как обычно говорят, это означает, что ничто не должно утверждаться без основания и даже что ничто не делается без основания.

Так как истинное предложение является тождественным или может быть доказано из тождественных с помощью определений, отсюда следует, что реальное определение существования состоит в том, что существует наиболее совершенное из всего, что может существовать, т. е. то, что содержит в себе больше сущности. А природа возможности, или сущности, будет состоять в требовании существования. Иначе невозможно было бы найти никакого основания для существования вещей ³.

Благо есть то, что содействует совершенству.

Совершенство же есть то, что содержит больше сущности.

Привативное есть то, что выражает отрицание последующей непрерывности.

Позитивное — то, что выражает утвердительное.

Всякая конечная прямая линия выражает отрицание последующей непрерывности.

Подлинное есть то, что полагается тем, что оно есть; неподлинное, или кажущееся,— то, что [в действительности] есть другое, ибо кажущееся имеет некоторые свойства того, что предполагается существующим, а именно те свойства, которые могут легче наблюдаться, но лишено других, отличающих данный предмет от всех иных, как, например, золото, которое имеет цвет пламени, однако жара пламени не несет.

Актуальное — то, что выражает существование, потенциальное — только сущность.

Бесконечное есть то, что имеет величину абсолютно, конечное заключает в себе отрицание чего-то того же самого

 

==124

рода. Но это, по-видимому, имеет место только в непрерывных; в дискретном количество, видимо, не может быть постигнуто абсолютно, как некоторое целое. Как величина есть число частей, так бесконечное,; поскольку оно заключает в себе что-то помимо тех частей; число которых дается,: есть большее любого заданного.

Прирожденное и произведенное, или, как обычно говорят, естественное и искусственное, различаются тем, что произведенное делается таким, каково оно есть, по воле людей. Творения людей являются произведенными, дети же не являются, ибо, если отец и породил сына, он все же не породил такого, какого хотел бы. Если бы какой-то мед рождался без участия пчел, он мог бы называться прирожденным, и, наоборот, мед пчел называется произведенным.

Простое — то, части чего подобны. Смешанное — то, части чего не подобны.

То же самое (Idem) — если одно всюду может подставляться на место другого. Если что-то всюду может замещаться другим, то и это другое может в свою очередь им замещаться.

Равные — те, количество которых то же самое, т. е. которые могут замещаться друг другом, сохраняя количество.

Подобные—те, которые могут замещаться друг другом,. сохраняя качество, т. е. те, которые не могут быть различимы иначе, как при их совместном рассмотрении.

Конгруэнтные — те, которые охватываются теми же самыми границами; если же они одной и той же материи, т. е. имеют части, подобные между собой, они подобны. Конгруэнтные всегда равны.

Совпадающие — те, что в действительности те же самые, однако кажутся различными.

Неподходящее (inconveniens) есть то, что содействует противоположному. Содействующее же (couferens) есть то, что является реквизитом для какого-нибудь способа произведения. Поэтому неподходящее контрарно содействующему. Подходящее же не есть тем самым содействующее, ибо нечто может подходить и тогда, когда оно лишь не вредит. Однако это зависит от словоупотребления. Ибо если кто-либо захочет называть подходящим небезразличное и, кроме того, захочет истолковать его как подходящее действие для причины, то подходящее и содействующее будут различаться как условие и реквизит, или как вводя-

 

==125

щее (Inferens) и вносящее вклад (importans), т. е. подходящее будет условием для какого-либо способа произведения и существования, тогда как содействующее будет реквизитом. И тогда то, что не является неподходящим, даже если оно не было бы подходящим, могло бы быть названо сообразным (conforme).

Полезное есть содействующее большему совершенству., хотя и не заключающее его в себе, в чем оно и отличается от блага самого по себе.

Приятное есть то, что влечет большее совершенство ощущающего, т. е. полезно ему, пусть даже за ним может случайно воспоследовать большее несовершенство, отчего оно сделается вредным. Из этого следует, что приятное есть то, что влечет к себе естественным образом, или само по себе вызывает влечение, если ничто не препятствует, т. е. если из него случайно не может воспоследовать большая неприятность или же лишение приятного.

Тягостное есть контрарное приятному.

Справедливое есть то, что сообразно или подходяще всеобщему благу, т. е. то, что является нравственно возможным. Должное — то, что нравственно необходимо. Нравственно значит с уважением к общему благу, насколько мы можем о нем судить. Так, благополучное злодеяние, т. е. преступление, которым кто-либо, желая нанести вред, способствовал вопреки своему намерению всеобщему благу, не становится от этого менее несправедливым. Более того, даже если бы нечто было возможным без ущерба для общего блага, то оно все же было бы несправедливо, если бы не было достойно [всеобщего] одобрения, т. е. если бы его свершение не было безопасно.

Значительное (important) ⁴ — то, из чего следует что-либо замечательное, т. е. вносящее какой-либо великий вклад. Пустое — ничего не вносящее или вносящее незначительное. Вносящее вклад есть вводящее первенствующее по природе (inferens natura prius).

Невозможное есть то, что заключает противоречие.

Ценное есть значительное с точки зрения блага.

Ничтожное — пустое с точки зрения блага.

 

==126

00.php - glava10

TENTAMEN ANAGOGICUM

АНАГОГИЧЕСКИЙ ОПЫТ ИССЛЕДОВАНИЯ ПРИЧИН

То, что ведет к высшей причине, и у философов, и у теологов называется анагогическим. Итак, здесь мы приступаем к доказательству того, что понять основание законов природы возможно, только предполагая существование некоей разумной причины. Мы показываем также, что при исследовании конечных причин бывают случаи, когда приходится принимать во внимание самое простое или самое определенное, безразлично, является ли оно наибольшим или же наименьшим. И то же самое можно наблюдать в исчислении разностей, чему хорошим примером служит общий закон направления луча, выведенный из конечных причин, без различения при этом случаев отражения и преломления, а также изогнутой или плоской поверхности. Из этого мы выводим несколько новых общих теорем, равно подходящих как для случая преломления, так и для случая отражения. Мы показываем, что анализ законов природы и исследование причин ведут нас к Богу, а также каким образом на пути к конечным основаниям, так же как и при исчислении разностей, мы рассматриваем не только наибольшее или наименьшее, но и вообще самое простое и самое определенное. Я уже по многим поводам отмечал, что познание законов природы приводит нас в конечном итоге к более высоким принципам порядка и совершенства, которые указывают на то, что вселенная является результатом универсальной разумной силы. Это познание и есть главный плод нашего исследования, и так полагали уже древние. Не говоря о Пифагоре и Платоне, которые в особенности отстаивали эту мысль, сам Аристотель стремился в своих трудах — особенно в своей «Метафизике» — доказать существование перводвигателя ¹. Правда, древним, которые не были в отличие от нас столь сведущи в законах природы, недоставало многих средств, которыми располагаем мы и которыми мы должны воспользоваться.

Познание природы рождает искусство, оно предоставляет нам множество средств для сохранения жизни, а

 

==127

также обеспечивает нам жизненные удобства; но, помимо того что познание приносит духовное удовлетворение, проистекающее из мудрости и добродетели, что само по себе является наибольшим удовольствием в жизни, оно возводит нас к вечному взамен того, что эта жизнь слишком коротка. А следовательно, то, что служит установлению правил, полагающих счастье в добродетели, и то, что выводит всё из принципа совершенства, бесконечно более полезно для человека и для государства, чем все то, что служит искусствам. Так что полезные для жизни открытия зачастую являются всего лишь следствиями более важных познаний, и воистину кто ищет царство божие, обретает остальное на своем пути.

Исследование конечных причин в физике является как раз исполнением того, что, как я полагаю, и должно делать, и те, кто желал изгнать их из своей философии, не очень-то осознали важность их использования. Ибо я не хотел бы обидеть их предположением, что, поступая таким образом, они имели дурные намерения. Однако появились и другие, которые, злоупотребив этим и не удовлетворившись исключением конечных причин из физики, вместо того чтобы рассмотреть их где-нибудь в ином месте, приложили усилия к тому, чтобы вообще устранить их, а также доказать, что творец вещей, даже если он воистину всемогущ, не обладает никаким разумом ². Были еще и такие, кто не признавал никакой всеобщей причины, как те древние, которые усматривали во вселенной только взаимодействие частиц ³, к чему, по-видимому, склонны те умы, в коих преобладает имагинативная способность, поскольку они полагают, что следует обходиться только математическими принципами и что нет никакой нужды ни в принципах метафизических, которые они считают химерами, ни в принципах блага, которые они относят к области человеческой морали, как будто совершенство и благо являются лишь неким особым результатом наших мыслей, а не находятся во всеобщей природе.

Я признаю, что очень легко впасть в эту ошибку, и это происходит всякий раз, когда в размышлениях останавливаются на том, что может быть получено одним воображением, т. е. на величинах, фигурах и их видоизменениях. Но когда исследование продолжается до поисков основании, оказывается, что законы движения не могут быть объяснены ни чисто геометрическими принципами, ни одним только воображением. А потому и случилось так,

 

==128

шей линии, соединяющей две данные точки, мы возьмем на выбор еще две, то заключенная между ними часть исходной линии опять-таки с необходимостью оказывается наикратчайшей по отношению к этим точкам. Подобным же образом и мельчайшие части вселенной устроены согласно порядку наибольшего совершенства; иначе целое не существовало бы.

Именно поэтому я утверждаю, что в самой телесной природе присутствуют, если можно так выразиться, два царства, которые взаимопроникают, не сливаясь и не мешая друг другу: царство силы, где все можно объяснить механически, с помощью действующих причин, если мы достаточно глубоко в них проникаем, и царство мудрости, где все можно объяснить архитектонически, с помощью, так сказать, конечных причин, если мы познаем их достаточно хорошо. И как раз поэтому можно утверждать не только то, что высказывал и Лукреций, а именно: животные видят потому, что у них есть глаза ⁹; но также и то,. что глаза им были даны для того, чтобы видеть, хотя я знаю, что многие принимают только первое утверждение, дабы показать силу своего ума. Однако те, кто более подробно разбирается в природных машинах, нуждаются в немалых предохранительных мерах, чтобы противостоять притягательной силе их красоты, и сам Гален, узнав кое-что о функциях частей тел животных, настолько проникся восхищением, что поверил, что их объяснение уподобилось бы пению гимнов во славу Божества. И у меня часто возникало желание, чтобы какой-нибудь искушенный врач взялся написать подробное сочинение, название которого или по крайней мере цель могли бы быть гимном Галена.

Более того, наши размышления не раз позволяли нам провести такие изыскания, которые заставляют признать полезность конечных причин не только для того, чтобы усилить восхищение перед высшим творцом, но и для свершения открытий в его творении. Однажды я представил подтверждение этого, когда предложил общий принцип оптики, а именно что луч вдет от одной точки к другой путем, который оказывается наиболее легким для случая плоских поверхностей, что должно послужить правилом и для других. Ибо следует учесть, что если этот принцип рассматривать как действующую причину, а среди всех возможных и как бы взвешенных лучей считать перевешивающим наилегчайший, то следовало бы рассмотреть всю поверхность такой, какая она есть, не рассматривая

 

К оглавлению

==130

касающейся ее плоскости; но и в этом случае не всегда удастся добиться успеха, что быстро и обнаружится. Однако, вовсе не скрывая, что этот принцип имеет нечто общее с конечной причиной — как уже некогда было указано г-ну Ферма, когда он использовал его в диоптрике ¹⁰, я нахожу его красивее и значительнее для более тонкого использования, чем принцип механизма. И некий искушенный автор, опубликовавший в Англии книгу по оптике, выразил мне по этому поводу признательность ¹¹. Порядок требует, чтобы с кривыми линиями и поверхностями обращались так же, как если бы они были составлены из прямых линий и плоскостей. И путь луча определяется той плоскостью, куда он падает, которая рассматривается как образующая здесь кривую поверхность. Но тот же самый порядок требует, чтобы эффект наибольшей легкости достигался по крайней мере на плоскостях, которые служат элементами других поверхностей, хотя на последних он и не может быть достигнут. Более того, таким образом по отношению к указанным плоскостям удовлетворяется и еще один принцип, следующий за предыдущим и указывающий, что, когда нет наименьшего, следует держаться наиболее определенного, которое может быть наипростейшим, даже и будучи при этом наибольшим.

Оказывается, что древние, и в их числе Птолемей, уже пользовались этой гипотезой о наилегчайшем пути падающего на плоскость луча для обоснования равенства углов падения и отражения, что является основанием катоптрики. И, воспользовавшись именно этой гипотезой, г-н Ферма обосновал закон преломления по синусам или (изложив это обоснование косвенно, как и Снеллиус ¹²) по секансам. Но, более того, я нисколько не сомневаюсь в том, что данный закон и был в самом начале выведен Ери помощи этого способа. Известно, что Виллеброрд Снеллиус, один из наиболее крупных геометров своего времени, к тому же глубоко проникший в методы древних, открыл этот закон и даже написал об этом работу, которая по причине смерти автора не была опубликована, но так как содержание ее было изложено его учениками, то, по всей видимости, г-н Декарт, некоторое время спустя приехавший в Голландию и интересовавшийся подобными вещами более, чем кто-либо другой, ознакомился с ней. Ибо способ, каким Декарт пытался это обосновать с помощью действующих причин или с помощью сложения направлений, по аналогии с отражением шаров, был

 

==131



настолько натянутым и, чтобы не сказать больше, малопонятным, что становится совершенно ясно, что это рассуждение лишь позднее было кое-как подогнано к выводу,, который в нем на самом деле не содержится. Поэтому следует полагать, что мы не пришли бы к столь прекрасному открытию так давно, если бы не метод конечных причин. Я припоминаю, что некоторые искушенные авторы часто выдвигали против этого принципа тот аргумент, что его не удается применить даже в случае отражения, если он прилагается к кривым, и что в случае вогнутых зеркал оказывается, что путь отраженного луча наидлиннейший. Но кроме уже сказанного мною, что, согласно архитектоническим принципам, кривые поверхности должны сообразоваться с касающимися в их плоскостями, я намерен

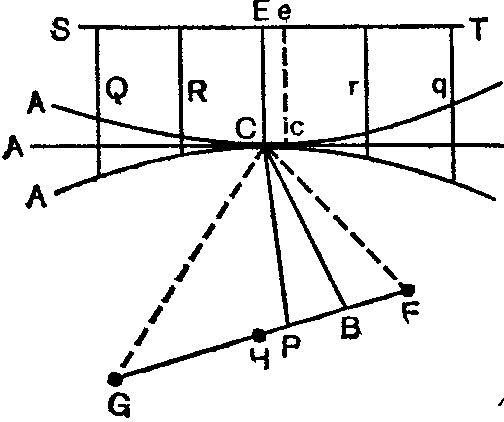
сейчас объяснить, каким образом всегда остается в силе. то положение, что луч идет наиболее определенным, или единственным, путем даже в случае кривизны поверхностей. Замечательно, что и в анализе de maximis et mini mis¹³ проделывается та же операция и для наибольшего, и для наименьшего, различают же их лишь в приложениях к тем или иным случаям, поскольку всегда отыскивается только наиболее определенное по величине, могущее быть как наибольшим, так и наименьшим в своем порядке, ибо анализ основывается лишь на исчезновении разности двух величин или на их совпадении, но никоим образом не на сравнении со всеми другими величинами. Так, пусть имеется (рис. 1) выпуклая либо вогнутая кривая АВ, a ST — ось, с которой на кривую опущены ординаты; при этом видно, что ординате Q (или R) соответствует равная ей и являющаяся как бы ее двойником некоторая другая q (или г). Но имеется особый случай ординаты ЕС, которая оказывается единственной определенной, единственной по своей величине и не имеет двойника, поскольку две ординаты ЕС и ее сливаются, образуя одну ординату, и эта ордината ЕС оказывается наибольшей в случае вогнутой кривой и наименьшей в случае выпуклой. И в то время как в других случаях две бесконечно близкие орди-

 

==132

наты отличаются на разность dm — если величину ординаты обозначить срез т, — отношение которой к Ее, бесконечно малой части оси, задает угол между кривой или ее касательной и осью ST, здесь, в точке С, бесконечно близкие ординаты оказываются двойниками, или совпадающими, разность между ними отсутствует, dm становится равной 0, а касательная в точке С — параллельной оси. Таким образом, основанием анализа является именно эта единственность как результат слияния ординат-двойников; *при этом не важно, будет ли данная ордината наибольшей или же наименьшей. Это уже определяется вычислением в каждом конкретном случае. Пусть (см. рис. 1) имеется некоторое зеркало АСВ, плоское, выпуклое либо вогнутое, и две данные точки: точка F и точка G', от точки отражения С требуется, чтобы путь FCG был уникальным, единственным, или определенным по своей величине, который уже древние называли р.(т/6 ¹⁴, т. е. наибольшим либо наименьшим (в зависимости от условий), так как для всякого иного пути находится парный, или его двойник,; который ему соответствует и имеет ту же длину. Соединим точки F -а G, пусть точка Н будет серединой отрезка